2010中考数学试题分类汇编共28专题23圆中的计算 25页

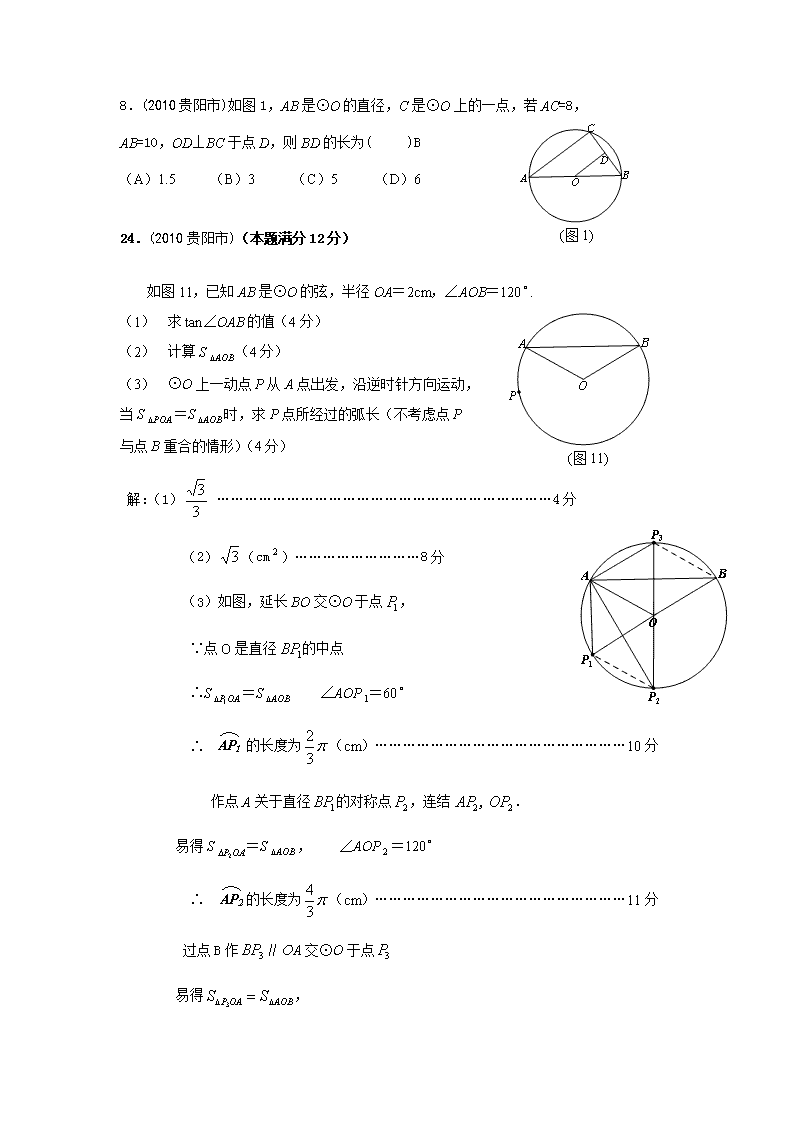
‎(图1)‎ ‎8．(2010贵阳市)如图1，AB是⊙O的直径，C是⊙O上的一点，若AC=8，‎ AB=10，OD⊥BC于点D，则BD的长为( )B ‎（A）1.5         （B）3          （C）5          （D）6 ‎ ‎24．(2010贵阳市)（本题满分12分）‎ ‎(图11)‎ 如图11，已知AB是⊙O的弦，半径OA＝‎2cm，∠AOB＝120.‎ （1） 求tan∠OAB的值（4分）‎ （2） 计算S（4分）‎ （3） ‎⊙O上一动点P从A点出发，沿逆时针方向运动，‎ 当S＝S时，求P点所经过的弧长（不考虑点P 与点B重合的情形）（4分）‎ 解：（1） ………………………………………………………………4分 ‎ （2）（cm）………………………8分 ‎ （3）如图，延长BO交⊙O于点，‎ ‎ ∵点O是直径的中点 ‎∴S＝S ∠AOP＝60‎ ‎∴ 的长度为（cm）………………………………………………10分 作点A关于直径的对称点，连结,．‎ 易得S＝S，  ∠AOP＝120‎ ‎∴ 的长度为（cm）………………………………………………11分 ‎ 过点B作∥交⊙O于点 易得，  ‎ ‎∴ 的长度为（cm）………………………………………………12分 ‎（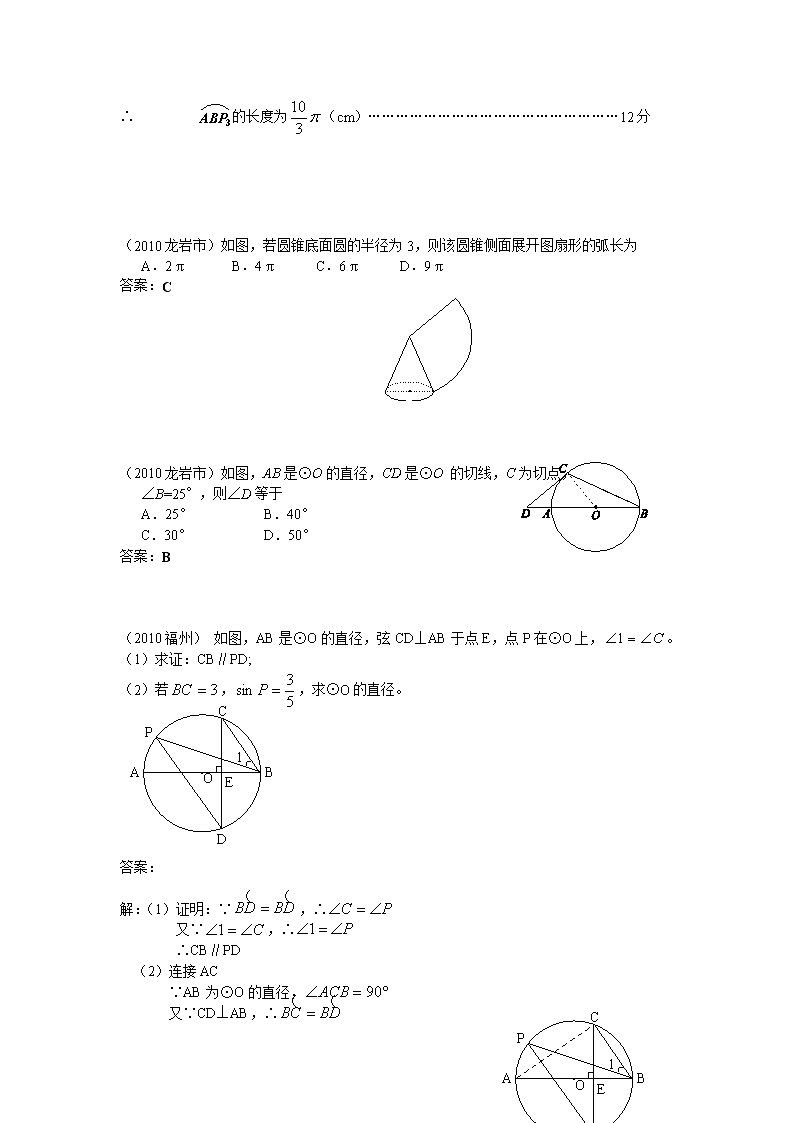2010龙岩市）如图，若圆锥底面圆的半径为3，则该圆锥侧面展开图扇形的弧长为 ‎ A．2 π B．4 π C．6 π D．9 π 答案：C ‎（2010龙岩市）如图，AB是⊙O的直径，CD是⊙O 的切线，C为切点，‎ ‎∠B=25°，则∠D等于 A．25° B．40° ‎ C．30° D．50°‎ 答案：B ‎（2010福州） 如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，。‎ ‎（1）求证：CB∥PD;‎ ‎·‎ O A B D C P E ‎1‎ ‎（2）若，，求⊙O的直径。‎ 答案：‎ ‎（‎ ‎（‎ 解：（1）证明：∵，∴‎ ‎ 又∵，∴‎ ‎ ∴CB∥PD ‎ （2）连接AC ‎（‎ ‎（‎ ‎ ∵AB为⊙O的直径，‎ ‎·‎ O A B D C P E ‎1‎ ‎ 又∵CD⊥AB，∴‎ ‎ ∴，‎ ‎ 在Rt△ABC中，‎ ‎ ∵，∴‎ ‎ 又∵，‎ ‎ 即⊙O的直径为5‎ ‎（2010年江苏盐城）16．已知圆锥的底面半径为3，侧面积为15，则这个圆锥的高为 ▲ ．‎ 答案：4‎ ‎（2010年南京中考数学题）‎ ‎25.（8分）如图，AB是⊙O的直径，点D在⊙O上，∠DAB=45°，BC∥AD，CD∥AB。‎ ‎（1）判断直线CD与⊙O的位置关系，并说明理由；‎ ‎（2）若⊙O的半径为1，求图中阴影部分的面积（结果保留）‎ ‎2010丽水 ‎24cm ‎(第9题)‎ 9.　小刚用一张半径为‎24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计)，如果做成的圆锥形小丑帽子的底面半径为‎10cm，那么 这张扇形纸板的面积是 A．120πcm2 B．240πcm2‎ C．260πcm2 D．480πcm2‎ 答案： B ‎2010丽水 A B O H C ‎(第20题)‎ l 20. 如图，直线l与⊙O相交于A，B两点，且与半径OC垂直，垂足 为H ，已知AB=‎16cm，．‎ ‎(1)　求⊙O的半径；‎ ‎(2)　如果要将直线l向下平移到与⊙O相切的位置，平移的距离 应是多少？请说明理由．‎ 答案： 0. (本题8分)‎ 解：(1)　∵　直线l与半径OC垂直，∴　． ……2分 A B O H C ‎(第20题)‎ l ‎∵　，‎ ‎∴　OB=HB=×8= 10． ……2分 ‎(2)　在Rt△OBH中，‎ ‎． ……2分 ‎∴　．‎ 所以将直线l向下平移到与⊙O相切的位置时，平移的距离是‎4cm． ……2分 随州市2010 10．将半径为4cm的半圆围成一个圆锥，在圆锥内接一个圆柱（如图示），当圆柱的侧面的面积最大时，圆柱的底面半径是___________cm.‎ 答案： 10. 　‎ ‎ (2010年 丹东市)22．如图，已知在⊙O中，AB=4，AC是⊙O的直径，AC⊥BD于F，∠A=30°．‎ ‎（1）求图中阴影部分的面积；‎ ‎（2）若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径．‎ F 第22题图 解：（1）法一：过O作OE⊥AB于E，则AE=AB=2． 1分 F E ‎ 在RtAEO中，∠BAC=30°，cos30°=．‎ ‎∴OA===4． …………………………3分 又∵OA=OB，∴∠ABO=30°．∴∠BOC=60°． ‎ ‎∵AC⊥BD，∴．‎ ‎∴∠COD =∠BOC=60°．∴∠BOD=120°． 5分 ‎∴S阴影==． 6分 法二：连结AD． 1分 ‎∵AC⊥BD，AC是直径，‎ F ‎∴AC垂直平分BD． ……………………2分 ‎∴AB=AD，BF=FD，． ‎ ‎∴∠BAD=2∠BAC=60°，‎ ‎∴∠BOD=120°． ……………………3分 ‎∵BF=AB=2，sin60°=，‎ AF=AB·sin60°=4×=6．‎ ‎∴OB2=BF2+OF2．即．‎ ‎∴OB=4． 5分 ‎∴S阴影=S圆=． 6分 法三：连结BC．………………………………………………………………………………1分 ‎ ∵AC为⊙O的直径， ∴∠ABC=90°．‎ F ‎∵AB=4，‎ ‎∴． ……………………3分 ‎∵∠A=30°， AC⊥BD， ∴∠BOC=60°， ‎ ‎∴∠BOD=120°．‎ ‎∴S阴影=π·OA2=×42·π=．……………………6分 以下同法一．‎ ‎（2）设圆锥的底面圆的半径为r，则周长为2πr，‎ ‎ ∴． ‎ ‎∴． 10分 ‎(2010年 威海市)5．一个圆锥的底面半径为6㎝，圆锥侧面展开图扇形的圆心角为240°，则圆锥的母线长为 （ ） 答案：A ‎ A．9㎝ B．12㎝ C．15㎝ D．18㎝ ‎ ‎﹙第14题图﹚‎ A B D O C ‎(2010年 威海市)14. 如图，AB为⊙O的直径，点C，D在⊙O上．若 ‎ ‎∠AOD＝30°，则∠BCD的度数是 ． 答案： 105° ‎ ‎（2010哈尔滨）１．将一个底面半径为‎5cm，母线长为‎12cm 的圆锥形纸筒沿一条母线剪开并展平，所得的侧面展开图的圆心角是 度．150‎ ‎（2010红河自治州）14. 已知圆锥的底面直径为4，母线长为6，则它的侧面展开图的圆心角为 120° .‎ ‎（2010红河自治州）23.（本小题满分14分）如图9，在直角坐标系xoy中，O是坐标原点，点A在x正半轴上，OA=cm，点B在y轴的正半轴上，OB=‎12cm，动点P从点O开始沿OA以cm/s的速度向点A移动，动点Q从点A开始沿AB以‎4cm/s的速度向点B移动，动点R从点B开始沿BO以‎2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动，移动时间为t（0＜t＜6）s.‎ ‎（1）求∠OAB的度数.‎ ‎（2）以OB为直径的⊙O‘与AB交于点M，当t为何值时，PM与⊙O‘相切？‎ ‎（3）写出△PQR的面积S随动点移动时间t的函数关系式，并求s的最小值及相应的t值.‎ ‎（4）是否存在△APQ为等腰三角形，若存在，求出相应的t值，若不存在请说明理由.‎ 解：（1）在Rt△AOB中：‎ tan∠OAB=‎ ‎∴∠OAB=30°‎ ‎（2）如图10，连接O‘P，O‘M. 当PM与⊙O‘相切时，有∠PM O‘=∠PO O‘=90°，‎ ‎ △PM O‘≌△PO O‘‎ 由（1）知∠OBA=60°‎ ‎∵O‘M= O‘B ‎∴△O‘BM是等边三角形 ‎∴∠B O‘M=60°‎ 可得∠O O‘P=∠M O‘P=60°‎ ‎∴OP= O O‘·tan∠O O‘P ‎ =6×tan60°=‎ 又∵OP=t ‎∴t=，t=3‎ 即：t=3时，PM与⊙O‘相切.‎ ‎（3）如图9，过点Q作QE⊥x于点E ‎ ∵∠BAO=30°，AQ=4t ‎ ∴QE=AQ=2t ‎ AE=AQ·cos∠OAB=4t×‎ ‎∴OE=OA-AE=-t ‎ ∴Q点的坐标为（-t，2t）‎ ‎ S△PQR= S△OAB -S△OPR -S△APQ -S△BRQ ‎ =‎ ‎ =‎ ‎ = （）‎ ‎ 当t=3时，S△PQR最小=‎ ‎ （4）分三种情况：如图11.‎ 当AP=AQ1=4t时，‎ ‎∵OP+AP=‎ ‎∴t+4t=‎ ‎∴t=‎ 或化简为t=-18‎ 当PQ2=AQ2=4t时 ‎ 过Q2点作Q2D⊥x轴于点D，‎ ‎∴PA=2AD=2A Q2·cosA=t 即t+t =‎ ‎∴t=2‎ 当PA=PQ3时，过点P作PH⊥AB于点H ‎ AH=PA·cos30°=（-t）·=18-3t AQ3=2AH=36-6t 得36-6t=4t，‎ ‎∴t=3.6‎ ‎ 综上所述，当t=2，t=3.6，t=-18时，△APQ是等腰三角形.‎ ‎（2010年镇江市）14．已知圆锥的母线长为4，底面半径为2，则圆锥的侧面积等于 （ A ）‎ ‎ A．8 B．‎9‎ C．10 D．11‎ ‎ (2010遵义市)如图,已知正方形的边长为,以对角的两个顶点为圆心, 长为半径画弧,则所得到的两条弧的长度之和为 ▲ (结果保留).‎ 答案：‎ ‎(2010遵义市)26．（12分）如图，在△ABC中，∠C=，AC+BC=8，点O是 ‎（26题图）‎ 斜边AB上一点，以O为圆心的⊙O分别与AC、BC相切于 点D、E．‎ ‎（1）当AC＝2时，求⊙O的半径；‎ ‎（2）设AC＝，⊙O的半径为，求与的函数关系式．‎ ‎26．（12分）(1)(5分) 解: 连接OD、OE、OC ‎∵D、E为切点 ‎∴OD⊥AC， OE⊥BC， OD=OE ‎∵‎ ‎∴AC·BC=AC·OD+BC·OE ‎∵AC+BC=8， AC=2，∴BC=6‎ ‎∴×2×6=×2×OD+×6×OE 而OD=OE， ‎ ‎∴OD=，即⊙O的半径为 ‎ ‎ ‎ （2）（7分）解：连接OD、OE、OC ‎∵D、E为切点 ‎∴OD⊥AC， OE⊥BC， OD=OE=‎ ‎∵‎ ‎∴AC·BC=AC·OD+BC·OE ‎∵AC+BC=8， AC=，∴BC=8-‎ ‎∴（8-）= +（8-）‎ 化简：‎ 即：‎ ‎（桂林2010）10．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是 （ C ）．‎ A． B． ‎ C． D． ‎ ‎（2010年兰州）9. 现有一个圆心角为，半径为的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计）.该圆锥底面圆的半径为 A． B． C． D．‎ 答案 C ‎（2010年无锡）5．已知圆锥的底面半径为‎2cm，母线长为‎5cm，则圆锥的侧面积是 （ ▲ ）‎ A． B． C． D．‎ 答案 C ‎（2010年兰州）18. 如图，扇形OAB，∠AOB=90，⊙P 与OA、OB分别相切于点F、E，并且与弧AB切于点C，则扇形OAB的面积与⊙P的面积比是 ．‎ ‎ ‎ A O D B F K E ‎(第16题)图)‎ G M CK ‎16. （2010年金华）如图在边长为2的正方形ABCD中，E，F，O分别是AB，CD，AD的中点， 以O为圆心，以OE为半径画弧EF.P是上的一个动点，连 结OP，并延长OP交线段BC于点K，过点P作⊙O 的切线，分别交射线AB于点M，交直线BC于点G. ‎ 若，则BK﹦ ▲ .‎ 答案：, .（每个2分）‎ ‎21．（2010年金华）(本题8分)‎ A C B D ‎(第21题图)‎ E F O 如图，AB是⊙O的直径，C是的中点，CE⊥AB于 E，BD交CE于点F．‎ ‎1‎ ‎2‎ ‎（1）求证：CF﹦BF；‎ ‎（2）若CD ﹦6， AC ﹦8，则⊙O的半径为 ▲ ， ‎ CE的长是 ▲ ．‎ 解：(1) 证明：∵AB是⊙O的直径，∴∠ACB﹦90°‎ ‎ 又∵CE⊥AB， ∴∠CEB﹦90°‎ ‎ ∴∠2﹦90°－∠A﹦∠1‎ ‎ 又∵C是弧BD的中点，∴∠1﹦∠A ‎ ∴∠1﹦∠2,‎ ‎ ∴ CF﹦BF﹒ …………………4分 ‎(2) ⊙O的半径为5 ， CE的长是﹒ ………4分（各2分）‎ ‎14．（2010年长沙）已知扇形的面积为，半径等于6，则它的圆心角等于 度．‎ 答案：120‎ ‎24．（2010年长沙）已知：AB是⊙O的弦，D是的中点，过B作AB的垂线交AD的延长线于C．‎ ‎（1）求证：AD＝DC；‎ ‎（2）过D作⊙O的切线交BC于E，若DE＝EC，求sinC．‎ O A D B E C 第24题图 证明：连BD∵∴∠A＝∠ABD∴AD＝BD …………………2分 ‎∵∠A+∠C＝90°，∠DBA+∠DBC＝90°∴∠C＝∠DBC∴BD＝DC ‎∴AD＝DC ………………………………………………………4分 ‎（2）连接OD∵DE为⊙O切线 ∴OD⊥DE …………………………5分 ‎ ‎∵，OD过圆心 ∴OD⊥AB 又∵AB⊥BC ∴四边形FBED为矩形∴DE⊥BC ……………………6分 ‎∵BD为Rt△ABC斜边上的中线∴BD＝DC ∴BE＝EC＝DE ‎∴∠C＝45° …………………………………………………7分 ‎∴sin∠C= ………………………………………………………………8分 ‎ (2010湖北省荆门市)10．如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN＝30°，B为AN弧的中点，P是直径MN上一动点，则PA＋PB的最小值为( )‎ ‎(A)2 (B) (C)1 (D)2‎ 第10题图 答案B ‎5．（2010年济宁市)已知⊙O1与⊙O2相切，⊙O1的半径为‎3 cm，⊙O2的半径为‎2 cm，则O1O2的长是 ‎（第9题）‎ 剪去 A．‎1 cm B．‎5 cm C．‎1 cm或‎5 cm D．‎0.5cm或‎2.5cm 答案：C ‎9．（2010年济宁市)如图，如果从半径为‎9cm的圆形纸片剪去圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为 A．‎6cm B．cm C．‎8cm D．cm 答案：B ‎6．（2010湖北省咸宁市）如图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C，D分别在两圆上，若，则的度数为 A． B． C． D．‎ 答案：B ‎7. （2010年郴州市）如图，是的直径，为弦，于，‎ 第7题 则下列结论中不成立的是 Ａ．　　　　Ｂ．‎ Ｃ．　　　Ｄ．‎ 答案：D ‎15. （2010年郴州市）一个圆锥的底面半径为，母线长为‎6cm，则圆锥的侧面积是____．（结果保留）‎ 答案：‎ ‎20．（2010年怀化市）如图6，已知直线AB是⊙O的切线，A为切点，‎ OB交⊙O于点C，点D在⊙O上，‎ 且∠OBA=40°，则∠ADC= ．‎ 答案：‎ ‎20．（2010年济宁市)如图，为外接圆的直径，，垂足为点，的平分线交于点，连接，.‎ ‎(1) 求证：； ‎ ‎(第20题)‎ ‎(2) 请判断，，三点是否在以为圆心，以为半径的圆上？并说明理由.‎ ‎（1）证明：∵为直径，，‎ ‎∴.∴. 3分 ‎（2）答：，，三点在以为圆心，以为半径的圆上. 4分 理由：由（1）知：，∴.‎ ‎∵，，，‎ ‎∴.∴. 6分 由（1）知：.∴.‎ ‎∴，，三点在以为圆心，以为半径的圆上.‎ 图8‎ ‎25. （2010年怀化市） 如图8，AB是⊙O的直径，C是⊙O上一点，于D,且AB=8,DB=2.‎ ‎ （1）求证：△ABC∽△CBD;‎ ‎ （2）求图中阴影部分的面积（结果精确到0.1，参考数据）.‎ ‎25. （1）证明：∵AB是⊙O的直径，‎ ‎ ∴∠ACB=,又，∴∠CDB=…………………………1分 在△ABC与△CBD中，‎ ‎∠ACB=∠CDB=,∠B=∠B, ∴△ABC∽△CBD……………………………3分 ‎(2)解：∵△ABC∽△CBD∴‎ ‎∴ ∵AB=8,DB=2, ∴CB=4.‎ 在Rt△ABC中，…………4分 ‎∴…………………………5分 ‎∴‎ ‎20．（2010湖北省咸宁市）如图，在⊙O中，直径AB垂直于弦CD，垂足为E，连接AC，‎ 将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．‎ A F C G O D E B ‎（第20题）‎ ‎（1）直线FC与⊙O有何位置关系？并说明理由；‎ ‎（2）若，求CD的长．‎ ‎20．解：（1）直线FC与⊙O相切．……1分 A F C G O D E B ‎（第20题）‎ ‎1‎ ‎3‎ ‎2‎ 理由如下：‎ 连接．‎ ‎∵， ∴……2分 由翻折得，，．‎ ‎∴． ∴OC∥AF．‎ ‎∴．‎ ‎∴直线FC与⊙O相切．……4分 ‎（2）在Rt△OCG中，，‎ ‎∴．……6分 在Rt△OCE中，．……8分 ‎∵直径AB垂直于弦CD，‎ ‎∴．‎ ‎（2010年成都）13．如图，在中，为的直径，，‎ 则的度数是_____________度．‎ 答案：100‎ ‎（2010年成都）15．若一个圆锥的侧面积是，侧面展开图是半圆，则该圆锥的底面圆半径是___________．‎ 答案：3‎ ‎（2010年成都）17．已知：如图，与相切于点，，的直径为．‎ ‎（1）求的长；‎ ‎（2）求的值．‎ 答案：17．.解：（1）由已知，OC=2，BC=4。‎ ‎ 在Rt△OBC中，由勾股定理，得 ‎ ‎ ‎ （2）在Rt△OAC中，∵OA=OB=，OC=2，‎ ‎ ∴sinA=‎ ‎（2010年成都）25．如图，内接于，，‎ 是上与点关于圆心成中心对称的点，是 边上一点，连结．已知，‎ ‎，是线段上一动点，连结并延长交 四边形的一边于点，且满足，则 的值为_______________．‎ 答案： 1和 ‎（2010年眉山）15．如图，∠A是⊙O的圆周角，∠A=40°，则∠OBC的度数为_______‎ ‎．‎ 答案：50°‎ ‎（2010年眉山）17．已知圆锥的底面半径为4cm，高为3cm，则这个圆锥的侧面积为__________cm2．‎ 答案：‎ ‎27．已知：如图，内接于，为直径，弦于，是的中点，连结并延长交的延长线于点，连结，分别交、于点、．‎ ‎ （1）求证：是的外心；‎ ‎ （2）若,求的长；‎ ‎ （3）求证：．‎ 答案：‎ ‎27. （1）证明：∵C是的中点，∴，‎ ‎∴∠CAD=∠ABC ‎∵AB是⊙O的直径，∴∠ACB=90°。‎ ‎∴∠CAD+∠AQC=90°‎ 又CE⊥AB，∴∠ABC+∠PCQ=90°‎ ‎∴∠AQC=∠PCQ ‎∴在△PCQ中，PC=PQ，‎ ‎∵CE⊥直径AB，∴‎ ‎∴‎ ‎∴∠CAD=∠ACE。‎ ‎∴在△APC中，有PA=PC，‎ ‎∴PA=PC=PQ ‎∴P是△ACQ的外心。‎ ‎（2）解：∵CE⊥直径AB于F，‎ ‎∴在Rt△BCF中，由tan∠ABC=，CF=8，‎ 得。‎ ‎∴由勾股定理，得 ‎∵AB是⊙O的直径，‎ ‎∴在Rt△ACB中，由tan∠ABC=，‎ ‎ 得。‎ 易知Rt△ACB∽Rt△QCA，∴‎ ‎∴。‎ ‎（3）证明：∵AB是⊙O的直径，∴∠ACB=90°‎ ‎∴∠DAB+∠ABD=90°‎ 又CF⊥AB，∴∠ABG+∠G=90°‎ ‎∴∠DAB=∠G；‎ ‎∴Rt△AFP∽Rt△GFB，‎ ‎∴，即 易知Rt△ACF∽Rt△CBF，‎ ‎∴（或由摄影定理得）‎ ‎∴‎ 由（1），知PC=PQ，∴FP+PQ=FP+PC=FC ‎∴。‎ 北京11. 如图，AB为圆O的直径，弦CD^AB，垂足为点E，连结OC，若OC=5，‎ ‎ CD=8，则AE= 。2‎ 北京20. 已知：如图，在△ABC中，D是AB边上一点，圆O过D、B、C三点，‎ ‎ ÐDOC=2ÐACD=90°。‎ ‎ (1) 求证：直线AC是圆O的切线；‎ ‎ (2) 如果ÐACB=75°，圆O的半径为2，求BD的长。‎ 毕节9．如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为‎16cm2,则该半圆的半径为（　C 　）‎ A. cm B. ‎9 cm C. cm D. cm 毕节10．已知圆锥的母线长是‎5cm，侧面积是15πcm2，则这个圆锥底面圆的半径是（ B ）‎ A．‎1.5cm B．‎3cm C．‎4cm D．‎‎6cm ‎25。(10湖南怀化)如图8，AB是⊙O的直径，C是⊙O上一点，于D,且AB=8,DB=2.‎ ‎ （1）求证：△ABC∽△CBD;‎ ‎ （2）求图中阴影部分的面积（结果精确到0.1，参考数据）.‎ 图8‎ ‎（1）证明：∵AB是⊙O的直径，‎ ‎ ∴∠ACB=,又，∴∠CDB=…………………………1分 在△ABC与△CBD中，‎ ‎∠ACB=∠CDB=,∠B=∠B, ∴△ABC∽△CBD……………………………3分 ‎(2)解：∵△ABC∽△CBD∴‎ ‎∴ ∵AB=8,DB=2, ∴CB=4.‎ 在Rt△ABC中，…………4分 ‎∴…………………………5分 ‎∴…………6分 ‎1、（2010年泉州南安市）⊙A的半径为‎2cm，AB=‎3cm．以B为圆心作⊙B，使得 ‎⊙A与 ⊙B外切，则⊙B的半径是　 　cm．‎ 答案：1‎ ‎2、（2010年杭州市）如图，5个圆的圆心在同一条直线上, 且互相相切，若大圆直径是12，4个 ‎ 小圆大小相等，则这5个圆的周长的和为 ‎ A. 48 B. 24 ‎ ‎ C. 12 D. 6‎ 答案：B ‎3、（2010年杭州市）如图, 已知△,，．是的中点，‎ ‎ ⊙与AC，BC分别相切于点与点．点F是⊙与的一 个交点，连并延长交的延长线于点. 则 . ‎ 答案：‎ ‎（2010山西17．图1是以AB为直径的半圆形纸片，AB＝‎6cm，沿着垂直于AB的半径OC剪开，将扇形OAC沿AB方向平移至扇形O’A’C’ ．如图2，其中O’是OB的中点．O’C’交于点F，则BF的长为_______cm．π ‎（第17题）‎ A B O C C B A O O’‎ C’‎ 图1‎ 图2‎ F ‎（2010宁夏11．矩形窗户上的装饰物如图所示，它是由半径均为b 的两个四分之一圆组成，则能射进阳光部分的面积是 ．‎ ‎（2010宁夏23．(8分)‎ 如图，已知：⊙O的直径AB与弦AC的夹角∠A=30°，过点C作⊙O的切线交AB的延长线于点P．‎ ‎(1) 求证：AC=CP；‎ ‎(2) 若PC=6,求图中阴影部分的面积（结果精确到0.1）． ‎ ‎（参考数据： ）‎ ‎ ‎ ‎23．证明：（1）连结OC ‎∵AO=OC ‎ ‎∴∠ACO=∠A=30°‎ ‎∴∠COP=2∠ACO=60°‎ ‎∵PC切⊙O于点C ‎ ‎ ∴OC⊥PC ‎∴∠P=30°‎ ‎∴∠A =∠P ‎ ‎ ∴AC =PC-----------------------------------------------------------------------------------4分 ‎（注：其余解法可参照此标准）‎ ‎（2）在Rt△OCP中，tan∠P= ∴OC=2‎ ‎∵S△OCP=CP·OC=×6×2= 且S扇形COB=‎ ‎∴S阴影= S△OCP －S扇形COB =--------------------------------------------8分 ‎·‎ A B C D O M 第17题图 ‎1.（2010宁德）如图，在直径AB＝12的⊙O中，弦CD⊥AB于M，且M是半径OB的中点，‎ 则弦CD的长是_______（结果保留根号）. 6‎ ‎2.（2010黄冈）将半径为‎4cm的半圆围成一个圆锥，在圆锥内接一个圆柱（如图示），当圆柱的侧面的面积最大时，圆柱的底面半径是___________cm. 　‎ 第8题图 ‎1．（2010昆明）如图，已知圆锥侧面展开图的扇形面积为‎65‎cm2，扇形的弧长为‎10‎cm，则圆锥母线长是( )‎ A．‎5cm B．‎10cm ‎ C．‎12cm D．‎‎13cm 答案：D 第9题图 A B C ‎2．（2010昆明）如图，在△ABC中，AB = AC，AB = 8，BC = 12，分别以 AB、AC为直径作半圆，则图中阴影部分的面积是（　 ）‎ ‎ A． B．‎ ‎ C． D．‎ 答案：D ‎3．（2010昆明）半径为r的圆内接正三角形的边长为 .（结果可保留根号）‎ 答案：r ‎1．（2010四川宜宾）‎ 将半径为5的圆(如图1)剪去一个圆心角为n°的扇形后围成如图2所示的圆锥则n的 值等于 ‎ ‎18题图 答案： 144；‎ ‎（2010年常州）12.已知扇形的半径为3cm，面积为cm2，则扇形的圆心角是 ，扇形的弧长是 cm（结果保留）.12.120°，2π.‎ ‎（2010河北省）20．（本小题满分8分）如图11-1，正方形ABCD是一个6 × 6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图11-2的程序移动．‎ ‎（1）请在图11-1中画出光点P经过的路径；‎ 绕点A顺时针旋转90°‎ 绕点B顺时针旋转90°‎ 绕点C顺时针旋转90°‎ 图11-2‎ 输入点P 输出点 绕点D顺时针旋转90°‎ A D 图11-1‎ B C P ‎（2）求光点P经过的路径总长（结果保留π）．‎ ‎（1）如图1；‎ A D 图1‎ B C P ‎【注：若学生作图没用圆规，所画路线光滑且基本准确即给4分】‎ ‎（2）∵，‎ ‎∴点P经过的路径总长为6 π．‎ ‎（2010年安徽）8. 如图，⊙O过点B 、C。圆心O在等腰直角△ABC的内部，∠BAC＝900，OA＝1，BC＝6，则⊙O的半径为………………（ C ）‎ A）B）C）D） ‎ ‎（第14题）‎ ‎（2010河南）14．如图矩形ABCD中，AD=1，AD=，以AD的长为半径的⊙A交BC于点E，则图中阴影部分的面积为______________________．‎ ‎（2010·珠海）21.如图，△ABC内接于⊙O，AB＝6,AC＝4,D是AB边上一点，P是优弧BAC的中点，连结PA、PB、PC、PD.‎ ‎(1)当BD的长度为多少时，△PAD是以AD为底边的等腰三角形？并证明；‎ ‎（2）若cos∠PCB=，求PA的长.‎ 解：（1）当BD＝AC＝4时，△PAD是以AD为底边的等腰三角形 ‎∵P是优弧BAC的中点 ∴弧PB＝弧PC ‎∴PB＝PC ‎∵BD＝AC＝4 ∠PBD=∠PCA ‎∴△PBD≌△PCA ‎∴PA=PD 即△PAD是以AD为底边的等腰三角形 ‎（2）由（1）可知，当BD＝4时，PD＝PA，AD＝AB-BD＝6-4＝2‎ 过点P作PE⊥AD于E，则AE＝AD=1‎ ‎∵∠PCB=∠PAD ‎∴cos∠PAD=cos∠PCB=‎ ‎∴PA=‎ ‎(苏州2010中考题16)．如图，在4×4的方格纸中(共有16个小方格)，每个小方格都是边长为1的正方形．‎ ‎ O、A、B分别是小正方形的顶点，则扇形OAB的弧长等于 ▲ ．(结果保留根号及)．‎ 答案：‎ ‎(苏州2010中考题27)．(本题满分9分)如图，在等腰梯形ABCD中，AD∥BC．O是CD边的中点，以O为圆心，OC长为半径作圆，交BC边于点E．过E作EH⊥AB，垂足为H．已知⊙O与AB边相切，切点为F ‎ (1)求证：OE∥AB；‎ ‎ (2)求证：EH=AB；‎ ‎(3)若，求的值．‎ 答案：‎ ‎（2010·绵阳）12．如图，等腰梯形ABCD内接于半圆D，且AB = 1，BC = 2，‎ C B A O D 则OA =（ A ）．‎ A． B． C． D．‎ 图5‎ ‎21. （上海）机器人“海宝”在某圆形区域表演“按指令行走”，如图5所示，“海宝”从圆心O出发，先沿北偏西67.4°方向行走‎13米至点A处，再沿正南方向行走‎14米至点B处，最后沿正东方向行走至点C处，点B、C都在圆O上.（1）求弦BC的长；（2）求圆O的半径长.‎ ‎（本题参考数据：sin 67.4° = ，cos 67.4° = ，tan 67.4° = ）‎ ‎（1）解：过点O作OD⊥AB，则∠AOD+∠AON=,即：sin∠AOD=cos∠AON= 即：AD=AO×=5,OD=AO×sin 67.4° =AO× =12‎ 又沿正南方向行走‎14米至点B处，最后沿正东方向行走至点C处 所以AB∥NS,AB⊥BC,所以E点位BC的中点，且BE=DO=12‎ ‎ 所以BC=24‎ ‎（2）解：连接OB，则OE=BD=AB-AD=14-5=9‎ 又在RT△BOE中，BE=12,‎ ‎ 所以 ‎ 即圆O的半径长为15 ‎ ‎8. （莱芜）已知圆锥的底面半径长为5，侧面展开后得到一个半圆，则该圆锥的母线长为（ C ）‎ ‎ A．2.5 B．‎5 ‎C．10 D．15‎