2018中考相似三角形汇编 47页

‎2018中考数学试题分类汇编：考点36 相似三角形 ‎　‎ 一．选择题（共28小题）‎ ‎1．（2018•重庆）制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大为原来的3倍，那么扩大后长方形广告牌的成本是（　　）‎ A．360元 B．720元 C．1080元 D．2160元 ‎【分析】根据题意求出长方形广告牌每平方米的成本，根据相似多边形的性质求出扩大后长方形广告牌的面积，计算即可．‎ ‎【解答】解：3m×2m=6m2，‎ ‎∴长方形广告牌的成本是120÷6=20元/m2，‎ 将此广告牌的四边都扩大为原来的3倍，‎ 则面积扩大为原来的9倍，‎ ‎∴扩大后长方形广告牌的面积=9×6=54m2，‎ ‎∴扩大后长方形广告牌的成本是54×20=1080m2，‎ 故选：C．‎ ‎　‎ ‎2．（2018•玉林）两三角形的相似比是2：3，则其面积之比是（　　）‎ A．： B．2：3 C．4：9 D．8：27‎ ‎【分析】根据相似三角形的面积比等于相似比的平方计算即可．‎ ‎【解答】解：∵两三角形的相似比是2：3，‎ ‎∴其面积之比是4：9，‎ 故选：C．‎ ‎　‎ ‎3．（2018•重庆）要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5cm，6cm和9cm，另一个三角形的最短边长为2.5cm，则它的最长边为（　　）‎ A．3cm B．4cm C．4.5cm D．5cm ‎【分析】根据相似三角形的对应边成比例求解可得．‎ ‎【解答】解：设另一个三角形的最长边长为xcm，‎ 根据题意，得： =，‎ 解得：x=4.5，‎ 即另一个三角形的最长边长为4.5cm，‎ 故选：C．‎ ‎　‎ ‎4．（2018•内江）已知△ABC与△A1B1C1相似，且相似比为1：3，则△ABC与△A1B1C1的面积比为（　　）‎ A．1：1 B．1：3 C．1：6 D．1：9‎ ‎【分析】利用相似三角形面积之比等于相似比的平方，求出即可．‎ ‎【解答】解：已知△ABC与△A1B1C1相似，且相似比为1：3，‎ 则△ABC与△A1B1C1的面积比为1：9，‎ 故选：D．‎ ‎　‎ ‎5．（2018•铜仁市）已知△ABC∽△DEF，相似比为2，且△ABC的面积为16，则△DEF的面积为（　　）‎ A．32 B．8 C．4 D．16‎ ‎【分析】由△ABC∽△DEF，相似比为2，根据相似三角形的面积的比等于相似比的平方，即可得△ABC与△DEF的面积比为4，又由△ABC的面积为16，即可求得△DEF的面积．‎ ‎【解答】解：∵△ABC∽△DEF，相似比为2，‎ ‎∴△ABC与△DEF的面积比为4，‎ ‎∵△ABC的面积为16，‎ ‎∴△DEF的面积为：16×=4．‎ 故选：C．‎ ‎　‎ ‎6．（2017•重庆）已知△ABC∽△DEF，且相似比为1：2，则△ABC与△DEF的面积比为（　　）‎ A．1：4 B．4：1 C．1：2 D．2：1‎ ‎【分析】利用相似三角形面积之比等于相似比的平方计算即可．‎ ‎【解答】解：∵△ABC∽△DEF，且相似比为1：2，‎ ‎∴△ABC与△DEF的面积比为1：4，‎ 故选：A．‎ ‎　‎ ‎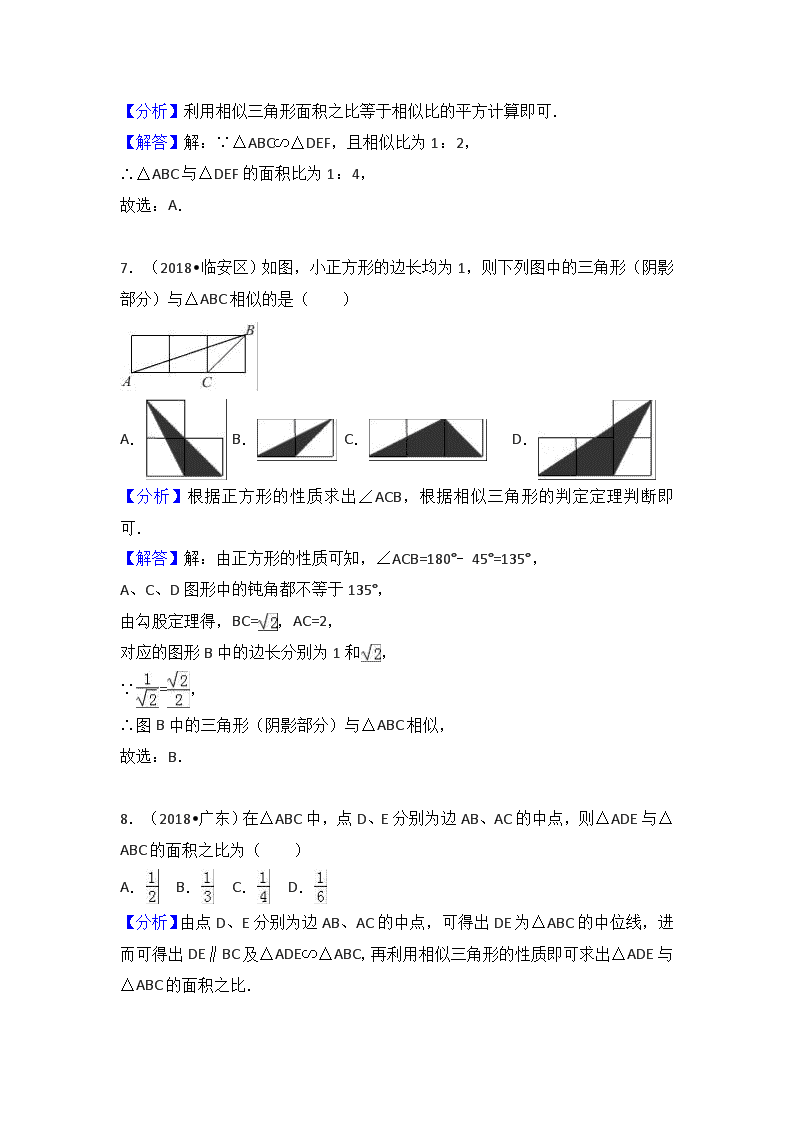7．（2018•临安区）如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（　　）‎ A． B． C． D．‎ ‎【分析】根据正方形的性质求出∠ACB，根据相似三角形的判定定理判断即可．‎ ‎【解答】解：由正方形的性质可知，∠ACB=180°﹣45°=135°，‎ A、C、D图形中的钝角都不等于135°，‎ 由勾股定理得，BC=，AC=2，‎ 对应的图形B中的边长分别为1和，‎ ‎∵=，‎ ‎∴图B中的三角形（阴影部分）与△ABC相似，‎ 故选：B．‎ ‎　‎ ‎8．（2018•广东）在△ABC中，点D、E分别为边AB、AC的中点，则△ADE与△ABC的面积之比为（　　）‎ A． B． C． D．‎ ‎【分析】由点D、E分别为边AB、AC的中点，可得出DE为△ABC的中位线，进而可得出DE∥BC及△ADE∽△ABC，再利用相似三角形的性质即可求出△ADE与△ABC的面积之比．‎ ‎【解答】解：∵点D、E分别为边AB、AC的中点，‎ ‎∴DE为△ABC的中位线，‎ ‎∴DE∥BC，‎ ‎∴△ADE∽△ABC，‎ ‎∴=（）2=．‎ 故选：C．‎ ‎　‎ ‎9．（2018•自贡）如图，在△ABC中，点D、E分别是AB、AC的中点，若△ADE的面积为4，则△ABC的面积为（　　）‎ A．8 B．12 C．14 D．16‎ ‎【分析】直接利用三角形中位线定理得出DE∥BC，DE=BC，再利用相似三角形的判定与性质得出答案．‎ ‎【解答】解：∵在△ABC中，点D、E分别是AB、AC的中点，‎ ‎∴DE∥BC，DE=BC，‎ ‎∴△ADE∽△ABC，‎ ‎∵=，‎ ‎∴=，‎ ‎∵△ADE的面积为4，‎ ‎∴△ABC的面积为：16，‎ 故选：D．‎ ‎　‎ ‎10．（2018•崇明县一模）如图，在平行四边形ABCD中，点E在边DC上，DE：EC=3：1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（　　）‎ A．3：4 B．9：16 C．9：1 D．3：1‎ ‎【分析】可证明△DFE∽△BFA，根据相似三角形的面积之比等于相似比的平方即可得出答案．‎ ‎【解答】解：∵四边形ABCD为平行四边形，‎ ‎∴DC∥AB，‎ ‎∴△DFE∽△BFA，‎ ‎∵DE：EC=3：1，‎ ‎∴DE：DC=3：4，‎ ‎∴DE：AB=3：4，‎ ‎∴S△DFE：S△BFA=9：16．‎ ‎ 故选：B．‎ ‎　‎ ‎11．（2018•随州）如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则的值为（　　）‎ A．1 B． C． 1 D．‎ ‎【分析】由DE∥BC可得出△ADE∽△ABC，利用相似三角形的性质结合S△ADE=S 四边形BCED，可得出=，结合BD=AB﹣AD即可求出的值，此题得解．‎ ‎【解答】解：∵DE∥BC，‎ ‎∴∠ADE=∠B，∠AED=∠C，‎ ‎∴△ADE∽△ABC，‎ ‎∴（）2=．‎ ‎∵S△ADE=S四边形BCED，‎ ‎∴=，‎ ‎∴===﹣1．‎ 故选：C．‎ ‎　‎ ‎12．（2018•哈尔滨）如图，在△ABC中，点D在BC边上，连接AD，点G在线段AD上，GE∥BD，且交AB于点E，GF∥AC，且交CD于点F，则下列结论一定正确的是（　　）‎ A． = B． = C． = D． =‎ ‎【分析】由GE∥BD、GF∥AC可得出△AEG∽△ABD、△DFG∽△DCA，根据相似三角形的性质即可找出==，此题得解．‎ ‎【解答】解：∵GE∥BD，GF∥AC，‎ ‎∴△AEG∽△ABD，△DFG∽△DCA，‎ ‎∴=， =，‎ ‎∴==．‎ 故选：D．‎ ‎　‎ ‎13．（2018•遵义）如图，四边形ABCD中，AD∥BC，∠ABC=90°，AB=5，BC=10，连接AC、BD，以BD为直径的圆交AC于点E．若DE=3，则AD的长为（　　）‎ A．5 B．4 C．3 D．2‎ ‎【分析】先求出AC，进而判断出△ADF∽△CAB，即可设DF=x，AD=x，利用勾股定理求出BD，再判断出△DEF∽△DBA，得出比例式建立方程即可得出结论．‎ ‎【解答】解：如图，在Rt△ABC中，AB=5，BC=10，‎ ‎∴AC=5‎ 过点D作DF⊥AC于F，‎ ‎∴∠AFD=∠CBA，‎ ‎∵AD∥BC，‎ ‎∴∠DAF=∠ACB，‎ ‎∴△ADF∽△CAB，‎ ‎∴，‎ ‎∴，‎ 设DF=x，则AD=x，‎ 在Rt△ABD中，BD==，‎ ‎∵∠DEF=∠DBA，∠DFE=∠DAB=90°，‎ ‎∴△DEF∽△DBA，‎ ‎∴，‎ ‎∴，‎ ‎∴x=2，‎ ‎∴AD=x=2，‎ 故选：D．‎ ‎　‎ ‎14．（2018•扬州）如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，CD与BE、AE分别交于点P，M．对于下列结论：‎ ‎①△BAE∽△CAD；②MP•MD=MA•ME；③2CB2=CP•CM．其中正确的是（　　）‎ A．①②③ B．① C．①② D．②③‎ ‎【分析】（1）由等腰Rt△ABC和等腰Rt△ADE三边份数关系可证；‎ ‎（2）通过等积式倒推可知，证明△PAM∽△EMD即可；‎ ‎（3）2CB2转化为AC2，证明△ACP∽△MCA，问题可证．‎ ‎【解答】解：由已知：AC=AB，AD=AE ‎∴‎ ‎∵∠BAC=∠EAD ‎∴∠BAE=∠CAD ‎∴△BAE∽△CAD 所以①正确 ‎∵△BAE∽△CAD ‎∴∠BEA=∠CDA ‎∵∠PME=∠AMD ‎∴△PME∽△AMD ‎∴‎ ‎∴MP•MD=MA•ME 所以②正确 ‎∵∠BEA=∠CDA ‎∠PME=∠AMD ‎∴P、E、D、A四点共圆 ‎∴∠APD=∠EAD=90°‎ ‎∵∠CAE=180°﹣∠BAC﹣∠EAD=90°‎ ‎∴△CAP∽△CMA ‎∴AC2=CP•CM ‎∵AC=AB ‎∴2CB2=CP•CM 所以③正确 故选：A．‎ ‎　‎ ‎15．（2018•贵港）如图，在△ABC中，EF∥BC，AB=3AE，若S四边形BCFE=16，则S△ABC=（　　）‎ A．16 B．18 C．20 D．24‎ ‎【分析】由EF∥BC，可证明△AEF∽△ABC，利用相似三角形的性质即可求出则S△ABC的值．‎ ‎【解答】解：∵EF∥BC，‎ ‎∴△AEF∽△ABC，‎ ‎∵AB=3AE，‎ ‎∴AE：AB=1：3，‎ ‎∴S△AEF：S△ABC=1：9，‎ 设S△AEF=x，‎ ‎∵S四边形BCFE=16，‎ ‎∴=，‎ 解得：x=2，‎ ‎∴S△ABC=18，‎ 故选：B．‎ ‎　‎ ‎16．（2018•孝感）如图，△ABC是等边三角形，△ABD是等腰直角三角形，∠BAD=90°，AE⊥BD于点E，连CD分别交AE，AB于点F，G，过点A作AH⊥CD交BD于点H．则下列结论：①∠ADC=15°；②AF=AG；③AH=DF；④△AFG∽△CBG；⑤AF=（﹣1）EF．其中正确结论的个数为（　　）‎ A．5 B．4 C．3 D．2‎ ‎【分析】①由等边三角形与等腰直角三角形知△CAD是等腰三角形且顶角∠CAD=150°，据此可判断；②求出∠AFP和∠FAG度数，从而得出∠AGF度数，据此可判断；③证△ADF≌△BAH即可判断；④由∠AFG=∠CBG=60°、∠AGF=∠CGB即可得证；⑤设PF=x，则AF=2x、AP==x，设EF=a，由△ADF≌△BAH知BH=AF=2x，根据△ABE是等腰直角三角形之BE=AE=a+2x，据此得出EH=a，证△PAF∽△EAH得=，从而得出a与x的关系即可判断．‎ ‎【解答】解：∵△ABC为等边三角形，△ABD为等腰直角三角形，‎ ‎∴∠BAC=60°、∠BAD=90°、AC=AB=AD，∠ADB=∠ABD=45°，‎ ‎∴△CAD是等腰三角形，且顶角∠CAD=150°，‎ ‎∴∠ADC=15°，故①正确；‎ ‎∵AE⊥BD，即∠AED=90°，‎ ‎∴∠DAE=45°，‎ ‎∴∠AFG=∠ADC+∠DAE=60°，∠FAG=45°，‎ ‎∴∠AGF=75°，‎ 由∠AFG≠∠AGF知AF≠AG，故②错误；‎ 记AH与CD的交点为P，‎ 由AH⊥CD且∠AFG=60°知∠FAP=30°，‎ 则∠BAH=∠ADC=15°，‎ 在△ADF和△BAH中，‎ ‎∵，‎ ‎∴△ADF≌△BAH（ASA），‎ ‎∴DF=AH，故③正确；‎ ‎∵∠AFG=∠CBG=60°，∠AGF=∠CGB，‎ ‎∴△AFG∽△CBG，故④正确；‎ 在Rt△APF中，设PF=x，则AF=2x、AP==x，‎ 设EF=a，‎ ‎∵△ADF≌△BAH，‎ ‎∴BH=AF=2x，‎ ‎△ABE中，∵∠AEB=90°、∠ABE=45°，‎ ‎∴BE=AE=AF+EF=a+2x，‎ ‎∴EH=BE﹣BH=a+2x﹣2x=a，‎ ‎∵∠APF=∠AEH=90°，∠FAP=∠HAE，‎ ‎∴△PAF∽△EAH，‎ ‎∴=，即=，‎ 整理，得：2x2=（﹣1）ax，‎ 由x≠0得2x=（﹣1）a，即AF=（﹣1）EF，故⑤正确；‎ 故选：B．‎ ‎　‎ ‎17．（2018•泸州）如图，正方形ABCD中，E，F分别在边AD，CD上，AF，BE相交于点G，若AE=3ED，DF=CF，则的值是（　　）‎ A． B． C． D．‎ ‎【分析】如图作，FN∥AD，交AB于N，交BE于M．设DE=a，则AE=3a，利用平行线分线段成比例定理解决问题即可；‎ ‎【解答】解：如图作，FN∥AD，交AB于N，交BE于M．‎ ‎∵四边形ABCD是正方形，‎ ‎∴AB∥CD，∵FN∥AD，‎ ‎∴四边形ANFD是平行四边形，‎ ‎∵∠D=90°，‎ ‎∴四边形ANFD是解析式，‎ ‎∵AE=3DE，设DE=a，则AE=3a，AD=AB=CD=FN=4a，AN=DF=2a，‎ ‎∵AN=BN，MN∥AE，‎ ‎∴BM=ME，‎ ‎∴MN=a，‎ ‎∴FM=a，‎ ‎∵AE∥FM，‎ ‎∴===，‎ 故选：C．‎ ‎　‎ ‎18．（2018•临安区）如图，在△ABC中，DE∥BC，DE分别与AB，AC相交于点D，E，若AD=4，DB=2，则DE：BC的值为（　　）‎ A． B． C． D．‎ ‎【分析】根据平行于三角形一边的直线和其他两边相交，所截得的三角形与原三角形相似，再根据相似三角形的对应边成比例解则可．‎ ‎【解答】解：∵DE∥BC，‎ ‎∴△ADE∽△ABC，‎ ‎∴===．‎ 故选：A．‎ ‎　‎ ‎19．（2018•恩施州）如图所示，在正方形ABCD中，G为CD边中点，连接AG并延长交BC边的延长线于E点，对角线BD交AG于F点．已知FG=2，则线段AE的长度为（　　）‎ A．6 B．8 C．10 D．12‎ ‎【分析】根据正方形的性质可得出AB∥CD，进而可得出△ABF∽△GDF，根据相似三角形的性质可得出==2，结合FG=2可求出AF、AG的长度，由CG∥AB、AB=2CG可得出CG为△EAB的中位线，再利用三角形中位线的性质可求出AE的长度，此题得解．‎ ‎【解答】解：∵四边形ABCD为正方形，‎ ‎∴AB=CD，AB∥CD，‎ ‎∴∠ABF=∠GDF，∠BAF=∠DGF，‎ ‎∴△ABF∽△GDF，‎ ‎∴==2，‎ ‎∴AF=2GF=4，‎ ‎∴AG=6．‎ ‎∵CG∥AB，AB=2CG，‎ ‎∴CG为△EAB的中位线，‎ ‎∴AE=2AG=12．‎ 故选：D．‎ ‎　‎ ‎20．（2018•杭州）如图，在△ABC中，点D在AB边上，DE∥BC，与边AC交于点E，连结BE．记△ADE，△BCE的面积分别为S1，S2（　　）‎ A．若2AD＞AB，则3S1＞2S2 B．若2AD＞AB，则3S1＜2S2‎ C．若2AD＜AB，则3S1＞2S2 D．若2AD＜AB，则3S1＜2S2‎ ‎【分析】根据题意判定△ADE∽△ABC，由相似三角形的面积之比等于相似比的平方解答．‎ ‎【解答】解：∵如图，在△ABC中，DE∥BC，‎ ‎∴△ADE∽△ABC，‎ ‎∴=（）2，‎ ‎∴若2AD＞AB，即＞时，＞，‎ 此时3S1＞S2+S△BDE，而S2+S△BDE＜2S2．但是不能确定3S1与2S2的大小，‎ 故选项A不符合题意，选项B不符合题意．‎ 若2AD＜AB，即＜时，＜，‎ 此时3S1＜S2+S△BDE＜2S2，‎ 故选项C不符合题意，选项D符合题意．‎ 故选：D．‎ ‎　‎ ‎21．（2018•永州）如图，在△ABC中，点D是边AB上的一点，∠ADC=∠ACB，AD=2，BD=6，则边AC的长为（　　）‎ A．2 B．4 C．6 D．8‎ ‎【分析】只要证明△ADC∽△ACB，可得=，即AC2=AD•AB，由此即可解决问题；‎ ‎【解答】解：∵∠A=∠A，∠ADC=∠ACB，‎ ‎∴△ADC∽△ACB，‎ ‎∴=，‎ ‎∴AC2=AD•AB=2×8=16，‎ ‎∵AC＞0，‎ ‎∴AC=4，‎ 故选：B．‎ ‎　‎ ‎22．（2018•香坊区）如图，点D、E、F分别是△ABC的边AB、AC、BC上的点，若DE∥BC，EF∥AB，则下列比例式一定成立的是（　　）‎ A． = B． = C． = D． =‎ ‎【分析】用平行线分线段成比例定理和相似三角形的判定即可得出结论．‎ ‎【解答】解：∵DE∥BC，‎ ‎∴，‎ ‎∵DE∥BC，‎ ‎∴△ADE∽△ABC，‎ ‎∴，‎ ‎∵EF∥AB，‎ ‎∴，‎ ‎∵EF∥AB，‎ ‎∴△CEF∽△CAB，‎ ‎∴，‎ ‎∵DE∥BC，EF∥AB，‎ ‎∴四边形BDEF是平行四边形，‎ ‎∴DE=BF，EF=BD，‎ ‎∴，，，，‎ ‎∴正确，‎ 故选：C．‎ ‎　‎ ‎23．（2018•荆门）如图，四边形ABCD为平行四边形，E、F为CD边的两个三等分点，连接AF、BE交于点G，则S△EFG：S△ABG=（　　）‎ A．1：3 B．3：1 C．1：9 D．9：1‎ ‎【分析】利用相似三角形的性质面积比等于相似比的平方即可解决问题；‎ ‎【解答】解：∵四边形ABCD是平行四边形，‎ ‎∴CD=AB，CD∥AB，‎ ‎∵DE=EF=FC，‎ ‎∴EF：AB=1：3，‎ ‎∴△EFG∽△BAG，‎ ‎∴=（）2=，‎ 故选：C．‎ ‎　‎ ‎24．（2018•达州）如图，E，F是平行四边形ABCD对角线AC上两点，AE=CF=AC．连接DE，DF并延长，分别交AB，BC于点G，H，连接GH，则的值为（　　）‎ A． B． C． D．1‎ ‎【分析】首先证明AG：AB=CH：BC=1：3，推出GH∥AC，推出△BGH∽△BAC，可得==（）2=（）2=， =，由此即可解决问题．‎ ‎【解答】解：∵四边形ABCD是平行四边形 ‎∴AD=BC，DC=AB，‎ ‎∵AC=CA，‎ ‎∴△ADC≌△CBA，‎ ‎∴S△ADC=S△ABC，‎ ‎∵AE=CF=AC，AG∥CD，CH∥AD，‎ ‎∴AG：DC=AE：CE=1：3，CH：AD=CF：AF=1：3，‎ ‎∴AG：AB=CH：BC=1：3，‎ ‎∴GH∥AC，‎ ‎∴△BGH∽△BAC，‎ ‎∴==（）2=（）2=，‎ ‎∵=，‎ ‎∴=×=，‎ 故选：C．‎ ‎　‎ ‎25．（2018•南充）如图，正方形ABCD的边长为2，P为CD的中点，连结AP，过点B作BE⊥AP于点E，延长CE交AD于点F，过点C作CH⊥BE于点G，交AB于点H，连接HF．下列结论正确的是（　　）‎ A．CE= B．EF= C．cos∠CEP= D．HF2=EF•CF ‎【分析】首先证明BH=AH，推出EG=BG，推出CE=CB，再证明△CEH≌△CBH，Rt△HFE≌Rt△HFA，利用全等三角形的性质即可一一判断．‎ ‎【解答】解：连接EH．‎ ‎∵四边形ABCD是正方形，‎ ‎∴CD=AB═BC=AD=2，CD∥AB，‎ ‎∵BE⊥AP，CH⊥BE，‎ ‎∴CH∥PA，‎ ‎∴四边形CPAH是平行四边形，‎ ‎∴CP=AH，‎ ‎∵CP=PD=1，‎ ‎∴AH=PC=1，‎ ‎∴AH=BH，‎ 在Rt△ABE中，∵AH=HB，‎ ‎∴EH=HB，∵HC⊥BE，‎ ‎∴BG=EG，‎ ‎∴CB=CE=2，故选项A错误，‎ ‎∵CH=CH，CB=CE，HB=HE，‎ ‎∴△ABC≌△CEH，‎ ‎∴∠CBH=∠CEH=90°，‎ ‎∵HF=HF，HE=HA，‎ ‎∴Rt△HFE≌Rt△HFA，‎ ‎∴AF=EF，设EF=AF=x，‎ 在Rt△CDF中，有22+（2﹣x）2=（2+x）2，‎ ‎∴x=，‎ ‎∴EF=，故B错误，‎ ‎∵PA∥CH，‎ ‎∴∠CEP=∠ECH=∠BCH，‎ ‎∴cos∠CEP=cos∠BCH==，故C错误．‎ ‎∵HF=，EF=，FC=‎ ‎∴HF2=EF•FC，故D正确，‎ 故选：D．‎ ‎　‎ ‎26．（2018•临沂）如图．利用标杆BE测量建筑物的高度．已知标杆BE高1.2m，测得AB=1.6m．BC=12.4m．则建筑物CD的高是（　　）‎ A．9.3m B．10.5m C．12.4m D．14m ‎【分析】先证明∴△ABE∽△ACD，则利用相似三角形的性质得=，然后利用比例性质求出CD即可．‎ ‎【解答】解：∵EB∥CD，‎ ‎∴△ABE∽△ACD，‎ ‎∴=，即=，‎ ‎∴CD=10.5（米）．‎ 故选：B．‎ ‎　‎ ‎27．（2018•长春）《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前，其中有首歌谣：今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？意即：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺，同时立一根一尺五寸的小标杆，它的影长五寸（提示：1丈=10尺，1尺=10寸），则竹竿的长为（　　）‎ A．五丈 B．四丈五尺 C．一丈 D．五尺 ‎【分析】根据同一时刻物高与影长成正比可得出结论．‎ ‎【解答】解：设竹竿的长度为x尺，‎ ‎∵竹竿的影长=一丈五尺=15尺，标杆长=一尺五寸=1.5尺，影长五寸=0.5尺，‎ ‎∴，解得x=45（尺）．‎ 故选：B．‎ ‎　‎ ‎28．（2018•绍兴）学校门口的栏杆如图所示，栏杆从水平位置BD绕O点旋转到AC位置，已知AB⊥BD，CD⊥BD，垂足分别为B，D，AO=4m，AB=1.6m，CO=1m，则栏杆C端应下降的垂直距离CD为（　　）‎ A．0.2m B．0.3m C．0.4m D．0.5m ‎【分析】由∠ABO=∠CDO=90°、∠AOB=∠COD知△ABO∽△CDO，据此得=，将已知数据代入即可得．‎ ‎【解答】解：∵AB⊥BD，CD⊥BD，‎ ‎∴∠ABO=∠CDO=90°，‎ 又∵∠AOB=∠COD，‎ ‎∴△ABO∽△CDO，‎ 则=，‎ ‎∵AO=4m，AB=1.6m，CO=1m，‎ ‎∴=，‎ 解得：CD=0.4，‎ 故选：C．‎ ‎　‎ 二．填空题（共7小题）‎ ‎29．（2018•邵阳）如图所示，点E是平行四边形ABCD的边BC延长线上一点，连接AE，交CD于点F，连接BF．写出图中任意一对相似三角形：　△ADF∽△ECF　．‎ ‎【分析】利用平行四边形的性质得到AD∥CE，则根据相似三角形的判定方法可判断△ADF∽△ECF．‎ ‎【解答】解：∵四边形ABCD为平行四边形，‎ ‎∴AD∥CE，‎ ‎∴△ADF∽△ECF．‎ 故答案为△ADF∽△ECF．‎ ‎　‎ ‎30．（2018•北京）如图，在矩形ABCD中，E是边AB的中点，连接DE交对角线AC于点F，若AB=4，AD=3，则CF的长为　　．‎ ‎【分析】根据矩形的性质可得出AB∥CD，进而可得出∠FAE=∠FCD，结合∠AFE=∠CFD（对顶角相等）可得出△AFE∽△CFD，利用相似三角形的性质可得出==2，利用勾股定理可求出AC的长度，再结合CF=•AC，即可求出CF的长．‎ ‎【解答】解：∵四边形ABCD为矩形，‎ ‎∴AB=CD，AD=BC，AB∥CD，‎ ‎∴∠FAE=∠FCD，‎ 又∵∠AFE=∠CFD，‎ ‎∴△AFE∽△CFD，‎ ‎∴==2．‎ ‎∵AC==5，‎ ‎∴CF=•AC=×5=．‎ 故答案为：．‎ ‎　‎ ‎31．（2018•包头）如图，在▱ABCD中，AC是一条对角线，EF∥BC，且EF与AB相交于点E，与AC相交于点F，3AE=2EB，连接DF．若S△AEF=1，则S△ADF的值为　　．‎ ‎【分析】由3AE=2EB可设AE=2a、BE=3a，根据EF∥BC得=（）2=，结合S△AEF=1知S△ADC=S△ABC=，再由==知=，继而根据S△ADF=S△ADC可得答案．‎ ‎【解答】解：∵3AE=2EB，‎ ‎∴可设AE=2a、BE=3a，‎ ‎∵EF∥BC，‎ ‎∴△AEF∽△ABC，‎ ‎∴=（）2=（）2=，‎ ‎∵S△AEF=1，‎ ‎∴S△ABC=，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴S△ADC=S△ABC=，‎ ‎∵EF∥BC，‎ ‎∴===，‎ ‎∴==，‎ ‎∴S△ADF=S△ADC=×=，‎ 故答案为：．‎ ‎　‎ ‎32．（2018•资阳）已知：如图，△ABC的面积为12，点D、E分别是边AB、AC的中点，则四边形BCED的面积为　9　．‎ ‎【分析】设四边形BCED的面积为x，则S△ADE=12﹣x，由题意知DE∥BC且DE=BC，从而得=（）2，据此建立关于x的方程，解之可得．‎ ‎【解答】解：设四边形BCED的面积为x，则S△ADE=12﹣x，‎ ‎∵点D、E分别是边AB、AC的中点，‎ ‎∴DE是△ABC的中位线，‎ ‎∴DE∥BC，且DE=BC，‎ ‎∴△ADE∽△ABC，‎ 则=（）2，即=，‎ 解得：x=9，‎ 即四边形BCED的面积为9，‎ 故答案为：9．‎ ‎　‎ ‎33．（2018•泰安）《九章算术》是中国传统数学最重要的著作，在“勾股”章中有这样一个问题：“今有邑方二百步，各中开门，出东门十五步有木，问：出南门几步面见木？”‎ 用今天的话说，大意是：如图，DEFG是一座边长为200步（“步”是古代的长度单位）的正方形小城，东门H位于GD的中点，南门K位于ED的中点，出东门15步的A处有一树木，求出南门多少步恰好看到位于A处的树木（即点D在直线AC上）？请你计算KC的长为　　步．‎ ‎【分析】证明△CDK∽△DAH，利用相似三角形的性质得=，然后利用比例性质可求出CK的长．‎ ‎【解答】解：DH=100，DK=100，AH=15，‎ ‎∵AH∥DK，‎ ‎∴∠CDK=∠A，‎ 而∠CKD=∠AHD，‎ ‎∴△CDK∽△DAH，‎ ‎∴=，即=，‎ ‎∴CK=．‎ 答：KC的长为步．‎ 故答案为．‎ ‎　‎ ‎34．（2018•岳阳）《九章算术》是我国古代数学名著，书中有下列问题：“今有勾五步，股十二步，问勾中容方几何？”其意思为：“今有直角三角形，勾（短直角边）长为5步，股（长直角边）长为12步，问该直角三角形能容纳的正方形边长最大是多少步？”该问题的答案是　　步．‎ ‎【分析】如图1，根据正方形的性质得：DE∥BC，则△ADE∽△ACB，列比例式可得结论；如图2，同理可得正方形的边长，比较可得最大值．‎ ‎【解答】解：如图1，∵四边形CDEF是正方形，‎ ‎∴CD=ED，DE∥CF，‎ 设ED=x，则CD=x，AD=12﹣x，‎ ‎∵DE∥CF，‎ ‎∴∠ADE=∠C，∠AED=∠B，‎ ‎∴△ADE∽△ACB，‎ ‎∴，‎ ‎∴，‎ x=，‎ 如图2，四边形DGFE是正方形，‎ 过C作CP⊥AB于P，交DG于Q，‎ 设ED=x，‎ S△ABC=AC•BC=AB•CP，‎ ‎12×5=13CP，‎ CP=，‎ 同理得：△CDG∽△CAB，‎ ‎∴，‎ ‎∴，‎ x=，‎ ‎∴该直角三角形能容纳的正方形边长最大是（步），‎ 故答案为：．‎ ‎　‎ ‎35．（2018•吉林）如图是测量河宽的示意图，AE与BC相交于点D，∠B=∠C=90°，测得BD=120m，DC=60m，EC=50m，求得河宽AB=　100　m．‎ ‎【分析】由两角对应相等可得△BAD∽△CED，利用对应边成比例可得两岸间的大致距离AB．‎ ‎【解答】解：∵∠ADB=∠EDC，∠ABC=∠ECD=90°，‎ ‎∴△ABD∽△ECD，‎ ‎∴，，‎ 解得：AB=（米）．‎ 故答案为：100．‎ ‎　‎ 三．解答题（共15小题）‎ ‎36．（2018•张家界）如图，点P是⊙O的直径AB延长线上一点，且AB=4，点M为上一个动点（不与A，B重合），射线PM与⊙O交于点N（不与M重合）‎ ‎（1）当M在什么位置时，△MAB的面积最大，并求岀这个最大值；‎ ‎（2）求证：△PAN∽△PMB．‎ ‎【分析】（1）当M在弧AB中点时，三角形MAB面积最大，此时OM与AB垂直，求出此时三角形面积最大值即可；‎ ‎（2）由同弧所对的圆周角相等及公共角，利用两对角相等的三角形相似即可得证．‎ ‎【解答】解：（1）当点M在的中点处时，△MAB面积最大，此时OM⊥AB，‎ ‎∵OM=AB=×4=2，‎ ‎∴S△ABM=AB•OM=×4×2=4；‎ ‎（2）∵∠PMB=∠PAN，∠P=∠P，‎ ‎∴△PAN∽△PMB．‎ ‎　‎ ‎37．（2018•株洲）如图，在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD，其中AM=AN．‎ ‎（1）求证：Rt△ABM≌Rt△AND；‎ ‎（2）线段MN与线段AD相交于T，若AT=，求tan∠ABM的值．‎ ‎【分析】（1）利用HL证明即可；‎ ‎（2）想办法证明△DNT∽△AMT，可得由AT=，推出，在Rt△ABM中，tan∠ABM=．‎ ‎【解答】解：（1）∵AD=AB，AM=AN，∠AMB=∠AND=90°‎ ‎∴Rt△ABM≌Rt△AND（HL）．‎ ‎（2）由Rt△ABM≌Rt△AND易得：∠DAN=∠BAM，DN=BM ‎∵∠BAM+∠DAM=90°；∠DAN+∠ADN=90°‎ ‎∴∠DAM=∠AND ‎∴ND∥AM ‎∴△DNT∽△AMT ‎∴‎ ‎∵AT=，‎ ‎∴‎ ‎∵Rt△ABM ‎∴tan∠ABM=．‎ ‎　‎ ‎38．（2018•大庆）如图，AB是⊙O的直径，点E为线段OB上一点（不与O，B重合），作EC⊥OB，交⊙O于点C，作直径CD，过点C的切线交DB的延长线于点P，作AF⊥PC于点F，连接CB．‎ ‎（1）求证：AC平分∠FAB；‎ ‎（2）求证：BC2=CE•CP；‎ ‎（3）当AB=4且=时，求劣弧的长度．‎ ‎【分析】（1）根据等角的余角相等证明即可；‎ ‎（2）只要证明△CBE∽△CPB，可得=解决问题；‎ ‎（3）作BM⊥PF于M．则CE=CM=CF，设CE=CM=CF=3a，PC=4a，PM=a，利用相似三角形的性质求出BM，求出tan∠BCM的值即可解决问题；‎ ‎【解答】（1）证明：∵AB是直径，‎ ‎∴∠ACB=90°，‎ ‎∴∠BCP+∠ACF=90°，∠ACE+∠BCE=90°，‎ ‎∵∠BCP=∠BCE，‎ ‎∴∠ACF=∠ACE，即AC平分∠FAB．‎ ‎（2）证明：∵OC=OB，‎ ‎∴∠OCB=∠OBC，‎ ‎∵PF是⊙O的切线，CE⊥AB，‎ ‎∴∠OCP=∠CEB=90°，‎ ‎∴∠PCB+∠OCB=90°，∠BCE+∠OBC=90°，‎ ‎∴∠BCE=∠BCP，‎ ‎∵CD是直径，‎ ‎∴∠CBD=∠CBP=90°，‎ ‎∴△CBE∽△CPB，‎ ‎∴=，‎ ‎∴BC2=CE•CP；‎ ‎（3）解：作BM⊥PF于M．则CE=CM=CF，设CE=CM=CF=3a，PC=4a，PM=a，‎ ‎∵∠MCB+∠P=90°，∠P+∠PBM=90°，‎ ‎∴∠MCB=∠PBM，‎ ‎∵CD是直径，BM⊥PC，‎ ‎∴∠CMB=∠BMP=90°，‎ ‎∴△BMC∽△PMB，‎ ‎∴=，‎ ‎∴BM2=CM•PM=3a2，‎ ‎∴BM=a，‎ ‎∴tan∠BCM==，‎ ‎∴∠BCM=30°，‎ ‎∴∠OCB=∠OBC=∠BOC=60°，∠BOD=120°‎ ‎∴的长==π．‎ ‎　‎ ‎39．（2018•江西）如图，在△ABC中，AB=8，BC=4，CA=6，CD∥AB，BD是∠ABC的平分线，BD交AC于点E，求AE的长．‎ ‎【分析】根据角平分线定义和平行线的性质求出∠D=∠CBD，求出BC=CD=4，证△AEB∽△CED，得出比例式，求出AE=2CE，即可得出答案．‎ ‎【解答】解：∵BD为∠ABC的平分线，‎ ‎∴∠ABD=∠CBD，‎ ‎∵AB∥CD，‎ ‎∴∠D=∠ABD，‎ ‎∴∠D=∠CBD，‎ ‎∴BC=CD，‎ ‎∵BC=4，‎ ‎∴CD=4，‎ ‎∵AB∥CD，‎ ‎∴△ABE∽△CDE，‎ ‎∴=，‎ ‎∴=，‎ ‎∴AE=2CE，‎ ‎∵AC=6=AE+CE，‎ ‎∴AE=4．‎ ‎　‎ ‎40．（2018•上海）已知：如图，正方形ABCD中，P是边BC上一点，BE⊥AP，DF⊥AP，垂足分别是点E、F．‎ ‎（1）求证：EF=AE﹣BE；‎ ‎（2）联结BF，如课=．求证：EF=EP．‎ ‎【分析】（1）利用正方形的性质得AB=AD，∠BAD=90°，根据等角的余角相等得到∠1=∠3，则可判断△ABE≌△DAF，则BE=AF，然后利用等线段代换可得到结论；‎ ‎（2）利用=和AF=BE得到=，则可判定Rt△BEF∽Rt△DFA，所以∠4=∠3，再证明∠4=∠5，然后根据等腰三角形的性质可判断EF=EP．‎ ‎【解答】证明：（1）∵四边形ABCD为正方形，‎ ‎∴AB=AD，∠BAD=90°，‎ ‎∵BE⊥AP，DF⊥AP，‎ ‎∴∠BEA=∠AFD=90°，‎ ‎∵∠1+∠2=90°，∠2+∠3=90°，‎ ‎∴∠1=∠3，‎ 在△ABE和△DAF中 ‎，‎ ‎∴△ABE≌△DAF，‎ ‎∴BE=AF，‎ ‎∴EF=AE﹣AF=AE﹣BE；‎ ‎（2）如图，∵=，‎ 而AF=BE，‎ ‎∴=，‎ ‎∴=，‎ ‎∴Rt△BEF∽Rt△DFA，‎ ‎∴∠4=∠3，‎ 而∠1=∠3，‎ ‎∴∠4=∠1，‎ ‎∵∠5=∠1，‎ ‎∴∠4=∠5，‎ 即BE平分∠FBP，‎ 而BE⊥EP，‎ ‎∴EF=EP．‎ ‎　‎ ‎41．（2018•东营）如图，CD是⊙O的切线，点C在直径AB的延长线上．‎ ‎（1）求证：∠CAD=∠BDC；‎ ‎（2）若BD=AD，AC=3，求CD的长．‎ ‎【分析】（1）连接OD，由OB=OD可得出∠OBD=∠ODB，根据切线的性质及直径所对的圆周角等于180°，利用等角的余角相等，即可证出∠CAD=∠BDC；‎ ‎（2）由∠C=∠C、∠CAD=∠CDB可得出△CDB∽△CAD，根据相似三角形的性质结合BD=AD、AC=3，即可求出CD的长．‎ ‎【解答】（1）证明：连接OD，如图所示．‎ ‎∵OB=OD，‎ ‎∴∠OBD=∠ODB．‎ ‎∵CD是⊙O的切线，OD是⊙O的半径，‎ ‎∴∠ODB+∠BDC=90°．‎ ‎∵AB是⊙O的直径，‎ ‎∴∠ADB=90°，‎ ‎∴∠OBD+∠CAD=90°，‎ ‎∴∠CAD=∠BDC．‎ ‎（2）解：∵∠C=∠C，∠CAD=∠CDB，‎ ‎∴△CDB∽△CAD，‎ ‎∴=．‎ ‎∵BD=AD，‎ ‎∴=，‎ ‎∴=，‎ 又∵AC=3，‎ ‎∴CD=2．‎ ‎　‎ ‎42．（2018•南京）如图，在正方形ABCD中，E是AB上一点，连接DE．过点A作AF⊥DE，垂足为F，⊙O经过点C、D、F，与AD相交于点G．‎ ‎（1）求证：△AFG∽△DFC；‎ ‎（2）若正方形ABCD的边长为4，AE=1，求⊙O的半径．‎ ‎【分析】（1）欲证明△AFG∽△DFC，只要证明∠FAG=∠FDC，∠AGF=∠FCD；‎ ‎（2）首先证明CG是直径，求出CG即可解决问题；‎ ‎【解答】（1）证明：在正方形ABCD中，∠ADC=90°，‎ ‎∴∠CDF+∠ADF=90°，‎ ‎∵AF⊥DE，‎ ‎∴∠AFD=90°，‎ ‎∴∠DAF+∠ADF=90°，‎ ‎∴∠DAF=∠CDF，‎ ‎∵四边形GFCD是⊙O的内接四边形，‎ ‎∴∠FCD+∠DGF=180°，‎ ‎∵∠FGA+∠DGF=180°，‎ ‎∴∠FGA=∠FCD，‎ ‎∴△AFG∽△DFC．‎ ‎（2）解：如图，连接CG．‎ ‎∵∠EAD=∠AFD=90°，∠EDA=∠ADF，‎ ‎∴△EDA∽△ADF，‎ ‎∴=，即=，‎ ‎∵△AFG∽△DFC，‎ ‎∴=，‎ ‎∴=，‎ 在正方形ABCD中，DA=DC，‎ ‎∴AG=EA=1，DG=DA﹣AG=4﹣1=3，‎ ‎∴CG==5，‎ ‎∵∠CDG=90°，‎ ‎∴CG是⊙O的直径，‎ ‎∴⊙O的半径为．‎ ‎　‎ ‎43．（2018•滨州）如图，AB为⊙O的直径，点C在⊙O上，AD⊥CD于点D，且AC平分∠DAB，求证：‎ ‎（1）直线DC是⊙O的切线；‎ ‎（2）AC2=2AD•AO．‎ ‎【分析】（1）连接OC，由OA=OC、AC平分∠DAB知∠OAC=∠OCA=∠‎ DAC，据此知OC∥AD，根据AD⊥DC即可得证；‎ ‎（2）连接BC，证△DAC∽△CAB即可得．‎ ‎【解答】解：（1）如图，连接OC，‎ ‎∵OA=OC，‎ ‎∴∠OAC=∠OCA，‎ ‎∵AC平分∠DAB，‎ ‎∴∠OAC=∠DAC，‎ ‎∴∠DAC=∠OCA，‎ ‎∴OC∥AD，‎ 又∵AD⊥CD，‎ ‎∴OC⊥DC，‎ ‎∴DC是⊙O的切线；‎ ‎（2）连接BC，‎ ‎∵AB为⊙O的直径，‎ ‎∴AB=2AO，∠ACB=90°，‎ ‎∵AD⊥DC，‎ ‎∴∠ADC=∠ACB=90°，‎ 又∵∠DAC=∠CAB，‎ ‎∴△DAC∽△CAB，‎ ‎∴=，即AC2=AB•AD，‎ ‎∵AB=2AO，‎ ‎∴AC2=2AD•AO．‎ ‎　‎ ‎44．（2018•十堰）如图，△ABC中，AB=AC，以AB为直径的⊙‎ O交BC于点D，交AC于点E，过点D作FG⊥AC于点F，交AB的延长线于点G．‎ ‎（1）求证：FG是⊙O的切线；‎ ‎（2）若tanC=2，求的值．‎ ‎【分析】（1）欲证明FG是⊙O的切线，只要证明OD⊥FG；‎ ‎（2）由△GDB∽△GAD，设BG=a．可得===，推出DG=2a，AG=4a，由此即可解决问题；‎ ‎【解答】（1）证明：连接AD、OD．‎ ‎∵AB是直径，‎ ‎∴∠ADB=90°，即AD⊥BC，‎ ‎∵AC=AB，‎ ‎∴CD=BD，‎ ‎∵OA=OB，‎ ‎∴OD∥AC，‎ ‎∵DF⊥AC，‎ ‎∴OD⊥DF，‎ ‎∴FG是⊙O的切线．‎ ‎（2）解：∵tanC==2，BD=CD，‎ ‎∴BD：AD=1：2，‎ ‎∵∠GDB+∠ODB=90°，∠ADO+∠ODB=90°，‎ ‎∵OA=OD，‎ ‎∴∠OAD=∠ODA，‎ ‎∴∠GDB=∠GAD，‎ ‎∵∠G=∠G，‎ ‎∴△GDB∽△GAD，设BG=a．‎ ‎∴===，‎ ‎∴DG=2a，AG=4a，‎ ‎∴BG：GA=1：4．‎ ‎　‎ ‎45．（2018•杭州）如图，在△ABC中，AB=AC，AD为BC边上的中线，DE⊥AB于点E．‎ ‎（1）求证：△BDE∽△CAD．‎ ‎（2）若AB=13，BC=10，求线段DE的长．‎ ‎【分析】（1）想办法证明∠B=∠C，∠DEB=∠ADC=90°即可解决问题；‎ ‎（2）利用面积法： •AD•BD=•AB•DE求解即可；‎ ‎【解答】解：（1）∵AB=AC，BD=CD，‎ ‎∴AD⊥BC，∠B=∠C，‎ ‎∵DE⊥AB，‎ ‎∴∠DEB=∠ADC，‎ ‎∴△BDE∽△CAD．‎ ‎（2）∵AB=AC，BD=CD，‎ ‎∴AD⊥BC，‎ 在Rt△ADB中，AD===12，‎ ‎∵•AD•BD=•AB•DE，‎ ‎∴DE=．‎ ‎　‎ ‎46．（2018•烟台）如图，已知D，E分别为△ABC的边AB，BC上两点，点A，C，E在⊙D上，点B，D在⊙E上．F为上一点，连接FE并延长交AC的延长线于点N，交AB于点M．‎ ‎（1）若∠EBD为α，请将∠CAD用含α的代数式表示；‎ ‎（2）若EM=MB，请说明当∠CAD为多少度时，直线EF为⊙D的切线；‎ ‎（3）在（2）的条件下，若AD=，求的值．‎ ‎【分析】（1）根据同圆的半径相等和等边对等角得：∠EDB=∠EBD=α，∠CAD=∠ACD，∠DCE=∠DEC=2α，再根据三角形内角和定理可得结论；‎ ‎（2）设∠MBE=x，同理得：∠EMB=∠MBE=x，根据切线的性质知：∠DEF=90°，所以∠CED+∠MEB=90°，同理根据三角形内角和定理可得∠CAD=45°；‎ ‎（3）由（2）得：∠CAD=45°；根据（1）的结论计算∠MBE=30°，证明△CDE是等边三角形，得CD=CE=DE=EF=AD=，求EM=1，MF=EF﹣EM=﹣1，根据三角形内角和及等腰三角形的判定得：EN=CE=，代入化简可得结论．‎ ‎【解答】解：（1）连接CD、DE，⊙E中，∵ED=EB，‎ ‎∴∠EDB=∠EBD=α，‎ ‎∴∠CED=∠EDB+∠EBD=2α，‎ ‎⊙D中，∵DC=DE=AD，‎ ‎∴∠CAD=∠ACD，∠DCE=∠DEC=2α，‎ ‎△ACB中，∠CAD+∠ACD+∠DCE+∠EBD=180°，‎ ‎∴∠CAD==；‎ ‎（2）设∠MBE=x，‎ ‎∵EM=MB，‎ ‎∴∠EMB=∠MBE=x，‎ 当EF为⊙D的切线时，∠DEF=90°，‎ ‎∴∠CED+∠MEB=90°，‎ ‎∴∠CED=∠DCE=90°﹣x，‎ ‎△ACB中，同理得，∠CAD+∠ACD+∠DCE+∠EBD=180°，‎ ‎∴2∠CAD=180°﹣90∴=90∴，‎ ‎∴∠CAD=45°；‎ ‎（3）由（2）得：∠CAD=45°；‎ 由（1）得：∠CAD=；‎ ‎∴∠MBE=30°，‎ ‎∴∠CED=2∠MBE=60°，‎ ‎∵CD=DE，‎ ‎∴△CDE是等边三角形，‎ ‎∴CD=CE=DE=EF=AD=，‎ Rt△DEM中，∠EDM=30°，DE=，‎ ‎∴EM=1，MF=EF﹣EM=﹣1，‎ ‎△ACB中，∠NCB=45°+30°=75°，‎ ‎△CNE中，∠CEN=∠BEF=30°，‎ ‎∴∠CNE=75°，‎ ‎∴∠CNE=∠NCB=75°，‎ ‎∴EN=CE=，‎ ‎∴===2+．‎ ‎　‎ ‎47．（2018•陕西）周末，小华和小亮想用所学的数学知识测量家门前小河的宽．测量时，他们选择了河对岸岸边的一棵大树，将其底部作为点A，在他们所在的岸边选择了点B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB的延长线上选择点D，竖起标杆DE，使得点E与点C、A共线．‎ 已知：CB⊥AD，ED⊥AD，测得BC=1m，DE=1.5m，BD=8.5m．测量示意图如图所示．请根据相关测量信息，求河宽AB．‎ ‎【分析】由BC∥DE，可得=，构建方程即可解决问题．‎ ‎【解答】解：∵BC∥DE，‎ ‎∴△ABC∽△ADE，‎ ‎∴=，‎ ‎∴=，‎ ‎∴AB=17（m），‎ 经检验：AB=17是分式方程的解，‎ 答：河宽AB的长为17米．‎ ‎　‎ ‎48．（2018•济宁）如图，在正方形ABCD中，点E，F分别是边AD，BC的中点，连接DF，过点E作EH⊥DF，垂足为H，EH的延长线交DC于点G．‎ ‎（1）猜想DG与CF的数量关系，并证明你的结论；‎ ‎（2）过点H作MN∥CD，分别交AD，BC于点M，N，若正方形ABCD的边长为10，点P是MN上一点，求△PDC周长的最小值．‎ ‎【分析】（1）结论：CF=2DG．只要证明△DEG∽△CDF即可；‎ ‎（2）作点C关于NM的对称点K，连接DK交MN于点P，连接PC，此时△PDC的周长最短．周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK；‎ ‎【解答】解：（1）结论：CF=2DG．‎ 理由：∵四边形ABCD是正方形，‎ ‎∴AD=BC=CD=AB，∠ADC=∠C=90°，‎ ‎∵DE=AE，‎ ‎∴AD=CD=2DE，‎ ‎∵EG⊥DF，‎ ‎∴∠DHG=90°，‎ ‎∴∠CDF+∠DGE=90°，∠DGE+∠DEG=90°，‎ ‎∴∠CDF=∠DEG，‎ ‎∴△DEG∽△CDF，‎ ‎∴==，‎ ‎∴CF=2DG．‎ ‎（2）作点C关于NM的对称点K，连接DK交MN于点P，连接PC，此时△PDC的周长最短．周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK．‎ 由题意：CD=AD=10，ED=AE=5，DG=，EG=，DH==，‎ ‎∴EH=2DH=2，‎ ‎∴HM==2，‎ ‎∴DM=CN=NK==1，‎ 在Rt△DCK中，DK===2，‎ ‎∴△PCD的周长的最小值为10+2．‎ ‎　‎ ‎49．（2018•聊城）如图，正方形ABCD中，E是BC上的一点，连接AE，过B点作BH⊥AE，垂足为点H，延长BH交CD于点F，连接AF．‎ ‎（1）求证：AE=BF．‎ ‎（2）若正方形边长是5，BE=2，求AF的长．‎ ‎【分析】（1）根据ASA证明△ABE≌△BCF，可得结论；‎ ‎（2）根据（1）得：△ABE≌△BCF，则CF=BE=2，最后利用勾股定理可得AF的长．‎ ‎【解答】（1）证明：∵四边形ABCD是正方形，‎ ‎∴AB=BC，∠ABE=∠BCF=90°，‎ ‎∴∠BAE+∠AEB=90°，‎ ‎∵BH⊥AE，‎ ‎∴∠BHE=90°，‎ ‎∴∠AEB+∠EBH=90°，‎ ‎∴∠BAE=∠EBH，‎ 在△ABE和△BCF中，‎ ‎，‎ ‎∴△ABE≌△BCF（ASA），‎ ‎∴AE=BF；‎ ‎（2）解：∵AB=BC=5，‎ 由（1）得：△ABE≌△BCF，‎ ‎∴CF=BE=2，‎ ‎∴DF=5﹣2=3，‎ ‎∵四边形ABCD是正方形，‎ ‎∴AB=AD=5，∠ADF=90°，‎ 由勾股定理得：AF====．‎ ‎　‎ ‎50．（2018•乌鲁木齐）如图，AG是∠HAF的平分线，点E在AF上，以AE为直径的⊙O交AG于点D，过点D作AH的垂线，垂足为点C，交AF于点B．‎ ‎（1）求证：直线BC是⊙O的切线；‎ ‎（2）若AC=2CD，设⊙O的半径为r，求BD的长度．‎ ‎【分析】（1）根据角平分线的定义和同圆的半径相等可得OD∥AC，证明OD⊥CB，可得结论；‎ ‎（2）在Rt△ACD中，设CD=a，则AC=2a，AD=a，证明△ACD∽△ADE，表示a=，由平行线分线段成比例定理得：，代入可得结论．‎ ‎【解答】（1）证明：连接OD，‎ ‎∵AG是∠HAF的平分线，‎ ‎∴∠CAD=∠BAD，‎ ‎∵OA=OD，‎ ‎∴∠OAD=∠ODA，‎ ‎∴∠CAD=∠ODA，‎ ‎∴OD∥AC，‎ ‎∵∠ACD=90°，‎ ‎∴∠ODB=∠ACD=90°，即OD⊥CB，‎ ‎∵D在⊙O上，‎ ‎∴直线BC是⊙O的切线；（4分）‎ ‎（2）解：在Rt△ACD中，设CD=a，则AC=2a，AD=a，‎ 连接DE，‎ ‎∵AE是⊙O的直径，‎ ‎∴∠ADE=90°，‎ 由∠CAD=∠BAD，∠ACD=∠ADE=90°，‎ ‎∴△ACD∽△ADE，‎ ‎∴，‎ 即，‎ ‎∴a=，‎ 由（1）知：OD∥AC，‎ ‎∴，即，‎ ‎∵a=，解得BD=r．（10分）‎ ‎　‎