2019中考数学专题练习圆的切线长定理含解析 9页

‎ 2019中考数学专题练习-圆的切线长定理（含解析）‎ 一、单选题 ‎1.如图，△ABC是一张周长为17cm的三角形的纸片，BC=5cm，⊙O是它的内切圆，小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，则剪下的三角形的周长为（   ） ‎ A. 12cm                          B. 7cm                          C. 6cm                          D. 随直线MN的变化而变化 ‎2.下列说法正确的是(   ) ‎ A. 过任意一点总可以作圆的两条切线                      B. 圆的切线长就是圆的切线的长度 C. 过圆外一点所画的圆的两条切线长相等               D. 过圆外一点所画的圆的切线长一定大于圆的半径 ‎3.如图，PA，PB切⊙O于A，B两点，CD切⊙O于点E，交PA，PB于C，D．若⊙O的半径为1，△PCD的周长等于2 ，则线段AB的长是（   ） ‎ A.                                        B. 3                                       C. 2                                        D. 3 ‎ ‎4.如图,圆和四边形ABCD的四条边都相切,且AB=16,CD=10,则四边形ABCD的周长为(   ) ‎ A. 50                                         B. 52                                         C. 54                                         D. 56‎ ‎5.如图，PA，PB，CD与⊙O相切于点为A，B，E，若PA=7，则△PCD的周长为（   ） ‎ A. 7                                        B. 14                                        C. 10.5                                        D. 10‎ ‎6.如图，PA,PB切⊙O于点A,B，PA=8，CD切⊙O于点E，交PA,PB于C,D两点，则△PCD的 周长是（    ）‎ A.8 B.18 C.16 D.14‎ ‎7.如图，四边形ABCD中，AD平行BC，∠ABC=90°，AD=2，AB=6，以AB为直径的半⊙O 切CD于点E，F为弧BE上一动点，过F点的直线MN为半⊙O的切线，MN交BC于M，交CD于N，则△MCN的周长为（   ） ‎ A. 9                                      B. 10                                      C. 3                                       D. 2 ‎ ‎8.圆外切等腰梯形的一腰长是8，则这个等腰梯形的上底与下底长的和为（　　） ‎ A. 4                                          B. 8                                          C. 12                                          D. 16‎ ‎9.如图，△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，已知AD=10cm ， 小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形（△AMN），则剪下的△AMN的周长为（　　） ‎ A. 20cm                        B. 15cm                        C. 10cm                        D. 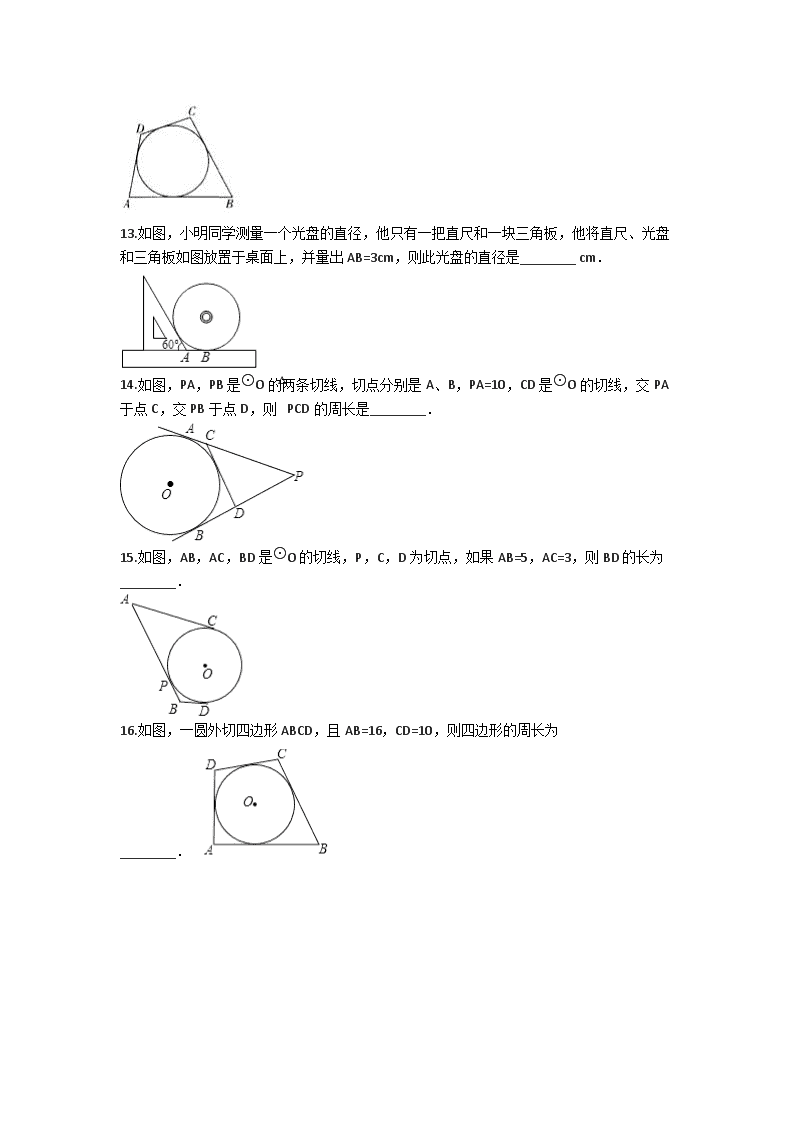随直线MN的变化而变化 二、填空题 ‎10.如图，PA、PB是⊙O的两条切线，A、B是切点，若∠APB=60°，PO=2，则⊙O的半径等于________． ‎ ‎11.PA、PB分别切⊙O于点A、B，若PA=3cm，那么PB=________cm． ‎ ‎12.如图，一圆内切于四边形ABCD，且AB=16，CD=10，则四边形ABCD的周长为________． ‎ ‎13.如图，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB=3cm，则此光盘的直径是________ cm． ‎ ‎14.如图，PA，PB是⊙O的两条切线，切点分别是A、B，PA=10，CD是⊙O的切线，交PA于点C，交PB于点D，则△PCD的周长是________． ‎ ‎15.如图，AB，AC，BD是⊙O的切线，P，C，D为切点，如果AB=5，AC=3，则BD的长为________． ‎ ‎16.如图，一圆外切四边形ABCD，且AB=16，CD=10，则四边形的周长为________． ‎ 答案解析部分 一、单选题 ‎1.【答案】B ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：设E、F分别是⊙O的切点， ∵△ABC是一张三角形的纸片，AB+BC+AC=17cm，⊙O是它的内切圆，点D是其中的一个切点，BC=5cm， ∴BD+CE=BC=5cm，则AD+AE=7cm， 故DM=MF，FN=EN，AD=AE， ∴AM+AN+MN=AD+AE=7（cm）． 故选：B． 【分析】利用切线长定理得出BC=BD+EC，DM=MF，FN=EN，AD=AE，进而得出答案．‎ ‎2.【答案】C ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解 ：A、过圆外任意一点总可以作圆的两条切线，过圆上一点只能做圆的一条切线，过圆内一点不能做圆的切线；故A错误，不符合题意； B、圆的切线长就是，过圆外一点引圆的一条切线，这点到切点之间的线段的长度就是圆的切线长；故B错误，不符合题意； C、根据切线长定理：过圆外一点所画的圆的两条切线长相等；故C是正确的符合题意； D、过圆外一点所画的圆的切线长取决于点离圆的距离等，故不一定大于圆的半径；故D错误，不符合题意； 故答案为：C。 【分析】根据切线长定理及定义即可一一判断。‎ ‎3.【答案】A ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：∵PA，PB切⊙O于A、B两点，CD切⊙O于点E，交PA，PB于C，D， ∴AC=EC，DE=DB，PA=PB， ∵△PCD的周长等于3， ∴PA+PB=2 ， ∴PA=PB= ， 连接PA和AO， ‎ ‎ ∵⊙O的半径为1， ∴sin∠APO= = = ， ∴∠APO=30°， ∴∠APB=60°， ∴△APB是等边三角形， ∴AB=PA=PB= ． 故选：A． 【分析】直接利用切线长定理得出AC=EC，DE=DB，PA=PB，进而求出PA的长，然后判定三角形APB为等边三角形即可确定AB的长．‎ ‎4.【答案】B ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解 ：设,圆与四边形ABCD的四条边AB,BC,CD,DA分别相切于点E,F,G,H,∵AB切圆于点E ,BC切圆于点F，∴BE=BF,同理CF=CG,DG=DH,AG=AE,∴AE＋BE＋CG＋DG=AH＋DH＋BF＋CF,即AB＋DC=AD＋BC=26,∴四边形ABCD的周长=AB＋BC＋CD＋DA=52. 故答案为：52. 【分析】根据切线长定理得出BE=BF,同理CF=CG,DG=DH,AG=AE,根据等式的性质得出AE＋BE＋CG＋DG=AH＋DH＋BF＋CF，即AB＋DC=AD＋BC=26,根据四边形的周长计算方法得出答案。‎ ‎5.【答案】B ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：∵PA、PB、CD与⊙O相切于点为A、B、E， ∴PB=PA=7，CA=CE，DE=DB， ∴△PCD的周长=PC+CD+PB =PC+CE+DE+PD =PC+CA+DB+PD =PA+PB=14， 故选：B． 【分析】根据从圆外一点引圆的两条切线，它们的切线长相等和三角形的周长公式计算即可．‎ ‎6.【答案】C ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：∵PA,PB切⊙O于点A,B，CD切⊙O于点E ∴PA=PB=8，AC=CE，DB=DE △PCD的周长为：PC+CE+DE+PD=PC=CA+DB+PD=PA+PB=8+8=16 故答案为：C【分析】利用切线长定理可得出PA=PB=8，AC=CE，DB=DE，从而可求△PCD的周长就转化为求PA+PB的值。‎ ‎7.【答案】A ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：作DH⊥BC于H，如图， ∵四边形ABCD中，AD平行BC，∠ABC=90°， ∴AB⊥AD，AB⊥BC， ∵AB为直径， ∴AD和BC为⊙O 切线， ∵CD和MN为⊙O 切线， ∴DE=DA=2，CE=CB，NE=NF，MB=MF， ∵四边形ABHD为矩形， ∴BH=AD=2，DH=AB=6， 设BC=x，则CH=x﹣2，CD=x+2， 在Rt△DCH中，∵CH2+DH2=DC2 ， ∴（x﹣2）2+62=（x+2）2 ， 解得x= ， ∴CB=CE= ， ∴△MCN的周长=CN+CM+MN =CN+CM+NF+MF =CN+CM+NF+MB =CE+CB =9． 故选A． ‎ ‎【分析】作DH⊥BC于H，如图，利用平行线的性质得AB⊥AD，AB⊥BC，则根据切线的判定得到AD和BC为⊙O切线，根据切线长定理得DE=DA=2，CE=CB，NE=NF，MB=MF，利用四边形ABHD为矩形得BH=AD=2，DH=AB=6，设BC=x，则CH=x﹣2，CD=x+2，在Rt△DCH中根据勾股定理得（x﹣2）2+62=（x+2）2 ， 解得x= ，即CB=CE= ，然后由等线段代换得到△MCN的周长=CE+CB=9．‎ ‎8.【答案】D ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】 ∵圆外切等腰梯形的一腰长是8，∴梯形对边和为：8+8=16， 则这个等腰梯形的上底与下底长的和为16． 故选：D． 【分析】直接利用圆外切四边形对边和相等，进而求出即可．‎ ‎9.【答案】A ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】 如图： ∵△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，AD=10cm ， ∴设E、F分别是⊙O的切点， 故DM=MF ， FN=EN ， AD=AE ， ∴AM+AN+MN=AD+AE=10+10=20（cm）． 故答案为：A． 【分析】 利用切线长定理得出DM=MF ， FN=EN ， AD=AE ， 进而得出答案．‎ 二、填空题 ‎10.【答案】1 ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：∵PA、PB是⊙O的两条切线， ∴∠APO=∠BPO= ∠APB，∠PAO=90° ∵∠APB=60°， ∴∠APO=30°， ∵PO=2， ∴AO=1． 故答案为：1． 【分析】根据切线的性质求得∠APO=30°，∠PAO=90°，再由直角三角形的性质得AO=1．‎ ‎11.【答案】3 ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】根据切线长定理得：   故答案为：3. ‎ ‎【分析】根据切线长定理即可求解。‎ ‎12.【答案】52 ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：∵一圆内切于四边形ABCD ∴AD+BC=DC+AB=10+16=26 ∴四边形ABCD的周长为：2（DC+AB）=2×26=52 故答案为：52 【分析】根据圆外切四边形的对边之和相等，就可得出AD+BC=DC+AB，就可求出四边形ABCD的周长。‎ ‎13.【答案】6 ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：如图所示： ∵∠CAD=60°， ∴∠CAB=120°， ∵AB和AC与⊙O相切， ∴∠OAB=∠OAC， ∴∠OAB= ∠CAB=60° ∵AB=3cm， ∴OA=6cm， ∴由勾股定理得OB=3 cm， ∴光盘的直径6 cm． 故答案为：6 ． 【分析】先画图，根据题意求出∠OAB=60°，再根据直角三角形的性质和勾股定理求得OB，从而得出光盘的直径．‎ ‎14.【答案】20 ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：∵PA、PB切⊙O于点A、B，CD切⊙O于点E， ‎ ‎ ∴PA=PB=10，CA=CE，DE=DB， ∴△PCD的周长是PC+CD+PD =PC+AC+DB+PD =PA+PB =10+10 =20． 故答案为：20． 【分析】根据切线长定理知：PA=PB=10，CA=CE，DE=DB ，根据三角形的周长=PC+CD+PD=PC+AC+DB+PD=PA+PB，计算即可。‎ ‎15.【答案】2 ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：∵AC、AP为⊙O的切线， ∴AC=AP， ∵BP、BD为⊙O的切线， ∴BP=BD， ∴BD=PB=AB﹣AP=5﹣3=2． 故答案为：2． 【分析】本题考查了切线长定理，由于AB、AC、BD是⊙O的切线，运用切线长定理并利用等式的性质可得，AC=AP，BP=BD，求出BP的长即可求出BD的长．‎ ‎16.【答案】52 ‎ ‎【考点】切线长定理 ‎ ‎【解析】【解答】解：根据圆外切四边形的性质定理可以得出，四边形的周长是对边和的2倍， ∴AB+BC+CD+AD=52 故填：52 【分析】利用圆外切四边形的性质定理可以得出，四边形的周长是对边和的2倍，即可得．‎