2014江苏省南京市中考数学试卷 10页

‎2014年江苏省南京市中考数学试卷 ‎（满分120分，考试时间120分钟）‎ 一、选择题（本大题共6小题，每小题2分，满分12分，在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）‎ ‎1．（2014江苏省南京市，1，2分）下列图形中，既是轴对称图形，又是中心对称图形的是（ ）‎ ‎ ‎ ‎ A． B． C． D．‎ ‎【答案】C ‎2．（2014江苏省南京市，2，2分）计算(－a2)3的结果是 A．a5 B．－a5 C．a6 D．－a6‎ ‎【答案】D；‎ ‎3．（2014江苏省南京市，3，2分）若△ABC∽△A′B′C′，相似比为1∶2，则△ABC与△A′B′C′的面积的比为 ‎ A．1∶2 B．2∶1 C．1∶4 D．4∶1‎ ‎【答案】C ‎4．（2014江苏省南京市，4，2分）下列无理数中，在－2与1之间的是 ‎ A．－ B．－ C． D．‎ ‎【答案】B ‎5．（2014江苏省南京市，5，2分）8的平方根是 ‎ A．4 B．±4 C． D．±‎ ‎【答案】D ‎6．（2014江苏省南京市，6，2分）如图，在矩形AOBC中，点A的坐标是（－2，1），点C的纵坐标是4，则B、C两点的坐标分别是 ‎ A．（，3），（－，4） B．（，3），（－，4）‎ ‎ C．（，），（－，4） D．（，），（－，4）‎ ‎ ‎ ‎【答案】B．‎ 二、填空题（本大题共10小题，每小题2分，共20分，不需写出解答过程，请把答案直接填写在答题卡相应的位置上．）‎ ‎7．（2014江苏省南京市，7，2分）－2的相反数是____________，－2的绝对值是____________．‎ ‎【答案】2；2．‎ ‎8．（2014江苏省南京市，8，2分）截止2013年底，中国高速铁路营运里程达到11000km，居世界首位，将11000用科学记数法表示为______________．‎ ‎【答案】1.1×104．‎ ‎9．（2014江苏省南京市，9，2分）使式子1＋有意义的x的取值范围是_____________．‎ ‎【答案】x≥0．‎ ‎10．（2014江苏省南京市，10，2分）2014年南京青奥会某项目6名礼仪小姐的身高如下（单位：cm）168，166，168，167，169，168，则他们的身高的众数是_______cm，极差是_______cm．‎ ‎【答案】168；3．‎ ‎11．（2014江苏省南京市，11，2分）已知反比例函数的图象经过点A(－2，3)，则当x＝－3时，y＝_______．‎ ‎【答案】2；‎ ‎12．（2014江苏省南京市，12，2分）如图，AD是正五边形ABCDE的一条对角线，则∠BAD＝_______°．‎ ‎【答案】72°‎ ‎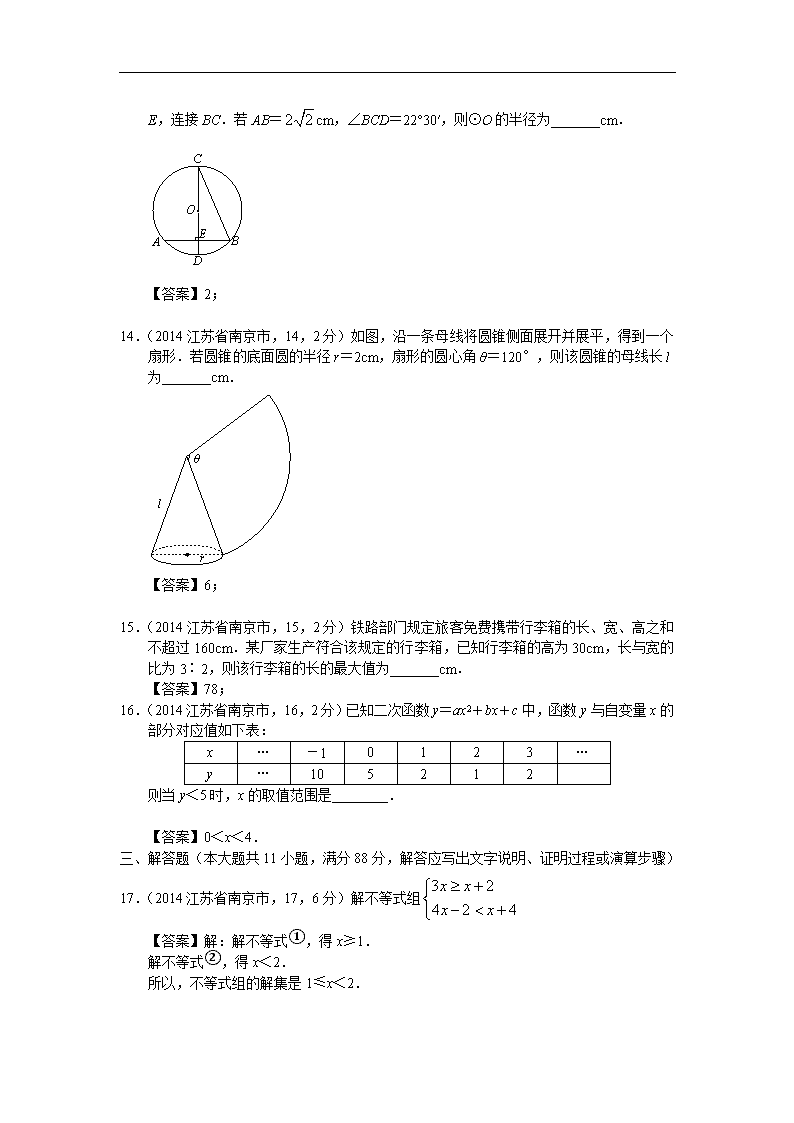13．（2014江苏省南京市，13，2分）如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为 E，连接BC．若AB＝cm，∠BCD＝22°30′，则⊙O的半径为_______cm．‎ ‎【答案】2；‎ ‎14．（2014江苏省南京市，14，2分）如图，沿一条母线将圆锥侧面展开并展平，得到一个扇形．若圆锥的底面圆的半径r＝2cm，扇形的圆心角θ＝120°，则该圆锥的母线长l为_______cm．‎ ‎【答案】6；‎ ‎15．（2014江苏省南京市，15，2分）铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm．某厂家生产符合该规定的行李箱，已知行李箱的高为30cm，长与宽的比为3∶2，则该行李箱的长的最大值为_______cm．‎ ‎【答案】78；‎ ‎16．（2014江苏省南京市，16，2分）已知二次函数y＝ax2＋bx＋c中，函数y与自变量x的部分对应值如下表：‎ x ‎…‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎…‎ y ‎…‎ ‎10‎ ‎5‎ ‎2‎ ‎1‎ ‎2‎ ‎ 则当y＜5时，x的取值范围是________．‎ ‎【答案】0＜x＜4．‎ 三、解答题（本大题共11小题，满分88分，解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（2014江苏省南京市，17，6分）解不等式组 ‎【答案】解：解不等式①，得x≥1．‎ 解不等式②，得x＜2．‎ 所以，不等式组的解集是1≤x＜2．‎ ‎18．（2014江苏省南京市，18，6分）先化简，再求值：，其中a＝1．‎ ‎【答案】解：＝‎ ‎ ＝＝＝．‎ ‎ 当a＝1时，＝．‎ ‎19．（2014江苏省南京市，19，8分）如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．‎ ‎ （1）求证：四边形DBFE是平行四边形；‎ ‎ （2）当△ABC满足什么条件时，四边形DBFE是菱形？为什么？‎ ‎【答案】证明：（1）∵D、E分别是AB、AC的中点，即DE是△ABC的中位线，∴DE∥BC．‎ 又∵EF∥AB，∴四边形DBFE是平行四边形．‎ ‎（2）本题答案不唯一，下列解法供参考．‎ 当AB＝BC时，四边形DBFE是菱形．‎ ‎∵D是AB的中点，∴BD＝AB，∵DE是△ABC的中位线，∴DE＝BC．∵AB＝BC，∴BD＝DE，又∵四边形DBFE是平行四边形，∴四边形DBFE是菱形．‎ ‎20．（2014江苏省南京市，20，8分）从甲、乙、丙3名同学中随机抽取环保志愿者，求下列事件的概率．‎ ‎ （1）抽取1名，恰好是甲；‎ ‎ （2）抽取2名，甲在其中．‎ ‎【答案】（1）从甲、乙、丙3名同学中随机抽取1名环保志愿者，恰好是甲的概率是．‎ ‎（2）从甲、乙、丙3名同学中随机抽取2名环保志愿者，所有可能出现的结果有：（甲，乙）、（甲，丙），（乙，丙），共3中，它们出现的可能性相同．所有的结果中，满足“甲在其中”（记为事件A）的结果只有2种．所以P(A)＝．‎ ‎21．（2014江苏省南京市，21，8分）为了了解某市120000名初中学生的视力情况，某校数学兴趣小组收集有关数据，并进行数据分析．‎ ‎ （1）小明在眼镜店调查了1000名初中学生的视力，小刚在邻居中调查了20名初中学生的视力．他们的抽样是否合理？‎ ‎ （2）该校学生兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查，整理他们的视力情况数据．得到如下的折线统计图．‎ 某市七、八、九年级各抽取的1000名学生 视力不良率的折线统计图 请你根据抽样调查的结果，估计该市120 000名初中学生视力不良的人数是多少？‎ ‎【答案】解：（1）他们的抽样都不合理．‎ 因为如果1000名初中学生全部在眼睛店抽取，那么该市每个学生被抽到的机会不相等，样本不具有代表性；如果只抽取20名初中学生，那么样本的容量过小，样本不具有广泛性．‎ ‎（2）×120000＝72000（名）．‎ 答：估计该市120000名初中学生视力不良的人数是72000名．‎ ‎22．（2014江苏省南京市，22，8分）某养殖户每年的养殖成本包括固定成本和可变成本，其中固定成本每年均为4万，可变成本逐年增长．已知该养殖户第1年的可变成本为2.6万元．设可变成本平均每年增长的百分率为x．‎ ‎ （1）用含x的代数式表示第3年的可变成本为_______万元；‎ ‎ （2）如果该养殖户第3年的养殖成本为7.146万元，求可变成本平均每年增长的百分率x．‎ ‎【答案】解：（1）2.6(1＋x)2．‎ ‎（2）根据题意，得4＋2.6(1＋x)2=7.146．‎ 解这个方程，得x1＝0.1，x2＝－2.1（不合题意，舍去）．‎ ‎23．（2014江苏省南京市，23，8分）如图，梯子斜靠在与地面垂直（垂足为O）的墙上，当梯子位于AB位置时，它与地面所成的角∠ABO＝60°；当梯子底端向右滑动1m（即BD＝1m）到达CD位置时，它与地面所成的角∠CDO＝51°18′，求梯子的长．‎ ‎（参考数据：sin51°18′≈0.780，cos51°18′≈0.625，tan51°18′≈1.248）‎ D B C A O ‎【答案】解：设梯子的长为xm．‎ 在Rt△ABO中，cos∠ABO＝，∴OB＝AB·cos∠ABO＝x·cos60°＝x．‎ 在Rt△CDO中，cos∠CDO＝，∴OD＝CD·cos∠CDO＝x·cos51°18′≈0.625x．‎ ‎∵BD＝OD－OB，∴0.625x－x＝1．‎ 解得x＝8．‎ 答：梯子的长约为8m．‎ ‎24．（2014江苏省南京市，24，8分）已知二次函数（m是常数）‎ ‎（1）求证：不论m为何值，该函数的图象与x轴没有公共点；‎ ‎（2）把该函数的图象沿y轴向下平移多少个单位长度后，得到的函数的图象与x轴只有一个公共点？‎ ‎【答案】（1）证法一：因为(－2m)2－4(m2＋3)＝－12＜0．‎ ‎ 所以方程x2－2mx＋m2＋3＝0没有实数根．‎ 所以不论m为何值，该函数的图象与x轴没有公共点．‎ 证法二：因为a＝1＞0，所以该函数的图象开口向上．‎ 又因为＝(x－m)2＋3≥3．‎ 所以该函数的图象在x轴的上方．‎ 所以不论m为何值，该函数的图象与x轴没有公共点．‎ ‎（2）解：＝(x－m)2＋3‎ 把函数y＝(x－m)2＋3的图象沿y轴向下平移3个单位长度后，得到函数y＝(x－m)2的图象，它的顶点坐标是(m，0)，因此这个函数的图象与x轴只有一个公共点．‎ 所以把该函数的图象沿y轴向下平移3个单位长度后，得到的函数的图象与x轴只有一个公共点．‎ ‎25．（2014江苏省南京市，25，9分）从甲地到乙地，先是一段平路，然后是一段上坡路．小明骑车从甲地出发，到达乙地后立即原路返回甲地，途中休息了一段时间．假设小明骑车在平路、上坡、下坡时分别保持匀速前进．已知小明骑车上坡的速度比平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km．设小明出发x ‎ h后，到达离甲地y km的地方，图中的折线OABCDE表示y于x之间的函数关系．‎ ‎（1）小明骑车在平路上的速度为_________km/h；他途中休息了_________h；‎ ‎（2）求线段AB，BC所表示的y与之间的函数关系式；‎ ‎ （3）如果小明两次经过途中某一地点的时间间隔为0.15h，那么该地点离甲地多远？‎ y/m C B ‎4.5‎ ‎6.5‎ O ‎0.3‎ x/h ‎1‎ A D ‎【答案】解：（1）15；0.1．‎ ‎（2）因为小明汽车在平路上的速度为15km/h，所以小明骑车上坡的速度为10km/h，下坡的速度为20 km/h．‎ 由图象可知，小明骑车上坡所用的时间是（h），下坡所用的时间是（h）．所以B、C两点的坐标分别是（0.5，6.5）、（0.6，6.5）．当x＝0.3时，y＝4.5．所以线段AB所表示的y与x之间的函数关系式为y＝4.5＋10(x－0.3)，即y＝10x＋1.5（0.3≤x≤0.5）；当x＝0.5时，y＝6.5，所以线段BC所表示的y与x之间的函数关系式为y＝6.5－20(x－0.5)，即y＝－20x＋16.5（0.5≤x≤06）．‎ ‎（3）小明两次经过图中某一地点的时间间隔为0.15h，根据题意，这个地点只能在坡路上．设小明第一次经过该地点的时间为th，则第二次经过该地点的时间为(t＋0.15)h．‎ 根据题意，得10t＋1.5＝－20(t＋0.15)＋16.5．解得t＝0.4．‎ 所以y＝10×0.4＋1.5＝5.5．‎ 答：该地点离甲地5.5km．‎ ‎26．（2014江苏省南京市，26，8分）如图，在直角三角形ABC中，∠ACB＝90°，AC＝4 cm，BC＝3 cm，圆O为三角形ABC的内切圆。‎ ‎（1）求圆O的半径；‎ ‎（2）点P从点B沿边BA向点A以点1cm/s 的速度匀速运动，以点P为圆心，PB长为半径作图．设点P运动的时间为 t s．若圆P与圆O相切，求t的值．‎ ‎【答案】解：（1）如图①，设⊙O与AB、BC、CA的切点分别是D、E、F，连接 OD、OE、OF．则AD＝AF，BD＝BE，CE＝CF．‎ ‎∵⊙O为△ABC的内切圆．∴OF⊥AC，OE⊥BC．即∠OFC＝∠OEC＝90°．‎ 又∵∠C＝90°，∴四边形CEOF是矩形．‎ 又∵OE＝OF，∴四边形CEOF是正方形．‎ 设⊙O的半径为rcm，则FC＝EC＝OE＝rcm．‎ 在Rt△ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm．‎ ‎∴AB＝＝5cm．‎ ‎∵AD＝AF＝AC－FC＝4－r，BD＝BE＝BC－EC＝3－r，∴4－r＋3－r＝5．‎ 解得r＝1，即⊙O的半径为1cm．‎ ‎ 图① 图②‎ ‎（2）过点P作PG⊥BC，垂足为G．‎ ‎∵∠PGB＝∠C＝90°，∴PG∥AC．∴△PBG∽△ABC．∴．‎ 又∵BP＝t，∴PG＝，BG＝．‎ 若⊙P与⊙O相切，则可分为两种情况：⊙P与⊙O外切，⊙P与⊙D内切．‎ 如图②，当⊙P与⊙O外切时，连接OP，则OP＝1＋t．‎ 过点P作PH⊥OE，垂足为H．‎ ‎∵∠PHE＝∠HEG＝∠PGE＝90°．∴四边形PHEG是矩形．‎ ‎∴HE＝PG，PH＝GE．‎ ‎∴OH＝OE－HE＝1－，PH＝GE＝BC－EC－BG＝3－1－＝2－．‎ 在Rt△OPH中，由勾股定理，得．解得t＝．‎ 如图③，当⊙P与⊙O内切时，连接OP，则OP＝t－1．‎ 过点O作OM⊥PG，垂足为M，‎ ‎∵∠MGE＝∠OEG＝∠OMG＝90°．∴四边形OEGM是矩形．∴MG＝OE，OM＝EG．∴PM＝PG－MG＝，OM＝EG＝BC－EC－BG＝3－1－．‎ 在Rt△OPM中，由勾股定理，得．解得t＝2．‎ ‎ 图③‎ 综上，若⊙P与⊙O相切，t＝s或2s．‎ ‎27．（2014江苏省南京市，27，11分）【问题提出】‎ 学习了三角形全等的判定方法（即“SAS”“ASA”“AAS”“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究。‎ ‎【初步思考】‎ 我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC＝DF，BC＝EF，‎ ‎∠B＝∠E，然后，对∠B进行分类，可以分为“∠B是直角、钝角、锐角”三种情况进行探究。 ‎ B C A E F D 图①‎ ‎【深入探究】‎ 第一种情况：当∠B为直角时，△ABC≌△DEF ‎（1）如图①，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E＝90°，根据_____，可以知道Rt△ABC≌Rt△DEF。‎ 第二种情况：当为钝角时，△ABC≌△DEF ‎（2）如图②，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是钝角，求证：△ABC≌△DEF。‎ 第三种情况：当∠B为锐角时，△ABC和△DEF不一定全等 ‎（3）如图③，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是锐角，请你用尺规在图③中作出△DEF，△DEF和△ABC不全等。（不写作法，保留作图痕迹）。‎ ‎ ‎ ‎ 图② 图③‎ ‎（4）∠B还要满足什么条件，就可以使得△ABC≌△DEF，请直接填写结论：‎ 在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是锐角，若_____，则△ABC≌△DEF．‎ ‎【答案】解：（1）HL；‎ ‎（2）证明：如图，过点C作CG⊥AB交AB的延长线于G，过点F作DH⊥DE交DE的延长线于H，‎ ‎∵∠B＝∠E，且∠B、∠E都是钝角，∴180°﹣∠B=180°﹣∠E，即∠CBG＝∠FEH，‎ 在△CBG和△FEH中，，∴△CBG≌△FEH（AAS），∴CG＝FH，‎ 在Rt△ACG和Rt△DFH中，，∴Rt△ACG≌Rt△DFH（HL），∴∠A＝∠D，‎ 在△ABC和△DEF中，，∴△ABC≌△DEF（AAS）；‎ ‎（3）解：如图，△DEF和△ABC不全等；‎ ‎（4）解：若∠B≥∠A，则△ABC≌△DEF．‎ 故答案为：（1）HL；（4）∠B≥∠A．‎ ‎ ‎ ‎ 第（2）题图 第（3）题图