2008年南通市中考数学试卷(含答案) 13页

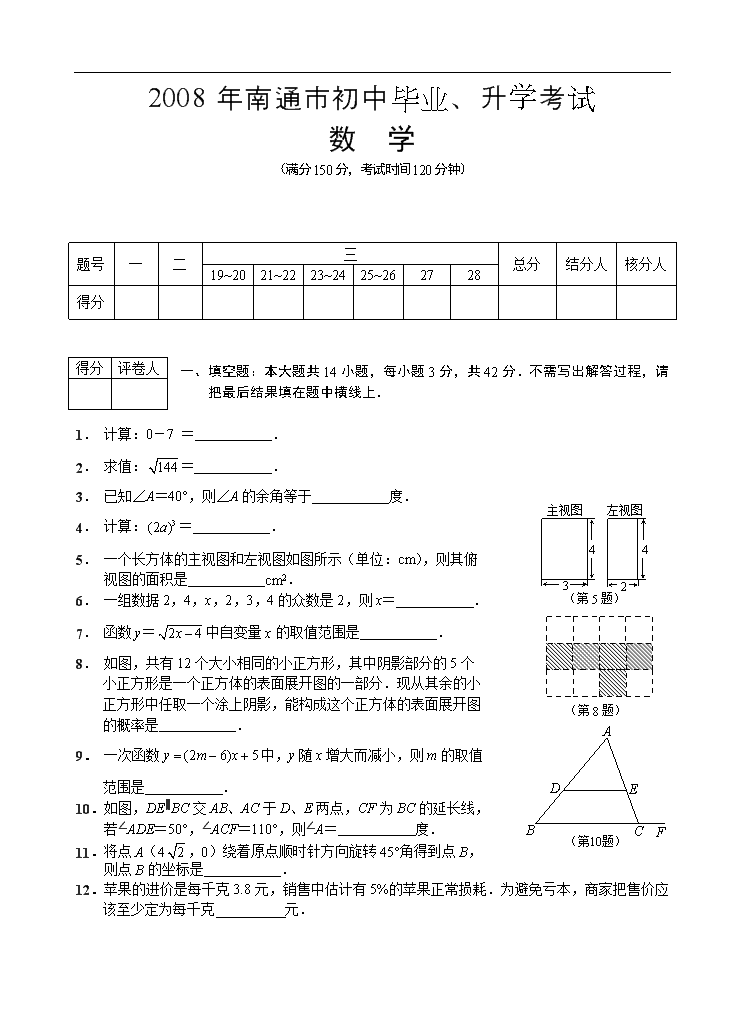
‎2008年南通市初中毕业、升学考试 数 学 ‎（满分150分，考试时间120分钟）‎ 题号 一 二 三 总分 结分人 核分人 ‎19~20‎ ‎21~22‎ ‎23~24‎ ‎25~26‎ ‎27‎ ‎28‎ 得分 得分 评卷人 一、填空题：本大题共14小题，每小题3分，共42分．不需写出解答过程，请 把最后结果填在题中横线上．‎ ‎1． 计算：0－7 ＝ ．‎ ‎2． 求值：＝ ．‎ ‎3‎ ‎2‎ ‎4‎ ‎4‎ 主视图 左视图 ‎（第5题）‎ ‎3． 已知∠A＝40°，则∠A的余角等于 度．‎ ‎4． 计算：＝ ．‎ ‎5． 一个长方体的主视图和左视图如图所示（单位：cm），则其俯 视图的面积是 cm2．‎ ‎6． 一组数据2，4，x，2，3，4的众数是2，则x＝ ．‎ ‎（第8题）‎ ‎7． 函数y＝中自变量x的取值范围是 ．‎ ‎8． 如图，共有12个大小相同的小正方形，其中阴影部分的5个 小正方形是一个正方体的表面展开图的一部分．现从其余的小 正方形中任取一个涂上阴影，能构成这个正方体的表面展开图 A B C F E D ‎（第10题）‎ 的概率是 ．‎ ‎9． 一次函数中，y随x增大而减小，则m的取值 范围是 ．‎ ‎10．如图，DE∥BC交AB、AC于D、E两点，CF为BC的延长线，‎ 若∠ADE＝50°，∠ACF＝110°，则∠A＝ 度．‎ ‎11．将点A（4，0）绕着原点顺时针方向旋转45°角得到点B，‎ 则点B的坐标是 ．‎ ‎12．苹果的进价是每千克3.8元，销售中估计有5%的苹果正常损耗．为避免亏本，商家把售价应该至少定为每千克 元．‎ O A B C D E ‎（第13题）‎ ‎13．已知：如图，△OAD≌△OBC，且∠O＝70°，∠C＝25°，则 ‎∠AEB＝ 度．‎ ‎14．已知三角形三个顶点坐标，求三角形面积通常有以下三种方法：‎ 方法1：直接法．计算三角形一边的长，并求出该边上的高．‎ 方法2：补形法．将三角形面积转化成若干个特殊的四边形和 三角形的面积的和与差．‎ 方法3：分割法．选择一条恰当的直线，将三角形分割成两个便于计算面积的三角形．‎ 现给出三点坐标：A（－1，4），B（2，2），C（4，－1），请你选择一种方法计算△ABC的面积，你的答案是S△ABC ＝ ．‎ 得分 评卷人 二、选择题：本大题共4小题，每小题4分，共16分．在每小题给出的四个选 项中，恰有一项是符合题目要求的，请将正确选项的代号填入题后括号内．‎ ‎15．下列命题正确的是 【 】‎ A．对角线相等且互相平分的四边形是菱形 B．对角线相等且互相垂直的四边形是菱形 C．对角线相等且互相平分的四边形是矩形 D．对角线相等的四边形是等腰梯形 ‎ ‎·‎ P（1，1）‎ ‎1‎ ‎1‎ ‎2‎ ‎2‎ ‎3‎ ‎3‎ ‎－1‎ ‎－1‎ O ‎（第16题）‎ ‎16．用图象法解某二元一次方程组时，在同一直角坐标系中作出相应的两个一次函数的图象（如图所示），则所解的二元一次方程组是 【 】‎ A． B．‎ C． D．‎ ‎17．已知△ABC和△A′B′C′是位似图形．△A′B′C′的面积为‎6cm2，‎ 周长是△ABC的一半．AB＝‎8cm，则AB边上高等于 【 】‎ A．‎3 cm B．‎6 cm ‎ C．‎9cm D．‎‎12cm ‎18．设、是关于的一元二次方程的两个实数根，且，，则 【 】‎ A． B． ‎ 座位号 C． D．‎ 三、解答题：本大题共10小题，共92分．解答时应写出文字说明、证明过程或演算步骤．‎ 得分 评卷人 ‎（19~20题，第19题10分，第20题6分，共16分）‎ ‎19．（1）计算÷； （2）分解因式．‎ ‎20．解分式方程．‎ 得分 评卷人 ‎（21~22题，第21题7分，第22题8分，共15分）‎ ‎21．如图，海上有一灯塔P，在它周围6海里内有暗礁．一艘海轮以18海里/时的速度由西向东方向航行，行至A点处测得灯塔P在它的北偏东60°的方向上，继续向东行驶20分钟后，到达B处又测得灯塔P在它的北偏东45°方向上，如果海轮不改变方向继续前进有没有触礁的危险?‎ A B P 北 东 ‎（第21题）‎ ‎（第22题）‎ A B C M N O ‎·‎ ‎22．已知：如图，M是的中点，过点M的弦MN交AB于点C，设⊙O的半径为‎4cm，MN＝‎4‎cm．‎ ‎（1）求圆心O到弦MN的距离；‎ ‎（2）求∠ACM的度数． ‎ 得分 评卷人 ‎（23~24题，第23题7分，第24题8分，共15分）‎ ‎23．某省为解决农村饮用水问题，省财政部门共投资20亿元对各市的农村饮用水的“改水工程”予以一定比例的补助．2008年，A市在省财政补助的基础上投入600万元用于“改水工程”，计划以后每年以相同的增长率投资，2010年该市计划投资“改水工程”1176万元．‎ ‎（1）求A市投资“改水工程”的年平均增长率；‎ ‎（2）从2008年到2010年，A市三年共投资“改水工程”多少万元？‎ ‎24．已知点A（－2，－c）向右平移8个单位得到点，A与两点均在抛物线上，且这条抛物线与轴的交点的纵坐标为－6，求这条抛物线的顶点坐标．‎ 得分 评卷人 ‎（25~26题，第25题10分，第26题12分，共22分）‎ ‎25．随着我国人民生活水平和质量的提高，百岁寿星日益增多.某市是中国的长寿之乡，截至2008年2月底，该市五个地区的100周岁以上的老人分布如下表（单位：人）：‎ ‎ 地区 性别 一 二 三 四 五 男性 ‎21‎ ‎30‎ ‎38‎ ‎42‎ ‎20‎ 女性 ‎39‎ ‎50‎ ‎73‎ ‎70‎ ‎37‎ ‎50‎ ‎42‎ 地区一 地区二 地区三 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎60‎ ‎50‎ ‎70‎ ‎80‎ 地区四 地区五 ‎39‎ ‎21‎ ‎38‎ ‎73‎ ‎20‎ ‎37‎ 地区 人数 ‎0‎ 男性 女性 ‎（第25题）‎ 根据表格中的数据得到条形图如下：‎ 解答下列问题：‎ ‎（1）请把统计图中地区二和地区四中缺失的数据、图形补充完整； ‎ ‎（2）填空：该市五个地区100周岁以上老人中，男性人数的极差是 人，女性人数的中位数是 人；‎ ‎（3）预计2015年该市100周岁以上的老人将比2008年2月的统计数增加100人，请你估算2015年地区一增加100周岁以上的男性老人多少人？‎ ‎26．如图，四边形ABCD中，AD＝CD，∠DAB＝∠ACB＝90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．‎ ‎（1）求证：AB·AF＝CB·CD；‎ ‎（2）已知AB＝‎15 cm，BC＝‎9 cm，P是射线DE上的动点．设DP＝x cm（），四边形BCDP的面积为y cm2．‎ ‎①求y关于x的函数关系式；‎ A B C D E F P ‎·‎ ‎（第26题）‎ ‎②当x为何值时，△PBC的周长最小，并求出此时y的值．‎ 得分 评卷人 ‎（第27题10分）‎ ‎27．在一次数学探究性学习活动中，某学习小组要制作一个圆锥体模型，操作规则是：在一块边长为‎16cm的正方形纸片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面．他们首先设计了如图所示的方案一，发现这种方案不可行，于是他们调整了扇形和圆的半径，设计了如图所示的方案二．（两个方案的图中，圆与正方形相邻两边及扇形的弧均相切．方案一中扇形的弧与正方形的两边相切）‎ ‎（1）请说明方案一不可行的理由；‎ ‎（2）判断方案二是否可行？若可行，请确定圆锥的母线长及其底面圆半径；若不可行，请说明理由‎（第27题）‎ 方案一 A B C D 方案二 A B C D ‎·‎ O1‎ ‎·‎ O2‎ ．‎ 得分 评卷人 ‎（第28题14分）‎ ‎28．已知双曲线与直线相交于A、B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线上的动点．过点B作BD∥y轴交x轴于点D．过N（0，－n）作NC∥x轴交双曲线于点E，交BD于点C．‎ ‎（1）若点D坐标是（－8，0），求A、B两点坐标及k的值．‎ ‎（2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式．‎ ‎（第28题）‎ y O ‎·‎ A D x B C E N M ‎·‎ ‎（3）设直线AM、BM分别与y轴相交于P、Q两点，且MA=pMP，MB=qMQ，求p－q的值．‎ ‎ ‎ ‎2008年南通市初中毕业、升学考试 数学试题参考答案与评分标准 说明：本评分标准每题只提供一种解法，如有其他解法，请参照本标准的精神给分．‎ 一、填空题：本大题共14小题，每小题3分，共42分．‎ ‎1．－7 2．12 3．50 4． 5．6 6．2 7．x≥2 8．‎ ‎9．m＜3 10．60 11．（4，－4） 12．4 13． 120 14．‎ 二、选择题：本大题共4小题，每小题4分，共16分．‎ ‎15．C 16．D 17．B 18．C 三、解答题：本大题共10小题，共92分．‎ ‎19．（1）解：原式＝÷ ……………………………………………………4分 ‎＝8÷4＝2．………………………………………………………………5分 ‎（2）解：原式＝ …………………………………………………7分 ‎＝ ………………………………………………………………9分 ‎＝．………………………………………………………………10分 ‎20．解：方程两边同乘以x(x+3)(x－1)，得5（x－1）－（x+3）＝0．…………………………2分 解这个方程，得．……………………………………………………………………4分 检验：把代入最简公分母，得2×5×1＝10≠0．‎ ‎∴原方程的解是．……………………………………………………………………6分 ‎21．解： 过P作PC⊥AB于C点，根据题意，得 A B P 北 东 C AB＝18×＝6，∠PAB＝90°－60°＝30°，‎ ‎∠PBC＝90°－45°＝45°，∠PCB＝90°，‎ ‎∴PC＝BC． ……………………………2分 在Rt△PAC中，‎ ‎（第21题）‎ tan30°＝， …………4分 即，解得PC＝． 6分 ‎∵＞6，∴海轮不改变方向继续前进无触礁危险．……………………………7分 ‎ ‎22．解：（1）连结OM．∵点M是的中点，∴OM⊥AB． …………………………………1分 过点O作OD⊥MN于点D，‎ ‎（第22题）‎ A B C M N O ‎·‎ D 由垂径定理，得． ………………………3分 ‎ 在Rt△ODM中，OM＝4，，∴OD＝．‎ 故圆心O到弦MN的距离为‎2 cm． …………………………5分 ‎（2）cos∠OMD＝，…………………………………6分 ‎∴∠OMD＝30°，∴∠ACM＝60°．……………………………8分 ‎23．解：（1）设A市投资“改水工程”年平均增长率是x，则 ‎．…………………………………………………………………………2分 解之，得或（不合题意，舍去）．………………………………………4分 所以，A市投资“改水工程”年平均增长率为40%． …………………………………5分 ‎（2）600＋600×1.4＋1176＝2616（万元）．‎ A市三年共投资“改水工程”2616万元． ………………………………………………7分 ‎24．解：由抛物线与轴交点的纵坐标为－6，得＝－6．……………………1分 ‎∴A（－2，6），点A向右平移8个单位得到点（6，6）． …………………………3分 ‎∵A与两点均在抛物线上，‎ ‎∴ 解这个方程组，得 ……………………………………6分 故抛物线的解析式是．‎ ‎∴抛物线的顶点坐标为（2，－10）． ……………………………………………………8分 ‎50‎ ‎42‎ 地区一 地区二 地区三 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎60‎ ‎50‎ ‎70‎ ‎80‎ 地区四 地区五 ‎39‎ ‎21‎ ‎38‎ ‎73‎ ‎20‎ ‎37‎ 地区 人数 ‎0‎ 男性 女性 ‎（第25题）‎ ‎30‎ ‎70‎ ‎25．解：（1）‎ ‎……………………4分 ‎（2）22，50； ……………………………………………………………………………………8分 ‎（3）[21÷（21＋30＋38＋42＋20＋39＋50＋73＋70＋37）]×100＝5，‎ 预计地区一增加100周岁以上男性老人5人. …………………………………………10分 ‎26．（1）证明：∵，，∴DE垂直平分AC，‎ ‎∴,∠DFA＝∠DFC ＝90°，∠DAF＝∠DCF．……………………………1分 ‎∵∠DAB＝∠DAF＋∠CAB＝90°，∠CAB＋∠B＝90°，∴∠DCF＝∠DAF＝∠B．2分 在Rt△DCF和Rt△ABC中，∠DFC＝∠ACB＝90°，∠DCF＝∠B，‎ ‎∴△DCF∽△ABC． ……………………………………………………………………3分 ‎∴，即．∴AB·AF＝CB·CD． ………………………………4分 ‎（2）解：①∵AB＝15，BC＝9，∠ACB＝90°，‎ ‎ ∴，∴．……………………………5分 ‎∴（）． ………………………………………………7分 ‎②∵BC＝9（定值），∴△PBC的周长最小，就是PB＋PC最小．由（1）知，点C关于直线DE的对称点是点A，∴PB+PC＝PB+PA，故只要求PB+PA最小．‎ 显然当P、A、B三点共线时PB+PA最小．此时DP＝DE，PB+PA＝AB． ………8分 由（1），，，得△DAF∽△ABC．‎ EF∥BC，得，EF=．‎ ‎∴AF∶BC＝AD∶AB，即6∶9＝AD∶15．∴AD＝10．……………………………10分 Rt△ADF中，AD＝10，AF＝6，∴DF＝8．‎ ‎∴． ………………………………………………………11分 ‎∴当时，△PBC的周长最小，此时．………………………………12分 ‎27．解：（1）理由如下：‎ ‎∵扇形的弧长＝16×＝8π，圆锥底面周长＝2πr，∴圆的半径为‎4cm．………2分 由于所给正方形纸片的对角线长为 cm，而制作这样的圆锥实际需要正方形纸片的对角线长为cm，，‎ ‎∴方案一不可行． ………………………………………………………………………5分 ‎ （2）方案二可行．求解过程如下：‎ 设圆锥底面圆的半径为rcm，圆锥的母线长为Rcm，则 ‎， ① ． ② …………………………7分 由①②，可得，． ………………9分 故所求圆锥的母线长为cm，底面圆的半径为cm． ………10分 ‎28．解：（1）∵D（－8，0），∴B点的横坐标为－8，代入中，得y=－2．‎ ‎∴B点坐标为（－8，－2）．而A、B两点关于原点对称，∴A（8，2）．‎ 从而．……………………………………………………………………3分 ‎（2）∵N（0，－n），B是CD的中点，A、B、M、E四点均在双曲线上，‎ ‎∴，B（－‎2m，－），C（－‎2m，－n），E（－m，－n）． ……………4分 ‎ S矩形DCNO，S△DBO=，S△OEN =， ………………7分 ‎ ∴S四边形OBCE= S矩形DCNO－S△DBO－ S△OEN=k．∴． …………………………8分 由直线及双曲线，得A（4，1），B（－4，－1），‎ ‎∴C（－4，－2），M（2，2）．………………………………………………………9分 设直线CM的解析式是，由C、M两点在这条直线上，得 ‎ 解得．‎ ‎∴直线CM的解析式是．………………………………………………11分 ‎（3）如图，分别作AA1⊥x轴，MM1⊥x轴，垂足分别为A1、M1．‎ 设A点的横坐标为a，则B点的横坐标为－a．于是 ‎（第28题）‎ y O ‎·‎ A x B M ‎·‎ Q A1‎ P M1‎ ‎．‎ 同理，……………………………13分 ‎∴．……………………14分