2019年中考数学模拟试卷 6页

‎2019年中考数学模拟试卷-苏科版 一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号涂在答题卡相应位置上）‎ ‎1．-2.5的倒数是（ ）‎ A. B. C. D. ‎ ‎2. “黑发不知勤学早，白首方悔读书迟。”自2018年扬州市教育局正式发布《关于大力倡导实施“五个一百工程”的指导意见》以来，全市中小学生累计阅读了中外名著约4250000本，4250000用科学记数法并精确到十万位表示为 （ ） ‎ A. B. C. D. ‎ ‎3.“横看成岭侧成峰，远近高低各不同。”表达的是从不同角度看同一个物体，可能看到不同的结果。下图是某几何体的三视图，则这个几何体是( )‎ A.圆柱 B.正方体 C.球 D.圆锥 ‎4. 实数a、b在数轴上的位置如图所示，则化简代数式–a的结果是（ ）‎ A．‎2a+b B．‎2a C．a D．b ‎5. 如图，将边长为2个单位的等边△ABC沿边BC向右平移1个单位得到△DEF，则四边形ABFD的周长为（　　）‎ A．6 B． ‎8 ‎ 　　C．10 D．12‎ ‎6. “又是烟花三月初，暖风醺醉瘦西湖。”为了解游客对景区的满意程度，瘦西湖景区管理部门随机调查了1000名游客，其中有800人对景区表示满意．对于这次调查以下说法正确的是（ ）‎ A．若随机访问一位游客，则该游客表示满意的概率约为0.8‎ B．到景区的所有游客中，只有800名游客表示满意 C．若随机访问10位游客，则一定有8位游客表示满意 D．本次调查采用的方式是普查 ‎7. 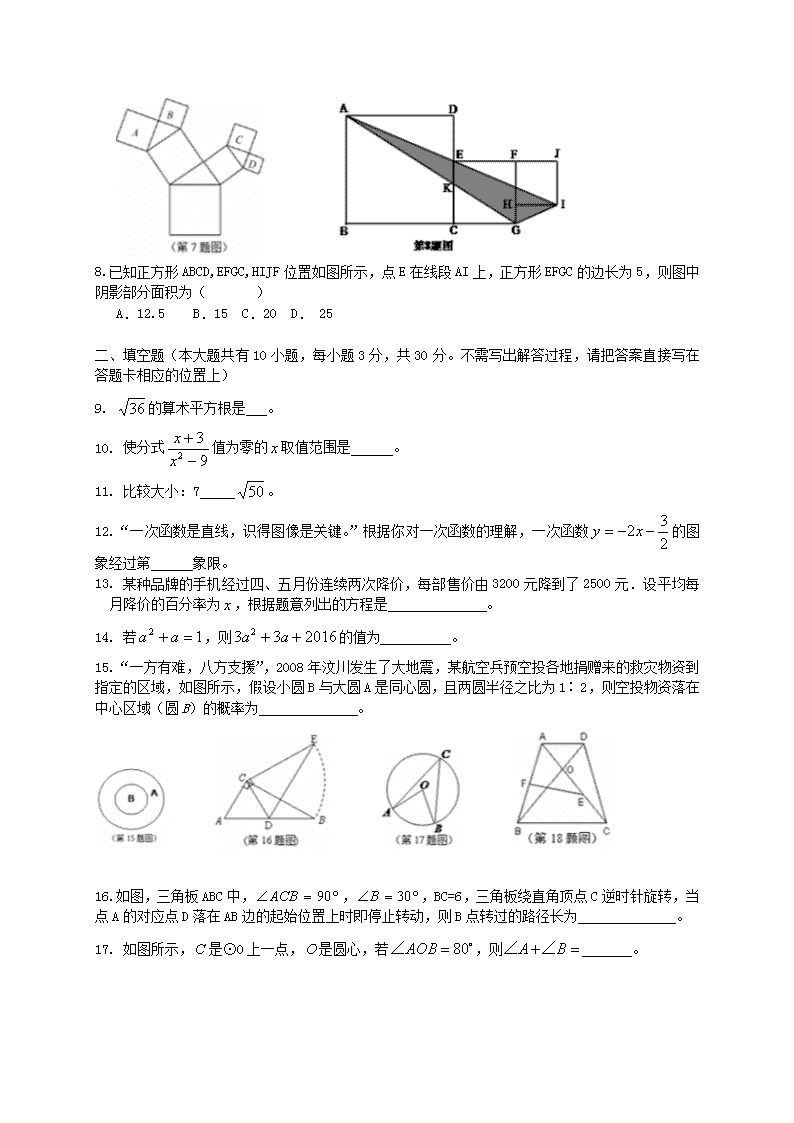如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为‎10cm，正方形A的边长为‎6cm、B的边长为‎5cm、C的边长为‎5cm，则正方形D的边长为（ ）‎ A． cm B．‎4cm C． cm D． ‎‎3cm ‎8. 已知正方形ABCD,EFGC,HIJF位置如图所示，点E在线段AI上，正方形EFGC的边长为5，则图中阴影部分面积为（ ）‎ A．12.5 B．‎15 C．20 D． 25‎ 二、填空题（本大题共有10小题，每小题3分，共30分。不需写出解答过程，请把答案直接写在答题卡相应的位置上）‎ ‎9. 的算术平方根是 。‎ ‎10. 使分式值为零的取值范围是 。‎ ‎11. 比较大小：7 。‎ ‎12.“一次函数是直线，识得图像是关键。”根据你对一次函数的理解，一次函数的图象经过第 象限。‎ ‎13. 某种品牌的手机经过四、五月份连续两次降价，每部售价由3200元降到了2500元．设平均每月降价的百分率为，根据题意列出的方程是 。‎ ‎14. 若，则的值为 。‎ ‎15. “一方有难，八方支援”，2008年汶川发生了大地震，某航空兵预空投各地捐赠来的救灾物资到指定的区域，如图所示，假设小圆B与大圆A是同心圆，且两圆半径之比为1∶2，则空投物资落在中心区域（圆B）的概率为 。‎ ‎16. 如图，三角板ABC中，，，BC=6，三角板绕直角顶点C逆时针旋转，当点A的对应点D落在AB边的起始位置上时即停止转动，则B点转过的路径长为 。‎ ‎17. 如图所示，是⊙O上一点，是圆心，若，则 。‎ ‎18. 如图，在梯形ABCD中，AD∥BC，AB=DC=‎8cm，AC、BD相交于O点，且∠AOD＝60°，设E、F分别为CO、AB的中点，则EF＝ 。‎ 三、解答题（本大题共有10小题，共96分。请在答题卡指定区域内答题，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19.计算（本题8分）：‎ ‎（1）； ‎ ‎ （2）解方程：‎ ‎20. （本题8分）“天下三分明月夜，二分无赖是扬州。”扬州是一座美丽的旅游城市，吸引了很多的外地游客，某旅行社对5月份该社接待的外地游客来扬州旅游的首选景点作了一次抽样调查，调查结果如下：‎ ‎（1）此次共调查了多少人？‎ ‎（2）请将以上图表补充完整．‎ ‎（3）该旅行社预计6月份接待外地来扬的游客2500人，请你估计首选去茱萸湾的人数约有多少人。‎ ‎21. （本题8分） 小聪与小慧共同发明了一种“字母棋”，进行比胜负的游戏。她们利用三个字母做成棋子，其中A棋、B棋、C棋各1枚。“字母棋”的游戏规则为：‎ ‎ ①游戏时两人各摸一枚棋进行比赛称一轮比赛；‎ ‎ ②A棋胜B棋、B棋胜C棋、C棋胜A棋；‎ ‎ ③相同棋子不分胜负。‎ 已知小聪与小慧约定：第一轮由小慧先摸，小聪后摸，先摸者摸出的棋不放回；第二轮由小聪先摸，小玲后摸，先摸者摸出的棋需放回，问两轮比赛下来，小聪与小慧获胜的机会是否均等?为什么？‎ ‎22. （本题8分）猪八戒是《西游记》中的人物，这里有一首关于他吃仙果的诗，请你解决诗中提出的数学问题。‎ 八戒吃仙果 三种仙果红紫黄，八戒共吃十一双；‎ 黄果占紫三分一，紫果正是红二倍；‎ 三种仙果各多少? 看谁算得快又对？（注：“三分一”指）‎ ‎23. （本题10分）如图，折叠直角三角形纸片，使点A与点D重合，为直角，AC=BC,AB=‎4cm,折痕为EF,D为BC中点，求阴影部分的面积。‎ ‎24. （本题10分）我们已经知道特殊角（）的三角函数值，如 ，等，如果给你的不是一个特殊角，比如角，你又怎样能知道它的三角函数值呢？为了解决这个问题，我们不妨运用“构造法”，先构造一个特殊的三角形，如图：△ABC中，AB=AC,点D在AC上，且BD=BC=AD,（1）求△ABC各内角的度数。（2）证明△ABC∽△BDC。（3）结合（1）、（2）的结论，求的值（计算结果精确到0.1）。‎ ‎25.（本题10分）如图，直线:与轴、轴分别交于A、B两点，直线：‎ 与轴、轴分别交于C、D两点，点P（1,m）为、的交点，（1）试求的值（2）已知上有一点Q,且的面积等于的面积，求点Q的坐标。‎ ‎26. （本题10分）如图，在矩形ABCD中，AB=3，BC=5，把矩形沿着CE折叠，使B点落在矩形外面，如果已知BE=2.5，求AG,DH的长。 ‎ ‎27. （本题12分）如图，抛物线经过点A（-1，0），B(3，0)和正半轴上点C，线段AC⊥BC，‎ ‎（1）求点C的坐标及抛物线的解析式.‎ ‎（2）△ABC绕点C旋转一周过程中线段AB所扫过的图形的面积.‎ ‎（3）若△ABC绕点C旋转后点A恰好落在x 轴上点D处，得△DCE，直线DE与抛物线交于点F。问此时抛物线的对称轴上是否存在点P使△PDF是等腰三角形.若存在，求点P坐标；若不存在，说明理由.‎ ‎28. （本题12分） “理财有风险,投资需谨慎”，在经济学中，人们常常要计算投资的“平均收益”和“风险”，这可以用我们已经学过的“平均数”，“方差”等相关数学知识来理解。‎ ‎（1）已知一组数据20,20,20,25,25,,这组数据的平均数为__________，方差为_________.‎ ‎（2）计算_______，___________‎ ‎（3）请你根据做以上两小题的经验解决以下问题.‎ ‎ 张先生打算投资购买A、B两种债券，据了解，这两种债券可能的收益情况如下表.‎ 类型 收益（元）‎ 获得收益的概率 债券A ‎－30‎ ‎30‎ 债券B ‎－20‎ ‎40‎ ‎①如果张先生只打算购买A、B中的一种债券，请你通过计算说明购买那种债券较好？（注：收益越大越好，风险越小越好）.‎ ‎②如果张先生打算组合购买两种债券，请帮他设计最佳的组合比例。‎ ‎（第28题图）‎