中考数学最新最密试题及答案6 13页

‎ 2014年中考数学最新最密试题 ‎（本试卷满分120分，考试时间120分钟）‎ 第1卷 (选择题 共36分)‎ 一、选择题(本题共12个小题，在每个小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来。每小题选对得3分，选错、不选或选出的答案超出一个均记0分）‎ ‎3．（2013山东潍坊3分）某班6名同学参加体能测试的成绩如下(单位：分)：75，95，75，75，80，80．关于这组数据的表述错误的是【 】．‎ A．众数是75 B．中位数是75 C．平均数是80 D．极差是20‎ ‎【答案】B。‎ ‎【考点】众数，中位数，平均数，极差。‎ ‎【分析】根据众数，中位数，平均数，极差的概念逐项分析：‎ A．75出现的次数最多，所以众数是75，A正确；‎ B．把数据按大小排列为：75，75，75，80，80，95，中间两个数为75，80，所以中位数是77.5， B错误；‎ C．平均数（75＋95＋75＋75＋80＋80）÷6=80，C正确；‎ D．极差是95－75=20，D正确。‎ 故选B。‎ ‎4．（2013山东潍坊3分）右图空心圆柱体的主视图的画法正确的是【 】．‎ A. B. C. D. ‎ ‎【答案】C。‎ ‎【考点】简单组合体的三视图。‎ ‎【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中：‎ 从正面观察物体可以发现：它的主视图应为矩形，又因为该几何体为空心圆柱体，故中间的两条棱在主视图中应为虚线。故选C。‎ ‎5．（2013山东潍坊3分）不等式组的解等于【 】．‎ A． 11 C． x<2 D． x<1或x>2‎ ‎【答案】A。‎ ‎【考点】解一元一次不等式组。‎ ‎【分析】解一元一次不等式组，先求出不等式组中每一个不等式的解集，再利用口诀求出这些解集的公共部分：同大取大，同小取小，大小小大中间找，大大小小解不了（无解）。因此，‎ 解2x＋3＞5得，x＞1；解3x－2＜4得，x＜2，∴此不等式组的解集为：1＜x＜2。故选A。‎ ‎6．（2013山东潍坊3分）许多人由于粗心，经常造成水龙头“滴水”或“流水”不断．根据测定，一般情况下一个水龙头“滴水”1个小时可以流掉3．5千克水．若1年按365天计算，这个水龙头1年可以流掉【 】千克水．(用科学计数法表示，保留3个有效数字)‎ ‎ A．3.1×104 B．0.31×105 C．3.06×104 D．3.07×104‎ ‎【答案】D。‎ ‎【考点】科学记数法。‎ ‎【分析】根据科学记数法的定义，科学记数法的表示形式为a×10n，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值。在确定n的值时，看该数是大于或等于1还是小于1。当该数大于或等于1时，n为它的整数位数减1；当该数小于1时，－n为它第一个有效数字前0的个数（含小数点前的1个0）。‎ 有效数字的计算方法是：从左边第一个不是0的数字起，后面所有的数字都是有效数字。‎ 因此3.5×24×365=30660=3.066×104≈3.07×104。故选D。 ‎ ‎7．（2013山东潍坊3分）已知两圆半径r1、r2分别是方程x2—7x+10=0的两根，两圆的圆心距为7，则两圆的位置关系是【 】．‎ ‎ A．相交 B．内切 C．外切 D．外离 ‎【答案】C。‎ ‎【考点】圆与圆的位置关系，因式分解法解一元二次方程。‎ ‎【分析】首先解方程x2—7x+10=0，求得两圆半径r1、r2的值，又由两圆的圆心距为7，根据两圆位置关系与圆心距d，两圆半径r1、r2的数量关系间的联系即可得出两圆位置关系：‎ ‎∵，∴两圆半径r1、r2分别是2，5。‎ ‎∵2＋5=7，两圆的圆心距为7，∴两圆的位置关系是外切。故选C。‎ ‎8．（2013山东潍坊3分）已知矩形ABCD中，AB=1，在BC上取一点E，沿AE将ΔABE向上折叠，使B点落在AD上的F点，若四边形EFDC与矩形ABCD相似，则AD=【 】．‎ ‎ A． B． C . D．2‎ ‎【答案】B。‎ ‎【考点】翻折变换（折叠问题），折叠的性质，矩形的性质，正方形的判定和性质，相似多边形的性质。‎ ‎【分析】∵矩形ABCD中，AF由AB折叠而得，∴ABEF是正方形。又∵AB=1，∴AF= AB=EF=1。‎ 设AD=x，则FD=x－1。‎ ‎∵四边形EFDC与矩形ABCD相似，∴，即。‎ 解得，（负值舍去）。‎ 经检验是原方程的解。故选B。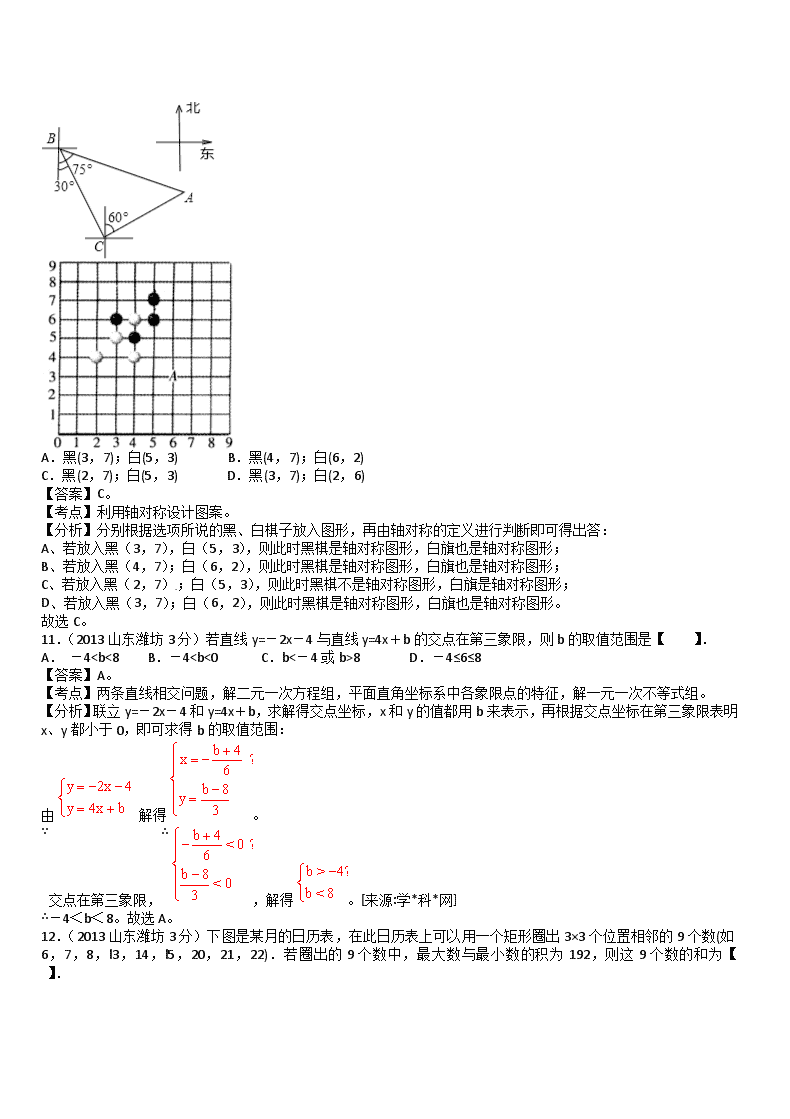‎ ‎9．（2013山东潍坊3分）轮船从B处以每小时50海里的速度沿南偏东300方向匀速航行，在B处观测灯塔A位于南偏东750方向上，轮船航行半小时到达C处，在C处观测灯塔A位于北偏东600方向上，则C处与灯塔A的距离是【 】海里．‎ A．黑(3，7)；白(5，3) B．黑(4，7)；白(6，2)‎ C．黑(2，7)；白(5，3) D．黑(3，7)；白(2，6)‎ ‎【答案】C。‎ ‎【考点】利用轴对称设计图案。‎ ‎【分析】分别根据选项所说的黑、白棋子放入图形，再由轴对称的定义进行判断即可得出答：‎ A、若放入黑（3，7），白（5，3），则此时黑棋是轴对称图形，白旗也是轴对称图形；‎ B、若放入黑（4，7）；白（6，2），则此时黑棋是轴对称图形，白旗也是轴对称图形；‎ C、若放入黑（2，7）；白（5，3），则此时黑棋不是轴对称图形，白旗是轴对称图形；‎ D、若放入黑（3，7）；白（6，2），则此时黑棋是轴对称图形，白旗也是轴对称图形。‎ 故选C。‎ ‎11．（2013山东潍坊3分）若直线y=－2x－4与直线y=4x＋b的交点在第三象限，则b的取值范围是【 】．‎ A． －48 D．－4≤6≤8‎ ‎【答案】A。‎ ‎【考点】两条直线相交问题，解二元一次方程组，平面直角坐标系中各象限点的特征，解一元一次不等式组。 ‎ ‎【分析】联立y=－2x－4和y=4x＋b，求解得交点坐标，x和y的值都用b来表示，再根据交点坐标在第三象限表明x、y都小于0，即可求得b的取值范围：‎ 由解得。‎ ‎∵交点在第三象限，∴，解得。[来源:学*科*网]‎ ‎∴－4＜b＜8。故选A。‎ ‎12．（2013山东潍坊3分）下图是某月的日历表，在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6，7，8，l3，14，l5，20，21，22)．若圈出的9个数中，最大数与最小数的积为192，则这9个数的和为【 】．‎ A．32 B．126 C．135 D．144‎ ‎【答案】D。‎ ‎【考点】分类归纳（数字的变化类），一元二次方程的应用。‎ ‎【分析】由日历表可知，圈出的9个数中，最大数与最小数的差总为16，又已知最大数与最小数的积为192，所以设最大数为x，则最小数为x－16。‎ ‎ ∴x（x－16）=192，解得x=24或x=－8（负数舍去）。‎ ‎ ∴最大数为24，最小数为8。‎ ‎ ∴圈出的9个数为8，9，10，15，16，17，22，23，24。和为144。故选D。‎ 第Ⅱ卷 (非选择题 共84分)‎ 二、填空题(本大题共5个小题，共15分，只要求填写最后结果，每小题填对得3分）‎ ‎13．（2013山东潍坊3分）分解因式：x3—4x2—12x= ▲ .‎ ‎【答案】x（x＋2）（x－6）。‎ ‎【考点】提公因式法和十字相乘法因式分解。‎ ‎【分析】因式分解常用方法有① 提取公因式法； ② 应用公式法； ③ 配方法； ④十字相乘法等。由题目特点，先提取公因式x，然后利用十字相乘法求解即可求得答案：‎ x3－4x2－12x=x（x2－4x－12）=x（x＋2）（x－6）。‎ ‎14．（2013山东潍坊3分）点P在反比例函数 (k≠0)的图象上，点Q(2，4)与点P关于y轴对称，则反比例函数的解析式为 ▲ .‎ ‎【答案】。‎ ‎【考点】关于y轴对称的点的坐标特征，曲线上点的坐标与方程的关系。‎ ‎【分析】根据轴对称的定义，利用点Q（2，4），求出P点坐标，将P点坐标代入解析式，即可求出反比例函数解析式：‎ ‎∵点Q（2，4）和点P关于y轴对称，关于y轴对称的点的坐标特征是纵坐标不变，横坐标互为相反数 ‎∴P点坐标为（－2，4）。‎ 将（－2，4）解析式得，k=xy=－2×4=－8。‎ ‎∴函数解析式为。‎ ‎15．（2013山东潍坊3分）方程的根是 ▲ .‎ ‎【答案】x=30。‎ ‎【考点】解分式方程。‎ ‎【分析】方程的两边都乘以x（x+3）得出66x-60（x+3）=0，求出这个方程的解，再代入代入x（x+3）进行检验即可：‎ ‎。‎ 检验：把x=30代入x（x+3）=990≠0，‎ ‎∴原方程的解为x=30。[来源:Zxxk.Com]‎ ‎16．（2013山东潍坊3分）如图所示，AB=DB，∠ABD=∠CBE，请你添加一个适当的条件 ▲ ， 使ΔABC≌ΔDBE． (只需添加一个即可)‎ ‎【答案】∠BDE=∠BAC（答案不唯一）。‎ ‎【考点】全等三角形的判定，开放型。‎ ‎【分析】根据∠ABD=∠CBE可以证明得到∠ABC=∠DBE，然后根据利用的证明方法，“ASA”“SAS”“AAS”分别写出第三个条件即可：‎ ‎∵∠ABD=∠CBE，∴∠ABD+∠ABE=∠CBE+∠ABE，即∠ABC=∠DBE。‎ ‎∵AB=DB，‎ ‎∴①用“ASA”，需添加∠BDE=∠BAC；‎ ‎②用“SAS”，需添加BE=BC；‎ ‎③用“AAS”，需添加∠ACB=∠DEB。‎ ‎17．（2013山东潍坊3分）下图中每一个小方格的面积为l，则可根据面积计算得到如下算式：1+3+5+7+…+(2n－1)= ▲ .(用n表示，n是正整数)‎ ‎【答案】n2。‎ ‎【考点】分类归纳（图形的变化类）。‎ ‎【分析】由图可知：‎ ‎ 当k=1时，面积为12=1；当k=2时，面积为1＋3=22=4；当k=3时，面积为1＋3＋5=32=9；‎ 当k=4时，面积为1＋3＋5＋7=42=16；······‎ 当k=n时，面积为1＋3＋5＋···＋（2n－1）=n2。‎ 三、解答题(本大题共7个小题，共69分。解答要写必要的文字说明、证明过程或演算步骤.）‎ ‎18．（2013山东潍坊9分）如图，三角形ABC的两个顶点B、C在圆上，顶点A在圆外，AB、AC分别交圆于E、D两点，连结EC、BD．‎ ‎ (1)求证：ΔABD∽ΔACE；‎ ‎ (2)若ΔBEC与ΔBDC的面积相等，试判定三角形ABC的形状．‎ ‎【答案】（1）证明：∵弧ED所对的圆周角相等，∴∠EBD=∠ECD，‎ 又∵∠A=∠A，∴△ABD∽△ACE。 （2）解：△ABC为等腰三角形。理由如下：‎ ‎∵S△BEC=S△BCD，S△ACE=S△ABC－S△BEC，S△ABD=S△ABC－S△BCD，‎ ‎∴S△ACE=S△ABD。‎ 又由（1）知△ABD∽△ACE，∴对应边之比等于1。‎ ‎∴AB=AC，即△ABC为等腰三角形。‎ ‎【考点】圆周角定理，相似三角形的判定和性质，等腰三角形的判定。‎ ‎【分析】（1）利用圆周角定理得出∠EBD=∠ECD，再利用∠A=∠A，得出△ABD∽△ACE。‎ ‎（2）根据△BEC与△BDC的面积相等，得出S△ACE=S△ABD，进而求出AB=AC，得出答案。‎ ‎19．（2013山东潍坊9分）为了援助失学儿童，初三学生李明从2013年1月份开始，每月一次将相等数额的零用钱存入已有部分存款的储蓄盒内，准备每6个月一次将储蓄盒内存款一并汇出(汇款手续费不计)．已知2月份存款后清点储蓄盒内有存款80元，5月份存款后清点储蓄盒内有存款125元．‎ ‎ (1)在李明2013年1月份存款前，储蓄盒内已有存款多少元?‎ ‎ (2)为了实现到2015年6月份存款后存款总数超过1000元的目标，李明计划从2013年1月份开始，每月存款都比2013年每月存款多t元(t为整数)，求t的最小值．‎ ‎20．（2013山东潍坊10分）校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道上确定点D，使CD与垂直，测得CD的长等于21米，在上点D的同侧取点A、B，使∠CAD=300，∠CBD=600．‎ ‎ (1)求AB的长(精确到0.1米，参考数据：)；‎ ‎ (2)已知本路段对校车限速为40千米／小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速?说明理由． ‎ ‎【答案】解：（1）由題意得，[来源:学科网ZXXK]‎ 在Rt△ADC中，，‎ 在Rt△BDC中，，‎ ‎∴AB=AD－BD= （米）。‎ ‎（2）∵汽车从A到B用时2秒，∴速度为24.2÷2=12.1（米/秒），‎ ‎∵12.1米/秒=43.56千米/小时，∴该车速度为43.56千米/小时。‎ ‎∵43.56千米/小时大于40千米/小时，∴此校车在AB路段超速。‎ ‎【考点】解直角三角形的应用。[来源:Zxxk.Com]‎ ‎【分析】（1）分别在Rt△ADC与Rt△BDC中，利用正切函数，即可求得AD与BD的长，从而求得AB的长。[来源:学.科.网]‎ ‎（2）由从A到B用时2秒，即可求得这辆校车的速度，比较与40千米/小时的大小，即可确定这辆校车是否超速。‎ ‎21．（2013山东潍坊10分）田忌赛马的故事为我们所熟知．小亮与小齐学习概率初步知识后设计了如下游戏：小亮手中有方块l0、8、6三张扑克牌，小齐手中有方块9、7、5三张扑克牌．每人从各自手中取一张牌进行比较，数字大的为本“局”获胜，每次取的牌不能放回．‎ ‎(1)若每人随机取手中的一张牌进行比赛，求小齐本“局”获胜的概率；‎ ‎(2)若比赛采用三局两胜制，即胜2局或3局者为本次比赛获胜者．当小亮的三张牌出牌顺序为先出6，再出8，最后出l0时，小齐随机出牌应对，求小齐本次比赛获胜的概率．‎ ‎【答案】解：（1）画树状图得：‎ ‎ ∵每人随机取一张牌共有9种情况，小齐获胜的情况有（8，9），（6，9），（6，7）共3种，‎ ‎∴小齐获胜的概率为。‎ ‎（2）根据题意，小明出牌顺序为6、8、10时，小齐随机出牌的情况有6种情况：（9，7，5），（9，5，7），（7，9，5），（7，5，9），（5，9，7），（5，7，9）， ‎ ‎∵小齐获胜的情况只有（7，9，5）一种，‎ ‎∴小齐获胜的概率为。‎ ‎【考点】列表法或树状图法，概率。‎ ‎【分析】（1）首先根据题意画出树状图或列表，然后由图表求得所有等可能的结果与小齐本“局”获胜的情况，利用概率公式即可求得答案。‎ ‎（2）根据题意，小明出牌顺序为6、8、10时，小齐随机出牌的情况有：（9，7，5），（9，5，7），（7，9，5），（7，5，9），（5，9，7），（5，7，9），又由小齐获胜的情况只有（7，9，5）一种，利用概率公式即可求得答案。‎ ‎22．（2013山东潍坊10分）如图，已知平行四边形ABCD，过A作AM⊥BC于M，交BD于E，过C作CN⊥AD于N，交BD于F，连结AF、CE．‎ ‎ (1)求证：四边形AECF为平行四边形；‎ ‎ (2)当AECF为菱形，M点为BC的中点时，求AB：AE的值．‎ ‎【答案】（1）证明∵四边形ABCD是平行四边形（已知），‎ ‎∴BC∥AD（平行四边形的对边相互平行）。‎ 又∵AM丄BC（已知），∴AM⊥AD。‎ ‎∵CN丄AD（已知），∴AM∥CN。∴AE∥CF。‎ 又由平行得∠ADE=∠CBD，又AD=BC（平行四边形的对边相等）。‎ 在△ADE和△CBF中， ∠DAE=∠BCF=90 ，AD=CB，∠ADE=∠FBC，‎ ‎∴△ADE≌△CBF（ASA），∴AE=CF（全等三角形的对应边相等）。‎ ‎∴四边形AECF为平行四边形（对边平行且相等的四边形是平行四边形）。‎ ‎（2）如图，连接AC交BF于点0，当AECF为菱形时，‎ ‎ 则AC与EF互相垂直平分。‎ ‎∵BO=OD（平行四边形的对角线相互平分），‎ ‎∴AC与BD互相垂直平分。‎ ‎∴ABCD是菱形（对角线相互垂直平分的平行四边形是菱形）。‎ ‎∴AB=BC（菱形的邻边相等）。‎ ‎∵M是BC的中点，AM丄BC（已知），∴△ABM≌△CAM。‎ ‎∴AB=AC（全等三角形的对应边相等）。∴△ABC为等边三角形。‎ ‎∴∠ABC=60°，∠CBD=30°。 ‎ 在Rt△BCF中，CF：BC=tan∠CBF=。‎ 又∵AE=CF，AB=BC，∴AB：AE=。‎ ‎【考点】平行四边形的判定和性质，全等三角形的判定和性质，等边三角形的判定和性质，解直角三角形 ‎【分析】（1）根据平行四边形的性质、垂直的定义、平行线的判定定理可以推知AE∥CF；然后由ASA推知△ADE≌△CBF；最后根据全等三角形的对应边相等知AE=CF，根据对边平行且相等的四边形是平行四边形的判定得出结论。‎ ‎（2）如图，连接AC交BF于点0．由菱形的判定定理推知平行四边形ABCD是菱形，根据菱形的邻边相等知AB=BC；然后结合已知条件“M是BC的中点，AM丄BC”证得△ADE≌△CBF（ASA），所以AE=CF（全等三角形的对应边相等），从而证得△ABC是正三角形；最后在Rt△BCF中，利用锐角三角函数的定义求得CF：BC=tan∠CBF= ，利用等量代换知（AE=CF，AB=BC）AB：AE=。‎ ‎23．（2013山东潍坊10分）许多家庭以燃气作为烧水做饭的燃料，节约用气是我们日常生活中非常现实的问题．某款燃气灶旋钮位置从0度到90度(如图)，燃气关闭时，燃气灶旋钮的位置为0度，旋钮角度越大，燃气流量越大，燃气开到最大时，旋钮角度为90度．为测试燃气灶旋钮在不同位置上的燃气用量，在相同条件下，选择在燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时，其火力不能够将水烧开，故选择旋钮角度x度的范围是18≤x≤90)，记录相关数据得到下表：‎ 旋钮角度(度)‎ ‎ 20‎ ‎ 50‎ ‎ 70‎ ‎ 80‎ ‎ 90‎ 所用燃气量(升)‎ ‎ 73‎ ‎ 67‎ ‎ 83‎ ‎ 97‎ ‎ 115‎ ‎ (1)请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律?说明确定是这种函数而不是其它函数的理由，并求出它的解析式；‎ ‎ (2)当旋钮角度为多少时，烧开一壶水所用燃气量最少?最少是多少?‎ ‎ (3)某家庭使用此款燃气灶，以前习惯把燃气开到最大，现采用最节省燃气的旋钮角度，每月平均能节约燃气10立方米，求该家庭以前每月的平均燃气用量．‎ ‎【答案】解：（1）若设y=kx+b（k≠0），‎ 由解得 。∴y= x+77。‎ 把x=70代入得y=65≠83，∴一次函数不符合。‎ 若设（k≠0），由解得k=1460。∴ 。‎ 把x=50代入得y=29.2≠67，∴反比例函数不符合。‎ 若设y=ax2＋bx＋c，‎ 由 解得。∴y=x2 x＋97（18≤x≤90）。‎ 把x=80代入得y=97，把x=90代入得y=115，符合题意。‎ ‎∴二次函数能表示所用燃气量y升与旋钮角度x度的变化规律。‎ ‎（2）由（1）得：y=x2 x＋97=（x－40）2+65，‎ ‎∴当x=40时，y取得最小值65。‎ 答：当旋钮角度为40°时，烧开一壶水所用燃气量最少，最少为65升。‎ ‎ （3）由（2）及表格知，采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115－65=50（升），设该家庭以前每月平均用气量为a立方米，则由题意得：‎ ‎，解得a=23。‎ 答：该家庭以前每月平均用气量为23立方米。‎ ‎【考点】待定系数法，曲线上点的坐标与方程的关系，二次函数的性质。‎ ‎【分析】（1）先假设函数为一次函数，任选两点求出函数解析式，再将各点代入验证；再假设函数为二次函数，任选三求出函数解析式，再将各点代入验证 ‎（2）将（1）所求二次函数解析式，化为顶点式，转化为二次函数最值的问题。‎ ‎（3）由（2）及表格知，采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115－65=50，再设该家庭以前每月平均用气量为a立方米，据此解答即可。‎ ‎24．（2013山东潍坊11分）如图，已知抛物线与坐标轴分别交于A(－2，O)、B(2，0)、C(0，－l)三点，过坐标原点O的直线y=kx与抛物线交于M、N两点．分别过点C、D(0，－2)作平行于x轴的直线、．‎ ‎ (1)求抛物线对应二次函数的解析式；‎ ‎ (2)求证以ON为直径的圆与直线相切；‎ ‎ (3)求线段MN的长(用k表示)，并证明M、N两点到直线的距离之和等于线段MN的长．‎ ‎【答案】解：（1）设抛物线对应二次函数的解析式为y=ax2＋bx＋c，‎ 则 解得。‎ ‎∴抛物线对应二次函数的解析式 所以。‎ ‎ （2）设M(x1，y1)，N(x2，y2)，因为点M、N在抛物线上，‎ ‎ ∴，∴x22=4(y2+1)。‎ 又∵，∴。‎ 又∵y2≥－l，∴ON=2＋y2。‎ 设ON的中点E，分别过点N、E向直线作垂线，垂足为P、F， 则 ，‎ ‎∴ON=2EF，‎ 即ON的中点到直线的距离等于ON长度的一半，‎ ‎∴以ON为直径的圆与相切。‎ 相关信息链接:北达教育|百度百科|百度贴吧 北达教育学校简介 北达教育总部位于北京大学校内,分校遍及北京各城区40多所,多年来被家长认可的教育机构,法制晚报曾报道：是什么让北达教育成为京城良好口碑课外辅导品牌?为此北达教育被法制晚报评为：公众最信赖知名教育品牌！曾多次被新浪网，中国网评为课外绿色发展机构！北达教育旗下北京中考网（www.beijing518.com)为北京咨询；报考；体育咨询；体检；填报志愿等综合门户网站，论坛在线人数已超35896位。‎ 开课背景：针对每年京籍外地回京家长求学难现状特开设2014年外地回京全日制班，以满足外地回京考生尽快适应北京中考考点、难点及最新中考动态等。同时针对北京公立中学班级人数过多、成绩层次不同、部分潜力学生成为学校忽视对象等，也可以报名。‎ 教学大纲：以2014年北京中考《考试说明》为风向标，兼顾每个考点，详细讲解重点难点。在授课过程中融入中考思维、答题思路、考试技巧等知识的传授。‎ 授课讲义：各科老师总结多年北京中考经验整理编排出独家讲义、习题，根据学生学习情况和中考考点设置难易程度，目的性强，阶段性提高。‎ 办学成绩：13年的中考培优经历，有多年辅导中考经验的优秀教师，上千位优秀学员的坚定选择，成就了北达教育。‎ 教学效果：学生的努力，专业老师辅导，共同创造中考辉煌！‎ 外辅导部 北达教育初高中课外辅导部是专门从事初、高中特别是中考、高考考试成功等教学辅导、学习方法研究的机构。办学来该校成功举办多年初中高中假期（暑假、寒假）辅导班、初中高中（春季、秋季）周末班、中考高考复读班、中考高考考前冲刺班中考高考（压题）串讲班、家教一对一。‎ 北达教育学校中学部以中考高考成功为中心，以突破学生学习瓶颈，提高学生成绩获得考试成功为宗旨，坚持诚信教学，育人为本，积极打造北达教育知名品牌，多年来经过全体教职工的不懈努力，取得了辉煌的成绩。现在已发展成为北京实力最大、师资精良、教学过硬、口碑良好、学生成绩在短期提高成绩最快的专业化中学生教学辅导学校。‎ 北京高考网|北京中考网|论坛|QQ群|新浪微博 联系电话：400-668-7882‎ ‎★2014中考寒假班、春季高频考点冲刺班、五一串讲班、中考压题班、‎ 报名已启动名额有限欲报从速★‎ 办学成绩 北达教育 ‎2011年人数 ‎2012年人数 ‎2013年人数 ‎2014年人数目标 中考状元 ‎5‎ ‎8‎ ‎10‎ ‎12‎ 单科满分 ‎102‎ ‎159‎ ‎159‎ ‎240‎ ‎560分以上 ‎6‎ ‎12‎ ‎29‎ ‎41‎ ‎555分以上 ‎12‎ ‎35‎ ‎68‎ ‎120‎ ‎550分以上 ‎26‎ ‎31‎ ‎135‎ ‎235‎ ‎540分以上 ‎266‎ ‎358‎ ‎658‎ ‎858‎ ‎530分以上 ‎498‎ ‎562‎ ‎1231‎ ‎1438‎ 重点中学入学率 ‎96%‎ ‎97%‎ ‎97%‎ ‎98%‎ 门户网站 ‎ 北达教育是北京中考网、北京高考网、北京小学奥数网的合法拥有者和创办者，现已发展成北京地区乃至全国知名的中小学门户网站，北达教育致力于打造中国最权威的中小学门户网站和最大的中高考网络信息中心。‎ 北达教育校区 北京大学校内教室 西直门校区 东直门东方银座写字楼K 亚运村校区 北京大学北大资源东楼层 玉泉路校区 北京大学北大资源东楼 牛栏山一中 公主坟天行建大厦校区 丰台中校区 北京师范大学校区 北大地校区 北京大学万柳校区 天通苑校区 崇文新成文化大厦 回龙观校区 朝阳八十中校区 九棵树校区 惠新东桥校区 望京校区 西单小学校区 双井校区 联合大学校区 管庄校区 清河小营校区 人大校区 四季青校区 上地校区 五道口校区 劲松校区 航天桥校区 长城大厦 三元桥校区 方庄校区 灯市口校区 古城