天津市中考数学试卷 19页

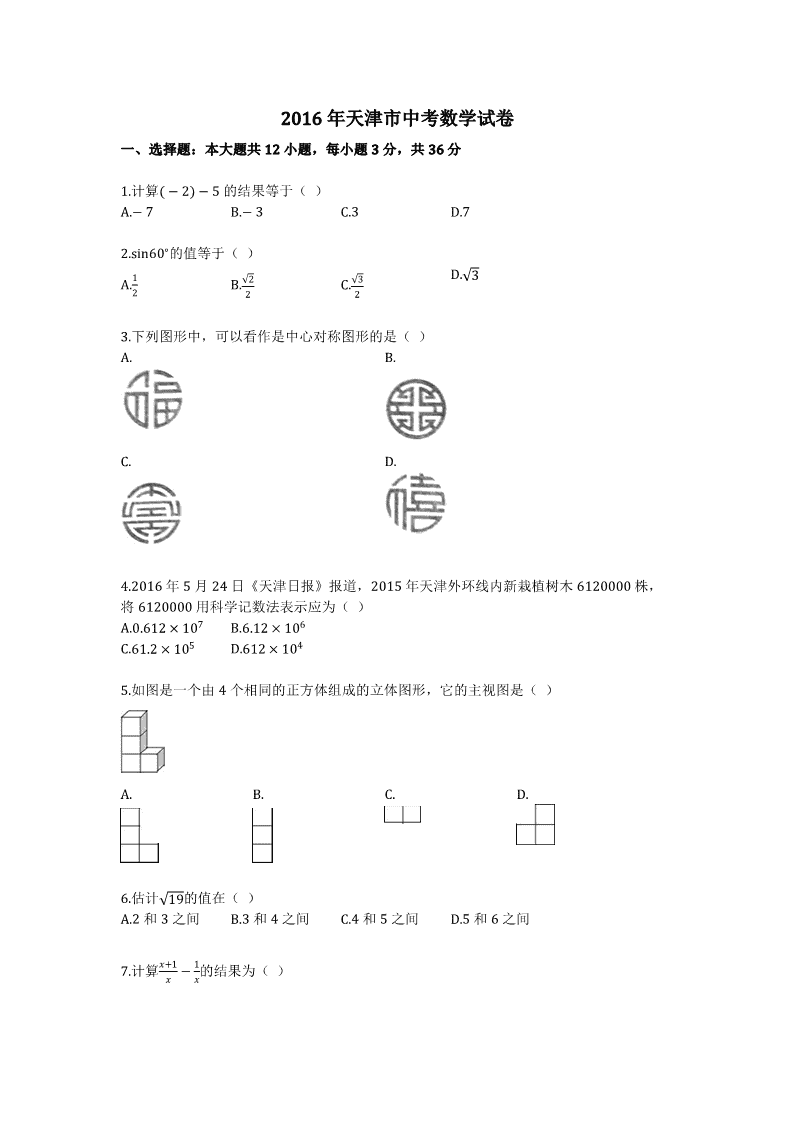
‎2016年天津市中考数学试卷 一、选择题：本大题共12小题，每小题3分，共36分 ‎ ‎ ‎1.计算‎(−2)−5‎的结果等于（ ）‎ A.‎‎−7‎ B.‎‎−3‎ C.‎‎3‎ D.‎‎7‎ ‎ ‎ ‎2.sin‎60‎‎∘‎的值等于（ ）‎ A.‎‎1‎‎2‎ B.‎‎2‎‎2‎ C.‎‎3‎‎2‎ D.‎‎3‎ ‎ ‎ ‎3.下列图形中，可以看作是中心对称图形的是（ ）‎ A.‎ B.‎ C.‎ D.‎ ‎ ‎ ‎4.‎2016‎年‎5‎月‎24‎日《天津日报》报道，‎2015‎年天津外环线内新栽植树木‎6120000‎株，将‎6120000‎用科学记数法表示应为（ ）‎ A.‎‎0.612×‎‎10‎‎7‎ B.‎‎6.12×‎‎10‎‎6‎ C.‎‎61.2×‎‎10‎‎5‎ D.‎‎612×‎‎10‎‎4‎ ‎ ‎ ‎5.如图是一个由‎4‎个相同的正方体组成的立体图形，它的主视图是（ ）‎ A.‎ B.‎ C.‎ D.‎ ‎ ‎ ‎6.估计‎19‎的值在（ ）‎ A.‎2‎和‎3‎之间 B.‎3‎和‎4‎之间 C.‎4‎和‎5‎之间 D.‎5‎和‎6‎之间 ‎ ‎ ‎7.计算x+1‎x‎−‎‎1‎x的结果为（ ）‎ A.‎‎1‎ B.‎x C.‎‎1‎x D.‎x+2‎x ‎ ‎ ‎8.方程x‎2‎‎+x−12=0‎的两个根为（ ）‎ A.x‎1‎‎=−2‎，‎x‎2‎‎=6‎ B.x‎1‎‎=−6‎，‎x‎2‎‎=2‎ C.x‎1‎‎=−3‎，‎x‎2‎‎=4‎ D.x‎1‎‎=−4‎，‎x‎2‎‎=3‎ ‎ ‎ ‎9.实数a，b在数轴上的对应点的位置如图所示，把‎−a，‎−b，‎0‎按照从小到大的顺序排列，正确的是（ ）‎ A.‎‎−a<0<−b B.‎‎0<−a<−b C.‎‎−b<0<−a D.‎‎0<−b<−a ‎ ‎ ‎10.如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′‎，AB′‎与DC相交于点E，则下列结论一定正确的是（ ）‎ A.‎‎∠DAB′=∠CAB′‎ B.‎‎∠ACD=∠B′CD C.‎AD=AE D.‎AE=CE ‎ ‎ ‎11.若点A(−5, y‎1‎)‎，B(−3, y‎2‎)‎，C(2, y‎3‎)‎在反比例函数y=‎‎3‎x的图象上，则y‎1‎，y‎2‎，y‎3‎的大小关系是（ ）‎ A.‎y‎1‎‎−b，‎−b<0‎，‎−a>0‎，即可得出答案．‎ ‎【解答】解：∵从数轴可知：a<0−b，‎−b<0‎，‎−a>0‎， ∴‎−b<0<−a， 故选C．‎ ‎10. 【答案】D ‎【解析】根据翻折变换的性质可得‎∠BAC=∠CAB′‎，根据两直线平行，内错角相等可得‎∠BAC=∠ACD，从而得到‎∠ACD=∠CAB′‎，然后根据等角对等边可得AE=CE，从而得解．‎ ‎【解答】解：∵矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′‎， ∴‎∠BAC=∠CAB′‎， ∵AB // CD， ∴‎∠BAC=∠ACD， ∴‎∠ACD=∠CAB′‎， ∴AE=CE， 所以，结论正确的是D选项． 故选D．‎ ‎11. 【答案】D ‎【解析】直接利用反比例函数图象的分布，结合增减性得出答案．‎ ‎【解答】解：∵点A(−5, y‎1‎)‎，B(−3, y‎2‎)‎，C(2, y‎3‎)‎在反比例函数y=‎‎3‎x的图象上， ∴A，B点在第三象限，C点在第一象限，每个图象上y随x的增大减小， ∴y‎3‎一定最大，y‎1‎‎>‎y‎2‎， ∴y‎2‎‎h时，y随x的增大而增大、当xh时，y随x的增大而增大，当x1.60m， ∴能进入复赛．‎ ‎【解析】‎(1)‎用整体‎1‎减去其它所占的百分比，即可求出a的值；; ‎(2)‎根据平均数、众数和中位数的定义分别进行解答即可；; ‎(3)‎根据中位数的意义可直接判断出能否进入复赛．‎ ‎【解答】解：‎(1)‎根据题意得： ‎1−20%−10%−15%−30%=25%‎； 则a的值是‎25‎； ; ‎(2)‎观察条形统计图得： x‎=‎1.50×2+1.55×4+1.60×5+1.65×6+1.70×3‎‎2+4+5+6+3‎=1.61‎； ∵在这组数据中，‎1.65‎出现了‎6‎ 次，出现的次数最多， ∴这组数据的众数是‎1.65‎； 将这组数据从小到大排列为，其中处于中间的两个数都是‎1.60‎， 则这组数据的中位数是‎1.60‎．; ‎(3)‎能； ∵共有‎20‎个人，中位数是第‎10‎、‎11‎个数的平均数， ∴根据中位数可以判断出能否进入前‎9‎名； ∵‎1.65m>1.60m， ∴能进入复赛．‎ ‎21. 【答案】‎ 解：‎(1)‎如图，连接OC， ∵‎⊙O与PC相切于点C， ∴OC⊥PC，即‎∠OCP=‎‎90‎‎∘‎， ∵‎∠CAB=‎‎27‎‎∘‎， ∴‎∠COB=2∠CAB=‎‎54‎‎∘‎， 在Rt△AOE中，‎∠P+∠COP=‎‎90‎‎∘‎， ∴‎∠P=‎90‎‎∘‎−∠COP=‎‎36‎‎∘‎；; ‎(2)‎∵E为AC的中点， ∴OD⊥AC，即‎∠AEO=‎‎90‎‎∘‎， 在Rt△AOE中，由‎∠EAO=‎‎10‎‎∘‎， 得‎∠AOE=‎90‎‎∘‎−∠EAO=‎‎80‎‎∘‎， ∴‎∠ACD=‎1‎‎2‎∠AOD=‎‎40‎‎∘‎， ∵‎∠ACD是‎△ACP的一个外角， ∴‎∠P=∠ACD−∠A=‎40‎‎∘‎−‎10‎‎∘‎=‎‎30‎‎∘‎．‎ ‎【解析】‎(1)‎连接OC，首先根据切线的性质得到‎∠OCP=‎‎90‎‎∘‎，利用‎∠CAB=‎‎27‎‎∘‎得到‎∠COB=2∠CAB=‎‎54‎‎∘‎，然后利用直角三角形两锐角互余即可求得答案；; ‎(2)‎根据E为AC的中点得到OD⊥AC，从而求得‎∠AOE=‎90‎‎∘‎−∠EAO=‎‎80‎‎∘‎，然后利用圆周角定理求得‎∠ACD=‎1‎‎2‎∠AOD=‎‎40‎‎∘‎，最后利用三角形的外角的性质求解即可．‎ ‎【解答】‎ 解：‎(1)‎如图，连接OC， ∵‎⊙O与PC相切于点C， ∴OC⊥PC，即‎∠OCP=‎‎90‎‎∘‎， ∵‎∠CAB=‎‎27‎‎∘‎， ∴‎∠COB=2∠CAB=‎‎54‎‎∘‎， 在Rt△AOE中，‎∠P+∠COP=‎‎90‎‎∘‎，‎ ‎ ∴‎∠P=‎90‎‎∘‎−∠COP=‎‎36‎‎∘‎；; ‎(2)‎∵E为AC的中点， ∴OD⊥AC，即‎∠AEO=‎‎90‎‎∘‎， 在Rt△AOE中，由‎∠EAO=‎‎10‎‎∘‎， 得‎∠AOE=‎90‎‎∘‎−∠EAO=‎‎80‎‎∘‎， ∴‎∠ACD=‎1‎‎2‎∠AOD=‎‎40‎‎∘‎， ∵‎∠ACD是‎△ACP的一个外角， ∴‎∠P=∠ACD−∠A=‎40‎‎∘‎−‎10‎‎∘‎=‎‎30‎‎∘‎．‎ ‎22. 【答案】AC的长约为‎38.2cm，CB的长约等于‎45.0m．‎ ‎【解析】根据锐角三角函数，可用CD表示AD，BD，AC，BC，根据线段的和差，可得关于CD的方程，根据解方程，可得CD的长，根据AC=‎2‎CD，CB=‎CD‎0.60‎，可得答案．‎ ‎【解答】解：过点C作CD⊥AB垂足为D ‎， 在Rt△ACD中，tanA=tan‎45‎‎∘‎=CDAD=1‎，CD=AD， sinA=sin‎45‎‎∘‎=CDAC=‎‎2‎‎2‎，AC=‎2‎CD． 在Rt△BCD中，tanB=tan‎37‎‎∘‎=CDBD≈0.75‎，BD=‎CD‎0.75‎； sinB=sin‎37‎‎∘‎=CDBC≈0.60‎，CB=‎CD‎0.60‎． ∵AD+BD=AB=63‎， ∴CD+CD‎0.75‎=63‎， 解得CD≈27‎， AC=‎2‎CD≈1.414×27=38.178≈38.2‎， CB=CD‎0.60‎≈‎27‎‎0.60‎=45.0‎， ‎ ‎23. 【答案】表一：‎315‎，‎45x，‎30‎，‎−30x+240‎； 表二：‎1200‎，‎400x，‎1400‎，‎−280x+2240‎；; ‎(2)‎能完成此项运送任务的最节省费用的租车方案是甲车‎6‎辆，乙车‎2‎辆， 理由：当租用甲种货车x辆时，设两种货车的总费用为y元， 则两种货车的总费用为：y=400x+(−280x+2240)=120x+2240‎， 又∵‎45x+(−30x+240)≥330‎，解得x≥6‎， ∵‎120>0‎， ∴在函数y=120x+2240‎中，y随x的增大而增大， ∴当x=6‎时，y取得最小值， ‎ 即能完成此项运送任务的最节省费用的租车方案是甲种货车‎6‎辆，乙种货车‎2‎辆．‎ ‎【解析】‎(1)‎根据计划租用甲、乙两种货车共‎8‎辆，已知每辆甲种货车一次最多运送机器‎45‎台、租车费用为‎400‎元，每辆乙种货车一次最多运送机器‎30‎台、租车费用为‎280‎元 ，可以分别把表一和表二补充完整；; ‎(2)‎由‎(1)‎中的数据和公司有‎330‎台机器需要一次性运送到某地，可以解答本题．‎ ‎【解答】解：‎(1)‎由题意可得， 在表一中，当甲车‎7‎辆时，运送的机器数量为：‎45×7=315‎（台），则乙车‎8−7=1‎辆，运送的机器数量为：‎30×1=30‎（台）， 当甲车x辆时，运送的机器数量为：‎45×x=45x（台），则乙车‎(8−x)‎辆，运送的机器数量为：‎30×(8−x)=−30x+240‎（台）， 在表二中，当租用甲货车‎3‎辆时，租用甲种货车的费用为：‎400×3=1200‎（元），则租用乙种货车‎8−3=5‎辆，租用乙种货车的费用为：‎280×5=1400‎（元）， 当租用甲货车x辆时，租用甲种货车的费用为：‎400×x=400x（元），则租用乙种货车‎(8−x)‎辆，租用乙种货车的费用为：‎280×(8−x)=−280x+2240‎（元）， ; ‎(2)‎能完成此项运送任务的最节省费用的租车方案是甲车‎6‎辆，乙车‎2‎辆， 理由：当租用甲种货车x辆时，设两种货车的总费用为y元， 则两种货车的总费用为：y=400x+(−280x+2240)=120x+2240‎， 又∵‎45x+(−30x+240)≥330‎，解得x≥6‎， ∵‎120>0‎， ∴在函数y=120x+2240‎中，y随x的增大而增大， ∴当x=6‎时，y取得最小值， 即能完成此项运送任务的最节省费用的租车方案是甲种货车‎6‎辆，乙种货车‎2‎辆．‎ ‎24. 【答案】解：‎(1)‎如图①， ∵点A(4, 0)‎，点B(0, 3)‎， ∴OA=4‎，OB=3‎， ∴AB=‎3‎‎2‎‎+‎‎4‎‎2‎=5‎， ∵‎△ABO绕点B逆时针旋转‎90‎‎∘‎，得‎△A′BO′‎， ∴BA=BA′‎，‎∠ABA′=‎‎90‎‎∘‎， ∴‎△ABA′‎为等腰直角三角形， ∴AA′=‎2‎BA=5‎‎2‎； ‎(2)‎作O′H⊥y轴于H，如图②， ∵‎△ABO绕点B逆时针旋转‎120‎‎∘‎，得‎△A′BO′‎， ∴BO=BO′=3‎，‎∠OBO′=‎‎120‎‎∘‎， ∴‎∠HBO′=‎‎60‎‎∘‎， 在Rt△BHO′‎中，∵‎∠BO′H=‎90‎‎∘‎−∠HBO′=‎‎30‎‎∘‎， ∴BH=‎1‎‎2‎BO′=‎‎3‎‎2‎，O′H=‎3‎BH=‎‎3‎‎3‎‎2‎， ∴OH=OB+BH=3+‎3‎‎2‎=‎‎9‎‎2‎， ∴O′‎点的坐标为‎(‎3‎‎3‎‎2‎, ‎9‎‎2‎)‎； ‎(3)‎∵‎△ABO绕点B逆时针旋转‎120‎‎∘‎，得‎△A′BO′‎，点P的对应点为P′‎， ∴BP=BP′‎， ∴O′P+BP′=O′P+BP， 作B点关于x轴的对称点C，连结O′C交x轴于P点，如图②， 则O′P+BP=O′P+PC=O′C，此时O′P+BP的值最小， ∵点C与点B关于x轴对称， ∴C(0, −3)‎， 设直线O′C的解析式为y=kx+b， 把O′(‎3‎‎3‎‎2‎, ‎9‎‎2‎)‎，C(0, −3)‎代入得‎3‎‎3‎‎2‎k+b=‎‎9‎‎2‎b=−3‎，解得k=‎‎5‎‎3‎‎3‎b=−3‎， ∴直线O′C的解析式为y=‎5‎‎3‎‎3‎x−3‎， 当y=0‎时，‎5‎‎3‎‎3‎x−3=0‎，解得x=‎‎3‎‎3‎‎5‎，则P(‎3‎‎3‎‎5‎, 0)‎， ∴OP=‎‎3‎‎3‎‎5‎， ∴O′P′=OP=‎‎3‎‎3‎‎5‎，‎ ‎ 作P′D⊥O′H于D， ∵‎∠BO′A′=∠BOA=‎‎90‎‎∘‎，‎∠BO′H=‎‎30‎‎∘‎， ∴‎∠DP′O′=‎‎30‎‎∘‎， ∴O′D=‎1‎‎2‎O′P′=‎‎3‎‎3‎‎10‎，P′D=‎3‎O′D=‎‎9‎‎10‎， ∴DH=O′H−O′D=‎3‎‎3‎‎2‎−‎3‎‎3‎‎10‎=‎‎6‎‎3‎‎5‎， ∴P′‎点的坐标为‎(‎6‎‎3‎‎5‎, ‎27‎‎5‎)‎．‎ ‎【解析】‎(1)‎如图①，先利用勾股定理计算出AB=5‎，再根据旋转的性质得BA=BA′‎，‎∠ABA′=‎‎90‎‎∘‎，则可判定‎△ABA′‎为等腰直角三角形，然后根据等腰直角三角形的性质求AA′‎的长； ‎(2)‎作O′H⊥y轴于H，如图②，利用旋转的性质得BO=BO′=3‎，‎∠OBO′=‎‎120‎‎∘‎，则‎∠HBO′=‎‎60‎‎∘‎，再在Rt△BHO′‎中利用含‎30‎度的直角三角形三边的关系可计算出BH和O′H的长，然后利用坐标的表示方法写出O′‎点的坐标； ‎(3)‎由旋转的性质得BP=BP′‎，则O′P+BP′=O′P+BP，作B点关于x轴的对称点C，连结O′C交x轴于P点，如图②，易得O′P+BP=O′C，利用两点之间线段最短可判断此时O′P+BP的值最小，接着利用待定系数法求出直线O′C的解析式为y=‎5‎‎3‎‎3‎x−3‎，从而得到P(‎3‎‎3‎‎5‎, 0)‎，则O′P′=OP=‎‎3‎‎3‎‎5‎，作P′D⊥O′H于D，然后确定‎∠DP′O′=‎‎30‎‎∘‎后利用含‎30‎度的直角三角形三边的关系可计算出P′D和DO′‎的长，从而可得到P′‎点的坐标．‎ ‎【解答】解：‎(1)‎如图①， ∵点A(4, 0)‎，点B(0, 3)‎， ∴OA=4‎，OB=3‎， ∴AB=‎3‎‎2‎‎+‎‎4‎‎2‎=5‎， ∵‎△ABO绕点B逆时针旋转‎90‎‎∘‎，得‎△A′BO′‎， ∴BA=BA′‎，‎∠ABA′=‎‎90‎‎∘‎， ∴‎△ABA′‎为等腰直角三角形， ∴AA′=‎2‎BA=5‎‎2‎； ‎(2)‎作O′H⊥y轴于H，如图②， ∵‎△ABO绕点B逆时针旋转‎120‎‎∘‎，得‎△A′BO′‎， ∴BO=BO′=3‎，‎∠OBO′=‎‎120‎‎∘‎， ∴‎∠HBO′=‎‎60‎‎∘‎， 在Rt△BHO′‎中，∵‎∠BO′H=‎90‎‎∘‎−∠HBO′=‎‎30‎‎∘‎， ∴BH=‎1‎‎2‎BO′=‎‎3‎‎2‎，O′H=‎3‎BH=‎‎3‎‎3‎‎2‎， ∴OH=OB+BH=3+‎3‎‎2‎=‎‎9‎‎2‎， ∴O′‎点的坐标为‎(‎3‎‎3‎‎2‎, ‎9‎‎2‎)‎； ‎(3)‎∵‎△ABO绕点B逆时针旋转‎120‎‎∘‎，得‎△A′BO′‎，点P的对应点为P′‎， ∴BP=BP′‎， ∴O′P+BP′=O′P+BP， 作B点关于x轴的对称点C，连结O′C交x轴于P点，如图②， 则O′P+BP=O′P+PC=O′C，此时O′P+BP的值最小， ∵点C与点B关于x轴对称， ∴C(0, −3)‎， 设直线O′C的解析式为y=kx+b， 把O′(‎3‎‎3‎‎2‎, ‎9‎‎2‎)‎，C(0, −3)‎代入得‎3‎‎3‎‎2‎k+b=‎‎9‎‎2‎b=−3‎，解得k=‎‎5‎‎3‎‎3‎b=−3‎， ∴直线O′C的解析式为y=‎5‎‎3‎‎3‎x−3‎， 当y=0‎时，‎5‎‎3‎‎3‎x−3=0‎，解得x=‎‎3‎‎3‎‎5‎，则P(‎3‎‎3‎‎5‎, 0)‎， ∴OP=‎‎3‎‎3‎‎5‎， ∴O′P′=OP=‎‎3‎‎3‎‎5‎，‎ ‎ 作P′D⊥O′H于D， ∵‎∠BO′A′=∠BOA=‎‎90‎‎∘‎，‎∠BO′H=‎‎30‎‎∘‎， ∴‎∠DP′O′=‎‎30‎‎∘‎， ∴O′D=‎1‎‎2‎O′P′=‎‎3‎‎3‎‎10‎，P′D=‎3‎O′D=‎‎9‎‎10‎， ∴DH=O′H−O′D=‎3‎‎3‎‎2‎−‎3‎‎3‎‎10‎=‎‎6‎‎3‎‎5‎， ∴P′‎点的坐标为‎(‎6‎‎3‎‎5‎, ‎27‎‎5‎)‎．‎ ‎25. 【答案】解：‎(I)‎∵y=x‎2‎−2x+1=(x−1‎‎)‎‎2‎ ∴顶点P(1, 0)‎， ∵当x=0‎时，y=1‎， ∴Q(0, 1)‎，; ‎(II)‎①设抛物线C′‎的解析式为y=x‎2‎−2x+m， ∴Q′(0, m)‎其中m>1‎， ∴OQ′=m， ∵F(1, ‎1‎‎2‎)‎， 过F作FH⊥OQ′‎，如图： ‎ ‎ ∴FH=1‎，Q′H=m−‎‎1‎‎2‎， 在Rt△FQ′H中，FQ‎′‎‎2‎=(m−‎1‎‎2‎‎)‎‎2‎+1=m‎2‎−m+‎‎5‎‎4‎， ∵FQ′=OQ′‎， ∴m‎2‎‎−m+‎5‎‎4‎=‎m‎2‎， ∴m=‎‎5‎‎4‎， ∴抛物线C′‎的解析式为y=x‎2‎−2x+‎‎5‎‎4‎， ②设点A(x‎0‎, y‎0‎)‎，则y‎0‎‎=x‎0‎‎2‎−2x‎0‎+‎‎5‎‎4‎， 过点A作x轴的垂线，与直线Q′F 相交于点N，则可设N(x‎0‎, n)‎， ‎ ‎ ∴AN=y‎0‎−n，其中y‎0‎‎>n， 连接FP， ∵F(1, ‎1‎‎2‎)‎，P(1, 0)‎， ∴FP⊥x轴， ∴FP // AN， ∴‎∠ANF=∠PFN， 连接PK，则直线Q′F是线段PK的垂直平分线， ∴FP=FK，有‎∠PFN=∠AFN， ∴‎∠ANF=∠AFN，则AF=AN， 根据勾股定理，得，AF‎2‎=(x‎0‎−1‎)‎‎2‎+(y‎0‎−‎‎1‎‎2‎‎)‎‎2‎， ∴‎(x‎0‎−1‎)‎‎2‎+(y‎0‎−‎1‎‎2‎‎)‎‎2‎=(x ‎2‎‎0‎ −2x‎0‎+‎5‎‎4‎)+y ‎2‎‎0‎ −y‎0‎=y ‎2‎‎0‎ ‎， ∴AF=‎y‎0‎， ∴y‎0‎‎=y‎0‎−n， ∴n=0‎， ∴N(x‎0‎, 0)‎， 设直线Q′F的解析式为y=kx+b， 则b=‎‎5‎‎4‎k+b=‎‎1‎‎2‎， 解得k=−‎‎3‎‎4‎b=‎‎5‎‎4‎， ∴y=−‎3‎‎4‎x+‎‎5‎‎4‎， 由点N在直线Q′F上，得，‎0=−‎3‎‎4‎x‎0‎+‎‎5‎‎4‎， ∴x‎0‎‎=‎‎5‎‎3‎， 将x‎0‎‎=‎‎5‎‎3‎代入y‎0‎‎=x ‎2‎‎0‎ −2x‎0‎+‎‎5‎‎4‎， ∴y‎0‎‎=‎‎25‎‎36‎， ∴‎A(‎5‎‎3‎, ‎25‎‎36‎)‎ ‎【解析】‎(1)‎令x=0‎，求出抛物线与y轴的交点，抛物线解析式化为顶点式，求出点P坐标； ‎(2)‎①设出Q′(0, m)‎，表示出Q′H，根据FQ′=OQ′‎，用勾股定理建立方程求出m，即可． ②根据AF=AN，用勾股定理，‎(x−1‎)‎‎2‎+(y−‎1‎‎2‎‎)‎‎2‎=(x‎2‎−2x+‎5‎‎4‎)+y‎2‎−y=‎y‎2‎，求出AF=y，再求出直线Q′F的解析式，即可．;‎ ‎【解答】解：‎(I)‎∵y=x‎2‎−2x+1=(x−1‎‎)‎‎2‎ ∴顶点P(1, 0)‎， ∵当x=0‎时，y=1‎， ∴Q(0, 1)‎，; ‎(II)‎①设抛物线C′‎的解析式为y=x‎2‎−2x+m， ∴Q′(0, m)‎其中m>1‎， ∴OQ′=m， ∵F(1, ‎1‎‎2‎)‎， 过F作FH⊥OQ′‎，如图： ‎ ‎ ∴FH=1‎，Q′H=m−‎‎1‎‎2‎， 在Rt△FQ′H中，FQ‎′‎‎2‎=(m−‎1‎‎2‎‎)‎‎2‎+1=m‎2‎−m+‎‎5‎‎4‎， ∵FQ′=OQ′‎， ∴m‎2‎‎−m+‎5‎‎4‎=‎m‎2‎， ∴m=‎‎5‎‎4‎， ∴抛物线C′‎的解析式为y=x‎2‎−2x+‎‎5‎‎4‎， ②设点A(x‎0‎, y‎0‎)‎，则y‎0‎‎=x‎0‎‎2‎−2x‎0‎+‎‎5‎‎4‎， 过点A作x轴的垂线，与直线Q′F 相交于点N，则可设N(x‎0‎, n)‎， ‎ ‎ ∴AN=y‎0‎−n，其中y‎0‎‎>n， 连接FP， ∵F(1, ‎1‎‎2‎)‎，P(1, 0)‎， ∴FP⊥x轴， ∴FP // AN， ∴‎∠ANF=∠PFN， 连接PK，则直线Q′F是线段PK的垂直平分线， ∴FP=FK，有‎∠PFN=∠AFN， ∴‎∠ANF=∠AFN，则AF=AN， 根据勾股定理，得，AF‎2‎=(x‎0‎−1‎)‎‎2‎+(y‎0‎−‎‎1‎‎2‎‎)‎‎2‎， ∴‎(x‎0‎−1‎)‎‎2‎+(y‎0‎−‎1‎‎2‎‎)‎‎2‎=(x ‎2‎‎0‎ −2x‎0‎+‎5‎‎4‎)+y ‎2‎‎0‎ −y‎0‎=y ‎2‎‎0‎ ‎， ∴AF=‎y‎0‎， ∴y‎0‎‎=y‎0‎−n， ∴n=0‎， ∴N(x‎0‎, 0)‎， 设直线Q′F的解析式为y=kx+b， 则b=‎‎5‎‎4‎k+b=‎‎1‎‎2‎， 解得k=−‎‎3‎‎4‎b=‎‎5‎‎4‎， ∴y=−‎3‎‎4‎x+‎‎5‎‎4‎， 由点N在直线Q′F上，得，‎0=−‎3‎‎4‎x‎0‎+‎‎5‎‎4‎， ∴x‎0‎‎=‎‎5‎‎3‎， 将x‎0‎‎=‎‎5‎‎3‎代入y‎0‎‎=x ‎2‎‎0‎ −2x‎0‎+‎‎5‎‎4‎， ∴y‎0‎‎=‎‎25‎‎36‎， ∴‎A(‎5‎‎3‎, ‎25‎‎36‎)‎