2014嘉兴中考数学试卷及答案 7页

‎2014年浙江省初中毕业生学业考试（嘉兴卷）‎ 数学 试题卷 考生须知：‎ 1． 全卷满分150分，考试时间120分钟，试题卷共6页，有三大题，共24小题。‎ 2． 全卷答案必须做在答题卷Ⅰ、卷Ⅱ的相应位置上，做在试题卷上无效。‎ 3． 本次考试不使用计算器。‎ 参考公式：二次函数图象的顶点坐标是。‎ 温馨提示：请仔细审题，细心答题，答题前仔细阅读答题纸上的“注意事项”。‎ 卷Ⅰ（选择题）‎ 一、 选择题（本题有10小题，每小题4分，共40分，请选出各题中唯的正确选项，不选、多选、错选，均不得分）‎ ‎1.的绝对值为（ ▲ ）‎ ‎(A) (B) (C) (D)‎ ‎2.如图，AB//CD,EF分别为交AB，CD于点Ｅ，Ｆ，∠1=50°，则∠2的度数为（ ▲ ）2·1·c·n·j·y ‎(A) 50° (B) 120° (C) 130° (D) 150°‎ ‎3.一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9，这5个数据的中位数是（ ▲ ）‎ ‎(A) 6 (B) 7 (C) 8 (D) 9‎ ‎4.2013年12月15日，我国“玉兔号”月球车顺利抵达月球表面，月球离地球平均距离是 ‎ 384 400 000米，数据384 400 000用科学计数法表示为（ ▲ ）‎ ‎(A) (B) (C) (D) ‎ ‎5.小红同学将自己5月份和各项消费情况制作成扇形统计图（如图），从图中可看出（ ▲ ）‎ 小红5月份消费情况扇形统计图 ‎(第5题)‎ ‎(A) 各项消费金额占消费总金额的百分比 ‎ ‎(B) 各项消费的金额 ‎(C) 消费的总金额 ‎(D) 各项消费金额的增减变化情况 ‎(第6题)‎ ‎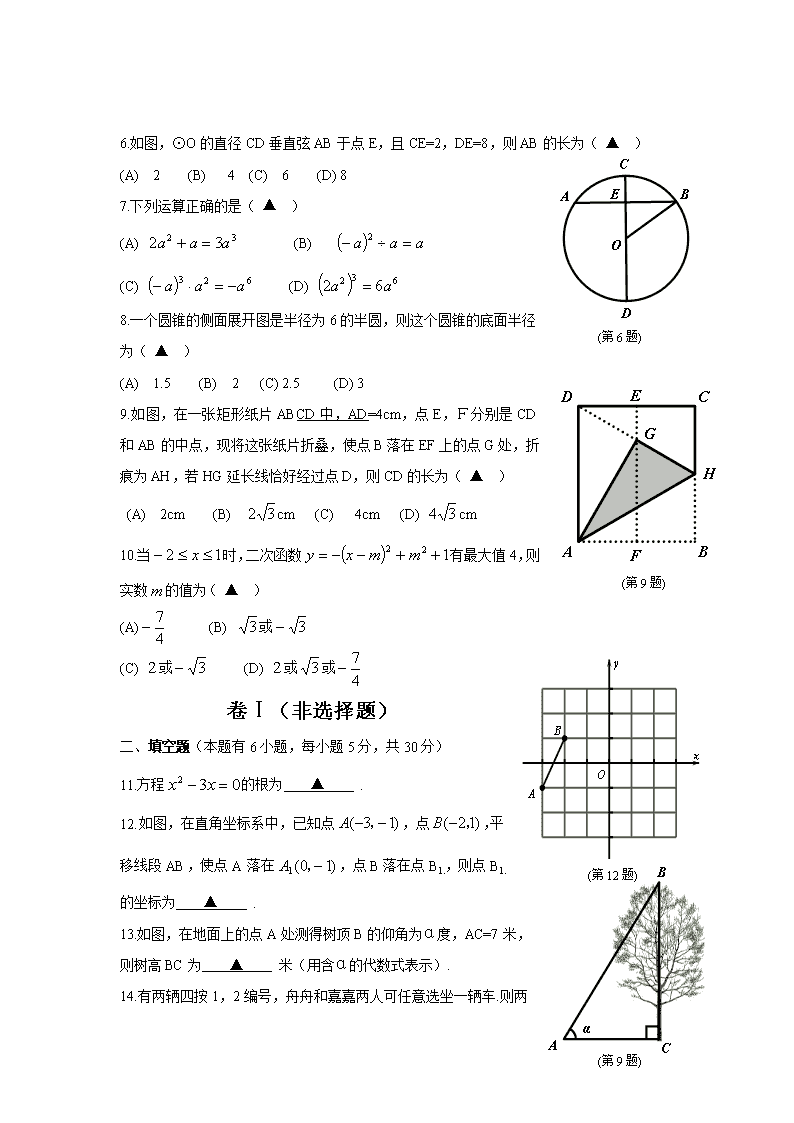6.如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为（ ▲ ）‎ ‎(A) 2 (B) 4 (C) 6 (D) 8‎ ‎7.下列运算正确的是（ ▲ ）‎ ‎(A) (B) ‎ ‎(C) (D) ‎ ‎8.一个圆锥的侧面展开图是半径为6的半圆，则这个圆锥的底面半径 为（ ▲ ）‎ ‎(第9题)‎ ‎(A) 1.5 (B) 2 (C) 2.5 (D) 3‎ ‎9.如图，在一张矩形纸片ABCD中，AD=4cm，点E，Ｆ分别是CD和AB的中点，现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH，若HG延长线恰好经过点D，则CD的长为（ ▲ ）【‎ ‎ (A) 2cm (B) cm (C) 4cm (D) cm ‎10.当时，二次函数有最大值4，则实数的值为（ ▲ ）‎ ‎(A) (B) 或 ‎ ‎(第12题)‎ ‎(C) 或 (D) 或或 卷Ⅰ（非选择题）‎ ‎(第9题)‎ ‎(第9题)‎ 一、 填空题（本题有6小题，每小题5分，共30分）‎ ‎11.方程的根为 ▲ .‎ ‎(第9题)‎ ‎12.如图，在直角坐标系中，已知点，点，平移线段AB，使点A落在，点B落在点B1.，则点B1.的坐标为 ▲ .‎ ‎13.如图，在地面上的点A处测得树顶B的仰角为α度，AC=7米，‎ 则树高BC为 ▲ 米（用含α的代数式表示）.‎ ‎14.有两辆四按1，2编号，舟舟和嘉嘉两人可任意选坐一辆车.则两人同坐2号车的概率为 ▲ .www-2-1-cnjy-com ‎15.点，是直线上的两点，则 ▲ 0（填“>”或“<”）.‎ ‎(第16题)‎ ‎16.如图，点C在以AB为直径的半圆上，AB=8，∠CBA=30°，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F.下列结论：①CE=CF；②线段EF的最小值为；③当AD=2时，EF与半圆相切；④若点F恰好落在B C上，则AD=；⑤当点D从点A运动到点B时，线段EF扫过的面积是.其中正确结论的序号是 ▲ .2-1-c-n-j-y 友情提示：做解答题，别忘了写出必要的过程；作图（包括添加辅助线）最后必须用黑色字迹的签字笔可钢笔将线条描黑.‎ 三、解答题（本题有8小题，第17～20题每小题8分，第21题10分，第22，23题每小题12分，第24题14分，共80分）　‎ ‎17.（1）计算：； （2）化简：‎ ‎18.解方程：‎ ‎19.某校为了了解学生孝敬父母的情况（选项：A.为父母洗一次脚；B.帮父母做一次家务；‎ ‎ C.给父母买一件礼物；D.其它），在全校范围内随机抽取了若干名学生进行调查，得到如下图表（部分信息未给出）：‎ 学生孝敬父母情况条形统计图 学生孝敬父母情况统计表 根据以上信息解答下列问题：‎ 选项 频数 频率 A ‎0.15‎ B ‎60‎ C ‎0.4‎ D ‎48‎ ‎0.2‎ ‎(第19题)‎ （1） 这次被调查的学生有多少人？‎ （2） 求表中，，的值，并补全条形统计图.‎ （3） 该校有1600名学生，估计该校全体学生中选择B选项的有多少人？‎ ‎20.已知：如图，在□ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF.‎ ‎（1）求证：△DOE≌△BOF.‎ ‎（2）当∠DOE等于多少度时，四边形BFED为菱形？请说明理由.‎ ‎(第20题)‎ ‎21.某汽车专卖店销售A，B两种型号的新能源汽车．上周售出１辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．‎ ‎（1）求每辆A型车和B型车的售价各为多少元．‎ ‎（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案？‎ ‎22实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量(毫克/百毫升)与时间（时）的关系可近似地用二次函数刻画；1.5小时后（包括1.5小时）与可近似地用反比例函数刻画（如图所示）．‎ ‎(第22题)‎ ‎（1）根据上述数学模型计算：‎ ‎ ①喝酒后几时血液中的酒精含量达到最大值？最大值 为多少？‎ ‎②当时，，求的值．‎ ‎（2）按国家规定，车辆驾驶人员血液中的酒精含量大于 ‎ 或等于20毫克/百毫升时属于“酒后驾驶”，不能驾 ‎ 车上路．参照上述数学模型，假设某驾驶员晚上 ‎ 20：00在家喝完半斤低度白酒，第二天早上7：00能 ‎ 否驾车去上班？请说明理由．‎ ‎23.类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形” ．‎ ‎（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，‎ ‎∠B=80°．求∠C，∠D的度数．‎ ‎ （2）在探究“等对角四边形”性质时：‎ ‎ ①小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．请你证明此结论；‎ ‎②由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等” ．你认为她的猜想正确吗？若正确，请证明；若不正确，请举出反例．‎ ‎(3)已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4．‎ 求对角线AC的长．‎ 第23题图1‎ 第23题图2‎ ‎ ‎ ‎24.如图，在平面直角坐标系中，A是抛物线上的一个动点，且点A在第一象限内．‎ AE⊥轴于点E，点B坐标为（0，2），直线AB交轴于点C，点D与点C关于轴对称，直线DE与AB相交于点F，连结BD．设线段AE的长为，△BED的面积为．‎ ‎（1）当时，求的值．‎ ‎ (2)求关于的函数解析式．‎ ‎（3）①若时，求的值；‎ ‎②当时，设，猜想与的数量关系并证明．‎