九年级数学中考压轴题练习1及答案 18页

‎2017年九年级数学中考综合题练习 今年“五一”小黄金周期间，我市旅游公司组织50名游客分散到A、B、C三个景点游玩．三个景点的门票价格如表所示：‎ 景点 A B C 门票单价 ‎30‎ ‎55‎ ‎75‎ 所购买的50张票中，B种票张数是A种票张数的3倍还多1张，设需购A种票张数为x，C种票张数为y．‎ ‎（1）写出y与x之间的函数关系式；‎ ‎（2）设购买门票总费用为w（元），求出w与x之间的函数关系式；‎ ‎（3）若每种票至少购买1张，且A种票不少于10张，则共有几种购票方案？并求出购票总费用最少时，购买A、B、C三种票的张数．‎ A、B两个水果市场各有荔枝13吨，现从A、B向甲、乙两地运送荔枝，其中甲地需要荔枝14吨，乙地需要荔枝12吨，从A到甲地的运费为50元/吨，到乙地的运费为30元/吨，从B到甲地的运费为60元/吨，到乙地的运费为45元/吨．‎ ‎（1）设A地到甲地运送荔枝x吨，请完成下表： ‎ 调往甲地（单位：吨）‎ 调往乙地（单位：吨）‎ A x ‎ ‎ B ‎ ‎ ‎ ‎ ‎（2）设总运费为W元，请写出W与x的函数关系式，并直接写出x的取值范围．‎ ‎（3）怎样调送荔枝才能使运费最少？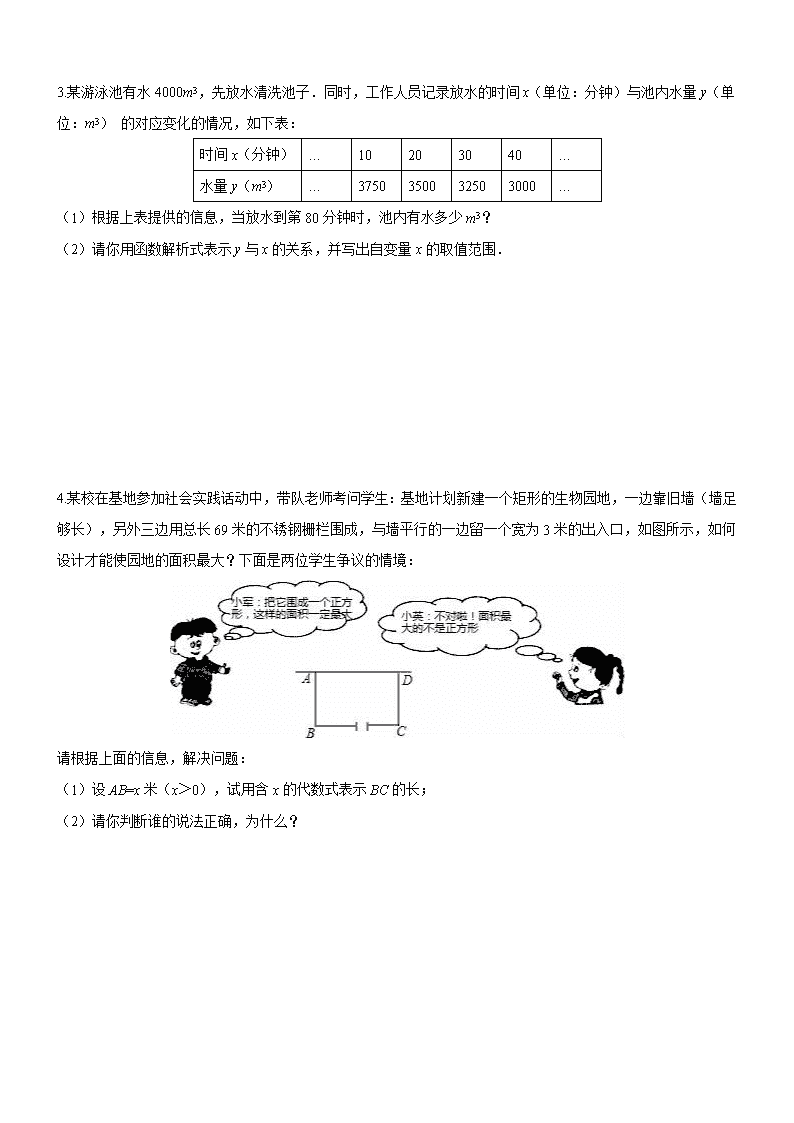‎ 某游泳池有水‎4000m3‎，先放水清洗池子．同时，工作人员记录放水的时间x（单位：分钟）与池内水量y（单位：m3） 的对应变化的情况，如下表：‎ 时间x（分钟）‎ ‎…‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎…‎ 水量y（m3）‎ ‎…‎ ‎3750‎ ‎3500‎ ‎3250‎ ‎3000‎ ‎…‎ ‎（1）根据上表提供的信息，当放水到第80分钟时，池内有水多少m3？‎ ‎（2）请你用函数解析式表示y与x的关系，并写出自变量x的取值范围．‎ 某校在基地参加社会实践话动中，带队老师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长‎69米的不锈钢栅栏围成，与墙平行的一边留一个宽为‎3米的出入口，如图所示，如何设计才能使园地的面积最大？下面是两位学生争议的情境：‎ 请根据上面的信息，解决问题：‎ ‎（1）设AB=x米（x＞0），试用含x的代数式表示BC的长；‎ ‎（2）请你判断谁的说法正确，为什么？‎ 某市某楼盘准备以每平方米6 000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4 860元的均价开盘销售.‎ ‎（1）求平均每次下调的百分率.‎ ‎（2）某人准备以开盘价均价购买一套‎100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？‎ 如图,要设计一个宽‎20cm,长‎30cm的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3，如果要使彩条所占面积是图案面积9/25,应如何设计彩条的宽度？‎ ‎ ‎ 某商品交易会上，一商人将每件进价为5元的纪念品，按每件9元出售，每天可售出32‎ 件．他想采用提高售价的办法来增加利润，经试验，发现这种纪念品每件提价2元，每天的销售量会减少8件．‎ ‎（1）当售价定为多少元时，每天的利润为140元？‎ ‎（2）写出每天所得的利润y（元）与售价x（元/件）之间的函数关系式，每件售价定为多少元，才能使一天所得的利润最大？最大利润是多少元？（利润=（售价﹣进价）×售出件数）‎ 如图是一种窗框的设计示意图,矩形ABCD被分成上下两部分,上部的矩形CDFE由两个正方形组成,制作窗框的材料总长为‎6m．‎ ‎（1）若AB为‎1m,直接写出此时窗户的透光面积 m2； ‎ ‎（2）设AB=x,求窗户透光面积S关于x的函数表达式,并求出S的最大值．‎ 如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，经过A、D两点的圆的圆心O恰好落在AB上，⊙O分别与AB、AC相交于点E、F．‎ ‎（1）判断直线BC与⊙O的位置关系并证明；‎ ‎（2）若⊙O的半径为2，AC=3，求BD的长度．‎ 已知：AB是⊙O的直径，点P在线段AB的延长线上，BP=OB=2，点Q在⊙O上，连接PQ．‎ ‎（1）如图①，线段PQ所在的直线与⊙O相切，求线段PQ的长；‎ ‎（2）如图②，线段PQ与⊙O还有一个公共点C，且PC=CQ，连接OQ，AC交于点D．‎ ‎ ①判断OQ与AC的位置关系，并说明理由；‎ ‎ ②求线段PQ的长．‎ 如图，在Rt△ABC中，∠ABC=90°，以AB为直径的⊙O与AC边交于点D，过点D作⊙O的切线交BC于点E，连接OE ‎（1）证明OE∥AD；‎ ‎（2）①当∠BAC= °时，四边形ODEB是正方形．‎ ‎ ②当∠BAC= °时，AD=3DE．‎ 如图，DC是⊙O的直径，点B在圆上，直线AB交CD延长线于点A，且∠ABD=∠C．‎ ‎（1）求证：AB是⊙O的切线；‎ ‎（2）若AB=‎4cm，AD=‎2cm，求tanA的值和DB的长．‎ 如图，⊙O是△ABC的外接圆，AC是⊙O的直径，弦BD=BA，AB=12，BC=5，BE⊥DC，交DC的延长线于点E．‎ ‎（1）求证：∠BCA=∠BAD；‎ ‎（2）求证：BE是⊙O的切线；‎ ‎（3）求DE的长．‎ 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E．‎ ‎（1）求证：AD2=AB•AE；‎ ‎（2）若AD=2，AF=3,求⊙O的半径．‎ 如图，⊙O是等腰三角形ABC的外接圆，AB=AC，延长BC到点D，使CD＝AC，连接AD交⊙O于点E，连接BE与AC交于点F.‎ ‎ （1）判断BE是否平分∠ABC，并说明理由；‎ ‎ （2）若AE=6，BE=8，求EF的长. ‎ 已知抛物线y=x2﹣2mx+m2+m﹣1（m是常数）的顶点为P，直线l：y=x﹣1‎ ‎（1）求证：点P在直线l上；‎ ‎（2）当m=﹣3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图），求点M的坐标；‎ ‎（3）若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值．‎ ‎ ‎ 如图，在平面直角坐标系中，二次函数y=ax2+bx﹣4（a≠0）的图象与x轴交于A（﹣2，0）、C（8，0）两点，与y轴交于点B，其对称轴与x轴交于点D．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）如图1，连结BC，在线段BC上是否存在点E，使得△CDE为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；‎ ‎（3）如图2，若点P（m，n）是该二次函数图象上的一个动点（其中m＞0，n＜0），连结PB，PD，BD，求△BDP面积的最大值及此时点P的坐标．‎ 如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与x轴相交于A，B两点，与y轴相交于点C，直线y=kx+n（k≠0）经过B，C两点，已知A（1，0），C（0，3），且BC=5．‎ ‎（1）分别求直线BC和抛物线的解析式（关系式）；‎ ‎（2）在抛物线的对称轴上是否存在点P，使得以B，C，P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．‎ 如图，已知矩形OABC在坐标系中，A(0，4),C(2，0),等腰Rt△OAD，D(-4，0)，∠E=90°.‎ ‎ （1）直接写出点B、E坐标：B（ ， ），E（ ， ）‎ ‎ （2）将△ODE从O点出发，沿x轴正方形平移，速度为1个单位/秒，当D与C重合时停止运动，设△ODE与矩形OABC重叠面积为S.‎ ‎ ①当t为几秒时，AE+BE值最小？当AE+BE最小时，此时重叠面积S为多少？‎ ‎ ②找出S与t之间的函数关系式.‎ ‎ ‎ 如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上，OA=1,OC=2,点D在边OC上且OD=1.25．‎ ‎（1）求直线AC的解析式．‎ ‎（2）在y轴上是否存在点P,直线PD与矩形对角线AC交于点M,使得△DMC为等腰三角形？若存在,直接写出所有符合条件的点P的坐标；若不存在，请说明理由．‎ ‎（3）抛物线y=-x2经过怎样平移,才能使得平移后的抛物线过点D和点E（点E在y轴正半轴上）,且△ODE沿DE折叠后点O落在边AB上O/处？‎ ‎ ‎ 参考答案 ‎1.略 ‎2.解：（1）如下表：‎ 故答案为：13﹣x，14﹣x，x﹣1．‎ ‎（2）根据题意得，W=50x+30（13﹣x）+60（14﹣x）+45（x﹣1）=5x+1185，‎ 由，解得：1≤x≤13．‎ ‎（3）在函数W=5x+1185中，k=5＞0，∴W随x的增大而增大，‎ 当x=1时，W取得最小值，最小值为5×1+1185=1190．‎ 此时A调往甲地1吨，调往乙地12吨，B调往甲地13吨．‎ ‎3.解：（1）由图表可知，每10分钟放水‎250m3‎，‎ 所以，第80分钟时，池内有水4000﹣8×250=‎2000m3‎；答：池内有水‎2000m3‎．‎ ‎（2）设函数关系式为y=kx+b，‎ ‎∵x=20时，y=3500，x=40时，y=3000，∴，解得：，‎ 所以，y=﹣25x+4000（0≤x≤160）．‎ ‎4.解：（1）设AB=x米，可得BC=69+3﹣2x=72﹣2x；‎ ‎（2）小英说法正确；矩形面积S=x（72﹣2x）=﹣2（x﹣18）2+648，‎ ‎∵72﹣2x＞0，∴x＜36，∴0＜x＜36，‎ ‎∴当x=18时，S取最大值，此时x≠72﹣2x，∴面积最大的不是正方形．‎ ‎5.解：（1）设平均每次下调的百分率为x，则6000(1-x)2=4860,‎ 解得：x1=0.1,x2=1.9（舍去）.‎ ‎∴ 平均每次下调的百分率为10%.‎ ‎（2）方案①可优惠：4860×100×(1-0.98)=9720(元)，‎ 方案②可优惠：100×80=8000（元），∴ 方案①更优惠.‎ ‎6.解：设横彩条宽为2x cm，则竖彩条宽为3x cm，由题意得 ‎ (20－4x)(30－6x)＝×600，解得x1＝1，x2＝9 当x＝9时，宽为18‎ ‎ ∵18×2＞20（舍去） ∴x＝1 答：使横彩条宽为‎7 cm，竖彩条宽为‎3 cm ‎7.解：（1）设售价定为x元时，每天的利润为140元，‎ 根据题意得：（x﹣5）[32﹣0.5×8（x﹣9）]=140，解得：x1=12，x2=10，‎ 答：售价定为12元或10元时，每天的利润为140元；‎ ‎（2）根据题意得；y=（x﹣5）[32﹣0.5×8（x﹣9）]，即y=﹣4x2+88x﹣340；‎ y=﹣4（x﹣11）2+144，故当x=11时，y最大=144元，‎ 答：售价为11元时，利润最大，最大利润是144元．‎ ‎8.解：（1）∵AB=1，∴AD=（6﹣3﹣0.5）×=，‎ ‎∴窗户的透光面积=AB•AD=×1=．故答案为：．‎ ‎（2）∵AB=x，∴AD==3﹣x．∴S=x（3﹣x）=﹣x2+3x．‎ ‎∵S=﹣x2+3x=﹣（x﹣）2+，∴当x=时，S的最大值=．‎ ‎9.解：（1）BC与⊙O相切．证明：连接OD．‎ ‎∵AD是∠BAC的平分线，∴∠BAD=∠CAD．又∵OD=OA，∴∠OAD=∠ODA．‎ ‎∴∠CAD=∠ODA．∴OD∥AC．∴∠ODB=∠C=90°，即OD⊥BC．‎ 又∵BC过半径OD的外端点D，∴BC与⊙O相切．‎ ‎（2）由（1）知OD∥AC．∴△BDO∽△BCA．∴OB:AB=OD:AC．‎ ‎∵⊙O的半径为2，∴DO=OE=2，AE=4．∴(BE+2):(BE+4)=2：3．∴BE=2．∴BO=4，‎ ‎∴在Rt△BDO中，BD=2．‎ ‎10.解：（1）如图①，连接OQ．‎ ‎∵线段PQ所在的直线与⊙O相切，点Q在⊙O上，∴OQ⊥OP．‎ 又∵BP=OB=OQ=2，∴PQ=2，即PQ=2；‎ ‎（2）OQ⊥AC．理由如下：如图②，连接BC．‎ ‎∵BP=OB，∴点B是OP的中点，又∵PC=CQ，∴点C是PQ的中点，‎ ‎∴BC是△PQO的中位线，∴BC∥OQ．‎ 又∵AB是直径，∴∠ACB=90°，即BC⊥AC，∴OQ⊥AC．‎ ‎（3）如图②，PC•PQ=PB•PA，即0.5PQ2=2×6，解得PQ=2．‎ ‎11.‎ ‎12.‎ ‎13.（1）证明：∵BD=BA，∴∠BDA=∠BAD．∵∠BCA=∠BDA，∴∠BCA=∠BAD．‎ ‎（2）证明：连结OB，如图，∵∠BCA=∠BDA，又∵∠BCE=∠BAD，∴∠BCA=∠BCE，‎ ‎∵OB=OC，∴∠BCO=∠CBO，∴∠BCE=∠CBO，∴OB∥ED．‎ ‎∵BE⊥ED，∴EB⊥BO．∴BE是⊙O的切线．‎ ‎（3）解：∵AC是⊙O的直径，∴∠ABC=90°，∴AC===13．‎ ‎∵∠BDE=∠CAB，∠BED=∠CBA=90°，∴△BED∽△CBA，‎ ‎∴，即，∴DE=．‎ ‎14.解：（1）如图，连接OD，DF．‎ ‎∵AB是直径，∴∠ADB=90°，∴AD⊥BC，∵AB=AC，∴BD=DC，‎ ‎∵AO=OB，∴OD∥AC，DO=AC，∵DE是切线，∴OD⊥DE，∵OD∥AC，‎ ‎∴DE⊥AC，∴∠AED=90°，∵∠DAE=∠DAC，∠AED=∠ADC=90°，‎ ‎∴△ADE∽△ACD，∴=，∴AD2=AE•AC=AB•AE．‎ ‎（2）∵AB=AC，∴∠B=∠C，‎ ‎∵∠DFC=∠B，∴∠C=∠DFC，∴DF=DC，∵DE⊥CF，∴EF=EC，设FE=EC=x，‎ ‎∵DE是切线∴DE2=EF•EA=AD2﹣AE2，∴x（x+3）=（2）2﹣（x+3）2，∴x=，‎ ‎∴AC=AF+FC=3+=，由（1）可知OD=AC=，∴⊙O的半径为．‎ ‎15.解：（1）BE平分∠ABC. 理由：∵CD＝AC，∴∠D=∠CAD. ‎ ‎∵AB＝AC，∴∠ABC=∠ACB ∵∠EBC=∠CAD，∴∠EBC=∠D=∠CAD. ‎ ‎∵∠ABC=∠ABE+∠EBC，∠ACB=∠D+∠CAD， ∴∠ABE=∠EBC，即BE平分∠ABC. ‎ ‎（2） 由（1）知∠CAD=∠EBC =∠ABE. ∵∠AEF=∠AEB，∴△AEF∽△BEA. ‎ ‎ ∴，∵AE=6， BE=8.∴EF=.‎ ‎16.‎ ‎17.‎ ‎ ‎ ‎ ‎ ‎18.‎ ‎19.略 ‎20.略