2009年福建省莆田市初中毕业、升学考试试卷及答案 14页

‎2009年莆田市初中毕业、升学考试试卷 数 学 ‎（满分：150分，考试时间：120分钟）‎ 一、细心填一填（本大题共10小题，每小题4分，共40分．直接把答案填在题中的横线上．）‎ ‎1．的相反数是 ．‎ ‎2．2009年莆田市参加初中毕业、升学考试的学生总人数约为43000人，将43000用科学记数法表示是___________．‎ A E C F B ‎(第4题图)‎ ‎3．在组成单词“”（概率）的所有字母中任意取出一个字母，则取到字母“”的概率是 ．‎ ‎4．如图，两处被池塘隔开，为了测量两处的距离，在外选一适当的点，连接，并分别取线段的中点，测得=‎20m，则=__________m．‎ ‎5．一罐饮料净重‎500克，罐上注有“蛋白质含量”，则这罐饮料中蛋白质的含量至少为__________克． ‎ A B C D D C B A O ‎（第6题图）‎ O ‎6．如图，菱形的对角线相交于点请你添加一个条件： ，使得该菱形为正方形． ‎ ‎7．甲、乙两位同学参加跳高训练，在相同条件下各跳10次，统计各自成绩的方差得，则成绩较稳定的同学是___________．（填“甲”或“乙”） ‎ ‎8．已知和的半径分别是一元二次方程的两根，且则和的位置关系是 ．‎ ‎9．出售某种文具盒，若每个获利元，一天可售出个，则当 元时，一天出售该种文具盒的总利润最大．‎ y x O P1‎ P2‎ P3‎ P4‎ P5‎ A1‎ A2‎ A3‎ A4‎ A5‎ ‎（第10题图）‎ ‎10．如图，在轴的正半轴上依次截取，过点分别作轴的垂线与反比例函数的图象相交于点，得直角三角形并设其面积分别为则的值为 ．‎ 二、精心选一选（本大题共6小题，每小题4分，共24分，每小题给出的四个选项中有且只有一个是正确的，请把正确选项的代号写在题后的括号内，答对的得4分；答错、不答或答案超过一个的一律得0分）．‎ ‎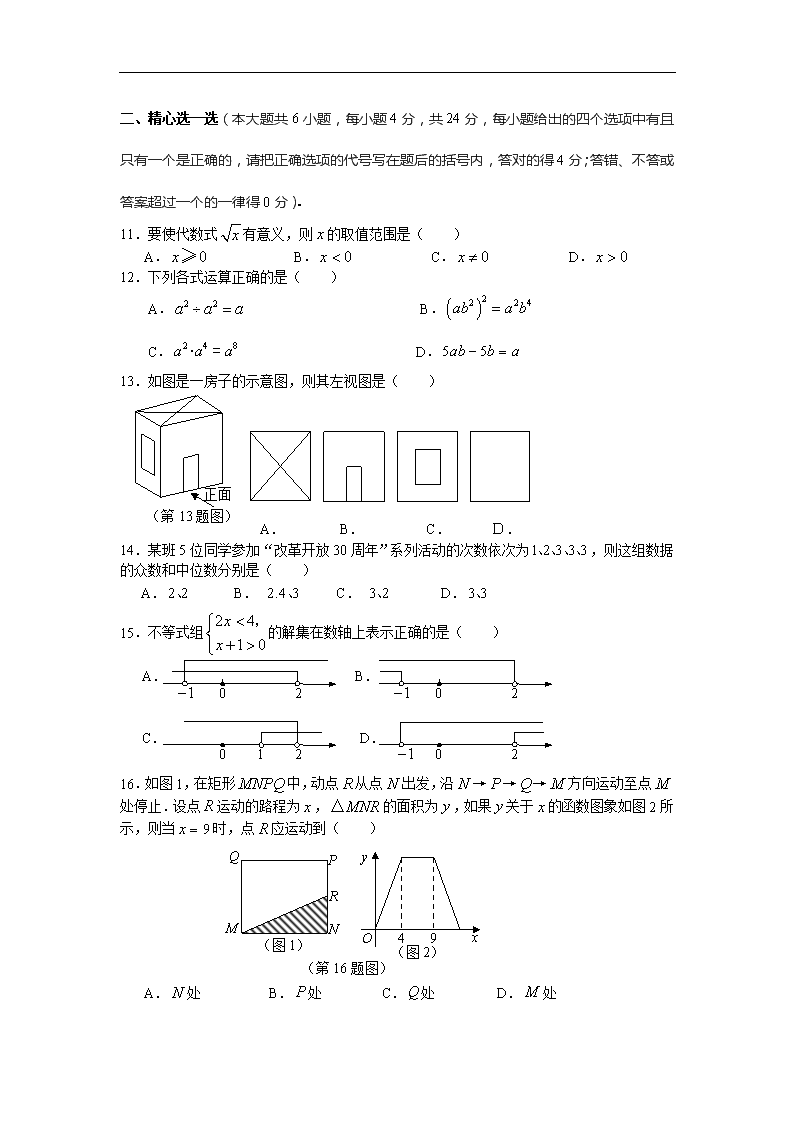11．要使代数式有意义，则的取值范围是（ ）‎ A． B． C． D．‎ ‎12．下列各式运算正确的是（ ）‎ A． B．‎ C． D．‎ ‎13．如图是一房子的示意图，则其左视图是（ ）‎ ‎（第13题图）‎ 正面 ‎ ‎ ‎ A． B． C．　　　Ｄ．‎ ‎14．某班5位同学参加“改革开放30周年”系列活动的次数依次为，则这组数据的众数和中位数分别是（ ）‎ A． B． C． D． ‎ ‎1‎ ‎0‎ ‎2‎ ‎0‎ ‎2‎ ‎0‎ ‎2‎ ‎0‎ ‎2‎ ‎15．不等式组的解集在数轴上表示正确的是（ ）‎ ‎ A． B． ‎ C． D． ‎ ‎16．如图1，在矩形中，动点从点出发，沿→→→方向运动至点处停止．设点运动的路程为，的面积为，如果关于的函数图象如图2所示，则当时，点应运动到（ ）‎ ‎（第16题图）‎ Q P R M N ‎（图1）‎ ‎（图2）‎ ‎4‎ ‎9‎ y x O ‎ A．处 B．处 C．处 D．处 三、耐心做一做（本大题共9小题，共86分．解答应写出必要的文字说明、证明过程或演算步骤．）‎ ‎17．（8分）计算：‎ ‎18．（8分）先化简，再求值：其中．‎ ‎19．（8分）已知：如图在中，过对角线的中点作直线分别交的延长线、的延长线于点 ‎（1）观察图形并找出一对全等三角形：____________________，请加以证明；‎ E B M O D N F C ‎（第19题图）‎ A ‎（2）在（1）中你所找出的一对全等三角形，其中一个三角形可由另一个三角形经过怎样的变换得到？‎ ‎20．（8分）（1）根据下列步骤画图并标明相应的字母:（直接在图１中画图）‎ ‎①以已知线段（图1）为直径画半圆；‎ ‎②在半圆上取不同于点的一点，连接；‎ ‎③过点画交半圆于点 ‎（2）尺规作图：（保留作图痕迹，不要求写作法、证明）‎ 已知：（图2）．‎ 求作：的平分线．‎ 图2‎ O B A B A 图1‎ ‎（第20题图）‎ ‎21．（8分）某校课题研究小组对本校九年级全体同学体育测试情况进行调查，他们随机抽查部分同学体育测试成绩（由高到低分四个等级），根据调查的数据绘制成如下的条形统计图和扇形统计图．‎ ‎0‎ ‎4‎ ‎8‎ ‎12‎ ‎16‎ ‎20‎ ‎24‎ ‎28‎ ‎32‎ ‎20‎ ‎32‎ ‎4‎ A级 C级 D级 等级 B级 D级，d=5%‎ C级，‎ c=30%‎ A级，‎ a=25%‎ B级，‎ b=?‎ ‎（第21题图）‎ 频数（人数）‎ 请根据以上不完整的统计图提供的信息，解答下列问题：‎ ‎（1）该课题研究小组共抽查了__________名同学的体育测试成绩，扇形统计图中级所占的百分比=___________；‎ ‎（2）补全条形统计图；‎ ‎（3）若该校九年级共有400名同学，请估计该校九年级同学体育测试达标（测试成绩级以上，含级）约有___________名．‎ ‎22．（10分）已知，如图，是以线段为直径的的切线，交于点，过点作弦垂足为点，连接．‎ ‎（1）仔细观察图形并写出四个不同的正确结论：①________，②________ ，③________，④____________（不添加其它字母和辅助线，不必证明）；‎ C D O F A B E ‎（第22题图）‎ ‎（2）=，=，求的半径 ‎23．（10分）面对全球金融危机的挑战，我国政府毅然启动内需，改善民生．国务院决定从‎2009年2月1日起，“家电下乡”在全国范围内实施，农民购买人选产品，政府按原价购买总额的13%给予补贴返还．某村委会组织部分农民到商场购买人选的同一型号的冰箱、电视机两种家电，已知购买冰箱的数量是电视机的2倍，且按原价购买冰箱总额为40000元、电视机总额为15000元．根据“家电下乡”优惠政策，每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元，求冰箱、电视机各购买多少台？‎ ‎（1）设购买电视机台，依题意填充下列表格：‎ 项目 家电种类 购买数量（台）‎ 原价购买总额（元）‎ 政府补贴返还比例 补贴返还总金额（元）‎ 每台补贴返还金额（元）‎ 冰箱 ‎40 000‎ ‎13%‎ 电视机 ‎15 000‎ ‎13%‎ ‎（2）列出方程（组）并解答．‎ ‎24.（12分）已知：等边的边长为．‎ 探究（1）：如图１，过等边的顶点依次作的垂线围成求证：是等边三角形且； ‎ 探究（2）：在等边内取一点，过点分别作垂足分别为点 ‎ ‎①如图2，若点是的重心，我们可利用三角形面积公式及等边三角形性质得到两个正确结论（不必证明）：结论1．；结论2．；‎ ‎②如图3，若点是等边内任意一点，则上述结论是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由．‎ N M A G C B A F C E B D A F C E B D ‎（图1）‎ ‎（图2）‎ ‎（图3）‎ ‎（第24题图）‎ O A F C E B D ‎（图4）‎ O O ‎25．（14分）已知，如图1，过点作平行于轴的直线，抛物线上的两点的横坐标分别为1和4，直线交轴于点，过点分别作直线的垂线，垂足分别为点、，连接．‎ ‎（1）求点的坐标；‎ ‎（2）求证：；‎ E D C A F B x O y l E D C O F x y ‎（图1）‎ 备用图 ‎（第25题图）‎ ‎（3）点是抛物线对称轴右侧图象上的一动点，过点作交轴于点，是否存在点使得与相似？若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．‎ ‎2009年莆田市初中毕业、升学考试试卷 数学试卷参考答案及评分标准 说明：‎ ‎（一）考生的解法与“参考答案”不同时，可参照“答案的评分标准”的精神进行评分 ‎（二）如解答的某一步计算出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得分数的二分之一；如属严重的概念性错误，就不给分．‎ ‎（三）以下解答各行右端所注分数表示正确做完该步骤应得的累计分数．‎ ‎（四）评分的最小单位是１分，得分或扣分都不能出现小数．‎ 一、细心填一填（本大题共10小题，每小题4分，共40分．）‎ ‎1．3 2．（不必考虑有效数字） 3． 4．40 5．2‎ ‎6．或或等 7．甲 8．相交 9．3 10．‎ 二、精心选一选（本大题共6小题，每小题4分，共24分．）‎ ‎11．A 12．B 13．C 14．D 15．A 16．C 三、耐心做一做（本题共9小题，共86分）‎ ‎17．（1）解：原式= 6分 ‎ = 8分 注：（2分），（2分），=1（2分）‎ ‎18.解：原式= 6分 ‎ = 7分 ‎ 当时原式= 8分 E B M O D N F C ‎（第19题图）‎ A 注：（各2分）‎ ‎19． （1）； 2分 证明：∵四边形是平行四边形 ∴ 3分 ‎∴ 4分 又∵‎ ‎∴ 5分 ‎ 2分 证明：∵四边形是平行四边形 ∴ 3分 ‎∴ 4分 又∵‎ ‎∴ 5分 ‎； 2分 证明：∵四边形是平行四边形 ∴ 3分 又∵ 4分 ‎∴ 5分 ‎（2）绕点旋转后得到或以点为中心作对称变换得到． 8分 ‎20．（1）正确完成步骤，各得1分，字母标注完整得1分，满分4分．‎ ‎ （2）说明：以点为圆心，以适当长为半径作弧交于两点 5分 ‎ 分别以点为圆心，以大于长为半径作弧，‎ 两弧相交于点 7分 B A 图1‎ ‎（第20题图）‎ 图2‎ O B A E D O C C D ‎ 作射线 8分 ‎0‎ ‎4‎ ‎8‎ ‎12‎ ‎16‎ ‎20‎ ‎24‎ ‎28‎ ‎32‎ ‎20‎ ‎32‎ ‎4‎ A级 C级 D级 等级 B级 ‎（第21题图）‎ ‎24‎ 频数（人数）‎ ‎21．（1）80 2分 ‎40% 4分 ‎（2）补全条形图（如右图） 6分 ‎（3）380 8分 ‎22．（1）‎ 等 ‎（每写出一个正确结论得１分，满分４分．）‎ C D O F A B E ‎（第22题图）‎ ‎（2）解:是的直径 5分 又 ‎ ‎ 6分 ‎ 7分 又是的切线 ‎ 8分 在中，‎ ‎ 9分 ‎ 10分 ‎23．（1）每个空格填对得1分，满分5分．‎ ‎40 000‎ ‎13%‎ 或5200‎ 或或 ‎15 000‎ ‎13%‎ ‎15 000×13%或1950‎ 或 ‎（2）解:依题意得- 7分 解得 8分 经检验是原分式方程的解 9分 N M A G C B ‎（图1）‎ 答:冰箱、电视机分别购买20台、10台 10分 ‎24．证明：如图1，为等边三角形 ‎∴‎ ‎ 1分 ‎ 2分 同理：‎ 为等边三角形． 3分 在中，‎ 在中， 4分 ‎ 5分 ‎（2）：结论1成立.‎ A F C E B D ‎（图2）‎ O H 证明；方法一：如图2，连接 由= 7分 作垂足为，‎ 则 ‎ 8分 方法二：如图3，过点作分别交于点，过点 作于点，‎ 是等边三角形 ‎ 6分 四边形是矩形 ‎ 7分 在中，‎ A F C E B D ‎（图3）‎ O M H G 在中，‎ 在中，‎ ‎ 8分 A F C E B D ‎（图4）‎ O M G N ‎（2）结论2成立．‎ 证明：方法一：如图４，过顶点依次作边的垂线围成由（1）得为等边三角形且 9分 过点分别作于,于于点于点 由结论1得： ‎ ‎ 10分 又 四边形为矩形 同理：， 11分 ‎ 12分 方法二：（同结论1方法二的辅助线）‎ A F C E B D ‎（图3）‎ O M H G 在中，‎ 在中， 9分 同理： 10分 ‎=‎ ‎= 11分 由结论1得：‎ A F C E B D ‎（图5）‎ O ‎ 12分 方法三：如图5，连接，根据勾股定理得：‎ ‎ 9分 ‎：‎ ‎ 10分 ‎ 11分 整理得：‎ ‎ 12分 ‎25．（1）解:方法一，如图1，当时,‎ 当时, ‎ E D C A F B x O y l ‎（图1）‎ ‎∴ 1分 ‎ 2分 设直线的解析式为 3分 则　　　解得 ‎∴直线的解析式为 4分 当时,‎ E D C A F B x O y l ‎（图2）‎ G H M ‎ 5分 方法二:求两点坐标同方法一,如图2,作,,垂足分别为、,交轴于点,则四边形和四边形均为矩形,设 3分 ‎ 4分 解得 ‎ 5分 ‎(2)证明：方法一：在中，‎ ‎ 6分 在中，‎ 由（1）得 ‎ 7分 ‎ 8分 方法二：由 （1）知 ‎ 6分 同理：‎ ‎ 7分 同理：‎ 即 8分 ‎（3）存在.‎ 解：如图3，作轴，垂足为点 9分 E D C O F x y 图3‎ M P l Q 又 ‎ 10分 设，则 ‎①当时，‎ ‎ 11分 解得 ‎ 12分 ‎②当时，‎ ‎ 13分 解得 综上，存在点、使得与相似. 14分