黄石市2008年初中毕业生学业考试数学试卷 10页

黄石市2008年初中毕业生学业考试 数学试卷 ‎（闭卷 考试时间：120分钟 满分120分）‎ 一、单项选择题（本大题共12个小题，每小题3分，满分36分）‎ 1．的相反数是（ ）‎ A． B． C． D．‎ ‎2．在实数，，，，中，无理数有（ ）‎ A B C D O A．1个 B．2个 C．3个 D．4个 3．如图，，和相交于点，，，‎ 则等于（ ）‎ A． B． C． D．‎ ‎4．下列图形中既是轴对称图形，又是中心对称图形的是（ ）‎ ‎ A． B． C． D．‎ 5．若不等式组有实数解，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎6．在反比例函数中，当时，随的增大而减小，则二次函数的图象大致是下图中的（ ）‎ x y O A．‎ x y O B．‎ x y O C．‎ x y O D．‎ 7．下面左图所示的几何体的俯视图是（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎8．如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与左图中相似的是（ ）‎ A．‎ B．‎ C．‎ D．‎ A B C 9．若一组数据2，4，，6，8的平均数是6，则这组数据的方差是（ ）‎ A． B．‎8 ‎ C． D．40‎ ‎10．若，则的大小关系为（ ）‎ A． B． C． D．不能确定 11．已知是关于的一元二次方程的两实数根，则式子的值是（ ）‎ A． B． C． D．‎ A B C P M N ‎12．如图，在等腰三角形中，，点是底 边上一个动点，分别是的中点，若 的最小值为2，则的周长是（ ）‎ A． B． C． D．‎ 二、填空题（本大题共6个小题，每小题3分，满分18分）‎ ‎1‎ ‎0‎ ‎2‎ ‎3‎ ‎5‎ 13．分解因式： ．‎ ‎14．已知是的一次函数，右表列出了部分对应值，‎ 则 ．‎ A C D O B ‎15．如图，在中，，，点为中点，将绕点按逆时针方向旋转得到，则点在旋转过程中所经过的路程为 ．（结果保留）‎ B A C D 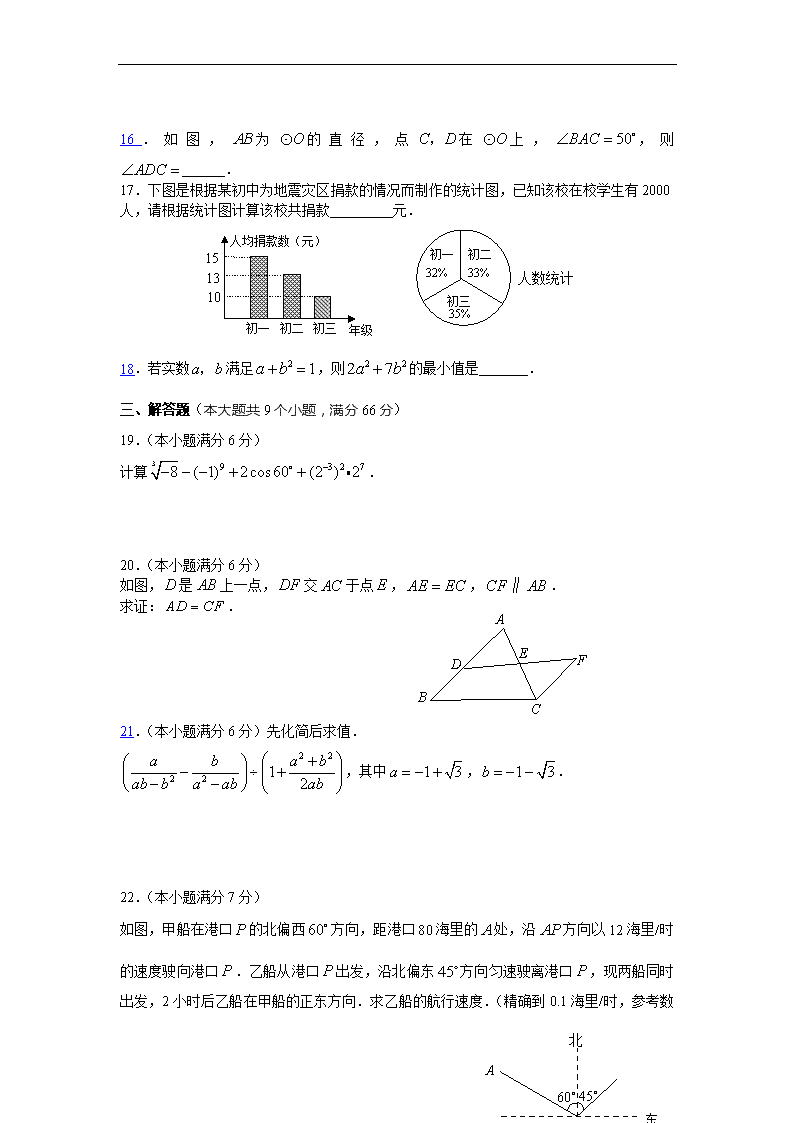16．如图，为的直径，点在上，，则 ．‎ ‎17．下图是根据某初中为地震灾区捐款的情况而制作的统计图，已知该校在校学生有2000人，请根据统计图计算该校共捐款 元．‎ 初一 初二 初三 年级 ‎10‎ ‎13‎ ‎15‎ 人均捐款数（元）‎ 初三 初二 初一 ‎32%‎ ‎33%‎ ‎35%‎ 人数统计 18．若实数满足，则的最小值是 ．‎ 三、解答题（本大题共9个小题，满分66分）‎ ‎19．（本小题满分6分）‎ 计算．‎ ‎20．（本小题满分6分）‎ 如图，是上一点，交于点，，．‎ A B C D E F 求证：．‎ 21．（本小题满分6分）先化简后求值．‎ ‎，其中，．‎ ‎22．（本小题满分7分）‎ A P 东 北 如图，甲船在港口的北偏西方向，距港口海里的处，沿方向以12海里/时的速度驶向港口．乙船从港口出发，沿北偏东方向匀速驶离港口，现两船同时出发，2小时后乙船在甲船的正东方向．求乙船的航行速度．（精确到0.1海里/时，参考数据，）‎ 23．（本小题满分7分）‎ 某车间要生产220件产品，做完100件后改进了操作方法，每天多加工10件，最后总共用4天完成了任务．求改进操作方法后，每天生产多少件产品？‎ ‎24．（本小题满分7分）‎ 在一个口袋中有个小球，其中两个是白球，其余为红球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，从袋中随机地取出一个球，它是红球的概率是．‎ ‎（1）求的值；‎ ‎（2）把这个球中的两个标号为1，其余分别标号为2，3，…，，随机地取出一个小球后不放回，再随机地取出一个小球，求第二次取出小球标号大于第一次取出小球标号的概率．‎ 25．（本小题满分8分）‎ 某公司有型产品40件，型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完．两商店销售这两种产品每件的利润（元）如下表：‎ 型利润 型利润 甲店 ‎200‎ ‎170‎ 乙店 ‎160‎ ‎150‎ ‎（1）设分配给甲店型产品件，这家公司卖出这100件产品的总利润为（元），求关于的函数关系式，并求出的取值范围；‎ ‎（2）若公司要求总利润不低于17560元，说明有多少种不同分配方案，并将各种方案设计出来；‎ ‎（3）为了促销，公司决定仅对甲店型产品让利销售，每件让利元，但让利后型产品的每件利润仍高于甲店型产品的每件利润．甲店的型产品以及乙店的型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大？‎ ‎26．（本小题满分9分）‎ 如图，为直角，点为线段的中点，点是射线上的一个动点（不与点重合），连结，作，垂足为，连结，过点作，交于．‎ ‎（1）求证：；‎ ‎（2）在什么范围内变化时，四边形是梯形，并说明理由；‎ A B C D F E M ‎（3）在什么范围内变化时，线段上存在点，满足条件，并说明理由．‎ ‎27．（本小题满分10分）‎ 如图，已知抛物线与轴交于点，，与轴交于点．‎ ‎（1）求抛物线的解析式及其顶点的坐标；‎ ‎（2）设直线交轴于点．在线段的垂直平分线上是否存在点，使得点到直线的距离等于点到原点的距离？如果存在，求出点的坐标；如果不存在，请说明理由；‎ ‎（3）过点作轴的垂线，交直线于点，将抛物线沿其对称轴平移，使抛物线与线段总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？‎ A B C O x y 黄石市2008年初中毕业生学业考试 数学试卷答案及评分标准 一、单项选择题（每小题3分，满分36分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C B C B A A D B B A D D 二、填空题（每小题3分，满分18分）‎ 13． 14．1 15． ‎ ‎16． 17．25180 18．2‎ 三、解答题（本大题共9小题，满分66分）‎ 19．解：原式 （4分）‎ ‎ （5分）‎ ‎ ． （6分）‎ ‎20．证明：，． （2分）‎ 又，，‎ ‎． （5分） ‎ ‎． （6分）‎ 21．解：原式 ‎ （2分）‎ ‎ ‎ ‎ ． （4分）‎ 当，时，‎ 原式． （6分）‎ A P 东 北 B Q C 22．依题意，设乙船速度为海里/时，2小时后甲船在点处，乙船在点处，作于，则海里，海里．‎ 在中，，‎ ‎． （2分）‎ 在中，，‎ ‎． （4分）‎ ‎，‎ ‎．‎ ‎．‎ 答：乙船的航行速度约为19.7海里/时． （7分）‎ 23．设改进操作方法后每天生产件产品，则改进前每天生产件产品．‎ 依题意有． （3分）‎ 整理得．‎ 解得或． （5分）‎ 时，，舍去．‎ ‎．‎ 答：改进操作方法后每天生产60件产品． （7分）‎ 24．（1）依题意． （3分）‎ ‎（2）当时，这5个球两个标号为1，其余标号分别为2，3，4．‎ 两次取球的小球标号出现的所有可能的结果如下表：‎ ‎（1，4）‎ ‎（1，4）‎ ‎（2，4）‎ ‎（3，4）‎ ‎（1，3）‎ ‎（1，3）‎ ‎（2，3）‎ ‎（4，3）‎ ‎（1，2）‎ ‎（1，2）‎ ‎（3，2）‎ ‎（4，2）‎ ‎（1，1）‎ ‎（2，1）‎ ‎（3，1）‎ ‎（4，1）‎ ‎（1，1）‎ ‎（2，1）‎ ‎（3，1）‎ ‎（4，1）‎ 第2个球的标号 ‎4‎ ‎3‎ ‎2‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 第1个球的标号 由上表知所求概率为． （7分）‎ 25．依题意，甲店型产品有件，乙店型有件，型有件，则 ‎（1）‎ ‎．‎ 由解得． （2分）‎ ‎（2）由，‎ ‎．‎ ‎，，39，40．‎ 有三种不同的分配方案．‎ ‎①时，甲店型38件，型32件，乙店型2件，型28件．‎ ‎②时，甲店型39件，型31件，乙店型1件，型29件．‎ ‎③时，甲店型40件，型30件，乙店型0件，型30件．‎ ‎（3）依题意：‎ ‎．‎ ‎①当时，，即甲店型40件，型30件，乙店型0件，型30件，能使总利润达到最大．‎ ‎②当时，，符合题意的各种方案，使总利润都一样．‎ ‎③当时，，即甲店型10件，型60件，乙店型30件，型0件，能使总利润达到最大． （8分）‎ 26．（1）在中，，，，．‎ A B C D F E M G H ‎，‎ ‎，．‎ ‎，，‎ ‎．‎ ‎．‎ ‎． （3分）‎ ‎（2）由（1），而，‎ ‎，即．‎ 若，则，．‎ ‎，．‎ 当或时，四边形为梯形． （6分）‎ ‎（3）作，垂足为，则．‎ ‎，．‎ 又为中点，为的中点．‎ 为的中垂线．‎ ‎．‎ 点在h上，．‎ ‎，‎ ‎．‎ ‎．‎ ‎．‎ 又，‎ ‎．‎ 当时，上存在点，满足条件． （9分）‎ ‎27．（1）设抛物线解析式为，把代入得．‎ ‎，‎ 顶点 （2分）‎ ‎（2）假设满足条件的点存在，依题意设，‎ 由求得直线的解析式为，‎ 它与轴的夹角为，设的中垂线交于，则．‎ 则，点到的距离为．‎ 又． （4分）‎ ‎．‎ 平方并整理得：‎ ‎．‎ 存在满足条件的点，的坐标为． （6分）‎ ‎（3）由上求得．‎ ‎①若抛物线向上平移，可设解析式为．‎ 当时，．‎ 当时，．‎ A B C O x y D F H P E 或．‎ ‎． （8分）‎ ‎②若抛物线向下移，可设解析式为．‎ 由，‎ 有．‎ ‎，．‎ 向上最多可平移72个单位长，向下最多可平移个单位长． （10分）‎