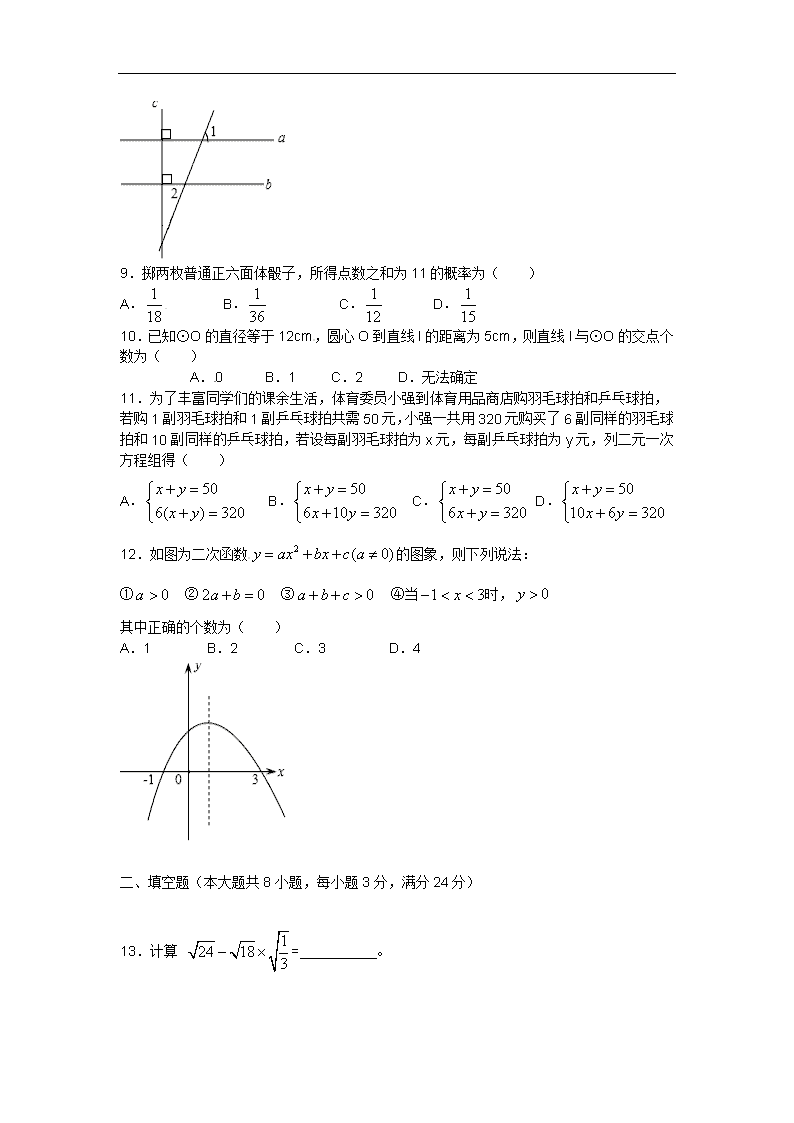2012年衡阳中考数学试卷 7页

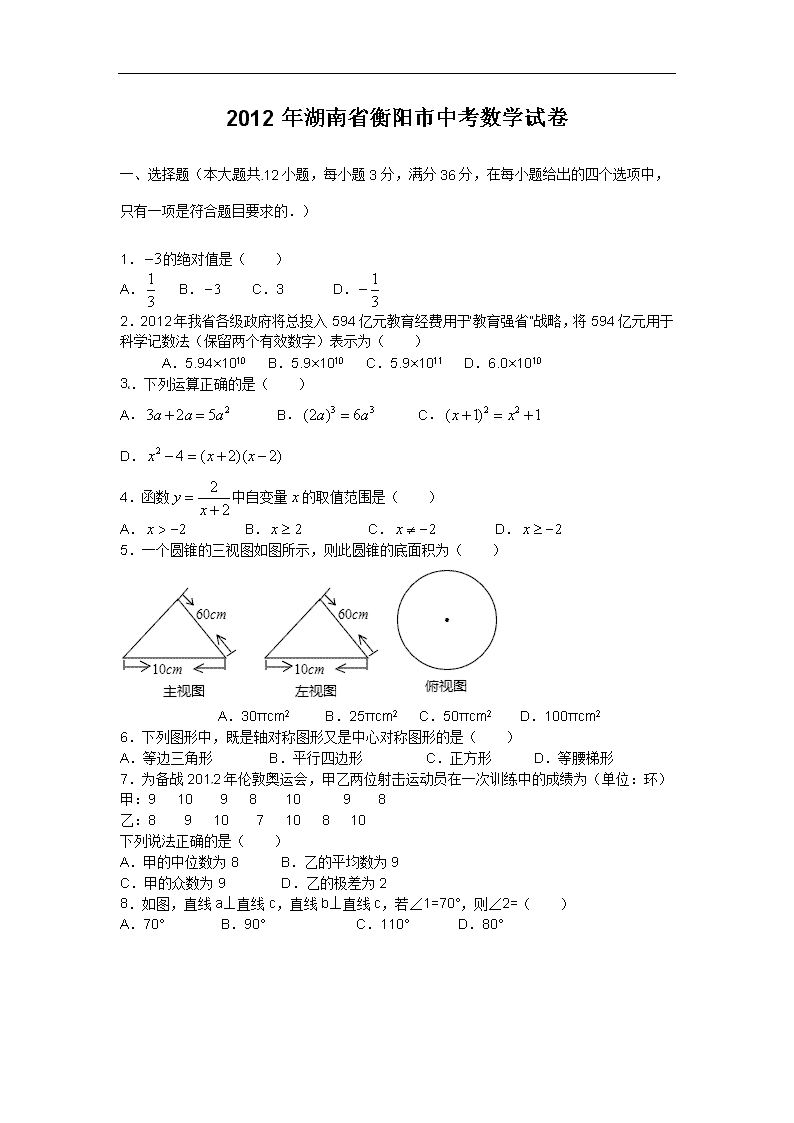
‎2012年湖南省衡阳市中考数学试卷 一、选择题（本大题共12小题，每小题3分，满分36分，在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1．的绝对值是（　　）‎ A． B． C．3 D．‎ ‎2．2012年我省各级政府将总投入594亿元教育经费用于“教育强省”战略，将594亿元用于科学记数法（保留两个有效数字）表示为（　　）‎ A．5.94×1010 B．5.9×1010 C．5.9×1011 D．6.0×1010‎ ‎3．下列运算正确的是（　　）‎ A． B． C． D．‎ ‎4．函数中自变量的取值范围是（　　）‎ A． B． C． D．‎ ‎5．一个圆锥的三视图如图所示，则此圆锥的底面积为（　　） ‎ A．30πcm2 B．25πcm2 C．50πcm2 D．100πcm2‎ ‎6．下列图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A．等边三角形 B．平行四边形 C．正方形 D．等腰梯形 ‎7．为备战2012年伦敦奥运会，甲乙两位射击运动员在一次训练中的成绩为（单位：环） 甲：9 10 9 8 10 9 8‎ 乙：8 9 10 7 10 8 10 ‎ 下列说法正确的是（　　）‎ A．甲的中位数为8 B．乙的平均数为9 ‎ C．甲的众数为9 D．乙的极差为2‎ ‎8．如图，直线a⊥直线c，直线b⊥直线c，若∠1=70°，则∠2=（　　）‎ A．70° B．90° C．110° D．80°‎ ‎9．掷两枚普通正六面体骰子，所得点数之和为11的概率为（　　）‎ A． B． C． D．‎ ‎10．已知⊙O的直径等于12cm，圆心O到直线l的距离为5cm，则直线l与⊙O的交点个数为（　　）‎ A．0 B．1 C．2 D．无法确定 ‎11．为了丰富同学们的课余生活，体育委员小强到体育用品商店购羽毛球拍和乒乓球拍，若购1副羽毛球拍和1副乒乓球拍共需50元，小强一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍，若设每副羽毛球拍为x元，每副乒乓球拍为y元，列二元一次方程组得（　　）‎ A． B． C． D．‎ ‎12．如图为二次函数的图象，则下列说法：‎ ‎① ② ③ ④当时，‎ 其中正确的个数为（　　）‎ A．1 B．2 C．3 D．4‎ 二、填空题（本大题共8小题，每小题3分，满分24分）‎ ‎13．计算 = 。‎ ‎14．分式方程 的解为 。 [来源:学,科,网][来源:学.科.网Z.X.X.K]‎ ‎15．如图，反比例函数的图象经过点P，则= 。‎ ‎16．某校为了丰富学生的课外体育活动，欲增购一批体育器材，为此该校对一部分学生进行了一次题为“你喜欢的体育活动”的问卷调查（每人限选一项） 根据收集到的数据，绘制成如图的统计图（不完整）： 根据图中提供的信息得出“跳绳”部分学生共有 人．[来源:学。科。网Z。X。X。K]‎ ‎17．如图，⊙O的半径为6cm，直线AB是⊙O的切线，切点为点B，弦BC∥AO，‎ 若∠A=30°，则劣弧的长为 cm．‎ ‎ ‎ ‎18．如图，一次函数的图象与正比例函数的图象平行且经过点A（1，-2），则 ．‎ ‎19．如图，菱形ABCD的周长为20cm，且，则菱形ABCD的面积为 cm2．‎ ‎ ‎ ‎20．观察下列等式 ① ‎ ‎② ‎ ‎ ③ … 根据上述规律，计算 。‎ 三、解答题（本大题共8小题，满分60分）‎ ‎21．计算：‎ ‎22．解不等式组 ，并把解集在数轴上表示出来．‎ ‎23．如图，AF=DC，BC∥EF，请只补充一个条件，使得△ABC≌△DEF，并说明理由．‎ ‎24．如图，一段河坝的横截面为梯形ABCD，试根据图中数据，求出坝底宽AD．（i=CE：ED，单位：m）‎ ‎25．在一个不透明的口袋里装有分别标有数字1，2，3，4四个小球，除数字不同外，小球没有任何区别，每次实验先搅拌均匀． （1）若从中任取一球，球上的数字为偶数的概率为多少？ （2）若从中任取一球（不放回），再从中任取一球，请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率． （3）若设计一种游戏方案：从中任取两球，两个球上的数字之差的绝对值为1为甲胜，否则为乙胜，请问这种游戏方案设计对甲、乙双方公平吗？说明理由．‎ ‎ 显示解析 [来源:Z&xx&k.Com][来源:学科网ZXXK]‎ ‎26．如图，AB是⊙O的直径，动弦CD垂直AB于点E，过点B作直线BF∥CD交AD的延长线于点F，若AB=10cm． （1）求证：BF是⊙O的切线． （2）若AD=8cm，求BE的长． （3）若四边形CBFD为平行四边形，则四边形ACBD为何种四边形？并说明理由．‎ ‎ ‎ ‎27．如图，A、B两点的坐标分别是（8，0）、（0，6），点P由点B出发沿BA方向向点A作匀速直线运动，速度为每秒3个单位长度，点Q由A出发沿AO（O为坐标原点）方向向点O作匀速直线运动，速度为每秒2个单位长度，连接PQ，若设运动时间为秒．解答如下问题： （1）当t为何值时，PQ∥BO？ （2）设△AQP的面积为S， ①求S与t之间的函数关系式，并求出S的最大值； ②若我们规定：点P、Q的坐标分别为，则新坐标称为“向量PQ”的坐标．当S取最大值时，求“向量PQ”的坐标．‎ ‎ ‎ ‎28．如图所示，已知抛物线的顶点为坐标原点O，矩形ABCD的顶点A，D在抛物线上，且AD平行x轴，交y轴于点F，AB的中点E在x轴上，B点的坐标为（2，1），点P（a，b）在抛物线上运动．（点P异于点O） （1）求此抛物线的解析式． （2）过点P作CB所在直线的垂线，垂足为点R， ①求证：PF=PR； ②是否存在点P，使得△PFR为等边三角形？若存在，求出点P的坐标；若不存在，请说明理由； ③延长PF交抛物线于另一点Q，过Q作BC所在直线的垂线，垂足为S，试判断△RSF的形状．‎ ‎ ‎