中考数学总复习几何综合问题 21页

‎2019届中考数学总复习：几何综合问题 ‎【中考展望】‎ ‎ 几何综合题是中考试卷中常见的题型，大致可分为几何计算型综合题与几何论证型综合题，它主要考查学生综合运用几何知识的能力.这类题型在近几年全国各地中考试卷中占有相当的分量，不仅有选择题、填空题、几何推理计算题以及代数与几何的综合计算题,还有更注重考查学生分析问题和解决问题能力的探究性的问题、方案设计的问题等等.主要特点是图形较复杂，覆盖面广、涉及的知识点较多，题设和结论之间的关系较隐蔽，常常需要添加辅助线来解答.‎ 几何综合题的呈现形式多样，如折叠类型、探究型、开放型、运动型、情景型等，背景鲜活，具有实用性和创造性，考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力.‎ 以几何为主的综合题常常在一定的图形背景下研究以下几个方面的问题：‎ ‎1、证明线段、角的数量关系（包括相等、和、差、倍、分及比例关系等）；‎ ‎2、证明图形的位置关系（如点与线、线与线、线与圆、圆与圆的位置关系等）；‎ ‎3、几何计算问题；‎ ‎4、动态几何问题等.‎ ‎【方法点拨】‎ 一、几何计算型综合问题，常常涉及到以下各部分的知识：‎ ‎1、与三角形有关的知识；‎ ‎2、等腰三角形，等腰梯形的性质；‎ ‎3、直角三角形的性质与三角函数；‎ ‎4、平行四边形的性质；‎ ‎5、全等三角形，相似三角形的性质；‎ ‎6、垂径定理，切线的性质，与正多边形有关的计算；‎ ‎7、弧长公式与扇形面积公式.‎ 二、几何论证型综合题的解答过程，要注意以下几个方面：‎ ‎1、注意图形的直观提示，注意观察、分析图形，把复杂的图形分解成几个基本图形，通过 添加辅助线补全或构造基本图形；‎ ‎2、注意分析挖掘题目的隐含条件、发展条件，为解题创造条件打好基础，要由已知联想经 验，由未知联想需要，不断转化条件和结论来探求思路，找到解决问题的突破点；‎ ‎3、要运用转化的思想解决几何证明问题，运用方程的思想解决几何计算问题，还要灵活运用 数学思想方法如数形结合、分类讨论、转化、方程等思想来解决问题.‎ ‎【典型例题】‎ 类型一、动态几何型问题 ‎1．如图，在矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从点A开始向点B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发，用t(s)表示移动的时间（0≤t≤6），那么：‎ ‎⑴当t为何值时，△QAP为等腰直角三角形？‎ ‎⑵求四边形QAPC的面积；提出一个与计算结果有关的结论；‎ ‎⑶当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似？‎ D A B C Q P ‎【思路点拨】⑴中应由△QAP为等腰直角三角形这一结论，需补充条件AQ=AP，由AQ=6－t，AP=2t，可求出t的值；‎ ‎⑵中四边形QAPC是一个不规则图形，其面积可由矩形面积减去△DQC与△PBC的面积求出；‎ ‎⑶中由于题目中未给出三角形的相似对应方式，因此需分类讨论.‎ ‎【答案与解析】‎ 解：（1）对于任何时刻t，AP=2t，DQ=t，QA=6-t． 当QA=AP时，△QAP为等腰直角三角形，即6-t=2t，解得：t=2（s）， 所以，当t=2s时，△QAP为等腰直角三角形．‎ ‎（2）在△QAC中，QA=6-t，QA边上的高DC=12， ∴S△QAC=QA•DC=（6-t）•12=36-6t． 在△APC中，AP=2t，BC=6， ∴S△APC=AP•BC=•2t•6=6t． ∴S四边形QAPC=S△QAC+S△APC=（36-6t）+6t=36（cm2）． 由计算结果发现：在P、Q两点移动的过程中，四边形QAPC的面积始终保持不变．（也可提出：P、Q两点到对角线AC的距离之和保持不变）‎ ‎（3）根据题意，可分为两种情况，在矩形ABCD中： ①当时，△QAP∽△ABC，则有： ，解得t=1.2（s）， 即当t=1.2s时，△QAP∽△ABC； ②当时，△PAQ∽△ABC，则有： ，解得t=3（s）， 即当t=3s时，△PAQ∽△ABC； 所以，当t=1.2s或3s时，以点Q、A、P为顶点的三角形与△ABC相似．‎ ‎【总结升华】本题是动态几何题，同时也是一道探究题．要求学生具有一定的发现、归纳和表达能力，这就要求我们通过计算分析，抓住其本质，揭示出变中不变的规律．四边形QAPC的面积也可由△QAC与△CAP的面积求出，；⑶中考查了分类讨论的数学思想，结论具有一定的开放性.‎ ‎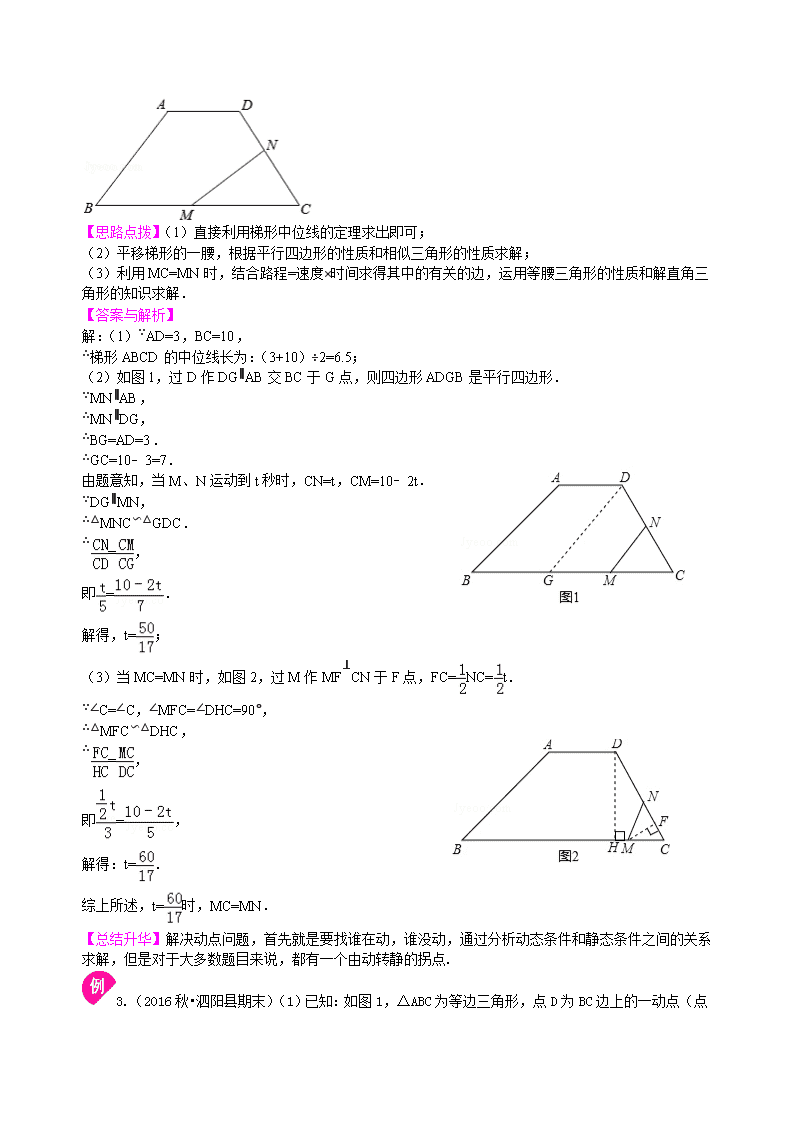2．（永春县校级月考）如图，在梯形ABCD中，AD∥BC，AD=3，CD=5，BC=10，梯形的高为4，动点M从点B出发沿线段BC以每秒2个单位长度向终点C运动；动点N同时从点C出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t秒 ‎（1）直接写出梯形ABCD的中位线长；‎ ‎（2）当MN∥AB时，求t的值；‎ ‎（3）试探究：t为何值时，使得MC=MN．‎ ‎【思路点拨】（1）直接利用梯形中位线的定理求出即可；‎ ‎（2）平移梯形的一腰，根据平行四边形的性质和相似三角形的性质求解；‎ ‎（3）利用MC=MN时，结合路程=速度×时间求得其中的有关的边，运用等腰三角形的性质和解直角三角形的知识求解．‎ ‎【答案与解析】‎ 解：（1）∵AD=3，BC=10，‎ ‎∴梯形ABCD的中位线长为：（3+10）÷2=6.5；‎ ‎（2）如图1，过D作DG∥AB交BC于G点，则四边形ADGB是平行四边形．‎ ‎∵MN∥AB，‎ ‎∴MN∥DG，‎ ‎∴BG=AD=3．‎ ‎∴GC=10﹣3=7．‎ 由题意知，当M、N运动到t秒时，CN=t，CM=10﹣2t．‎ ‎∵DG∥MN，‎ ‎∴△MNC∽△GDC．‎ ‎∴=，‎ 即=．‎ 解得，t=；‎ ‎（3）当MC=MN时，如图2，过M作MF⊥CN于F点，FC=NC=t．‎ ‎∵∠C=∠C，∠MFC=∠DHC=90°，‎ ‎∴△MFC∽△DHC，‎ ‎∴=，‎ 即=，‎ 解得：t=．‎ 综上所述，t=时，MC=MN．‎ ‎【总结升华】解决动点问题，首先就是要找谁在动，谁没动，通过分析动态条件和静态条件之间的关系求解，但是对于大多数题目来说，都有一个由动转静的拐点.‎ ‎3.（2016秋•泗阳县期末）（1）已知：如图1，△‎ ABC为等边三角形，点D为BC边上的一动点（点D不与B、C重合），以AD为边作等边△ADE，连接CE．求证：①BD=CE，②AC=CE+CD；聪明的小明做完上题后进行了进一步变式探究．‎ ‎（2）如图2，在△ABC中，∠BAC=90°，AC=AB，点D为BC上的一动点（点D不与B、C重合），以AD为边作等腰Rt△ADE，∠DAE=90°（顶点A、D、E按逆时针方向排列），连接CE，类比题（1），请你猜想线段BD、CD、DE之间会有怎样的关系，请直接写出，不需论证；‎ ‎（3）如图3，在（2）的条件下，若D点在BC的延长线上运动，以AD为边作等腰Rt△ADE，∠DAE=90°（顶点A、D、E按逆时针方向排列），连接CE．‎ ‎①题（2）的结论还成立吗？请说明理由；‎ ‎②连结BE，若BE=10，BC=6，求AE的长．‎ ‎【思路点拨】（1）①根据等边三角形的性质就可以得出∠BAC=∠DAE=60°，AB=BC=AC，AD=DE=AE，进而就可以得出△ABD≌△ACE，即可得出结论；②由△ABD≌△ACE，以及等边三角形的性质，就可以得出AC=DC+CE；‎ ‎（2）先判定△ABD≌△ACE（SAS），得出∠B=∠ACE=45°，BD=CE，在Rt△DCE中，根据勾股定理得出CE2+CD2=DE2，即可得到BD2+CD2=DE2；‎ ‎（3）①运用（2）中的方法得出BD2+CD2=DE2；②根据Rt△BCE中，BE=10，BC=6，求得CE==8，进而得出CD=8﹣6=2，在Rt△DCE中，求得DE==，最后根据△ADE是等腰直角三角形，即可得出AE的长．‎ ‎【答案与解析】‎ 解：（1）①如图1，∵△ABC和△ADE是等边三角形，‎ ‎∴∠BAC=∠DAE=60°，AB=BC=AC，AD=DE=AE，‎ ‎∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，‎ ‎∴∠BAD=∠EAC．‎ 在△ABD和△ACE中，‎ ‎，‎ ‎∴△ABD≌△ACE（SAS），‎ ‎∴BD=CE；‎ ‎②∵BD=CE，AC=BC，‎ 又∵BC=BD+CD，‎ ‎∴AC=CE+CD；‎ ‎（2）BD2+CD2=DE2．‎ 证明：如图2，∵∠BAC=∠DAE=90°，‎ ‎∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，‎ 即∠BAD=∠CAE，‎ 在△ABD与△ACE中，‎ ‎，‎ ‎∴△ABD≌△ACE（SAS），‎ ‎∴∠B=∠ACE=45°，BD=CE，‎ ‎∴∠B+∠ACB=∠ACE+∠ACB=90°，‎ ‎∴∠BCE=90°，‎ ‎∴Rt△DCE中，CE2+CD2=DE2，‎ ‎∴BD2+CD2=DE2；‎ ‎（3）①（2）中的结论还成立．‎ 理由：如图3，∵∠BAC=∠DAE=90°，‎ ‎∴∠BAC+∠DAC=∠DAE+∠DAC，‎ 即∠BAD=∠CAE，‎ 在△ABD与△ACE中，‎ ‎，‎ ‎∴△ABD≌△ACE（SAS），‎ ‎∴∠ABC=∠ACE=45°，BD=CE，‎ ‎∴∠ABC+∠ACB=∠ACE+∠ACB=90°，‎ ‎∴∠BCE=90°=∠ECD，‎ ‎∴Rt△DCE中，CE2+CD2=DE2，‎ ‎∴BD2+CD2=DE2；‎ ‎②∵Rt△BCE中，BE=10，BC=6，‎ ‎∴CE==8，‎ ‎∴BD=CE=8，‎ ‎∴CD=8﹣6=2，‎ ‎∴Rt△DCE中，DE==，‎ ‎∵△ADE是等腰直角三角形，‎ ‎∴AE=．‎ ‎【总结升华】本题属于三角形综合题，主要考查了全等三角形的判定与性质，等边三角形的性质，等腰直角三角形的性质以及勾股定理的综合应用.‎ 举一反三：‎ ‎【变式】△ABC是等边三角形，P为平面内的一个动点，BP=BA，若＜∠PBC＜180°，且∠PBC平分线上的一点D满足DB=DA，‎ ‎（1）当BP与BA重合时（如图1），∠BPD= °；‎ ‎（2）当BP在∠ABC的内部时（如图2），求∠BPD的度数；‎ ‎（3）当BP在∠ABC的外部时，请你直接写出∠BPD的度数，并画出相应的图形．‎ ‎ ‎ ‎ ‎ ‎【答案】（1）∠BPD= 30°； ‎ ‎（2）如图3，连结CD． ‎ ‎ ‎ ‎∵ 点D在∠PBC的平分线上，‎ ‎ ∴ ∠1=∠2．‎ ‎ ∵ △ABC是等边三角形，‎ ‎ ∴ BA=BC=AC，∠ACB= 60°．‎ ‎ ∵ BP=BA，‎ ‎ ∴ BP=BC．‎ ‎ ∵ BD= BD，‎ ‎ ∴ △PBD≌△CBD．‎ ‎ ∴ ∠BPD=∠3．‎ ‎ ∵ DB=DA，BC=AC，CD=CD，‎ ‎ ∴ △BCD≌△ACD．‎ ‎ ∴ ． ‎ ‎ ∴ ∠BPD =30°． ‎ ‎ （3）∠BPD= 30°或 150°. ‎ ‎ ‎ 类型二、几何计算型问题 ‎【高清课堂：几何综合问题 例1 】‎ ‎4.如图，直角三角形纸片ABC中，∠ACB=90°，AC=8，BC=6．折叠该纸片使点B与点C重合，折痕与AB、BC的交点分别为D、E. ‎ ‎(1) DE的长为 ；‎ ‎(2) 将折叠后的图形沿直线AE剪开，原纸片被剪成三块，其中最小一块的面积等于 ．‎ ‎ ‎ ‎【思路点拨】（1）由题意可得：DE是线段BC的垂直平分线，易证DE∥AC，即DE是△ABC的中位线，即可求得DE的长； （2）由DE∥AC，DE=AC，易证△AOC∽△EOD，根据相似三角形的对应边成比例，即可求得OA：OE=2，然后求得△ACE的面积，利用等高三角形的面积比等于对应底的比，即可求得答案．‎ ‎【答案与解析】‎ ‎（1）根据题意得：DE⊥BC，CE=BE， ∵∠ACB=90°， 即AC⊥BC， ∴DE∥AC， ∴AD=BD， ∴DE=AC=×8=4；‎ ‎（2）∵DE∥AC，DE=AC， ∴△AOC∽△EOD， ∴OA：OE=AC：DE=2， ∵CE=BC=×6=3， ∵∠ACB=90°，AC=8， ∴S△ACE=CE•AC=×3×8=12， ∴S△OCE=S△ACE=4， ∴S△ADE+S△ODE=S△ABC-4-12=8， ∴其中最小一块的面积等于4．‎ ‎【总结升华】考查了折叠的性质、直角三角形的性质、三角形中位线的性质以及相似三角形的判定与性质．此题难度适中，注意数形结合思想的应用，注意掌握折叠前后图形的对应关系,是一道典型的几何综合题．‎ 举一反三 ‎【变式】在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，将△ABE沿AE所在直线翻折得△AB′E，那么△AB′E与四边形AECD重叠部分的面积是 . ‎ ‎【答案】在Rt△ABE中，∵∠B=45°，AB=2，‎ ‎∴AE=BE= ，∴S△ABE=1．‎ 由翻折的性质可知：△AB′E≌△ABE，∴EB′=EB=‎ ‎∴B′C=BB′－BC=2－2，‎ ‎∵四边形ABCD是菱形，∴CF∥BA．‎ ‎∴∠ B′FC=∠B′AB=90°, ∠B′CF=∠B=45°‎ ‎∴CF=， ∴S ==3－2 ‎ ‎∴S阴=S－S=2－2．‎ ‎ ‎ ‎5．如图，在等腰梯形ABCD中，AB∥DC，∠A=45°，AB=10 cm，CD=4 cm，等腰直角△PMN的斜边MN=10 cm， A点与N点重合， MN和AB在一条直线上，设等腰梯形ABCD不动，等腰直角△PMN沿AB所在直线以1 cm／s的速度向右移动，直到点N与点B重合为止. (1)等腰直角△PMN在整个移动过程中与等腰梯形ABCD重叠部分的形状由________形变化为________形； (2)设当等腰直角△PMN移动x (s)时，等腰直角△PMN与等腰梯形ABCD重叠部分的面积为y(cm2)，求y与x之间的函数关系式； (3)当x=4 (s)时，求等腰直角△PMN与等腰梯形ABCD重叠部分的面积. 　 　　‎ ‎【思路点拨】（1）根据已知求出∠PNM=∠DAB=45°，求出∠AEN，根据等腰直角三角形的判定判断即可；推出∠DAB=∠PNM=45°，根据等腰梯形的判定判断即可； （2）可分为以下两种情况： ①当0＜x≤6时，重叠部分的形状为等腰直角△EAN，AN=x（cm），过点E作EH⊥AB于点H，则EH平分AN，求出EH，根据三角形的面积公式求出即可；②当6＜x≤10时，重叠部分的形状是等腰梯形ANED，求出AN=x（cm），CE=BN=10-x，DE=x-6，过点D作DF⊥AB于F，过点C作CG⊥AB于G，求出DF，代入梯形面积公式求出即可.‎ ‎【答案与解析】‎ ‎(1)等腰直角三角形；等腰梯形. (2)等腰直角△‎ PMN在整个移动过程中与等腰梯形ABCD重合部分图形的形状可分为以下两种情况： 　 　　①当0＜x≤6时，重叠部分的形状为等腰直角△EAN(如图①).此时AN=x(cm)，过点E作EH⊥AB于点H，则EH平分AN， 　　∴EH=AN=x，　 ∴y=S△ANE=AN·EH=x·x=. 　　②当6＜x≤10时，重叠部分的形状是等腰梯形ANED(如图②)． 　　　此时，AN=x(cm)，∵∠PNM=∠B=45°，∴EN∥BC， 　　　∵CE∥BN，∴四边形ENBC是平行四边形， 　　　CE=BN=10-x，DE=4-(10-x)=x-6， 　　　过点D作DF⊥AB于F，过点C作CG⊥AB于G， 　　　则AF=BG，DF=AF=(10-4)=3， 　　　∴y=S梯形ANED=(DE+AN)·DF=(x-6+x)×3=3x-9. 　　　综上，. 　　(3)当等腰直角△PMN运动到PN边经过点D时，移动时间为6(s)， 　　　 ∴当x=4 (s)时，y=x2=×42=4. 　　 　∴当x=4 (s)时，等腰直角△PMN与等腰梯形ABCD重叠部分的面积是4cm2.‎ ‎【总结升华】本题主要考查对等腰梯形的性质和判定，等腰三角形的性质和判定，三角形的内角和定理，三角形的面积，平移的性质，等腰直角三角形等知识点的理解和掌握，综合运用这些性质进行推理和计算是解此题的关键．‎ 举一反三：‎ ‎【变式】如图，等腰梯形ABCD中，AB=15，AD=20，∠C=30°．点M、N同时以相同速度分别从点A、点D开始在AB、AD(包括端点)上运动. 　　　　 　　(1)设ND的长为x，用x表示出点N到AB的距离，并写出x的取值范围； 　　(2)当五边形BCDNM面积最小时，请判断△AMN的形状.‎ ‎【答案】　‎ ‎(1)过点N作BA的垂线NP，交BA的延长线于点P.则AM=x，AN=20-x. 　　　 ∵四边形ABCD是等腰梯形，AB∥CD，∠D=∠C=30°， 　 　　∴∠PAN=∠‎ D=30°. 　　　 在Rt△APN中，PN=AN×sin∠PAN=(20-x)，即N到AB距离为(20-x). 　　　 ∵点N在AD上，0≤x≤20，点M在AB上，0≤x≤15，∴x取值范围是0≤x≤15. 　　(2)∵S五边形BCDNM=S梯形-S△AMN且S梯形为定值， 　　　 ∴当S五边形BCDMN最小时，应使S△AMN最大 　　　 据(1)，S△AMN=AM·NP=. 　　　 ∵＜0，∴当x=10时，S△AMN有最大值. 　　　 ∴当x=10时，S五边形BCDNM有最小值． 　　　 当x=10时， 即ND=AM=10，AN=AD-ND=10，即AM=AN． 　　　 则当五边形BCDNM面积最小时，△AMN为等腰三角形.‎ ‎【巩固练习】‎ 一、选择题 ‎1.（2016•天水）如图，边长为2的等边△ABC和边长为1的等边△A′B′C′，它们的边B′C′，BC位于同一条直线l上，开始时，点C′与B重合，△ABC固定不动，然后把△A′B′C′自左向右沿直线l平移，移出△ABC外（点B′与C重合）停止，设△A′B′C′平移的距离为x，两个三角形重合部分的面积为y，则y关于x的函数图象是（　　）‎ A． B． C． D．‎ ‎2.如图，将直角三角形ABC沿着斜边AC的方向平移到△DEF的位置（A、D、C、F四点在同一条直线上）．直角边DE交BC于点G．如果BG=4，EF=12，△BEG的面积等于4，那么梯形ABGD的面积是（　　）‎ A.16 B.20 C.24 D.28‎ 二、填空题 ‎3.（2016•海淀区二模）据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度．如图所示，木杆EF的长为2m，它的影长FD为3m，测得OA为201m，则金字塔的高度BO为　 　 m．‎ ‎4.如图，线段AB=8cm，点C是AB上任意一点（不与点A、B重合），分别以AC、BC为斜边在AB的同侧作等腰直角三角形（△AMC和△CNB），则当BC=_____________cm时，两个等腰直角三角形的面积和最小．‎ 三、解答题 ‎5.有一根直尺的短边长2cm，长边长10cm，还有一块锐角为45°‎ 的直角三角形纸板，它的斜边长12cm．如图①，将直尺的短边DE与直角三角形纸板的斜边AB重合，且点D与点A重合； 将直尺沿AB方向平移（如图②），设平移的长度为xcm（ 0≤x≤0 ），直尺和三角形纸板的重叠部分（图中阴影部分）的面积为Scm2． （1）当x=0时（如图①），S=________； （2）当0＜x≤4时（如图②），求S关于x的函数关系式； （3）当4＜x＜6时，求S关于x的函数关系式； （4）直接写出S的最大值． ‎ ‎6. 问题情境：如图①，在△ABD与△CAE中，BD=AE，∠DBA=∠EAC，AB=AC，易证：△ABD≌△CAE．（不需要证明） 特例探究：如图②，在等边△ABC中，点D、E分别在边BC、AB上，且BD=AE，AD与CE交于点F．求证：△ABD≌△CAE． 归纳证明：如图③，在等边△ABC中，点D、E分别在边CB、BA的延长线上，且BD=AE．△ABD与△CAE是否全等？如果全等，请证明；如果不全等，请说明理由． 拓展应用：如图④，在等腰三角形中，AB=AC，点O是AB边的垂直平分线与AC的交点，点D、E分别在OB、BA的延长线上．若BD=AE，∠BAC=50°，∠AEC=32°，求∠BAD的度数．‎ ‎ ‎ ‎7.如图正三角形ABC的边长为6cm,⊙O的半径为rcm，当圆心O从点A出发，沿着线路AB－BC－CA运动，回到点A时，⊙O随着点O的运动而移动.‎ ‎⑴若r=cm,求⊙O首次与BC边相切时，AO的长；‎ ‎⑵在⊙O移动过程中，从切点的个数来考虑，相切有几种不同的情况？写出不同情况下r的取值范围及相应的切点的个数；‎ ‎⑶设⊙O在整个移动过程中，在△ABC内部，⊙O未经过的部分面积为S，在S＞0时，求关于r的函数解析式，并写出自变量r的取值范围.‎ A(O)‎ O B C ‎8.（2015•德州）（1）问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°，求证：AD•BC=AP•BP．‎ ‎（2）探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．‎ ‎（3）应用：请利用（1）（2）获得的经验解决问题：‎ 如图3，在△ABD中，AB=6，AD=BD=5，点P以每秒1个单位长度的速度，由点A出了，沿边AB向点B运动，且满足∠DPC=∠A，设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切时，求t的值．‎ ‎9.如图，直角梯形ABCD中，AD∥BC，∠B=90°，AB=12 cm，BC=9 cm，DC=13 cm，点P是线段AB上一个动点.设BP为x cm，△PCD的面积为y cm2．‎ ‎(1)求AD 的长；‎ ‎(2)求y与x之间的函数关系式，并求出当x为何值时，y有最大值？最大值是多少？‎ ‎(3)在线段AB上是否存在点P，使得△PCD是直角三角形？若存在，求出x的值；若不存在，‎ 请说明理由. 　 　　　 　　‎ ‎10.如图，平行四边形ABCD中，AB=10，AD=6，∠A=60°，点P从点A出发沿边线AB—BC以每秒1个单位长的速度向点C运动，当P与C重合时停下运动，过点P作AB的垂线PQ交AD或DC于Q.设P运动时间为t秒，直线PQ扫过平行四边形ABCD的面积为S.求S关于t的函数解析式. 　 　　　 ‎ ‎【答案与解析】‎ 一、选择题 ‎1.【答案】B.‎ ‎【解析】如图1所示：当0＜x≤1时，过点D作DE⊥BC′．‎ ‎∵△ABC和△A′B′C′均为等边三角形，‎ ‎∴△DBC′为等边三角形．‎ ‎∴DE=BC′=x．‎ ‎∴y=BC′•DE=x2．‎ 当x=1时，y=，且抛物线的开口向上．‎ 如图2所示：1＜x≤2时，过点A′作A′E⊥B′C′，垂足为E．‎ ‎∵y=B′C′•A′E=×1×=．‎ ‎∴函数图象是一条平行与x轴的线段．‎ 如图3所示：2＜x≤3时，过点D作DE⊥B′C，垂足为E．‎ y=B′C•DE=（x﹣3）2，‎ 函数图象为抛物线的一部分，且抛物线开口向上．‎ 故选：B．‎ ‎2.【答案】B.‎ 二、填空题 ‎3.【答案】134.‎ ‎4.【答案】4.‎ 三、解答题 ‎5.【答案与解析】‎ ‎（1）由题意可知： 当x=0时， ∵△ABC是等腰直角三角形， ∴AE=EF=2， 则阴影部分的面积为：S=×2×2=2； 故答案为：2；‎ ‎（2）在Rt△ADG中，∠A=45°， ∴DG=AD=x，同理EF=AE=x+2， ∴S梯形DEFG=（x+x+2）×2=2x+2． ∴S=2x+2； （3）①当4＜x＜6时（图1）， ‎ GD=AD=x，EF=EB=12-（x+2）=10-x， 则S△ADG=AD•DG=x2，‎ S△BEF=（10-x）2， 而S△ABC=×12×6=36，‎ S△BEF=（10-x）2， ‎ ‎∴S=36-x2-（10-x）2=-x2+10x-14， S=-x2+10x-14=-（x-5）2+11， ∴当x=5，（4＜x＜6）时，S最大值=11． （4）S最大值=11．‎ ‎6.【答案与解析】‎ 特例探究： 证明：∵△ABC是等边三角形， ∴AB=AC，∠DBA=∠EAC=60°， 在△ABD与△CAE中，‎ ‎， ∴△ABD≌△CAE（SAS）； 归纳证明：△ABD与△CAE全等．理由如下： ∵在等边△ABC中，AB=AC，∠ABC=∠BAC=60°， ∴∠DBA=∠EAC=120°． 在△ABD与△CAE中，‎ ‎， ∴△ABD≌△CAE（SAS）； 拓展应用：∵点O在AB的垂直平分线上， ∴OA=OB， ∴∠OBA=∠BAC=50°， ∴∠EAC=∠DBC． 在△ABD与△CAE中，， ∴△ABD≌△CAE（SAS）， ∴∠BDA=∠AEC=32°， ∴∠BAD=∠OBA-∠BDA=18°．‎ ‎7.【答案与解析】‎ ‎(1).设⊙O首次与BC相切于点D，则有OD⊥BC． 且OD=r=． 在直角三角形BDO中， ∵∠OBD=60°， ∴OB==2． ∴AO=AB-OB=6-2=4（厘米）； ‎ ‎（2）由正三角形的边长为6厘米．可得出它的一边上的高为3厘米． ①当⊙O的半径r=3厘米时，⊙O在移动中与△ABC的边共相切三次，即切点个数为3； ②当0＜r＜3时，⊙O在移动中与△ABC的边相切六次，即切点个数为6； ③当r＞3时，⊙O与△ABC不能相切，即切点个数为0． （3）如图，易知在S＞0时，⊙O在移动中，在△ABC内部为经过的部分为正三角形．‎ ‎ 记作△A′B′C′，这个正三角形的三边分别于原正三角形三边平行，且平行线间的距离等于r． 连接AA′，并延长AA′，分别交B′C′，BC于E，F两点． 则AF⊥BC，A′E⊥B′C′，且EF=r． 又过点A′作A′G⊥AB于G，则A′G=r． ∵∠GAA′=30°， ∴AA′=2x． ∴△A′B′C′的高A′E=AF-3r=9-3r， B′C′=‎ A′E=2（3-r）． ∴△A′B′C′的面积S=B′C′•A′E=3‎ ‎（3-r）2． ∴所求的解析式为S=3（3-r）2（0＜r＜3）．‎ ‎8.【答案与解析】‎ 解：（1）如图1，‎ ‎∵∠DPC=∠A=∠B=90°，‎ ‎∴∠ADP+∠APD=90°，‎ ‎∠BPC+∠APD=90°，‎ ‎∴∠ADP=∠BPC，‎ ‎∴△ADP∽△BPC，‎ ‎∴=，‎ ‎∴AD•BC=AP•BP；‎ ‎（2）结论AD•BC=AP•BP仍然成立．‎ 理由：如图2，‎ ‎∵∠BPD=∠DPC+∠BPC，∠BPD=∠A+∠ADP，‎ ‎∴∠DPC+∠BPC=∠A+∠ADP．‎ ‎∵∠DPC=∠A=∠B=θ，‎ ‎∴∠BPC=∠ADP，‎ ‎∴△ADP∽△BPC，‎ ‎∴=，‎ ‎∴AD•BC=AP•BP；‎ ‎（3）如图3，‎ 过点D作DE⊥AB于点E．‎ ‎∵AD=BD=5，AB=6，‎ ‎∴AE=BE=3．‎ 由勾股定理可得DE=4．‎ ‎∵以点D为圆心，DC为半径的圆与AB相切，‎ ‎∴DC=DE=4，‎ ‎∴BC=5﹣4=1．‎ 又∵AD=BD，‎ ‎∴∠A=∠B，‎ ‎∴∠DPC=∠A=∠B．‎ 由（1）、（2）的经验可知AD•BC=AP•BP，‎ ‎∴5×1=t（6﹣t），‎ 解得：t1=1，t2=5，‎ ‎∴t的值为1秒或5秒．‎ ‎9.【答案与解析】‎ ‎(1)如图1，作DE⊥BC于点E． 据题意知，四边形ABED是矩形，AB=DE，AD=BE. 在Rt△DEC中，∠DEC=90°，DE=12，CD=13， ∴ EC=5．　　　 ∴AD=BE=BC-EC=4． (2)若BP为x，则AP=12-x. S△BPC=BP·BC=x.　 S△APD=AP·AD=24-2x. ∴S△PCD=S梯形ABCD-S△BPC-S△APD=78-x-24+2x=-x+54. 即　 y=-x+54，0≤x≤12. 当x=0时，y取得最大值为54 cm2. (3)若△PCD是直角三角形，∵∠BCP＜90°，∴∠PCD≠90° ∴分两种情况讨论，如图2. ①当∠DPC=90°时 ∵∠APD+∠BPC=90°，∠BPC+∠PCB=90°， ∴∠APD=∠PCB.∴ △APD∽△BCP. ∴.即.解得x=6. ∠APD=∠BPC=45°的情况不存在，不考虑. ②当∠P1DC=90°时， 在Rt△P1BC中，P1C2=BP12+BC2=x2+92， 在Rt△P1AD中，P1D2=P1A2+AD2=(12-x)2+42‎ ‎， ∵∠P1DC=90°，CD2+P1D2=P1C2. 即132+(12-x)2+42=x2+92.解得. 综上，当x=6或，△PCD是直角三角形.‎ ‎10.【答案与解析】‎ 当Q点与D点重合时，AQ=AD=6，此时AP=AQ=3=t 　当P与B点重合时，t=10， 　当P点运动到C时，t=16， 　∴分三类情况讨论 (1)当0≤t≤3时，如图： 　 　AP=t，PQ=t， 　∴S=AP·PQ=t2 (2)当3＜t≤10时，示意图： 过D作DH⊥AB于H，AD=t， 则DH=ADsinA=6·=3，AH=ADcosA=3 ∴DQ=PH=AP-AH=t-3 ∴S=(AP+DQ)·DH 　 =(t+t-3)·3=3t- 　(3)当10＜t≤16时，如 图： 　 　　AB+BP=t 　　CP=AB+BC-(AB+BP)=16-t 　　∴CQ=CP=8- 　　QP=·CQ=8-t 　　∴S=S□ABCD-S△CPQ 　　　=AB·h-·CQ·PQ 　　 =10·3-·(8-)·(8-) 　　　=30-(64-8t+) 　　　= 　　综上，. ‎