中考数学基础热点专题 统计与概率含答案 5页

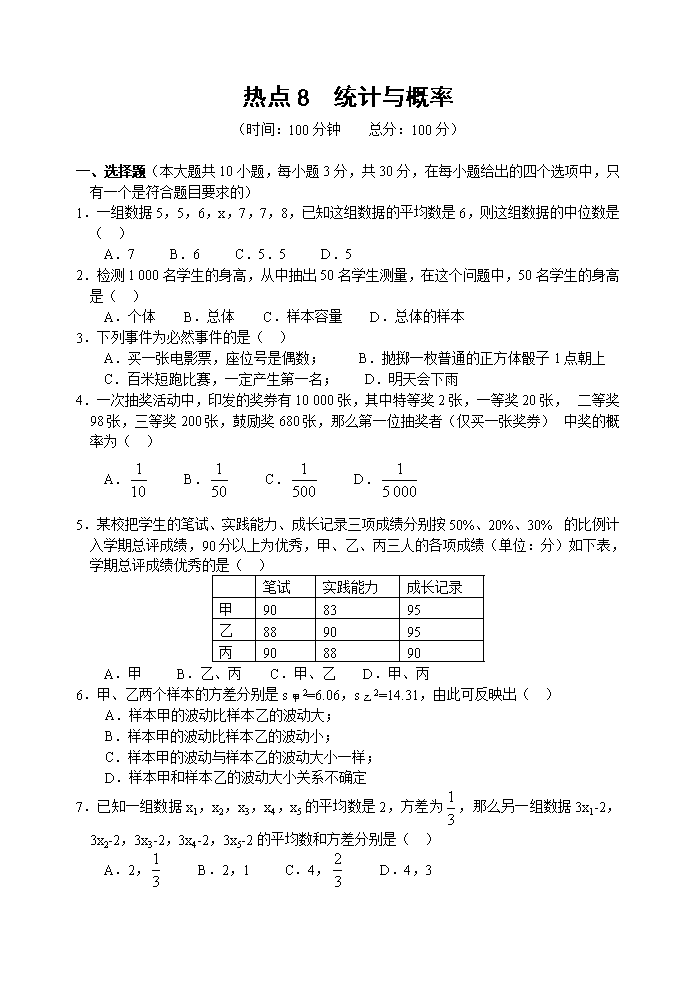
热点8 统计与概率 ‎（时间：100分钟 总分：100分）‎ 一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是符合题目要求的）‎ ‎1．一组数据5，5，6，x，7，7，8，已知这组数据的平均数是6，则这组数据的中位数是（ ）‎ ‎ A．7 B．‎6 C．5．5 D．5‎ ‎2．检测1 000名学生的身高，从中抽出50名学生测量，在这个问题中，50名学生的身高是（ ）‎ ‎ A．个体 B．总体 C．样本容量 D．总体的样本 ‎3．下列事件为必然事件的是（ ）‎ ‎ A．买一张电影票，座位号是偶数； B．抛掷一枚普通的正方体骰子1点朝上 ‎ C．百米短跑比赛，一定产生第一名； D．明天会下雨 ‎4．一次抽奖活动中，印发的奖券有10 000张，其中特等奖2张，一等奖20张，二等奖98张，三等奖200张，鼓励奖680张，那么第一位抽奖者（仅买一张奖券）中奖的概率为（ ）‎ ‎ A． B． C． D．‎ ‎5．某校把学生的笔试、实践能力、成长记录三项成绩分别按50%、20%、30%的比例计入学期总评成绩，90分以上为优秀，甲、乙、丙三人的各项成绩（单位：分）如下表，学期总评成绩优秀的是（ ）‎ 笔试 实践能力 成长记录 甲 ‎90‎ ‎83‎ ‎95‎ 乙 ‎88‎ ‎90‎ ‎95‎ 丙 ‎90‎ ‎88‎ ‎90‎ ‎ A．甲 B．乙、丙 C．甲、乙 D．甲、丙 ‎6．甲、乙两个样本的方差分别是s甲2=6.06，s乙2=14.31，由此可反映出（ ）‎ A．样本甲的波动比样本乙的波动大； ‎ B．样本甲的波动比样本乙的波动小；‎ C．样本甲的波动与样本乙的波动大小一样；‎ D．样本甲和样本乙的波动大小关系不确定 ‎7．已知一组数据x1，x2，x3，x4，x5的平均数是2，方差为，那么另一组数据3x1-2，3x2-2，3x3-2，3x4-2，3x5-2的平均数和方差分别是（ ）‎ ‎ A．2， B．2，‎1 C．4， D．4，3‎ ‎8．某班一次数学测验，其成绩统计如下表：‎ 分数 ‎50‎ ‎60‎ ‎70‎ ‎80‎ ‎90‎ ‎100‎ 人数 ‎1‎ ‎6‎ ‎12‎ ‎11‎ ‎15‎ ‎5‎ ‎ 则这个班此次测验的众数为（ ）‎ ‎ A．90分 B．‎15 C．100分 D．50分 ‎9．一组数据1，-1，0，-1，1的方差和标准差分别是（ ）‎ ‎ A．0，0 B．0.8，‎0.64 C．1，1 D．0.8，‎ ‎10．由小到大排列一组数据y1，y2，y3，y4，y5，其中每个数都小于-2，则对于样本1，y1，-y2，y3，-y4，y5的中位数是（ ）‎ ‎ A． B． C． D．‎ 二、填空题（本大题共8题，每题3分，共24分）‎ ‎11．若你想设计一个月内你家里丢弃塑料袋数目的情况，你一定不能选择_______统计图（填扇形、折线和条形）．‎ ‎12．如图，是世界人口扇形统计图，关系中国部分的圆心角的度数为______．‎ ‎13．在100件产品中有5件次品，则从中任取一件次品的概率为________．‎ ‎14．要了解全市中考生的数学成绩在某一范围内的学生所占比例的大小，需知道相应样本的________（填“平均数”“方差”或“频率分布”）．‎ ‎15．随机掷一枚均匀的硬币两次，至少有一次正面朝上的概率是_____．‎ ‎16．在一个有10万人的小镇上，随机调查了2 000人，其中有250人看中央电视台的早间新闻，在该镇随便问一人，他看早间新闻的概率大约是________．‎ ‎17．已知一组数据的方差是s2=[（x1-2.5）2+（x2-2.5）2+（x3-2.5）2+…+（x25-2.5）2]，则这组数据的平均数是_________．‎ ‎18．一组数据的方差为s2，将这组数据的每个数据都乘2，所得到的一组新数据的方差是________．‎ 三、解答题（本大题共46分，19～23题每题6分，24题、25题每题8分．解答题应写出文字说明、证明过程或演算步骤）‎ ‎19．已知一组数据6，2，4，2，3，5，2，4．‎ ‎（1）这组数据的样本容量是多少？（2）写出这组数据的众数和平均数．‎ ‎20．请你设计一个转盘游戏，使获一等奖的机会为，获二等奖的机会为，获得三等奖的机会为，并说明你的转盘游戏的中奖概率．‎ ‎21．根据下表制作扇形统计图，表示各种果树占果园总树木的百分比．‎ ‎ （1）计算各种果树面积与总面积的百分比；‎ ‎ （2）计算各种果树对应的圆心角的度数；‎ ‎ （3）制作扇形统计图．‎ 果树名 梨树 苹果树 葡萄树 桃树 面积（单位：公顷）‎ ‎30‎ ‎60‎ ‎15‎ ‎15‎ ‎22．某餐厅共有7名员工，所有员工的工资情况如下表所示（单位：元）．解答下列问题．‎ 人员 经理 厨师甲 厨师乙 会计 服务员甲 服务员乙 服务员丙 人数 ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ 工资额 ‎3000‎ ‎700‎ ‎500‎ ‎450‎ ‎360‎ ‎340‎ ‎320‎ ‎ （1）餐厅所有员工的平均工资是多少？工资的中位数是多少？‎ ‎ （2）用平均数还是用中位数描述所有员工的工资的一般水平比较恰当？‎ ‎ （3）去掉经理工资以后，其他员工的平均工资是多少？是否也能反映员工工资的一般水平？‎ ‎ ‎ ‎23．下表是某校九年级（1）班20名学生某次数学测验的成绩统计表：‎ 成绩（单位：分）‎ ‎60‎ ‎70‎ ‎80‎ ‎90‎ ‎100‎ 人数（单位：人）‎ ‎1‎ ‎5‎ x y ‎2‎ ‎ （1）若这20名学生的平均分是84分，求x和y的值．‎ ‎（2）这20名学生的本次测验成绩的众数和中位数分别是多少？‎ ‎24．有三面小旗，分别为红、黄、蓝三种颜色．‎ ‎ （1）把三面小旗按不同顺序排列，共有多少种不同排法？把它们排列出来．‎ ‎（2）如果把小旗从左至右排列，红色小旗排在最左端的概率是多少？‎ ‎25．中小学生的视力状况受到社会的关注，某市有关部门对全市4万名初中生的视力状况进行了一次抽样调查，统计所得到的有关数据绘制成频率分布直方图，如图10-2，从左至右五个小组的频率之比依次是2：4：9：7：3，第五小组的频率是30．‎ ‎ （1）本次调查共抽测了多少名学生？‎ ‎ （2）本次调查抽测的数据的中位数应在哪个小组？说明理由．‎ ‎ （3）如果视力在4.9～5.1（包括4.9、5.1）均属正常，那么全市初中生视力正常约有多少人？‎ 答案 一、选择题 ‎ 1．B 2．D 3．C 4．A 5．C 6．B 7．D 8．A 9．D 10．C 二、填空题 ‎ 11．扇形 12．72° 13． 14．频率分布 15． 16． 17．2.5 18．4s2‎ 三、解答题 ‎19．解：（1）8． （2）众数为2，平均数为3.5．‎ ‎20．解：设计略，中奖概率为．‎ ‎21．解：（1）梨树25%，苹果树50%，葡萄树12．5%，桃树12．5%．‎ ‎ （2）梨树90°，苹果树180°，葡萄树45°，桃树45°．（3）图略．‎ ‎22．解：（1）平均工资为810元，中位数为450．‎ ‎ （2）中位数．（3）445，能反映员工工资的一般水平．‎ ‎23．解：（1）由题意知 解得 ‎ （2）众数为90分，中位数为90分．‎ ‎24．解：（1）共有6种不同排法，分别为红黄蓝、红蓝黄、黄红蓝、黄蓝红、蓝红黄、蓝黄红．（2）．‎ ‎25．解：（1）设5个小组的频率依次为2x，4x，9x，7x，3x，则2x+4x+9x+7x+3x=1，解得x=．30÷=250（人）．‎ ‎ （2）第三小组，理由略．（3）4×=1.12万人．毛