2014上海中考二模试题附答案金山数学 19页

‎2014年上海市金山区中考数学二模试卷 ‎　‎ 一、选择题：（本大题共6题，每题4分，满分24分）【四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答题纸相应位置上】‎ ‎1．（4分）（2014•金山区二模）下列各数中是有理数的是（　　）‎ ‎　‎ A．‎ ‎3.14‎ B．‎ C．‎ D．‎ ‎　‎ ‎2．（4分）（2014•金山区二模）将直线y=x+2向下平移2个单位后，所得直线的解析式为（　　）‎ ‎　‎ A．‎ y=x+4‎ B．‎ y=x﹣2‎ C．‎ y=x D．‎ y=x﹣4‎ ‎　‎ ‎3．（4分）（2014•金山区二模）下列一元二次方程中，有两个相等的实数根的是（　　）‎ ‎　‎ A．‎ x2+2x﹣1=0‎ B．‎ x2﹣2x+1=0‎ C．‎ x2+2x+4=0‎ D．‎ x2﹣2x﹣4=0‎ ‎　‎ ‎4．（4分）（2014•金山区二模）在本学期的“献爱心”的捐款活动中，九（1）班学生捐款情况如图，那么捐款金额的众数和中位数分别是（　　）‎ ‎　‎ A．‎ ‎15和13.5‎ B．‎ ‎8元和6.5元 C．‎ ‎15和8元 D．‎ ‎8元和8元 ‎　‎ ‎5．（4分）（2014•金山区二模）下列命题中，真命题是（　　）‎ ‎　‎ A．‎ 平行四边形是轴对称图形 ‎　‎ B．‎ 正多边形是中心对称图形 ‎　‎ C．‎ 正多边形都是轴对称图形 ‎　‎ D．‎ 是轴对称图形的四边形都是中心对称图形 ‎　‎ ‎6．（4分）（2014•金山区二模）在同一平面内，已知线段AO=2，⊙A的半径为r，将⊙A绕点O按逆时针方向旋转90°，得到的圆记作⊙B，如果⊙A与⊙B外切，那么r的值为（　　）‎ ‎　‎ A．‎ ‎1‎ B．‎ ‎2‎ C．‎ D．‎ ‎　‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎7．（4分）（2014•金山区二模）计算：（a3）2=　_________　．‎ ‎　‎ ‎8．（4分）（2014•宝坻区二模）计算：（a+2）（a﹣2）=　_________　．‎ ‎　‎ ‎9．（4分）（2014•金山区二模）方程=的解是　_________　．‎ ‎　‎ ‎10．（4分）（2014•金山区二模）计算：+2（+）=　_________　．‎ ‎　‎ ‎11．（4分）（2014•金山区二模）已知函数f（x）=，那么f（）=　_________　．‎ ‎　‎ ‎12．（4分）（2014•金山区二模）已知反比例函数的图象经过点（﹣1，2），那么该反比例函数的图象的两个分支在第　_________　象限．‎ ‎　‎ ‎13．（4分）菱形的两条对角线长分别为6和8，则这个菱形的周长为　_________　．‎ ‎　‎ ‎14．（4分）（2014•金山区二模）某班共有学生36人，在迎新年庆祝会上，随机抽取1名一等奖，3名二等奖，5名三等奖，以上统称为等第奖，该班每一名学生获得等第奖的概率是　_________　．‎ ‎　‎ ‎15．（4分）（2014•金山区二模）为了了解学生课外阅读的喜好，某校随机抽取部分学生进行问卷调查，调查时要求每人只选取一种喜欢的书籍，如果没有喜欢的书籍或者喜欢其他类型的书籍，则都选“其他”，图2是整理数据后绘制的不完整的统计图，如果还知道喜欢漫画的有60人，选“其他”的有30人，那么喜欢小说的人数为　_________　．‎ ‎　‎ ‎16．（4分）（2014•金山区二模）如图，在△ABC中，AB=4，BC=6，BD是∠ABC的角平分线，DE∥BC．DE交AB于点E，那么DE的长为　_________　．‎ ‎　‎ ‎17．（4分）（2014•金山区二模）如果一个三角形的一边长等于另一边长的两倍，我们把这样的三角形成为“倍边三角形”．如果一个直角三角形是倍边三角形，那么这个直角三角形的较小的锐角的正切值为　_________　．‎ ‎　‎ ‎18．（4分）（2014•金山区二模）如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，D是边AB上一点，联结CD，把△ACD沿CD所在的直线翻折，点A落在点E的位置，如果DE∥BC，那么AD的长为　_________　．‎ ‎　‎ 三、解答题：（本大题共7题，满分78分）第15题 ‎19．（10分）（2014•金山区二模）计算：﹣cos30°﹣2﹣1+（π﹣）0．‎ ‎　‎ ‎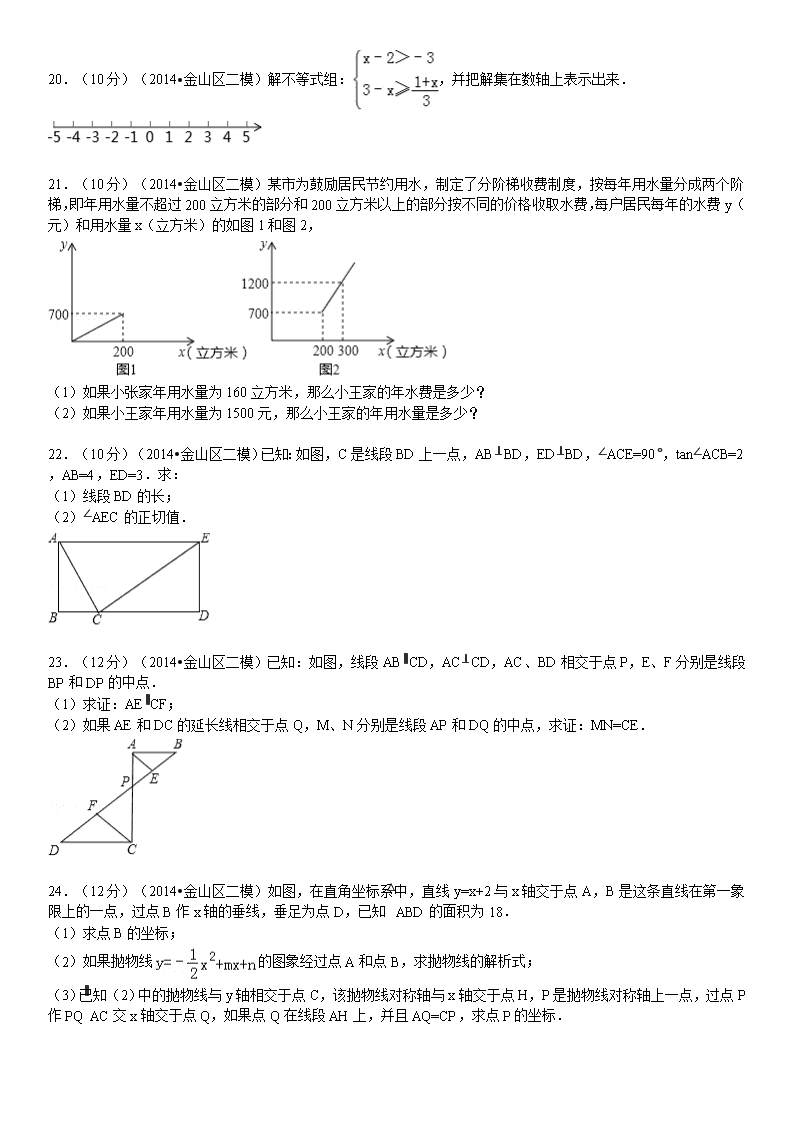20．（10分）（2014•金山区二模）解不等式组：，并把解集在数轴上表示出来．‎ ‎　‎ ‎21．（10分）（2014•金山区二模）某市为鼓励居民节约用水，制定了分阶梯收费制度，按每年用水量分成两个阶梯，即年用水量不超过200立方米的部分和200立方米以上的部分按不同的价格收取水费，每户居民每年的水费y（元）和用水量x（立方米）的如图1和图2，‎ ‎（1）如果小张家年用水量为160立方米，那么小王家的年水费是多少？‎ ‎（2）如果小王家年用水量为1500元，那么小王家的年用水量是多少？‎ ‎　‎ ‎22．（10分）（2014•金山区二模）已知：如图，C是线段BD上一点，AB⊥BD，ED⊥BD，∠ACE=90°，tan∠ACB=2，AB=4，ED=3．求：‎ ‎（1）线段BD的长；‎ ‎（2）∠AEC的正切值．‎ ‎　‎ ‎23．（12分）（2014•金山区二模）已知：如图，线段AB∥CD，AC⊥CD，AC、BD相交于点P，E、F分别是线段BP和DP的中点．‎ ‎（1）求证：AE∥CF；‎ ‎（2）如果AE和DC的延长线相交于点Q，M、N分别是线段AP和DQ的中点，求证：MN=CE．‎ ‎　‎ ‎24．（12分）（2014•金山区二模）如图，在直角坐标系中，直线y=x+2与x轴交于点A，B是这条直线在第一象限上的一点，过点B作x轴的垂线，垂足为点D，已知△ABD的面积为18．‎ ‎（1）求点B的坐标； ‎ ‎（2）如果抛物线的图象经过点A和点B，求抛物线的解析式；‎ ‎（3）已知（2）中的抛物线与y轴相交于点C，该抛物线对称轴与x轴交于点H，P是抛物线对称轴上一点，过点P作PQ∥AC交x轴交于点Q，如果点Q在线段AH上，并且AQ=CP，求点P的坐标．‎ ‎　‎ ‎25．（14分）（2014•金山区二模）如图，已知在梯形ABCD中，AD∥BC，AB⊥BC，AB=4，AD=3，sin∠DCB=，P是边CD上一点（点P与点C、D不重合），以PC为半径的⊙P与边BC相交于点C和点Q．‎ ‎（1）如果BP⊥CD，求CP的长；‎ ‎（2）如果PA=PB，试判断以AB为直径的⊙O与⊙P的位置关系；‎ ‎（3）联结PQ，如果△ADP和△BQP相似，求CP的长．‎ ‎　‎ ‎2014年上海市金山区中考数学二模试卷 参考答案与试题解析 ‎　‎ 一、选择题：（本大题共6题，每题4分，满分24分）【四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答题纸相应位置上】‎ ‎1．（4分）（2014•金山区二模）下列各数中是有理数的是（　　）‎ ‎　‎ A．‎ ‎3.14‎ B．‎ C．‎ D．‎ 考点：‎ 实数．菁优网版权所有 分析：‎ 根据有理数是有限小数或无限循环小，可得答案．‎ 解答：‎ 解：A、是有限小数，故A是有理数；‎ B、C、D是无限不循环小数，故B、C、D是无理数；‎ 故选：A．‎ 点评：‎ 本题考查了有理数，有限小数或无限循环小数是有理数．‎ ‎　‎ ‎2．（4分）（2014•金山区二模）将直线y=x+2向下平移2个单位后，所得直线的解析式为（　　）‎ ‎　‎ A．‎ y=x+4‎ B．‎ y=x﹣2‎ C．‎ y=x D．‎ y=x﹣4‎ 考点：‎ 一次函数图象与几何变换．菁优网版权所有 分析：‎ 根据平移k值不变，只有b只发生改变解答即可．‎ 解答：‎ 解：根据题意知，平移后的直线解析式为：y=x+2﹣2=x，即y=x．‎ 故选：C．‎ 点评：‎ 本题考查图形的平移变换和函数解析式之间的关系，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标左移加，右移减；纵坐标上移加，下移减．平移后解析式有这样一个规律“左加右减，上加下减”．关键是要搞清楚平移前后的解析式有什么关系．‎ ‎　‎ ‎3．（4分）（2014•金山区二模）下列一元二次方程中，有两个相等的实数根的是（　　）‎ ‎　‎ A．‎ x2+2x﹣1=0‎ B．‎ x2﹣2x+1=0‎ C．‎ x2+2x+4=0‎ D．‎ x2﹣2x﹣4=0‎ 考点：‎ 根的判别式．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 分别计算四个方程的根的判别式，然后根据判别式的意义进行判断．‎ 解答：‎ 解：A、△=22﹣4×（﹣1）=8＞0，方程有两个不相等的实数根，所以A选项错误；‎ B、△=22﹣4×1=0，方程有两个相等的实数根，所以B选项正确；‎ C、△=22﹣4×4=﹣12＜0，方程没有实数根，所以C选项错误；‎ D、△=22﹣4×（﹣4）=20＞0，方程有两个不相等的实数根，所以D选项错误．‎ 故选B．‎ 点评：‎ 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2﹣‎4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．‎ ‎　‎ ‎4．（4分）（2014•金山区二模）在本学期的“献爱心”的捐款活动中，九（1）班学生捐款情况如图，那么捐款金额的众数和中位数分别是（　　）‎ ‎　‎ A．‎ ‎15和13.5‎ B．‎ ‎8元和6.5元 C．‎ ‎15和8元 D．‎ ‎8元和8元 考点：‎ 条形统计图；中位数；众数．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 根据条形统计图中的数据求出众数与中位数即可．‎ 解答：‎ 解：根据条形统计图得到捐8元的学生数最多，为15个，故捐款金额的众数为8元，‎ 将捐款数按照从小到大顺序排列得到3，3，3，3，3，3，3，3，5，5，5，5，5，5，5，5，5，5，5，5，8，8，8，8，8，8，8，8，8，8，8，8，8，8，8，10，10，10，10，10，其中最中间的两个数为5和8，平均数为6.5，即中位数为6.5，‎ 故选B 点评：‎ 此题考查了条形统计图，众数，以及中位数，弄清题中的数据是解本题的关键．‎ ‎　‎ ‎5．（4分）（2014•金山区二模）下列命题中，真命题是（　　）‎ ‎　‎ A．‎ 平行四边形是轴对称图形 ‎　‎ B．‎ 正多边形是中心对称图形 ‎　‎ C．‎ 正多边形都是轴对称图形 ‎　‎ D．‎ 是轴对称图形的四边形都是中心对称图形 考点：‎ 命题与定理．菁优网版权所有 分析：‎ 根据轴对称图形和中心对称图形的定义以及平行四边形、正多边形和等腰梯形的性质分别进行判断．‎ 解答：‎ 解：A、平行四边形是中心对称图形，不是轴对称图形，所以A选项错误；‎ B、当正多边形的边数为偶数时，它是中心对称图形，所以B选项错误；‎ C、正多边形都是轴对称图形，所以C选项正确；‎ D、等腰梯形是轴对称图形，但不是中心对称图形，所以D选项错误．‎ 故选C．‎ 点评：‎ 本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．‎ ‎　‎ ‎6．（4分）（2014•金山区二模）在同一平面内，已知线段AO=2，⊙A的半径为r，将⊙A绕点O按逆时针方向旋转90°，得到的圆记作⊙B，如果⊙A与⊙B外切，那么r的值为（　　）‎ ‎　‎ A．‎ ‎1‎ B．‎ ‎2‎ C．‎ D．‎ 考点：‎ 圆与圆的位置关系．菁优网版权所有 分析：‎ 根据旋转的性质得到△OAB为等腰直角三角形，则AB=OA=2，从而求得线段AB的长，然后利用两圆外切两圆的圆心距等于两圆的半径之和直接求解．‎ 解答：‎ 解：∵⊙A绕点O按逆时针方向旋转90°得到的⊙B，‎ ‎∴△OAB为等腰直角三角形，‎ ‎∵AO=2，‎ ‎∴OB=OA=2，AB=2，‎ ‎∵⊙A、⊙B外切，‎ ‎∴AB等于两圆半径之和，‎ ‎∴r=．‎ 故选C．‎ 点评：‎ 本题考查了圆与圆的位置关系：两圆的半径分别为R、r，两圆的圆心距为d，若d=R+r，则两圆外切．也考查了旋转的性质．‎ ‎　‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎7．（4分）（2014•金山区二模）计算：（a3）2=　a6　．‎ 考点：‎ 幂的乘方与积的乘方．菁优网版权所有 分析：‎ 按照幂的乘方法则：底数不变，指数相乘计算．即（am）n=amn（m，n是正整数）‎ 解答：‎ 解：（a3）2=a6．‎ 故答案为：a6．‎ 点评：‎ 本题考查了幂的乘方法则：底数不变，指数相乘．（am）n=amn（m，n是正整数），牢记法则是关键．‎ ‎　‎ ‎8．（4分）（2014•宝坻区二模）计算：（a+2）（a﹣2）=　a2﹣4　．‎ 考点：‎ 平方差公式．菁优网版权所有 分析：‎ 利用平方差公式直接求解即可求得答案．‎ 解答：‎ 解：（a+2）（a﹣2）=a2﹣4．‎ 故答案为：a2﹣4．‎ 点评：‎ 本题考查了平方差公式．注意运用平方差公式计算时，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方．‎ ‎　‎ ‎9．（4分）（2014•金山区二模）方程=的解是　x=﹣1　．‎ 考点：‎ 解分式方程．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．‎ 解答：‎ 解：去分母得：x2=1，‎ 解得：x=1或x=﹣1，‎ 经检验x=1是增根，分式方程的解为x=﹣1．‎ 故答案为：x=﹣1‎ 点评：‎ 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．‎ ‎　‎ ‎10．（4分）（2014•金山区二模）计算：+2（+）=　3+2　．‎ 考点：‎ ‎*平面向量．菁优网版权所有 分析：‎ 先去掉括号，然后进行加法运算即可．‎ 解答：‎ 解：+2（+）‎ ‎=+2+2‎ ‎=3+2．‎ 故答案为：3+2．‎ 点评：‎ 本题考查了平面向量，主要是向量的加法运算，是基础题．‎ ‎　‎ ‎11．（4分）（2014•金山区二模）已知函数f（x）=，那么f（）=　　．‎ 考点：‎ 函数值．菁优网版权所有 分析：‎ 把x=代入函数解析式进行计算即可得解．‎ 解答：‎ 解：f（）==．‎ 故答案为：．‎ 点评：‎ 本题考查了函数值求解，把自变量的值代入函数关系式计算即可，比较简单．‎ ‎　‎ ‎12．（4分）（2014•金山区二模）已知反比例函数的图象经过点（﹣1，2），那么该反比例函数的图象的两个分支在第　二、四　象限．‎ 考点：‎ 反比例函数的性质．菁优网版权所有 分析：‎ 根据反比例函数图象在一、三象限或在二、四象限，根据（﹣1，2）所在象限即可作出判断．‎ 解答：‎ 解：点（﹣1，2）在第二象限，则该反比例函数的图象的两个分支在第二、四象限．‎ 故答案是：二、四．‎ 点评：‎ 本题考查了反比例函数的性质，对于反比例函数（k≠0），（1）k＞0，反比例函数图象在一、三象限；（2）k＜0，反比例函数图象在第二、四象限内．‎ ‎　‎ ‎13．（4分）（2012•肇庆）菱形的两条对角线长分别为6和8，则这个菱形的周长为　20　．‎ 考点：‎ 菱形的性质；勾股定理．菁优网版权所有 分析：‎ 根据菱形的对角线互相垂直平分的性质，利用对角线的一半，根据勾股定理求出菱形的边长，再根据菱形的四条边相等求出周长即可．‎ 解答：‎ 解：如图所示，‎ 根据题意得AO=×8=4，BO=×6=3，‎ ‎∵四边形ABCD是菱形，‎ ‎∴AB=BC=CD=DA，AC⊥BD，‎ ‎∴△AOB是直角三角形，‎ ‎∴AB===5，‎ ‎∴此菱形的周长为：5×4=20．‎ 故答案为：20．‎ 点评：‎ 本题主要考查了菱形的性质，利用勾股定理求出菱形的边长是解题的关键，同学们也要熟练掌握菱形的性质：①菱形的四条边都相等；②菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．‎ ‎　‎ ‎14．（4分）（2014•金山区二模）某班共有学生36人，在迎新年庆祝会上，随机抽取1名一等奖，3名二等奖，5名三等奖，以上统称为等第奖，该班每一名学生获得等第奖的概率是　　．‎ 考点：‎ 概率公式．菁优网版权所有 分析：‎ 共36人，其中有1+3+5=9个等第奖，利用概率公式直接求解即可．‎ 解答：‎ 解：∵共36人，其中有1+3+5=9个等第奖，‎ ‎∴该班每一名学生获得等第奖的概率是=，‎ 故答案为：．‎ 点评：‎ 综合考查了概率的求法．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．‎ ‎　‎ ‎15．（4分）（2014•金山区二模）为了了解学生课外阅读的喜好，某校随机抽取部分学生进行问卷调查，调查时要求每人只选取一种喜欢的书籍，如果没有喜欢的书籍或者喜欢其他类型的书籍，则都选“其他”，图2是整理数据后绘制的不完整的统计图，如果还知道喜欢漫画的有60人，选“其他”的有30人，那么喜欢小说的人数为　120　．‎ 考点：‎ 扇形统计图．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 根据扇形统计图，列出算式，计算即可得到结果．‎ 解答：‎ 解：根据题意得：（30÷10%）﹣60﹣30﹣（30÷10%）×30%=300﹣60﹣30﹣90=120（人），‎ 则喜欢小说的人数为120人．‎ 故答案为：120．‎ 点评：‎ 此题考查了扇形统计图，弄清题中的数据是解本题的关键．‎ ‎　‎ ‎16．（4分）（2014•金山区二模）如图，在△ABC中，AB=4，BC=6，BD是∠ABC的角平分线，DE∥BC．DE交AB于点E，那么DE的长为　2.4　．‎ 考点：‎ 相似三角形的判定与性质；等腰三角形的判定与性质．菁优网版权所有 分析：‎ 根据平行线的性质和角平分线定义求出∠EDB=∠EBD，推出DE=BE，设DE=BE=x，证相似，得出比例式，代入求出即可．‎ 解答：‎ 解：∵DE∥BC，‎ ‎∴∠EDB=∠CBD，‎ ‎∵BD是∠ABC的角平分线，‎ ‎∴∠CBD=∠ABD，‎ ‎∴∠EDB=∠EBD，‎ ‎∴DE=BE，‎ 设DE=BE=x，‎ ‎∵DE∥BC，‎ ‎∴△AED∽△ABC，‎ ‎∴=，‎ ‎∴=，‎ 解得：x=2.4，‎ ‎∴DE=2.4，‎ 故答案为：2.4．‎ 点评：‎ 本题考查了等腰三角形的性质和判定，平行线的性质，相似三角形的性质和判定的应用，解此题的关键是求出BE=DE和求出△AED∽△ABC．‎ ‎　‎ ‎17．（4分）（2014•金山区二模）如果一个三角形的一边长等于另一边长的两倍，我们把这样的三角形成为“倍边三角形”．如果一个直角三角形是倍边三角形，那么这个直角三角形的较小的锐角的正切值为　或　．‎ 考点：‎ 勾股定理；锐角三角函数的定义．菁优网版权所有 专题：‎ 分类讨论．‎ 分析：‎ 分两种情况考虑，当斜边为直角边2倍时，当直角边为直角边2倍时，求出最小角的正切值即可．‎ 解答：‎ 解：如图1所示，AC=2AB，‎ ‎∴最小角为∠C，根据勾股定理得：BC==AB，‎ 则tanC===；‎ 如图2所示，BC=2AB，‎ ‎∴tanC==，‎ 综上，这个直角三角形的较小的锐角的正切值为或．‎ 故答案为：或．‎ 点评：‎ 此题考查了勾股定理，锐角三角函数定义，熟练掌握勾股定理是解本题的关键．‎ ‎　‎ ‎18．（4分）（2014•金山区二模）如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，D是边AB上一点，联结CD，把△ACD沿CD所在的直线翻折，点A落在点E的位置，如果DE∥BC，那么AD的长为　2　．‎ 考点：‎ 翻折变换（折叠问题）．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 连结CE交AB于F点，根据勾股定理得AB=5，再根据折叠的性质得CE=CA=4，DE=AD，∠E=∠A，有DE∥BC得到∠1=∠B，则∠1+∠E=90°，得到CE⊥AB，于是可根据面积法计算出CF=，所以EF=CE﹣CF=，然后证明△DEF∽△BCF，利用相似比可计算出DE=2，于是得到AD=2．‎ 解答：‎ 解：连结CE交AB于F点，如图，‎ ‎∵∠ACB=90°，AC=4，BC=3，‎ ‎∴AB==5，‎ ‎∵△ACD沿CD所在的直线翻折，点A落在点E的位置，‎ ‎∴CE=CA=4，DE=AD，∠E=∠A，‎ ‎∵DE∥BC，‎ ‎∴∠1=∠B，‎ 而∠A+∠B=90°，‎ ‎∴∠1+∠E=90°，‎ ‎∴∠DFE=90°，‎ ‎∴CE⊥AB，‎ ‎∵CF•AB=AC•BC，‎ ‎∴CF==，‎ ‎∴EF=CE﹣CF=4﹣=，‎ ‎∵DE∥BC，‎ ‎∴△DEF∽△BCF，‎ ‎∴DE：BC=EF：CF，即DE：3=：，‎ ‎∴DE=2，‎ ‎∴AD=2．‎ 故答案为2．‎ 点评：‎ 本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理、相似三角形的判定与性质．‎ ‎　‎ 三、解答题：（本大题共7题，满分78分）第15题 ‎19．（10分）（2014•金山区二模）计算：﹣cos30°﹣2﹣1+（π﹣）0．‎ 考点：‎ 二次根式的混合运算；零指数幂；负整数指数幂；特殊角的三角函数值．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 根据零指数幂、负整数指数幂和特殊角的三角函数值得到原式=﹣﹣+1，然后合并即可．‎ 解答：‎ 解：原式=﹣﹣+1‎ ‎=0．‎ 点评：‎ 本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．也考查了零指数幂、负整数指数幂和特殊角的三角函数值．‎ ‎　‎ ‎20．（10分）（2014•金山区二模）解不等式组：，并把解集在数轴上表示出来．‎ 考点：‎ 解一元一次不等式组；在数轴上表示不等式的解集．菁优网版权所有 分析：‎ 求出每个不等式的解集，再找出不等式组的解集即可．‎ 解答：‎ 解：∵解不等式x﹣2＞﹣3得：x＞﹣1，‎ 解不等式3﹣x≥得：x≤4，‎ ‎∴不等式组的解集为﹣1＜x≤4，‎ 在数轴上表示为：．‎ 点评：‎ 本题考查了解一元一次不等式，在数轴上表示不等式组的解集的应用，关键是能求出不等式组的解集．‎ ‎　‎ ‎21．（10分）（2014•金山区二模）某市为鼓励居民节约用水，制定了分阶梯收费制度，按每年用水量分成两个阶梯，即年用水量不超过200立方米的部分和200立方米以上的部分按不同的价格收取水费，每户居民每年的水费y（元）和用水量x（立方米）的如图1和图2，‎ ‎（1）如果小张家年用水量为160立方米，那么小王家的年水费是多少？‎ ‎（2）如果小王家年用水量为1500元，那么小王家的年用水量是多少？‎ 考点：‎ 一次函数的应用．菁优网版权所有 分析：‎ ‎（1）根据图象可得当x≤200时，水价与水费成正比例函数关系，设y=kx，再把（200，700）代入可得k的值，进而得到函数解析式，然后再代入x=160，算出y即可；‎ ‎（2）根据函数图象可得x≥200时，水价与水费成一次函数关系，设y=ax+b，再把（200，700），（300，1200），代入算出a、b的值，进而得到函数解析式，然后再把y=1500代入算出x即可．‎ 解答：‎ 解：（1）当x≤200时，水价与水费成正比例函数关系，‎ 设y=kx，‎ ‎∵图象经过（200，700），‎ ‎∴700=200k，‎ 解得：k=3.5，‎ ‎∴y=3.5x，‎ 把x=160代入：y=160×3.5=560（元），‎ 答：小王家的年水费是560元；‎ ‎（2）当x≥200时，水价与水费成一次函数关系，‎ 设y=ax+b，‎ ‎∵图象经过（200，700），（300，1200），‎ ‎∴，‎ 解得：，‎ ‎∴y=5x﹣300，‎ 把y=1500代入：1500=5x﹣300，‎ 解得：x=360，‎ 答：小王家的年用水量是360立方米．‎ 点评：‎ 此题主要考查了一次函数的应用，关键是正确掌握待定系数法求一次函数解析式．‎ ‎　‎ ‎22．（10分）（2014•金山区二模）已知：如图，C是线段BD上一点，AB⊥BD，ED⊥BD，∠ACE=90°，tan∠ACB=2，AB=4，ED=3．求：‎ ‎（1）线段BD的长；‎ ‎（2）∠AEC的正切值．‎ 考点：‎ 解直角三角形．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ ‎（1）利用同角的余角相等得到一对角相等，再由一对直角相等，得到三角形ABC与三角形DCE相似，由相似得比例，根据锐角三角函数定义及tan∠ACB的值，求出BC与CD的值，根据BC+CD求出BD的值即可；‎ ‎（2）由三角形ABC与三角形DCE相似，根据AB与CD长求出相似比，进而求出AC与CE的比值，即为∠AEC的正切值．‎ 解答：‎ 解：（1）∵∠ACE=90°，AB⊥BD，ED⊥BD，‎ ‎∴∠ACB+∠ECD=90°，∠ACB+∠BAC=90°，∠B=∠D=90°，‎ ‎∴∠BAC=∠ECD，‎ ‎∴△ABC∽△CDE，‎ ‎∴=，‎ ‎∵tan∠ACB==2，AB=4，ED=3，‎ ‎∴=2，即BC=2，CD=6，‎ 则BD=BC+CD=2+6=8；‎ ‎（2）∵△ABC∽△CDE，‎ ‎∴===，‎ 则tan∠AEC==．‎ 点评：‎ 此题属于解直角三角形题型，涉及的知识有：锐角三角函数定义，相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解本题的关键．‎ ‎　‎ ‎23．（12分）（2014•金山区二模）已知：如图，线段AB∥CD，AC⊥CD，AC、BD相交于点P，E、F分别是线段BP和DP的中点．‎ ‎（1）求证：AE∥CF；‎ ‎（2）如果AE和DC的延长线相交于点Q，M、N分别是线段AP和DQ的中点，求证：MN=CE．‎ 考点：‎ 相似三角形的判定与性质．菁优网版权所有 分析：‎ ‎（1）根据直角三角形斜边上中线性质求出AE=BE=PE，CF=PF，推出∠EAP=∠EPA，∠CPF=∠FCP，求出∠EAP=∠FCP，根据平行线的判定推出即可；‎ ‎（2）求出ME∥CN，EN∥CM，得出矩形MCNE，根据矩形的判定推出即可．‎ 解答：‎ ‎（1）证明：∵AB∥CD，AC⊥CD，‎ ‎∴∠BAP=∠DCP=90°，‎ ‎∵E、F分别是线段BP和DP的中点，‎ ‎∴AE=PE=BE，CF=PF，‎ ‎∴∠EAP=∠EPA，∠CPF=∠FCP，‎ ‎∵∠EPA=∠CPF，‎ ‎∴∠EAP=∠FCP，‎ ‎∴AE∥CF；‎ ‎（2）证明：连接EM、EN，‎ ‎∵M、E分别为AP、BP的中点，‎ ‎∴EM∥AB，‎ ‎∵AB∥CD，‎ ‎∴ME∥DC，即EM∥CN，‎ ‎∵AB∥CD，‎ ‎∴△AEB∽△QED，‎ ‎∴=，‎ ‎∵AE=BE，‎ ‎∴DE=EQ，‎ ‎∵N为DQ的中点，‎ ‎∴EN⊥AQ，‎ ‎∵∠ACD=90°，‎ ‎∴EN∥MC，‎ ‎∴四边形MCNE是矩形，‎ ‎∴MN=CE．‎ 点评：‎ 本题考查了直角三角形斜边上中线性质，矩形的性质和判定，相似三角形的性质和判定的应用，主要考查学生综合运用性质进行推理的能力，题目比较好，难度适中．‎ ‎　‎ ‎24．（12分）（2014•金山区二模）如图，在直角坐标系中，直线y=x+2与x轴交于点A，B是这条直线在第一象限上的一点，过点B作x轴的垂线，垂足为点D，已知△ABD的面积为18．‎ ‎（1）求点B的坐标； ‎ ‎（2）如果抛物线的图象经过点A和点B，求抛物线的解析式；‎ ‎（3）已知（2）中的抛物线与y轴相交于点C，该抛物线对称轴与x轴交于点H，P是抛物线对称轴上一点，过点P作PQ∥AC交x轴交于点Q，如果点Q在线段AH上，并且AQ=CP，求点P的坐标．‎ 考点：‎ 二次函数综合题．菁优网版权所有 分析：‎ ‎（1）由直线y=x+2可知斜率为1，则AD=BD，然后根据三角形的面积求得B点的纵坐标，因为直线与x轴交点是（2，0）求得OA的长，从而求得OD的长，最后求得P点的坐标．‎ ‎（2）用待定系数法把A、B的坐标代入即可．‎ ‎（3）由A、C点的坐标可得AC的斜率为3，设PQ直线为y=3x+b，可解出b值以及Q点的x坐标，AQ可得，CP可用勾股定理获得，然后AQ=CP，求出点P的坐标．‎ 解答：‎ 解：（1）∵直线y=x+2的斜率为1，‎ ‎∴AD=BD，‎ ‎∴S△ABC=AD•BD=BD2，‎ ‎∴18=BD2，解得BD=6，‎ ‎∴AD=BD=6，‎ ‎∵直线y=x+2与x轴的交点A的坐标为（﹣2，0），‎ ‎∴OD=4，‎ ‎∴点B的坐标为（4，6）．‎ ‎（2）把A、B点的坐标代入得：‎ ‎，‎ 解得：，‎ ‎∴抛物线的解析式为y=﹣x2+2x+6．‎ ‎（3）可设P点为（a，），可得AC的斜率为3，设PQ直线为y=3x+b，可解出b值以及Q点的x坐标，AQ可得，CP可用勾股定理获得，然后AQ=CP，求出点P的坐标 ‎∵抛物线的解析式为y=﹣x2+2x+6与y轴的交点C为（0，6），对称轴为x=2．‎ ‎∴直线AC的斜率为3，‎ ‎∵PQ∥AC，‎ ‎∴直线PQ的斜率也为3，‎ 设直线PQ的解析式为y=3x+b，则Q（﹣，0），‎ ‎∴AQ=2﹣，‎ 当x=2时，y=3x+b=6+b，‎ ‎∴P（2，6+b），‎ ‎∴PC2=22+【6﹣（6+b）】2=4+b2，‎ 当y=0时，y=3x+b的x=﹣，‎ ‎∴AQ=2﹣，‎ ‎∵AQ=CP，‎ ‎∴（2﹣）2=4+b2，‎ 解得：b=﹣，‎ ‎∴P（2，）‎ 点评：‎ 本题考查了二次函数的综合运用，考查用待定系数法求二次函数解析式以及勾股定理的应用；‎ ‎　‎ ‎25．（14分）（2014•金山区二模）如图，已知在梯形ABCD中，AD∥BC，AB⊥BC，AB=4，AD=3，sin∠DCB=，P是边CD上一点（点P与点C、D不重合），以PC为半径的⊙P与边BC相交于点C和点Q．‎ ‎（1）如果BP⊥CD，求CP的长；‎ ‎（2）如果PA=PB，试判断以AB为直径的⊙O与⊙P的位置关系；‎ ‎（3）联结PQ，如果△ADP和△BQP相似，求CP的长．‎ 考点：‎ 圆的综合题．菁优网版权所有 专题：‎ 综合题．‎ 分析：‎ ‎（1）作DH⊥BC于H，如图1，利用矩形的性质得DH=4，BH=3，在Rt△DHC中，利用正弦的定义可计算出DC=5，再利用勾股定理计算出CH=3，则BC=BH+CH=6，然后证明Rt△DCH∽Rt△BCP，利用相似比可计算出PC=；‎ ‎（2）作PE⊥AB于E，如图2，由于PA=PB，根据等腰三角形的性质得AE=BE=AB=2，也可判断PE为梯形ABCD的中位线，所以PD=PC=，PE=（AD+BC）=，于是得到EA+PC=PE，根据两圆外切的判定方法得到以AB为直径的⊙O与⊙P外切；‎ ‎（3）如图1，作PF⊥BC于F，根据垂径定理得CF=QF，设PC=x，则DP=5﹣x，先证明△CPF∽△CDH，利用相似比可计算出CF=，则CQ=2CF=，BQ=BC﹣CQ=6﹣，由PQ=PC得∠PQC=∠PCQ，而∠ADP+∠PCQ=180°，∠PQC+∠PQB=180°，所以∠ADP=∠PQB，然后讨论：当△ADP∽△BQP，根据相似的性质得，解得x1=，x2=10（舍去），得到PC=；当△ADP∽△PQB，利用相似的性质得=，解得x1=，x2=5（舍去），得到PC=．‎ 解答：‎ 解：（1）作DH⊥BC于H，如图1，‎ ‎∵AD∥BC，AB⊥BC，AB=4，AD=3，‎ ‎∴DH=4，BH=3，‎ 在Rt△DHC中，sin∠DCH==，‎ ‎∴DC=5，‎ ‎∴CH==3，‎ ‎∴BC=BH+CH=6，‎ ‎∵BP⊥CD，‎ ‎∴∠BPC=90°，‎ 而∠DCH=∠BCP，‎ ‎∴Rt△DCH∽Rt△BCP，‎ ‎∴=，即=，‎ ‎∴PC=；‎ ‎（2）作PE⊥AB于E，如图2，‎ ‎∵PA=PB，‎ ‎∴AE=BE=AB=2，‎ ‎∵PE∥AD∥BC，‎ ‎∴PE为梯形ABCD的中位线，‎ ‎∴PD=PC，PE=（AD+BC）=（3+6）=，‎ ‎∴PC=BC=，‎ ‎∴EA+PC=PE，‎ ‎∴以AB为直径的⊙O与⊙P外切；‎ ‎（3）如图1，作PF⊥BC于F，则CF=QF，‎ 设PC=x，则DP=5﹣x，‎ ‎∵PF∥DH，‎ ‎∴△CPF∽△CDH，‎ ‎∴=，即=，解得CF=，‎ ‎∴CQ=2CF=，‎ ‎∴BQ=BC﹣CQ=6﹣，‎ ‎∵PQ=PC，‎ ‎∴∠PQC=∠PCQ，‎ ‎∵AD∥BC，‎ ‎∴∠ADP+∠PCQ=180°，‎ 而∠PQC+∠PQB=180°，‎ ‎∴∠ADP=∠PQB，‎ 当△ADP∽△BQP，‎ ‎∴=，即=，‎ 整理得2x2﹣25x+50=0，解得x1=，x2=10（舍去），‎ 经检验x=是原分式方程的解．‎ ‎∴PC=；‎ 当△ADP∽△PQB，‎ ‎∴=，即=‎ 整理得5x2﹣43x+90=0，解得x1=，x2=5（舍去），‎ 经检验x=是原分式方程的解．‎ ‎∴PC=，‎ ‎∴如果△ADP和△BQP相似，CP的长为或．‎ 点评：‎ 本题考查了圆的综合题：熟练掌握垂径定理、圆与圆的位置关系和梯形的性质；会运用勾股定理和相似比进行几何计算．‎ ‎　‎