中考总复习数学教材过关训练教材过关二十七 相似附答案 5页

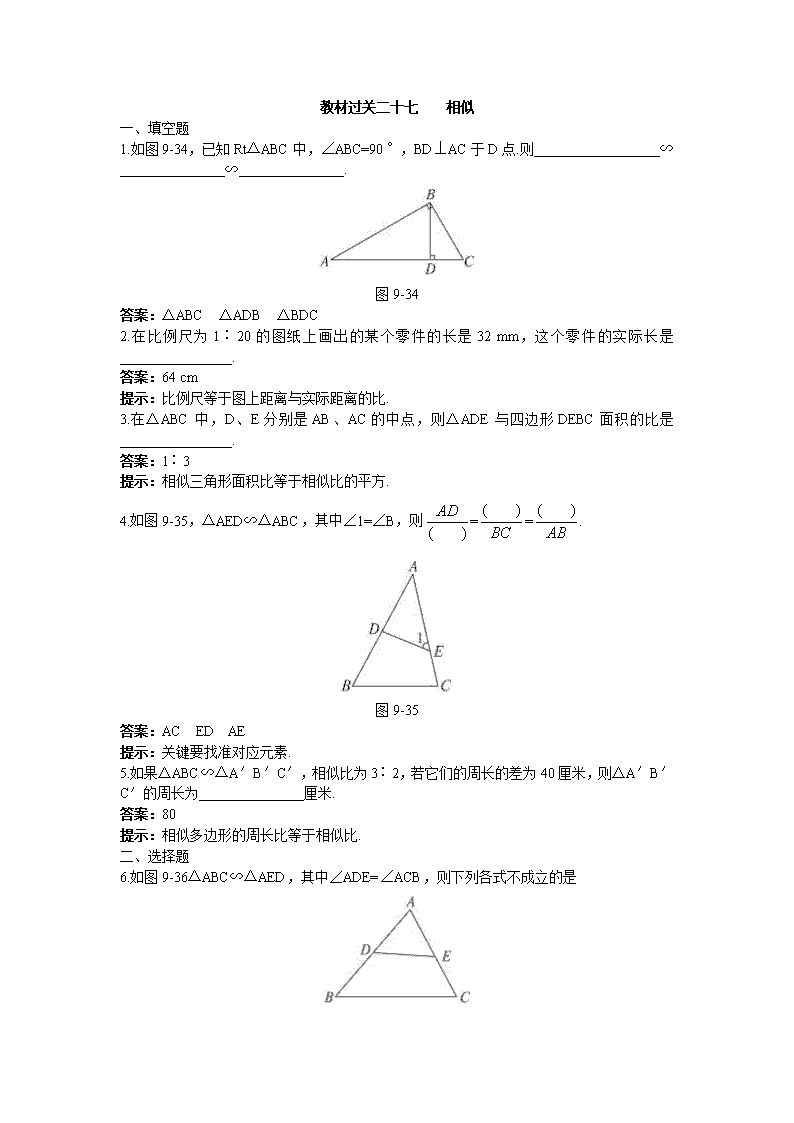
教材过关二十七 相似 一、填空题 ‎1.如图9-34，已知Rt△ABC中，∠ABC=90°，BD⊥AC于D点.则__________________∽_______________∽_______________.‎ 图9-34‎ 答案：△ABC △ADB △BDC ‎2.在比例尺为1∶20的图纸上画出的某个零件的长是32 mm，这个零件的实际长是________________.‎ 答案：64 cm 提示：比例尺等于图上距离与实际距离的比.‎ ‎3.在△ABC中，D、E分别是AB、AC的中点，则△ADE与四边形DEBC面积的比是________________.‎ 答案：1∶3‎ 提示：相似三角形面积比等于相似比的平方.‎ ‎4.如图9-35，△AED∽△ABC，其中∠1=∠B，则==.‎ 图9-35‎ 答案：AC ED AE 提示：关键要找准对应元素.‎ ‎5.如果△ABC∽△A′B′C′，相似比为3∶2，若它们的周长的差为40厘米，则△A′B′C′的周长为_______________厘米.‎ 答案：80‎ 提示：相似多边形的周长比等于相似比.‎ 二、选择题 ‎6.如图9-36△ABC∽△AED，其中∠ADE=∠ACB，则下列各式不成立的是 图9-36‎ A.= B.=‎ C.BC2=BD·DE D.=‎ 答案：C 提示：要搞清楚顶点B和E，C和D对应.‎ ‎7.△ABC中，AB=12，BC=18，CA=24，另一个和它相似的三角形最长的一边是36，则最短的一边是 A.27 B.12 C.18 D.20‎ 答案：C 提示：两个相似三角形的相似比为两个三角形最长边的比，即24与36的比.‎ ‎8.一个三角形三边长之比为4∶5∶6，三边中点连线组成的三角形的周长为30 cm，则原三角形最大边长为 A.44 cm B.40 cm C.36 cm D.24 cm 答案：D 解析：设出原三角形的三边为4x、5x、6x,再由三角形中位线性质得出答案.‎ ‎9.如图9-37,AB是斜靠在墙上的长梯,梯脚B距墙脚1.6 m,梯上点D距墙1.4 m,BD长0.55 m,则梯子的长为 图9-37‎ A.3.85 m B.4.00 m C.4.40 m D.4.50 m 答案：A 解：设梯子长为x m，据题意△ADE∽△ABC，则=,即=.‎ 三、解答题 ‎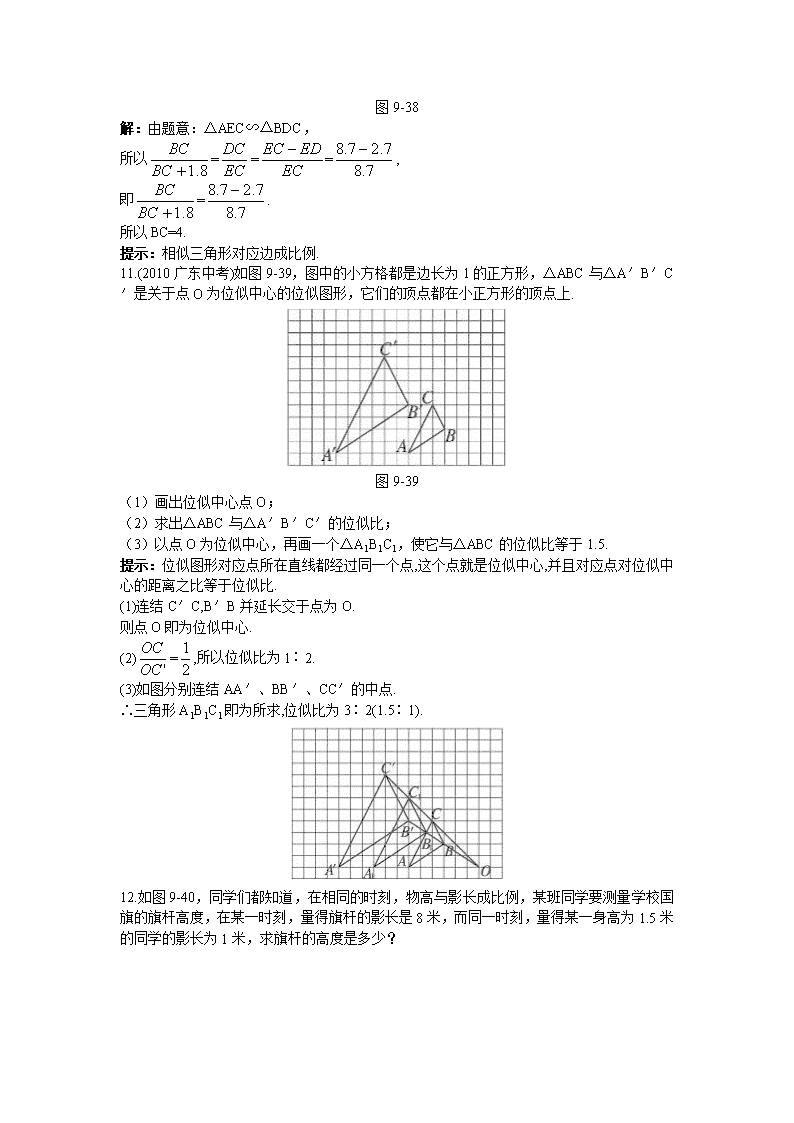10.如图9-38，阳光通过窗口照射到室内,在地面上留下2.7 m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7 m,窗口高AB=1.8 m,求窗口底边离地面的高BC.‎ 图9-38‎ 解：由题意：△AEC∽△BDC，‎ 所以===,‎ 即=.‎ 所以BC=4.‎ 提示：相似三角形对应边成比例.‎ ‎11.(2010广东中考)如图9-39，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′是关于点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上.‎ 图9-39‎ ‎（1）画出位似中心点O；‎ ‎（2）求出△ABC与△A′B′C′的位似比；‎ ‎（3）以点O为位似中心，再画一个△A1B1C1，使它与△ABC的位似比等于1.5.‎ 提示：位似图形对应点所在直线都经过同一个点,这个点就是位似中心,并且对应点对位似中心的距离之比等于位似比.‎ ‎(1)连结C′C,B′B并延长交于点为O.‎ 则点O即为位似中心.‎ ‎(2)=,所以位似比为1∶2.‎ ‎(3)如图分别连结AA′、BB′、CC′的中点.‎ ‎∴三角形A1B1C1即为所求,位似比为3∶2(1.5∶1).‎ ‎12.如图9-40，同学们都知道，在相同的时刻，物高与影长成比例，某班同学要测量学校国旗的旗杆高度，在某一时刻，量得旗杆的影长是8米，而同一时刻，量得某一身高为1.5米的同学的影长为1米，求旗杆的高度是多少？‎ 图9-40‎ 解：设旗杆的高度是x米，则=.‎ 得x=12.‎ 提示：关键是同一时刻物高与影长成正比.‎ ‎13.如图9-41,△ABC中，DE∥BC，EF∥AB，试说明△ADE∽△EFC.‎ 图9-41‎ 解：∵DE∥BC,‎ ‎∴∠AED=∠C,∠ADE=∠B.‎ ‎∵EF∥AB,∴∠B=∠CFE.‎ ‎∴∠ADE=∠CFE.‎ ‎∴△ADE∽△EFC.‎ 提示：两角对应相等,两三角形相似.‎ ‎14.如图9-42,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.求证:△ABC∽△FCD.‎ 图9-42‎ 证明：∵D是BC的中点，DE⊥BC,‎ ‎∴BE=EC.‎ ‎∴∠BCE=∠B.‎ ‎∵AD=AC,‎ ‎∴∠ACD=∠ADC.‎ ‎∴△ABC∽△FCD.‎ 提示：两角对应相等两三角形相似.‎