2018平行四边形中考专题 30页

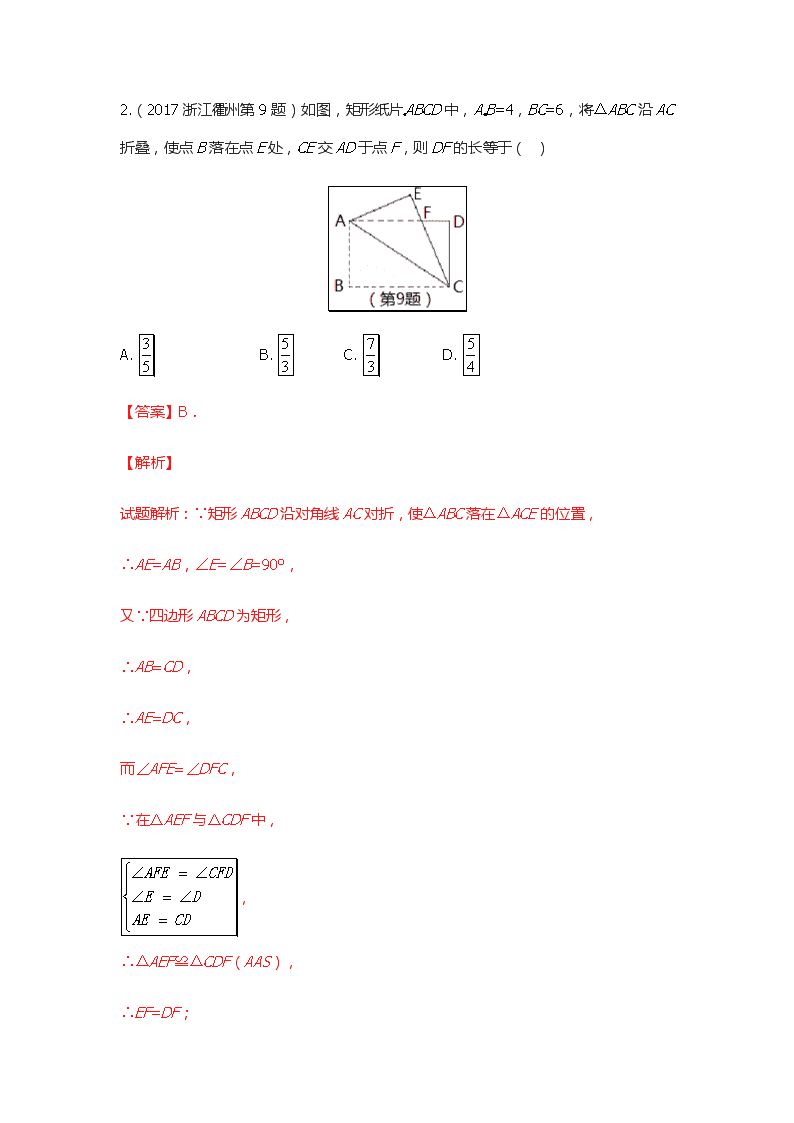
2.（2017 浙江衢州第 9 题）如图，矩形纸片 ABCD 中，A B=4，BC=6，将△ABC 沿 AC 折叠，使点 B 落在点 E 处，CE 交 AD 于点 F，则 DF 的长等于（ ） A. B. C. D. [来源:学。科。网] 【答案】B． 【解析】 试题解析：∵矩形 ABCD 沿对角线 AC 对折，使△ABC 落在△ACE 的位置， ∴AE=AB，∠E=∠B=90°， 又∵四边形 ABCD 为矩形， ∴AB=CD， ∴AE=DC， 而∠AFE=∠DFC， ∵在△AEF 与△CDF 中， ， ∴△AEF≌△CDF（AAS）， ∴EF=DF； 5 3 3 5 3 7 4 5 AFE CFD E D AE CD ∠ = ∠ ∠ = ∠  = ∵四边形 ABCD 为矩形， ∴AD=BC=6，CD=AB=4， ∵Rt△AEF≌Rt△CDF， ∴FC=FA， 设 FA=x，则 FC=x，FD=6﹣x， 在 Rt△CDF 中，CF2=CD2+DF2，即 x2=42+（6﹣x）2，解得 x= ， 则 FD=6﹣x= ． 故选 B． 考点：1.矩形的性质；2.折叠问题. 14.（2017 四川宜宾第 7 题）如图，在矩形 ABCD 中 BC=8，CD=6，将△ABE 沿 BE 折 叠，使点 A 恰好落在对角线 BD 上 F 处，则 DE 的长是（　　） A．3 B． C．5 D． 【答案】C. 【解析】 试题解析：∵矩形 ABCD， 13 3 5 3 24 5 89 16 ∴∠BAD=90°， 由折叠可得△BEF≌△BAE， ∴EF⊥BD，AE=EF，AB=BF， 在 Rt△ABD 中，AB=CD=6，BC=AD=8， 根据勾股定理得：BD=10，即 FD=10﹣6=4， 设 EF=AE=x，则有 ED=8﹣x， 根据勾股定理得：x2+42=（8﹣x）2， 解得：x=3（负值舍去）， 则 DE=8﹣3=5， 故选 C. 考点：1. 翻折变换（折叠问题）；2.矩形的性质． 38.（2017 湖南株洲第 9 题）如图，点 E、F、G、H 分别为四边形 ABCD 的四边 AB、 BC、CD、DA 的中点，则关于四边形 EFGH，下列说法正确的为（　　） A．一定不是平行四边形 　　　　　　　　B．一定不是中心对称图形 C．可能是轴对称图形 　　　　　　　　　　D．当 AC=BD 时它是矩形 【答案】C. 考点：中点四边形；平行四边形的判定；矩形的判定；轴对称图形 7. （2017 青海西宁第 7 题）如图，点 是矩形 的对角线 的中点， 交 于点 ，若 ，则 的长为（ ） A． 5 B． 4 C. D． 【答案】D O ABCD AC / /OM AB AD M 3, 10OM BC= = OB 34 2 34 考点：矩形的性质． 9. （2017 海南第 11 题）如图，在菱形 ABCD 中，AC=8，BD=6，则△ABC 的周长是 （ ） A．14 B．16 C．18 D．20 【答案】C. 考点：菱形的性质，勾股定理. 3.（2017 贵州安顺第 17 题）如图所示，正方形 ABCD 的边长为 6，△ABE 是等边 三角形，点 E 在正方形 ABCD 内，在对角线 AC 上有一点 P，使 PD+PE 的和最 小，则这个最小值为　 　． 【答案】6. 【解析】设 BE 与 AC 交于点 P，连接 BD， ∵点 B 与 D 关于 AC 对称， ∴PD=PB， ∴PD+PE=PB+PE=BE 最小． 即 P 在 AC 与 BE 的交点上时，PD+PE 最小，为 BE 的长度； ∵正方形 ABCD 的边长为 6， ∴AB=6． 又∵△ABE 是等边三角形， ∴BE=AB=6． 故所求最小值为 6． 考点：轴对称﹣最短路线问题；等边三角形的性质；正方形的性质． 14..(2017 天津第 17 题)如图，正方形 和正方形 的边长分别为 3 和 1，点 分别在边 上， 为 的中点，连接 ，则 的长为 . ABCD EFCG GF, CDBC, P AE PG PG 【答案】 . 【解析】 试题分析：连结 AC,根据正方形的性质可得 A、E、C 三点共线，连结 FG 交 AC 于点 M， 因正方形 和正方形 的边长分别为 3 和 1，根据勾股定理可求得 EC=FG= ,AC=3 ,即可得 AE=2 ,因 为 的中点，可得 PE=AP= ,再由正方形的性质 可得 GM=EM= ,FG 垂直于 AC，在 Rt△PGM 中，PM= ,由勾股定理即可求得 PG= . 15.(2017 福建第 15 题)两个完全相同的正五边形都有一边在直线 上，且有一个公共 顶点 ，其摆放方式如图所示，则 等于 度． 8. （2017 黑龙江齐齐哈尔第 16 题）如图，在等腰三角形纸片 中， ， ，沿底边 上的高 剪成两个三角形，用这两个三角形 拼成平行四边形，则这个平行四边形较长的对角线的长是 ． 5 ABCD EFCG 2 2 2 P AE 2 2 2 3 2 2 5 l O AOB∠ ABC 10AB AC= = 12BC = BC AD 【答案】10cm 或 2 cm 或 4 cm． 【解析】 试题分析：如图： ， 过点 A 作 AD⊥BC 于点 D， ∵△ABC 边 AB=AC=10cm，BC=12cm，∴BD=DC=6cm，∴AD=8cm， 如图①所示：可得四边形 ACBD 是矩形，则其对角线长为：10cm， 如图②所示：AD=8cm， 连接 BC，过点 C 作 CE⊥BD 于点 E，则 EC=8cm，BE=2BD=12cm，则 BC=4 cm， 如图③所示：BD=6cm， 由题意可得：AE=6cm，EC=2BE=16cm， 故 AC= =2 cm， 故答案为：10cm 或 2 cm 或 4 cm． 考点：图形的剪拼．. 73 13 13 2 26 16+ 73 73 13 14. （2017 湖南张家界第 14 题）如图，在正方形 ABCD 中，AD= ，把边 BC 绕点 B 逆时针旋转 30°得到线段 BP，连接 AP 并延长交 CD 于点 E，连接 PC，则三角形 PCE 的面积为 ． 【答案】 ． 考点：旋转的性质；正方形的性质；综合题． 4.（2017 甘肃庆阳第 26 题）如图，矩形 ABCD 中，AB=6，BC=4，过对角线 BD 中点 O 的直线分别交 AB，CD 边于点 E，F． （1）求证：四边形 BEDF 是平行四边形； （2）当四边形 BEDF 是菱形时，求 EF 的长． 2 3 9 5 3− 【答案】(1)证明见解析.（2） ． 【解析】 试题分析：（1）根据平行四边形 ABCD 的性质，判定△BOE≌△DOF（ASA），得出 四边形 BEDF 的对角线互相平分，进而得出结论； （2）在 Rt△ADE 中，由勾股定理得出方程，解方程求出 BE，由勾股定理求出 BD，得 出 OB，再由勾股定理求出 EO，即可得出 EF 的长． （2）当四边形 BEDF 是菱形时，BE⊥EF， 设 BE=x，则 DE=x，AE=6﹣x， 在 Rt△ADE 中，DE2=AD2+AE2， 4 13 3 ∴x2=42+（6﹣x）2， 解得：x= ， ∵BD= ， ∴OB= BD= ， ∵BD⊥EF， ∴EO= ， ∴EF=2EO= ． 考点：矩形的性质；平行四边形的判定与性质；菱形的性质． 6.（2017 贵州安顺第 21 题）如图，DB∥AC，且 DB= AC，E 是 AC 的中点， （1）求证：BC=DE； （2）连接 AD、BE，若要使四边形 DBEA 是矩形，则给△ABC 添加什么条件， 为什么？ 【答案】（1）证明见解析；（2）添加 AB=BC． 13 3 2 2 2 13AD AB+ = 1 2 13 2 2 2 13 3BE OB− = 4 13 3 1 2 【解析】 试题分析：（1）要证明 BC=DE，只要证四边形 BCED 是平行四边形．通过给出的已 知条件便可． （2）矩形的判定方法有多种，可选择利用“对角线相等的平行四边形为矩形”来解决． 试题解析：（1）证明：∵E 是 AC 中点， ∴EC= AC． ∵DB= AC， ∴DB∥EC． 又∵DB∥EC， ∴四边形 DBCE 是平行四边形． ∴BC=DE． （2）添加 AB=BC． 理由：∵DB∥AE，DB=AE ∴四边形 DBEA 是平行四边形． ∵BC=DE，AB=BC， ∴AB=DE． ∴▭ADBE 是矩形． 考点：矩形的判定；平行四边形的判定与性质． 1 2 1 2 10.（2017 江苏盐城第 22 题）如图，矩形 ABCD 中，∠ABD、∠CDB 的平分线 BE、 DF 分别交边 AD、BC 于点 E、F． （1）求证：四边形 BEDF 是平行四边形； （2）当∠ABE 为多少度时，四边形 BEDF 是菱形？请说明理由． 【答案】（1）证明见解析；（2）当∠ABE=30°时，四边形 BEDF 是菱形，理由见解 析. 试题解析：（1）∵四边形 ABCD 是矩形， ∴AB∥DC、AD∥BC， ∴∠ABD=∠CDB， ∵BE 平分∠ABD、DF 平分∠BDC， ∴∠EBD= ∠ABD，∠FDB= ∠BDC，1 2 1 2 ∴∠EBD=∠FDB， ∴BE∥DF， 又∵AD∥BC， ∴四边形 BEDF 是平行四边形； （2）当∠ABE=30°时，四边形 BEDF 是菱形， ∵BE 平分∠ABD， ∴∠ABD=2∠ABE=60°，∠EBD=∠ABE=30°， ∵四边形 ABCD 是矩形， ∴∠A=90°， ∴∠EDB=90°-∠ABD=30°， ∴∠EDB=∠EBD=30°， ∴EB=ED， 又∵四边形 BEDF 是平行四边形， ∴四边形 BEDF 是菱形． 考点：矩形的性质；平行四边形的判定与性质；菱形的判定． 11.（2017 甘肃兰州第 26 题）如图，1，将一张矩形纸片 沿着对角线 向上折 叠，顶点 落到点 处， 交 于点 . (1)求证： 是等腰三角形； ABCD BD C E BE AD F BDF△ (2)如图 2，过点 作 ，交 于点 ，连结 交 于点 . ①判断四边形 的形状，并说明理由； ②若 ， ，求 的长. 【答案】(1)证明见解析;(2) ． 【解析】 试题分析: （1）根据两直线平行内错角相等及折叠特性判断； （2）①根据已知矩形性质及第一问证得邻边相等判断； ②根据折叠特性设未知边，构造勾股定理列方程求解． 试题解析：（1）证明：如图 1，根据折叠，∠DBC=∠DBE， 又 AD∥BC， ∴∠DBC=∠ADB， ∴∠DBE=∠ADB， D DG BE∥ BC G FG BD O BFDG 6AB = 8AD = FG 15 2 ∴DF=BF， ∴△BDF 是等腰三角形； （2）①∵四边形 ABCD 是矩形， ∴AD∥BC， ∴FD∥BG， 又∵FD∥BG， ∴四边形 BFDG 是平行四边形， ∵DF=BF， ∴四边形 BFDG 是菱形； ②∵AB=6，AD=8， ∴BD=10． ∴OB= BD=5． 假设 DF=BF=x，∴AF=AD﹣DF=8﹣x． ∴在直角△ABF 中，AB2+A2=BF2，即 62+（8﹣x）2=x2， 解得 x= ， 即 BF= ， ∴FO= = ， 1 2 25 4 25 4 2 2252 2 ( ) 54BF OB− = − 15 4 ∴FG=2FO= ． 考点：四边形综合题． 13.（2017 江苏徐州第 23 题）如图，在平行四边形 中，点 是边 的中 点，连接 并延长，交 延长线于点 连接 . （1）求证：四边形 是平行四边形； （2）若 ，则当 时，四边形 是矩形. 【答案】（1）证明见解析；（2）100° 【解析】 试题分析：（1）由 AAS 证明△BOE≌△COD，得出 OE=OD，即可得出结论； （2）由平行四边形的性质得出∠BCD=∠A=50°，由三角形的外角性质求出 ∠ODC=∠BCD，得出 OC=OD，证出 DE=BC，即可得出结论． 试题解析:（1）∵四边形 ABCD 为平行四边形， 15 2 ABCD O BC DO AB E ,BD EC BECD 50A∠ =  BOD∠ =  BECD ∴AB∥DC，AB=CD， ∴∠OEB=∠ODC， 又∵O 为 BC 的中点， ∴BO=CO， 在△BOE 和△COD 中， ， ∴△BOE≌△COD（AAS）； ∴OE=OD， ∴四边形 BECD 是平行四边形； （2）若∠A=50°，则当∠BOD=100°时，四边形 BECD 是矩形．理由如下： ∵四边形 ABCD 是平行四边形， ∴∠BCD=∠A=50°， ∵∠BOD=∠BCD+∠ODC， ∴∠ODC=100°-50°=50°=∠BCD， ∴OC=OD， ∵BO=CO，OD=OE， ∴DE=BC， ∵四边形 BECD 是平行四边形， ∴四边形 BECD 是矩形； 16. (2017 北京第 22 题)如图，在四边形 中， 为一条对角线， ， 为 的中点，连接 . OEB＝ ODC BOE＝ COD BO＝CO ∠ ∠ ∠ ∠    ABCD BD 0/ / , 2 , 90AD BC AD BC ABD= ∠ = E AD BE （1）求证：四边形 为菱形； （2）连接 ，若 平分 ，求 的长. 【答案】（1）证明见解析.（2） . 【解析】 试题分析：（1）先证四边形是平行四边形，再证其为菱形；（2）利用等腰三角形的 性质，锐角三角函数，即可求解. 本题解析：(1)证明：∵E 为 AD 中点，AD=2BC,∴BC=ED, ∵AD∥BC, ∴四边形 ABCD 是平 行四边形，∵AD=2BE, ∠ABD=90°,AE=DE∴BE=ED, ∴四边形 ABCD 是菱形. (2)∵AD∥BC,AC 平分∠BAD ∴∠BAC=∠DAC=∠BCA,∴BA=BC=1, ∵AD=2BC=2， ∴sin∠ADB= ,∠ADB=30°, ∴∠DAC=30°, ∠ADC=60°.在 RT△ACD 中，AD=2，CD=1， AC= . 考点：平行线性质，菱形判定，直角三角形斜边中线定理. 考点：1.矩形的判定；2.平行四边形的判定与性质． BCDE AC AC , 1BAD BC∠ = AC 3 1 2 3 17.(2017 天津第 24 题)将一个直角三角形纸片 放置在平面直角坐标系中，点 ，点 ，点 . 是边 上的一点（点 不与点 重合），沿 着 折叠该纸片，得点 的对应点 . （1）如图①，当点 在第一象限，且满足 时，求点 的坐标； （2）如图②，当 为 中点时，求 的长； （3）当 时，求点 的坐标（直接写出结果即可）. 【答案】（1）点 A’的坐标为（ ，1）；（2）1；（3） 或 . 【解析】 试题分析：（1）因点 ，点 ，可得 OA= ,OB=1，根据折叠的性质 可得△A’OP≌△AOP，由全等三角形的性质可得 OA’=OA= ,在 Rt△A’OB 中，根据 勾股定理求得 的长，即可求得点 A 的坐标；（2）在 Rt△AOB 中，根据勾股定理 求得 AB=2，再证△BOP 是等边三角形，从而得∠OPA =120°.在判定四边形 OPA’B 是平 行四边形，根据平行四边形的性质即可得 的长； 试题解析：（1）因点 ，点 ， ABO )0,3(A )1,0(B )0,0(O P AB P BA, OP A 'A 'A OBBA ⊥' 'A P AB BA' 030'=∠BPA P 2 3 3 3 3( , )2 2 − − 2 3 3 3( , )2 2 − )0,3(A )1,0(B 3 3 'A B BA' )0,3(A )1,0(B ∴OA= ,OB=1. 根据题意，由折叠的性质可得△A’OP≌△AOP. ∴OA’=OA= , 由 ，得∠A’BO=90°. 在 Rt△A’OB 中， , ∴点 A’的坐标为（ ，1）. (2) 在 Rt△AOB 中，OA= ,OB=1, ∴ ∵当 为 中点， ∴AP=BP=1,OP= AB=1. ∴OP=OB=BP, ∴△BOP 是等边三角形 ∴∠BOP=∠BPO=60°， ∴∠OPA=180°-∠BPO=120°. 由（1）知，△A’OP≌△AOP， ∴∠OPA’=∠OPA=120°，P’A=PA=1， 又 OB=PA’=1， ∴四边形 OPA’B 是平行四边形. ∴A’B=OP=1. 3 3 OBBA ⊥' 2 2' ' 2A B OA OB= − = 2 3 2 2 2AB OA OB= + = P AB 1 2 (3) 或 . 21.（2017 山东青岛第 21 题）（本小题满分 8 分） 已知：如图，在菱形 ABCD 中，点 E，O，F 分别是边 AB，AC，AD 的中点，连接 CE、CF、OF． （1）求证：△ BCE≌△DCF； （2）当 AB 与 BC 满足什么条件时，四边形 AEOF 正方形？请说明理由． 【答案】（1）证明见解析（2）四边形 AEOF 是正方形 【解析】 试题分析：（1）利用 SAS 证明△ BCE≌△DCF； （2）先证明 AEOF 为菱形，当 BC⊥AB，得∠BAD＝90°，再利用知识点：有一个角是 90°的菱形是正方形。 试题解析：（1）∵四边形 ABCD 为菱形 ∴AB=BC=CD=DA，∠B=∠D 又 E、F 分别是 AB、AD 中点，∴BE=DF ∴△ABE≌△CDF（SAS） 3 3 3 3( , )2 2 − − 2 3 3 3( , )2 2 − 考点：1、菱形，2、全等三角形，3、正方形 29．（2017 四川省达州市）如图，在△ABC 中，点 O 是边 AC 上一个动点，过点 O 作 直线 EF∥BC 分别交∠ACB、外角∠ACD 的平分线于点 E、F． （1）若 CE=8，CF=6，求 OC 的长； （2）连接 AE、AF．问：当点 O 在边 AC 上运动到什么位置时，四边形 AECF 是矩形？ 并说明理由． 【答案】（1）5；（2）当点 O 在边 AC 上运动到 AC 中点时，四边形 AECF 是矩形． 【解析】 试题分析：（1）根据平行线的性质以及角平分线的性质得出∠OEC=∠OCE， ∠OFC=∠OCF，证出 OE=OC=OF，∠ECF=90°，由勾股定理求出 EF，即可得出答案； （2）解：当点 O 在边 AC 上运动到 AC 中点时，四边形 AECF 是矩形．理由如下： 连接 AE、AF，如图所示： 当 O 为 AC 的中点时，AO=CO，∵EO=FO，∴四边形 AECF 是平行四边形， ∵∠ECF=90°，∴平行四边形 AECF 是矩形． 考点：1．矩形的判定；2．平行线的性质；3．等腰三角形的判定与性质；4．探究 型；5．动点型． 31．（2017 山东省济宁市）实验探究： （1）如图 1，对折矩形纸片 ABCD，使 AD 与 BC 重合，得到折痕 EF，把纸片展开； 再一次折叠纸片，使点 A 落在 EF 上，并使折痕经过点 B，得到折痕 BM，同时得到线 段 BN，MN．请你观察图 1，猜想∠MBN 的度数是多少，并证明你的结论． （2）将图 1 中的三角形纸片 BMN 剪下，如图 2，折叠该纸片，探究 MN 与 BM 的数量 关系，写出折叠方案，并结合方案证明你的结论． 【答案】（1）∠MBN=30°；（2）MN= BM． 【解析】 试题分析：（1）猜想：∠MBN=30°．只要证明△ABN 是等边三角形即可； （2）结论：MN= BM． 折纸方案：如图 2 中，折叠△BMN，使得点 N 落在 BM 上 O 处，折痕为 MP，连接 OP． 理由：由折叠可知△MOP≌△MNP，∴MN=OM，∠OMP=∠NMP= ∠OMN=30°=∠B， ∠MOP=∠MNP=90°，∴∠BOP=∠MOP=90°，∵OP=OP，∴△MOP≌△BOP，∴MO=BO= BM，∴MN= BM． 1 2 1 2 1 2 1 2 1 2 考点：1．翻折变换（折叠问题）；2．矩形的性质；3．剪纸问题． 32．（2017 广东省）如图所示，已知四边形 ABCD，ADEF 都是菱形，∠BAD=∠FAD， ∠BAD 为锐角． （1）求证：AD⊥BF； （2）若 BF=BC，求∠ADC 的度数． 【答案】（1）证明见解析；（2）150°． 【解析】 试题分析：（1）连结 DB、DF．根据菱形四边相等得出 AB=AD=FA，再利用 SAS 证明 △BAD≌△FAD，得出 DB=DF，那么 D 在线段 BF 的垂直平分线上，又 AB=AF，即 A 在 线段 BF 的垂直平分线上，进而证明 AD⊥BF； （2）如图，设 AD⊥BF 于 H，作 DG⊥BC 于 G，则四边形 BGDH 是矩形，∴DG=BH= BF．∵BF=BC，BC=CD，∴DG= CD．在直角△CDG 中，∵∠CGD=90°，DG= CD， ∴∠C=30°，∵BC∥AD，∴∠ADC=180°﹣∠C=150°． 考点：菱形的性质． 5. （2017 广西百色第 22 题）矩形 中， 分别是 的中点， 分别交 于 两点. 求证：（1）四边形 是平行四边形； （2） 1 2 1 2 1 2 ABCD ,E F ,AD BC ,CE AF BD ,G H AFCE .EG FH= 【答案】（1）证明见解析；（2）证明见解析. 考点：1.矩形的性质；2.平行四边形的判定与性质． 12. （2017 上海第 23 题）已知：如图，四边形 ABCD 中，AD∥BC，AD=CD，E 是对角 线 BD 上一点，且 EA=EC． （1）求证：四边形 ABCD 是菱形； （2）如果 BE=BC，且∠CBE：∠BCE=2：3，求证：四边形 ABCD 是正方形． 【答案】（1）证明见解析；（2）证明见解析. 考点：1.正方形的判定与性质；2.菱形的判定及性质. 13. （2017 湖南张家界第 17 题）如图，在平行四边形 ABCD 中，边 AB 的垂直平分线 交 AD 于点 E，交 CB 的延长线于点 F，连接 AF，BE． （1）求证：△AGE≌△BGF； （2）试判断四边形 AFBE 的形状，并说明理由． 【答案】（1）证明见解析；（2）四边形 AFBE 是菱形． 考点：平行四边形的性质；全等三角形的判定与性质；线段垂直平分线的性质；探究 型．