2009年湖南省湘西自治州初中毕业学业考试卷及答案 7页

‎2009年湘西自治州初中毕业学业考试数学试题卷 姓名： 准考证号： ‎ ‎-----------------------------------------------------------------------------------------------------------------‎ 注意事项：‎ ‎1、本卷为试题卷，考生应在答题卡上作答，在试题卷、草稿纸上答题无效．‎ ‎2、答题前，考生须先将自己的姓名、准考证号分别在试题卷和答题卡上填写清楚．‎ ‎3、答题完成后，请将试题卷、答题卡、草稿纸放在桌上，由监考老师统一收回．‎ ‎4、本试卷三大题，25小题，时量120分钟，满分120分．‎ ‎-----------------------------------------------------------------------------------------------------------------‎ 一、填空题（本大题8小题，每小题3分，共24分． 将正确答案填在答题卡相应横线上）‎ ‎1．数3的绝对值是 ．‎ ‎2．用代数式表示“a与b的和”，式子为 ．‎ ‎3．如果x－y＜0，那么x与y的大小关系是x y ．（填＜或＞符号）‎ ‎4．一个圆的半径是4，则圆的面积是 ．（答案保留π）‎ ‎5．一次函数的图像过坐标原点，则b的值为 ．‎ ‎6．长方形一条边长为‎3cm，面积为‎12cm2，则该长方形另一条边长为 cm．‎ ‎7．截止到2008年底，湘西州在校小学生中的少数民族学生数约为21.2万人，约占全州小学生总数的80%，则全州的小学生总数大致为 万．（保留小数点后一位）‎ ‎8．对于任意不相等的两个数a，b，定义一种运算※如下：a※b=，‎ 如3※2=．那么12※4= ．‎ 二、选择题（本大题8个小题，每小题3分，共24分． 将每个小题所给四个选项中惟一正确选项的代号在答题卡上填涂）‎ ‎9． 一个角是80°，它的余角是（　　）‎ A．10° B．100° C．80° D．120°‎ ‎10．要了解一批电视机的使用寿命，从中任意抽取40台电视机进行试验，在这个问题中，40是（　　）‎ A．个体 B．总体 C．样本容量 D．总体的一个样本 ‎11．在下列运算中，计算正确的是（　　）‎ A． B． ‎ C． D． ‎ ‎12．在直角坐标系中，点M（sin50°，－cos70°）所在的象限是（　　）‎ A． 第一象限 B． 第二象限 C． 第三象限 D． 第四象限 ‎13．在下列命题中，是真命题的是（　　）‎ A．两条对角线相等的四边形是矩形 ‎ B．两条对角线互相垂直的四边形是菱形 C．两条对角线互相平分的四边形是平行四边形 D．两条对角线互相垂直且相等的四边形是正方形 ‎14．的半径为‎10cm，弦AB＝‎12cm，则圆心到AB的距离为（　　）‎ ‎ A． ‎2cm B． ‎6cm C． ‎8cm D． ‎‎10cm ‎15．一个不透明的袋中装有除颜色外均相同的3个红球和2个黄球，从中随机摸出一个，摸到黄球的概率是（　　）‎ A． B． C． D．‎ l1‎ l2‎ ‎1‎ ‎2‎ ‎3‎ ‎16．如图，，∠1=120°，∠2=100°，则∠3= （　　） ‎ ‎ A．20° B．40°‎ ‎ C．50° 　　D．60°‎ 三、 解答题（本大题9小题，共72分，每个题目都要求在答题卡的相应位置写出计算或证明的主要步骤）‎ ‎17．（本题5分）先化简再计算：，其中=3，=2．‎ A B C D E F ‎18．（本题5分）解方程： ‎ ‎19．（本题6分）如图，在△ABC中，DE∥BC，‎ ‎ EF∥AB，求证：△ADE∽△EFC．‎ ‎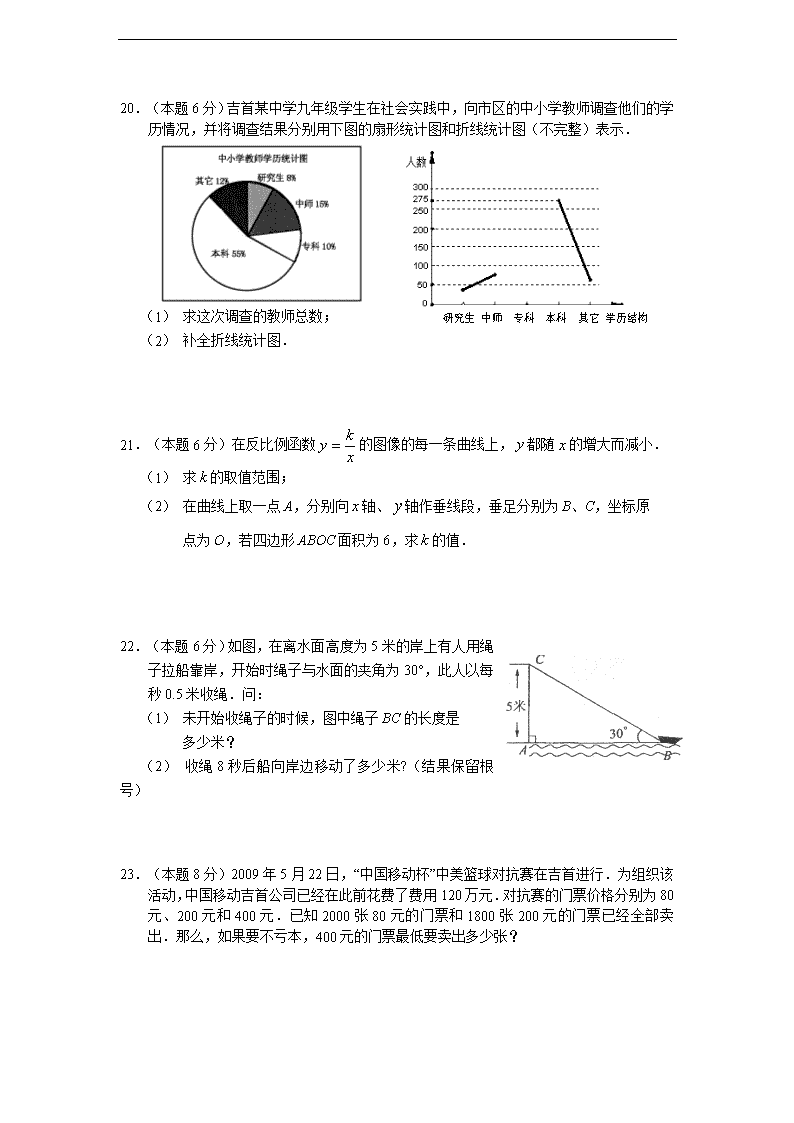20．（本题6分）吉首某中学九年级学生在社会实践中，向市区的中小学教师调查他们的学历情况，并将调查结果分别用下图的扇形统计图和折线统计图（不完整）表示． ‎ 研究生 中师 专科 本科 其它 学历结构 ‎ （1） 求这次调查的教师总数； ‎ ‎ （2） 补全折线统计图．‎ ‎21．（本题6分）在反比例函数的图像的每一条曲线上，都随的增大而减小．‎ ‎（1） 求的取值范围；‎ ‎ （2） 在曲线上取一点A，分别向轴、轴作垂线段，垂足分别为B、C，坐标原 ‎ 点为O，若四边形ABOC面积为6，求的值． ‎ ‎22．（本题6分）如图，在离水面高度为‎5米的岸上有人用绳子拉船靠岸，开始时绳子与水面的夹角为30°，此人以每秒‎0.5米收绳．问：‎ ‎（1） 未开始收绳子的时候，图中绳子BC的长度是 ‎ 多少米？‎ ‎（2） 收绳8秒后船向岸边移动了多少米?（结果保留根号）‎ ‎23．（本题8分）‎2009年5月22日，“中国移动杯”中美篮球对抗赛在吉首进行．为组织该活动，中国移动吉首公司已经在此前花费了费用120万元．对抗赛的门票价格分别为80元、200元和400元．已知2000张80元的门票和1800张200元的门票已经全部卖出．那么，如果要不亏本，400元的门票最低要卖出多少张？‎ ‎24．（本题10分）如图，等腰直角△ABC腰长为a，现分别按图1、图2方式在△ABC内内接一个正方形ADFE和正方形PMNQ．设△ABC的面积为S，正方形ADFE的面积为S1，正方形PMNQ的面积为S2，‎ ‎ （1） 在图1 中，求AD∶AB的值；在图2中，求AP∶AB的值；‎ ‎ （2） 比较S1+S2与S的大小．‎ ‎ 图1 图2‎ A E C F B D A Q C M B N P ‎ ‎ ‎25．（本题20分）在直角坐标系xoy中，抛物线与x轴交于两点A、B，与y轴交于点C，其中A在B的左侧，B的坐标是（3，0）．将直线沿y轴向上平移3个单位长度后恰好经过点B、C．‎ （1） 求k的值；‎ （2） 求直线BC和抛物线的解析式；‎ （3） 求△ABC的面积；‎ （4） 设抛物线顶点为D，点P在抛物线的对称轴上，且∠APD=∠ACB，求点P的坐标．‎ ‎2009年湘西自治州初中毕业学业考试数学参考答案 一、（本题8小题，每题3分，共24分，填错记0分）‎ ‎ 1．3； 2．a+b； 3．＜； 4．16π； 5．0； 6．4； 7．26.5； 8．1/2‎ 二、（本题8小题，每题3分，共24分，选错记0分）‎ ‎ 9．A 10．C 11．D 12．D 13．C 14．C 15．C 16．B ‎ 三、（本题9个题，共72分）‎ ‎ 17．（本题5分）‎ 解：原式＝ 2分 ‎ ＝x＋y－2x＋y ‎ ＝－x＋2y 4分 ‎ 因为 x＝3，y＝2‎ ‎ 所以原式＝－3＋4＝1 5分 ‎ 18．（本题5分）‎ ‎ 解：①＋② 得 4x＝12，即 x＝3 2分 ‎ 代入① 有6－y＝7，即 y＝－1 4分 ‎ 所以原方程的解是： 5分 ‎ 19．（本题6分）‎ ‎ 证明：∵DE∥BC，∴DE∥FC，∴∠AED＝∠C 3分 又∵EF∥AB，∴EF∥AD，∴∠A＝∠FEC 5分 ‎∴△ADE∽△EFC 6分 ‎ 20．（本题6分）‎ ‎ 解：（1）总人数＝人 3分 ‎（2）教师中专科学历的人数＝人 4分 作图： 6分 注：第(2)问虽然没明确指出专科人数为50，但只要作图准确就可得6分．‎ ‎ 研究生 中师 专科 本科 其它 学历结构 ‎21．（本题6分）‎ ‎ 解（1）因为y的值随x的增大而减小，所以k＞0　 2分 ‎ （2）设A（x0，y0）‎ ‎　　　　则由已知，应有｜x0y0｜＝6 4分 ‎　　　　即｜k｜＝6‎ ‎　　　　而k＞０‎ ‎　　　　所以k＝6． 6分 ‎22．（本题6分）‎ ‎ 解（1）如图，在Rt△ABC中，＝sin30° 2分 ‎ ∴ BC＝＝‎10米 3分 ‎ （2）收绳8秒后，绳子BC缩短了‎4米，只有‎6米， 4分 ‎ 这时，船到河岸的距离为米． 6分 ‎23．（本题8分）‎ ‎ 解：2000张80元的门票收入为2000×80＝160000元； 2分 ‎ 1800张200元的门票收入为1800×200＝360000元； 4分 ‎ 1200000－160000－360000＝680000元， 5分 ‎ 故400元的门票至少要卖出：680000÷400＝1700张．‎ ‎ 答：400元的门票最少要卖出1700张． 8分 ‎24．（本题10分）‎ ‎ 解（1）图1中，∵AD＝DF，∠B＝45°，从而DF＝DB，∴AD＝DB，‎ ‎ ∴AD∶AB＝1∶2　 2分 ‎ 图2中，∵PM＝MN，∠B＝45°，从而PM＝MB，∴MN＝MB，‎ ‎ ∴MN＝MB＝NC，‎ ‎∴AP∶AB＝PQ∶BC＝MN∶BC＝1∶3 4分 ‎ （2）图1中，S１＝ 6分 又PQ∶BC=AP∶AB=1∶3，‎ ‎∴PQ=，∴S２＝ 8分 从而S1+S2= 又S=　‎ ‎∴S1+S2＜S 10分 ‎25．（本题20分）‎ ‎ 解（1）直线沿y轴向上平移3个单位后，过两点B，C 从而可设直线BC的方程为 2分 令，得C（0，3） 3分 又B（3，0）在直线上，‎ ‎∴‎ ‎∴ 5分 ‎（2）由（1），直线BC的方程为 7分 又抛物线过点B，C ‎∴‎ ‎∴抛物线方程为 10分 ‎（3）由（2），令 得 12分 即A（1，0），B（3，0），而C（0，3）‎ ‎∴△ABC的面积S△ABC=（3-1）·3=3平方单位 15分 ‎ （4）由（2），D（2，），设对称轴与x轴交于点F，与BC交于E，可得E（2，1），‎ 连结AE．‎ ‎∵‎ ‎∴AE⊥CE，且AE=，CE=‎ ‎（或先作垂线AE⊥BC，再计算也可）‎ 在Rt△AFP与Rt△AEC中，‎ ‎∵∠ACE=∠APE（已知） ‎ ‎∴ 即= ‎ ‎∴ 18分 ‎∴点P的坐标为（2，2）或（2，） 20分 ‎（x轴上、下方各一个）‎ ‎（注：只有一个点扣1分）‎