2017年江苏省徐州市中考数学试卷 6页

‎2017年江苏省徐州市中考数学试卷 一、选择题（每小题3分，共24分）‎ ‎1、－5的倒数是（ ）‎ ‎ A、－5 B、5 C、 D、‎ ‎2、下列图形中，既是轴对称图形，又是中心对称图形的是（ ）‎ ‎ A、 B、 C、 D、‎ ‎3、肥皂泡的泡壁厚度大约是0.00000071米，数字0.00000071用科学记数法表示为（ ）‎ ‎ A、7.1×107 B、0.71×10-6 C、7.1×10-7 D、71×10-8‎ ‎4、下列运算正确的是（ ）‎ ‎ A、 B、 C、 D、‎ ‎5、在“朗读者”节目的影响下，某中学开展了“好书伴我成长”读书活动。为了解5月份八年级300名学生读书情况，随机调查了八年级50名学生读书的册数，统计数据如下表所示：‎ 册数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 人数 ‎4‎ ‎12‎ ‎16‎ ‎17‎ ‎1‎ 关于这组数据，下列说法正确的是（ ）‎ ‎ A、中位数是2 B、众数是17 C、平均数是2 D、方差是2‎ ‎6、如图，点A、B、C在⊙O上，∠AOB＝72°，则∠ACB等于（ ）‎ ‎ A、28° B、54° C、18° D、36°‎ ‎7、如图，在平面直角坐标系中，函数（）与（）的图象相交于点A（2，3），B（－6，－1），则不等式的解集为（ ）‎ ‎ A、 B、或 C、 D、或 ‎8、若函数的图象与坐标轴有三个交点，则的取值范围是（ ）‎ ‎ A、或 B、 C、 D、‎ 二、填空题（每小题3分，共30分）‎ ‎9、4是 的算术平方根。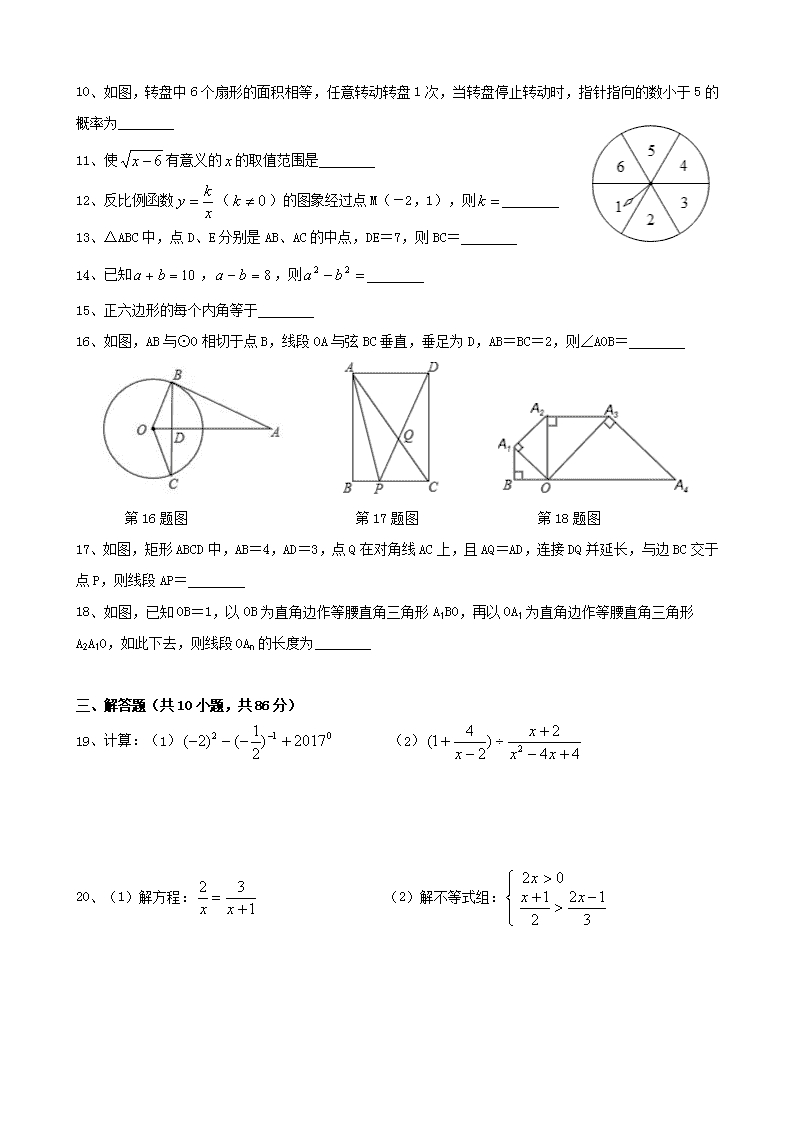‎ ‎10、如图，转盘中6个扇形的面积相等，任意转动转盘1次，当转盘停止转动时，指针指向的数小于5的概率为 ‎ ‎11、使有意义的的取值范围是 ‎ ‎12、反比例函数（）的图象经过点M（－2，1），则 ‎ ‎13、△ABC中，点D、E分别是AB、AC的中点，DE＝7，则BC＝ ‎ ‎14、已知，，则 ‎ ‎15、正六边形的每个内角等于 ‎ ‎16、如图，AB与⊙O相切于点B，线段OA与弦BC垂直，垂足为D，AB＝BC＝2，则∠AOB＝ ‎ ‎ ‎ ‎ 第16题图 第17题图 第18题图 ‎17、如图，矩形ABCD中，AB＝4，AD＝3，点Q在对角线AC上，且AQ＝AD，连接DQ并延长，与边BC交于点P，则线段AP＝ ‎ ‎18、如图，已知OB＝1，以OB为直角边作等腰直角三角形A1BO，再以OA1为直角边作等腰直角三角形A2A1O，如此下去，则线段OAn的长度为 ‎ 三、解答题（共10小题，共86分）‎ ‎19、计算：（1） （2）‎ ‎20、（1）解方程： （2）解不等式组：‎ ‎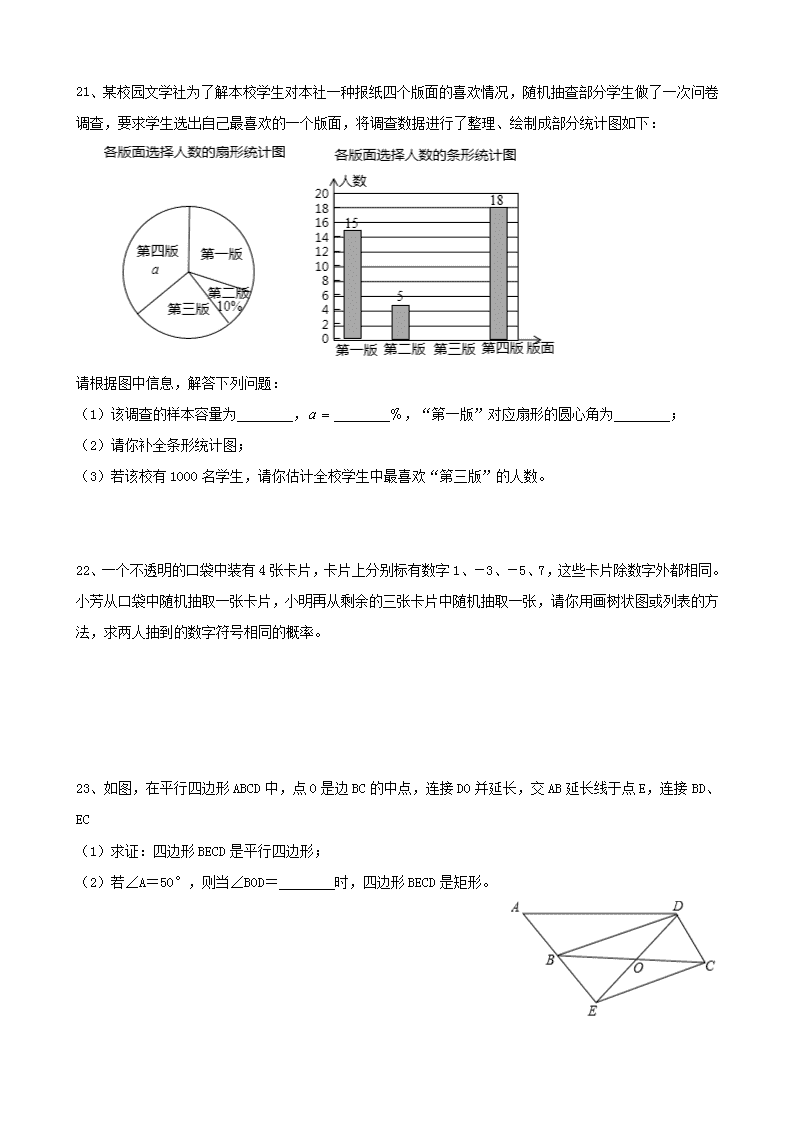21、某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况，随机抽查部分学生做了一次问卷调查，要求学生选出自己最喜欢的一个版面，将调查数据进行了整理、绘制成部分统计图如下：‎ ‎ ‎ 请根据图中信息，解答下列问题：‎ ‎（1）该调查的样本容量为 ， ﹪，“第一版”对应扇形的圆心角为 ；‎ ‎（2）请你补全条形统计图；‎ ‎（3）若该校有1000名学生，请你估计全校学生中最喜欢“第三版”的人数。‎ ‎22、一个不透明的口袋中装有4张卡片，卡片上分别标有数字1、－3、－5、7，这些卡片除数字外都相同。小芳从口袋中随机抽取一张卡片，小明再从剩余的三张卡片中随机抽取一张，请你用画树状图或列表的方法，求两人抽到的数字符号相同的概率。‎ ‎23、如图，在平行四边形ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线于点E，连接BD、EC ‎（1）求证：四边形BECD是平行四边形；‎ ‎（2）若∠A＝50°，则当∠BOD＝ 时，四边形BECD是矩形。‎ ‎24、4月9日上午8时，2017徐州国际马拉松赛鸣枪开跑，一名34岁的男子带着他的两个孩子一同参加了比赛，下面是两个孩子与记者的对话：‎ ‎ ‎ 根据对话内容，请你用方程的知识帮记者求出哥哥和妹妹的年龄。‎ ‎25、如图，已知AC⊥BC，垂足为C，AC＝4，BC＝，将线段AC绕点A按逆时针方向旋转60°，得到线段AD，连接DC、DB ‎（1）线段DC＝ ；‎ ‎（2）求线段DB的长度。‎ ‎26、如图①，菱形ABCD中，AB＝5 cm，动点P从点B出发，沿折线BC-CD-DA运动到点A停止，动点Q从点A出发，沿线段AB运动到点B停止，它们运动的速度相同，设点P出发 s时，△BPQ的面积为 cm2。已知与之间的函数关系如图②所示，其中OM、MN为线段，曲线NK为抛物线的一部分。请根据图中的信息，解答下列问题：‎ ‎（1）当1＜＜2时，△BPQ的面积 （填“变”或“不变”）；‎ ‎（2）分别求出线段OM，曲线NK所对应的函数表达式；‎ ‎（3）当为何值时，△BPQ的面积是5 cm2 ？‎ ‎27、如图，将边长为6的正三角形纸片ABC按如下顺序进行两次折叠、展平后，得折痕AD、BE（如图①），点O为其交点。‎ ‎（1）探求AO与OD的数量关系，并说明理由；‎ ‎（2）如图②，若P、N分别为BE、BC上的动点。‎ ‎ ①当PN＋PD的长度取得最小值时，求BP的长度；‎ ‎ ②如图③，若点Q在线段BO上，BQ＝1，则QN＋NP＋PD的最小值＝ ‎ ‎28、如图，已知二次函数的图象与轴交于A、B两点，与轴交于点C，⊙C的半径为，P为⊙C上一动点。‎ ‎（1）点B、C的坐标分别为B（ ）、C（ ）；‎ ‎（2）是否存在点P，使得△PBC为直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；‎ ‎（3）连接PB，若E为PB的中点，连接OE，则OE的最大值＝ ‎