中考数学模拟试卷一含解析1 16页

‎2016年河南省信阳市新县一中中考数学模拟试卷（一）‎ 一、选择题（共8小题，每小题3分，满分24分）‎ ‎1．在，0，﹣1，这四个实数中，最大的是（　　）‎ A． B．0 C．﹣1 D．‎ ‎2．世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微笑的无花果，质量只有0.000000076克，将0.000000076克用科学记数法表示为（　　）‎ A．7.6×10﹣8 B．0.76×10﹣9 C．7.6×108 D．0.76×109‎ ‎3．如图，直线AB∥CD，直线EF分别与直线AB，CD相交于点G，H．若∠1=135°，则∠2的度数为（　　）‎ A．65° B．55° C．45° D．35°‎ ‎4．如图是某工厂要设计生产的正六棱柱的立体图形，它的主视图是（　　）‎ A． B． C． D．‎ ‎5．为了解本地区老年人一年中生病次数，下列样本抽取方式最合适的是（　　）‎ A．到公园里调查100名晨练老人 B．到医院调查100名老年病人 C．到某小区调查10名老年居民 D．利用户籍资料，按规则抽查10%的老年人 ‎6．已知点P（a+1，﹣+1）关于原点的对称点在第四象限，则a的取值范围在数轴上表示正确的是（　　）‎ A． B． C． D．‎ ‎7．如图，菱形ABCD的对角线AC，BD相交于O点，E，F分别是AB，BC边上的中点，连接EF．若EF=，BD=4，则菱形ABCD的周长为（　　）‎ A．4 B．4 C．4 D．28‎ ‎8．如图，边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上，A1、A2、A3、…、An﹣1为OA的n等分点，B1、B2、B3、…Bn﹣1为CB的n等分点，连接A1B1、A2B2、A3B3、…、An﹣1Bn﹣1，分别交y=x2（x≥0）于点C1、C2、C3、…、Cn﹣1，当B25C25=8C25A25时，则n的值为（　　）‎ A．75 B．15 C．25 D．50‎ ‎　‎ 二、填空题（共7小题，每小题3分，满分21分）‎ ‎9．计算：2﹣1﹣3×=　　　　　　．‎ ‎10．如图，AD∥BE∥CF，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F， =，DE=6，则EF=　　　　　　．‎ ‎11．若点P1（﹣1，m），P2（﹣2，m﹣2）在反比例函数y=的图象上，则m=　　　　　　．‎ ‎12．已知点A（x1，y1），点（x2，y2）是二次函数y=x2﹣2x+3上不重合的两个点，且y1=y2，则x=x1+x2，y的值为　　　　　　．‎ ‎13．若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数，如796就是一个“中高数”，若十位上数字为7，则从5，6，8，9中任选两数，与7组成“中高数”的概率是　　　　　　．‎ ‎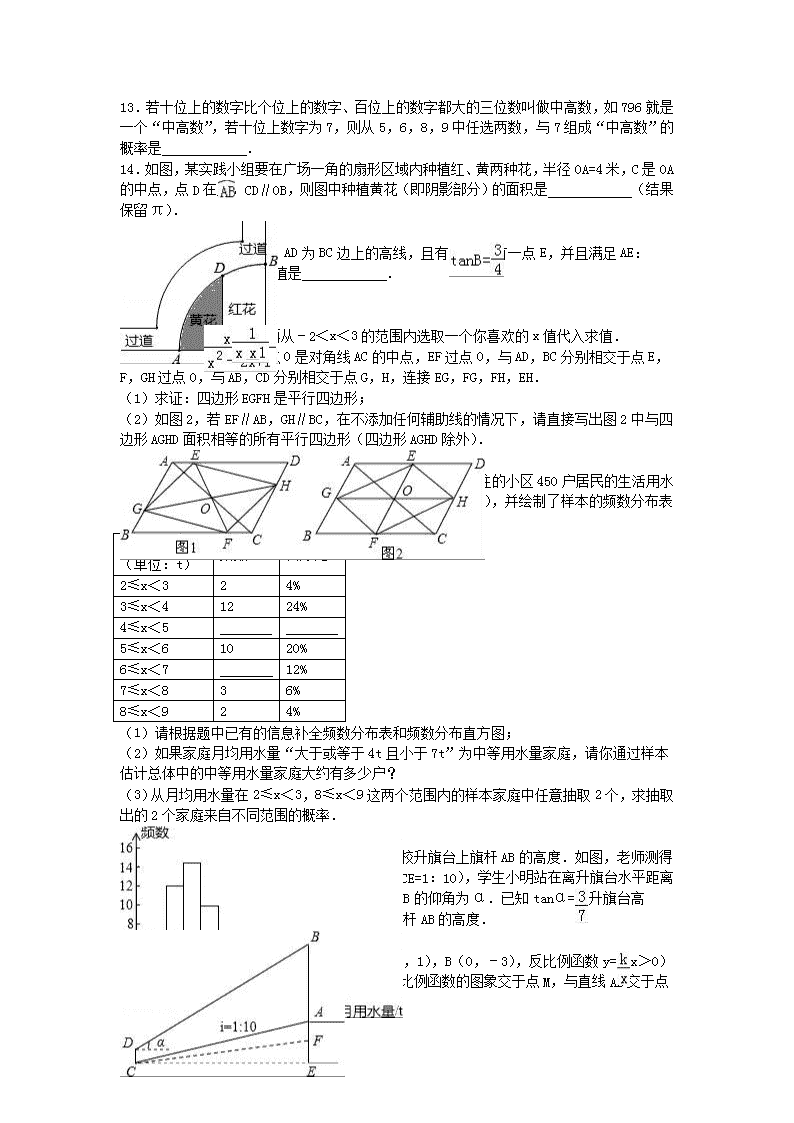14．如图，某实践小组要在广场一角的扇形区域内种植红、黄两种花，半径OA=4米，C是OA的中点，点D在上，CD∥OB，则图中种植黄花（即阴影部分）的面积是　　　　　　（结果保留π）．‎ ‎15．已知等腰三角形ABC，AD为BC边上的高线，且有，AC上有一点E，并且满足AE：EC=2：3，则tan∠ADE的值是　　　　　　．‎ ‎　‎ 三、解答题 ‎16．先化简：÷（﹣），再从﹣2＜x＜3的范围内选取一个你喜欢的x值代入求值．‎ ‎17．如图1，▱ABCD中，点O是对角线AC的中点，EF过点O，与AD，BC分别相交于点E，F，GH过点O，与AB，CD分别相交于点G，H，连接EG，FG，FH，EH．‎ ‎（1）求证：四边形EGFH是平行四边形；‎ ‎（2）如图2，若EF∥AB，GH∥BC，在不添加任何辅助线的情况下，请直接写出图2中与四边形AGHD面积相等的所有平行四边形（四边形AGHD除外）．‎ ‎18．小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）．‎ 月均用水量（单位：t）‎ 频数 百分比 ‎2≤x＜3‎ ‎2‎ ‎4%‎ ‎3≤x＜4‎ ‎12‎ ‎24%‎ ‎4≤x＜5‎ ‎　　　　　　‎ ‎　　　　　　‎ ‎5≤x＜6‎ ‎10‎ ‎20%‎ ‎6≤x＜7‎ ‎　　　　　　‎ ‎12%‎ ‎7≤x＜8‎ ‎3‎ ‎6%‎ ‎8≤x＜9‎ ‎2‎ ‎4%‎ ‎（1）请根据题中已有的信息补全频数分布表和频数分布直方图；‎ ‎（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有多少户？‎ ‎（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，求抽取出的2个家庭来自不同范围的概率．‎ ‎19．数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度．如图，老师测得升旗台前斜坡FC的坡比为iFC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α．已知tanα=，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．‎ ‎20．如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数y=（x＞0）的图象经过点A，动直线x=t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．‎ ‎（1）求k的值；‎ ‎（2）求△BMN面积的最大值；‎ ‎（3）若MA⊥AB，求t的值．‎ ‎21．某文具店购进A，B两种钢笔，若购进A种钢笔2支，B种钢笔3支，共需90元；购进A种钢笔3支，B种钢笔5支，共需145元．‎ ‎（1）求A、B两种钢笔每支各多少元？‎ ‎（2）若该文具店要购进A，B两种钢笔共90支，总费用不超过1588元，并且A种钢笔的数量少于B种钢笔的数量，那么该文具店有哪几种购买方案？‎ ‎（3）文具店以每支30元的价格销售B种钢笔，很快销售一空，于是，文具店决定在进价不变的基础上再购进一批B种钢笔，涨价卖出，经统计，B种钢笔售价为30元时，每月可卖68支；每涨价1元，每月将少卖4支，设文具店将新购进的B种钢笔每支涨价a元（a为正整数），销售这批钢笔每月获得W元，试求W与a之间的函数关系式，并且求出B种铅笔销售单价定为多少元时，每月获利最大？最大利润是多少元？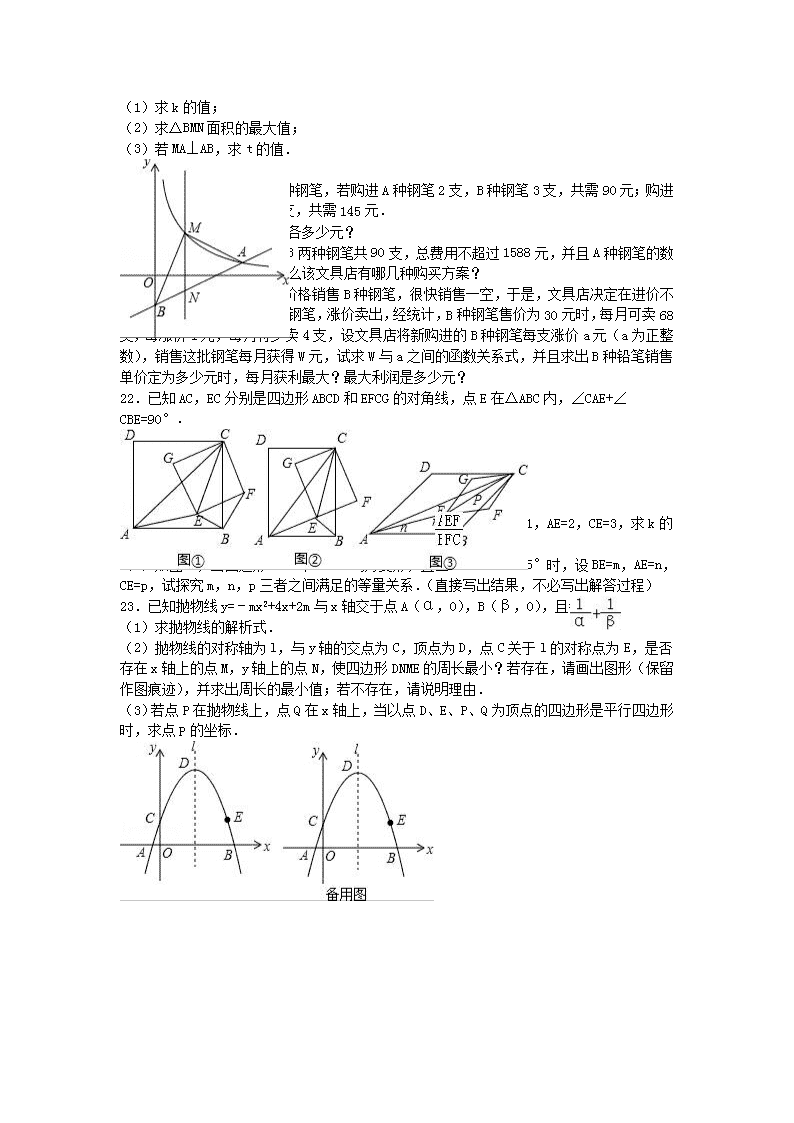‎ ‎22．已知AC，EC分别是四边形ABCD和EFCG的对角线，点E在△ABC内，∠CAE+∠CBE=90°．‎ ‎（1）如图①，当四边形ABCD和EFCG均为正方形时，连接BF．‎ ‎（i）求证：△CAE∽△CBF；‎ ‎（ii）若BE=1，AE=2，求CE的长；‎ ‎（2）如图②，当四边形ABCD和EFCG均为矩形，且==k时，若BE=1，AE=2，CE=3，求k的值；‎ ‎（3）如图③，当四边形ABCD和EFCG均为菱形，且∠DAB=∠GEF=45°时，设BE=m，AE=n，CE=p，试探究m，n，p三者之间满足的等量关系．（直接写出结果，不必写出解答过程）‎ ‎23．已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0），B（β，0），且=﹣2，‎ ‎（1）求抛物线的解析式．‎ ‎（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．‎ ‎（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．‎ ‎　‎ ‎2016年河南省信阳市新县一中中考数学模拟试卷（一）‎ 参考答案与试题解析 ‎　‎ 一、选择题（共8小题，每小题3分，满分24分）‎ ‎1．在，0，﹣1，这四个实数中，最大的是（　　）‎ A． B．0 C．﹣1 D．‎ ‎【考点】实数大小比较．‎ ‎【分析】利用任意两个实数都可以比较大小，正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小进行比较即可．‎ ‎【解答】解：∵正实数都大于0，负实数都小于0，正实数大于一切负实数，‎ ‎0＜＜1，1＜＜2，‎ ‎∴﹣1＜0＜＜，‎ 故选D．‎ ‎　‎ ‎2．世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微笑的无花果，质量只有0.000000076克，将0.000000076克用科学记数法表示为（　　）‎ A．7.6×10﹣8 B．0.76×10﹣9 C．7.6×108 D．0.76×109‎ ‎【考点】科学记数法—表示较小的数．‎ ‎【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．‎ ‎【解答】解：0.000000076=7.6×10﹣8．‎ 故选：A．‎ ‎　‎ ‎3．如图，直线AB∥CD，直线EF分别与直线AB，CD相交于点G，H．若∠1=135°，则∠2的度数为（　　）‎ A．65° B．55° C．45° D．35°‎ ‎【考点】平行线的性质．‎ ‎【分析】根据平行线的性质求出∠2的度数即可．‎ ‎【解答】解：∵AB∥CD，∠1=135°，‎ ‎∴∠2=180°﹣135°=45°．‎ 故选C．‎ ‎　‎ ‎4．如图是某工厂要设计生产的正六棱柱的立体图形，它的主视图是（　　）‎ A． B． C． D．‎ ‎【考点】简单几何体的三视图．‎ ‎【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．依此即可求解．‎ ‎【解答】解：根据主视图的定义，可得它的主视图为：．‎ 故选：A．‎ ‎　‎ ‎5．为了解本地区老年人一年中生病次数，下列样本抽取方式最合适的是（　　）‎ A．到公园里调查100名晨练老人 B．到医院调查100名老年病人 C．到某小区调查10名老年居民 D．利用户籍资料，按规则抽查10%的老年人 ‎【考点】抽样调查的可靠性．‎ ‎【分析】采取抽样调查时，应能够保证被抽中的调查样本在总体中的合理、均匀分布，调查出现倾向性偏差的可能性是极小的，样本对总体的代表性很强．‎ ‎【解答】解：A，B选项选择的地点没有代表性，公园里的老人都比较注意远动，身体比较健康，医院的病人太多；‎ C、选项调查10人数量太少；‎ D、随机抽查了本地区10%的老年人，具有代表性．‎ 故选D．‎ ‎　‎ ‎6．已知点P（a+1，﹣+1）关于原点的对称点在第四象限，则a的取值范围在数轴上表示正确的是（　　）‎ A． B． C． D．‎ ‎【考点】关于原点对称的点的坐标；在数轴上表示不等式的解集．‎ ‎【分析】根据关于原点对称点的性质得出对应点坐标，再利用第四象限点的坐标性质得出答案．‎ ‎【解答】解：∵点P（a+1，﹣+1）关于原点的对称点坐标为：（﹣a﹣1，﹣1），该点在第四象限，‎ ‎∴，‎ 解得：a＜﹣1，‎ 则a的取值范围在数轴上表示为：‎ ‎．‎ 故选：C．‎ ‎　‎ ‎7．如图，菱形ABCD的对角线AC，BD相交于O点，E，F分别是AB，BC边上的中点，连接EF．若EF=，BD=4，则菱形ABCD的周长为（　　）‎ A．4 B．4 C．4 D．28‎ ‎【考点】菱形的性质；三角形中位线定理．‎ ‎【分析】首先利用三角形的中位线定理得出AC，进一步利用菱形的性质和勾股定理求得边长，得出周长即可．‎ ‎【解答】解：∵E，F分别是AB，BC边上的中点，EF=，‎ ‎∴AC=2EF=2，‎ ‎∵四边形ABCD是菱形，‎ ‎∴AC⊥BD，OA=AC=，OB=BD=2，‎ ‎∴AB==，‎ ‎∴菱形ABCD的周长为4．‎ 故选：C．‎ ‎　‎ ‎8．如图，边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上，A1、A2、A3、…、An﹣1为OA的n等分点，B1、B2、B3、…Bn﹣1为CB的n等分点，连接A1B1、A2B2、A3B3、…、An﹣1Bn﹣1，分别交y=x2（x≥0）于点C1、C2、C3、…、Cn﹣1，当B25C25=8C25A25时，则n的值为（　　）‎ A．75 B．15 C．25 D．50‎ ‎【考点】二次函数图象上点的坐标特征．‎ ‎【分析】根据题意表示出OA25，B25A25的长，由B25C25=8C25A25确定点C25的坐标，代入解析式计算得到答案．‎ ‎【解答】解：∵正方形OABC的边长为n，点A1，A2，…，An﹣1为OA的n等分点，点B1，B2，…，Bn﹣1为CB的n等分点，‎ ‎∴OA25=•n=25，A25B25=n，‎ ‎∵B25C25=8C25A25，‎ ‎∴C25（25，），‎ ‎∵点C25在y=x2（x≥0）上，‎ ‎∴=×（25）2，‎ 解得n=75．‎ 故选A．‎ ‎　‎ 二、填空题（共7小题，每小题3分，满分21分）‎ ‎9．计算：2﹣1﹣3×=　﹣1　．‎ ‎【考点】立方根；负整数指数幂．‎ ‎【分析】先依据负整数指数幂的性质、立方根的性质进行计算，然后再依据有理数的乘法和减法法则计算即可．‎ ‎【解答】解：原式=﹣3×=﹣1．‎ 故答案为：﹣1．‎ ‎　‎ ‎10．如图，AD∥BE∥CF，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F， =，DE=6，则EF=　9　．‎ ‎【考点】平行线分线段成比例．‎ ‎【分析】根据平行线分线段成比例定理得到=，即=，然后根据比例性质求EF．‎ ‎【解答】解：∵AD∥BE∥CF，‎ ‎∴=，即=，‎ ‎∴EF=9．‎ 故答案为9．‎ ‎　‎ ‎11．若点P1（﹣1，m），P2（﹣2，m﹣2）在反比例函数y=的图象上，则m=　4　．‎ ‎【考点】反比例函数图象上点的坐标特征．‎ ‎【分析】根据反比例函数图象上的点纵横坐标之积为定值列出m的一元一次方程，求出m的值即可．‎ ‎【解答】解：∵P1（﹣1，m），P2（﹣2，m﹣2）在反比例函数y=的图象上，‎ ‎∴﹣m=﹣2×（m﹣2），‎ ‎∴m=4，‎ 故答案为4．‎ ‎　‎ ‎12．已知点A（x1，y1），点（x2，y2）是二次函数y=x2﹣2x+3上不重合的两个点，且y1=y2，则x=x1+x2，y的值为　3　．‎ ‎【考点】二次函数图象上点的坐标特征．‎ ‎【分析】根据点在函数图象上的意义求出x=x1+x2 的值，再代入二次函数的解析式求得对应的y的值．‎ ‎【解答】解：∵点（x1，y1）与点（x2，y2）是二次函数y=x2﹣2x+3上不重合的两个点，‎ ‎∴y1=y=x12﹣2x1+3，y2=x22﹣2x2+3．‎ 又∵y1=y2，‎ ‎∴x12﹣2x1+3=x22﹣2x2+3，‎ x12﹣x22=2（x1﹣x2 ），‎ ‎∵点（x1，y1）与点（x2，y2）是二次函数y=x2﹣2x+3上不重合的两个点，‎ ‎∴x1﹣x2≠0，‎ ‎∴x1+x2=2，‎ ‎∴x=x1+x2=2，则：y=22﹣2×2+3=3．‎ 即：当x=x1+x2 时，y的值为3‎ ‎　‎ ‎13．若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数，如796就是一个“中高数”，若十位上数字为7，则从5，6，8，9中任选两数，与7组成“中高数”的概率是　　．‎ ‎【考点】列表法与树状图法．‎ ‎【分析】先画树状图展示所有12种等可能的结果数，再找出任选两个不同的数，与7组成“中高数”的结果数，然后根据概率公式求解．‎ ‎【解答】解：画树状图为：‎ ‎，‎ 一共有12种可能，与7组成“中高数”的有2种，故与7组成“中高数”的概率是： =．‎ 故答案为：．‎ ‎　‎ ‎14．如图，某实践小组要在广场一角的扇形区域内种植红、黄两种花，半径OA=4米，C是OA的中点，点D在上，CD∥OB，则图中种植黄花（即阴影部分）的面积是　π﹣2　（结果保留π）．‎ ‎【考点】扇形面积的计算．‎ ‎【分析】连接OD，根据直角三角形的性质求出∠ODC的度数，根据扇形面积公式和三角形面积公式得到答案．‎ ‎【解答】解：连接OD，‎ ‎∵C是OA的中点，OA=OD，‎ ‎∴OC=OD=2，CD=2，‎ ‎∴∠ODC=30°，则∠DOA=60°，‎ 种植黄花（即阴影部分）的面积=扇形AOD的面积﹣△DOC的面积 ‎=﹣×2×2‎ ‎=π﹣2，‎ 故答案为：π﹣2．‎ ‎　‎ ‎15．已知等腰三角形ABC，AD为BC边上的高线，且有，AC上有一点E，并且满足AE：EC=2：3，则tan∠ADE的值是　或或　．‎ ‎【考点】解直角三角形．‎ ‎【分析】分三种情况进行讨论：①如果AB=AC，过E点作CD的平行线交AD于F．②如果BA=BC，过E点作CD的平行线交AD于F．③如果CA=CB，过E点作CD的平行线交AD于F，作CG⊥AB于G．利用锐角三角函数的定义、平行线分线段成比例定理可求出∠ADE的正切值．‎ ‎【解答】解：分三种情况：‎ ‎①如果AB=AC，过E点作CD的平行线交AD于F．如图1．‎ ‎∵AD为BC边上的高线，tan∠B=，‎ ‎∴EF⊥AD，tan∠C=．‎ 设AE=2a，‎ ‎∵AE：CE=2：3，‎ ‎∴CE=3a，AC=5a．‎ ‎∵tan∠C=，‎ ‎∴sin∠C=，cos∠C=．‎ 在直角△ADC中，‎ AD=ACsin∠C=5a×=3a．‎ 在直角△AFE中，‎ AF=AE×sin∠AEF=AE×sin∠C=2a×=a．‎ EF=AE×cos∠AEF=AE×cos∠C=2a×=a．‎ DF=AD﹣AF=3a﹣a=a．‎ 在直角△DFE中，‎ tan∠ADE===；‎ ‎②如果BA=BC，过E点作CD的平行线交AD于F．如图2．‎ ‎∵AD为BC边上的高线，tan∠B==，‎ ‎∴可设AD=3k，则BD=4k，‎ 由勾股定理得AB=5k，‎ ‎∴BC=AB=5k，DC=AC﹣BD=k．‎ ‎∵EF∥CD，AE：EC=2：3，‎ ‎∴===，‎ ‎∴==，‎ ‎∴AF=k，EF=k，‎ ‎∴DF=AD﹣AF=3k﹣k=k．‎ 在直角△DFE中，‎ tan∠ADE===；‎ ‎③如果CA=CB，过E点作CD的平行线交AD于F，作CG⊥AB于G．如图2．‎ ‎∵在直角△BCG中，tan∠B==，‎ ‎∴可设CG=3b，则BG=4b，AB=2BG=8b，‎ 由勾股定理得BC=5b，则AC=BC=5b，‎ ‎∵AE：EC=2：3，‎ ‎∴AE=2b，EC=3b．‎ ‎∵在直角△ABD中，tan∠B==，AB=8b，‎ ‎∴AD=×8b=b，BD=×8b=b，‎ ‎∴CD=BD﹣BC=b﹣5b=b．‎ ‎∵EF∥CD，‎ ‎∴===，‎ ‎∴==，‎ ‎∴AF=b，EF=b，‎ ‎∴DF=AD﹣AF=b﹣b=b．‎ 在直角△DFE中，‎ tan∠ADE===．‎ 故答案为或或．‎ ‎　‎ 三、解答题 ‎16．先化简：÷（﹣），再从﹣2＜x＜3的范围内选取一个你喜欢的x值代入求值．‎ ‎【考点】分式的化简求值．‎ ‎【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，确定出x的值，代入计算即可求出值．‎ ‎【解答】解：原式=÷=•=，‎ 当x=2时，原式=4（x≠﹣1，0，1）．‎ ‎　‎ ‎17．如图1，▱ABCD中，点O是对角线AC的中点，EF过点O，与AD，BC分别相交于点E，F，GH过点O，与AB，CD分别相交于点G，H，连接EG，FG，FH，EH．‎ ‎（1）求证：四边形EGFH是平行四边形；‎ ‎（2）如图2，若EF∥AB，GH∥BC，在不添加任何辅助线的情况下，请直接写出图2中与四边形AGHD面积相等的所有平行四边形（四边形AGHD除外）．‎ ‎【考点】平行四边形的判定与性质；全等三角形的判定与性质．‎ ‎【分析】（1）由四边形ABCD是平行四边形，得到AD∥BC，根据平行四边形的性质得到∠EAO=∠FCO，证出△OAE≌△OCF，得到OE=OF，同理OG=OH，根据对角线互相平分的四边形是平行四边形得到结论；‎ ‎（2）根据两组对边分别平行的四边形是平行四边形即可得到结论．‎ ‎【解答】（1）证明：∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，‎ ‎∴∠EAO=∠FCO，‎ 在△OAE与△OCF中，‎ ‎∴△OAE≌△OCF，‎ ‎∴OE=OF，‎ 同理OG=OH，‎ ‎∴四边形EGFH是平行四边形；‎ ‎（2）解：与四边形AGHD面积相等的所有平行四边形有▱GBCH，▱ABFE，▱EFCD，▱EGFH；‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，AB∥CD，‎ ‎∵EF∥AB，GH∥BC，‎ ‎∴四边形GBCH，ABFE，EFCD，EGFH为平行四边形，‎ ‎∵EF过点O，GH过点O，‎ ‎∵OE=OF，OG=OH，‎ ‎∴▱GBCH，▱ABFE，▱EFCD，▱EGFH，▱ACHD它们面积=▱ABCD的面积，‎ ‎∴与四边形AGHD面积相等的所有平行四边形有▱GBCH，▱ABFE，▱EFCD，▱EGFH．‎ ‎　‎ ‎18．小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）．‎ 月均用水量（单位：t）‎ 频数 百分比 ‎2≤x＜3‎ ‎2‎ ‎4%‎ ‎3≤x＜4‎ ‎12‎ ‎24%‎ ‎4≤x＜5‎ ‎　15　‎ ‎　30%　‎ ‎5≤x＜6‎ ‎10‎ ‎20%‎ ‎6≤x＜7‎ ‎　6　‎ ‎12%‎ ‎7≤x＜8‎ ‎3‎ ‎6%‎ ‎8≤x＜9‎ ‎2‎ ‎4%‎ ‎（1）请根据题中已有的信息补全频数分布表和频数分布直方图；‎ ‎（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有多少户？‎ ‎（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，求抽取出的2个家庭来自不同范围的概率．‎ ‎【考点】频数（率）分布直方图；用样本估计总体；频数（率）分布表；列表法与树状图法．‎ ‎【分析】（1）根据第一组的频数是2，百分比是4%即可求得总人数，然后根据百分比的意义求解；‎ ‎（2）利用总户数540乘以对应的百分比求解；‎ ‎（3）在2≤x＜3范围的两户用a、b表示，8≤x＜9这两个范围内的两户用1，2表示，利用树状图法表示出所有可能的结果，然后利用概率公式求解．‎ ‎【解答】解：（1）调查的总数是：2÷4%=50（户），‎ 则6≤x＜7部分调查的户数是：50×12%=6（户），‎ 则4≤x＜5的户数是：50﹣2﹣12﹣10﹣6﹣3﹣2=15（户），所占的百分比是：×100%=30%．‎ 月均用水量（单位：t）‎ 频数 百分比 ‎2≤x＜3‎ ‎2‎ ‎4%‎ ‎3≤x＜4‎ ‎12‎ ‎24%‎ ‎4≤x＜5‎ ‎15‎ ‎30%‎ ‎5≤x＜6‎ ‎10‎ ‎20%‎ ‎6≤x＜7‎ ‎6‎ ‎12%‎ ‎7≤x＜8‎ ‎3‎ ‎6%‎ ‎8≤x＜9‎ ‎2‎ ‎4%‎ ‎（2）中等用水量家庭大约有450×（30%+20%+12%）=279（户）；‎ ‎（3）在2≤x＜3范围的两户用a、b表示，8≤x＜9这两个范围内的两户用1，2表示．‎ 则抽取出的2个家庭来自不同范围的概率是： =．‎ ‎　‎ ‎19．数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度．如图，老师测得升旗台前斜坡FC的坡比为iFC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α．已知tanα=，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．‎ ‎【考点】解直角三角形的应用-仰角俯角问题；解直角三角形的应用-坡度坡角问题．‎ ‎【分析】首先根据题意分析图形，本题涉及到两个直角三角形，分别解可得BG与EF的大小，进而求得BE、AE的大小，再利用AB=BE﹣AE可求出答案．‎ ‎【解答】解：作DG⊥AE于G，则∠BDG=α，‎ 易知四边形DCEG为矩形．‎ ‎∴DG=CE=35m，EG=DC=1.6m 在直角三角形BDG中，BG=DG•×tanα=35×=15m，‎ ‎∴BE=15+1.6=16.6m．‎ ‎∵斜坡FC的坡比为iFC=1：10，CE=35m，‎ ‎∴EF=35×=3.5，‎ ‎∵AF=1，‎ ‎∴AE=AF+EF=1+3.5=4.5，‎ ‎∴AB=BE﹣AE=16.6﹣4.5=12.1m．‎ 答：旗杆AB的高度为12.1m．‎ ‎　‎ ‎20．如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数y=（x＞0）的图象经过点A，动直线x=t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．‎ ‎（1）求k的值；‎ ‎（2）求△BMN面积的最大值；‎ ‎（3）若MA⊥AB，求t的值．‎ ‎【考点】反比例函数综合题．‎ ‎【分析】（1）把点A坐标代入y=（x＞0），即可求出k的值；‎ ‎（2）先求出直线AB的解析式，设M（t，），N（t， t﹣3），则MN=﹣t+3，由三角形的面积公式得出△BMN的面积是t的二次函数，即可得出面积的最大值；‎ ‎（3）求出直线AM的解析式，由反比例函数解析式和直线AM的解析式组成方程组，解方程组求出M的坐标，即可得出结果．‎ ‎【解答】解：（1）把点A（8，1）代入反比例函数y=（x＞0）得：‎ k=1×8=8，y=，‎ ‎∴k=8；‎ ‎（2）设直线AB的解析式为：y=kx+b，‎ 根据题意得：，‎ 解得：k=，b=﹣3，‎ ‎∴直线AB的解析式为：y=x﹣3；‎ 设M（t，），N（t， t﹣3），‎ 则MN=﹣t+3，‎ ‎∴△BMN的面积S=（﹣t+3）t=﹣t2+t+4=﹣（t﹣3）2+，‎ ‎∴△BMN的面积S是t的二次函数，‎ ‎∵﹣＜0，‎ ‎∴S有最大值，‎ 当t=3时，△BMN的面积的最大值为；‎ ‎（3）∵MA⊥AB，‎ ‎∴设直线MA的解析式为：y=﹣2x+c，‎ 把点A（8，1）代入得：c=17，‎ ‎∴直线AM的解析式为：y=﹣2x+17，‎ 解方程组得： 或（舍去），‎ ‎∴M的坐标为（，16），‎ ‎∴t=．‎ ‎　‎ ‎21．某文具店购进A，B两种钢笔，若购进A种钢笔2支，B种钢笔3支，共需90元；购进A种钢笔3支，B种钢笔5支，共需145元．‎ ‎（1）求A、B两种钢笔每支各多少元？‎ ‎（2）若该文具店要购进A，B两种钢笔共90支，总费用不超过1588元，并且A种钢笔的数量少于B种钢笔的数量，那么该文具店有哪几种购买方案？‎ ‎（3）文具店以每支30元的价格销售B种钢笔，很快销售一空，于是，文具店决定在进价不变的基础上再购进一批B种钢笔，涨价卖出，经统计，B种钢笔售价为30元时，每月可卖68支；每涨价1元，每月将少卖4支，设文具店将新购进的B种钢笔每支涨价a元（a为正整数），销售这批钢笔每月获得W元，试求W与a之间的函数关系式，并且求出B种铅笔销售单价定为多少元时，每月获利最大？最大利润是多少元？‎ ‎【考点】二次函数的应用；二元一次方程组的应用；一元一次不等式组的应用．‎ ‎【分析】（1）设A种钢笔每只x元，B种钢笔每支y元，由题意得方程组即可解得答案；‎ ‎（2）设购进A种钢笔每只z元，由题意得，求得42.4≤z＜45，由于z是整数，得到z=43，44于是得到共有两种方案：方案一：购进A种钢笔43支，购进B种钢笔47支，方案二：购进A种钢笔44只，购进B种钢笔46只，‎ ‎（3）根据二次函数的解析式W=（30﹣20+a）（68﹣4a）=﹣4a2+28a+680=﹣4（a﹣）2+729即可求得结果．‎ ‎【解答】解：（1）设A种钢笔每只x元，B种钢笔每支y元，‎ 由题意得，‎ 解得：，‎ 答：A种钢笔每只15元，B种钢笔每支20元；‎ ‎（2）设购进A种钢笔z支，‎ 由题意得：，‎ ‎∴42.4≤z＜45，‎ ‎∵z是整数 z=43，44，‎ ‎∴90﹣z=47，或46；‎ ‎∴共有两种方案：方案一：购进A种钢笔43支，购进B种钢笔47支，‎ 方案二：购进A种钢笔44只，购进B种钢笔46只；‎ ‎（3）W=（30﹣20+a）（68﹣4a）=﹣4a2+28a+680=﹣4（a﹣）2+729，‎ ‎∵﹣4＜0，∴W有最大值，∵a为正整数，‎ ‎∴当a=3，或a=4时，W最大，‎ ‎∴W最大=﹣4×（3﹣）2+729=728，30+a=33，或34；‎ 答：B种铅笔销售单价定为33元或34元时，每月获利最大，最大利润是728元．‎ ‎　‎ ‎22．已知AC，EC分别是四边形ABCD和EFCG的对角线，点E在△ABC内，∠CAE+∠CBE=90°．‎ ‎（1）如图①，当四边形ABCD和EFCG均为正方形时，连接BF．‎ ‎（i）求证：△CAE∽△CBF；‎ ‎（ii）若BE=1，AE=2，求CE的长；‎ ‎（2）如图②，当四边形ABCD和EFCG均为矩形，且==k时，若BE=1，AE=2，CE=3，求k的值；‎ ‎（3）如图③，当四边形ABCD和EFCG均为菱形，且∠DAB=∠GEF=45°时，设BE=m，AE=n，CE=p，试探究m，n，p三者之间满足的等量关系．（直接写出结果，不必写出解答过程）‎ ‎【考点】四边形综合题．‎ ‎【分析】（1）（i）首先根据四边形ABCD和EFCG均为正方形，可得，∠ACE=∠BCF；然后根据相似三角形判定的方法，推得△CAE∽△CBF即可．‎ ‎（ii）首先根据△CAE∽△CBF，判断出∠CAE=∠CBF，再根据∠CAE+∠CBE=90°，判断出∠EBF=90°；然后在Rt△BEF中，根据勾股定理，求出EF的长度，再根据CE、EF的关系，求出CE的长是多少即可．‎ ‎（2）首先根据相似三角形判定的方法，判断出△ACE∽△BCF，即可判断出，据此求出BF的长度是多少；然后判断出∠EBF=90°，在Rt△BEF中，根据勾股定理，求出EF的值是多少，进而求出k的值是多少即可．‎ ‎（3）首先根据∠DAB=45°，可得∠ABC=180°﹣45°=135°，在△ABC中，根据勾股定理可求得AB2、BC2，AC2之间的关系，EF2、FC2，EC2之间的关系；然后根据相似三角形判定的方法，判断出△ACE∽△BCF，即可用n表示出BF的值；最后判断出EBF=90°，在Rt△BEF中，根据勾股定理，判断出m，n，p三者之间满足的等量关系即可．‎ ‎【解答】（1）（i）证明：∵四边形ABCD和EFCG均为正方形，‎ ‎∴，‎ ‎∴∠ACB=∠ECF=45°，‎ ‎∴∠ACE=∠BCF，‎ 在△CAE和△CBF中，‎ ‎，‎ ‎∴△CAE∽△CBF．‎ ‎（ii）解：∵△CAE∽△CBF，‎ ‎∴∠CAE=∠CBF，，‎ 又∵∠CAE+∠CBE=90°，‎ ‎∴∠CBF+∠CBE=90°，‎ ‎∴∠EBF=90°，‎ 又∵，AE=2‎ ‎∴，‎ ‎∴，‎ ‎∴EF2=BE2+BF2==3，‎ ‎∴EF=，‎ ‎∵CE2=2EF2=6，‎ ‎∴CE=．‎ ‎（2）如图②，连接BF，‎ ‎∵==k，‎ ‎∴BC=a，AB=ka，FC=b，EF=kb，‎ ‎∴AC=，‎ CE==，‎ ‎∴，∠ACE=∠BCF，‎ 在△ACE和△BCF中，‎ ‎，‎ ‎∴△ACE∽△BCF，‎ ‎∴，∠CAE=∠CBF，‎ 又∵AE=2，‎ ‎∴，‎ ‎∴BF=，‎ ‎∵∠CAE=∠CBF，∠CAE+∠CBE=90°，‎ ‎∴∠CBE+∠CBF=90°，‎ ‎∴∠EBF=90°，‎ ‎∴EF2=BE2+BF2=1，‎ ‎∵，‎ ‎∴=，CE=3，‎ ‎∴EF=，‎ ‎∴1，‎ ‎∴，‎ 解得k=±，‎ ‎∵==k＞0，‎ ‎∴k=．‎ ‎（3）连接BF，同理可得∠EBF=90°，过C点作CH⊥AB延长线于H，‎ ‎∵四边形ABCD为菱形，‎ ‎∴AB=BC，设AB=BC=x，‎ ‎∵∠CBH=∠DAB=45°，∴BH=CH=x，‎ ‎∴AC2=AH2+CH2=（x+x）2+（x）2，=（2+）x2，‎ ‎∴AB2：BC2：AC2=1：1：（2+），‎ 同理可得EF2：FC2：EC2=1：1：（2+），‎ ‎∴EF2==，‎ 在△ACE和△BCF中，‎ ‎，‎ ‎∴△ACE∽△BCF，‎ ‎∴==2+，∠CAE=∠CBF，‎ 又∵AE=n，‎ ‎∴，‎ ‎∵∠CAE=∠CBF，∠CAE+∠CBE=90°，‎ ‎∴∠CBE+∠CBF=90°，‎ ‎∴∠EBF=90°，‎ ‎∴EF2=BE2+BF2，‎ ‎∴，‎ ‎∴（2）m2+n2=p2，‎ 即m，n，p三者之间满足的等量关系是：（2）m2+n2=p2．‎ ‎　‎ ‎23．已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0），B（β，0），且=﹣2，‎ ‎（1）求抛物线的解析式．‎ ‎（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．‎ ‎（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）利用根据与系数的关系得出α+β=，αβ=﹣2，进而代入求出m的值即可得出答案；‎ ‎（2）利用轴对称求最短路线的方法，作点D关于y轴的对称点D′，点E关于x轴的对称点E′，得出四边形DNME的周长最小为：D′E′+DE，进而利用勾股定理求出即可；‎ ‎（3）利用平行四边形的判定与性质结合P点纵坐标为±4，进而分别求出即可．‎ ‎【解答】解：（1）由题意可得：α，β是方程﹣mx2+4x+2m=0的两根，由根与系数的关系可得，‎ α+β=，αβ=﹣2，‎ ‎∵=﹣2，‎ ‎∴=﹣2，即=﹣2，‎ 解得：m=1，‎ 故抛物线解析式为：y=﹣x2+4x+2；‎ ‎（2）存在x轴上的点M，y轴上的点N，使得四边形DNME的周长最小，‎ ‎∵y=﹣x2+4x+2=﹣（x﹣2）2+6，‎ ‎∴抛物线的对称轴l为x=2，顶点D的坐标为：（2，6），‎ 又∵抛物线与y轴交点C的坐标为：（0，2），点E与点C关于l对称，‎ ‎∴E点坐标为：（4，2），‎ 作点D关于y轴的对称点D′，点E关于x轴的对称点E′，‎ 则D′的坐标为；（﹣2，6），E′坐标为：（4，﹣2），‎ 连接D′E′，交x轴于M，交y轴于N，‎ 此时，四边形DNME的周长最小为：D′E′+DE，如图1所示：‎ 延长E′E，′D交于一点F，在Rt△D′E′F中，D′F=6，E′F=8，‎ 则D′E′===10，‎ 设对称轴l与CE交于点G，在Rt△DGE中，DG=4，EG=2，‎ ‎∴DE===2，‎ ‎∴四边形DNME的周长最小值为：10+2；‎ ‎（3）如图2，P为抛物线上的点，过点P作PH⊥x轴，垂足为H，‎ 若以点D、E、P、Q为顶点的四边形为平行四边形，则△PHQ≌△DGE，‎ ‎∴PH=DG=4，‎ ‎∴|y|=4，‎ ‎∴当y=4时，﹣x2+4x+2=4，‎ 解得：x1=2+，x2=2﹣，‎ 当y=﹣4时，﹣x2+4x+2=﹣4，‎ 解得：x3=2+，x4=2﹣，‎ 故P点的坐标为；（2﹣，4），（2+，4），（2﹣，﹣4），（2+，﹣4）．‎