上海中考数学压轴题集锦20102012 47页

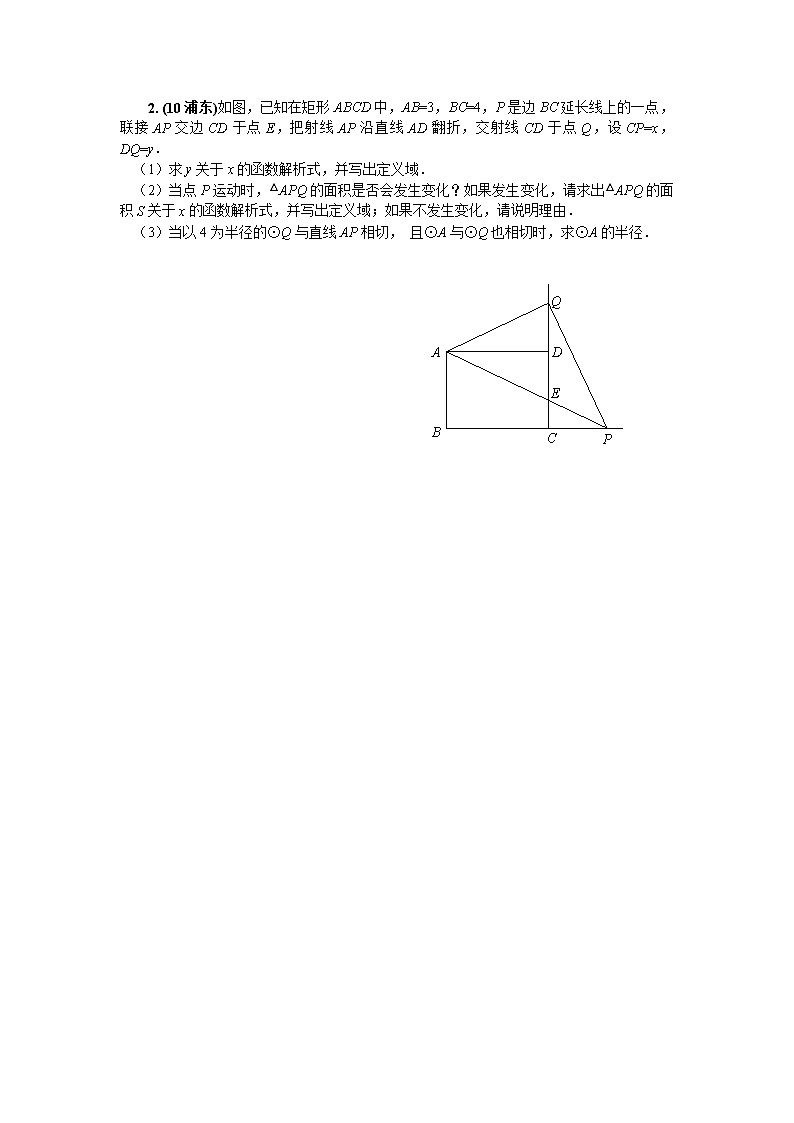
压轴题集锦 ‎2013年2月---2013年6月 一．圆背景下的综合题：‎ ‎1.（10金山）如图1，在Rt△ABC中，∠C=90°，AC=BC，D是AB边上一点，E是在AC边上的一个动点（与点A、C不重合），DF⊥DE，DF与射线BC相交于点F。‎ ‎（1）如图2，如果点D是边AB的中点，求证：DE=DF；‎ ‎（2）如果AD∶DB=m，求DE∶DF的值；‎ ‎（3）如果AC=BC=6，AD∶DB=1∶2，设AE=x，BF=y，‎ ‎①求y关于x的函数关系式，并写出定义域；‎ C A B D E F 图2‎ C A B D E F 图1‎ ‎②以CE为直径的圆与直线AB是否可相切，若可能，求出此时x的值，若不可能，请说明理由。‎ C A B D 备用图1‎ C A B D 备用图2‎ ‎2. (10浦东)如图，已知在矩形ABCD中，AB=3，BC=4，P是边BC延长线上的一点，联接AP交边CD于点E，把射线AP沿直线AD翻折，交射线CD于点Q，设CP=x，DQ=y．‎ ‎（1）求y关于x的函数解析式，并写出定义域．‎ ‎（2）当点P运动时，△APQ的面积是否会发生变化？如果发生变化，请求出△APQ的面积S关于x的函数解析式，并写出定义域；如果不发生变化，请说明理由．‎ ‎（3）当以4为半径的⊙Q与直线AP相切， 且⊙A与⊙Q也相切时，求⊙A的半径．‎ A B C Q D P E ‎3. （10青浦）如图，已知△ABC中，AB=AC=，BC=4，点O在BC边上运动，以O为圆心，OA为半径的圆与边AB交于点D（点A除外），设OB，AD ．‎ ‎（1）求的值；‎ ‎（2）求关于的函数解析式，并写出函数的定义域；‎ C O D B A ‎（3）当点O在BC边上运动时，⊙O是否可能与以C为圆心，BC长为半径的⊙C相切？如果可能，请求出两圆相切时的值；如果不可能，请说明理由．‎ ‎4. （11松江）如图，在Rt△ABC中，∠C=90°，AC=4，BC=5，D是BC边上一点，CD=3，点P在边AC上（点P与A、C不重合），过点P作PE// BC，交AD于点E．‎ ‎（1）设AP=x，DE=y，求y关于x的函数解析式，并写出x的取值范围；‎ ‎（2）当以PE为半径的⊙E与DB为半径的⊙D外切时，求的正切值；‎ 备用图 D C B A ‎（3）将△ABD沿直线AD翻折，得到△AB/D，联结B/C．如果∠ACE=∠BCB/，求AP的值．‎ E P D C B A ‎5. （11浦东）如图，已知在△ABC中，AB=4，BC=2，以点B为圆心，线段BC长为半径的弧交边AC于点D，且∠DBC=∠BAC，P是边BC延长线上一点，过点P作PQ⊥BP，交线段BD的延长线于点Q．设CP=x，DQ=y．‎ ‎（1）求CD的长；‎ ‎（2）求y关于x的函数解析式，并写出它的定义域；‎ A B C D Q P ‎（3）当∠DAQ=2∠BAC时，求CP的值．‎ ‎6. （11徐汇）在中，，，，⊙的半径长为1，⊙交边 于点，点是边上的动点．‎ ‎（1）如图，将⊙绕点旋转得到⊙，请判断⊙与直线的位置关系；‎ ‎（2）如图，在（1）的条件下，当是等腰三角形时，求的长； ‎ ‎（3）如图，点是边上的动点，如果以为半径的⊙和以为半径的 B O A C P B O A C P O N B A C ‎⊙外切，设，，求关于的函数关系式及定义域．‎ ‎7. O A C D B E （12静安）如图，⊙O的半径为6，线段AB与⊙O相交于点C、D，AC=4，∠BOD=∠A，OB与⊙O相交于点E，设OA=，CD=．‎ （1） 求BD长；‎ （2） 求关于的函数解析式，并写出定义域；‎ （3） 当CE⊥OD时，求AO的长．‎ ‎8. （12黄浦）如图，已知中，，，，是边上的中点，是边上的点（不与端点重合），是边上的点，且∥，延长与直线相交于点，点是延长线上的点，且，联结，设，.‎ ‎（1）求关于的函数关系式及其定义域；‎ ‎（2）联结，当以为半径的和以为半径的外切时，求的正切值；‎ ‎（3）当与相似时，求的长.‎ 备用图b 备用图a ‎9.（10崇明）已知：如图，直角梯形ABCD中，AD∥BC，，，，，AM∥DC，E、F分别是线段AD、AM上的动点（点E与A、D不重合）且，设，.‎ ‎（1）求证：；‎ ‎（2）求与的函数关系式并写出定义域；‎ ‎（3）若点E在边AD上移动时， 为等腰三角形，求的值；‎ ‎（4）若以BM为半径的⊙M和以ED为半径的⊙E相切，求的面积.‎ A E F D B ‎ M C ‎10. （10奉贤）已知，在边长为6的正方形ABCD的两侧如图作正方形BEFG、正方形DMNK，恰好使得N、A、F三点在一直线上，联结MF交线段AD于点P，联结NP，设正方形BEFG的边长为x，正方形DMNK的边长为y，‎ ‎（1）求y关于x的函数关系式及自变量x的取值范围；‎ ‎（2）当△NPF的面积为32时，求x的值；‎ ‎（3）以P为圆心，AP为半径的圆能否与以G为圆心，GF为半径的圆相切，若能请求x的值，若不能，请说明理由。‎ A B C D E F G M N K P ‎ ‎ ‎11．（10静安）在半径为4的⊙O中，点C是以AB为直径的半圆的中点，OD⊥AC，垂足为D，点E是射线AB上的任意一点，DF//AB，DF与CE相交于点F，设EF=，DF=． ‎ A B E F C D O （1） 如图，当点E在射线OB上时，求关于的函数解析式，并写出函数定义域；‎ （2） 如图，当点F在⊙O上时，求线段DF的长；‎ （3） 如果以点E为圆心、EF为半径的圆与⊙O相切，求线段DF的长．‎ A B E F C D O ‎12. (10普陀)如图，已知Sin∠ABC=，⊙O的半径为2，圆心O在射线BC上，⊙O与射线BA相交于E、F两点，EF=，‎ （1） 求BO的长；‎ （2） 点P在射线BC上，以点P为圆心作圆，使得⊙P同时与⊙O和射线BA相切，‎ D C F A B O E G 求所有满足条件的⊙P的半径.‎ ‎13. （10杨浦）已知线段AB=10，点P在线段AB上，且AP=6，以A为圆心AP为半径作⊙A，点C在⊙A上，以B为圆心BC为半径作⊙B，射线BC与⊙A交于点Q（不与点C重合）。‎ ‎（1）当⊙B过点A时，求CQ的长；‎ ‎（2）当点Q在线段BC上时，设BC=x，CQ=y，试求y关于x的函数关系式，并写出定义域；‎ ‎（3）当由A、P、Q、C四点构成的四边形是梯形时，求BC的长。‎ C C Q Q P B A P B A A B P ‎（备用图）‎ ‎14.(11杨浦)已知△ABC中，AB=4，BC=6，AC＞AB，点D为AC边上一点，且DC=AB，E为BC边的中点，联结DE，设AD=x。‎ （1） 当DE⊥BC时，求x的值；‎ （2） 设，求y关于x的函数关系式，并写出定义域；‎ （3） 取AD的中点M，联结EM并延长交BA的延长线于点P，以A为圆心AM为半径作⊙A，试问：当AD的长改变时，点P与⊙A的位置关系变化吗？若不变化，请说明具体的位置关系，并证明你的结论；若变化，请说明理由。‎ A B C D E ‎（备用图）‎ D C E B A ‎15.（11宝山）如图，已知⊙O的半径长为1，PQ是⊙O的直径，点M是PQ延长线上一点，以点M为圆心作圆，与⊙O交于A、B两点，联结PA并延长，交⊙M于另外一点C.‎ ‎(1) 若AB恰好是⊙O的直径，设OM=x，AC=y，试在图中画出符合要求的大致图形，并求y关于x的函数解析式；‎ ‎(2) 联结OA、MA、MC，若OA⊥MA，且△OMA与△PMC相似，求OM的长度和⊙M的半径长；‎ ‎(3) 是否存在⊙M，使得AB、AC恰好是一个正五边形的两条边？若存在，试求OM的长度和⊙M的半径长；若不存在，试说明理由.‎ A B C Q P O M Q P O M 备用图 Q P O ‎16. （11静安）如图，在半径为5的⊙O中，点A、B在⊙O上，∠AOB=90º，点C是AB上的一个动点，AC与OB的延长线相交于点D，设AC=，BD=． ‎ ‎（1）求关于的函数解析式，并写出它的定义域；‎ ‎（2）如果⊙与⊙O相交于点A、C，且⊙与⊙O的圆心距为2，当BD=OB时，求⊙的半径；‎ ‎（3）是否存在点C，使得△DCB∽△DOC？如果存在，请证明；如果不存在，请简要说明理由．‎ B D C A O ‎17. （10虹口）如图，在直角梯形中，，,，．动点、分别从点、同时出发，动点沿射线的方向以每秒2个单位长的速度运动，动点在线段上以每秒1个单位长的速度向点运动，当点运动到点时，点随之停止运动．设运动的时间为（秒）．‎ ‎（1）当点在线段上运动时，联结，若=，求的值；‎ ‎（2）当点在线段上运动时，若以为直径的圆与以为直径的圆外切，求的值；‎ C D B A 备用图2‎ C D B A 备用图1‎ C D B A Q P ‎（3）设射线与射线相交于点，能否为等腰三角形？如果能，请直接写出的值；如果不能，请说明理由.‎ ‎18. （10闵行）已知：如图，△ABC为等边三角形，，AH⊥BC，垂足为点H， 点D在线段HC上，且HD = 2，点P为射线AH上任意一点，以点P为圆心，线段PD的长为半径作⊙P，设AP = x．‎ ‎（1）当x = 3时，求⊙P的半径长；‎ ‎（2）如图1，如果⊙P与线段AB相交于E、F两点，且EF = y，求y关于x的函数解析式，并写出它的定义域；‎ ‎（3）如果△PHD与△ABH相似，求x的值（直接写出答案即可）．‎ A B C P D H E F A B C H ‎（备用图）‎ A B C P D H ‎19 （10徐汇）在梯形ABCD中，AD//BC，AB⊥AD，AB=4，AD=5，CD=5．E为底边BC上一点，以点E为圆心，BE为半径画⊙E交直线DE于点F． ‎ (1) 如图，当点F在线段DE上时，设BE，DF，试建立关于的函数关系式，‎ 并写出自变量的取值范围； ‎ (2) 当以CD直径的⊙O与⊙E与相切时，求的值；‎ (3) 联接AF、BF，当△ABF是以AF为腰的等腰三角形时，求的值。‎ ‎20． （11杨浦）已知半径为6的⊙O1与半径为4的⊙O2相交于点P、Q，且∠O1P O2= 120°，点A为⊙O1上异于点P、Q的动点，直线AP与⊙O2交于点B，直线O1A与直线O2B交于点M。‎ （1） 如图，求∠AM B的度数；‎ （2） 当点A在⊙O1上运动时，是否存在∠AM B的度数不同于（1）中结论的情况？若存在，请在图2中画出一种该情况的示意图，并求出∠AM B的度数；若不存在，请在图中再画出一个符合题意的图形，并证明∠AM B的度数同于（1）中结论；‎ P O1‎ O2‎ Q （3） 当点A在⊙O1上运动时，若△APO1与△BPO2相似，求线段AB的长。‎ P O1‎ O2‎ A B M Q P O1‎ O2‎ Q 备用图 ‎21. （10中考）已知点P在线段AB上，点O在线段AB的延长线上。以点O为圆心，OP为半径作圆，点C是圆O上的一点。‎ （1） 如图，如果AP=2PB，PB=BO。求证：△CAO∽△BCO；‎ （2） 如果AP=m（m是常数，且m〉1），BP=1，OP是OA、OB的比例中项。当点C在圆O上运动时，求AC：BC的值（结果用含m的式子表示）；‎ （3） 在（2）的条件下，讨论以BC为半径的圆B和以CA为半径的圆C的位置关系，并写出相应m的取值范围。‎ A P B O C ‎22. （07中考）已知：，点在射线上，（如图）．为直线上一动点，以为边作等边三角形（点按顺时针排列），是的外心．‎ ‎（1）当点在射线上运动时，求证：点在的平分线上；‎ ‎（2）当点在射线上运动（点与点不重合）时，与交于点，设，，求关于的函数解析式，并写出函数的定义域；‎ ‎（3）若点在射线上，，圆为的内切圆．当的边或与圆相切时，请直接写出点与点的距离．‎ 备用图 ‎23. （10中考）如图，在Rt△ABC中，∠ACB＝90°.半径为1的圆A与边AB相交于点D，与边AC相交于点E，连结DE并延长，与线段BC的延长线交于点P.‎ ‎（1）当∠B＝30°时，连结AP，若△AEP与△BDP相似，求CE的长；‎ ‎（2）若CE=2，BD=BC，求∠BPD的正切值；‎ ‎（3）若，设CE=x，△ABC的周长为y，求y关于x的函数关系式.‎ ‎[来源:学*科*网]‎ ‎ 图11(备用)‎ ‎24. （11卢湾）已知：如图，在直角梯形ABCD中，BC∥AD ，BC⊥AB，AB=8，BC=6．动点E、F分别在边BC和AD上，且AF=2EC．线段EF与AC相交于点G，过点G作GH∥AD，交CD于点H，射线EH交AD的延长线于点M，交于点，设EC=x．‎ ‎（1）求证：；‎ ‎（2）当时，用含的代数式表达的长；‎ ‎（3）在（2）题条件下，若以为半径的与以为半径的相切，求的值.‎ 二．三角形背景下的综合题 ‎1.1 （09中考）已知为线段上的动点，点在射线上，且满足（如图所示）．‎ ‎（1）当，且点与点重合时（如图所示），求线段的长；‎ ‎（2）在图中，联结．当，且点在线段上时，设点之间的距离为，，其中表示的面积，表示的面积，求关于的函数解析式，并写出函数定义域；‎ A D P C B Q D A P C B ‎（Q）‎ ‎）‎ C A D P B Q ‎（3）当，且点在线段的延长线上时（如图10所示），求的大小．‎ ‎ ‎ ‎1.2 （10松江）如图，正方形ABCD中， AB=1，点P是射线DA上的一动点， DE⊥CP,垂足为E， EF⊥BE与射线DC交于点F．‎ ‎（1）若点P在边DA上（与点D、点A不重合）． ‎ ‎①求证：△DEF∽△CEB；‎ ‎②设AP=x，DF=y，求与的函数关系式，并写出函数定义域；‎ A B C D A B C D E F P ‎（2）当时，求AP的长．‎ ‎1.3 （11金山）如图，正方形的边长是，是的中点．动点在线段上运动．连接并延长交射线于点，过作的垂线交射线于点，连、接、.‎ ‎（1）求证：是等腰三角形；‎ ‎（2）设时，的面积为．求关于的函数关系式，并写出自变量的取值范围；‎ ‎（3）在点运动过程中是否可以成为等边三角形？请说明理由.‎ G M F E D C B A ‎1.4 （11普陀）直角三角板ABC中，∠A=30°，BC＝1.将其绕直角顶点C逆时针旋转一个角（且≠ 90°），得到Rt△， ‎ ‎（1）如图，当边经过点B时，求旋转角的度数；‎ ‎（2）在三角板旋转的过程中，边与AB所在直线交于点D，过点 D作DE∥交边于点E，联结BE.‎ ‎①当时，设，，求与之间的函数解析式及定义域；‎ ‎②当时，求的长. ‎ ‎ ‎ 备用图 备用图 ‎1.5 （10嘉定）在△中，，，，点在△内，且，点是斜边上的中点，直线与边的交点为，点是直线上的一动点．‎ ‎（1）试判断直线与的位置关系，并证明你的结论；‎ ‎（2）当在△的外部时，已知由点、、组成的三角形与△相似，求的长；‎ ‎（3）当不在△的边上时，设，△的面积为，请直接写出与的函数关系式及函数的定义域．‎ C D B P A M 备用图 C D B P A M 备用图 C D B P A M ‎1．6 (11虹口)如图，在Rt△ABC中，∠BAC= 90°，AB=3，AC=4，AD是BC边上的高，点E、F分别是AB边和AC边上的动点，且∠EDF= 90°．‎ ‎（1）求DE︰DF的值；‎ ‎（2）联结EF，设点B与点E间的距离为，△DEF的面积为，求关于的函数解析式，并写出的取值范围；‎ ‎（3）设直线DF与直线AB相交于点G，△EFG能否成为等腰三角形？若能，请直接写出线段BE的长；若不能，请说明理由.‎ 备用图2‎ B C D A 备用图1‎ B C D A B C D E F A ‎2.1 （09徐汇）已知如图，在等腰梯形ABCD中， AD∥BC，AB=CD，AD=3，BC=9，，直线MN是梯形的对称轴，点P是线段MN上一个动点（不与M、N重合），射线BP交线段CD于点E，过点C作CF∥AB 交射线BP于点F．‎ ‎（1） 求证：；‎ （2） 设PN，CE，试建立和之间的函数关系式，并求出定义域；‎ （3） 联结PD，在点P运动过程中，如果和相似，求出PN的长．‎ ‎2.2 （11闸北）直线分别交x轴、y轴于A、B两点，△AOB绕点O按逆时针方向旋转90°后得到△COD，抛物线经过A、C、D三点．‎ ‎(1) 写出点A、B、C、D的坐标；‎ ‎(2) 求经过A、C、D三点的抛物线表达式，并求抛物线顶点G的坐标；‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎-1·1‎ ‎-2·1‎ ‎-3·1‎ ‎-4·1‎ x y ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎-1·1‎ ‎-2·1‎ ‎-3·1‎ ‎-4·1‎ O ‎(3) 在直线BG上是否存在点Q，使得以点A、B、Q为顶点的三角形与△COD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．‎ ‎ ‎ ‎2.3 （12金山）如图，中，，，过点作∥，点、分别是射线、线段上的动点，且，过点作∥交线段于点，联接，设面积为，．‎ ‎（1）用的代数式表示；‎ ‎（2）求与的函数关系式，并写出定义域； ‎ B P D Q C A O E ‎（3）联接，若与相似，求的长．‎ ‎2.4 （13奉贤）如图(1)，已知∠MON=90°,点P为射线ON上一点，且OP=4，B、C为射线OM和ON上的两个动点（），过点P作PA⊥BC，垂足为点A，且PA=2，联结BP ．‎ ‎（1）若时，求tan∠BPO的值； ‎ ‎（2）设求与之间的函数解析式，并写出定义域；‎ ‎（3）如图(2)，过点A作BP的垂线，垂足为点H，交射线ON于点Q，点B、C在射线OM和ON上运动时，探索线段OQ的长是否发生变化？若不发生变化，求出它的值。若发生变化，试用含x的代数式表示OQ的长．‎ P C A B M O P C A B M O Q H N N ‎2.5（12虹口）如图，△ABC中，∠ABC=90°，AB=BC=4，点O为AB边的中点，点M是BC边上一动点（不与点B、C重合），AD⊥AB，垂足为点A.联结MO，将△BOM沿直线MO翻折，点B落在点B1处，直线M B1与AC、AD分别交于点F、N..‎ ‎（1）当∠CMF=120°时，求的长；‎ ‎（2）设，，求关于的函数关系式，并写出自变量取 值范围；‎ O A B C M D N B1‎ F ‎（3）联结NO，与AC边交于点E，当△FMC∽△AEO时，求的长.‎ ‎2.6 （10长宁）如图，抛物线交x轴于A、B两点（A点在B点左侧），交y轴于点C。已知B（8，0），，△ABC的面积为8.‎ （1） 求抛物线的解析式；‎ （2） 若动直线EF（EF//x轴）从点C开始，以每秒1个长度单位的速度沿y轴负方向平移，且交y轴、线段BC于E、F两点，动点P同时从点B出发，在线段OB上以每秒2个单位的速度向原点O运动。联结FP，设运动时间t秒。当t为何值时，的值最小，求出最大值；‎ （3） 在满足（2）的条件下，是否存在t的值，使以P、B、F为顶点的三角形与△ABC相似。若存在，试求出t的值；若不存在，请说明理由。‎ ‎2.7（11普陀）已知，，是的平分线，点P在上，．将三角板的直角顶点放置在点P处，绕着点P旋转，三角板的一条直角边与射线CB交于点E，另一条直角边与直线CA、直线CB分别交于点F、点G．‎ ‎（1）如图，当点F在射线CA上时，‎ ①求证： PF = PE．‎ ②设CF= x，EG=y，求y与x的函数解析式并写出函数的定义域． ‎ ‎（2）联结EF，当△CEF与△EGP相似时，求EG的长．‎ 备用图 ‎2.8 （11中考）在中，，，。点是边上任意一点，直线，与边或边相交于点，点在线段上，点在线段上，，‎ ‎⑴ 当点与点重合时，求的长 ‎⑵ 当点在边上时，点不与点重合，设，，求关于的函数关系式，并写出函数的定义域 ‎⑶ 若(的顶点、、分别与的顶点、、对应)，求的长 ‎3.1 （11黄浦）如图，在△ABC中，∠ACB=，AC=BC=2，M是边AC的中点，CH⊥BM于H.‎ ‎ （1）试求sin∠MCH的值；‎ ‎ （2）求证：∠ABM=∠CAH；‎ M A B C D H ‎ （3）若D是边AB上的点，且使△AHD为等腰三角形，请直接写出AD的长为________.‎ ‎3.2（10黄浦）如图，一把“T型”尺（图8），其中MN⊥OP，将这把“T型”尺放置于矩形ABCD中（其中AB=4,AD=5），使边OP始终经过点A，且保持OA=AB，“T型”尺在绕点A转动的过程中，直线MN交边BC、CD于E、F两点.(图9)‎ ‎ （1）试问线段BE与OE的长度关系如何？并说明理由；‎ ‎ （2）当△CEF是等腰直角三角形时,求线段BE的长；‎ P O N M F E D C B A P O N M ‎ （3）设BE=x,CF=y，试求y关于x的函数解析式，并写出函数定义域.‎ ‎3.3（10闸北）如图七，在直角坐标平面内有点A(6, 0)，B(0, 8)，C(-4, 0)，点M、N分别为线段AC和射线AB上的动点，点M以2个单位长度/秒的速度自C向A方向作匀速运动，点N以5个单位长度/秒的速度自A向B方向作匀速运动，MN交OB于点P．‎ ‎(1)求证：MN∶NP为定值；‎ ‎(2)若△BNP与△MNA相似，求CM的长；‎ ‎(3)若△BNP是等腰三角形，求CM的长．‎ ‎3.4 （10宝山）如图，矩形ABCD中，，点E是BC边上的一个动点，联结AE，过点D作，垂足为点F . ‎ ‎（1）设，的余切值为y，求y关于x的函数解析式；‎ ‎（2）若存在点，使得ABE 、ADF与四边形CDFE的面积比是3：4：5，‎ 试求矩形ABCD的面积；‎ ‎(备用图)‎ · D C B A E F · D C B A E F ‎（3）对（2）中求出的矩形ABCD，联结CF，当BE的长为多少时，CDF是等腰三角形？‎ 三．四边形背景下的综合题 ‎1.(11青浦)如图，在直角坐标平面内，为原点，抛物线经过点（，），且顶点（，）在直线上． ‎ ‎（1）求的值和抛物线的解析式；‎ ‎（2）如在线段上有一点，满足，在轴上有一点（，），联结，且直线与轴交于点．‎ ‎①求直线的解析式；‎ ‎②如点M是直线上的一个动点，在x轴上方的平面内有另一点N，且以O、E、M、N为顶点的四边形是菱形，请求出点N的坐标．（直接写出结果，不需要过程．）‎ A B E C 备用图 D O x y A B E C D O x y ‎2.（12普陀）将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．‎ ‎（1）如图①，对△ABC作变换[60°，]得△AB′C′，那么=　 　；‎ 直线BC与直线B′C′所夹的锐角为　 　度．‎ ‎（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC作变换[θ，n]得△AB'C'，‎ 使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值．‎ （1） 如图③，△ABC中，AB=AC，∠BAC=36°，BC=l，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ和n的值．‎ ‎3.（10卢湾）数学课上，张老师出示了问题1：‎ 如图，四边形ABCD是正方形， BC =1，对角线交点记作O，点E是边BC延长线上一点．联结OE交CD边于F，设，，求关于的函数解析式及其定义域．‎ ‎（1）经过思考，小明认为可以通过添加辅助线——过点O作OM⊥BC，垂足为M求解．你认为这个想法可行吗？请写出问题1的答案及相应的推导过程；‎ ‎（2）如果将问题1中的条件“四边形ABCD是正方形，BC =1”改为“四边形ABCD是平行四边形，BC=3，CD=2，”其余条件不变，请直接写出条件改变后的函数解析式；‎ ‎（3）如果将问题1中的条件“四边形ABCD是正方形，BC =1”进一步改为：“四边形ABCD是梯形，AD∥BC，，，(其中，，为常量)”其余条件不变，请你写出条件再次改变后关于的函数解析式以及相应的推导过程．‎ ‎4.（10闵行）如图，在△ABC中，AB = BC = 5，AC = 6，BO⊥AC，垂足为点O．过点A作射线AE // BC，点P是边BC上任意一点，联结PO并延长与射线AE相交于点Q，设B、P两点间的距离为x．‎ ‎（1）如图1，如果四边形ABPQ是平行四边形，求x的值；‎ ‎（2）过点Q作直线BC的垂线，垂足为点R，当为何值时，△PQR∽△CBO？‎ ‎（3）设△AOQ的面积为y，求y与x的函数关系式，并写出函数的定义域．‎ C O P B Q A E C O B A E Q P C O B A E ‎（备用图）‎ ‎5.（11闵行）如图，在矩形ABCD中，点E在边AD上，联结BE，∠ABE = 30°，BE = DE，联结BD．点M为线段DE上的任意一点，过点M作MN // BD，与BE相交于点N．‎ ‎（1）如果，求边AD的长；‎ ‎（2）如图，在（1）的条件下，如果点M为线段DE的中点，联结CN．过点M作MF⊥CN，垂足为点F，求线段MF的长；‎ ‎（3）试判断BE、MN、MD这三条线段的长度之间有怎样的数量关系？请证明你的结论．‎ A B C D E M N F A B C D E M N ‎ ‎