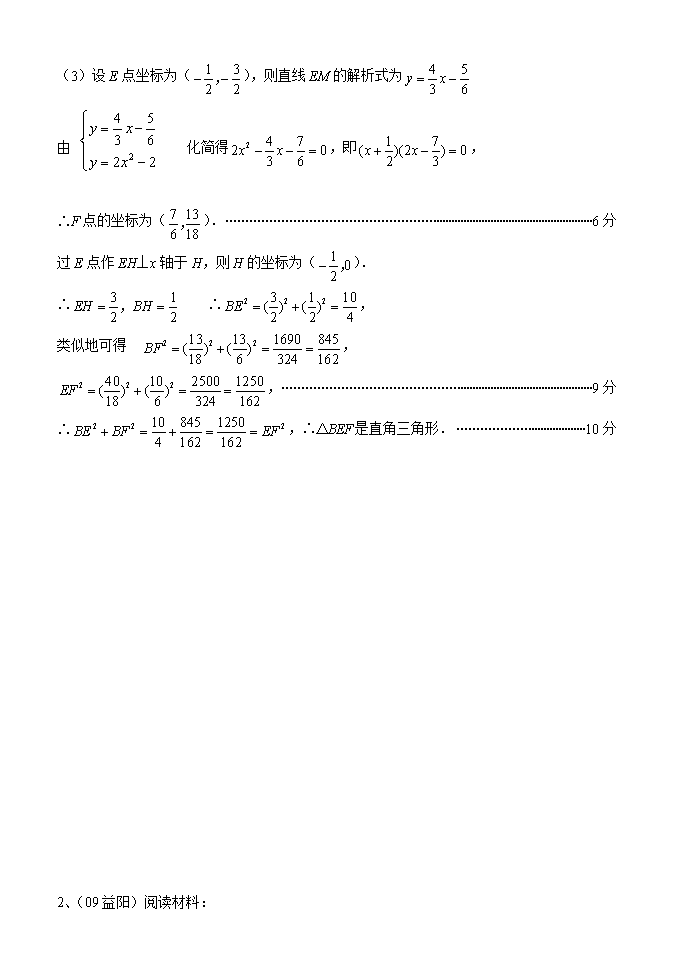中考数学压轴专题 二次函数类 11页

中考数学压轴专题 二次函数类 ‎1、已知二次函数过点A （0，），B（，0），C（）．‎ ‎（1）求此二次函数的解析式；‎ ‎（2）判断点M（1，）是否在直线AC上？‎ 图8‎ ‎（3）过点M（1，）作一条直线与二次函数的图象交于E、F两点（不同于A，B，C三点），请自已给出E点的坐标，并证明△BEF是直角三角形．‎ 解析：‎ ‎（1）设二次函数的解析式为（）， ‎ 把A （0，），B（，0），C（）代入得 解得 a=2 ， b=0 ， c=－2，‎ ‎∴ 3分 ‎（2）设直线AC的解析式为 ，‎ 把A （0，－2），C（）代入得 ‎，解得 ，∴‎ 当x=1时， ∴M（1，）在直线AC上 5分 ‎（3）设E点坐标为（），则直线EM的解析式为 由 化简得，即，‎ ‎∴F点的坐标为（）． 6分 过E点作EH⊥x轴于H，则H的坐标为（）．‎ ‎∴ ∴，‎ 类似地可得 ，‎ ‎， 9分 ‎∴，∴△BEF是直角三角形． 10分 ‎2、（09益阳）阅读材料：‎ 如图12-1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半.‎ 解答下列问题：‎ 如图12-2，抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.‎ ‎(1)求抛物线和直线AB的解析式；‎ ‎(2)点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及；‎ 图12-2‎ x C O y A B D ‎1‎ ‎1‎ ‎(3)是否存在一点P，使S△PAB=S△CAB，若存在，求出P点的坐标；若不存在，请说明理由.‎ 解：‎ ‎(1)设抛物线的解析式为： 1分 把A（3,0）代入解析式求得 所以 3分 设直线AB的解析式为：‎ 由求得B点的坐标为 4分 把，代入中 解得：‎ 所以 6分 ‎(2)因为C点坐标为(１,4)‎ 所以当x＝１时，y1＝4，y2＝2‎ 所以CD＝4-2＝2 8分 ‎(平方单位) 10分 ‎(3)假设存在符合条件的点P，设P点的横坐标为x，△PAB的铅垂高为h，‎ 则 12分 由S△PAB=S△CAB 得：‎ 化简得：‎ 解得，‎ 将代入中，‎ 解得P点坐标为 14分 ‎3、（07龙岩）“便民”水泥代销点销售某种水泥，每吨进价为250元．如果每吨销售价定为290元时，平均每天可售出16吨．‎ ‎（1）若代销点采取降低促销的方式，试建立每吨的销售利润（元）与每吨降低（元）之间的函数关系式．‎ ‎（2）若每吨售价每降低5元，则平均每天能多售出4吨．问：每吨水泥的实际售价定为多少元时，每天的销售利润平均可达720元．‎ 解：‎ ‎（1）依题意，得 5分 ‎（2）依题意，得 8分 解得 11分 ‎ 12分 答：每吨水泥的实际售价应定为元时，每天的销售利润平均可达720元． 13分 注：第（1）题中函数关系式写为者不扣分．‎ A B C N M P A B C N M P A B C N M P 图24—1‎ 图24—2‎ 图24—3‎ ‎4、（07龙岩）如图24－1，在中，，，．是边上的动点（不与重合），交于点，关于的对称图形是．设．‎ ‎（1）用含的式子表示的面积（不必写出过程）；‎ ‎（2）当为何值时，点恰好落在边上；‎ ‎（3）在动点的运动过程中，记与梯形重叠部分的面积为，试求关于的函数关系式；并求为何值时，重叠部分的面积最大，最大面积是多少？‎ 解：‎ ‎（1） 3分 ‎（2）如图24－2，由轴对称性质知：， 4分 A B C N M P 图 A B C N M P 图 又，， 5分 ‎ 6分 点是中点，即当时，点恰好落在边上． 7分 ‎（3）i）以下分两种情况讨论：‎ ‎①当时，易见 8分 ‎②当时，如图24－3，设，分别交于、，‎ 由（2）知 由题意知 ‎ ‎ （此步无写不扣分）10分 ii）当时， 易知 11分 又当时，‎ 当时（符合）， 12分 综上所述，当时，重叠部分的面积最大，其值为． 13分 ‎5、（07龙岩）如图，抛物线经过的三个顶点，已知轴，点在轴上，点在轴上，且．‎ ‎（1）求抛物线的对称轴；‎ ‎（2）写出三点的坐标并求抛物线的解析式；‎ ‎（3）探究：若点是抛物线对称轴上且在轴下方的动点，是否存在是等腰三角形．若存在，求出所有符合条件的点坐标；不存在，请说明理由．‎ A C B y x ‎0‎ ‎1‎ ‎1‎ 解：‎ ‎（1）抛物线的对称轴 2分 ‎（2） 5分 把点坐标代入中，解得 6分 A C B x ‎0‎ ‎1‎ ‎1‎ Ｑ Ｎ Ｍ Ｋ y ‎ 7分 ‎（3）存在符合条件的点共有3个．以下分三类情形探索．‎ 设抛物线对称轴与轴交于，与交于．‎ 过点作轴于，易得，，，‎ ① 以为腰且顶角为角的有1个：．‎ ‎ 8分 在中，‎ ‎ 9分 ‎②以为腰且顶角为角的有1个：．‎ 在中， 10分 ‎ 11分 ‎③以为底，顶角为角的有1个，即．‎ 画的垂直平分线交抛物线对称轴于，此时平分线必过等腰的顶点．‎ 过点作垂直轴，垂足为，显然．‎ ‎．‎ ‎ 于是 13分 ‎ 14分 注：第（3）小题中，只写出点的坐标，无任何说明者不得分．‎ ‎5、（06 烟台）如图，已知抛物线L1: y=x2-4的图像与x有交于A、C两点.‎ ‎（1）若抛物线l2与l1关于x轴对称，求l2的解析式；‎ ‎（2）若点B是抛物线l1上的一动点（B不与A、C重合），以AC为对角线，A、B、C三点为顶点的平行四边形的第四个顶点定为D，求证：点D在l2上；‎ ‎（3）探索：当点B分别位于l1在x轴上、下两部分的图像上时，平行四边形ABCD的面积是否存在最大值和最小值？若存在，判断它是何种特殊平行四边形，并求出它的面积；若不存在，请说明理由。‎ 解析：‎ 设l2的解析式为y=a(x-h)2+k ‎∵l2与x轴的交点A(-2,0),C(2,0),顶点坐标是(0，-4),l1与l2关于x轴对称，‎ ‎∴l2过A(-2,0),C(2,0),顶点坐标是（0，4）‎ ‎∴y=ax2+4‎ ‎∴0=‎4a+4 得 a=-1‎ ‎∴l2的解析式为y=-x2+4‎ ‎(2)设B(x1 ,y1)‎ ‎∵点B在l1上 ‎∴B(x1 ,x12-4) ‎ ‎∵四边形ABCD是平行四边形，A、C关于O对称 ‎∴B、D关于O对称 ‎∴D(-x1 ,-x12+4).‎ 将D(-x1 ,-x12+4)的坐标代入l2：y=-x2+4‎ ‎∴左边=右边 ‎∴点D在l2上.‎ ‎(3)设平行四边形ABCD的面积为S,则 S=2S△ABC =AC|y1|=4|y1|‎ A）.当点B在x轴上方时，y1＞0‎ ‎∴S=4y1 ,它是关于y1的正比例函数且S随y1的增大而增大，‎ ‎∴S既无最大值也无最小值 B）.当点B在x轴下方时，-4≤y1＜0‎ ‎∴S=-4y1 ,它是关于y1的正比例函数且S随y1的增大而减小，‎ ‎∴当y1 =-4时，S由最大值16，但他没有最小值 此时B(0,-4)在y轴上，它的对称点D也在y轴上.‎ ‎∴AC⊥BD ‎∴平行四边形ABCD是菱形此时S最大=16.‎ ‎8、（06潍坊）已知二次函数图象的顶点在原点，对称轴为轴．一次函数的图象与二次函数的图象交于两点（在的左侧），且点坐标为．平行于轴的直线过点．‎ ‎（1）求一次函数与二次函数的解析式；‎ ‎（2）判断以线段为直径的圆与直线的位置关系，并给出证明；‎ ‎（3）把二次函数的图象向右平移个单位，再向下平移个单位，二次函数的图象与轴交于两点，一次函数图象交轴于点．当为何值时，过三点的圆的面积最小？最小面积是多少？‎ 解析：‎ ‎（1）把代入得，‎ 一次函数的解析式为；‎ 二次函数图象的顶点在原点，对称轴为轴，‎ 设二次函数解析式为，‎ 把代入得，‎ 二次函数解析式为． 3分 ‎（2）由 解得或，‎ ‎，‎ 过点分别作直线的垂线，垂足为，‎ 则，‎ 直角梯形的中位线长为，‎ 过作垂直于直线于点，则，，‎ ‎，‎ 的长等于中点到直线的距离的2倍，‎ 以为直径的圆与直线相切．‎ ‎（3）平移后二次函数解析式为，‎ 令，得，，，‎ 过三点的圆的圆心一定在直线上，点为定点，‎ 要使圆面积最小，圆半径应等于点到直线的距离，‎ 此时，半径为2，面积为，‎ 设圆心为中点为，连，则，‎ 在三角形中，，‎ ‎，而，‎ ‎，‎ 当时，过三点的圆面积最小，最小面积为．‎