南京市2008年初中毕业生学业考试含答案 12页

南京市 2008 年初中毕业生学业考试 数 学 注意事项： 1．本试卷共 6 页．全卷满分 120 分．考试时间为 120 分钟．考生答题全部答在答题卡上， 答在本试卷上无效． 2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再 将自己的姓名、准考证号用 0.5 毫米黑色墨水签字笔填写在答题卡及本试卷上． 3．答选择题必须用 2B 铅笔将答题卡上对应的答案标号涂黑．如需改动，请用橡皮擦干净 后，再选涂其他答案．答非选择题必须用 0.5 毫米黑色墨水签字笔写在答题卡上的指定位置， 在其他位置答题一律无效． 4．作图必须用 2B 铅笔作答，并请加黑加粗，描写清楚． 一、选择题（本大题共 10 小题，每小题 2 分，共计 20 分．在每小题所给出的四个选项中， 恰有一项是符合题目要求的，请将正确选项的序号填涂在答题卡上） 1． 的绝对值是（ ） A． B． C． D． 2．2008 年 5 月 27 日，北京 2008 年奥运会火炬接力传递活动在南京境内举行，火炬传递路 线全程约 12 900m，将 12 900m 用科学记数法表示应为（ ） A． B． C． D． 3．计算 的结果是（ ） A． B． C． D． 4．2 的平方根是（ ） A．4 B． C． D． 5．已知反比例函数的图象经过点 ，则这个函数的图象位于（ ） A．第一、三象限 B．第二、三象限 C．第二、四象限 D．第三、四象限 6．如图，将一张等腰梯形纸片沿中位线剪开，拼成一个新的图形， 这个新的图形可以是下列图形中的（ ） A．三角形 B．平行四边形 C．矩形 D．正方形 7．小刚身高 1.7m，测得他站立在阳光下的影子长为 0.85m，紧接着他把手臂竖直举起，测 得影子长为 1.1m，那么小刚举起的手臂超出头顶（ ） A．0.5m B．0.55m C．0.6m D．2.2m 8．如图， 是等边三角形 的外接圆， 的半径为 2， 则等边三角形 的边长为（ ） A． B． C． D． 9．超市为了制定某个时间段收银台开放方案，统计了这个时间段本超市顾客在收银台排队 3− 3− 3 1 3 − 1 3 50.129 10× 41.29 10× 312.9 10× 2129 10× 2 3( )ab 5ab 6ab 3 5a b 3 6a b 2 2− 2± ( 21)P − ， O ABC O ABC 3 5 2 3 2 5 （第 6 题） （第 8 题） A B C O 付款的等待时间，并绘制成如下的频数分布直方图（图中等待时间 6 分钟到 7 分钟表示大于 或等于 6 分钟而小于 7 分钟，其它类同）．这个时间段内顾客等待时间不少于 6 分钟的人数 为（ ） A．5 B．7 C．16 D．33 10 ． 如 图 ， 已 知 的 半 径 为 1 ， 与 相 切 于 点 ， 与 交 于 点 ， ，垂足为 ，则 的值等于（ ） A． B． C． D． 二、填空题（本大题共 6 小题，每小题 3 分，共计 18 分．不需写出解答过程，请把答案直 接填写在答题卡相应位置上） 11．计算 的结果是 ． 12．函数 中，自变量 的取值范围是 ． 13．已知 和 的半径分别为 3cm 和 5cm，且它们内切，则圆心距 等于 cm． 14．若等腰三角形的一个外角为 ，则它的底角为 度． 15．口袋内装有一些除颜色外完全相同的红球、白球和黑球，从中摸出一 球，摸出红球的概率是 0.2，摸出白球的概率是 0.5，那么摸出黑球的概率 是 ． 16．如图，有一圆形展厅，在其圆形边缘上的点 处安装了一台监视器， 它的监控角度是 ．为了监控整个展厅，最少需在圆形边缘上共安装 这样的监视器 台． 三、解答题（本大题共 12 小题，共计 82 分．请在答题卡指定区域内作答，解答时应写出 文字说明、证明过程或演算步骤） 17．（6 分）先化简，再求值： ，其中 ． （第 9 题） 0 1 2 3 4 5 6 7 8 等待时间/min 4 8 12 16 人数 2 3 6 8 16 9 5 2 （第 10 题） A B C O D O AB O A OB O C OD OA⊥ D cos AOB∠ OD OA CD AB 12 3− 1 xy x −= x 1O 2O 1 2O O 70 A 65 2(2 1) 2(2 1) 3a a+ − + + 2a = （第 16 题） A 65 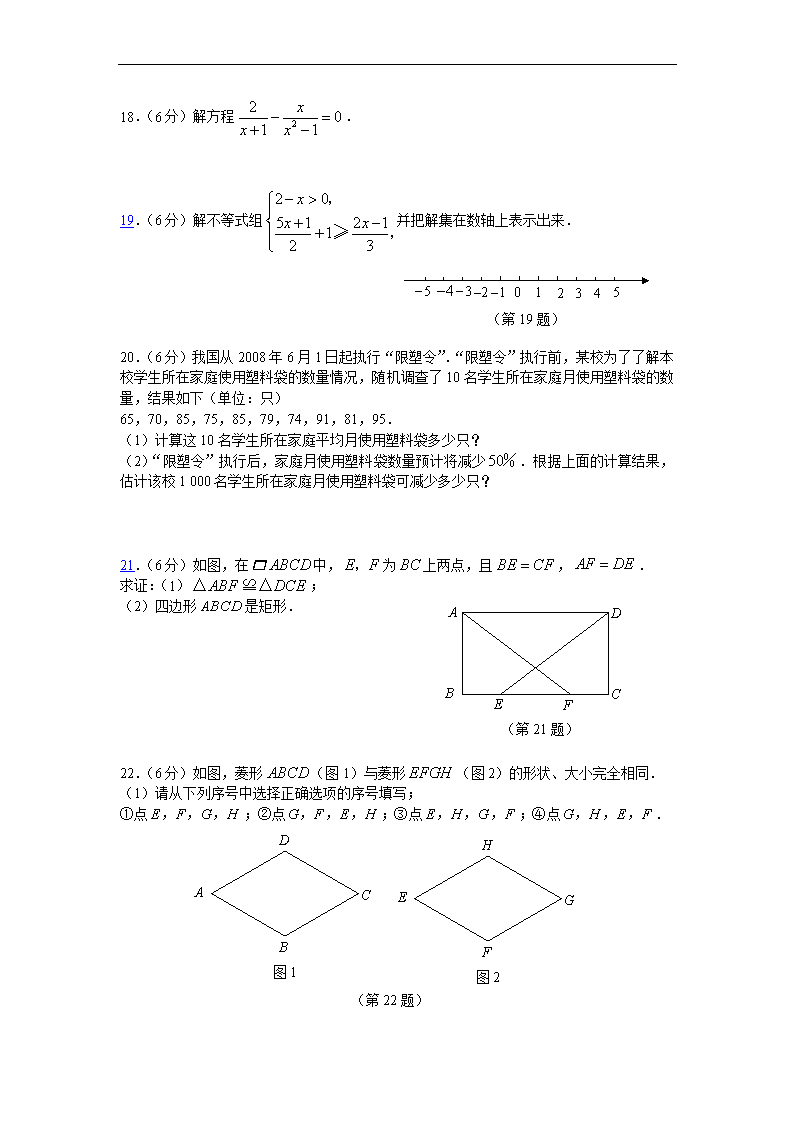18．（6 分）解方程 ． 19．（6 分）解不等式组 并把解集在数轴上表示出来． 20．（6 分）我国从 2008 年 6 月 1 日起执行“限塑令”．“限塑令”执行前，某校为了了解本 校学生所在家庭使用塑料袋的数量情况，随机调查了 10 名学生所在家庭月使用塑料袋的数 量，结果如下（单位：只） 65，70，85，75，85，79，74，91，81，95． （1）计算这 10 名学生所在家庭平均月使用塑料袋多少只？ （2）“限塑令”执行后，家庭月使用塑料袋数量预计将减少 ．根据上面的计算结果， 估计该校 1 000 名学生所在家庭月使用塑料袋可减少多少只？ 21．（6 分）如图，在 中， 为 上两点，且 ， ． 求证：（1） ； （2）四边形 是矩形． 22．（6 分）如图，菱形 （图 1）与菱形 （图 2）的形状、大小完全相同． （1）请从下列序号中选择正确选项的序号填写； ①点 ；②点 ；③点 ；④点 ． 2 2 01 1 x x x − =+ − 2 0 5 1 2 112 3 x x x − > + − + ， ≥ ， 50％ ABCD E F， BC BE CF= AF DE= ABF DCE△ ≌△ ABCD ABCD EFGH E F G H， ， ， G F E H， ， ， E H G F， ， ， G H E F， ， ， （第 19 题） 5− 4− 3− 2− 1− 0 1 2 3 4 5 （第 21 题） A B C D E F 图 1 A （第 22 题） B C D 图 2 E F G H 如果图 1 经过一次平移后得到图 2，那么点 对应点分别是 ； 如果图 1 经过一次轴对称后得到图 2，那么点 对应点分别是 ； 如果图 1 经过一次旋转后得到图 2，那么点 对应点分别是 ； （2）①图 1，图 2 关于点 成中心对称，请画出对称中心（保留画图痕迹，不写画法）； ②写出两个图形成中心对称的一条性质： ．（可以结合所画图形叙述） 23．（6 分）如图，山顶建有一座铁塔，塔高 ，某人在点 处测得塔底 的仰角 为 ，塔顶 的仰角为 ，求此人距 的水平距离 ． （参考数据： ， ， ， ， ， ） 24．（7 分）小明和小颖做掷骰子的游戏，规则如下： ①游戏前，每人选一个数字； ②每次同时掷两枚均匀骰子； ③如果同时掷得的两枚骰子点数之和，与谁所选数字相同，那么谁就获胜． （1）在下表中列出同时掷两枚均匀骰子所有可能出现的结果： 1 2 3 4 5 6 1 2 3 4 5 6 （2）小明选的数字是 5，小颖选的数字是 6．如果你也加入游戏，你会选什么数字，使自己 获胜的概率比他们大？请说明理由． 25．（7 分）某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为 ．在温室内， A B C D， ， ， A B C D， ， ， A B C D， ， ， O 30mCD = A C 20 D 23 CD AB sin 20 0.342 ≈ cos20 0.940 ≈ tan 20 0.364 ≈ sin 23 0.391 ≈ cos23 0.921 ≈ tan 23 0.424 ≈ 2:1 （第 23 题） A B C D 20 23 第 2 枚骰子 掷得的点数第 1 枚骰子 掷得的点数 沿前侧内墙保留 3m 宽的空地，其它三侧内墙各保留 1m 宽的通道．当矩形温室的长与宽各 为多少时，蔬菜种植区域的面积是 ？ 26．（8 分）已知二次函数 中，函数 与自变量 的部分对应值如下表： … … … … （1）求该二次函数的关系式； （2）当 为何值时， 有最小值，最小值是多少？ （3）若 ， 两点都在该函数的图象上，试比较 与 的大小． 27．（8 分）如图，已知 的半径为 6cm，射线 经过点 ， ，射线 与 相切于点 ． 两点同时从点 出发，点 以 5cm/s 的速度沿射线 方向运动， 点 以 4cm/s 的速度沿射线 方向运动．设运动时间为 s． （1）求 的长； （2）当 为何值时，直线 与 相切？ 2288m 2y x bx c= + + y x x 1− 0 1 2 3 4 y 10 5 2 1 2 5 x y 1( )A m y， 2( 1 )B m y+ ， 1y 2y O PM O 10cmOP = PN O Q A B， P A PM B PN t PQ t AB O （第 25 题） 蔬菜种植区域 前 侧 空 地 （第 27 题） A B Q OP N M 28．（10 分）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车 行驶的时间为 ，两车之间的距离为 ，图中的折线表示 与 之间的函数关系． 根据图象进行以下探究： 信息读取 （1）甲、乙两地之间的距离为 km； （2）请解释图中点 的实际意义； 图象理解 （3）求慢车和快车的速度； （4）求线段 所表示的 与 之间的函数关系式，并写出自变量 的取值范围； 问题解决 （5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车 相遇 30 分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？ 南京市 2008 年初中毕业生学业考试 数学试题参考答案及评分标准 说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参 照本评分标准的精神给分． 一、选择题（每小题 2 分，共计 20 分） 题号 1 2 3 4 5 6 7 8 9 10 答案 B B D D C B A C B A 二、填空题（每小题 3 分，共计 18 分） 11． 12． 13． 14． 15． 16． 三、解答题（本大题共 12 小题，共计 82 分） 17．（本题 6 分） (h)x (km)y y x B BC y x x 3 0x ≠ 2 35 0.3 3 （第 28 题） A B C D O y/km 900 12 x/h4 解：原式 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 当 时， ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 18．（本题 6 分） 解：方程两边同乘 ，得 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 解这个方程，得 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 检验：当 时， ． 所以 是原方程的解．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 19．（本题 6 分） 解：解不等式①，得 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 解不等式②，得 ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 所以，不等式组的解集是 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 不等式组的解集在数轴上表示如下： ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 20．（本题 6 分） 解：（1） ． 答：这 10 名学生所在家庭平均月使用塑料袋 80 只．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2） ． 答：执行“限塑令”后，估计 1 000 名学生所在家庭月使用塑料袋可减少 40 000 只．∙∙∙∙∙6 分 21．（本题 6 分） 解：（1） ， ， ， ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 四边形 是平行四边形， ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 在 和 中， ， ， ， ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）解法一： ， ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 四边形 是平行四边形， 24 4 1 4 2 3a a a= + + − − + 24 2a= + 2a = 2 24 2 4 ( 2) 2 10a + = × + = ( 1)( 1)x x− + 2( 1) 0x x− − = 2x = 2x = ( 1)( 1) 0x x− + ≠ 2x = 2x < 1x −≥ 1 2x− <≤ 1 (65 70 85 75 85 79 74 91 81 95) 8010 + + + + + + + + + = 80 1000 50 40 000× × =％ BE CF= BF BE EF= + CE CF EF= + BF CE∴ =  ABCD AB DC∴ = ABF△ DCE△ AB DC= BF CE= AF DE= ABF DCE∴△ ≌△ ABF DCE△ ≌△ B C∴∠ = ∠  ABCD 5− 4− 3− 2− 1− 0 1 2 3 4 5 ． ． ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 四边形 是矩形．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 解法二：连接 ． ， ． ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 在 和 中， ， ， ， ． ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 四边形 是平行四边形， 四边形 是矩形．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 22．（本题 6 分） 解：（1）①；②；④；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）①画图正确；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 ②答案不惟一，例如：对应线段相等， 等．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 23．（本题 6 分） 解：在 中， ， ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 在 中， ， ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 ． ． 答：此人距 的水平距离 约为 500m． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 24．（本题 7 分） 解：（1）填表正确；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）由上表可以看出，同时投掷两枚骰子，可能出现的结果有 36 种，它们出现的可能性相 同． 所有的结果中，满足两枚骰子点数和为 5（记为事件 ）的结果有 4 种，即（1，4），（2， 3），（3，2）（4，1），所以小明获胜的概率为 ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 满足两枚骰子点数和为 6（记为事件 ）的结果有 5 种，即（1，5），（2，4），（3，3）（4， AB CD∴ ∥ 180B C∴∠ + ∠ =  90B C∴∠ = ∠ =  ∴ ABCD AC DB， ABF DCE△ ≌△ AFB DEC∴∠ = ∠ AFC DEB∴∠ = ∠ AFC△ DEB△ AF DE= AFC DEB∠ = ∠ CF BE= AFC DEB∴△ ≌△ AC DB∴ =  ABCD ∴ ABCD OC OE= Rt ABC△ 20CAB∠ =  tan tan 20BC AB CAB AB∴ = ∠ =   Rt ABD△ 23DAB∠ =  tan tan 23BD AB DAB AB∴ = ∠ =   tan 23 tan 20 (tan 23 tan 20 )CD BD BC AB AB AB∴ = − = − = −     30 500(m)tan 23 tan 20 0.424 0.364 CDAB∴ = =− −  ≈ CD AB A 4 1( ) 36 9P A = = B 2），（5，1），所以小颖获胜的概率为 ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 要想使自己获胜的概率比他们大，必须满足两枚骰子点数和出现的结果多于 5 种，由所列表 格可知，只有两枚骰子点数和为 7（记为事件 ）的结果多于 5 种，有 6 种，即（1，6）， （2，5），（3，4）（4，3），（5，2），（6，1），所以 ．因此，要想使自己获胜 的概率比他们大，所选数字应为 7．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 25．（本题 7 分） 解法一：设矩形温室的宽为 ，则长为 ．根据题意，得 ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 解这个方程，得 （不合题意，舍去）， ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 所以 ， ． 答：当矩形温室的长为 28m，宽为 14m 时，蔬菜种植区域的面积是 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 解法二：设矩形温室的长为 ，则宽为 ．根据题意，得 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 解这个方程，得 （不合题意，舍去）， ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 所以 ， ． 答：当矩形温室的长为 28m，宽为 14m 时，蔬菜种植区域的面积是 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 26．（本题 8 分） 解：（1）根据题意，当 时， ；当 时， ． 所以 解得 所以，该二次函数关系式为 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 （2）因为 ， 所以当 时， 有最小值，最小值是 1．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 5( ) 36P B = C 6 1( ) 36 6P C = = mx 2 mx ( 2) (2 4) 288x x− − = 1 10x = − 2 14x = 14x = 2 2 14 28x = × = 2288m mx 1 m2 x 1 2 ( 4) 2882 x x − − =   1 20x = − 2 28x = 28x = 1 1 28 142 2x = × = 2288m 0x = 5y = 1x = 2y = 5 2 1 . c b c =  = + + ， 4 5. b c = −  = ， 2 4 5y x x= − + 2 24 5 ( 2) 1y x x x= − + = − + 2x = y （3）因为 ， 两点都在函数 的图象上， 所以， ， ． ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 所以，当 ，即 时， ； 当 ，即 时， ； 当 ，即 时， ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 27．（本题 8 分） （1）连接 ． 与 相切于点 ， ，即 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 ， ， ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 （2）过点 作 ，垂足为 ． 点 的运动速度为 5cm/s，点 的运动速度为 4cm/s，运动时间为 s， ， ． ， ， ． ， ． ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 ， 四边形 为矩形． ． 的半径为 6， 时，直线 与 相切． 1( )A m y， 2( 1 )B m y+ ， 2 4 5y x x= − + 2 1 4 5y m m= − + 2 2 2 ( 1) 4( 1) 5 2 2y m m m m= + − + + = − + 2 2 2 1 ( 2 2) ( 4 5) 2 3y y m m m m m− = − + − − + = − 2 3 0m − < 3 2m < 1 2y y> 2 3 0m − = 3 2m = 1 2y y= 2 3 0m − > 3 2m > 1 2y y< OQ PN O Q OQ PN∴ ⊥ 90OQP∠ =  10OP = 6OQ = 2 210 6 8(cm)PQ∴ = − = O OC AB⊥ C  A B t 5PA t∴ = 4PB t= 10PO = 8PQ = PA PB PO PQ ∴ = P P∠ = ∠ PAB POQ∴△ ∽△ 90PBA PQO∴∠ = ∠ =  90BQO CBQ OCB∠ = ∠ = ∠ =  ∴ OCBQ BQ OC∴ = O 6BQ OC∴ = = AB O ①当 运动到如图 1 所示的位置． ． 由 ，得 ． 解得 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 ②当 运动到如图 2 所示的位置． ． 由 ，得 ． 解得 ． 所以，当 为 0.5s 或 3.5s 时直线 与 相切．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 28．（本题 10 分） 解：（1）900；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 （2）图中点 的实际意义是：当慢车行驶 4h 时，慢车和快车相遇．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 （3）由图象可知，慢车 12h 行驶的路程为 900km， 所以慢车的速度为 ； ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 当慢车行驶 4h 时，慢车和快车相遇，两车行驶的路程之和为 900km，所以慢车和快车行驶 的速度之和为 ，所以快车的速度为 150km/h．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 （4）根据题意，快车行驶 900km 到达乙地，所以快车行驶 到达乙地，此时两 车之间的距离为 ，所以点 的坐标为 ． 设线段 所表示的 与 之间的函数关系式为 ，把 ， 代入得 AB 8 4BQ PQ PB t= − = − 6BQ = 8 4 6t− = 0.5(s)t = AB 4 8BQ PB PQ t= − = − 6BQ = 4 8 6t − = 3.5(s)t = t AB O B 900 75(km / h)12 = 900 225(km / h)4 = 900 6(h)150 = 6 75 450(km)× = C (6 450)， BC y x y kx b= + (4 0)， (6 450)， 图 2 A B Q OP N M C 图 1 A B Q OP N M C 解得 所以，线段 所表示的 与 之间的函数关系式为 ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 自变量 的取值范围是 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 （5）慢车与第一列快车相遇 30 分钟后与第二列快车相遇，此时，慢车的行驶时间是 4.5h． 把 代入 ，得 ． 此时，慢车与第一列快车之间的距离等于两列快车之间的距离是 112.5km，所以两列快车出 发的间隔时间是 ，即第二列快车比第一列快车晚出发 0.75h．∙∙∙∙∙10 分 0 4 450 6 . k b k b = +  = + ， 225 900. k b =  = − ， BC y x 225 900y x= − x 4 6x≤ ≤ 4.5x = 225 900y x= − 112.5y = 112.5 150 0.75(h)÷ =