中考数学模拟试题无答案 5页

九年级数学模拟试题（5）‎ 一、选择题（共8小题，每小题3分，满分24分）‎ ‎1．的算术平方根为 ( )‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎2．下列运算正确的是 ( )‎ Ａ． Ｂ．‎ Ｃ． Ｄ．‎ ‎3．如图，由几个小正方体组成的立体图形的左视图是 ( )‎ Ａ．‎ Ｂ．‎ Ｃ．‎ Ｄ．‎ ‎4．下列事件中确定事件是 ( )‎ Ａ．掷一枚均匀的硬币，正面朝上 Ｂ．买一注福利彩票一定会中奖 Ｃ．把4个球放入三个抽屉中，其中一个抽屉中至少有个球 Ｄ．掷一枚六个面分别标有，，，，，的均匀正方体骰子，骰子停止转动后奇数点朝上 ‎5．只用下列哪一种正多边形，可以进行平面镶嵌（ ）‎ A．正五边形 B．正六边形 C．正八边形 D．正十边形 ‎6. 解分式方程时，去分母后变形正确的为（ ）‎ A．2+（x+2）=3（x-1） B．2-x+2=3（x-1）‎ C．2-（x+2）=3 D． 2-（x+2）=3（x-1） ‎ ‎7．将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（ ）‎ ‎ ‎ A．‎ ‎140°‎ B．‎ ‎160°‎ C．‎ ‎170°‎ D．‎ ‎150°‎ ‎8．在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B‎1C‎1C，延长C1B1交x轴于点A2，作正方形A2B‎2C‎2C1,………按这样的规律进行下去，‎ 第2012个正方形的面积为（ ）‎ A. B.‎ C. D.‎ 二、填空题 ‎9. 若式子有意义，则x的取值范围为_______________________‎ ‎10. 已知且，则的取值范围为_____________‎ ‎11. 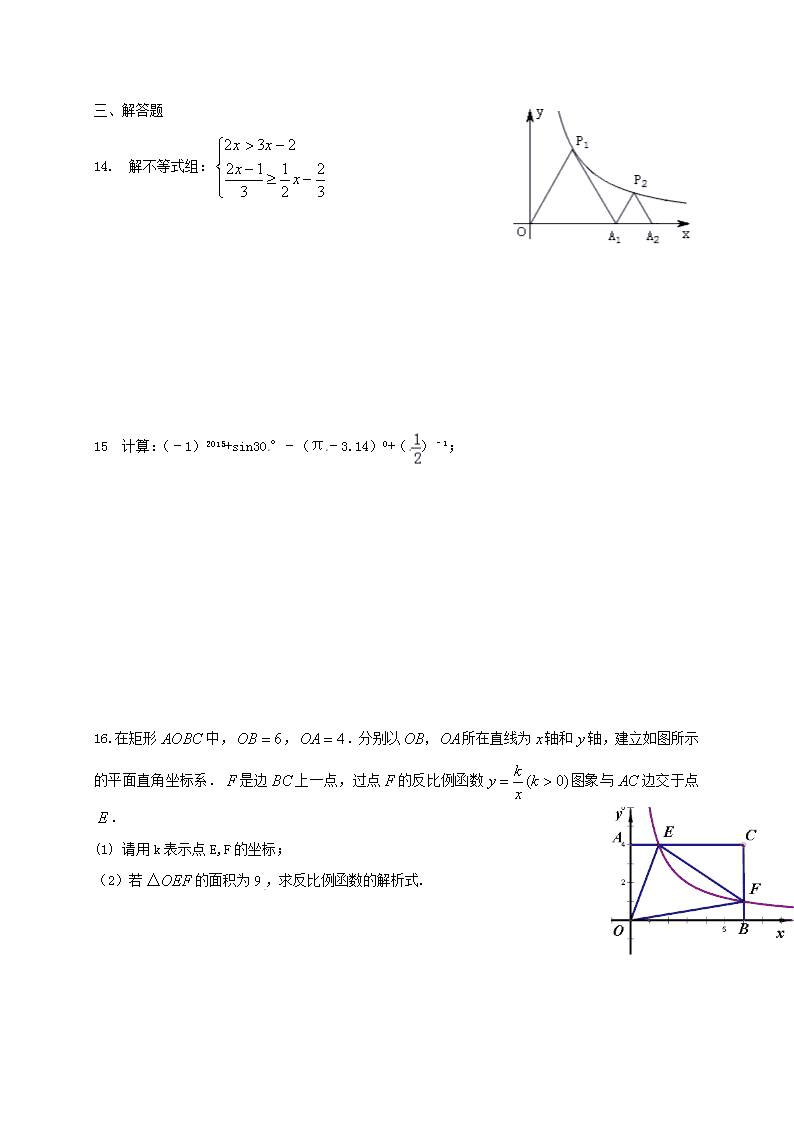二次函数的图像与图像的形状、开口方向相同，只是位置不同，则二次函数的顶点坐标是___________________________ ‎ ‎12.如图，斜面AC的坡度（CD与AD的比）为1:2，AC=米，坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带相连，若AB=‎10米，则旗杆BC的高度为__________________‎ ‎13. 如图，P1是反比例函数在第一象限图像上的一点，点A1 的坐标为 ‎(2，0)．若△P1O A1与△P‎2 A‎1 A2均为等边三角形，则A2点的坐标为______________________-‎ 三、解答题 ‎14. 解不等式组：‎ ‎15 计算：（﹣1）2015+sin30°﹣（π﹣3.14）0+（）﹣1；‎ ‎16. （_______________________________________________________________________________________________________________________________在矩形中，，．分别以所在直线为轴和轴，建立如图所示的平面直角坐标系．是边上一点，过点的反比例函数图象与边交于点．‎ ‎(1) 请用k表示点E,F的坐标；‎ ‎（2）若的面积为，求反比例函数的解析式.‎ ‎ ‎ ‎17．根据某网站调查，2014年网民们最关注的热点话题分别有：消费、教育、环保、反腐及其他共五类．根据调查的部分相关数据，绘制的统计图表如下：‎ 根据所给信息解答下列问题：‎ ‎（1）请补全条形统计图并在图中标明相应数据；‎ ‎（2）若菏泽市约有880万人口，请你估计最关注环保问题的人数约为多少万人？‎ ‎（3）在这次调查中，某单位共有甲、乙、丙、丁四人最关注教育问题，现准备从这四人中随机抽取两人进行座谈，试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率．‎ ‎18.已知：如图，在△ABC中，AB=AC，以AC为直径的⊙O 交AB 于点M，交BC 于点N，连接AN,过点 C 的切线交AB 的延长线于点P.‎ ‎（1）求证：∠BCP=∠BAN;‎ ‎（2）求证：‎ ‎19．如图，抛物线与x轴交于A（5,0）、B（-1,0）两点，过点A作直线AC⊥x轴，交直线于点C；‎ 求该抛物线的解析式；‎ 求点A关于直线的对称点的坐标，判定点是否在抛物线上，并说明理由；‎ 点P是抛物线上一动点，过点P作y轴的平行线，交线段于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.‎ ‎ ‎ ‎（第22 题）‎