上海市奉贤区2014年中考数学二模试题目 8页

上海市奉贤区2014年中考二模数学试题 ‎（满分150分，考试时间100分钟） ‎ ‎ ‎ 考生注意：‎ ‎1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．‎ ‎2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．下列各数中，属于无理数的是（▲）‎ A. ； B. ； C.； D. ；‎ ‎2．下列根式中，属于最简二次根式的是（▲）‎ A．； B．； Ｃ． ； Ｄ．；‎ ‎3．不等式的解集在数轴上表示正确的是（▲）‎ A．‎ B．‎ C．‎ D．‎ 第4题 ‎4． 右图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图，那么该班40名同学一周体育锻炼时间的众数、中位数分别是（▲） ‎ A.16、10.5；　　 B.8、9；‎ C.16、8.5； 　D.8、8.5；‎ ‎5．在数学活动课上，老师要同学们判断一个四边形门框是否为矩形，‎ 下面是某学习小组的4位同学拟定的方案，其中正确的是（▲）‎ A．测量对角线是否相互平分； B．测量两组对边是否分别相等；‎ C．测量一组对角是否都为直角； D．测量其中三个角是否都为直角；‎ 第6题 ‎6．如图，直线∥，⊥．下列命题中真命题是（▲）‎ A．； B．；‎ C．； D．；‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎7．计算： = ▲ ；‎ ‎8．分解因式：= ▲ ；‎ ‎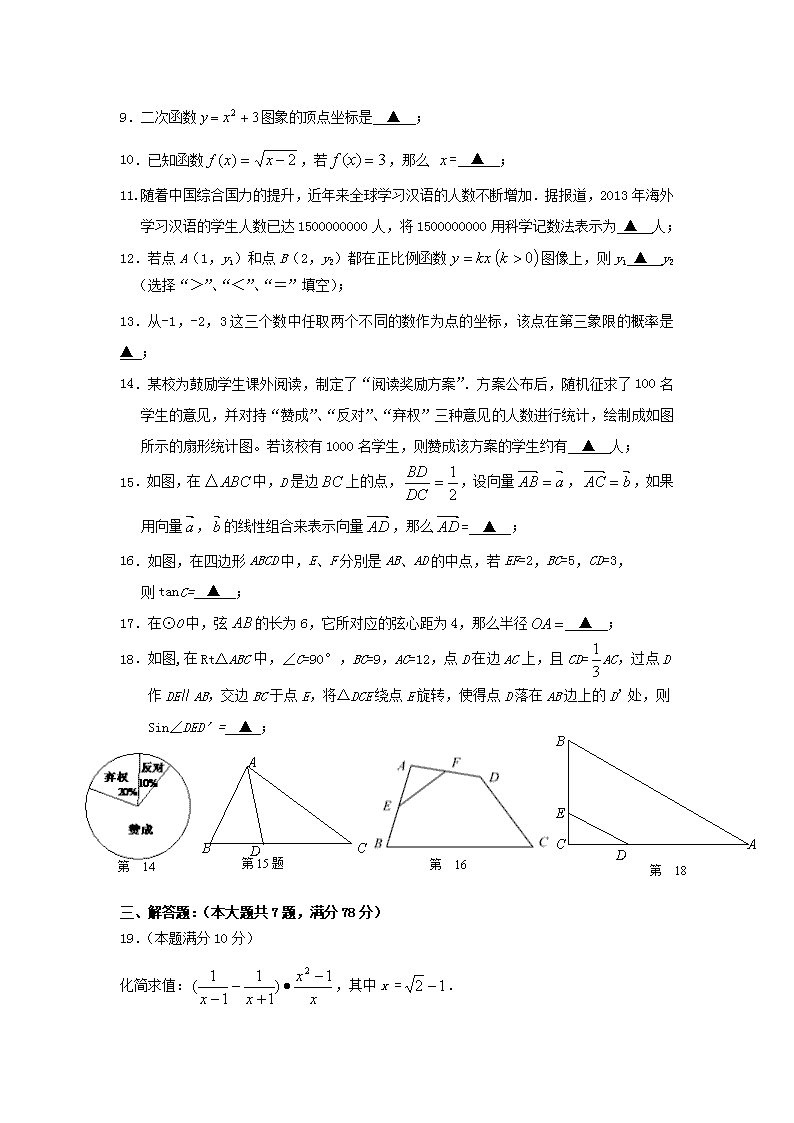9．二次函数图象的顶点坐标是 ▲ ；‎ ‎10．已知函数，若，那么 = ▲ ；‎ ‎11.随着中国综合国力的提升，近年来全球学习汉语的人数不断增加．据报道，2013年海外学习汉语的学生人数已达1500000000人，将1500000000用科学记数法表示为 ▲ 人；‎ ‎12．若点A（1，y1）和点B（2，y2）都在正比例函数图像上，则y1 ▲ y2（选择“＞”、“＜”、“＝”填空）；‎ ‎13．从-1，-2，3这三个数中任取两个不同的数作为点的坐标，该点在第三象限的概率是 ▲ ；‎ ‎14．某校为鼓励学生课外阅读，制定了“阅读奖励方案”．方案公布后，随机征求了100名学生的意见，并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计，绘制成如图所示的扇形统计图。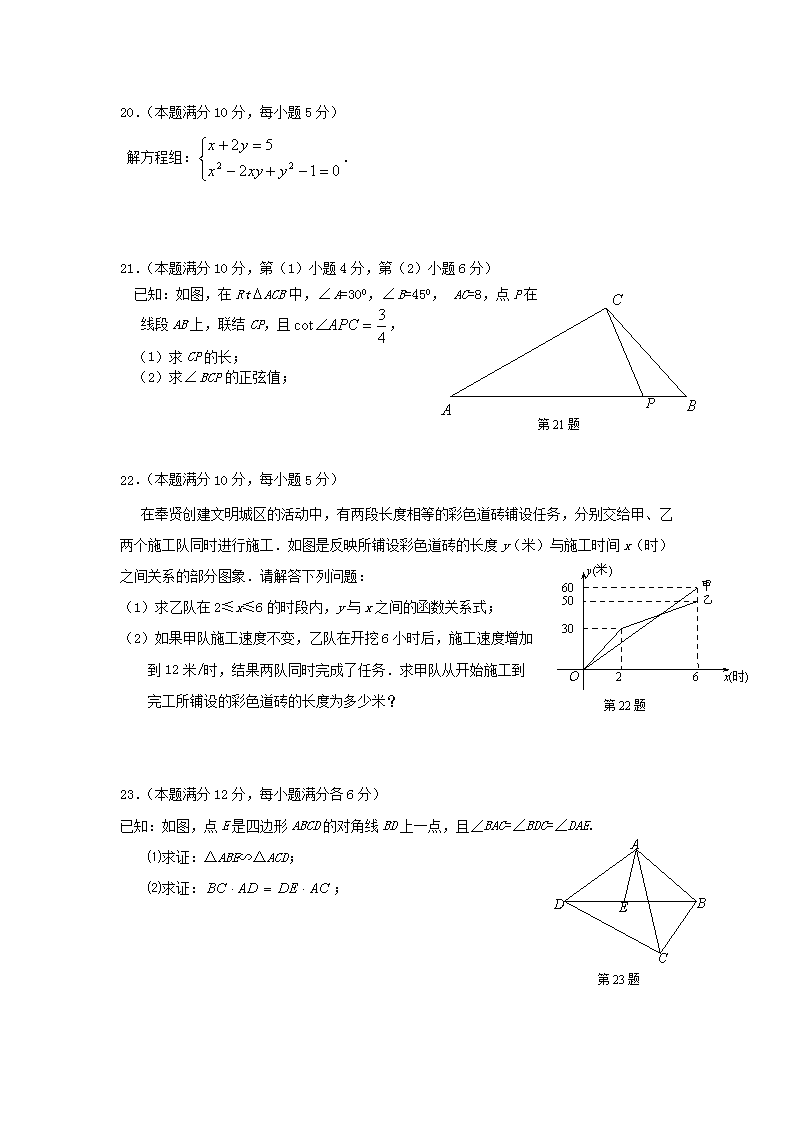若该校有1000名学生，则赞成该方案的学生约有 ▲ 人；‎ ‎15．如图，在中，D是边上的点，，设向量，，如果用向量，的线性组合来表示向量，那么= ▲ ；‎ ‎16．如图，在四边形ABCD中，E、F分別是AB、AD的中点，若EF=2，BC=5，CD=3，‎ 则tanC= ▲ ；‎ ‎17．在⊙O中，弦的长为6，它所对应的弦心距为4，那么半径 ▲ ；‎ 第14题 A D C B 第15题 第16题 C A B E D 第18题 ‎18．如图,在Rt△ABC中，∠C=90°，BC=9，AC=12，点D在边AC上，且CD=AC，过点D作DE∥AB，交边BC于点E，将△DCE绕点E旋转，使得点D落在AB边上的D’处，则Sin∠DED’= ▲ ；‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ 化简求值：，其中x =．‎ ‎20．（本题满分10分，每小题5分）‎ ‎ 解方程组：．‎ ‎21．（本题满分10分，第（1）小题4分，第（2）小题6分）‎ C A B P 第21题 已知：如图，在RtACB中，A=300，B=450， AC=8，点P在 线段AB上，联结CP，且，‎ ‎（1）求CP的长；‎ ‎（2）求BCP的正弦值；‎ ‎22．（本题满分10分，每小题5分）‎ ‎6‎ ‎2‎ O x(时)‎ y(米)‎ ‎30‎ ‎60‎ 乙 甲 ‎50‎ 第22题 在奉贤创建文明城区的活动中，有两段长度相等的彩色道砖铺设任务，分别交给甲、乙两个施工队同时进行施工．如图是反映所铺设彩色道砖的长度y（米）与施工时间x（时）之间关系的部分图象．请解答下列问题：‎ ‎（1）求乙队在2≤x≤6的时段内，y与x之间的函数关系式； ‎ ‎（2）如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加 到‎12米/时，结果两队同时完成了任务．求甲队从开始施工到 完工所铺设的彩色道砖的长度为多少米？‎ ‎23．（本题满分12分，每小题满分各6分）‎ EA 第23题 DA C B A 已知：如图，点E是四边形ABCD的对角线BD上一点，且∠BAC=∠BDC=∠DAE.‎ ‎⑴求证：△ABE∽△ACD；‎ ‎⑵求证：；‎ ‎24．（本题满分12分，每小题6分）‎ 第24题 已知：如图，在平面直角坐标系中，抛物线 交轴于A、B两点，交轴于点C.‎ ‎（1）求抛物线的表达式和它的对称轴；‎ ‎（2）若点P是线段OA上一点（点P不与点O和点A 重合），点Q是射线AC上一点，且，‎ 在轴上是否存在一点D，使得与 相似，如果存在，请求出点D的坐标；如不存在，‎ 请说明理由．‎ ‎25．（本题满分14分，第（1）小题5分，第（2）小题5分，第（3）小题4分）‎ 已知：如图1，在梯形ABCD中，∠A=90°,AD∥BC, AD=2,AB=3, tanC=,点P是AD延长线上一点，F为DC的中点， 联结BP，交线段DF于点G．‎ ‎（1）若以AB为半径的⊙B与以PD为半径的⊙P外切，求PD的长；‎ ‎（2）如图2，过点F作BC的平行线交BP于点E，‎ ‎①若设DP=，EF=，求与的函数关系式并写出自变量的取值范围；‎ ‎②联结DE和PF，若DE=PF，求PD的长．‎ A P 第25题图1‎ DA C B FA G C EA A P 第25题图2‎ DA B FA G A 备用图 DA C B FA 奉贤区初三调研考数学卷参考答案 201404‎ 一 、选择题：（本大题共8题，满分24分）‎ ‎1．B ； 2．B； 3．C ； 4．B； 5．D； 6．A；‎ 二、填空题：（本大题共12题，满分48分）‎ ‎7．； 8．； 9．（0,3）； 10．11； ‎ ‎11．； 12．＜； 13．； 14．700； ‎ ‎ 15．； 16．； 17．5； 18．； ‎ 三．（本大题共7题，满分78分）‎ ‎19． （本题满分10分）‎ 解：=………………………2分 ‎= ……………………………………………………………4分 当时…………………………………………4分 ‎20. （本题满分10分）解：‎ 由(2)得：或…………………………………………………2分 原方程组可化为和…………………………………2分 ‎ 解这两个方程组得原方程组得解：，…………………………6分 ‎21. （本题满分10分）‎ ‎（1）解：过点C作CH⊥AB于点H，………………………………………………1分 ‎∵A=300， AC=8，∴CH＝4………………………………………………………1分 ‎∵在直角三角形CHP中， ∴PH=3………………………………1分 ‎∴CP=5 ………………………………………………………………………………1分 ‎（2）∵在直角三角形CHB中，B=450 ，CH＝4 ∴BH＝4…………………1分 ‎∴PB＝1，……………………………………………………………………………1分 过点P作PG⊥BC于点G，……………………………………………………………1分 ‎∵在直角三角形PGB中，B=450 ，PB＝1 ∴PG＝…………………………1分 ‎∴在直角三角形PGC中=………………………………………2分 ‎22．（本题满分10分）‎ ‎（1）设乙队在2≤x≤6的时段内y与x之间的函数关系式为y =kx+b，……1分 由图可知，函数图象过点（2，30）、（6，50），‎ ‎∴ 解得 ……………………………………………3分 ‎∴y =5x＋20． ……………………………………………………………………1分 ‎（2）由图可知，甲队速度是：60÷6=10（米/时）． ……………………………1分 设甲队从开始到完工所铺设彩色道砖的长度为z米，依题意，得……………1分 ‎ ……………………………………………………2分 ‎ 解得 =110．………………………………………………………1分 答：甲队从开始到完工所铺设彩色道砖的长度为‎110米． ‎ EA 第23题 DA C B A O ‎23．（本题满分12分，每小题满分各6分）‎ 证明：（1）∵∠BAC=∠DAE ∴∠BAE=∠DAC…………………………2分 ‎ ∵ ∠BAC=∠BDC，∠BOA=∠DOC ‎∴∠ABE=∠ACD…………………………………………………2分 ‎∴△ABE∽△ACD………………………………………………2分 ‎(2) ∵△ABE∽△ACD ∴……………………………2分 ‎∵∠BAC=∠DAE ∴△ABC∽△AED………………………1分 ‎∴……………………………………………………2分 ‎∴…………………………………………1分 ‎ 24．（本题满分12分，每小题6分）‎ ‎(1)∵抛物线交轴于A、B两点 ‎∴ 解得：……………………………………3分 ‎∴抛物线的表达式：…………………………………………1分 它的对称轴是：直线…………………………………………………………2分 ‎（2）假设在轴上是否存在一点D，使得与相似 ‎∵∠A=∠A ‎ ‎ 则①△APQ∽△ACD ∴‎ ‎∵ ∴AC=CD ‎ ‎∵A ∴………………………………………………………3分 ‎②△APQ∽△ADC ∴‎ ‎∵C (0，3) ， ‎ ‎∴AD=CD ∴…………………………………………………………3分 ‎∴点D的坐标时，△ACD与△APQ相似。‎ ‎ 25．（本题满分14分，第（1）小题5分，第（2）小题5分，第（3）小题4分）‎ 解：（1）∵在直角三角形ABP中，AD=2,AB=3, DP=‎ ‎ ∴BP=………………………………………………………1分 ‎∵以AB为半径的⊙B与以PD为半径的⊙P外切 ‎∴BP=AB+PD………………………………………………………………1分 ‎∴…………………………………………………2分 解得： ……………………………………………………………1分 ‎∴PD的长为2时，以AB为半径的⊙B与以PD为半径的⊙P外切。‎ ‎（2）联结DE并延长交BC于点G，………………………………………………1分 ‎∵F为DC的中点，EF∥BC ∴DE=EG ‎ ‎∴CG=2EF ‎∵AD∥BC ∴‎ ‎∴DP=BG…………………………………………………………………………1分 过D作DH⊥BC于点H，∵tanC=，DH=3 ∴CH=6‎ ‎∵AD=BH=2 ∴BC=8…………………………………………………………1分 ‎∵DP=，EF=, BC=BG+CG ‎∴ ∴………………………………………2分 ‎（3）∵AD∥EF ，DE=PF 当 DP=EF时，四边形DEFP为平行四边形 ‎∴= ∴…………………………………………………………………2分 当 DPEF时，四边形DEFP为等腰梯形 过E作EQ⊥AP于点Q， DQ=‎ ‎∵EQ∥AB，BE=PE ∴AQ= ∴DQ=‎ ‎∴= 解得：…………………………………………2分 ‎∴PD的长为或4.‎