2010沈阳中考数学试题 12页

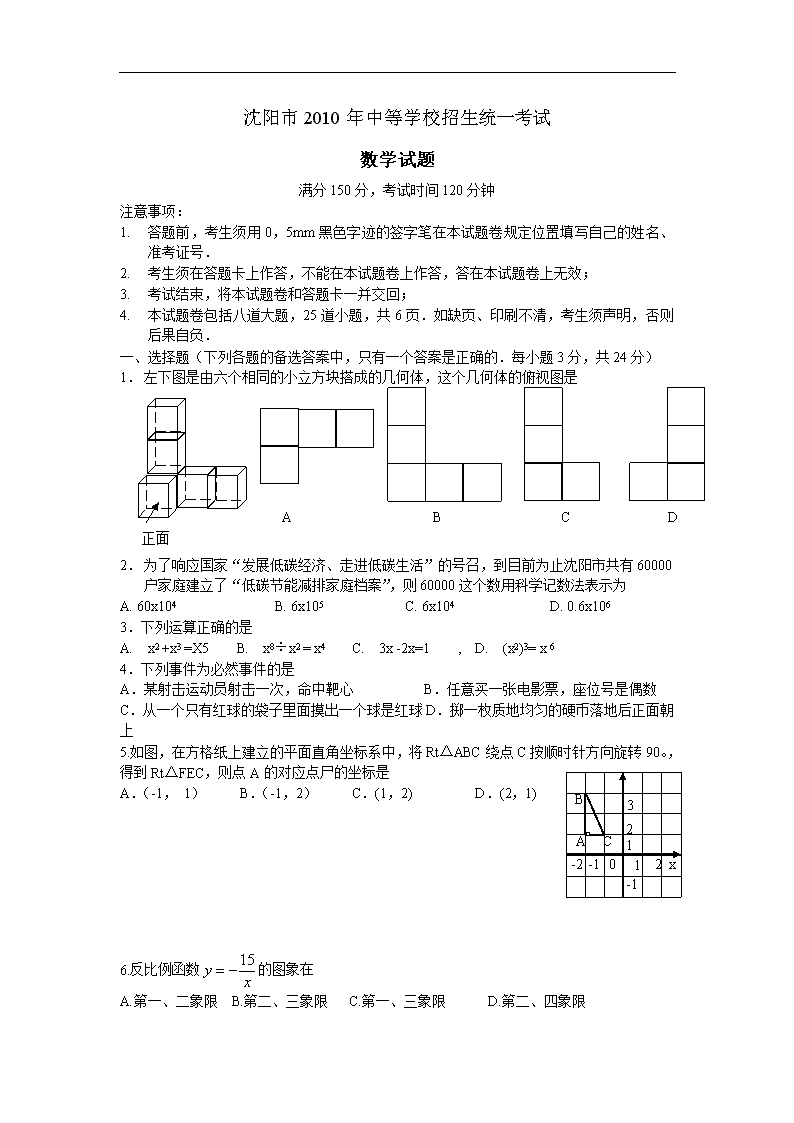
沈阳市2010年中等学校招生统一考试 数学试题 满分150分，考试时间120分钟 注意事项：‎ 1. 答题前，考生须用0，‎5mm黑色字迹的签字笔在本试题卷规定位置填写自己的姓名、准考证号．‎ 2. 考生须在答题卡上作答，不能在本试题卷上作答，答在本试题卷上无效；‎ 3. 考试结束，将本试题卷和答题卡一并交回；‎ 4. 本试题卷包括八道大题，25道小题，共6页．如缺页、印刷不清，考生须声明，否则后果自负．‎ 一、 选择题（下列各题的备选答案中，只有一个答案是正确的．每小题3分，共24分）‎ 1． 左下图是由六个相同的小立方块搭成的几何体，这个几何体的俯视图是 A B C D ‎ 正面 2． 为了响应国家“发展低碳经济、走进低碳生活”的号召，到目前为止沈阳市共有60000户家庭建立了“低碳节能减排家庭档案”，则60000这个数用科学记数法表示为 A. 60x104 B. 6x‎105 ‎‎ C. 6x104 D. 0.6x106‎ ‎3．下列运算正确的是 A. x2 +x3 =X5 B. x8÷x2 = x‎4 C. 3x -2x=1 , D. (x2)3= x 6‎ ‎4．下列事件为必然事件的是 A．某射击运动员射击一次，命中靶心 B．任意买一张电影票，座位号是偶数 C．从一个只有红球的袋子里面摸出一个球是红球D．掷一枚质地均匀的硬币落地后正面朝上 ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ x ‎-1‎ ‎1‎ ‎2‎ ‎3‎ A ‎ B ‎ C ‎ ‎5.如图，在方格纸上建立的平面直角坐标系中，将Rt△ABC绕点C按顺时针方向旋转90。，得到Rt△FEC，则点A的对应点尸的坐标是 A．（-1， 1） B．（-1，2） C．(1，2) D．(2，1)‎ ‎6.反比例函数的图象在 A.第一、二象限　B.第二、三象限 C.第一、三象限　　　D.第二、四象限 ‎7.在半径为12的中，圆心角所对的弧长是 A.6　　 　B. ‎4‎　　 　C. 2　　　 D.‎ ‎8.如图，在等边中，为边上一点，为边上一点，且则的边长为 A. 9　　 　B. ‎12　‎‎　　 ‎ C. 15　　　 D. 18‎ A C D E B 第8题图 二、填空题（每小题4分，共32分）‎ ‎9.一组数据3，4，4，6，这组数据的极差为______________.‎ ‎10.计算：____________.‎ ‎11.分解因式：______________.‎ ‎12.一次函数中，的值随值增大而____________.‎ ‎13.不等式组的解集是___________.‎ ‎14.如图，在中，点在边上，，连接交于点，则的面积与的面积之比为____________.‎ 第14题图 ‎15.在平面直角坐标系中，点……，用你发现的规律确定的坐标为__________.‎ ‎16.若等腰梯形的上、下底之和为2，并且两条对角线所成的锐角为，则等腰梯形的面积为_________.‎ 三、解答题（第17、18小题各8分，第19小题10分，共26分）‎ ‎17.先化简，再求值：其中 ‎18.小吴在放假期间去上海参观世博会．小吴根据游客流量，决定第一天从中国馆（）、日本馆（）、西班牙馆（）中随机选一个馆参观，第二天从法国馆（）、沙特馆（）、芬兰馆（）中随机选一个馆参观.请你用列表法或画树状图（树形图）法，求小吴恰好第一天参观中国馆（）且第二天参观芬兰馆（）的概率（各国家馆可用对应的字母表示）.‎ A B C D E F O ‎19.如图，菱形的对角线与相交于点，点、分别为边、的中点，连接、、.求证：四边形是菱形.‎ 第19题图 四、（每小题10分，共20分）‎ ‎20.‎2010年4月14日，国内成品油价格迎来今年的首次提价，某市93号汽油的价格由6.25元/升涨到了6.52元/升，某报纸调查员就“关于汽油涨价对用车会造成的影响”这一问题向有机动车的私家车车主进行了问卷调查，并制作了统计图表的一部分如下：‎ 车主的态度 百分比 A.没有影响 ‎4%‎ B.影响不大、还可以接受 C.有影响，现在用车次数减少了 ‎52%‎ D.影响很大，需要放弃用车 E.不关心这个问题 ‎10%‎ 第20题图 ‎（1）结合上述统计图表可得：=____________，=______________；‎ ‎（2）根据以上信息，请直接在答题卡中补全条形统计图；‎ ‎（3）2010年4月末，若该市有机动车的私家车车主约人，根据上述信息，请你估计一下持有“影响不大，还可以接受”这种态度的车主约有多少人？‎ ‎21.如图，是的直径，点在的延长线上，直线与相切于点，弦于点，线段，连接.‎ ‎（1）求证：；‎ ‎（2）若求的半径及的长.‎ 第21题图 五、（本题10分）‎ ‎22. 阅读下列材料，并解决后面的问题.‎ ‎★阅读材料：‎ ‎（1）等高线概念：在地图上，我们把地面上海拔高度相同的点连成的闭合曲线叫等高线.例如，如图1，把海拔高度是‎50米、‎100米、‎150米的点分别连接起来，就分别形成‎50米、‎100米、‎150米三条等高线.‎ ‎（2）利用等高线地形图求坡度的步骤如下：（如图2）‎ 步骤一：根据两点、 所在的等高线地形图，分别读出点、的高度；‎ ‎、两点的铅直距离=点、的高度差；‎ 步骤二：量出在等高线地形图上的距离为个单位，若等高线地形图的比例尺为：1，则、两点的水平距离=；‎ 步骤三：的坡度=；‎ 第22题图1‎ 第22题图2‎ 第22题图3‎ ‎★请按照下列求解过程完成填空，并把所得结果直接写在答题卡上.‎ 某中学学生小明和小丁生活在山城，如图3（示意图），小明每天上学从家经过沿着公路、到学校，小丁每天上学从家沿着公路到学校.该山城等高线地形图的比例尺为，在等高线地形图上量得厘米， 厘米，‎ 厘米.‎ ‎（1）分别求出、、的坡度（同一段路中间坡度的微小变化忽略不计）；‎ ‎（2）若他们早晨7点同时步行从家出发，中途不停留，谁先到学校？（假设当坡度在到之间时，小明和小丁步行的平均速度均约为‎1.3米/秒；当坡度在到之间时，小明和小丁步行的平均速度均约为‎1米/秒）‎ 解：（1）的水平距离=（厘米）=900（米），的坡度=；的水平距离=（厘米）=1 800（米），的坡度=；的水平距离=（厘米）=2 100（米），的坡度=__________.‎ ‎2）因为，所以小明在路段、上步行的平均速度均约为‎1.3米 ‎/秒，因为__________，所以小丁在路段上步行的平均速度约为___________米/秒，斜坡的距离=（米），斜坡的距离=（米），斜坡的距离=（米），所以小明从家到学校的时间=（秒）.小丁从家到学校的时间约为__________秒.因此，__________先到学校.‎ 六、（本题12分）‎ ‎23.某公司有甲、乙两个绿色农产品种植基地.在收获期这两个基地当天收获的某种农产品，一部分存入仓库，另一部分运往外地销售.根据经验，该农产品在收获过程中两个种植基地累积总产量（吨）与收获天数（天）满足函数关系（1≤≤10且为整数）.该农产品在收获过程中甲、乙两基地的累积产量分别占两基地累积总产量的百分比和甲、乙两基地累积存入仓库的量分别占甲、乙两基地的累积产量的百分比如下表：‎ ‎（1）请用含的代数式分别表示在收获过程中甲、乙两个基地累积存入仓库的量；‎ ‎（2）设在收获过程中甲、乙两基地累积存入仓库的该种农产品的总量为（吨）.请求出（吨）与收获天数（天）的函数关系式；‎ ‎（3）在（2）的基础上，若仓库内原有该种农产品42.6吨，为满足本地市场需求，在此收获期开始的同时，每天从仓库调出一部分该种农产品投入本地市场，若在本地市场售出的该种农产品总量（吨）与收获天数（天）满足函数关系（1≤≤‎ ‎10，且为整数）.问在此收获期内连续销售几天，该农产品库存量达到最低值？最低库存量是多少吨？‎ 七、（本题12分）‎ ‎24.如图1，在中，点为边中点，直线绕顶点旋转，若点在直线的异侧，直线于点，直线于点，连接 ‎（1）延长交于点（如图2），①求证：；②求证：；‎ ‎（2）若直线绕点旋转到图3的位置时，点在直线的同侧，其它条件不变.此时还成立吗？若成立，请给予证明；若不成立，请说明理由；‎ ‎（3）若直线绕点旋转到与边平行的位置时，其它条件不变，请直接判断四边形的形状及此时还成立吗？不必说明理由.‎ 第24题图1‎ 第24题图2‎ 第24题图3‎ 八、（本题14分）‎ ‎25.如图1，在平面直角坐标系中，抛物线与轴正半轴交于点、与轴正半轴交于点，边长为16的正方形的顶点与原点重合，顶点与点重合，顶点与点重合.‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）如图2，若正方形在平面内运动，并且边所在的直线始终与轴垂直，抛物线始终与边交于点且同时与边交于点（运动时，点不与两点重合，点不与两点重合）.设点的坐标为.‎ ‎①当时，分别求出点与点的坐标；‎ ‎②在①的基础上，当正方形左右平移时，请直接写出的取值范围；‎ ‎③当=7时，是否存在的值使点为边的中点.若存在，请求出的值；若不存在，请说明理由.‎ 第25题图1‎ 第25题图2‎ 第25题图3‎