茂名市2015年中考数学卷 9页

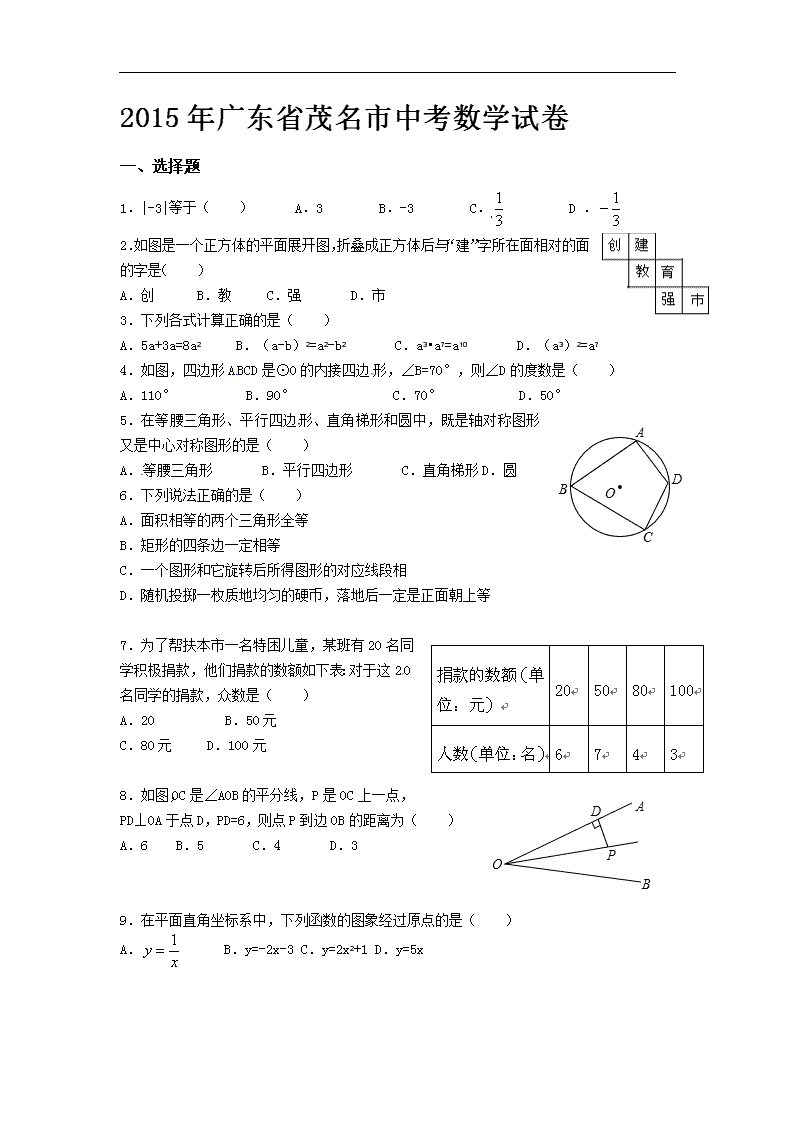
‎2015年广东省茂名市中考数学试卷 一、选择题 ‎1．|-3|等于（　　） A．3 B．-3 C． D ． ‎ ‎2．如图是一个正方体的平面展开图，折叠成正方体后与“建”字所在面相对的面的字是（　　）‎ A．创 B．教 C．强 D．市 ‎3．下列各式计算正确的是（　　）‎ A．5a+3a=8a2 B．（a-b）2=a2-b2 C．a3•a7=a10 D．（a3）2=a7‎ ‎4．如图，四边形ABCD是⊙O的内接四边形，∠B=70°，则∠D的度数是（　　）‎ A．110° B．90° C．70° D．50°‎ ‎5．在等腰三角形、平行四边形、直角梯形和圆中，既是轴对称图形又是中心对称图形的是（　　）‎ A．等腰三角形 B．平行四边形 C．直角梯形D．圆 ‎6．下列说法正确的是（　　）‎ A．面积相等的两个三角形全等 ‎ B．矩形的四条边一定相等 C．一个图形和它旋转后所得图形的对应线段相 D．随机投掷一枚质地均匀的硬币，落地后一定是正面朝上等 ‎7．为了帮扶本市一名特困儿童，某班有20名同学积极捐款，他们捐款的数额如下表：对于这20名同学的捐款，众数是（　　）‎ A．20 B．50元 ‎ C．80元 D．100元 ‎8．如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD=6，则点P到边OB的距离为（　　）‎ A．6 B．5 C．4 D．3‎ ‎9．在平面直角坐标系中，下列函数的图象经过原点的是（　　）‎ A． B．y=-2x-3 C．y=2x2+1 D．y=5x ‎10．张三和李四两人加工同一种零件，每小时张三比李四多加工5个零件，张三加工120个这种零件与李四加工100个这种零件所用时间相等，求张三和李四每小时各加工多少个这种零件？若设张三每小时经过这种零件x个，则下面列出的方程正确的是（　　）‎ A． B． C． D． ‎ 二、填空题（本大题共5小题，每小题3分，共15分）‎ ‎11．-8的立方根是 ‎ ‎12．一个多边形的内角和是720°，那么这个多边形是 ‎ ‎13．不等式x-4＜0的解集是 ‎ ‎14．如图，将矩形ABCD沿对角线BD折叠，使点C与C′重合．‎ 若AB=3，则C′D的长为 ．‎ ‎15．为了求1+3+32+33+…+3100的值，可令M=1+3+32+33+…+3100，则3M=3+32+33+34+…+3101，因此，3M-M=3101-1，所以，即，仿照以上推理计算：1+5+52+53+…+52015的值是 ．‎ 三、用心做一做（本大题共3小题，每小题7分，共21分）‎ ‎16．计算：‎ ‎17．设y=ax，若代数式（x+y）（x-2y）+3y（x+y）化简的结果为x2，请你求出满足条件的a值．‎ ‎18．补充完整三角形中位线定理，并加以证明： （1）三角形中位线定理：三角形的中位线 ； （2）已知：如图，DE是△ABC的中位线，求证：DE∥BC，‎ 四、沉着冷静，缜密思考（本大题共2小题，每小题7分，共14分）‎ ‎19．某校为了丰富学生的第二课堂，对学生参与演讲、舞蹈、书法和摄影活动的兴趣情况进行调查，学校采取随机抽样的方法进行问卷调查（每个被调查的学生必须选择而且只能选择其中最感兴趣的一项），对调查结果进行统计后，绘制了如下两个统计图： （1）此次调查抽取的学生人数m= 名，其中选择“书法”的学生占抽样人数的百分比n= （2）若该校有3000名学生，请根据以上数据估计该校对“书法”最感兴趣的学生人数．‎ ‎20．在一个不透明的袋中装有2个黄球，3个黑球和5个红球，它们除颜色外其他都相同． （1）将袋中的球摇均匀后，求从袋中随机摸出一个球是黄球的概率； （2）现在再将若干个红球放入袋中，与原来的10个球均匀混合在一起，使从袋中随机摸出一个球是红球的概率是 ，请求出后来放入袋中的红球的个数．‎ 五、满怀信心，再接再厉（本大题共3小题，每小题8分，共24分）‎ ‎21．如图，一条输电线路从A地到B地需要经过C地，图中AC=20千米，∠CAB=30°，∠CBA=45°，因线路整改需要，将从A地到B地之间铺设一条笔直的输电线路． （1）求新铺设的输电线路AB的长度；（结果保留根号） （2）问整改后从A地到B地的输电线路比原来缩短了多少千米？（结果保留根号）‎ ‎22．在平面直角坐标系中，我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”，例如点（-2，-4），（1，2），（3，6）…都是“理想点”，显然这样的“理想点”有有无数多个． （1）若点M（2，a）是反比例函数（k为常数，k≠0）图象上的“理想点”，求这个反比例函数的表达式； （2）函数y=3mx-1（m为常数，m≠0）的图象上存在“理想点”吗？若存在，请求出“理想点”的坐标；若不存在，请说明理由．‎ ‎23．某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息： ①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：‎ 时间（第x天）‎ ‎1‎ ‎3‎ ‎6‎ ‎10‎ ‎…‎ 日销售量（m件）‎ ‎198‎ ‎194‎ ‎188‎ ‎180‎ ‎…‎ ‎②该产品90天内每天的销售价格与时间（第x天）的关系如下表：‎ 时间（第x天）‎ ‎1≤x＜50‎ ‎50≤x≤90‎ 销售价格（元/件）‎ x+60‎ ‎100‎ ‎（1）求m关于x的一次函数表达式； （2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格-每件成本）】 （3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．‎ 六、灵动管理，超越自我（本大题共2小题，每小题8分，共16分）‎ ‎24．如图，Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．动点M从点B出发，在BA边上以每秒3cm的速度向定点A运动，同时动点N从点C出发，在CB边上以每秒2cm的速度向点B运动，运动时间为t秒（），连接MN． （1）若△BMN与△ABC相似，求t的值； （2）连接AN，CM，若AN⊥CM，求t的值． ‎ ‎25．如图，在平面直角坐标系中，⊙A与x轴相交于C（-2，0），‎ D（-8，0）两点，与y轴相切于点B（0，4）． （1）求经过B，C，D三点的抛物线的函数表达式； （2）设抛物线的顶点为E，证明：直线CE与⊙A相切； （3）在x轴下方的抛物线上，是否存在一点F，使△BDF面积最大，最大值是多少？并求出点F的坐标．‎