上海市闸北区中考数学二模卷及答案无水印 7页

九年级闸北数学学科期中练习卷（2010.5）‎ ‎（考试时间：100分钟，满分：150分）‎ 考生注意：‎ ‎1．本试卷含三个题，共25题：‎ ‎2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；‎ ‎3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎【下列各题的四个结论中，有且只有一个选项是正确的。选择正确项的代号并填涂在答题纸的相应位置上．】‎ ‎1．下列运算中，结果正确的是 ‎（A）； （B）； （C）； （D）．‎ ‎2．一个人的呼吸系统每天吸入和呼出大约‎20000升空气，20000用科学记数法可表示为 ‎（A）2×104； （B）2×105； （C）2×10－4； （D）2×10－5．‎ ‎3．一元二次方程x2＋2x＋1＝0根的情况是 ‎（A）有两个不相等的实数根； （B）有两个相等的实数根；‎ ‎（C）有一个实数根； （D）无实数根．‎ ‎4．反比例函数y＝的图像在一、三象限内，那么 ‎（A）k>0； （B）k≠0；‎ ‎（C）k<0； （D）k取一切实数．‎ C D B A ‎（图一）‎ ‎5．如图一，平行四边形ABCD中，AC、BD为对角线，那么等于 ‎（A）；‎ ‎（B）；‎ ‎（C）；‎ ‎（D）．‎ ‎（图二）‎ ‎6． 一个水池接有甲、乙、丙三个水管，先打开甲，一段时间后再打开乙，水池注满水后关闭甲，同时打开丙，直到水池中的水排空．水池中的水量与时间之间的函数关系如图二，则关于三个水管每小时的水流量，下列判断正确的是 ‎（A）乙>甲；‎ ‎（B）丙>甲；‎ ‎（C）甲>乙；‎ ‎（D）丙>乙．‎ 二、填空题：（本大题共12题，每小题4分，满分48分）‎ ‎【请将结果直接填入答题纸的相应位置．】‎ ‎7．计算：· ＝ ▲ ．‎ ‎8．分解因式：x2－9＝ ▲ ．‎ ‎9．方程的解是 ▲ ．‎ ‎10．某抗菌药原价30元，经过两次降价，现价格为10.8元，若平均每次降价率相同，且均为x，则可列出方程 ▲ ．‎ ‎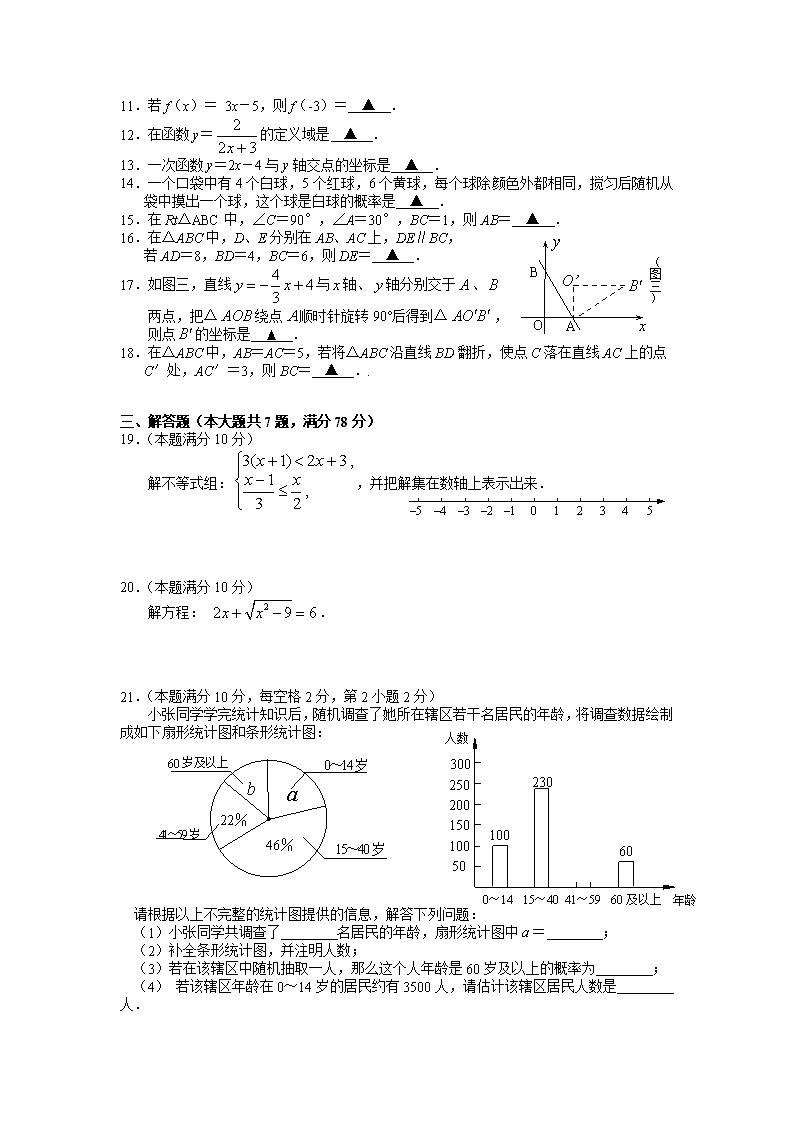11．若f（x）＝ 3x－5，则f（-3）＝ ▲ ．‎ ‎12．在函数y＝的定义域是 ▲ ． ‎ ‎13．一次函数y＝2x－4与y轴交点的坐标是 ▲ ．‎ ‎14．一个口袋中有4个白球，5个红球，6个黄球，每个球除颜色外都相同，搅匀后随机从袋中摸出一个球，这个球是白球的概率是 ▲ ． ‎ ‎15．在Rt△ABC中，∠C＝90°，∠A＝30°，BC＝1，则AB＝ ▲ ．‎ A B O ‎（图三）‎ O’‎ ‎16．在△ABC中，D、E分别在AB、AC上，DE∥BC，‎ 若AD＝8，BD＝4，BC＝6，则DE＝ ▲ ． ‎ ‎17．如图三，直线与轴、轴分别交于、‎ 两点，把△绕点顺时针旋转90°后得到△，‎ 则点的坐标是 ▲ ．‎ ‎18．在△ABC中，AB＝AC＝5，若将△ABC沿直线BD翻折，使点C落在直线AC上的点 C′处，AC′＝3，则BC＝ ▲ ．.‎ 三、解答题（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎–4‎ ‎–3‎ ‎–2‎ ‎–1‎ ‎–5‎ 解不等式组：，并把解集在数轴上表示出来．‎ ‎20．（本题满分10分）‎ 解方程： ．‎ ‎21．（本题满分10分，每空格2分，第2小题2分）‎ ‎200‎ ‎50‎ ‎250‎ ‎150‎ ‎100‎ ‎300‎ ‎0～14‎ ‎15～40‎ ‎41～59‎ ‎60及以上 年龄 ‎60‎ ‎230‎ ‎100‎ 人数 小张同学学完统计知识后，随机调查了她所在辖区若干名居民的年龄，将调查数据绘制成如下扇形统计图和条形统计图：‎ ‎46％‎ ‎22％‎ ‎0～14岁 ‎60岁及以上 ‎41～59岁 ‎15～40岁 请根据以上不完整的统计图提供的信息，解答下列问题：‎ ‎（1）小张同学共调查了 名居民的年龄，扇形统计图中＝ ；‎ ‎（2）补全条形统计图，并注明人数；‎ ‎（3）若在该辖区中随机抽取一人，那么这个人年龄是60岁及以上的概率为 ；‎ ‎（4） 若该辖区年龄在0～14岁的居民约有3500人，请估计该辖区居民人数是 人．‎ O D x C A.‎ y B ‎（图四）‎ ‎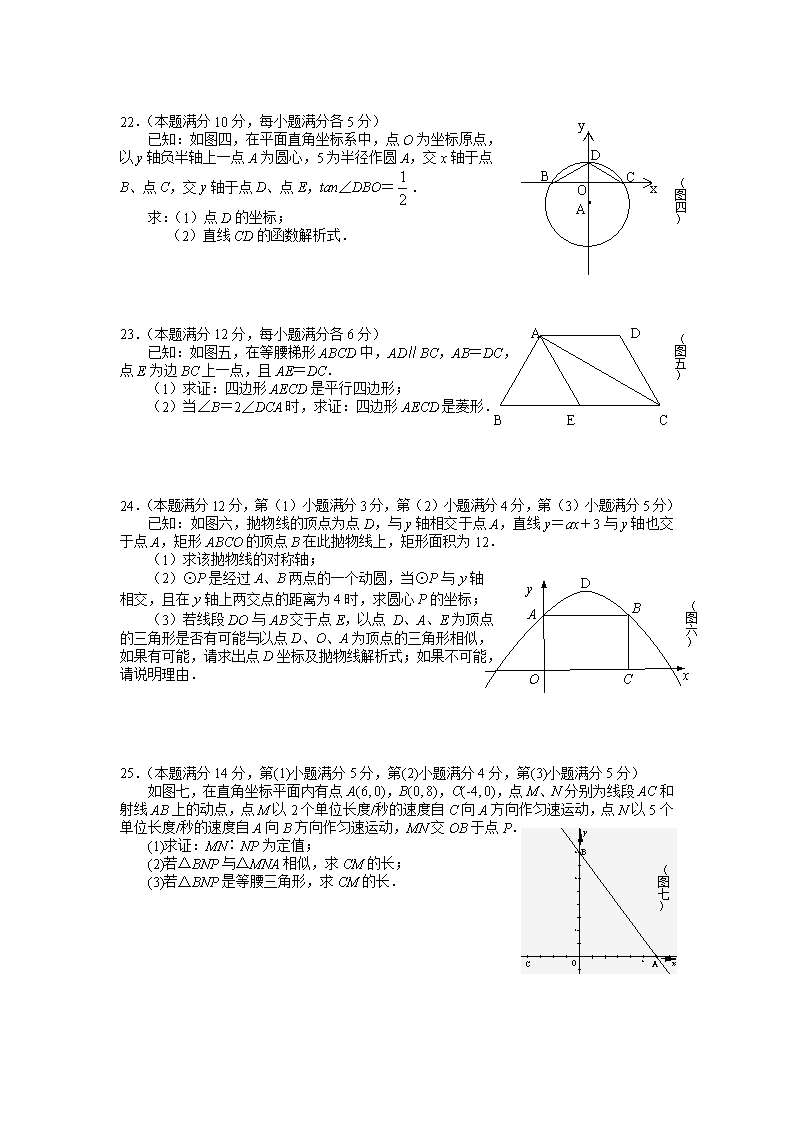22．（本题满分10分，每小题满分各5分）‎ 已知：如图四，在平面直角坐标系中，点O为坐标原点，‎ 以y轴负半轴上一点A为圆心，5为半径作圆A，交x轴于点 B、点C，交y轴于点D、点E，tan∠DBO＝．‎ 求：（1）点D的坐标；‎ ‎（2）直线CD的函数解析式．‎ A B C D E ‎（图五）‎ ‎23．（本题满分12分，每小题满分各6分）‎ 已知：如图五，在等腰梯形ABCD中，AD∥BC，AB＝DC，‎ 点E为边BC上一点，且AE＝DC．‎ ‎（1）求证：四边形AECD是平行四边形；‎ ‎（2）当∠B＝2∠DCA时，求证：四边形AECD是菱形．‎ ‎24．（本题满分12分，第（1）小题满分3分，第（2）小题满分4分，第（3）小题满分5分）‎ 已知：如图六，抛物线的顶点为点D，与y轴相交于点A，直线y＝ax＋3与y轴也交于点A，矩形ABCO的顶点B在此抛物线上，矩形面积为12．‎ BO CO O y AO x D ‎（图六）‎ ‎（1）求该抛物线的对称轴；‎ ‎（2）⊙P是经过A、B两点的一个动圆，当⊙P与轴 相交，且在轴上两交点的距离为4时，求圆心P的坐标；‎ ‎（3）若线段DO与AB交于点E，以点 D、A、E为顶点 的三角形是否有可能与以点D、O、A为顶点的三角形相似，‎ 如果有可能，请求出点D坐标及抛物线解析式；如果不可能，‎ 请说明理由．‎ ‎25．（本题满分14分，第(1)小题满分5分，第(2)小题满分4分，第(3)小题满分5分）‎ 如图七，在直角坐标平面内有点A(6, 0)，B(0, 8)，C(-4, 0)，点M、N分别为线段AC和 ‎（图七）‎ 射线AB上的动点，点M以2个单位长度/秒的速度自C向A方向作匀速运动，点N以5个单位长度/秒的速度自A向B方向作匀速运动，MN交OB于点P．‎ ‎(1)求证：MN∶NP为定值；‎ ‎(2)若△BNP与△MNA相似，求CM的长；‎ ‎(3)若△BNP是等腰三角形，求CM的长．‎ 闸北初中数学学科学业练习卷答案要点与评分标准（2010.4）‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．D； 2．A； 3．B； 4．A； 5．C； 6．C．‎ 二、填空题：（本大题共12题，每小题4分，满分48分）‎ ‎7．4； 8．(x+3)(x－3)； 9．1； 10．30（1－x）2＝10.8；‎ ‎11．－14； 12．x≠－； 13．（0, -4）； 14．； ‎ ‎15．2； 16．4； 17．（7, 3）； 18．或2．‎ 三、解答题（本大题共7题，满分78分）‎ ‎19．解：…………………………………………………………………2分 ‎ …………………………………………………………………………4分 所以不等式组的解集为－2≤x<0， …………………………………………………2分 解集在数轴上表示正确．…………………………………………………………… 2分 ‎20．解：＝6－2x…………………………………………………………………1分 x2－9＝36－24x＋4x2 …………………………………………………………………2分 x2－8x＋15＝0 …………………………………………………………………………2分 ‎(x－3)(x－5)＝0 ………………………………………………………………………1分 x1＝3，x2＝5（舍）……………………………………………………………………2分 经检验：原方程根为x＝3． …………………………………………………………2分 ‎21．解：（1）500，20％；（2）图略，人数为110人；（3）12％；（4）17500．‎ ‎22．解：（1）∵在Rt△BDO中，tan∠DBO＝‎ ‎∴＝，设DO＝a，则BO＝‎2a…………………………………………………1分 联结AB，∵圆A的半径为5，∴AB＝AD＝5，AO＝5－a …………………………1分 ‎∵在Rt△ABO中，AO2＋BO2＝AB2，∴（5－a）2＋（‎2a）2＝52 …………………1分 ‎∴a1＝2，a2＝0（舍） …………………………………………………………………1分 ‎∴D（0，2） ……………………………………………………………………………1分 ‎（2）∵AD⊥BC，∴BO＝CO＝2a=4 …………………………………………………1分 ‎∴C（4，0） ……………………………………………………………………………1分 设直线CD的函数解析式为y＝kx＋b（k≠0），把C（4，0），D（0，2）代入，‎ 得，∴ …………………………………………………………2分 ‎∴直线CD的函数解析式为y＝－x＋2 ……………………………………………1分 ‎23．证：（1）∵在等腰梯形ABCD中，AD∥BC，AB＝DC ‎∴∠B＝∠DCB…………………………………………………………………………1分 ‎∵AE＝DC， ∴AE=AB ………………………………………………………………1分 ‎∴∠B=∠AEB …………………………………………………………………………1分 ‎∴∠DCB =∠AEB………………………………………………………………………1分 ‎∴AE∥DC………………………………………………………………………………1分 ‎∴四边形AECD为平行四边形 ………………………………………………………1分 ‎（2）∵AE∥DC，∴∠EAC＝∠DCA ………………………………………………1分 ‎∵∠B＝2∠DCA，∠B＝∠DCB ‎∴∠DCB＝2∠DC ……………………………………………………………………1分 ‎∴∠ECA＝∠DCA ……………………………………………………………………1分 ‎∴∠EAC＝∠ECA ……………………………………………………………………1分 ‎∴AE＝C E………………………………………………………………………………1分 ‎∵四边形AECD为平行四边形 ‎∴四边形AECD为菱形．………………………………………………………………1分 ‎24．解：（1）∵直线y＝ax＋3与y轴交于点A，‎ ‎∴点A坐标为（0，3）……………………………………………………………………1分 ‎∴AO＝3，∵矩形ABCO的面积为12，∴AB＝4………………………………………1分 ‎∴点B的坐标为（4，3）∴抛物线的对称轴为直线x＝2 ……………………………1分 ‎（2）∵⊙P经过A、B两点，‎ ‎∴点P在直线x＝2上，即点P的坐标为（2，y）……………………………………1分 ‎∵⊙P与y轴相交，且在y轴上两交点的距离为4‎ 又∵AB＝4，‎ ‎∴点P到AB的距离等于点P到y轴的距离为2………………………………………1分 ‎∴点P的坐标为（2，1）或（2，5）……………………………………………………2分 ‎（3）①设△DAE∽△DAO，则∠DAE＝∠DAO，与已知条件矛盾，此情况不成立．‎ 过点D作DM⊥y轴，垂足为点M，DN⊥x轴，垂足为点N．………………………1分 设点D坐标为（2，y），则ON＝DM＝2，DN＝OM＝y，AM＝y－3‎ ‎②设△DAE∽△DOA，则∠DAE＝∠DOA，∴∠DAM＝∠DON ……………………1分 ‎∵∠DMA＝∠DNO＝90°，∴△DAM∽△DON ………………………………………1分 ‎∴，∴， ∴ ∴（舍），‎ E ‎∴点D坐标为（2，4） …………………………………………………………………1分 设抛物线解析式为 ‎∵顶点坐标为（2，4），∴m＝ －2，k＝4，则解析式为 将（0，3）代入，得a＝，∴抛物线解析式为．…………1分 ‎25．证明：(1) 过点N作NH⊥x轴于点H，…………………1分 设AN=5k，得：AH=3k，CM=2k ‎①　当点M在CO上时，点N在线段AB上时：‎ ‎ ∴OH=6-3k，OM=4-2k， ∴MH=10-5k，‎ ‎ ∵PO∥NH，∴………………2分 ‎ ②　当点M在OA上时，点N在线段AB的延长线上时：‎ ‎ ∴OH=3k-6，OM=2k-4，∴MH=5k-10，‎ ‎ ∵PO∥NH∴，………………2分 解：(2) 当△BNP与△MNA相似时：‎ ‎①　当点M在CO上时，只可能是∠MNB=∠MNA=90°，‎ ‎∴△BNP∽△MNA△∽BOA，‎ ‎，，， ……2分 ‎②　当点M在OA上时，只可能是∠NBP=∠NMA，∴∠PBA=∠PMO，‎ ‎∵‎ ‎∴，矛盾∴不成立. ………………………2分 ‎(3) ∵，，∴，，‎ ‎①　当点M在CO上时，， ‎ ‎(ⅰ) ，，， ………………………1分 ‎(ⅱ) ，则，∵，矛盾∴不成立…1分 ‎(ⅲ) ，则 ‎∵, ，∴‎ 又∵，可证△为等腰三角形，‎ ‎∴，∴，∴，……………………………1分 ‎②　当点M在OA上时，，‎ ‎(ⅰ) ，，， ………………………1分 ‎(ⅱ) 或∵，∴不成立．…………………………1分