中考圆知识点总结复习经典推荐打印版 4页

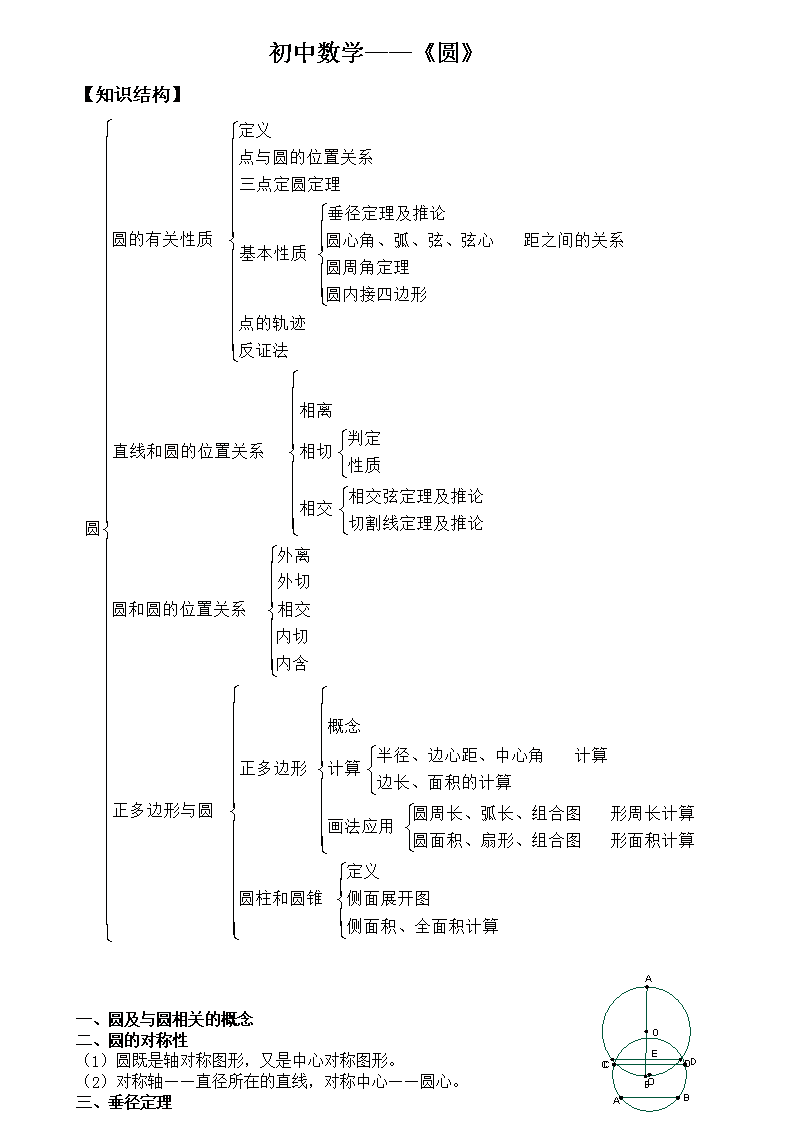
‎ 初中数学——《圆》‎ ‎【知识结构】‎ 一、 圆及与圆相关的概念 二、圆的对称性 ‎（1）圆既是轴对称图形，又是中心对称图形。‎ ‎（2）对称轴——直径所在的直线，对称中心——圆心。‎ 三、垂径定理 ‎ 垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。‎ 推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；‎ ‎ 知2推3定理： ①是直径 ② ③ ④ 弧弧 ⑤ 弧弧 ‎ 推论2：圆的两条平行弦所夹的弧相等。‎ 四、圆心角定理 ‎ 圆心角定理：同圆或等圆中，相等的圆心角所对的弦相等，所对的弧相等，弦心距相等。‎ ‎ 知1推3定理： ‎ ‎①；②； ③；④ 弧弧 五、圆周角定理 ‎1、圆周角定理：同弧所对的圆周角等于它所对的圆心的角的一半。‎ ‎2、推论：‎ ‎1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧是等弧；‎ ‎2：半圆或直径所对的圆周角是直角；圆周角是直角所对的弧是半圆，所对的弦是直径。‎ ‎3：若三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。‎ ‎ 六、圆内接四边形 圆的内接四边形定理：圆的内接四边形的对角互补，外角等于它的内对角。‎ 七、点与圆的位置关系 ‎1、点在圆内 点在圆内；‎ ‎2、点在圆上 点在圆上；‎ ‎3、点在圆外 点在圆外；‎ 八、 三点定圆定理——三角形外接圆 ‎ 1、三点定圆：不在同一直线上的三个点确定一个圆。‎ ‎ 2、三角形的外接圆：经过三角形的三个顶点的圆叫做三角形的外接圆。‎ ‎ 3、三角形的外心：三角形的外接圆的圆心是三角形三条边的垂直平分线的交点，它叫做这个三角形的外心。‎ 九、直线与圆的位置关系 ‎1、直线与圆相离 无交点；‎ ‎2、直线与圆相切 有一个交点；‎ ‎3、直线与圆相交 有两个交点；‎ 十、切线的性质与判定定理 ‎1、判定定理：过半径外端且垂直于半径的直线是切线 ‎ （两个条件，缺一不可）‎ ‎2、性质定理：切线垂直于过切点的半径 ‎ 推论1：过圆心垂直于切线的直线必过切点。‎ ‎ 推论2：过切点垂直于切线的直线必过圆心。‎ 十一、切线长定理 切线长定理： 从圆外一点引圆的两条切线，它们的切线长相等，这点和圆心的连线平分两条切线的夹角。‎ 十二、内切圆及有关计算。‎ ‎（1）三角形内切圆的圆心是三个内角平分线的交点，它到三边的距离相等。‎ ‎（2）△ABC中，∠C=90°，AC=b，BC=a，AB=c，则内切圆的半径r= 。 ‎ B ‎ O A D ‎（3）S△ABC=，其中a，b，c是边长，r是内切圆的半径。‎ ‎（4）弦切角：角的顶点在圆周上，角的一边是圆的切线，另一边是圆的弦。‎ ‎ 如图，BC切⊙O于点B，AB为弦，∠ABC叫弦切角，∠ABC=∠D。 ‎ 十三、圆与圆的位置关系 外离（图1） 无交点 ；‎ 外切（图2） 有一个交点 ；‎ 相交（图3） 有两个交点 ；‎ 内切（图4） 有一个交点 ；‎ 内含（图5） 无交点 ；‎ ‎ ‎ 十四、圆内正多边形的计算 ‎（1）正三角形 ‎ ‎ 在⊙中△是正三角形，有关计算在中进行：；‎ ‎（2）正四边形 同理，四边形的有关计算在中进行，：‎ ‎（3）正六边形 同理，六边形的有关计算在中进行，.‎ 十五、扇形、圆柱和圆锥的相关计算公式 ‎1、扇形：（1）弧长公式：；‎ ‎（2）扇形面积公式： ‎ ‎：圆心角 ：扇形多对应的圆的半径 ：扇形弧长 ：扇形面积 ‎2、圆柱： ‎ ‎（1）圆柱侧面展开图 ‎ =‎ ‎（2）圆柱的体积：‎ ‎3、圆锥侧面展开图 ‎（1）=‎ ‎（2）圆锥的体积：‎ 十六、补充定理 一、圆幂定理 ‎1、相交弦定理：圆内两弦相交，交点分得的两条线段的乘积相等。‎ 即：‎ 推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项。‎ ‎ 即：‎ ‎2、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。‎ ‎ 即：‎ ‎3、割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等 即：‎ 二、两圆公共弦定理 圆公共弦定理：两圆圆心的连线垂直并且平分这两个圆的的公共弦。‎ 三、圆的公切线 ‎ 两圆公切线长的计算公式：‎ ‎（1）公切线长：中，；‎ ‎（2）外公切线长：是半径之差； 内公切线长：是半径之和 ‎