2019中考物理知识点全突破系列专题66斜面的机械效率 12页

斜面的机械效率 一、单选题 ‎1.如图所示，将同一物体分别沿光滑的斜面AB、AC以相同的速度从底部匀速拉到顶点A，已知AB＞AC，施加的力分别为F1、F2拉力做的功为W1、W2 ， 拉力做功的功率分别为P1、P2 ， 则下列判断中正确的是（   ） ‎ ‎ ‎ A.F1＜F2 ， W1=W2 ， P1＞P2 B.F1＞F2 ， W1＞W2 ， P1＞P2 C.F1＜F2 ， W1＜W2 ， P1＜P2 D.F1＜F2 ， W1=W2 ， P1＜P2‎ ‎2.如图所示，斜面长3m，高0.6m，建筑工人用绳子在6s内将重500N的物体从其底端沿斜面向上匀速拉到顶端，拉力是150N（忽略绳子的重力）。则下列说法正确的是（  ）‎ A.斜面上的摩擦力是50N B.拉力的功率是50W C.拉力所做的功是300J D.斜面的机械效率是80%‎ ‎3.如图所示 ,有一斜面长为L，高为h,现 用力F沿斜面把物重为 G的木块从底端匀速拉到顶端。己知木块受到斜面的摩擦力为f。若不考虑其它阻力 ,则下列说法错误的是（   ） ‎ A. 减小斜面的倾斜程度,可以提高斜面机械效率            ‎ B. 减小木块与斜面间的摩擦,可以提高斜面机械效率   C. 斜面的机械效率为：                  ‎ D. 斜面的机械效率为： ‎ ‎4.用功率恒为160W的拉力，使质量为5kg的物体以4m/s的速度沿30°角的斜坡匀速拉到坡顶，已知斜坡长60m，则下列说法错误的是（    ）‎ A. 物体从斜坡底端到达坡顶的时间是15s                B. 物体上坡时的牵引力是40N C. 物体上坡时受到的摩擦力为15N                         D. 斜面的机械效率是50%‎ ‎5.一个斜面高为h ， 长为l ， 该斜面的机械效率为η.现把重为G的物体沿斜面匀速向上移动，则物体受到的滑动摩擦力的大小为(  ) ‎ A.＋G B.－G C. D. ‎ ‎6.在斜面上将一个质量为5kg的物体匀速拉到高处，如图所示，沿斜面向上的拉力为40N，斜面长2m、高1m。把重物直接提升h所做的功作有用功。g取10N/kg，下列说法正确的是（    ） ‎ A. 物体只受重力、拉力和摩擦力三个力的作用        B. 做的有用功是40J C. 此斜面的机械效率为62.5%                                 D. 物体受到的摩擦力大小为10N ‎7.如图所示，在斜面上将一个重9N的物体匀速拉到高处，沿斜面向上的拉力为5N，斜面长3m，高1m。则下列说法中不正确的是：（   ） ‎ ‎ ‎ A.该过程中做的有用功为9J B.这个斜面的机械效率为60% C.物体所受到的摩擦力是5N D.减小斜面与物体间的摩擦可以提高斜面的机械效率 ‎8.将一个重为4.5N的物体沿斜面从底端匀速拉到顶端（如图所示），斜面长1.2m，高0.4m，斜面对物体的摩擦力为0.3N（物体大小可忽略）．则下列说法正确的是（   ） ‎ ‎ ‎ A.沿斜面向上的拉力0.3N B.有用功0.36J，机械效率20% C.有用功1.8J，机械效率20% D.总功2.16J，机械效率83.3%‎ ‎9.在使用下列简单机械匀速提升同一物体的四种方式，所用动力最小的是（不计机械自重、绳重和摩擦）（  ） ‎ A. B.     C. D.‎ ‎10.如图所示，将一个重为10N的木块沿倾角为30°斜面匀速向上拉至顶端，拉力为8N，斜面高5m，下列说法中正确的是（　　） ‎ A. 拉力做功为40J             B. 摩擦力大小为3N             C. 摩擦力大小为8N             D. 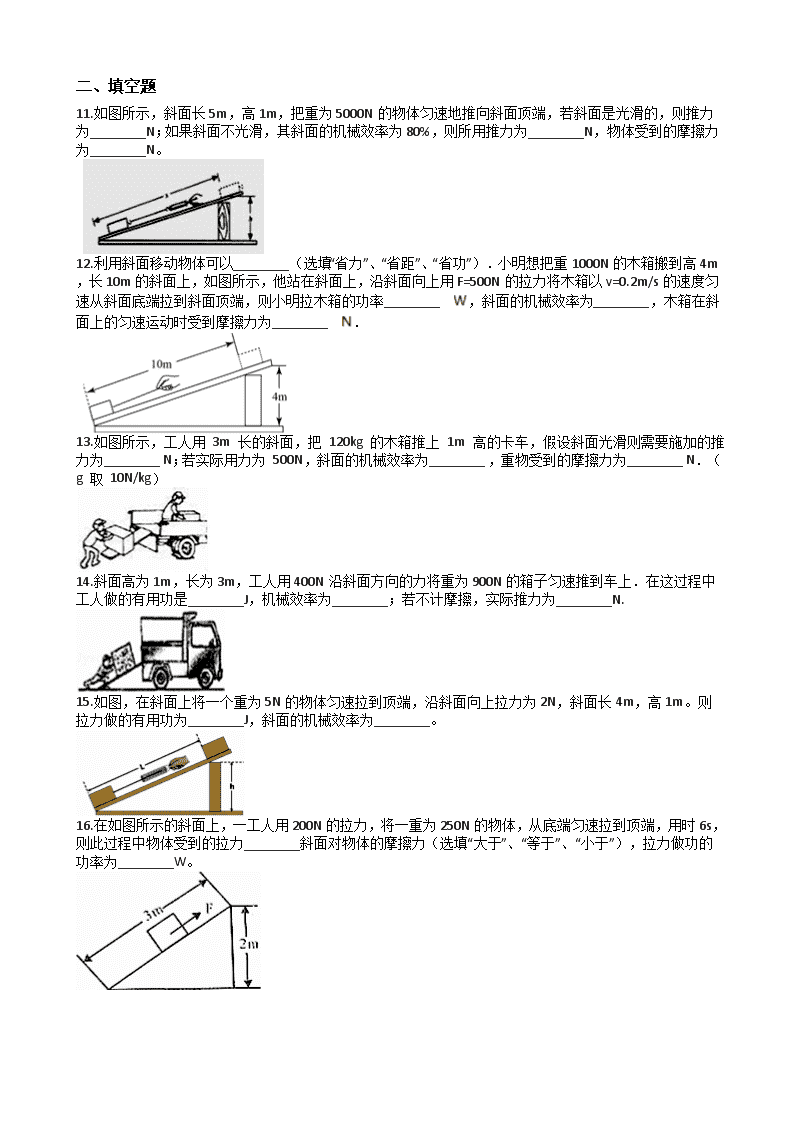机械效率为80%‎ 二、填空题 ‎11.如图所示，斜面长5m，高1m，把重为5000N的物体匀速地推向斜面顶端，若斜面是光滑的，则推力为________N；如果斜面不光滑，其斜面的机械效率为80%，则所用推力为________N，物体受到的摩擦力为________N。‎ ‎ ‎ ‎12.利用斜面移动物体可以________（选填“省力”、“省距”、“省功”）．小明想把重1000N的木箱搬到高4m，长10m的斜面上，如图所示，他站在斜面上，沿斜面向上用F=500N的拉力将木箱以v=0.2m/s的速度匀速从斜面底端拉到斜面顶端，则小明拉木箱的功率________ ，斜面的机械效率为________，木箱在斜面上的匀速运动时受到摩擦力为________ ． ‎ ‎ ‎ ‎13.如图所示，工人用 3m 长的斜面，把 120kg 的木箱推上 1m 高的卡车，假设斜面光滑则需要施加的推力为________ N；若实际用力为 500N，斜面的机械效率为________ ，重物受到的摩擦力为________ N．（g 取 10N/kg）‎ ‎14.斜面高为1m，长为3m，工人用400N沿斜面方向的力将重为900N的箱子匀速推到车上．在这过程中工人做的有用功是________J，机械效率为________；若不计摩擦，实际推力为________N. ‎ ‎15.如图，在斜面上将一个重为5N的物体匀速拉到顶端，沿斜面向上拉力为2N，斜面长4m，高1m。则拉力做的有用功为________J，斜面的机械效率为________。‎ ‎16.在如图所示的斜面上，一工人用200N的拉力，将一重为250N的物体，从底端匀速拉到顶端，用时6s，则此过程中物体受到的拉力________斜面对物体的摩擦力（选填“大于”、“等于”、“小于”），拉力做功的功率为________W。 ‎ ‎17.工人利用斜面和滑轮将物体从斜面底端匀速拉到顶端，斜面高1m，长2m，物体重500N，平行于斜面的拉力200N，所用时间10s。拉力的功率为________W，把物体直接提高到斜面顶端做的功为有用功，则这个装置的机械效率为________。‎ ‎ ‎ ‎18.如图所示，斜面长S=0.6m，高h=0.3m．用沿粗糙斜面方向的拉力F ， 将一个重为G=10N的小车由斜面底端匀速拉到顶端，运动过程中小车克服摩擦力做了1.2J的功．探究斜面是否省力，应比较________的关系；探究斜面能否省功，要比较________的关系；此斜面的机械效率是________，拉力F的大小________N.‎ ‎ ‎ ‎19.工人利用斜面和滑轮将物体从斜面底端匀速拉到顶端，斜面高1m，长2m，物体重500N，平行于斜面的拉力200N，所用时间10s。在此过程中，物体动能________（选填“增大”、“减小”或“不变”）。重力势能________（选填“增大”、“减小”或“不变”）。拉力的功率为________W，把物体直接提高到斜面顶端做的功为有用功，则这个装置的机械效率为________。‎ ‎20.如图所示，沿斜面把质量为12kg的一个物体匀速拉到最高处，沿斜面向上的拉力是F=100N，斜面长2m、高1m，则其机械效率是________%，物体所受摩擦力是________N．（取g=10N/kg） ‎ ‎21.如图所示，将质量为80kg的木箱，用一个平行于斜面向上的拉力从底端匀速拉到斜面顶端。斜面长10m、高3m，在此过程斜面的机械效率为80%．则拉力做的功为________J，拉力所做的额外功为________J．若换一个质量小一点的木箱，用力匀速拉到斜面顶端，此时斜面的机械效率将________。（选填“增大”、“不变”或“减小”） ‎ ‎22.如图所示，用一个长为1.2 m的斜面将重为45 N的物体沿斜面匀速拉到0.4 m的高台上，斜面的机械效率为60%，则把重物拉上高台时做的有用功是________J，物体与斜面间的摩擦力是________N. ‎ ‎23.如图所示，某同学用6N的拉力将重为8N的物体拉上高3m、长5m的斜面，则该斜面的机械效率________。 ‎ ‎24.如图所示，将一个重10N的物体用沿斜面向上的拉力F=7.5N匀速拉到斜面的顶端，物体沿斜面移动的距离s为5m，上升的高度h为3m，则这个过程人做的总功是________J，斜面的机械效率为________。‎ ‎ ‎ ‎25.如图所示，工人用沿斜面向上大小为500N的推力，将重800N的货物从A点匀速推至BC水平面上的B点；已知AB长3m，BC距地面高1.5m。则此斜面的机械效率为________。‎ ‎26.某同学利用长2m、高1.2m的斜面匀速拉动一重物，若其机械效率为75%，额外功仅为克服斜面对重物的摩擦力所做的功，则所受摩擦力与物体的重力之比为________。 ‎ ‎27.某人用平行于斜面的拉力，把一个重为1000N的物体，沿着长5m、高1m的斜面由底端匀速拉到顶端，拉力的大小为250N，则拉力所做的有用功为________ J，此斜面的机械效率为________。 ‎ ‎28.如图小明同学用弹簧测力计拉着重为8N的木块沿斜面向上做匀速直线运动，弹簧测力计的示数如图所示，则把木块由斜面底端拉到顶端时小明做功为________J，木块和斜面间的摩擦力为________N。 ‎ 答案解析部分 一、单选题 ‎1.【答案】D ‎ ‎【解析】【解答】将同一物体分别沿光滑斜面（无摩擦力）AB、AC以相同的速度，匀速拉到顶点A，拉力F1、F2对物体所做的功等于物体克服重力所做的功，而同一物体升高相同的高度克服重力做的功相同，故W1=W2；又因 ，W相同，AB＞AC，所以F1＜F2 ， 再由 知，速度相同，F1＜F2 ， 则P1＜P2.‎ 故答案为：D.‎ ‎【分析】斜面越长，越省力，利用物体的重力和上升的高度可以计算有用功，功和时间的比值计算功率。‎ ‎ ‎ ‎2.【答案】A ‎ ‎【解析】【解答】（1）拉力F做的功：W总＝Fs＝150N×3m＝450J；有用功：W有用＝Gh＝500N×0.6m＝300J，额外功：W额＝W总﹣W有用＝450J﹣300J＝150J，由W额＝fs可得，物体在斜面上受到的摩擦力：f＝  ＝  ＝50N，A符合题意、C不符合题意；（2）拉力的功率：P＝  ＝  ＝75W，B不符合题意；（3）斜面的机械效率：η＝  ×100% 66.7%，D不符合题意。‎ 故答案为：A。‎ ‎【分析】利用W=Fs计算该过程拉力F做的功；利用W有=Gh求出有用功，利用W额=W总-W有求出额外功，然后利用W额=fs计算货物箱在斜面上受的摩擦力大小；利用P=求拉力做功功率；斜面的机械效率等于有用功与总功之比.‎ ‎3.【答案】A ‎ ‎【解析】【解答】当减小斜面的倾斜程度时，木块对斜面的压力逐渐变大，在接触面粗糙程度不变时，压力越大，物体受到的滑动摩擦力就越大，所做的额外功就越多，斜面的机械效率就越低，A符合题意；减小斜面与物体间的摩擦，可以减小额外功，而有用功不变，总功减小，有用功与总功的比值变大，可以提高斜面的机械效率，B不符合题意；此过程中，克服物体重力所做功为有用功，即：W有=Gh；拉力做的功是总功，即：W总=FL；则斜面的机械效率为：， C不符合题意；克服斜面上的摩擦所做的功为额外功，即W额=fL；所以，总功：W总=W有+W额=Gh+fL，则斜面的机械效率为：， D不符合题意。故答案为A。【分析】摩擦力做的功为额外功，有用功不变时，额外功越大斜面的机械效率越低；根据功的计算公式W=Fs可表达拉力做的功，即总功；再根据W=Gh表达有用功；然后根据机械效率的计算公式可表达斜面的效率η；有用功与额外功之和为总功，由此根据机械效率的计算公式可表达斜面的效率η。‎ ‎4.【答案】D ‎ ‎【解析】【解答】A.物体从斜坡底端到达坡顶的路程为60m,速度为4m/s,所以是t===15s,故A正确； B.牵引力的功率恒为160W,物体的速度是4m/s,所以牵引力是F===40N,故B正确； C.根据30°角对应的直角边是斜边的一半,可知斜面的高为30m，此过程中拉力做的,总功为W总=Fs=40Nx60m=2400J, 有用功为W有用=Gh=mgh=5kgx10N/kgx30m=1500J,则做的额外功为W额外=W总-W有用=2400J-1500J=900J， 所以摩擦力大小为f=W额外/s==15N,故C正确；斜面的机械效率是η=W有用/W总==62.5%,故D错误。 故答案为：D 【分析】已知斜坡的长和物体运动速度，利用公式t=，即可求出物体从斜坡底端到达坡顶的时间；已知功率和速度，利用公式F=，即可求出牵引力；先根据30°角对应的直角边是斜边的一半,得出斜面的高，然后分别求出总功、有用功和额外功，再利用公式f=W额外/s，即可求出摩擦力；根据（3）中求出的总功和有用功，再利用公式η=W有用/W总 ， 即可求出斜面的机械效率。‎ ‎5.【答案】D ‎ ‎【解析】【解答】有用功为： ；‎ 根据 得总功为： ；‎ 则额外功为： ‎ 额外功为克服摩擦力所做的功，所以可得摩擦力为：‎ ‎。‎ D符合题意。‎ 故答案为：D ‎【分析】此题考查有关斜面机械效率的计算（W有用=Gh；W总=Fs），容易出错的是摩擦力的计算，我们要知道使用斜面时克服摩擦力做的功就是额外功，明确总功应等于有用功与额外功之和.‎ ‎6.【答案】C ‎ ‎【解析】【解答】A、将物体匀速拉到高处的过程中，物体受到了重力、支持力、摩擦力、拉力共4个力的作用；A不符合题意； B、所做的有用功： ；B不符合题意； C、所做的总功： ， 此斜面的机械效率： ，C符合题意； D、所做的额外功： ； 由 可得，物体受到的摩擦力： ，D不符合题意。 故答案为：C。 【分析】对物体进行受力分析，受重力、支持力、摩擦力和拉力；根据公式W=Gh可求提升物体所做的有用功；利用公式η=计算出机械效率；总功减去有用功即为克服摩擦力所做的额外功，根据W额=fs求出物体所受斜面的摩擦力.‎ ‎7.【答案】C ‎ ‎【解析】【解答】A、拉力做的有用功：W有用=Gh=9N×1m=9J，A不符合题意；‎ B、拉力F对物体做的总功：W总=Fs=5N×3m=15J，斜面的机械效率  ，B不符合题意；‎ C、克服摩擦力所做的额外功：W额=W总-W有=15J-9J=6J，由W额=fs得摩擦力  ，C错误，符合题意；‎ D、减小斜面与物体间的摩擦，可以减小额外功，有用功不变，总功减小，有用功与总功的比值变大，可以提高斜面的机械效率，D不符合题意。‎ 故答案为：C。‎ ‎【分析】利用W=Gh求有用功；利用W=Fs求总功，利用求斜面的机械效率；利用总功减去有用功求得额外功，利用W额=fs求摩擦力；提高斜面的机械效率的方法：减小摩擦力、增大斜面的倾斜程度.‎ ‎8.【答案】D ‎ ‎【解析】【解答】由题意知：物重G=4.5N，高h=0.4m，斜面长L=1.2m，受到的摩擦力f=0.3N，则所做的有用功W有=Gh=4.5N×0.4m=1.8J，所做的额外功W额=fL=0.3N×1.2m=0.36J。故总功为W总=W有+W额=1.8J+0.36J=2.16J，机械效率η=W有/W总=1.8J/2.16J=83.3%。‎ 故答案为：D。‎ ‎【分析】利用W=fs可求出额外功；再根据W=Gh求出有用功；额外功与有用功相加可得出总功，然后根据机械效率的计算公式求出斜面的机械效率.‎ ‎ ‎ ‎9.【答案】D ‎ ‎【解析】【解答】不计机械自重绳重和摩擦，即在理想状况下：A. 图示是一个定滑轮拉力F1＝G；B. 根据勾股定理知h＝ ＝3m,图中为斜面,F2×5m＝G×3m,得到F2＝0.6G；C. 如图所示,由图可知 ，由杠杆平衡条件可得：F3×L2＝G×LG,拉力F3＝G× G＝0.4G；D. 由图示可知,滑轮组承重绳子的有效股数n＝3,拉力F4＝ G；因此最小拉力是F4；‎ 故答案为：D。‎ ‎【分析】定滑轮可以改变力的方向，不省力，使用斜面时，斜面与高的比值越大越省力，根据动力臂是阻力臂的几倍，动力就是阻力的几分之一分析省力，使用滑轮组时，有几股绳承担物体重力，拉力就是总重的几分之一。‎ ‎10.【答案】B ‎ ‎【解析】【解答】A、因为斜面的倾角为30°，斜面高为h＝5m，所以，斜面的长度为：s＝2h＝2 5m＝10m，已知拉力F＝8N，则拉力做的总功为：W总＝Fs＝8N 10m＝80J．A不符合题意； BC、因为G＝10N，h＝5m，所以，做的有用功为：W ＝Gh＝10N 5m＝50J，则额外功为：W额外＝W总﹣W有用＝80J﹣50J＝30J，由W额外＝fs可得摩擦力的大小为：f＝ ＝3N．B符合题意，C不符合题意； D、该斜面的机械效率：η＝ 100%＝ 100%＝62.5%，D不符合题意。 故答案为：B 【分析】拉力做的总功W总＝Fs，做的有用功W ＝Gh，η＝ w 有 用/ w 总 ， W额外＝W总﹣W有用 ， W额外＝fs.‎ 二、填空题 ‎11.【答案】1000；1250；250    ‎ ‎【解析】【解答】物体的有用功为：W有=Gh=5000N×1m=5000J 若斜面光滑，则没有额外功，即推力的功W总=5000J 推力F= W总/L = 5000J/5m =1000N．‎ 效率为：η= W有/W1 ‎ 有用功为W总==W总/η=5000J/80%=6250J 推力F= W总/L = 6250J/5m =1250N 额外功：W额=W总-W有=6250J-5000J=1250J 摩擦力：f=W额/s=1250J/5m=250N 故答案为：1000；1250；250. 【分析】根据W=Gh求出有用功，根据W=Fs求出推力； 斜面不光滑，根据η＝×100%算出总功，根据W总=Fs算出推力；利用总功减去有用功求出额外功，再根据W=fs求出摩擦力的大小.‎ ‎ ‎ ‎12.【答案】省力；100；80%；100    ‎ ‎【解析】【解答】使用任何机械都不省功，但使用斜面可以省力；根据题意知道，小明沿斜面向上用力是F=500N，木箱的速度是v=0.2m/s，所以小明同学拉木箱的功率是：P=W总/t=Fs/t=Fv=500N×0.2m/s=100W；又因为箱子的重力是G=1000N，斜面的高是h=4m，所以小明同学做的有用功是：W有用 =Gh=1000N×4m=4000J，做的总功是W总 =Fs=500N×10m=5000J，故机械效率是：η=W有用/W总×100%=4000J/5000J×100%≈80%；因为额外功是：W额外 =W总 -W有用 =5000J-4000J=1000J，且W额外 =fL，所以摩擦力的大小是：f=W额/L=1000J/10m=100N。‎ 故答案为：省力；100；80%；100. 【分析】斜面越陡越省力；利用P=Fv求拉木箱的功率；利用公式W=Gh计算出有用功；再利用η=×100%计算出斜面的机械效率；有用功加上额外功（克服摩擦做功）等于总功，据此求出额外功；再利用W额外=fL计算出摩擦力大小.‎ ‎ ‎ ‎13.【答案】400；80%；100    ‎ ‎【解析】【解答】（1）有用功： ；斜面很光滑，由功的原理可知，推力对物体做的功等于人做的有用功即： ， 解得：； （2）若实际用力为 500N，人所做的总功： ；斜面的机械效率： ； （3） ，即： ，所以 ；‎ 故答案为：400；80%；100．‎ ‎【分析】根据斜面上力和距离计算功的大小，另一有用功和总功的比值计算机械效率。‎ ‎14.【答案】900；75%；300    ‎ ‎【解析】【解答】 (1)箱子重G＝900N，斜面高h＝1m，工人做的有用功为： ＝Gh＝900N×1m＝900J.(2)斜面的长度s＝3m，推力F＝400N，推力做的总功为： ＝Fs＝400N×3m＝1200J.斜面的机械效率为：η＝ ×100%＝75%.(3)若不计摩擦，则额外功为0，此时Gh＝F′s，即900N×1m＝F′×3m，解得：F′＝300N. 故答案为：900；75%；300. 【分析】根据W=Gh求出有用功；根据W=Fs求出总功，根据η=求出机械效率.若不计摩擦，额外功为0，W=Gh=Fs，据此求出推力大小.‎ ‎15.【答案】5；62.5% ‎ ‎【解析】【解答】（1）拉力做的有用功： ；（2）拉力F对物体做的总功： ，斜面的机械效率： 。‎ 故答案为：  (1). 5    (2). 62.5%‎ ‎【分析】利用W=Gh求拉力做的有用功；利用W=Fs求拉力F对物体做的总功，斜面的机械效率等于有用功与总功之比.‎ ‎16.【答案】大于；100 ‎ ‎【解析】【解答】当用力F沿斜面匀速向上拉动物体时，在沿斜面方向上，物体受到沿斜面向上的拉力、沿斜面向下的摩擦力和重力沿斜面向下的分力作用处于平衡状态，由力的平衡条件知道，拉力F等于摩擦力与重力沿斜面向下的分力之和，所以，物体所受到的拉力大于斜面对物体的摩擦力；拉力对木箱做的功是：W=Fs=200N×3m=600J，拉力对木箱做功的功率是：P=W/t=600J/6s=100W。 故答案为：大于；100. 【分析】使用斜面时，沿斜面向上的拉力要克服物体重力和摩擦力，利用拉力和距离计算功的大小，利用功和时间的比值计算功率.‎ ‎17.【答案】80；62.5% ‎ ‎【解析】【解答】由于用一动滑轮，绳子移动的距离l＝2s＝2×2m＝4m，拉力的功率为：P  。这个装置的机械效率为：η＝ ‎ 故答案为：80；62.5%. 【分析】根据W=FS求出总功；根据P=求出拉力的功率； 根据η=求出机械效率.‎ ‎ ‎ ‎18.【答案】F与G；FS与Gh；71.4%；7 ‎ ‎【解析】【解答】探究斜面是否省力，应比较拉力F与重力G关系的关系；探究斜面能否省功，要比较拉力F做的功与克服重力所做的功即：FS与Gh的关系的关系；人对小车做的有用功：W有＝Gh＝10N×0.3m＝3J；人做的总功：W总＝W有+W额＝3J+1.2J＝4.2J，斜面的机械效率：η＝ ≈71.4%；由W总＝Fs可得，推力的大小：F＝ ＝7N.‎ ‎【分析】明确使用斜面时有用功（克服物体重力做功）、总功（推力做功）、机械效率的计算（），知道克服摩擦力做的功是额外功.‎ ‎ ‎ ‎19.【答案】不变；增大；80；62.5% ‎ ‎【解析】【解答】（1）将物体从斜面底端匀速拉到顶端，质量不变，速度不变，则物体的动能不变。（2）物体沿斜面升高，质量不变，高度变大，所以其重力势能增大。（3）图中滑轮是动滑轮，则绳端通过的距离为： ；拉力做功为： ；拉力的功率为： （4）此过程的有用功为： ；这个装置的机械效率为： ；‎ 故答案为：(1). 不变    (2). 增大    (3). 80    (4). 62.5%‎ ‎【分析】动能大小的影响因素：质量、速度.质量越大，速度越大，动能越大；重力势能大小的影响因素：质量、被举得高度. 用公式W=Fs，再运用P=求功率；运用公式W=Gh，求出有用功，再运用机械效率的公式求得机械效率.‎ ‎20.【答案】60；40 ‎ ‎【解析】【解答】（1）有用功： ； 拉力做的总功： ； 斜面的机械效率： ； ⑵额外功： ， 由 可得，物体所受的摩擦力： 。 故答案为：60；40. 【分析】利用W=Fs求出总功，利用W=Gh求出有用功，利用效率公式求出斜面的机械效率；克服摩擦力做的功即为额外功，根据W额=W总-W有=fs求出摩擦力的大小.‎ ‎21.【答案】3000；600；不变 ‎ ‎【解析】【解答】木箱的重力为： ， 拉力做的有用功： ， 由 可得拉力做的总功： ；（2）拉力所做的额外功为： ，（3）如图，木箱对斜面的压力 ， 木箱受到的摩擦力与压力成正比、与接触面的粗糙程度成反比，设摩擦系数为μ（其大小由接触面的粗糙程度决定），则 ，斜面的机械效率： 可见，在斜面倾斜程度、接触面粗糙程度不变的情况下，斜面的机械效率与木箱的重力（质量）大小无关， 所以，若换一个质量小一点的木箱，机械效率不变。 故答案为：3000；600；不变. ‎ ‎【分析】利用W=Gh求拉力做的有用功，再利用η=求拉力做的总功；拉力所做的额外功等于总功减去有用功.‎ ‎22.【答案】18；10　 ‎ ‎【解析】【解答】有用功就是对物体所做的功为：W有=Gh=4.5N×0.4m=18J；由于斜面的机械效率为60％，可以得到总功为W总=W有/60%=18J/60%=30J，额外功为克服摩擦力所做的功为W额=W总-W有=12J，所以摩擦力的大小为f=W额/l=12J/1.2m=10N。 故答案为：18；10. 【分析】物体上升时，重力和高度的乘积计算有用功，拉力和斜面长计算总功，总功和有用功的差计算额外功，额外功和斜面的比值计算摩擦力。‎ ‎23.【答案】80％ ‎ ‎【解析】【解答】做的有用功为：   拉力所做的总功：   该斜面的机械效率： 。 故答案为： 80%。 【分析】物体重力和高度的乘积计算有用功，拉力和拉力上的距离计算总功，有用功和总功的比值计算机械效率.‎ ‎24.【答案】37.5；80% ‎ ‎【解析】【解答】根据题意知道，拉力所做的功是总功，由W=Fs知道，拉力做的总功是：W总 =Fs=7.5N×5m=37.5J；克服物体重力所做的功为有用功，即有用功是：W有=Gh=10N×3m=30J；所以，斜面的机械效率是：η=W有用/W总×100%=30J/37.5J×100%=80%。‎ 故答案为：37.5；80%. 【分析】利用W=Gh计算有用功；利用W=Fs计算拉力所做的功；利用计算机械效率.‎ ‎ ‎ ‎25.【答案】75% ‎ ‎【解析】【解答】沿斜面向上推动货物，此过程中推力所做的有用功为：W有=Gh=800N×1.5m=1200J；‎ 推力所做总功为：W总=Fs=500N×3m=1500J；‎ 则此斜面的机械效率： 。‎ 故答案为：75%. 【分析】根据功的计算公式W=Fs可求出总功；再根据W=Gh求出有用功；然后根据机械效率的计算公式可求出斜面的效率η.‎ ‎26.【答案】1：5 ‎ ‎【解析】【解答】使用斜面做的有用功：W有用=Gh ， 由η= =75%可得，做的总功：W总= = = Gh ， 则额外功：W额=fs=W总﹣W有用= Gh﹣Gh= Gh ， 所以可得：fs= Gh ， 因为s=2m，h=1.2m，所以h：s=1.2m：2m=3：5，所受摩擦力与物体的重力之比： = × = × =1：5。‎ 故答案为：1:5. 【分析】使用斜面做的有用功W有用=Gh，利用η==75%求做的总功，额外功W额=fs，等于总功减去有用功，进而求出摩擦力与物体的重力之比.‎ ‎27.【答案】1000；80％ ‎ ‎【解析】【解答】（1）W有用＝Gh＝1000N×1m＝1000J； （2）W总＝FS＝250N×5m＝1250J，‎ η＝ ＝＝80%． 故答案为：1000；80%.‎ ‎【分析】根据公式W有用＝Gh计算出有用功，根据公式W总＝Fs计算出总功；根据公式计算滑轮组的机械效率.‎ ‎28.【答案】2.88；0.8 ‎ ‎【解析】【解答】图中弹簧测力计的分度值为0.2N，指针对应刻度是4.8N，故此时弹簧测力计拉木块的力为4.8N，从图中可以看出，木块从低端拉到顶部移动了60cm=0.6m，故把木块由斜面底端拉到顶端时小明做功W=FS=4.8N×0.6m=2.88J；整个过程小明做的有用功W有=Gh=8N×0.3m=2.4J；则整个过程额外功W额=2.88J-2.4J=0.48J；W额=fS;     . 故答案为：2.88；0.8. 【分析】根据弹簧测力计的分度值读出拉力的大小，根据W=Fs求出总功，利用相似三角形对应边变成比例求出物体上升的高度，再根据W=Gh求出有用功，利用效率公式求出斜面的机械效率；摩擦力做的功即为额外功，根据W=Fs求出摩擦力的大小.‎