张家界市中考数学试题及答案Word版 11页

科目：数学（初中）‎ ‎（试题卷）‎ 注意事项：‎ ‎1、答题前，考生务必将自己的姓名、准考证号写在答题卡和该试题卷的封面上，并将准考证号下面相应的信息点用2B铅笔涂黑。‎ ‎2、考生作答时，选择题和非选择题均须写在答题卡上，在草稿纸和本试题卷上答题无效。考生在答题卡上按如下要求答题：‎ ‎（1）选择题部分用2B铅笔把对应题目的答案标号所在方框涂黑，修改时用橡皮擦干净，不留痕迹。‎ ‎（2）非选择题部分（包括填写填和解答题）请按题号用0.5毫米黑色墨水签字笔书写，否则作答无效。‎ ‎（3）保持字体工整、笔迹清晰、卡面清洁、不折叠。‎ ‎3、考试结束后，将本试题卷和答题卡一并交回。‎ ‎4、本试题卷共5页。如缺页，考生须声明，否则后果自负。‎ 姓 名 ‎ 准考证号 ‎ 张家界市2016年初中毕业学业考试试题 数 学 一、选择题（本大题共8个小题，每小题3分，满分24分，在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1．的倒数是（ ）‎ A． B． C． D．‎ ‎2．左下图是由4个完全相同的小正方体组成的立体图形，则它的俯视图是（ ）‎ 正面 A B C C D ‎3．下列运算正确的是（　　）‎ A． B． C． D．‎ ‎4. 如图，将一块直角三角板的直角顶点放在直尺的一边上，如果∠1=50°，那么∠2的度数是（　　）‎ ‎　 A．30° B． 40° C． 50° D． 60°‎ ‎5. 在校田径运动会上，小明和其他三名选手参加‎100米预赛，赛场共设1，2，3，4四条跑道，选手以随机抽签的方式决定各自的跑道，若小明首先抽签，则小明抽到1号跑道的概率是（　　）‎ A． B． C． D．‎ O A B C ‎6. 如图，AB是⊙O的直径，BC是⊙O的弦，若∠OBC=60°，则∠BAC的度数是( )‎ A．75° B．60° C． 45° D．30° ‎ ‎7. 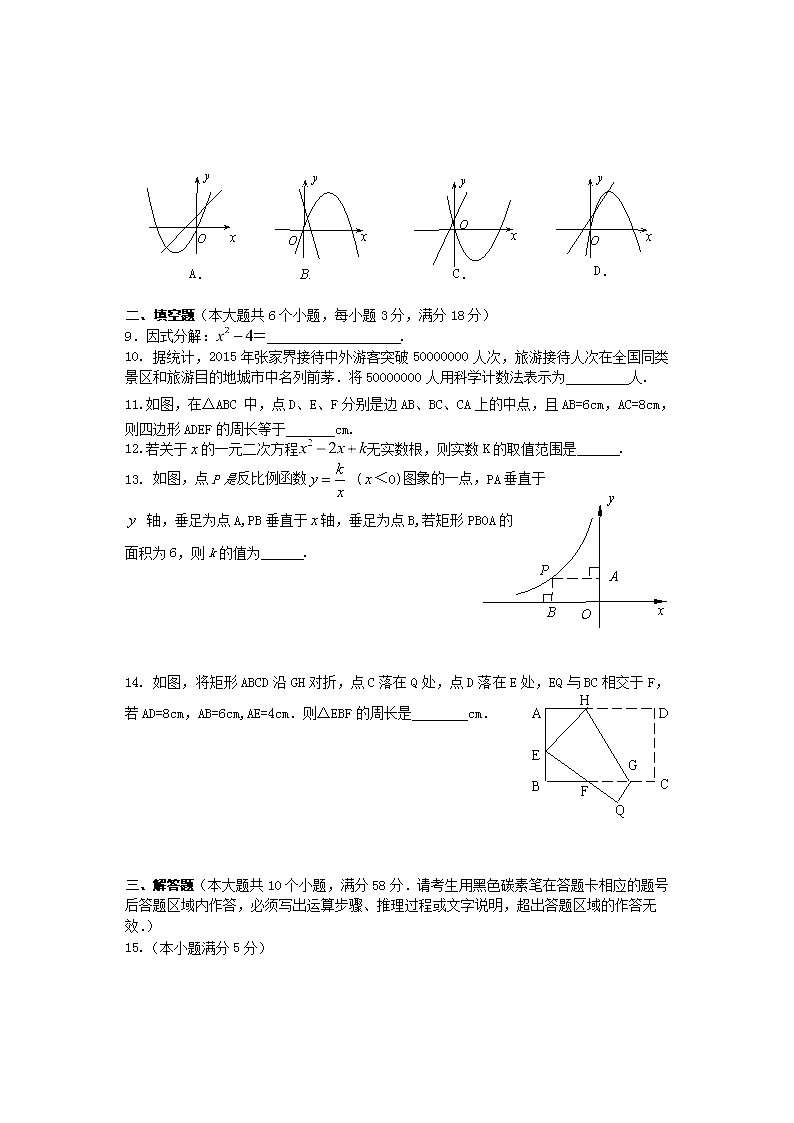下表是我市4个区县今年5月31日最高气温（℃）的统计结果：‎ 永定区 武陵源区 慈利县 桑植县 ‎32‎ ‎32‎ ‎33‎ ‎30‎ 该日最高气温的众数和中位数分别是（　　）‎ A．‎32℃‎，‎32℃‎ B．‎32℃‎，‎33℃‎ C．‎33℃‎，‎33℃‎ D．‎32℃‎，‎30℃‎[‎ ‎8. 在同一平面直角坐标系中，函数y=ax+b与y=ax2—bx的图象可能是（　　） ‎ O y x A．‎ O y x C．‎ O y x D．‎ O y x B.‎ B．‎ 二、填空题（本大题共6个小题，每小题3分，满分18分）‎ ‎9．因式分解：＝ .‎ ‎10. 据统计，2015年张家界接待中外游客突破50000000人次，旅游接待人次在全国同类景区和旅游目的地城市中名列前茅．将50000000人用科学计数法表示为 人.‎ ‎11.如图，在△ABC 中，点D、E、F分别是边AB、BC、CA上的中点，且AB=6cm，AC=8cm，则四边形ADEF的周长等于 cm.‎ B P A O Q x B．‎ y C ‎12.若关于的一元二次方程无实数根，则实数K的取值范围是 .‎ ‎13. 如图，点P是反比例函数 (＜0)图象的一点，PA垂直于 ‎ 轴，垂足为点A,PB垂直于轴，垂足为点B,若矩形PBOA的 面积为6，则k的值为 .‎ A E H B C D G F Q ‎14. 如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在E处，EQ与BC相交于F，若AD=‎8cm，AB=‎6cm,AE=‎4cm．则△EBF的周长是 cm．‎ 三、解答题（本大题共10个小题，满分58分．请考生用黑色碳素笔在答题卡相应的题号后答题区域内作答，必须写出运算步骤、推理过程或文字说明，超出答题区域的作答无效．）‎ ‎15.（本小题满分5分）‎ 计算：‎ ‎16.（本小题满分5分）‎ 已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（，）、B（，）、C（1，1）（正方形网格中每个小正方形的边长是1个单位长度）．‎ ‎（1）是绕点 逆时针旋转 度得到的，的坐标是 ；‎ A B C O A1‎ B1‎ ‎（2）求出线段AC旋转过程中所扫过的面积（结果保留）．‎ ‎（2）线段AC旋转过程中所扫过的面积为以点C为圆心，AC为半径的扇形的面积．‎ ‎17. （本小题满分5分）‎ 先化简，后求值：，其中满足．‎ ‎ ‎ ‎18.（本小题满分5分）‎ 在读书月活动中，某校号召全体师生积极捐书，为了解所捐书籍的种类，图书管理员对部分书籍进行了抽样调查，根据调查数据绘制了如下不完整的统计图表.请你根据统计 图表所提供的信息回答下面问题：‎ 某校师生捐书种类情况统计表 种类 频数 百分比 A．科普类 ‎12‎ B．文学类 ‎14‎ ‎35%‎ C．艺术类 ‎20%‎ D．其它类 ‎6‎ ‎15%‎ 某校师生捐书种类情况条形统计图 D ‎4‎ ‎16‎ 种类 A C B 本数 ‎0‎ ‎ 8‎ ‎12‎ ‎20‎ ‎ （1）统计表中的= ，= ；‎ ‎（2）补全条形统计图；‎ ‎（3）本次活动师生共捐书2000本，请估计有多少本科普类图书？‎ ‎19.（本小题满分5分）已知：如图，在四边形ABCD中，AB∥CD，E是BC的中点，直线AE交DC的延长线于点F．试判断四边形ABFC的形状，并证明你的结论。‎ ‎ ‎ ‎20.（本小题满分5分）求不等式组的解集，并把它们的解集在数轴上表示出来． ‎ ‎ ‎ 解：解不等式①得：；………………1分 解不等式②得：．………………2分 则不等式组的解集是：．………………3分 解集在数轴上表示如下： ‎ ‎-1-1‎ ‎44‎ ‎33‎ ‎22‎ ‎11‎ ‎00‎ ‎-2-2‎ ‎-3-3‎ ‎-4-4‎ ‎………………5分 ‎21. （本小题满分5分）如图，某建筑物AC顶部有一旗杆AB，且点A，B，C在同一条直线上，小明在地面D处观测旗杆顶端B的仰角为30°，然后他正对建筑物的方向前进了‎20米到达地面的E处，又测得旗杆顶端B的仰角为60°，已知建筑物的高度AC=‎12m，求旗杆AB的高度（结果精确到‎0.1米）．参考数据：≈1.73，≈1.41‎ ‎30‎ ° A B C D E ‎22. （本小题满分5分）张家界到长沙的距离约为320 ，小明开着大货车，小华开着小轿车，都从张家界同时去长沙，已知小轿车的速度是大货车的1.25倍，小华比小明提前1小时到达长沙．试问：大货车和小轿车的速度各是多少？‎ ‎23 .（本小题满分8分）如图，AB是⊙O的直径，C是⊙O上的一点，直线MN经过点C，过点A作直线MN的垂线，垂足为点D，且∠BAC=∠CAD．‎ ‎（1）求证：直线MN是⊙O的切线；‎ ‎（2）若CD=3，∠CAD= 30° ，求⊙O的半径．‎ ‎ ‎ ‎24. （本小题满分10分）‎ 已知抛物线2－3 (a0) 的图象与y轴交于点A(0，)，顶点为B.‎ ‎（1）试确定a的值，并写出B点的坐标；‎ ‎(2）若一次函数的图象经过A、B两点，试写出一次函数的解析式；‎ ‎(3）试在x轴上求一点P，使得△PAB的周长取最小值；‎ ‎(4）若将抛物线平移m（m0）个单位，所得新抛物线的顶点记作C，与原抛物线的交点记作D，问：点O、C、D能否在同一条直线上？若能，请求出m的值；若不能，请说明理由。‎ 湖南省张家界市2016年初中毕业学业水平考试试卷 数学参考答案 一、选择题（本大题共8个小题，每小题3分，满分24分，在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎ 1． A 2. C 3.　B　 4.B 5. B 6.D 7. A 8.D 二、填空题（本大题共6个小题，每小题3分，满分18分）‎ ‎ 9． 10. ‎ ‎ 11. 14 12. 13. -6 14. 8‎ 三、解答题（本大题共10个小题，满分58分．请考生用黑色碳素笔在答题卡相应的题号后答题区域内作答，必须写出运算步骤、推理过程或文字说明，超出答题区域的作答无效．）‎ ‎15.解：原式= …………4分 ‎ =3…………5分 ‎（说明：第一步计算每对一项得1分）‎ ‎16.解：（1）是绕点 C 逆时针旋转 90 度得到的.的坐标是 ‎ (1,-2) ；…………3分（每空1分）‎ ‎（2）线段AC旋转过程中所扫过的面积为以点C为圆心，AC为半径的扇形的面积．‎ ‎∵=，…………4分 ‎∴面积为：，即线段AC旋转过程中所扫过的面积为．…………5分 ‎17. 解：‎ 解方程，得：，…………3分 当时，原分式无意义．‎ 当时，‎ 原式=……………………5分 ‎18. 解：四边形ABFC是平行四边形……………………１分 因为AB //DF，所以∠EFC =∠EAB ∠ECF =∠EBA ‎ 又EC=EB 所以△EFC≌△EAB………………………………３分 所以AB=FC 在四边形ABFC中，AB=FC 且AB//FC ‎ 所以四边形ABFC是平行四边形………………………………５分 其它证法合理即给分 ‎19.解：解不等式①得： ；……………………1分 解不等式②得： ．……………………2分 则不等式组的解集是： ．……………………3分 解集在数轴上表示如下： ‎ …………………5分 ‎-4-4‎ ‎-3-3‎ ‎-2-2‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎-1-1‎ ‎20. 解：根据题意得： ， ， ．‎ ‎∴，‎ ‎∴．……………………2分 在Rt△中，‎ ‎（米）…………4分 ‎∴（米）‎ 答：旗杆的高度是5.3米．…………………………5分 ‎21. 解：设大货车的速度是x千米/时…………………………1分 由题意，得………………………2分 解得： x=64. ………………………………3分 经检验，x=64是原方程的解，且符合题意………………………………4分 则1.25 x=1.2564=80‎ 答：大货车的速度是80千米/时，小轿车的速度是100千米/时. …………5分 ‎22 . ‎ ‎ (1)证明：连接OC，因为OA=OC，所以∠BAC=∠ACO．…………１分 因为AC平分∠BAD，所以∠BAC=∠CAD，故∠ACO =∠CAD．所以 OC//AD，又已知AD丄MN，所以OC丄MN……………………2分 所以，直线MN是⊙O的切线……………………3分 ‎(2)解：已知AB是⊙O的直径，则∠ACB=90°,又AD丄MN，则 ‎∠ADC=90°.‎ 在Rt△ABC和Rt△ACD中，∠BAC= ∠CAD，所以Rt△ABC∽Rt△ACD，‎ 则………………………………5分 已知AD=4，AC=5，则AB= ，‎ 所以⊙O的直径为 ……………………6分 ‎23.解：（1）=8，= 30% ；……………………2分 ‎（2）如右图所示；……………………4分 ‎（3）2000×30%=600（本）……………………7分 ‎24. 解：（1）=1 B(1,-3) ……………………２分 (2) 设一次函数的解析式为 ‎ 将A、B两点的坐标代入解析式求得： 所以 …………5分 ‎（3）A点关于轴的对称点记作E，则E(0，2)，‎ 连接EB交轴于点P，则P点即为所求.‎ 理由：在△PAB中，AB为定值，只需PA+PB取最小值即可，而PA=PE，从而只需PE+PB取最小值即可，由于两点之间线段最短，所以PE+PB≤EB，所以E、P、B三点在同一条直线上时，取得最小值.‎ 由于过E、B点的一次函数解析式为，……………………６分 故P(，0)………………………………７分 ‎(4)设抛物线向右平移m（若m>0表示向右平移，若ｍ＜０表示向左平移）个单位，则所得新的抛物线的顶点C（1+m，-3），‎ 新抛物线解析式为 ‎ 两抛物线的交点D( )，……………………８分 经过O、C的一次函数解析式是 若 O、C、D在同一直线上，‎ 则 有，化简整理得，由于m≠0‎ 所以　解得 或　…………９分 故O、C、D三点能够在同一直线上，此时.即抛物线向右平移２个单位，或者向左平移３个单位，均满足题目要求.…………10分