- 372.00 KB
- 2021-05-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
闵行区2017学年第二学期九年级质量调研考试
数 学 试 卷
(考试时间100分钟,满分150分)
考生注意:
1.本试卷含三个大题,共25题.
2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答 题一律无效.
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证 明或计算的主要步骤.
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】
1.在下列各式中,二次单项式是
(A); (B); (C); (D).
2.下列运算结果正确的是
(A); (B);
(C); (D).
3.在平面直角坐标系中,反比例函数图像在每个象限内y随着x的增大而减小,那么它的图像的两个分支分别在
(A)第一、三象限; (B)第二、四象限;
(C)第一、二象限; (D)第三、四象限.
4.有9名学生参加校民乐决赛,最终成绩各不相同,其中一名同学想要知道自己是否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的
(A)平均数; (B)中位数; (C)众数; (D)方差.
5.已知四边形ABCD是平行四边形,下列结论中不正确的是
(A)当AB = BC时,四边形ABCD是菱形;
(B)当AC⊥BD时,四边形ABCD是菱形;
(C)当∠ABC = 90o时,四边形ABCD是矩形;
(D)当AC = BD时,四边形ABCD是正方形.
6.点A在圆O上,已知圆O的半径是4,如果点A到直线a的距离是8,那么圆O
与直线a的位置关系可能是
(A)相交; (B)相离; (C)相切或相交; (D)相切或相离.
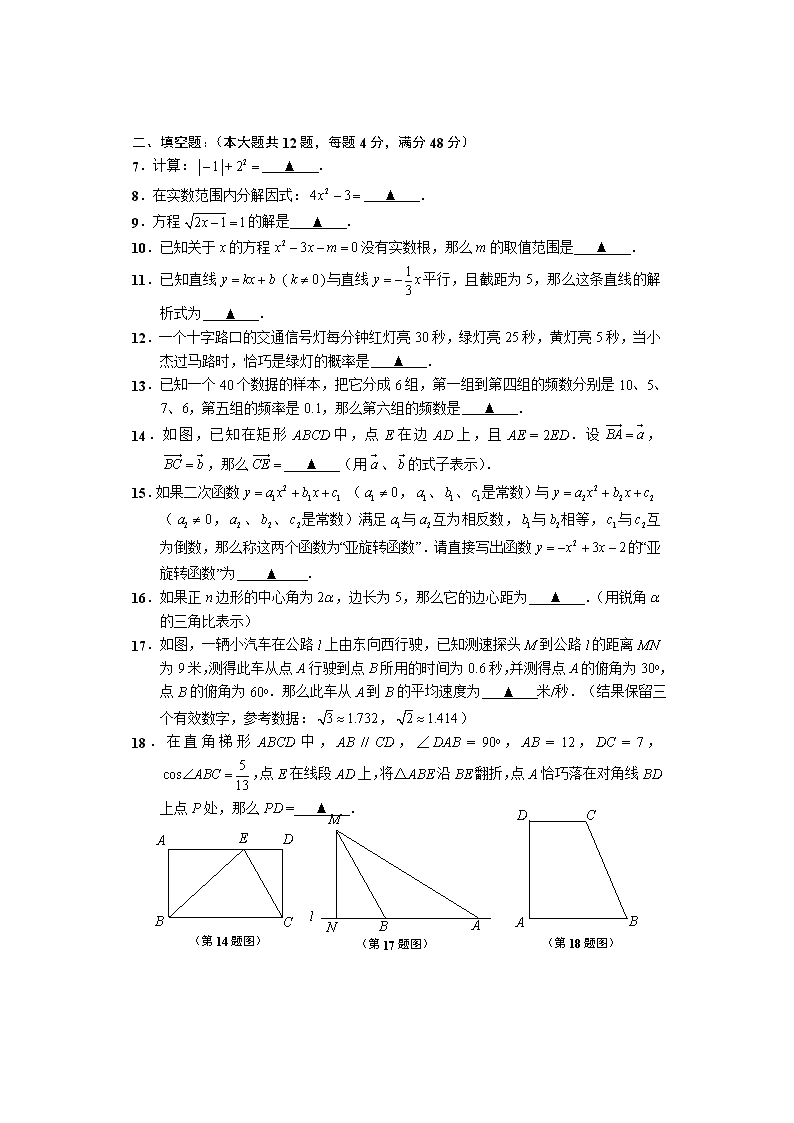
二、填空题:(本大题共12题,每题4分,满分48分)
7.计算: ▲ .
8.在实数范围内分解因式: ▲ .
9.方程的解是 ▲ .
10.已知关于x的方程没有实数根,那么m的取值范围是 ▲ .
11.已知直线与直线平行,且截距为5,那么这条直线的解析式为 ▲ .
12.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小杰过马路时,恰巧是绿灯的概率是 ▲ .
13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.1,那么第六组的频数是 ▲ .
14.如图,已知在矩形ABCD中,点E在边AD上,且AE = 2ED.设,,那么 ▲ (用、的式子表示).
15.如果二次函数(,、、是常数)与(,、、是常数)满足与互为相反数,与相等,与互为倒数,那么称这两个函数为“亚旋转函数”.请直接写出函数的“亚旋转函数”为 ▲ .
16.如果正n边形的中心角为,边长为5,那么它的边心距为 ▲ .(用锐角的三角比表示)
17.如图,一辆小汽车在公路l上由东向西行驶,已知测速探头M到公路l的距离MN为9米,测得此车从点A行驶到点B所用的时间为0.6秒,并测得点A的俯角为30o,点B的俯角为60o.那么此车从A到B的平均速度为 ▲ 米/秒.(结果保留三个有效数字,参考数据:,)
A
B
M
N
(第17题图)
l
A
B
D
C
(第18题图)
18.在直角梯形ABCD中,AB // CD,∠DAB = 90o,AB = 12,DC = 7,,点E在线段AD上,将△ABE沿BE翻折,点A恰巧落在对角线BD上点P处,那么PD = ▲ .
A
B
D
C
(第14题图)
E
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
计算:.
20.(本题满分10分)
解方程组:
21.(本题满分10分,其中第(1)小题4分,第(2)小题6分)
A
B
O
C
x
y
(第21题图)
已知一次函数的图像与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC = 90o,.
(1)求点的坐标;
(2)在第一象限内有一点M(1,m),且点M与点
C位于直线AB的同侧,使得,
求点M的坐标.
22.(本题满分10分)
为了响应上海市市政府“绿色出行”的号召,减轻校门口道路拥堵的现状,王强决定改父母开车接送为自己骑车上学.已知他家离学校7.5千米,上下班高峰时段,驾车的平均速度比自行车平均速度快15千米/小时,骑自行车所用时间比驾车所用时间多小时,求自行车的平均速度?
23.(本题满分12分,其中第(1)小题5分,第(2)小题7分)
A
B
E
G
C
F
D
(第23题图)
如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD相交于点F,FG∥AC,联结DG.
(1)求证:;
(2)求证:四边形ADGF是菱形.
24.(本题满分12分,其中每小题各4分)
A
B
O
C
x
y
(第24题图)
D
如图,已知在平面直角坐标系xOy中,抛物线与x轴交于
点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为
底的等腰三角形,求Q点的坐标.
25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)
如图,已知在Rt△ABC中,∠ACB = 90o,AC =6,BC = 8,点F在线段AB上,以点B为圆心,BF为半径的圆交BC于点E,射线AE交圆B于点D(点D、E不重合).
(1)如果设BF = x,EF = y,求y与x之间的函数关系式,并写出它的定义域;
(2)如果,求ED的长;
(3)联结CD、BD,请判断四边形ABDC是否为直角梯形?说明理由.
(第25题图)
C
B
E
F
D
A
(备用图)
C
B
A
闵行区2017学年第二学期九年级质量调研考试数学试卷
参考答案及评分标准
一、选择题:(本大题共6题,每题4分,满分24分)
1.C ;2.C ;3.A;4.B;5.D;6.D.
二、填空题:(本大题共12题,每题4分,满分48分)
7.5; 8.; 9.; 10.; 11.;
12.; 13.8; 14.; 15.; 16.(或);
17.17.3; 18..
三、解答题:(本大题共7题,满分78分)
19.解:原式……………………………………(2分+2分+2分+2分)
.……………………………………………………………………(2分)
20.解:由②得:,…………………………………………(2分)
原方程组可化为,………………………………(2分)
解得原方程组的解为,…………………………………(5分)
∴原方程组的解是,……………………………………(1分)
21.解:(1)令,则,解得:,∴点A坐标是(2,0).
令,则,∴点B坐标是(0,4).………………………(1分)
∴.………………………………(1分)
∵,,∴.
过C点作CD⊥轴于点D,易得.…………………(1分)
∴,,∴点C坐标是(4,1).………………………(1分)
(2).………………………………(1分)
∵,∴.……………………………………(1分)
∵,,∴点M在直线上;
令直线与线段AB交于点E,;……………………(1分)
分别过点A、B作直线的垂线,垂足分别是点F、G,
∴AF+BG = OA = 2;……………………………………………………(1分)
∴
…………………(1分)
∴,,,∴,.……………………(1分)
22.解:设自行车的平均速度是千米/时.………………………………………(1分)
根据题意,列方程得;……………………………………(3分)
化简得:;………………………………………………(2分)
解得:,;…………………………………………………(2分)
经检验,是原方程的根,且符合题意,不符合题意舍去.(1分)
答:自行车的平均速度是15千米/时.………………………………………(1分)
23.证明:(1)∵AE平分∠BAC,∴∠BAC=2∠BAF=2∠EAC.
∵∠BAC=2∠C,∴∠BAF=∠C=∠EAC.…………………………(1分)
又∵BD平分∠ABC,∴∠ABD=∠DBC.……………………………(1分)
∵∠ABF=∠C,∠ABD=∠DBC,
∴.…………………………………………………(1分)
∴.………………………………………………………(1分)
∴.………………………………………………(1分)
(2)∵FG∥AC,∴∠C=∠FGB,∴∠FGB=∠FAB.………………(1分)
∵∠BAF=∠BGF,∠ABD=∠GBD,BF=BF,
∴.∴AF=FG,BA=BG.…………………………(1分)
∵BA=BG,∠ABD=∠GBD,BD=BD,
∴.∴∠BAD=∠BGD.……………………………(1分)
∵∠BAD=2∠C,∴∠BGD=2∠C,∴∠GDC=∠C,
∴∠GDC=∠EAC,∴AF∥DG.……………………………………(1分)
又∵FG∥AC,∴四边形ADGF是平行四边形.……………………(1分)
∴AF=FG.……………………………………………………………(1分)
∴四边形ADGF是菱形.……………………………………………(1分)
24.解:(1)把B(1,0)和C(0,3)代入中,
得,解得.……………………………………(2分)
∴抛物线的解析式是:.……………………………(1分)
∴顶点坐标D(-1,4).……………………………………………(1分)
(2)令,则,,,∴A(-3,0)
∴,∴∠CAO=∠OCA.…………………………………(1分)
在中,.………………………………(1分)
∵,,,
∴,;
∴,是直角三角形且,
∴,
又∵∠DAC和∠OCB都是锐角,∴∠DAC=∠OCB.…………………(1分)
∴,
即.……………………………………………………(1分)
(3)令,且满足,,0),,4)
∵是以AD为底的等腰三角形,
∴,即,
化简得:.………………………………………………(1分)
由,……………………………………………………(1分)
解得,.
∴点Q的坐标是,.…(2分)
25.解:(1)在Rt△ABC中,,,
∴.……………………………………………………………(1分)
过E作EH⊥AB,垂足是H,
易得:,,.…………………………(1分)
在Rt△EHF中,,
∴.………………………………………(1分+1分)
(2)取的中点P,联结BP交ED于点G
∵,P是的中点,∴.
∴∠FBE =∠EBP =∠PBD.
∵,BP过圆心,∴BG⊥ED,ED =2EG =2DG.…………(1分)
又∵∠CEA =∠DEB,
∴∠CAE=∠EBP=∠ABC.……………………………………………(1分)
又∵BE是公共边,∴.∴.
在Rt△CEA中,∵AC = 6,,,
∴.……………………………(1分)
∴.……………………………………………(1分)
∴.……………………………………(1分)
(3)四边形ABDC不可能为直角梯形.…………………………………(1分)
①当CD∥AB时,如果四边形ABDC是直角梯形,
只可能∠ABD =∠CDB = 90o.
在Rt△CBD中,∵,
∴,
.
∴,;
∴.
∴CD不平行于AB,与CD∥AB矛盾.
∴四边形ABDC不可能为直角梯形.…………………………(2分)
②当AC∥BD时,如果四边形ABDC是直角梯形,
只可能∠ACD =∠CDB = 90o.
∵AC∥BD,∠ACB = 90o,
∴∠ACB =∠CBD = 90o.
∴∠ABD =∠ACB +∠BCD > 90o.
与∠ACD =∠CDB = 90o矛盾.
∴四边形ABDC不可能为直角梯形.…………………………(2分)