- 176.50 KB
- 2021-05-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
阿氏圆整理
例题讲解:
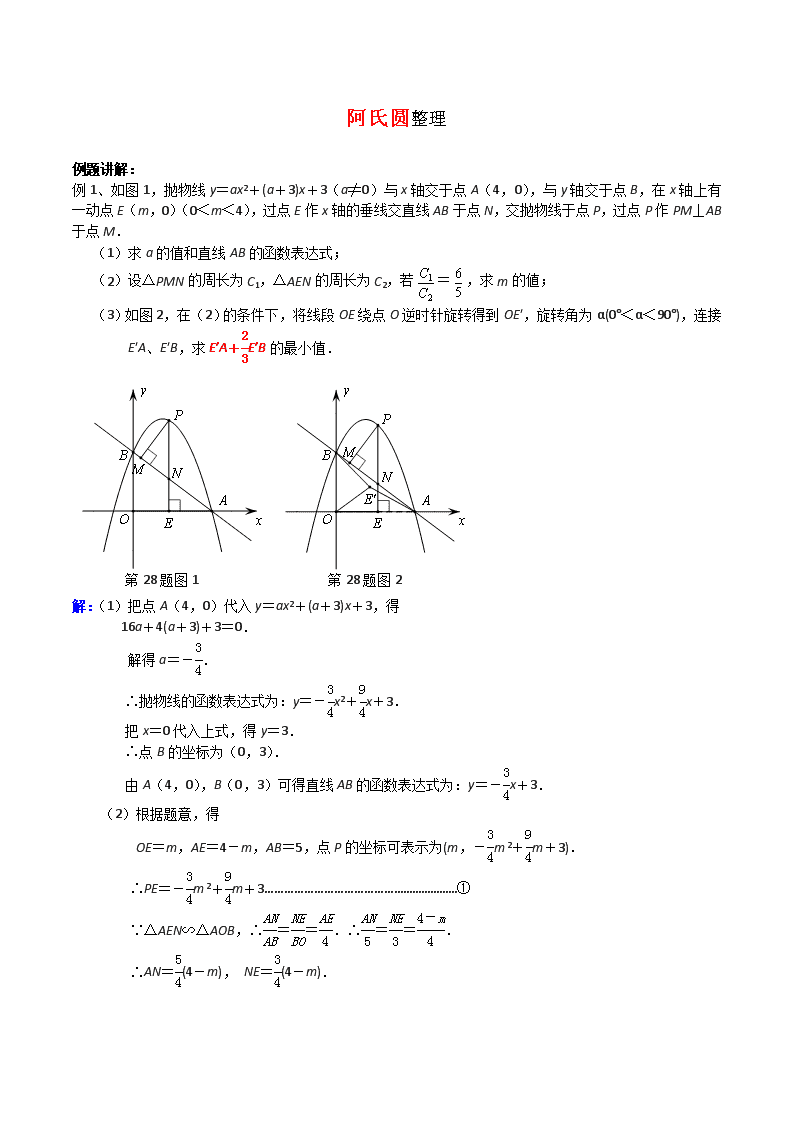
例1、如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求a的值和直线AB的函数表达式;
(2)设△PMN的周长为C1,△AEN的周长为C2,若=,求m的値;
(3)如图2,在(2)的条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E′A+E′B的最小值.
第28题图1
第28题图2
解:(1)把点A(4,0)代入y=ax2+(a+3)x+3,得
16a+4(a+3)+3=0.
解得a=-.
∴抛物线的函数表达式为:y=-x2+x+3.
把x=0代入上式,得y=3.
∴点B的坐标为(0,3).
由A(4,0),B(0,3)可得直线AB的函数表达式为:y=-x+3.
(2)根据题意,得
OE=m,AE=4-m,AB=5,点P的坐标可表示为(m,-m 2+m+3).
∴PE=-m 2+m+3……………………………………………………①
∵△AEN∽△AOB,∴==.∴==.
∴AN=(4-m), NE=(4-m).
∵△PMN∽△AEN,且=,
∴=.∴PN =AN=×(4-m)=(4-m).
∴PE=NE+PN=(4-m)+(4-m)=(4-m)………………………...②
由①、②,得
-m 2+m+3=(4-m).
解得m1=2,m2=4(不合题意,舍去).
∴m的値为2.
(3)在(2)的条件下,m的値为2,点E(2,0),OE=2.∴OE′=OE=2.
如图,取点F(0,),连接FE′、AF.则OF=,AF==.
第28题答案图
∵==,=,且∠FOE′=∠E′OB,∴△FOE′∽△E′OB.∴=.∴FE′=E′B.
∴E′A+E′B=E′A+FE′≥AF=.
∴E′A+E′B的最小值为.
巩固练习:
1、如图,在Rt△ABC中,∠ACB﹦90°,CB﹦4,CA﹦6,圆C半径为2,P为圆上一动点,连接AP,BP, 最小值为( )
A、 B、 C、 D、
2、如图,在△ABC中,∠B﹦90°,AB﹦CB﹦2,以点B为圆心作圆B与AC相切,点P为圆B上任一动点,则的最小值是 .
3、如图,菱形ABCD的边长为2,锐角大小为60°,⊙A与BC相切于点E,在⊙A上任取一点P,则的最小值为 .
y
x
4、在平面直角坐标系中,A(2,0),B(0,2),C(4,0),D(3,2),P是△AOB外部的第一象限内一动点,且∠BPA﹦135°,则2PD﹢PC的最小值是 .
5、(1)如图1,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求的最小值和的最大值.
(2)如图2,已知正方形ABCD的边长为9,圆B的半径为6,点P是圆B上的一个动点,求的最小值和的最大值.
(3)如图3,已知菱形ABCD的边长为4,∠B﹦90°,圆B的半径为,2,点P是圆B上的一个动点,求的最小值和的最大值.
图1 图2 图3
套路总结
阿氏圆基本解法:构造相似
阿氏圆一般解题步骤:
第一步:连接动点至圆心O(将系数不为1的线段的两个端点分别与圆心相连接),则连接OP、OD;
第二步:计算出所连接的这两条线段OP、OD长度;
第三步:计算这两条线段长度的比;
第四步:在OD上取点M,使得;
第五步:连接CM,与圆O交点即为点P.
1.
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,AP+BP的最小值为( )
2.如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为上一动点,求PC+PD的最小值.