中考数学最后3大题试题及答案 6页

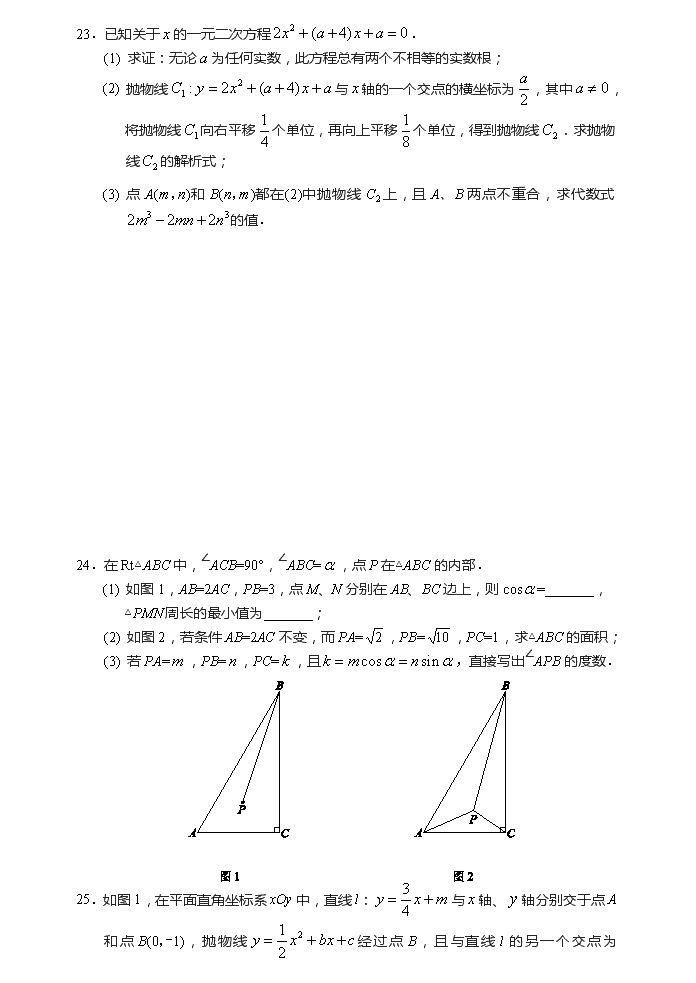
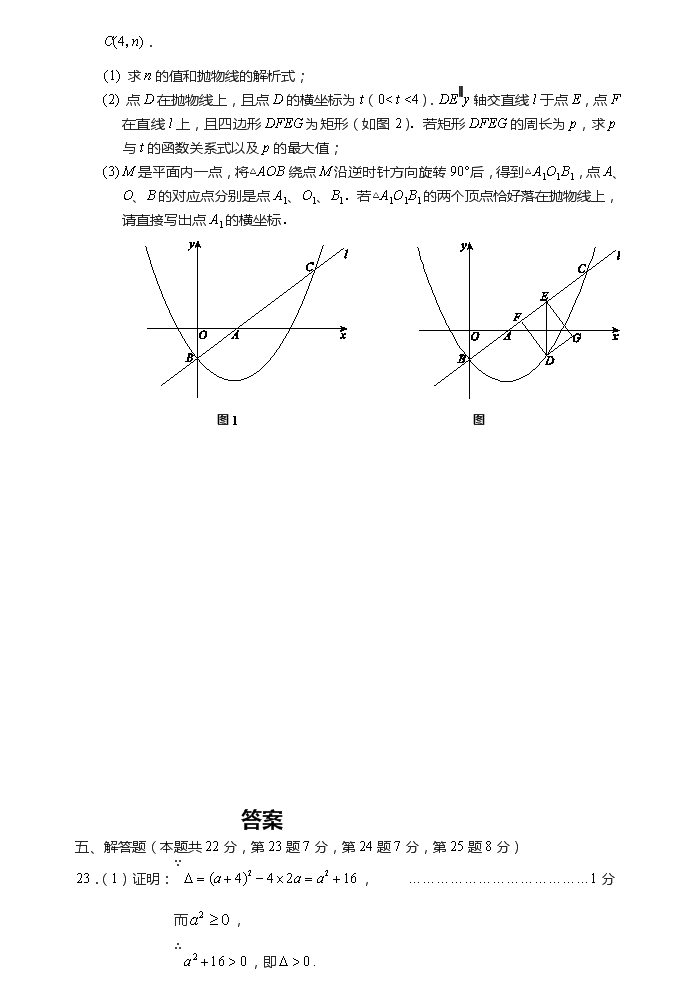
‎23．已知关于的一元二次方程．‎ ‎ (1) 求证：无论为任何实数，此方程总有两个不相等的实数根；‎ ‎(2) 抛物线与轴的一个交点的横坐标为，其中，将抛物线向右平移个单位，再向上平移个单位，得到抛物线．求抛物 线的解析式；‎ ‎(3) 点A(m,n)和B(n,m)都在(2)中抛物线C2上，且A、B两点不重合，求代数式 的值．‎ ‎24．在Rt△ABC中，∠ACB=90°，∠ABC=，点P在△ABC的内部．‎ ‎(1) 如图1，AB=2AC，PB=3，点M、N分别在AB、BC边上，则cos=_______，‎ ‎ △PMN周长的最小值为_______；‎ ‎(2) 如图2，若条件AB=2AC不变，而PA=，PB=，PC=1，求△ABC的面积；‎ ‎(3) 若PA=，PB=，PC=，且，直接写出∠APB的度数．‎ ‎25．如图1，在平面直角坐标系xOy中，直线l：与轴、轴分别交于点A和点B(0,-1)，抛物线经过点B，且与直线l的另一个交点为 C(4,n)．‎ ‎ (1) 求的值和抛物线的解析式；‎ ‎(2) 点D在抛物线上，且点D的横坐标为t（0< t <4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；‎ ‎(3) M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A1O1B1，点A、O、B的对应点分别是点A1、O1、B1．若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的横坐标．‎ 图1 图 答案 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23．（1）证明：∵， …………………………………1分 ‎ 而， ‎ ‎ ∴，即. ‎ ‎ ∴无论为任何实数，此方程总有两个不相等的实数根. …………2分 ‎（2）解：∵当时，，‎ ‎ ∴.‎ ‎ ∴，即.‎ ‎∵，‎ ‎ ∴. ………………………………………………………… 3分 ‎∴抛物线的解析式为.‎ ‎∴抛物线的顶点为.‎ ‎∴抛物线的顶点为.‎ ‎∴抛物线的解析式为. …………………………4分 ‎（3）解：∵点A（，）和B（，）都在抛物线上，‎ ‎ ∴，且.‎ ‎ ∴.‎ ‎ ∴.‎ ‎ ∴.‎ ‎ ∵A、B两点不重合，即，‎ ‎ ∴.‎ ‎ ∴. ……………………………………………………… 5分 ‎∵，，‎ ‎ ∴‎ ‎ ‎ ‎ ‎ ‎ ………………………………………………………………6分 ‎. ………………………………………………………………7分 ‎24．解：（1）=，△PMN周长的最小值为 3 ； ………………………2分 图6‎ ‎ （2）分别将△PAB、△PBC、△PAC沿直线AB、BC、AC翻折，点P的对称点分别是点D、E、F，连接DE、DF，（如图6）‎ ‎ 则△PAB≌△DAB，△PCB≌△ECB，△PAC≌△FAC.‎ ‎ ∴AD=AP=AF， BD=BP=BE，CE=CP=CF.‎ ‎ ∵由（1）知∠ABC=30°，∠BAC=60°，∠ACB=90°，‎ ‎ ∴∠DBE=2∠ABC=60°，∠DAF=2∠BAC=120°，‎ ‎ ∠FCE=2∠ACB=180°.‎ ‎ ∴△DBE是等边三角形，点F、C、E共线.‎ ‎ ∴DE=BD=BP=，EF=CE+CF=2CP=2.‎ ‎ ∵△ADF中，AD=AF=，∠DAF=120°，‎ ‎ ∴∠ADF=∠AFD=30°.‎ ‎∴DF=AD =.‎ ‎ ∴.‎ ‎ ∴∠DFE=90°. ………………………………………………………4分 ‎ ∵，‎ ‎ ∴.‎ ‎ ∴. ……………………………………………5分 ‎ （3）∠APB=150°. ………………………………………………………… 7分 ‎ 说明：作BM⊥DE于M，AN⊥DF于N.（如图7）‎ ‎ 由（2）知∠DBE=，∠DAF=.‎ 图7‎ ‎ ∵BD=BE=，AD=AF=，‎ ‎ ∴∠DBM=，∠DAN=.‎ ‎ ∴∠1=，∠3=.‎ ‎ ∴DM =，DN=.‎ ‎ ∴DE=DF=EF.‎ ‎ ∴∠2=60°.‎ ‎ ∴∠APB=∠BDA=∠1+∠2+∠3=150°.‎ ‎25．解：（1）∵直线l：经过点B（0，），‎ ‎ ∴.‎ ‎ ∴直线l的解析式为. ‎ ‎ ∵直线l：经过点C（4，n），‎ ‎∴. ………………………………………………1分 ‎ ∵抛物线经过点C（4，2）和点B（0，），‎ ‎ ∴ ‎ ‎ 解得 ‎ ‎ ∴抛物线的解析式为. …………………………2分 ‎ （2）∵直线l：与x轴交于点A，‎ 图8‎ ‎ ∴点A的坐标为（，0）. ‎ ‎∴OA=.‎ 在Rt△OAB中，OB=1，‎ ‎ ∴AB==. ‎ ‎ ∵DE∥轴，‎ ‎ ∴∠OBA=∠FED.‎ ‎ ∵矩形DFEG中，∠DFE=90°，‎ ‎ ∴∠DFE=∠AOB=90°.‎ ‎ ∴△OAB∽△FDE.‎ ‎ ∴.‎ ‎ ∴，‎ ‎ . …………………………………………4分 ‎ ∴=2(FD+ FE)=. ‎ ‎ ∵D（，），E（，），且，‎ ‎ ∴.‎ ‎ ∴. …………………………… 5分 ‎ ∵，且，‎ ‎ ∴当时，有最大值. …………………………………… 6分 ‎ （3）点A1的横坐标为或. ……………………………………………8分 ‎ 说明：两种情况参看图9和图10，其中O1B1与轴平行，O1A1与轴平行.‎ 图9‎ 图10‎ B ‎1‎ O ‎1‎ A ‎1‎ l C A B O x y y x O B A C l A ‎1‎ O ‎1‎ B ‎1‎ ‎ ‎