2008年上海市中考数学考试(1) 7页

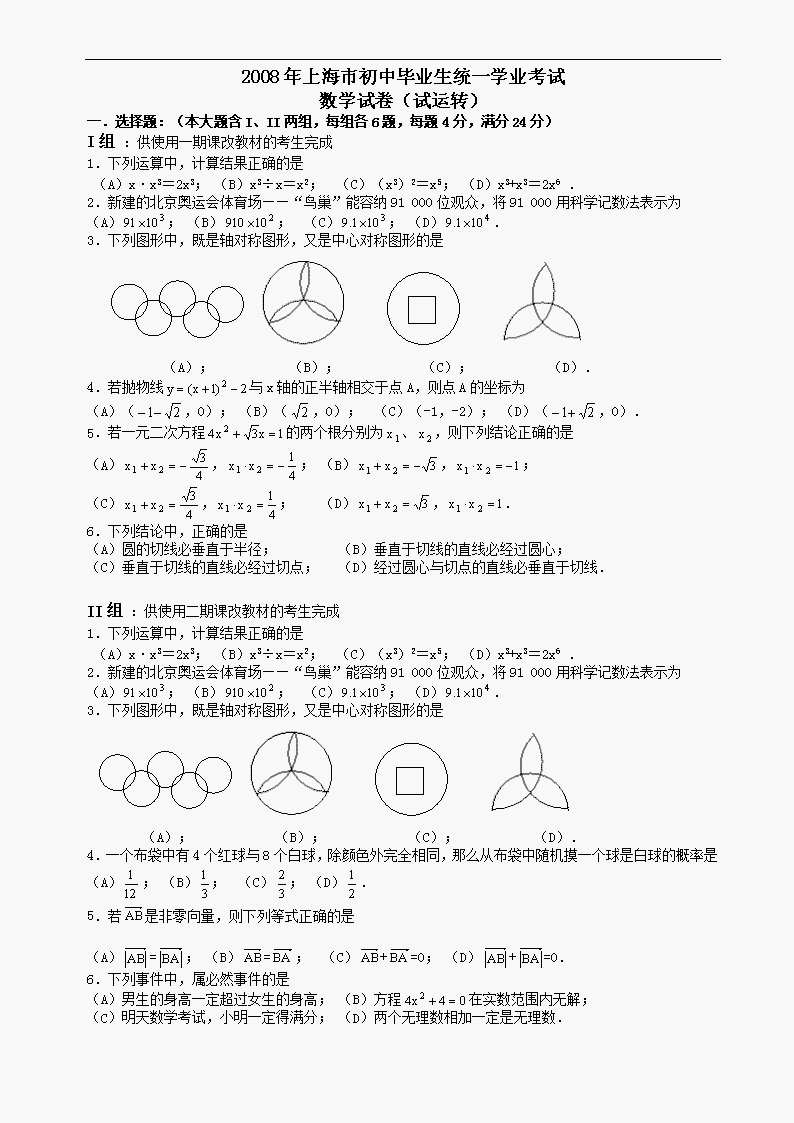
‎2008年上海市初中毕业生统一学业考试 数学试卷（试运转）‎ 一．选择题：（本大题含I、II两组，每组各6题，每题4分，满分24分）‎ I组 ：供使用一期课改教材的考生完成 ‎ ‎1．下列运算中，计算结果正确的是 ‎ （A）x·x3＝2x3； （B）x3÷x＝x2； （C）（x3）2＝x5； （D）x3+x3＝2x6 ． ‎ ‎2．新建的北京奥运会体育场——“鸟巢”能容纳91 000位观众，将91 000用科学记数法表示为 ‎（A）； （B）； （C）； （D）．‎ ‎3．下列图形中，既是轴对称图形，又是中心对称图形的是 ‎（A）； （B）； （C）； （D）．‎ ‎4．若抛物线与x轴的正半轴相交于点A，则点A的坐标为 ‎（A）（，0）； （B）（，0）； （C）（-1，-2）； （D）（，0）．‎ ‎5．若一元二次方程的两个根分别为、，则下列结论正确的是 ‎（A），； （B），； ‎ ‎（C），； （D），．‎ ‎6．下列结论中，正确的是 ‎（A）圆的切线必垂直于半径； （B）垂直于切线的直线必经过圆心； ‎ ‎（C）垂直于切线的直线必经过切点； （D）经过圆心与切点的直线必垂直于切线．‎ II组 ：供使用二期课改教材的考生完成 ‎1．下列运算中，计算结果正确的是 ‎ （A）x·x3＝2x3； （B）x3÷x＝x2； （C）（x3）2＝x5； （D）x3+x3＝2x6 ． ‎ ‎2．新建的北京奥运会体育场——“鸟巢”能容纳91 000位观众，将91 000用科学记数法表示为 ‎（A）； （B）； （C）； （D）．‎ ‎3．下列图形中，既是轴对称图形，又是中心对称图形的是 ‎（A）； （B）； （C）； （D）．‎ ‎4．一个布袋中有4个红球与8个白球，除颜色外完全相同，那么从布袋中随机摸一个球是白球的概率是 ‎（A）； （B）； （C）； （D）．‎ ‎5．若是非零向量，则下列等式正确的是 ‎ ‎ ‎（A）=； （B）=； （C）+=0； （D）+=0．‎ ‎6．下列事件中，属必然事件的是 ‎（A）男生的身高一定超过女生的身高； （B）方程在实数范围内无解； ‎ ‎（C）明天数学考试，小明一定得满分； （D）两个无理数相加一定是无理数．‎ 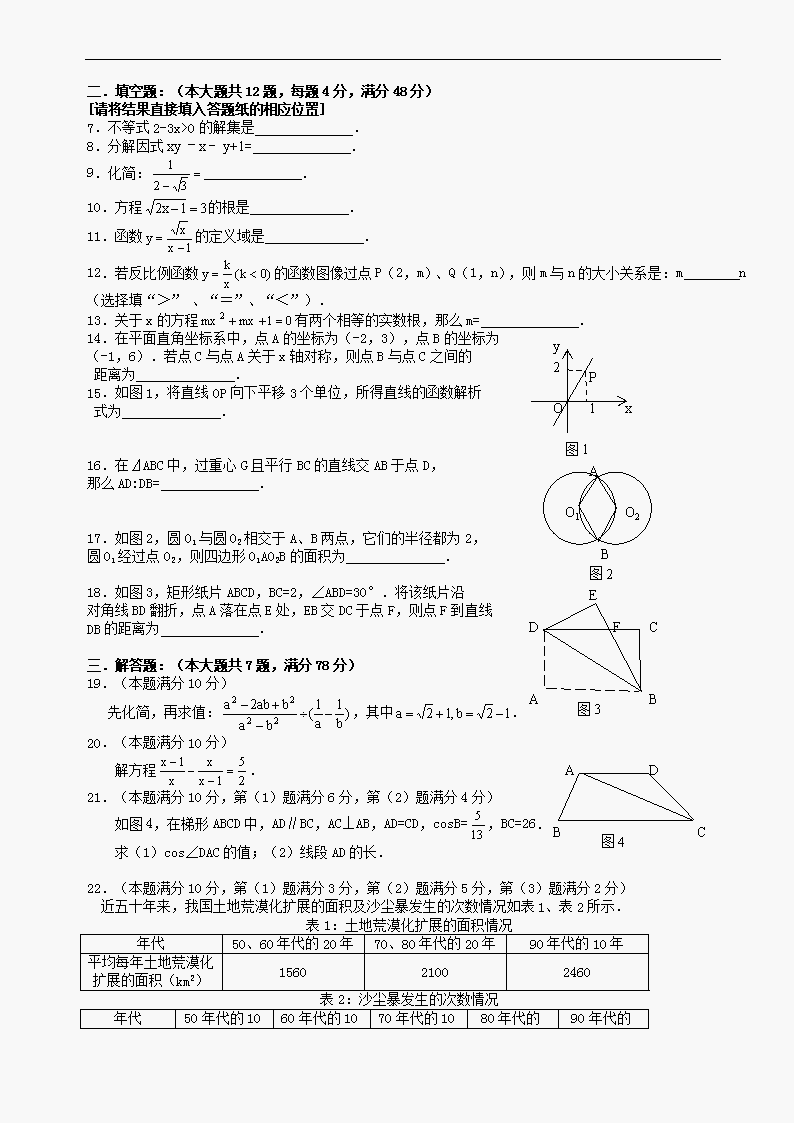二．填空题：（本大题共12题，每题4分，满分48分）‎ ‎[请将结果直接填入答题纸的相应位置]‎ ‎7．不等式2-3x>0的解集是 ．‎ ‎8．分解因式xy –x - y+1= ．‎ ‎9．化简： ．‎ ‎10．方程的根是 ．‎ ‎11．函数的定义域是 ．‎ ‎12．若反比例函数的函数图像过点P（2，m）、Q（1，n），则m与n的大小关系是：m n （选择填“＞” 、“＝”、“＜”）．‎ O P x ‎1‎ ‎2‎ y 图1‎ ‎13．关于x的方程有两个相等的实数根，那么m= ．‎ ‎14．在平面直角坐标系中，点A的坐标为（-2，3），点B的坐标为 ‎（-1，6）．若点C与点A关于x轴对称，则点B与点C之间的 距离为 ．‎ ‎15．如图1，将直线OP向下平移3个单位，所得直线的函数解析 式为 ．‎ O1‎ O2‎ B A 图2‎ ‎16．在⊿ABC中，过重心G且平行BC的直线交AB于点D，‎ 那么AD:DB= ．‎ ‎17．如图2，圆O1与圆O2相交于A、B两点，它们的半径都为2，‎ 圆O1经过点O2，则四边形O1AO2B的面积为 ．‎ F C B A 图3‎ D E ‎18．如图3，矩形纸片ABCD，BC=2，∠ABD=30°．将该纸片沿 对角线BD翻折，点A落在点E处，EB交DC于点F，则点F到直线 DB的距离为 ．‎ 三．解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ ‎ 先化简，再求值：，其中．‎ ‎20．（本题满分10分）‎ C B A 图4‎ D 解方程．‎ ‎21．（本题满分10分，第（1）题满分6分，第（2）题满分4分）‎ 如图4，在梯形ABCD中，AD∥BC，AC⊥AB，AD=CD，cosB=，BC=26．‎ 求（1）cos∠DAC的值；（2）线段AD的长．‎ ‎22．（本题满分10分，第（1）题满分3分，第（2）题满分5分，第（3）题满分2分）‎ 近五十年来，我国土地荒漠化扩展的面积及沙尘暴发生的次数情况如表1、表2所示．‎ 表1：土地荒漠化扩展的面积情况 年代 ‎50、60年代的20年 ‎70、80年代的20年 ‎90年代的10年 平均每年土地荒漠化扩展的面积（km2）‎ ‎1560‎ ‎2100‎ ‎2460‎ 表2：沙尘暴发生的次数情况 年代 ‎50年代的10年 ‎60年代的10年 ‎70年代的10年 ‎80年代的10年 ‎90年代的10年 每十年沙尘暴发生次数 ‎5‎ ‎8‎ ‎13‎ ‎14‎ ‎23‎ ‎50年代 ‎60年代 ‎70年代 ‎80年代 ‎90年代 ‎25‎ ‎20‎ ‎15‎ ‎10‎ ‎5‎ 次数 年代 图5‎ ‎（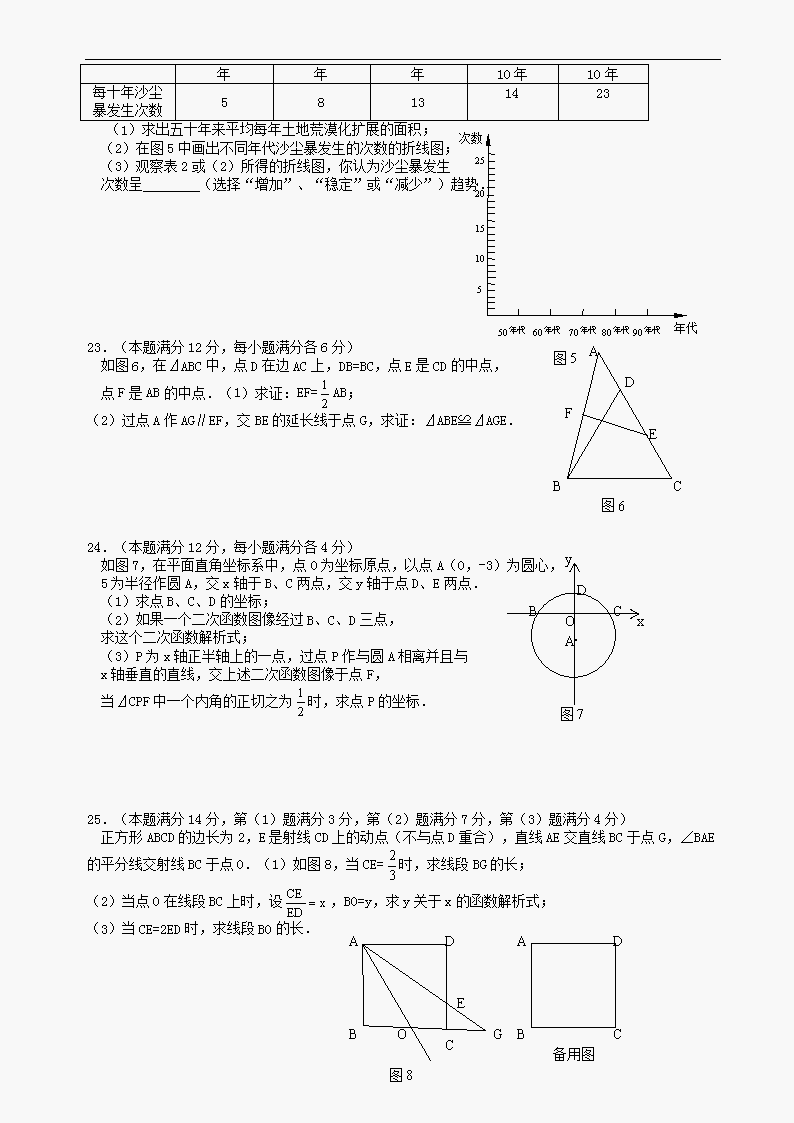1）求出五十年来平均每年土地荒漠化扩展的面积；‎ ‎（2）在图5中画出不同年代沙尘暴发生的次数的折线图；‎ ‎（3）观察表2或（2）所得的折线图，你认为沙尘暴发生 次数呈 （选择“增加”、“稳定”或“减少”）趋势．‎ A B F E D C 图6‎ ‎23．（本题满分12分，每小题满分各6分）‎ 如图6，在⊿ABC中，点D在边AC上，DB=BC，点E是CD的中点，‎ 点F是AB的中点．（1）求证：EF=AB；‎ ‎（2）过点A作AG∥EF，交BE的延长线于点G，求证：⊿ABE≌⊿AGE．‎ 图7‎ O D x C A.‎ y B ‎24．（本题满分12分，每小题满分各4分）‎ 如图7，在平面直角坐标系中，点O为坐标原点，以点A（0，-3）为圆心，‎ ‎5为半径作圆A，交x轴于B、C两点，交y轴于点D、E两点．‎ ‎（1）求点B、C、D的坐标；‎ ‎（2）如果一个二次函数图像经过B、C、D三点，‎ 求这个二次函数解析式；‎ ‎（3）P为x轴正半轴上的一点，过点P作与圆A相离并且与 x轴垂直的直线，交上述二次函数图像于点F，‎ 当⊿CPF中一个内角的正切之为时，求点P的坐标． ‎ ‎25．（本题满分14分，第（1）题满分3分，第（2）题满分7分，第（3）题满分4分）‎ 正方形ABCD的边长为2，E是射线CD上的动点（不与点D重合），直线AE交直线BC于点G，∠BAE的平分线交射线BC于点O．（1）如图8，当CE=时，求线段BG的长；‎ ‎（2）当点O在线段BC上时，设，BO=y，求y关于x的函数解析式；‎ 备用图 A B C D A D B G E C 图8‎ O ‎（3）当CE=2ED时，求线段BO的长．‎ ‎2008年上海市初中毕业生统一学业考试 数学模拟卷答案要点与评分标准 说明：‎ 1． 解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答中评分标准相应评分；‎ 2． 第一、二大题若无特别说明，每题评分只有满分或零分；‎ 3． 第三大题中各题右端所注分数，表示考生正确做对这一步应得分数；‎ 4． 评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅．如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定后继部分的给分，但原则上不超过后继部分应得分数的一半；‎ 5． 评分时，给分或扣分均以1分为基本单位 一．选择题：（本大题含I、II两组，每组各6题，满分24分）‎ I组 1、B； 2、D； 3、C; 4、D; 5、A; 6、D．‎ II组 1、B； 2、D； 3、C; 4、C; 5、A; 6、B．‎ 二．填空题：（本大题共12题，满分48分）‎ ‎7、; 8、； 9、； 10、；‎ ‎11、 且； 12、； 13、4； 14、； ‎ ‎15、； 16、(或2)； 17、； 18、.‎ 三．解答题：（本大题共7题，满分78分）‎ ‎19．解：原式＝ －－－－－－－－－－－－－－－－－－－－(3分)‎ ‎ －－－－－－－－－－－－－－－－－－－－－－－ (2分)‎ ‎ ，－－－－－－－－－－－－－－－－－－－－－－－－－－－(2分)‎ ‎ 当时，原式＝－－－－－－－－－－－－－－(3分)‎ ‎20．解: [方法一]设，－－－－－－－－－－－－－－－－－－－－－－－(2分)‎ ‎ 则原方程化为， 整理得， －－－－－－－－－－ (2分)‎ ‎∴， ；－－－－－－－－－－－－－－－－－－－－－－－－－(2分)‎ 当时， ， 得 ，－－－－－－－－－－－－－－－－ (1分)‎ 当时， 得 ，－－－－－－－－－－－－－－－－－ (1分)‎ ‎ 经检验 ，是原方程的根；　－－－－－－－－－－－－－－－－(2分)‎ ‎ [方法二]去分母得 ，　－－－－－－－－－－－－－－（3分）‎ ‎ 整理得 ，　－－－－－－－－－－－－－－－－－－－－－－－－（2分）‎ ‎ 解得 ，，－－－－－－－－－－－－－－－－－－－－－－－－（3分）‎ ‎ 经检验 ，是原方程的根．－－－－－－－－－－－－－－－－－－（2分）‎ ‎21．解：（1）在Rt△ABC中，，cosB=．－－－－－－－－－ (1分)‎ ‎∵BC=26，∴AB=10． －－－－－－－－－－－－－－－－－－－－－－－－－ (1分)‎ ‎∴AC=．－－－－－－－－－－－－－－－－ (2分)‎ ‎∵AD//BC，∴∠DAC=∠ACB．－－－－－－－－－－－－－－－－－－－－－ (1分)‎ ‎∴cos∠DAC= cos∠ACB=；－－－－－－－－－－－－－－－－－－ (1分)‎ ‎(2)过点D作DE⊥AC，垂足为E．－－－－－－－－－－－－－－－－－－－－(1分)‎ ‎∵AD=DC， AE=EC=．－－－－－－－－－－－－－－－－－－－－(1分)‎ 在Rt△ADE中，cos∠DAE=，－－－－－－－－－－－－－－－－－ (1分)‎ ‎∴AD=13． －－－－－－－－－－－－－－－－－－－－－－－－－－－－－－(1分)‎ ‎50年代 ‎60年代 ‎70年代 ‎80年代 ‎90年代 ‎25‎ ‎20‎ ‎15‎ ‎10‎ ‎5‎ 次数 年代 ‎22．解：（1）平均每年土地荒漠化扩展的面积为 ‎ （2分）‎ ‎（km2）， －－－－－－－－－(1分)‎ ‎ 答：所求平均每年土地荒漠化扩展的面积为‎1956 km2；‎ ‎（2）右图； －－－－－－－－－－－－－ (5分)‎ ‎（3）增加．－－－－－－－－－－－－－－(2分)‎ ‎23．证明：(1) 连结BE，－－－－－－－－－－ (1分)‎ ‎∵DB=BC，点E是CD的中点，∴BE⊥CD．(2分)‎ ‎∵点F是Rt△ABE中斜边上的中点，∴EF=； ‎ ‎－－－－－－－－－－－－ (3分)‎ ‎(2) [方法一]在△中，，，∴．－－－－－－（3分）‎ 在△和△中，,∠AEB=∠AEG=90°，∴△ABE≌△AGE；－－(3分)‎ ‎[方法二]由(1)得，EF=AF，∴∠AEF=∠FAE． －－－－－－－－－－－－－(1分)‎ ‎∵EF//AG，∴∠AEF=∠EAG． －－－－－－－－－－－－－－－－－－－－(1分)‎ ‎∴∠EAF=∠EAG．－－－－－－－－－－－－－－－－－－－－－－－－－－ (1分)‎ ‎∵AE=AE，∠AEB=∠AEG=90°，∴△ABE≌△AGE．－－－－－－－－－－－ (3分)‎ ‎24．解：（1）∵点A的坐标为，线段，∴点D的坐标．－－－－(1分)‎ ‎ 连结AC，在Rt△AOC中，∠AOC=90°，OA=3，AC=5，∴OC=4． －－－－－(1分)‎ ‎ ∴点C的坐标为；－－－－－－－－－－－－－－－－－－－－－－－－(1分)‎ ‎ 同理可得 点B坐标为．－－－－－－－－－－－－－－－－－－－－－ (1分)‎ ‎（2）设所求二次函数的解析式为，‎ 由于该二次函数的图像经过B、C、D三点，则 ‎ －－－－－－－－－－－－－－－－－－－－－－－－（3分）‎ ‎ 解得 ∴所求的二次函数的解析式为；－－－－－－－(1分)‎ ‎（3）设点P坐标为，由题意得，－－－－－－－－－－－－－－－－(1分)‎ 且点F的坐标为，，，‎ ‎∵∠CPF=90°，∴当△CPF中一个内角的正切值为时，‎ ‎①若时，即，解得 ， (舍)；－－－－－－－(1分)‎ ‎②当时， 解得 (舍)，(舍)，－－－－－－－ (1分)‎ 所以所求点P的坐标为(12，0)．－－－－－－－－－－－－－－－－－－－－－ (1分)‎ ‎25．解：（1）在边长为2的正方形中，，得，‎ 又∵，即，∴，得．－－－－－－－－（2分）‎ ‎∵，∴； －－－－－－－－－－－－－－－－－－－－－－－－（1分）‎ ‎（2）当点在线段上时，过点作，垂足为点，‎ ‎∵为的角平分线，，∴．－－－－－－（１分）‎ 在正方形中，，∴．‎ ‎∵，∴．－－－－－－－－－－－－－－－－－－－－－－－（１分）‎ 又∵，，得．－－－－－－－－－－－－－－（１分）‎ ‎∵在Rt△ABG中，，，，‎ ‎∴．‎ ‎∵，∴．－－－－－－－－－－（１分）‎ ‎∵，即，得，；（2分）(1分)‎ ‎（3）当时，‎ ‎①当点在线段上时，即，由（2）得；－－（1分）‎ ‎②当点在线段延长线上时，‎ ‎，，在 Rt△ADE中，．‎ 设交线段于点，∵是的平分线，即，‎ 又∵，∴．∴．‎ ‎∴．∴．－－－－－－－－－－－－－－－（1分）‎ ‎∵，∴，即，得． （2分）‎