福建省2020年中考数学真题试题（B卷，含解析） 26页

福建省2019年中考数学真题试题 一、选择题（本题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．（4.00分）在实数|﹣3|，﹣2，0，π中，最小的数是（　　）‎ A．|﹣3| B．﹣2 C．0 D．π ‎2．（4.00分）某几何体的三视图如图所示，则该几何体是（　　）‎ A．圆柱 B．三棱柱 C．长方体 D．四棱锥 ‎3．（4.00分）下列各组数中，能作为一个三角形三边边长的是（　　）‎ A．1，1，2 B．1，2，4 C．2，3，4 D．2，3，5‎ ‎4．（4.00分）一个n边形的内角和为360°，则n等于（　　）‎ A．3 B．4 C．5 D．6‎ ‎5．（4.00分）如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，则∠ACE等于（　　）‎ A．15° B．30° C．45° D．60°‎ ‎6．（4.00分）投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（　　）‎ A．两枚骰子向上一面的点数之和大于1‎ B．两枚骰子向上一面的点数之和等于1‎ C．两枚骰子向上一面的点数之和大于12‎ 26‎ D．两枚骰子向上一面的点数之和等于12‎ ‎7．（4.00分）已知m=+，则以下对m的估算正确的（　　）‎ A．2＜m＜3 B．3＜m＜4 C．4＜m＜5 D．5＜m＜6‎ ‎8．（4.00分）我国古代数学著作《增删算法统宗》记载”绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托“其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺，竿长y尺，则符合题意的方程组是（　　）‎ A． B．‎ C． D．‎ ‎9．（4.00分）如图，AB是⊙O的直径，BC与⊙O相切于点B，AC交⊙O于点D，若∠ACB=50°，则∠BOD等于（　　）‎ A．40° B．50° C．60° D．80°‎ ‎10．（4.00分）已知关于x的一元二次方程（a+1）x2+2bx+（a+1）=0有两个相等的实数根，下列判断正确的是（　　）‎ A．1一定不是关于x的方程x2+bx+a=0的根 B．0一定不是关于x的方程x2+bx+a=0的根 C．1和﹣1都是关于x的方程x2+bx+a=0的根 D．1和﹣1不都是关于x的方程x2+bx+a=0的根 ‎　‎ 二、填空题：本题共6小题，每小题4分，共24分）‎ ‎11．（4.00分）计算：（）0﹣1=　 　．‎ ‎12．（4.00分）某8种食品所含的热量值分别为：120，134，120，119，126，120，118，124，则这组数据的众数为　 　．‎ 26‎ ‎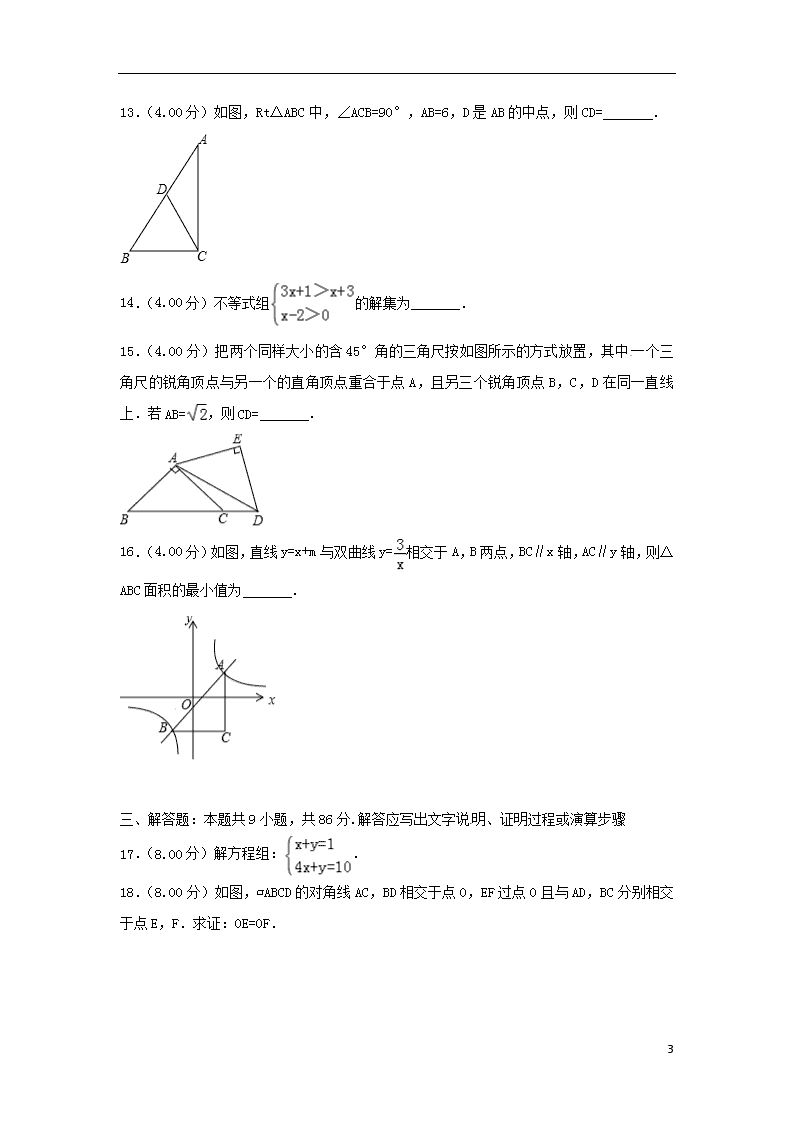13．（4.00分）如图，Rt△ABC中，∠ACB=90°，AB=6，D是AB的中点，则CD=　 　．‎ ‎14．（4.00分）不等式组的解集为　 　．‎ ‎15．（4.00分）把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB=，则CD=　 　．‎ ‎16．（4.00分）如图，直线y=x+m与双曲线y=相交于A，B两点，BC∥x轴，AC∥y轴，则△ABC面积的最小值为　 　．‎ ‎　‎ 三、解答题：本题共9小题，共86分.解答应写出文字说明、证明过程或演算步骤 ‎17．（8.00分）解方程组：．‎ ‎18．（8.00分）如图，▱ABCD的对角线AC，BD相交于点O，EF过点O且与AD，BC分别相交于点E，F．求证：OE=OF．‎ 26‎ ‎19．（8.00分）先化简，再求值：（﹣1）÷，其中m=+1．‎ ‎20．（8.00分）求证：相似三角形对应边上的中线之比等于相似比．‎ 要求：①根据给出的△ABC及线段A'B′，∠A′（∠A′=∠A），以线段A′B′为一边，在给出的图形上用尺规作出△A'B′C′，使得△A'B′C′∽△ABC，不写作法，保留作图痕迹；‎ ‎②在已有的图形上画出一组对应中线，并据此写出已知、求证和证明过程．‎ ‎21．（8.00分）如图，在Rt△ABC中，∠C=90°，AB=10，AC=8．线段AD由线段AB绕点A按逆时针方向旋转90°得到，△EFG由△ABC沿CB方向平移得到，且直线EF过点D．‎ ‎（1）求∠BDF的大小；‎ ‎（2）求CG的长．‎ ‎22．（10.00分）甲、乙两家快递公司揽件员（揽收快件的员工）的日工资方案如下：‎ 甲公司为“基本工资+揽件提成”，其中基本工资为70元/日，每揽收一件提成2元；‎ 乙公司无基本工资，仅以揽件提成计算工资．若当日揽件数不超过40，每件提成4元；若当日搅件数超过 ‎40，超过部分每件多提成2元．‎ 如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图：‎ 26‎ ‎（1）现从今年四月份的30天中随机抽取1天，求这一天甲公司揽件员人均揽件数超过40（不含40）的概率；‎ ‎（2）根据以上信息，以今年四月份的数据为依据，并将各公司揽件员的人均揽件数视为该公司各揽件员的 揽件数，解决以下问题：‎ ‎①估计甲公司各揽件员的日平均件数；‎ ‎②小明拟到甲、乙两家公司中的一家应聘揽件员，如果仅从工资收入的角度考虑，请利用所学的统计知识帮他选择，井说明理由．‎ ‎23．（10.00分）空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长为100米．‎ ‎（1）已知a=20，矩形菜园的一边靠墙，另三边一共用了100米木栏，且围成的矩形菜园面积为450平方米．‎ 如图1，求所利用旧墙AD的长；‎ ‎（2）已知0＜α＜50，且空地足够大，如图2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的矩 形菜园ABCD的面积最大，并求面积的最大值．‎ ‎24．（12.00分）如图，D是△ABC外接圆上的动点，且B，D位于AC的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG⊥‎ 26‎ AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．‎ ‎（1）求证：BG∥CD；‎ ‎（2）设△ABC外接圆的圆心为O，若AB=DH，∠OHD=80°，求∠BDE的大小．‎ ‎25．（14.00分）已知抛物线y=ax2+bx+c过点A（0，2），且抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且B在C的左侧，△ABC有一个内角为60°．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若MN与直线y=﹣2x平行，且M，N位于直线BC的两侧，y1＞y2，解决以下问题：‎ ‎①求证：BC平分∠MBN；‎ ‎②求△MBC外心的纵坐标的取值范围．‎ ‎　‎ 26‎ 参考答案与试题解析 一、选择题（本题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．（4.00分）在实数|﹣3|，﹣2，0，π中，最小的数是（　　）‎ A．|﹣3| B．﹣2 C．0 D．π ‎【分析】直接利用利用绝对值的性质化简，进而比较大小得出答案．‎ ‎【解答】解：在实数|﹣3|，﹣2，0，π中，‎ ‎|﹣3|=3，则﹣2＜0＜|﹣3|＜π，‎ 故最小的数是：﹣2．‎ 故选：B．‎ ‎　‎ ‎2．（4.00分）某几何体的三视图如图所示，则该几何体是（　　）‎ A．圆柱 B．三棱柱 C．长方体 D．四棱锥 ‎【分析】根据常见几何体的三视图逐一判断即可得．‎ ‎【解答】解：A、圆柱的主视图和左视图是矩形，但俯视图是圆，不符合题意；‎ B、三棱柱的主视图和左视图是矩形，但俯视图是三角形，不符合题意；‎ C、长方体的主视图、左视图及俯视图都是矩形，符合题意；‎ D、四棱锥的主视图、左视图都是三角形，而俯视图是四边形，不符合题意；‎ 故选：C．‎ ‎　‎ ‎3．（4.00分）下列各组数中，能作为一个三角形三边边长的是（　　）‎ A．1，1，2 B．1，2，4 C．2，3，4 D．2，3，5‎ ‎【分析】根据三角形中任意两边之和大于第三边，任意两边之差小于第三边．即可求解．‎ ‎【解答】解：A、1+1=2，不满足三边关系，故错误；‎ B、1+2＜4，不满足三边关系，故错误；‎ 26‎ C、2+3＞4，满足三边关系，故正确；‎ D、2+3=5，不满足三边关系，故错误．‎ 故选：C．‎ ‎　‎ ‎4．（4.00分）一个n边形的内角和为360°，则n等于（　　）‎ A．3 B．4 C．5 D．6‎ ‎【分析】n边形的内角和是（n﹣2）•180°，如果已知多边形的内角和，就可以得到一个关于边数的方程，解方程就可以求n．‎ ‎【解答】解：根据n边形的内角和公式，得：‎ ‎（n﹣2）•180=360，‎ 解得n=4．‎ 故选：B．‎ ‎　‎ ‎5．（4.00分）如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，则∠ACE等于（　　）‎ A．15° B．30° C．45° D．60°‎ ‎【分析】先判断出AD是BC的垂直平分线，进而求出∠ECB=45°，即可得出结论．‎ ‎【解答】解：∵等边三角形ABC中，AD⊥BC，‎ ‎∴BD=CD，即：AD是BC的垂直平分线，‎ ‎∵点E在AD上，‎ ‎∴BE=CE，‎ ‎∴∠EBC=∠ECB，‎ ‎∵∠EBC=45°，‎ ‎∴∠ECB=45°，‎ 26‎ ‎∵△ABC是等边三角形，‎ ‎∴∠ACB=60°，‎ ‎∴∠ACE=∠ACB﹣∠ECB=15°，‎ 故选：A．‎ ‎　‎ ‎6．（4.00分）投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（　　）‎ A．两枚骰子向上一面的点数之和大于1‎ B．两枚骰子向上一面的点数之和等于1‎ C．两枚骰子向上一面的点数之和大于12‎ D．两枚骰子向上一面的点数之和等于12‎ ‎【分析】根据事先能肯定它一定会发生的事件称为必然事件，事先能肯定它一定不会发生的事件称为不可能事件，在一定条件下，可能发生也可能不发生的事件，称为随机事件进行分析即可．‎ ‎【解答】解：A、两枚骰子向上一面的点数之和大于1，是必然事件，故此选项错误；‎ B、两枚骰子向上一面的点数之和等于1，是不可能事件，故此选项错误；‎ C、两枚骰子向上一面的点数之和大于12，是不可能事件，故此选项错误；‎ D、两枚骰子向上一面的点数之和等于12，是随机事件，故此选项正确；‎ 故选：D．‎ ‎　‎ ‎7．（4.00分）已知m=+，则以下对m的估算正确的（　　）‎ A．2＜m＜3 B．3＜m＜4 C．4＜m＜5 D．5＜m＜6‎ ‎【分析】直接化简二次根式，得出的取值范围，进而得出答案．‎ ‎【解答】解：∵m=+=2+，‎ ‎1＜＜2，‎ ‎∴3＜m＜4，‎ 故选：B．‎ ‎　‎ 26‎ ‎8．（4.00分）我国古代数学著作《增删算法统宗》记载”绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托“其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺，竿长y尺，则符合题意的方程组是（　　）‎ A． B．‎ C． D．‎ ‎【分析】设索长为x尺，竿子长为y尺，根据“索比竿子长一托，折回索子却量竿，却比竿子短一托”，即可得出关于x、y的二元一次方程组．‎ ‎【解答】解：设索长为x尺，竿子长为y尺，‎ 根据题意得：．‎ 故选：A．‎ ‎　‎ ‎9．（4.00分）如图，AB是⊙O的直径，BC与⊙O相切于点B，AC交⊙O于点D，若∠ACB=50°，则∠BOD等于（　　）‎ A．40° B．50° C．60° D．80°‎ ‎【分析】根据切线的性质得到∠ABC=90°，根据直角三角形的性质求出∠A，根据圆周角定理计算即可．‎ ‎【解答】解：∵BC是⊙O的切线，‎ ‎∴∠ABC=90°，‎ ‎∴∠A=90°﹣∠ACB=40°，‎ 由圆周角定理得，∠BOD=2∠A=80°，‎ 故选：D．‎ ‎　‎ ‎10．（4.00分）已知关于x的一元二次方程（a+1）x2+2bx+（a+‎ 26‎ ‎1）=0有两个相等的实数根，下列判断正确的是（　　）‎ A．1一定不是关于x的方程x2+bx+a=0的根 B．0一定不是关于x的方程x2+bx+a=0的根 C．1和﹣1都是关于x的方程x2+bx+a=0的根 D．1和﹣1不都是关于x的方程x2+bx+a=0的根 ‎【分析】根据方程有两个相等的实数根可得出b=a+1或b=﹣（a+1），当b=a+1时，﹣1是方程x2+bx+a=0的根；当b=﹣（a+1）时，1是方程x2+bx+a=0的根．再结合a+1≠﹣（a+1），可得出1和﹣1不都是关于x的方程x2+bx+a=0的根．‎ ‎【解答】解：∵关于x的一元二次方程（a+1）x2+2bx+（a+1）=0有两个相等的实数根，‎ ‎∴，‎ ‎∴b=a+1或b=﹣（a+1）．‎ 当b=a+1时，有a﹣b+1=0，此时﹣1是方程x2+bx+a=0的根；‎ 当b=﹣（a+1）时，有a+b+1=0，此时1是方程x2+bx+a=0的根．‎ ‎∵a+1≠0，‎ ‎∴a+1≠﹣（a+1），‎ ‎∴1和﹣1不都是关于x的方程x2+bx+a=0的根．‎ 故选：D．‎ ‎　‎ 二、填空题：本题共6小题，每小题4分，共24分）‎ ‎11．（4.00分）计算：（）0﹣1=　0　．‎ ‎【分析】根据零指数幂：a0=1（a≠0）进行计算即可．‎ ‎【解答】解：原式=1﹣1=0，‎ 故答案为：0．‎ ‎　‎ ‎12．（4.00分）某8种食品所含的热量值分别为：120，134，120，119，126，120，118，124，则这组数据的众数为　120　．‎ ‎【分析】根据众数的定义：一组数据中出现次数最多的数据即为众数．‎ ‎【解答】解：∵这组数据中120出现次数最多，有3次，‎ 26‎ ‎∴这组数据的众数为120，‎ 故答案为：120．‎ ‎　‎ ‎13．（4.00分）如图，Rt△ABC中，∠ACB=90°，AB=6，D是AB的中点，则CD=　3　．‎ ‎【分析】根据直角三角形斜边上的中线等于斜边的一半解答．‎ ‎【解答】解：∵∠ACB=90°，D为AB的中点，‎ ‎∴CD=AB=×6=3．‎ 故答案为：3．‎ ‎　‎ ‎14．（4.00分）不等式组的解集为　x＞2　．‎ ‎【分析】先求出每个不等式的解集，再求出不等式组的解集即可．‎ ‎【解答】解：‎ ‎∵解不等式①得：x＞1，‎ 解不等式②得：x＞2，‎ ‎∴不等式组的解集为x＞2，‎ 故答案为：x＞2．‎ ‎　‎ ‎15．（4.00分）把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB=，则CD=　﹣1　．‎ 26‎ ‎【分析】先利用等腰直角三角形的性质求出BC=2，BF=AF=1，再利用勾股定理求出DF，即可得出结论．‎ ‎【解答】解：如图，过点A作AF⊥BC于F，‎ 在Rt△ABC中，∠B=45°，‎ ‎∴BC=AB=2，BF=AF=AB=1，‎ ‎∵两个同样大小的含45°角的三角尺，‎ ‎∴AD=BC=2，‎ 在Rt△ADF中，根据勾股定理得，DF==‎ ‎∴CD=BF+DF﹣BC=1+﹣2=﹣1，‎ 故答案为：﹣1．‎ ‎　‎ ‎16．（4.00分）如图，直线y=x+m与双曲线y=相交于A，B两点，BC∥x轴，AC∥y轴，则△ABC面积的最小值为　6　．‎ ‎【分析】根据双曲线y=过A，B两点，可设A（a，），B（b，），则C（a，）．将y=x+m代入y=，整理得x2+mx﹣3=0，由于直线y=x+m与双曲线y=相交于A，B两点，所以a、b是方程x2+mx﹣3=0的两个根，根据根与系数的关系得出a+b=﹣m，ab=﹣3，那么（a﹣b）‎ 26‎ ‎2=（a+b）2﹣4ab=m2+12．再根据三角形的面积公式得出S△ABC=AC•BC=m2+6，利用二次函数的性质即可求出当m=0时，△ABC的面积有最小值6．‎ ‎【解答】解：设A（a，），B（b，），则C（a，）．‎ 将y=x+m代入y=，得x+m=，‎ 整理，得x2+mx﹣3=0，‎ 则a+b=﹣m，ab=﹣3，‎ ‎∴（a﹣b）2=（a+b）2﹣4ab=m2+12．‎ ‎∵S△ABC=AC•BC ‎=（﹣）（a﹣b）‎ ‎=••（a﹣b）‎ ‎=（a﹣b）2‎ ‎=（m2+12）‎ ‎=m2+6，‎ ‎∴当m=0时，△ABC的面积有最小值6．‎ 故答案为6．‎ ‎　‎ 三、解答题：本题共9小题，共86分.解答应写出文字说明、证明过程或演算步骤 ‎17．（8.00分）解方程组：．‎ ‎【分析】方程组利用加减消元法求出解即可．‎ ‎【解答】解：，‎ ‎②﹣①得：3x=9，‎ 解得：x=3，‎ 把x=3代入①得：y=﹣2，‎ 则方程组的解为．‎ ‎　‎ 26‎ ‎18．（8.00分）如图，▱ABCD的对角线AC，BD相交于点O，EF过点O且与AD，BC分别相交于点E，F．求证：OE=OF．‎ ‎【分析】由四边形ABCD是平行四边形，可得OA=OC，AD∥BC，继而可证得△AOE≌△COF（ASA），则可证得结论．‎ ‎【解答】证明：∵四边形ABCD是平行四边形，‎ ‎∴OA=OC，AD∥BC，‎ ‎∴∠OAE=∠OCF，‎ 在△OAE和△OCF中，‎ ‎，‎ ‎∴△AOE≌△COF（ASA），‎ ‎∴OE=OF．‎ ‎　‎ ‎19．（8.00分）先化简，再求值：（﹣1）÷，其中m=+1．‎ ‎【分析】根据分式的减法和除法可以化简题目中的式子，然后将m的值代入即可解答本题．‎ ‎【解答】解：（﹣1）÷‎ ‎=‎ ‎=‎ ‎=，‎ 当m=+1时，原式=．‎ ‎　‎ ‎20．（8.00分）求证：相似三角形对应边上的中线之比等于相似比．‎ 要求：①根据给出的△ABC及线段A'B′，∠A′（∠A′=∠A），以线段A′B′为一边，在给出的图形上用尺规作出△A'B′C′，使得△A'B′C′∽△ABC，不写作法，保留作图痕迹；‎ 26‎ ‎②在已有的图形上画出一组对应中线，并据此写出已知、求证和证明过程．‎ ‎【分析】（1）作∠A'B'C=∠ABC，即可得到△A'B′C′；‎ ‎（2）依据D是AB的中点，D'是A'B'的中点，即可得到=，根据△ABC∽△A'B'C'，即可得到=，∠A'=∠A，进而得出△A'C'D'∽△ACD，可得==k．‎ ‎【解答】解：（1）如图所示，△A'B′C′即为所求；‎ ‎（2）已知，如图，△ABC∽△A'B'C'，===k，D是AB的中点，D'是A'B'的中点，‎ 求证：=k．‎ 证明：∵D是AB的中点，D'是A'B'的中点，‎ ‎∴AD=AB，A'D'=A'B'，‎ ‎∴==，‎ ‎∵△ABC∽△A'B'C'，‎ ‎∴=，∠A'=∠A，‎ ‎∵=，∠A'=∠A，‎ 26‎ ‎∴△A'C'D'∽△ACD，‎ ‎∴==k．‎ ‎　‎ ‎21．（8.00分）如图，在Rt△ABC中，∠C=90°，AB=10，AC=8．线段AD由线段AB绕点A按逆时针方向旋转90°得到，△EFG由△ABC沿CB方向平移得到，且直线EF过点D．‎ ‎（1）求∠BDF的大小；‎ ‎（2）求CG的长．‎ ‎【分析】（1）由旋转的性质得，AD=AB=10，∠ABD=45°，再由平移的性质即可得出结论；‎ ‎（2）先判断出∠ADE=∠ACB，进而得出△ADE∽△ACB，得出比例式求出AE，即可得出结论．‎ ‎【解答】解：（1）∵线段AD是由线段AB绕点A按逆时针方向旋转90°得到，‎ ‎∴∠DAB=90°，AD=AB=10，‎ ‎∴∠ABD=45°，‎ ‎∵△EFG是△ABC沿CB方向平移得到，‎ ‎∴AB∥EF，‎ ‎∴∠BDF=∠ABD=45°；‎ ‎（2）由平移的性质得，AE∥CG，AB∥EF，‎ ‎∴∠DEA=∠DFC=∠ABC，∠ADE+∠DAB=180°，‎ ‎∵∠DAB=90°，‎ ‎∴∠ADE=90°，‎ ‎∵∠ACB=90°，‎ ‎∴∠ADE=∠ACB，‎ ‎∴△ADE∽△ACB，‎ ‎∴，‎ 26‎ ‎∵AB=8，AB=AD=10，‎ ‎∴AE=12.5，‎ 由平移的性质得，CG=AE=12.5．‎ ‎　‎ ‎22．（10.00分）甲、乙两家快递公司揽件员（揽收快件的员工）的日工资方案如下：‎ 甲公司为“基本工资+揽件提成”，其中基本工资为70元/日，每揽收一件提成2元；‎ 乙公司无基本工资，仅以揽件提成计算工资．若当日揽件数不超过40，每件提成4元；若当日搅件数超过 ‎40，超过部分每件多提成2元．‎ 如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图：‎ ‎（1）现从今年四月份的30天中随机抽取1天，求这一天甲公司揽件员人均揽件数超过40（不含40）的概率；‎ ‎（2）根据以上信息，以今年四月份的数据为依据，并将各公司揽件员的人均揽件数视为该公司各揽件员的 揽件数，解决以下问题：‎ ‎①估计甲公司各揽件员的日平均件数；‎ ‎②小明拟到甲、乙两家公司中的一家应聘揽件员，如果仅从工资收入的角度考虑，请利用所学的统计知识帮他选择，井说明理由．‎ ‎【分析】（1）根据概率公式计算可得；‎ ‎（2）分别根据平均数的定义及其意义解答可得．‎ ‎【解答】解：（1）因为今年四月份甲公司揽件员人均揽件数超过40的有4天，‎ 所以甲公司揽件员人均揽件数超过40（不含40）的概率为=；‎ 26‎ ‎（2）①甲公司各揽件员的日平均件数为=39件；‎ ‎②甲公司揽件员的日平均工资为70+39×2=148元，‎ 乙公司揽件员的日平均工资为 ‎=[40+]×4+×6‎ ‎=159.4元，‎ 因为159.4＞148，‎ 所以仅从工资收入的角度考虑，小明应到乙公司应聘．‎ ‎　‎ ‎23．（10.00分）空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长为100米．‎ ‎（1）已知a=20，矩形菜园的一边靠墙，另三边一共用了100米木栏，且围成的矩形菜园面积为450平方米．‎ 如图1，求所利用旧墙AD的长；‎ ‎（2）已知0＜α＜50，且空地足够大，如图2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的矩 形菜园ABCD的面积最大，并求面积的最大值．‎ ‎【分析】（1）按题意设出AD，表示AB构成方程；‎ ‎（2）根据旧墙长度a和AD长度表示矩形菜园长和宽，注意分类讨论s与菜园边长之间的数量关系．‎ ‎【解答】解：（1）设AD=x米，则AB=‎ 依题意得，‎ 解得x1=10，x2=90‎ ‎∵a=20，且x≤a 26‎ ‎∴x=90舍去 ‎∴利用旧墙AD的长为10米．‎ ‎（2）设AD=x米，矩形ABCD的面积为S平方米 ‎①如果按图一方案围成矩形菜园，依题意 得：‎ S=，0＜x＜a ‎∵0＜α＜50‎ ‎∴x＜a＜50时，S随x的增大而增大 当x=a时，S最大=50a﹣‎ ‎②如按图2方案围成矩形菜园，依题意得 S=，a≤x＜50+‎ 当a＜25+＜50时，即0＜a＜时，‎ 则x=25+时，S最大=（25+）2=‎ 当25+≤a，即时，S随x的增大而减小 ‎∴x=a时，S最大=‎ 综合①②，当0＜a＜时，‎ ‎﹣（）=‎ ‎＞，此时，按图2方案围成矩形菜园面积最大，最大面积为平方米 当时，两种方案围成的矩形菜园面积最大值相等．‎ 26‎ ‎∴当0＜a＜时，围成长和宽均为（25+）米的矩形菜园面积最大，最大面积为平方米；‎ 当时，围成长为a米，宽为（50﹣）米的矩形菜园面积最大，最大面积为（）平方米．‎ ‎　‎ ‎24．（12.00分）如图，D是△ABC外接圆上的动点，且B，D位于AC的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．‎ ‎（1）求证：BG∥CD；‎ ‎（2）设△ABC外接圆的圆心为O，若AB=DH，∠OHD=80°，求∠BDE的大小．‎ ‎【分析】（1）根据等边对等角得：∠PCB=∠PBC，由四点共圆的性质得：∠BAD+∠BCD=180°，从而得：∠BFD=∠PCB=∠PBC，根据平行线的判定得：BC∥DF，可得∠ABC=90°，AC是⊙O的直径，从而得：∠ADC=∠AGB=90°，根据同位角相等可得结论；‎ ‎（2）先证明四边形BCDH是平行四边形，得BC=DH，根据特殊的三角函数值得：∠ACB=60°，∠BAC=30°，所以DH=AC，分两种情况：‎ ‎①当点O在DE的左侧时，如图2，作辅助线，构建直角三角形，由同弧所对的圆周角相等和互余的性质得：∠AMD=∠ABD，则∠ADM=∠BDE，并由DH=OD，可得结论；‎ ‎②当点O在DE的右侧时，如图3，同理作辅助线，同理有∠ADE=∠BDN=20°，∠ODH=20°，得结论．‎ ‎【解答】（1）证明：如图1，∵PC=PB，‎ ‎∴∠PCB=∠PBC，‎ ‎∵四边形ABCD内接于圆，‎ ‎∴∠BAD+∠BCD=180°，‎ 26‎ ‎∵∠BCD+∠PCB=180°，‎ ‎∴∠BAD=∠PCB，‎ ‎∵∠BAD=∠BFD，‎ ‎∴∠BFD=∠PCB=∠PBC，‎ ‎∴BC∥DF，‎ ‎∵DE⊥AB，‎ ‎∴∠DEB=90°，‎ ‎∴∠ABC=90°，‎ ‎∴AC是⊙O的直径，‎ ‎∴∠ADC=90°，‎ ‎∵BG⊥AD，‎ ‎∴∠AGB=90°，‎ ‎∴∠ADC=∠AGB，‎ ‎∴BG∥CD；‎ ‎（2）由（1）得：BC∥DF，BG∥CD，‎ ‎∴四边形BCDH是平行四边形，‎ ‎∴BC=DH，‎ 在Rt△ABC中，∵AB=DH，‎ ‎∴tan∠ACB==，‎ ‎∴∠ACB=60°，∠BAC=30°，‎ ‎∴∠ADB=60°，BC=AC，‎ ‎∴DH=AC，‎ ‎①当点O在DE的左侧时，如图2，作直径DM，连接AM、OH，则∠DAM=90°，‎ ‎∴∠AMD+∠ADM=90°‎ ‎∵DE⊥AB，‎ ‎∴∠BED=90°，‎ ‎∴∠BDE+∠ABD=90°，‎ ‎∵∠AMD=∠ABD，‎ ‎∴∠ADM=∠BDE，‎ 26‎ ‎∵DH=AC，‎ ‎∴DH=OD，‎ ‎∴∠DOH=∠OHD=80°，‎ ‎∴∠ODH=20°‎ ‎∵∠AOB=60°，‎ ‎∴∠ADM+∠BDE=40°，‎ ‎∴∠BDE=∠ADM=20°，‎ ‎②当点O在DE的右侧时，如图3，作直径DN，连接BN，‎ 由①得：∠ADE=∠BDN=20°，∠ODH=20°，‎ ‎∴∠BDE=∠BDN+∠ODH=40°，‎ 综上所述，∠BDE的度数为20°或40°．‎ ‎　‎ 26‎ ‎25．（14.00分）已知抛物线y=ax2+bx+c过点A（0，2），且抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且B在C的左侧，△ABC有一个内角为60°．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若MN与直线y=﹣2x平行，且M，N位于直线BC的两侧，y1＞y2，解决以下问题：‎ ‎①求证：BC平分∠MBN；‎ ‎②求△MBC外心的纵坐标的取值范围．‎ ‎【分析】（1）由A的坐标确定出c的值，根据已知不等式判断出y1﹣y2＜0，可得出抛物线的增减性，确定出抛物线对称轴为y轴，且开口向下，求出b的值，如图1所示，可得三角形ABC为等边三角形，确定出B的坐标，代入抛物线解析式即可；‎ ‎（2）①设出点M（x1，﹣x12+2），N（x2，﹣x22+2），由MN与已知直线平行，得到k值相同，表示出直线MN解析式，进而表示出ME，BE，NF，BF，求出tan∠MBE与tan∠NBF的值相等，进而得到BC为角平分线；‎ ‎②三角形的外心即为三条垂直平分线的交点，得到y轴为BC的垂直平分线，设P为外心，利用勾股定理化简PB2=PM2，确定出△MBC外心的纵坐标的取值范围即可．‎ ‎【解答】解：（1）∵抛物线过点A（0，2），‎ ‎∴c=2，‎ 当x1＜x2＜0时，x1﹣x2＜0，由（x1﹣x2）（y1﹣y2）＞0，得到y1﹣y2＜0，‎ ‎∴当x＜0时，y随x的增大而增大，‎ 同理当x＞0时，y随x的增大而减小，‎ ‎∴抛物线的对称轴为y轴，且开口向下，即b=0，‎ ‎∵以O为圆心，OA为半径的圆与抛物线交于另两点B，C，如图1所示，‎ ‎∴△ABC为等腰三角形，‎ ‎∵△ABC中有一个角为60°，‎ ‎∴△ABC为等边三角形，且OC=OA=2，‎ 设线段BC与y轴的交点为点D，则有BD=CD，且∠OBD=30°，‎ ‎∴BD=OB•cos30°=，OD=OB•sin30°=1，‎ ‎∵B在C的左侧，‎ ‎∴B的坐标为（﹣，﹣1），‎ 26‎ ‎∵B点在抛物线上，且c=2，b=0，‎ ‎∴3a+2=﹣1，‎ 解得：a=﹣1，‎ 则抛物线解析式为y=﹣x2+2；‎ ‎（2）①由（1）知，点M（x1，﹣x12+2），N（x2，﹣x22+2），‎ ‎∵MN与直线y=﹣2x平行，‎ ‎∴设直线MN的解析式为y=﹣2x+m，则有﹣x12+2=﹣2x1+m，即m=﹣x12+2x1+2，‎ ‎∴直线MN解析式为y=﹣2x﹣x12+2x1+2，‎ 把y=﹣2x﹣x12+2x1+2代入y=﹣x2+2，解得：x=x1或x=2﹣x1，‎ ‎∴x2=2﹣x1，即y2=﹣（2﹣x1）2+2=﹣x12+4x1﹣10，‎ 作ME⊥BC，NF⊥BC，垂足为E，F，如图2所示，‎ ‎∵M，N位于直线BC的两侧，且y1＞y2，则y2＜﹣1＜y1≤2，且﹣＜x1＜x2，‎ ‎∴ME=y1﹣（﹣1）=﹣x12+3，BE=x1﹣（﹣）=x1+，NF=﹣1﹣y2=x12﹣4x1+9，BF=x2﹣（﹣）=3﹣x1，‎ 在Rt△BEM中，tan∠MBE===﹣x1，‎ 在Rt△BFN中，tan∠NBF=====﹣x1，‎ ‎∵tan∠MBE=tan∠NBF，‎ ‎∴∠MBE=∠NBF，‎ 则BC平分∠MBN；‎ ‎②∵y轴为BC的垂直平分线，‎ ‎∴设△MBC的外心为P（0，y0），则PB=PM，即PB2=PM2，‎ 根据勾股定理得：3+（y0+1）2=x12+（y0﹣y1）2，‎ ‎∵x12=2﹣y2，‎ ‎∴y02+2y0+4=（2﹣y1）+（y0﹣y1）2，即y0=y1﹣1，‎ 由①得：﹣1＜y1≤2，‎ ‎∴﹣＜y0≤0，‎ 26‎ 则△MBC的外心的纵坐标的取值范围是﹣＜y0≤0．‎ ‎　‎ 26‎