2013中考数学第一轮复习基础训练全集（中） 56页

第一部分　数与代数 第一章　数与式 第1讲　实数83‎ 第2讲　代数式 84‎ 第3讲　整式与分式85‎ 第1课时　整式85‎ 第2课时　因式分解86‎ 第3课时　分式87‎ 第4讲　二次根式89‎ 第二章　方程与不等式 第1讲　方程与方程组90‎ 第1课时　一元一次方程与二元一次方程组90‎ 第2课时　分式方程91‎ 第3课时　一元二次方程93‎ 第2讲　不等式与不等式组94‎ 第三章　函数 第1讲　函数与平面直角坐标系97‎ 第2讲　一次函数99‎ 第3讲　反比例函数101‎ 第4讲　二次函数103‎ 第二部分　空间与图形 第四章　三角形与四边形 第1讲　相交线和平行线106‎ 第2讲　三角形108‎ 第1课时　三角形108‎ 第2课时　等腰三角形与直角三角形110‎ 第3讲　四边形与多边形112‎ 第1课时　多边形与平行四边形112‎ 第2课时　特殊的平行四边形114‎ 第3课时　梯形116‎ 第五章　圆 第1讲　圆的基本性质118‎ 第2讲　与圆有关的位置关系120‎ 第3讲　与圆有关的计算122‎ 第六章　图形与变换 第1讲　图形的轴对称、平移与旋转124‎ 第2讲　视图与投影126‎ 第3讲　尺规作图127‎ 第4讲　图形的相似130‎ 第5讲　解直角三角形132‎ 第三部分　统计与概率 第七章　统计与概率 第1讲　统计135‎ 第2讲　概率137‎ 第四部分　中考专题突破 专题一　归纳与猜想140‎ 专题二　方案与设计141‎ 专题三　阅读理解型问题143‎ 专题四　开放探究题145‎ 专题五　数形结合思想147‎ 基础题强化提高测试 中考数学基础题强化提高测试1149‎ 中考数学基础题强化提高测试2151‎ 中考数学基础题强化提高测试3153‎ 中考数学基础题强化提高测试4155‎ 中考数学基础题强化提高测试5157‎ 中考数学基础题强化提高测试6159‎ ‎2013年中考数学模拟试题(一)161‎ ‎2013年中考数学模拟试题(二)165‎ ‎第五章　圆 第1讲　圆的基本性质 A级　基础题 ‎　　　 　　　　　 　　　　　 　　　‎ ‎1．下列四个命题：‎ ‎①直径是弦；‎ ‎②经过三个点一定可以作圆；‎ ‎③三角形的外心到三角形各顶点的距离都相等；‎ ‎④半径相等的两个半圆是等弧．‎ 其中正确的有(　　)‎ A．4个 B．3个 C．2个 D．1个 ‎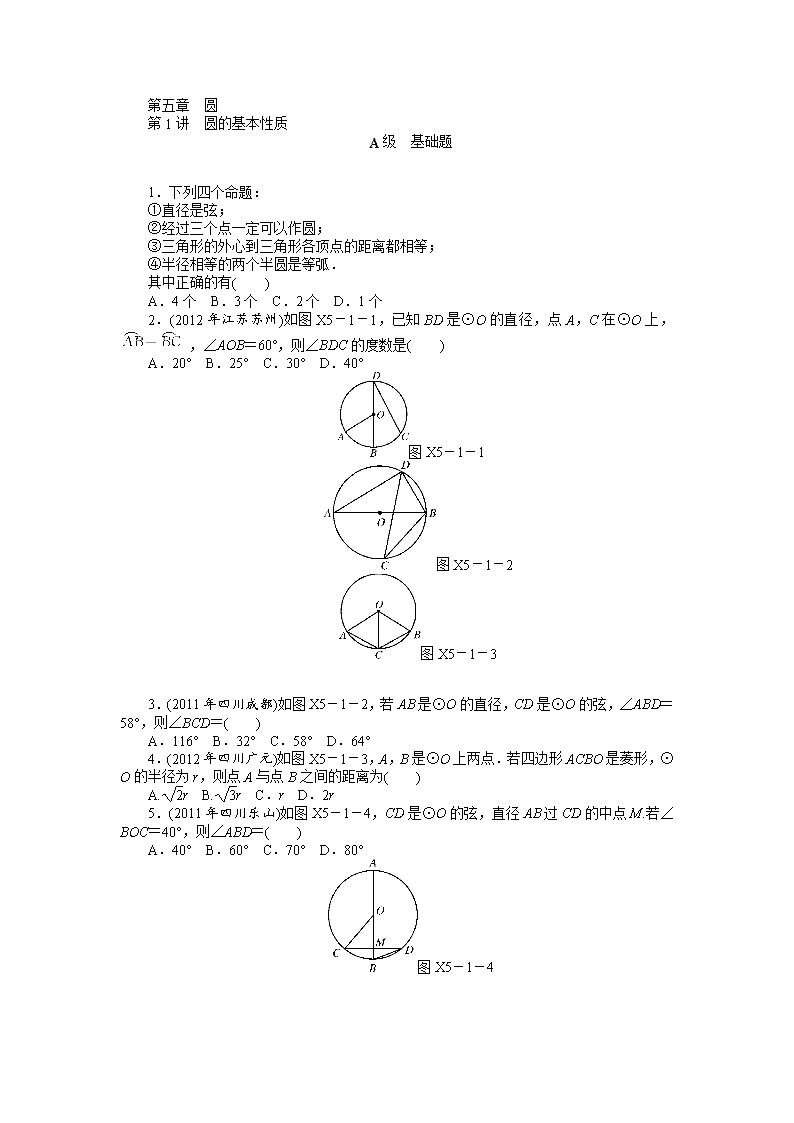2．(2012年江苏苏州)如图X5－1－1，已知BD是⊙O的直径，点A，C在⊙O上， ，∠AOB＝60°，则∠BDC的度数是(　　)‎ A．20° B．25° C．30° D．40°w 图X5－1－1‎ ‎　图X5－1－2‎ ‎　图X5－1－3‎ ‎3．(2011年四川成都)如图X5－1－2，若AB是⊙O的直径，CD是⊙O的弦，∠ABD＝58°，则∠BCD＝(　　)‎ A．116° B．32° C．58° D．64°‎ ‎4．(2012年四川广元)如图X5－1－3，A，B是⊙O上两点．若四边形ACBO是菱形，⊙O的半径为r，则点A与点B之间的距离为(　　)‎ A.r B.r C．r D．2r ‎ ‎5．(2011年四川乐山)如图X5－1－4，CD是⊙O的弦，直径AB过CD的中点M.若∠BOC＝40°，则∠ABD＝(　　)‎ A．40° B．60° C．70° D．80°‎ 图X5－1－4‎ ‎　　　　图X5－1－5‎ ‎6．(2012年山东泰安)如图X5－1－5，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是(　　)‎ A．CM＝DM B.‎ C．∠ACD＝∠ADC D．OM＝MD ‎7．(2011年甘肃兰州)如图X5－1－6，⊙O过点B，C，圆心O在等腰Rt△ABC的内部，∠BAC＝90°，OA＝1，BC＝6，则⊙O的半径为(　　)‎ A．6 B．13 C. D．2 图X5－1－6‎ ‎　图X5－1－7‎ ‎8．(2012年贵州六盘水)当宽为3 cm的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图X5－1－7(单位： cm)，那么该圆的半径为______ cm.‎ ‎9．(2011年福建漳州)如图X5－1－8，AB是⊙O的直径， ，∠COD＝60°.‎ ‎(1)△AOC是等边三角形吗？请说明理由；‎ ‎(2)求证：OC∥BD.‎ 图X5－1－8‎ ‎10．(2011年湖南长沙)如图X5－1－9，在⊙O中，直径AB与弦CD相交于点P，∠CAB＝40°，∠APD＝65°.‎ ‎(1)求∠B的大小；‎ ‎(2)已知圆心O到BD的距离为3，求AD的长. ‎ 图X5－1－9‎ ‎11．(2012年宁夏)如图X5－1－10，在⊙O中，直径AB⊥CD于点E，连接CO并延长交AD于点F，且CF⊥AD.求∠D的度数．‎ 图X5－1－10‎ ‎12．(2012年湖南长沙)如图X5－1－11，A，P，B，C是半径为8的⊙O上的四点，且满足∠BAC＝∠APC＝60°.‎ ‎(1)求证：△ABC是等边三角形；‎ ‎(2)求圆心O到BC的距离OD.‎ 图X5－1－11‎ B级　中等题 ‎13．(2012年安徽)如图X5－1－12，点A，B，C，D在⊙O上，点O在∠D的内部，四边形OABC为平行四边形，则∠OAD＋∠OCD＝________°.‎ 图X5－1－12‎ ‎　　图X5－1－13‎ ‎14．(2011年福建福州)如图X5－1－13，在以O为圆心的两个同心圆中，大圆的弦AB切小圆于点C若∠AOB＝120°，则大圆半径R与小圆半径r之间满足(　　)‎ A．R＝r B．R＝3r C．R＝2r D．R＝2 r X|k | B| 1 . c |O |m ‎15．(2011年云南曲靖)如图X5－1－14，点A，B，C，D都在⊙O上，OC⊥AB，∠ADC＝30°.‎ ‎(1)求∠BOC的度数；‎ ‎(2)求证：四边形AOBC是菱形．‎ 图X5－1－14‎ C级　拔尖题 ‎16．(2011年江苏南京)如图X5－1－15，在平面直角坐标系中，⊙P的圆心是(2，a)(a＞2)，半径为2，函数y＝x的图象被⊙P截得的弦AB的长为2 ，则a的值是(　　)‎ 图X5－1－15‎ A．2 B．2＋ C．2 D．2＋ ‎17．(2011年上海)如图X5－1－16，点C，D分别在扇形AOB的半径OA，OB的延长线上，且OA＝3，AC＝2，CD平行于AB，并与弧AB相交于点M，N.‎ ‎(1)求线段OD的长；‎ ‎(2)若tan∠C＝，求弦MN的长．‎ 图X5－1－16‎ ‎18．(2012年上海)如图X5－1－17，在半径为2的扇形AOB中，∠AOB＝90°，点C是弧AB上的一个动点(不与点A，B重合)，OD⊥BC，OE⊥AC，垂足分别为D，E.‎ ‎(1)当BC＝1时，求线段OD的长；‎ ‎(2)在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；‎ ‎(3)设BD＝x，△DOE的面积为y，求y关于x的函数关系式，并写出它的定义域．‎ 图X5－1－17‎ 第2讲　与圆有关的位置关系 A级　基础题 ‎　 　　　　　 　　　　　 　　　‎ ‎1．若⊙O的半径为4 cm，点A到圆心O的距离为3 cm，那么点A与⊙O的位置关系是(　　)‎ A．点A在圆内 B．点A在圆上 C．点A在圆外 D．不能确定 ‎2．(2012年江苏无锡)已知⊙O的半径为2，直线l上有一点P满足PO＝2，则直线l与⊙O的位置关系是(　　)‎ A．相切 B．相离 C．相离或相切 D．相切或相交 ‎3．(2012年湖南衡阳)已知⊙O的直径为12 cm，圆心O到直线l的距离为5 cm，则直线l与⊙O的交点个数为(　　)‎ A．0 B．1 C．2 D．无法确定 ‎4．(2010年浙江温州)如图X5－2－1，在△ABC中，AB＝BC＝2，以AB为直径的⊙O与BC相切于点B，则AC＝(　　)‎ 图X5－2－1‎ A. ‎ B. C．2 ‎ D．2 ‎5．(2010年甘肃兰州)如图X5－2－2，正三角形的内切圆半径为1，那么这个正三角形的边长为(　　)‎ 图X5－2－2‎ A．2 ‎ B．3 ‎ C. ‎ D．2 ‎6．(2012年黑龙江)如图X5－2－3，已知AB是⊙O的一条直径，延长AB至点C，使AC＝3BC，CD与⊙O相切，切点为D，若CD＝3 ，则线段BC＝________.‎ 图X5－2－3‎ ‎　　　图X5－2－4‎ ‎7．(2012年四川广元)平面上有⊙O及一点P，点P到⊙O上一点的距离最长为6 cm，最短为2 cm，则⊙O的半径为____________ cm.‎ ‎8．(2012年江苏扬州)如图X5－2－4，PA，PB是⊙O的切线，切点分别为A，B两点，点C在⊙O上，如果∠ACB＝70°，那么∠P的度数是__________． ‎ ‎9．(2012年湖南株洲)如图X5－2－5，已知AD为⊙O的直径，B为AD延长线上一点，BC与⊙O切于点C，∠A＝30°.‎ 求证：(1)BD＝CD；‎ ‎(2)△AOC≌△CDB.‎ 图X5－2－5‎ ‎10．(2010年广东中山)如图X5－2－6，PA与⊙O相切于点A，弦AB⊥OP，垂足为C，OP与⊙O相交于点D，已知OA＝2，OP＝4.‎ ‎(1)求∠POA的度数；‎ ‎(2)计算弦AB的长．‎ 图X5－2－6‎ B级　中等题 图X5－2－7‎ ‎11．(2012年山东济南)如图X5－2－7，在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，以其三边为直径向三角形外作三个半圆，矩形EFGH的各边分别与半圆相切且平行于AB或BC，则矩形EFGH的周长是______．‎ ‎12．(2012年四川自贡)如图X5－2－8，AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C.‎ ‎(1)若AB＝2，∠P＝30°，求AP的长；‎ ‎(2)若点D为AP的中点，求证：直线CD是⊙O的切线．‎ 图X5－2－8‎ C级　拔尖题 ‎13．如图X5－2－9(1)，一个圆形电动砂轮的半径是20 cm，转轴OA长是40 cm.砂轮未工作时停靠在竖直的档板OM上，边缘与挡板相切于点B.现在要用砂轮切割水平放置的薄铁片(铁片厚度忽略不计，ON是切痕所在的直线)．‎ ‎(1)在图X5－2－9(2)的坐标系中，求点A与点A1的坐标；‎ ‎(2)求砂轮工作前后，转轴OA旋转的角度和圆心A转过的弧长．‎ 注：图X5－2－9(1)是未工作时的示意图，图X5－1－26(2)是工作前后的示意图．‎ 图X5－2－9‎ 选做题 ‎14．(2012年江西)已知，纸片⊙O的半径为2，如图X5－2－10(1)，沿弦AB折叠操作．‎ ‎(1)如图X5－2－10(2)，当折叠后的 经过圆心O时，求的长；‎ ‎(2)如图X5－2－10(3)，当弦AB＝2时，求折叠后 所在圆的圆心O′到弦AB的距离；‎ ‎(3)在图X5－2－10(1)中，再将纸片⊙O沿弦CD折叠操作．‎ ‎①如图X5－2－10(4)，当AB∥CD，折叠后的 与所在圆外切于点P时，设点O到弦AB，CD的距离之和为d，求d的值；‎ ‎②如图X5－2－10(5)，当AB与CD不平行，折叠后的 与所在圆外切于点P时，设点M为AB的中点，点N为CD的中点．试探究四边形OMPN的形状，并证明你的结论．‎ ‎(1)‎ ‎　(2)‎ ‎　(3)‎ ‎(4)‎ ‎　　　(5)‎ 图X5－2－10‎ 第3讲　与圆有关的计算 A级　基础题 ‎　 　　　　　 　　　　　 　　　‎ ‎1．(2012年湖南衡阳)一个圆锥的三视图如图X5－3－1，则此圆锥的底面积为(　　)‎ ‎　　‎ 图X5－3－1‎ A．30π cm2 B．25π cm2 ‎ C．50π cm2 D．100π cm2 ‎ ‎2．(2012年四川自贡)如图X5－3－2，圆锥形冰淇淋盒的母线长是13 cm，高是12 cm，则该圆锥形底面圆的面积是(　　)‎ 图X5－3－2‎ A．10π cm2 ‎ B．25π cm2 ‎ C．60π cm2 ‎ D．65π cm2‎ ‎3．如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”，则半径为2的“等边扇形”的面积为(　　)‎ A．π B．1 C．2 D.π ‎4．(2012年湖南娄底)如图X5－3－3，正方形MNEF的四个顶点在直径为4的大圆上，小圆与正方形各边都相切，AB与CD是大圆的直径，AB⊥CD，CD⊥MN，则图中阴影部分的面积是(　　)‎ A．4π B．3π C．2π D．π 图X5－3－3‎ ‎　　　图X5－3－4‎ ‎5．(2012年福建漳州)如图X5－3－4，一枚直径为4 cm的圆形古钱币沿着直线滚动一周，圆心移动的距离是(　　)‎ A．2π cm B．4π cm C．8π cm D．16π cm 图X5－3－5‎ ‎6．(2012年湖南衡阳)如图X5－3－5，⊙O的半径为6 cm，直线AB是⊙O的切线，切点为B，弦BC∥AO.若∠A＝30°，则劣弧的长为__________cm.‎ ‎7．(2011年内蒙古乌兰察布)已知O为圆锥的顶点，M 为圆锥底面上一点，点P在OM上．一只蜗牛从点P出发，绕圆锥侧面爬行，回到点P时所爬过的最短路线的痕迹如图X5－3－6，若沿OM将圆锥侧面剪开并展开，所得的侧面展开图是(　　)‎ 图X5－3－6‎ ‎　　‎ ‎8．(2012年四川巴中)已知一个圆的半径为5 cm，则它的内接六边形的边长为________．‎ ‎9．(2011年山东聊城)如图X5－3－7，圆锥的底面半径OB为10 cm，它的展开图扇形的半径AB为30 cm，则这个扇形的圆心角α的度数为________．‎ 图X5－3－7‎ ‎10．(2012年浙江舟山)如图X5－3－8，已知⊙O的半径为2，弦AB⊥半径OC，沿AB将弓形ACB翻折，使点C与圆心O重合，则月牙形(图中实线围成的部分)的面积是__________．‎ 图X5－3－8‎ ‎　图X5－3－9‎ ‎11．(2011年江苏宿迁)如图X5－3－9，把一个半径为12 cm的圆形硬纸片等分成三个扇形，用其中一个扇形制作成一个圆锥形纸筒的侧面(衔接处无缝隙且不重叠)，则圆锥底面半径是________cm.‎ ‎12．(2011年浙江湖州)如图X5－3－10，已知AB是⊙O的直径，弦CD⊥AB，垂足为E，∠AOC＝60°，OC＝2.‎ ‎(1)求OE和CD的长；‎ ‎(2)求图中阴影部分的面积．‎ 图X5－3－10‎ B级　中等题 ‎13．某花园内有一块五边形的空地如图X5－3－11，为了美化环境，现计划在五边形各顶点为圆心，2 m长为半径的扇形区域(阴影部分)种上花草，那么种上花草的扇形区域总面积是(　　)‎ A．6π m2 B．5π m2 C．4π m2 D．3π m2‎ 图X5－3－11‎ ‎　　　图X5－3－12‎ ‎14．(2012年四川凉山州)如图X5－1－12，在由小正方形构成的网格中，半径为1的⊙O在格点上，则图中阴影部分两个小扇形的面积之和为________________________________________________________________________(结果保留π)．‎ ‎15．(2011年广东深圳)如图X5－3－13(1)，已知在⊙O中，点C为劣弧AB上的中点，连接AC并延长至D，使CD＝CA，连接DB并延长DB交⊙O于点E，连接AE.‎ ‎(1)求证：AE是⊙O的直径；‎ ‎(2)如图X5－3－13(2)，连接EC，⊙O半径为5，AC的长为4，求阴影部分的面积之和(结果保留π与根号)．‎ ‎(1)‎ ‎　　　(2)‎ 图X5－3－13‎ C级　拔尖题 ‎16．(2011年四川广安)如图X5－3－14，圆柱的底面周长为6 cm，AC是底面圆的直径，高BC＝6 cm，点P是母线BC上一点，且PC＝BC.一只蚂蚁从点A出发，沿着圆柱体的表面爬行到点P的最短距离是(　　)‎ 图X5－3－14‎ A. cm ‎ B．5 cm C．3 cm ‎ D．7 cm 选做题 ‎17．(2012年湖南岳阳)如图X5－3－15，在⊙O中，，弦AB与弦AC交于点A，弦CD与AB交于点F，连接BC.‎ ‎(1)求证：AC2＝AB·AF；‎ ‎(2)若⊙O的半径长为2 cm，∠B＝60°，求图中阴影部分的面积．‎ 图X5－3－15‎ 第六章　图形与变换 第1讲　图形的轴对称、平移与旋转 A级　基础题 ‎　 　　　　　 　　　　　 　　　‎ ‎1．下列图形中，是轴对称图形的是(　　)‎ ‎2．(2012年辽宁沈阳)在平面直角坐标系中，点P(－1,2)关于x轴的对称点的坐标为(　　)‎ A．(－1，－2) B．(1，－2) ‎ C．(2，－1) D．(－2,1)‎ ‎3．(2012年浙江义乌)如图X6－1－1，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为(　　)‎ 图X6－1－1‎ A．6‎ B．8‎ C．10‎ D．12‎ ‎4．(2012年贵州遵义)把一张正方形纸片按如图X6－1－2(1)、(2)对折两次后，再按如图X6－1－2(3)挖去一个三角形小孔，则展开后的图形是(　　)‎ 图X6－1－2‎ ‎5．(2012年四川资阳)下列图形：①平行四边形；②菱形；③圆；④梯形；⑤等腰三角形；⑥直角三角形；⑦国旗上的五角星．这些图形中既是轴对称图形又是中心对称图形的有(　　)‎ A．1种 B．2种 C．3种 D．4种 ‎6．(2012年湖北武汉)如图X6－1－3，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F处．若AE＝5，BF＝3，则CD的长是(　　)‎ A．7 B．8 C．9 D．10‎ 图X6－1－3‎ ‎　图X6－1－4‎ ‎　图X6－1－5‎ ‎7．(2012年广西玉林)在平面直角坐标系中，一青蛙从点A(－1,0)处向右跳2个单位长度，再向上跳2个单位长度到点A′处，则点A′的坐标为__________．‎ ‎8．(2012年福建厦门)如图X6－1－4，点D是等边△ABC内的一点，如果△ABD绕点A逆时针旋转后能与△ACE重合，那么旋转了________度．‎ ‎9．(2012年浙江温州)分别以正方形的各边为直径向其内部作半圆得到的图形如图X6－1－5.将该图形绕其中心旋转一个合适的角度后会与原图形重合，则这个旋转角的最小度数是__________ 度．‎ 图X6－1－6‎ ‎10．(2012年湖南岳阳)如图X6－1－6，在Rt△ABC中，∠B＝90°，沿AD折叠，使点B落在斜边AC上，若AB＝3，BC＝4，则BD＝__________.‎ ‎11．(2012年四川凉山州)如图X6－1－7，梯形ABCD是直角梯形．‎ ‎(1)直接写出点A，B，C，D的坐标；‎ ‎(2)画出直角梯形ABCD关于y轴的对称图形，使它与梯形ABCD构成一个等腰梯形；‎ ‎(3)将(2)中的等腰梯形向上平移四个单位长度，画出平移后的图形(不要求写作法)．‎ 图X6－1－7‎ ‎12．(2011年广东珠海)如图X6－1－8，将一个钝角△ABC(其中∠ABC＝120°)绕点B顺时针旋转得△A1BC1，使得点C落在AB的延长线上的点C1处，连接AA1.‎ ‎(1)写出旋转角的度数；‎ ‎(2)求证：∠A1AC＝∠C1.‎ 图X6－1－8‎ B级　中等题 图X6－1－9‎ ‎13．(2012年山东济南)如图X6－1－9，在Rt△ABC中，∠C＝90°，AC＝4，将△ABC沿CB向右平移得到△DEF，若平移距离为2，则四边形ABED的面积等于________．‎ ‎14．(2012年黑龙江大庆)在平面直角坐标系中，O为坐标原点，点A的坐标为(，1)，将OA绕原点按逆时针方向旋转30°得OB，则点B的坐标为(　　)‎ A．(1，) B．(－1，)‎ C．(0,2) D．(2,0)‎ ‎15．(2012年江苏南京)如图X6－1－10，在Rt△ABC中，∠ABC＝90°，点D在BC的延长线上，且BD＝AB，过点B作BE⊥AC，与BD的垂线DE交于点E.‎ ‎(1)求证：△ABC≌△BDE；‎ ‎(2)△BDE可由△ABC旋转得到，利用尺规作出旋转中心O(保留作图痕迹，不写作法)．‎ 图X6－1－10‎ C级　拔尖题 ‎16．(2012年山东济宁)如图X6－1－11，在平面直角坐标系中，有一Rt△ABC，且A(－1,3)，B(－3，－1)，C(－3,3)，已知△A1AC1是由△ABC旋转得到的．‎ ‎(1)请写出旋转中心的坐标是________，旋转角是________度；‎ ‎(2)以(1)中的旋转中心为中心，分别画出△A1AC1顺时针旋转90°、180°的三角形；‎ ‎(3)设Rt△ABC两直角边BC＝a，AC＝b，斜边AB＝c，利用变换前后所形成的图X6－案证明勾股定理．‎ 图X6－1－11‎ 选做题 ‎17．(2011年江苏南通)如图X6－1－12，O为正方形ABCD的中心，分别延长OA，OD到点F，E，使OF＝2OA，OE＝2OD，连接EF.将△EOF绕点O逆时针旋转α角得到△E1OF1(如图X6－1－13)．‎ ‎(1)探究AE1与BF1的数量关系，并给予证明；‎ ‎(2)当α＝30°时，求证：△AOE1为直角三角形．‎ 图X6－1－12‎ ‎　　图X6－1－13‎ 第2讲　视图与投影 A级　基础题 ‎　 　　　　　 　　　　　 　　　‎ ‎1．下列结论正确的是(　　)‎ ‎①物体在阳光照射下，影子的方向是相同的；‎ ‎②物体在任何光线照射下，影子的方向都是相同的；‎ ‎③物体在路灯照射下，影子的方向与路灯的位置有关；‎ ‎④物体在光线照射下，影子的长短仅与物体的长短有关．‎ A．1个 B．2个 C．3个 D．4个 ‎2．(2012年四川资阳)如图X6－2－1是一个正方体被截去一角后得到的几何体，它的俯视图是(　　)‎ 图X6－2－1‎ ‎　‎ ‎3．(2012年江苏宿迁)如图X6－2－2是一个用相同的小立方体搭成的几何体的三视图，则组成这个几何体的小立方体的个数是(　　)‎ 图X6－2－2‎ A．2个 B．3个 C．4个 D．5个 ‎4．(2012年福建厦门)如图X6－2－3是一个立体图形的三视图，则这个立体图形是(　　)‎ 图X6－2－3‎ A．圆锥 B．球 C．圆柱 D．三棱锥 ‎5．(2012年云南)如图X6－2－4是由6个相同的小正方体搭成的一个几何体，则它的俯视图是(　　)‎ 图X6－2－4‎ ‎　‎ ‎6．李刚同学拿一个矩形木框在阳光下摆弄，矩形木框在地面上形成的投影不可能的是(　　)‎ ‎7．(2011年浙江温州)如图X6－2－5所示的物体是由两个紧靠在一起的圆柱体组成，它的主视图是(　　)‎ 图X6－2－5‎ ‎ ‎ ‎8．(2010年浙江杭州)若一个所有棱长相等的三棱柱，它的主视图和俯视图分别是正方形和正三角形，则左视图是(　　)‎ A．矩形 B．正方形 C．菱形 D．正三角形 ‎9．一个几何体的三视图如图X6－2－6，那么这个几何体是(　　)‎ 图X6－2－6‎ ‎　图X6－2－7‎ ‎10．(2012年衢州)长方体的主视图、俯视图如图X6－2－7所示，则其左视图面积为(　　)‎ A．3 B．4 C．12 D．16 ‎ ‎11．(2012年四川自贡)画出如图X6－2－8所示立体图的三视图．‎ 图X6－2－8‎ ‎12．分别画出图X6－2－9中几何体的主视图、左视图和俯视图．‎ 图X6－2－9‎ B级　中等题 ‎13．关于盲区的说法正确的有(　　)‎ ‎①我们把视线看不到的地方称为盲区；‎ ‎②我们上山与下山时视野盲区是相同的；‎ ‎③我们坐车向前行驶，有时会发现一些高大的建筑物会被比它矮的建筑物挡住；‎ ‎④人们常说“站得高，看得远”，说明在高处视野盲区要小，视野范围大．‎ A．1个 B．2个 ‎ C．3个 D．4个 ‎14．若干桶方便面摆放在桌子上，如图X6－2－10所示是它的三视图，则这一堆方便面共有(　　)‎ 图X6－2－10‎ A．6桶 B．7桶 ‎ C．8桶 D．9桶 ‎15．(2012年黑龙江大庆)‎ 用八个同样大小的小立方体粘成一个大立方体如图X6－2－11，得到的几何体的三视图如图X6－2－12.若小明从八个小立方体中取走若干个，剩余的小立方体保持原位置不动，并使得到的新几何体的三视图仍是图X6－2－12，则他取走的小立方体最多可以是________个．‎ 图X6－2－11‎ ‎　　图X6－2－12‎ C级　拔尖题 ‎16．(2011年山东东营)如图X6－2－13，观察由棱长为1的小立方体摆成的图形，寻找规律：如图(1)中： 共有1个小立方体，其中1个看得见，0个看不见；如图(2)中：共有8个小立方体，其中7个看得见，1个看不见；如图(3)中：共有27个小立方体，其中19个看得见，8个看不见；…，则第(6)个图中，看得见的小立方体有________个．‎ 图X6－2－13‎ ‎17．如图X6－2－14，一段街道的两边沿所在直线分别为AB，PQ，并且AB∥PQ，建筑物的一端DE所在的直线MN⊥AB于点M，交PQ于点N，小亮从胜利街的A处，沿着AB方向前进，小明一直站在点P的位置等待小亮．‎ ‎(1)请你画出小亮恰好能看见小明的视线，以及此时小亮所在的位置(用点C标出)；‎ ‎(2)已知MN＝30 m，MD＝12 m，PN＝36 m，求(1)中的点C到胜利街口的距离．‎ 图X6－2－14‎ 第3讲　尺规作图 A级　基础题 ‎　 　　　　　 　　　　　 　　　‎ ‎1．下列各条件中，不能作出唯一三角形的条件是(　　)‎ A．已知两边和夹角 B．已知两边和其中一条边所对的角 C．已知两角和夹边 D．已知两角和其中一角的对边 ‎2．(2011年浙江绍兴)如图X6－3－1，在△ABC中，分别以点A和点B为圆心，大于AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD.若△ADC 的周长为10，AB＝7，则△ABC的周长为(　　)‎ 图X6－3－1‎ A．7　　 ‎ B．14 ‎ C．17　 ‎ D．20‎ ‎3．(2012年河北)如图X6－3－2，点C在∠AOB的OB边上，用尺规作出了CN∥OA，在作图痕迹中，是(　　)‎ 图X6－3－2‎ A．以点C为圆心，OD为半径的弧 ‎ B．以点C为圆心，DM为半径的弧 ‎ C．以点E为圆心，OD为半径的弧 ‎ D．以点E为圆心，DM为半径的弧 ‎4．下列关于作图的语句，正确的是(　　)‎ A．画直线AB＝10厘米 B．画射线OB＝10厘米 ‎ C．已知A，B，C三点，过这三点画一条直线 ‎ D．过直线AB外一点画一条直线和直线AB平行 ‎ ‎5．已知线段AB和CD，如图X6－3－3，求作一线段，使它的长度等于AB＋2CD.‎ 图X6－3－3‎ ‎6．试把如图X6－3－4所示的角四等分(不写作法)．‎ 图X6－3－4‎ ‎7．(2012年广西玉林)已知等腰△ABC的顶角∠A＝36°(如图X6－3－5)．‎ ‎(1)作底角∠ABC的平分线BD，交AC于点D(用尺规作图，不写作法，但保留作图痕迹，然后用墨水笔加墨)；‎ ‎(2)通过计算，说明△ABD和△BDC都是等腰三角形．‎ 图X6－3－5‎ ‎8．(2012年贵州铜仁)某市计划在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A，B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A，B，C的位置如图X6－3－6，请在原图上利用尺规作图作出音乐喷泉M的位置(要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图)．‎ 图X6－3－6‎ ‎9．(2012年山东青岛)如图X6－3－7已知：线段a，c，∠α.‎ 求作：△ABC，使BC＝a，AB＝c，∠ABC＝∠α.‎ 图X6－3－7‎ ‎10．(2012年浙江绍兴)如图X6－3－8，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M.‎ ‎(1)若∠ACD＝114°，求∠MAB的度数；‎ ‎(2)若CN⊥AM，垂足为N，求证：△ACN≌△MCN.‎ 图X6－3－8‎ ‎11．如图X6－3－9，已知△ABC，画它的内切圆⊙O.‎ 图X6－3－9‎ 作法：‎ ‎(1)分别作____________，两平分线交于点O；‎ ‎(2)过点O作____的垂线段，交BC于点D；‎ ‎(3)以点__为圆心，以____的长为半径，画圆，‎ 那么，所画的⊙O就是△ABC的______．‎ ‎12．(2011年山东青岛)如图X6－3－10，已知线段a和h.‎ 求作：△ABC，使得AB＝AC，BC＝a，且BC边上的高AD＝h.‎ 要求：尺规作图，不写作法，保留作图痕迹．‎ 图X6－3－10‎ X k B 1 . c o m B级　中等题 ‎13．如图X6－3－11，画一个等腰△ABC，使得底边BC＝a，它的高AD＝h.‎ 图X6－3－11‎ ‎14．为了推进农村新型合作医疗制度改革，准备在某镇新建一个医疗点P，使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A，B，C不在同一直线上，地理位置如图X6－3－12)，请你用尺规作图的方法确定点P的位置．‎ 要求： 写出已知，求作，不写作法，保留作图痕迹．‎ 解：已知：‎ 求作：‎ 图X6－3－12‎ C级　拔尖题 ‎15．(2012年广西贵港)如图X6－3－13，已知△ABC，且∠ACB＝90°.‎ ‎(1)请用直尺和圆规按要求作图(保留作图痕迹，不写作法和证明)：‎ ‎①以点A为圆心，BC边的长为半径作⊙A；‎ ‎②以点B为顶点，在AB边的下方作∠ABD＝∠BAC.‎ ‎(2)请判断直线BD与⊙A的位置关系(不必证明)．‎ 图X6－3－13‎ ‎16．(2011年甘肃兰州)如图X6－3－14，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A，B，C.‎ ‎(1)请完成如下操作：‎ ‎①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系；②用直尺和圆规画出该圆弧所在圆的圆心D的位置(不用写作法，保留作图痕迹)，并连接AD，CD；‎ ‎(2)请在(1)的基础上，完成下列问题：‎ ‎①写出点的坐标：C__________，D__________；‎ ‎②⊙D的半径＝____________(结果保留根号)；‎ ‎③若扇形ADC是一个圆锥的侧面展开图，则该圆锥的底面面积为________(结果保留π)；‎ ‎④若E(7,0)，试判断直线EC与⊙D的位置关系，并说明你的理由．‎ 图X6－3－14‎ 选做题 ‎17．(2012年四川达州)数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：‎ 作法：如图X6－3－15(1)，①在OA和OB上分别截取OD，OE，使OD＝OE.‎ ‎②分别以D，E为圆心，以大于 DE的长为半径作弧，两弧在∠AOB内交于点C.‎ ‎③作射线OC，则OC就是∠AOB的平分线．‎ 小聪的作法步骤：如图X6－3－15(2)，①利用三角板上的刻度，在OA和OB上分别截取OM，ON，使OM＝ON.‎ ‎②分别过M，N作OM，ON的垂线，交于点P.‎ ‎③作射线OP，则OP为∠AOB的平分线．‎ 小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线．‎ 根据以上情境，解决下列问题：‎ ‎(1)李老师用尺规作角平分线时，用到的三角形全等的判定方法是______；‎ ‎(2)小聪的作法正确吗？请说明理由；‎ ‎(3)请你帮小颖设计用刻度尺作角平分线的方法(要求：作出图形，写出作图步骤，不予证明)．‎ ‎(1)‎ ‎　　　(2)‎ 图X6－3－15‎ 第4讲　图形的相似 A级　基础题 ‎　 　　　　　 　　　　　 　　　‎ ‎1．(2010年广西桂林)如图X6－4－1，已知△ADE与△ABC的相似比为1∶2，则△ADE与△ABC的面积比为(　　)‎ 图X6－4－1‎ A．1∶2‎ B．1∶4‎ C．2∶1‎ D．4∶1‎ ‎2．若两个相似三角形的面积之比为1∶16，则它们的周长之比为(　　)‎ A．1∶2　　　　 B．1∶4　　　　 ‎ C．1∶5　　　 D．1∶16‎ ‎3．下列各组线段(单位：cm)中，是成比例线段的为(　　)‎ A．1,2,3,4　　　 B．1,2,2,4‎ C．3,5,9,13　　　 D．1,2,2,3‎ ‎4．(2011年湖南怀化)如图X6－4－2，在△ABC中，DE∥BC，AD＝5，BD＝10，AE＝3，则CE的值为(　　)‎ 图X6－4－2‎ A．9　　　‎ B．6‎ C．3‎ D．4‎ ‎5．若△ABC∽△DEF，它们的周长分别为6 cm和8 cm，那么下式中一定成立的是(　　)‎ A．3AB＝4DE B．4AC＝3DE C．3∠A＝4∠D D．4(AB＋BC＋AC)＝3(DE＋EF＋DF)‎ ‎6．如果△ABC∽△A′B′C′，BC＝3，B′C′＝1.8，则△A′B′C′与△ABC的相似比为(　　)‎ A．5∶3　 B．3∶2　 C．2∶3　 D．3∶5‎ ‎7．下列说法中：①所有的等腰三角形都相似；②所有的正三角形都相似；③所有的正方形都相似；④所有的矩形都相似．其中说法正确的序号是________________．‎ ‎8．如果两个相似三角形的相似比是3∶5，周长的差为4 cm，那么较小三角形的周长为________cm.‎ ‎9．(2012年湖南株洲)如图X6－4－3，在矩形ABCD中，AB＝6，BC＝8，沿直线MN对折，使A，C重合，直线MN交AC于点O.‎ ‎(1)求证：△COM∽△CBA；‎ ‎(2)求线段OM的长度．‎ 图X6－4－3‎ ‎10．(2011年湖南常德)如图X6－4－4，已知四边形ABCD是平行四边形．‎ ‎(1)求证：△MEF∽△MBA；‎ ‎(2)若AF，BE分别是∠DAB，∠CBA的平分线，求证：DF＝EC.‎ 图X6－4－4‎ ‎11．(2011年广西来宾)如图X6－4－5，在△ABC中，∠ABC＝80°，∠BAC＝40°，AB的垂直平分线分别与AC，AB交于点D，E.‎ ‎(1)用圆规和直尺在图中作出AB的垂直平分线DE，并连接BD；‎ ‎(2)证明：△ABC∽△BDC.‎ 图X6－4－5‎ ‎12．已知如图X6－4－6，在矩形ABCD中，E是BC上一点，F是BC的延长线上一点，且BE＝CF，BD与AE相交于点G.‎ 求证：(1)△ABE≌△DCF；‎ ‎(2)CF·AE＝BF·GE.‎ 图X6－4－6‎ B级　中等题 ‎13．如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3,4和x，那么x的值(　　)‎ A．只有1个　　　 B．可以有2个 C．有2个以上但有限 D．有无数个 ‎14．如图X6－4－7，已知在△ABC中，AD＝DB，∠1＝∠2.求证：△ABC∽△EAD.‎ 图X6－4－7‎ ‎15．如图X6－4－8，在△ABC中，AB＝AC，BD⊥AC于点D，试证明：BC2＝2CD·AC.‎ 图X6－4－8‎ ‎16．如图X6－4－9，大江的同一侧有A，B两个工厂，它们都有垂直于江边的小路AD，BE，长度分别为3千米和2千米，且两条小路之间的距离为5千米．现要在江边建一个供水站向A，B两厂送水，欲使供水管路最短，则供水站应建在距E处多远的位置？‎ 图X6－4－9‎ C级　拔尖题 ‎17．(2011年湖南怀化)如图X6－4－10，△ABC是一张锐角三角形的硬纸片，AD是边BC上的高，BC＝40 cm，AD＝30 cm，从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH，使它的一边EF在BC上，顶点G，H分别在AC，AB上，AD与HG的交点为M.‎ ‎(1)求证：＝；‎ ‎(2)求这个矩形EFGH的周长．‎ 图X6－4－10‎ 选做题 ‎18．(2012年湖南株洲)如图X6－4－11，在△ABC中，∠C＝90°，BC＝5米，AC＝12米．点M在线段CA上，从C向A运动，速度为1米/秒；同时点N在线段AB上，从A向B运动，速度为2米/秒，运动时间为t秒．‎ ‎(1)当t为何值时，∠AMN＝∠ANM?‎ ‎(2)当t为何值时，△AMN的面积最大？并求出这个最大值．‎ 图X6－4－11‎ 第5讲　解直角三角形 A级　基础题 ‎1．已知在Rt△ABC中，∠C＝90°，tanA＝，BC＝8，则AC＝(　　)‎ A．6　　　 B.　　　　 C．10　　　　 D．12‎ ‎2．(2010年黑龙江哈尔滨)在Rt△ABC中，∠C＝90°，∠B＝35°，AB＝7，则BC的长为(　　)‎ A．7sin35° B．7cot35°‎ C．7cos35° D．7tan35°‎ ‎3．(2011年山东东营)河堤横断面如图X6－5－1，堤高BC＝5米，迎水坡AB的坡比是1∶(坡比是坡面的铅直高度BC与水平宽度AC之比)，则AC的长是(　　)‎ A．5 米 B．10米 C．15米 D．10 米 图X6－5－1‎ ‎　　　图X6－5－2‎ ‎4．(2012年山东济南)如图X6－5－2，在8×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为(　　)‎ A. B. C. D．3‎ ‎5．(2011年山东滨州)在等腰△ABC中，∠C＝90°，则tanA＝________.‎ ‎6．在Rt△ABC中，∠C＝90°，BC＝5，AB＝12，sinA＝________.‎ ‎7．(2012年江苏常州)若∠α＝60°，则∠α的余角为________________________________________________________________________，‎ cosa的值为 ________.‎ ‎8．(2011年江苏南通)如图X6－5－3，为了测量河宽AB(假设河的两岸平行)，在点C测得∠ACB＝30°，在点D测得∠ADB＝60°，又CD＝60 m，则河宽AB为____________m(结果保留根号)．‎ 图X6－5－3‎ ‎9．(2011年广东汕头)如图X6－5－4，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路．现新修一条路AC到公路l，小明测量出∠ACD＝30°，∠ABD＝45°，BC＝50 m．请你帮小明计算他家到公路l的距离AD的长度(精确到0.1 m)．‎ ‎(参考数据：≈1.414，≈1.732)‎ 图X6－5－4‎ ‎10．(2011年广东湛江)如图X6－5－5，五一期间，小红到美丽的世界地质公园湖光岩参加社会实践活动，在景点P处测得景点B位于南偏东45°方向，然后沿北偏东60°方向走100米到达景点A，此时测得景点B正好位于景点A的正南方向，求景点A与景点B之间的距离(结果精确到0.1米)．‎ 图X6－5－5‎ ‎11．(2011年甘肃兰州)已知α是锐角，且sin(α＋15°)＝.计算－4cos α－(π－3.14)0＋tan α＋的值．‎ B级　中等题 ‎12．(2011年广东东莞)如图X6－5－6，在直角梯形纸片ABCD中，AD∥BC，∠A＝90°，∠C＝30°.折叠纸片，使BC经过点D，点C落在点E处，BF是折痕，且BF＝CF＝8.‎ 图X6－5－6‎ ‎(1)求∠BDF的度数；‎ ‎(2)求AB的长．‎ ‎13．(2011年安徽)如图X6－5－7，某高速公路建设中需要确定隧道AB的长度．已知在离地面1 500 m高的C处的飞机上，测量人员测得正前方A，B两点处的俯角分别为60°和45°，求隧道AB的长．‎ ‎(参考数据：≈1.73)‎ 图X6－5－7‎ ‎14．在△ABC中，∠C＝90°，若b＋c＝90，∠A－∠B＝30°，解这个直角三角形．‎ ‎15．如图X6－5－8，两座建筑物AB及CD，其中A，C距离为50米，在AB的顶点B处测得CD的顶部D的仰角β＝30°，测得其底部C的俯角α＝60°，求两座建筑物AB及CD的高(精确到0.1米)．‎ 图X6－5－8‎ C级　拔尖题 ‎16．(2011年江苏扬州)如图X6－5－9，是某品牌太阳能热水器的实物图和横断面示意图，已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心，支架CD与水平面AE垂直，AB＝150厘米，∠BAC＝30°，另一根辅助支架DE＝76厘米，∠CED＝60°.‎ ‎(1)求垂直支架CD的长度(结果保留根号)；‎ ‎(2)求水箱半径OD的长度(结果保留三个有效数字)．‎ ‎(参考数据：≈1.41，≈1.73)‎ ‎　　‎ 图X6－5－9‎ ‎17．如图X6－5－10，斜坡AC的坡度(坡比)为1∶，AC＝10米．坡顶有一旗杆BC，旗杆顶端点B与点A有一条彩带AB相连，AB＝14米，试求旗杆BC的高度．‎ 图X6－5－10‎ ‎18．某地区为提高某段海堤的防海潮能力，计划将长96 m的一堤段(原海堤的横断面如图X6－5－11中的梯形ABCD)的堤面加宽1.6 m，背水坡度由原来的1∶1改成1∶2.已知原背水坡长AD＝8.0 m，求完成这一工程所需的土方(保留两个有效数字)．‎ 图X6－5－11‎ 第三部分　统计与概率 第七章　统计与概率 第1讲　统计 A级　基础题 ‎ ‎1．(2011年浙江湖州)数据1,2,3,4,5的平均数是(　　)‎ A．1 B．2 C．3 D．4 ‎ ‎2．体育课上测量立定跳远，其中一组六个人的成绩(单位：米)分别是：1.0,1.3,2.2,2.0,1.8,1.6 ，则这组数据的中位数是(　　)‎ A．2.1 B．1.6 C．1.8 D．1.7‎ ‎3．(2012年江苏徐州)九(2)班“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别为：4,6,8,16,16.这组数据的中位数、众数分别为(　　)‎ A．16,16 B．10,16 ‎ C．8,8 D．8,16‎ ‎4．(2012年江苏无锡)下列调查中，须用普查的是(　　)‎ A．了解某市学生的视力情况 B．了解某市中学生课外阅读的情况 C．了解某市百岁以上老人的健康情况 D．了解某市老年人参加晨练的情况 ‎5．某市6月上旬前5天的最高气温如下(单位：℃)：28,29,31,29,32.对这组数据，下列说法正确的是(　　)‎ A．平均数为30 B．众数为29‎ C．中位数为31 D．无法确定 ‎6．(2011年江苏泰州)为了了解某市八年级学生的肺活量，从中抽样调查了500名学生的肺活量，这项调查中的样本是(　　) ‎ A．某市八年级学生的肺活量 B．从中抽取的500名学生的肺活量 C．从中抽取的500名学生 D．500‎ ‎7．(2011年山东威海)今年体育学业考试增加了跳绳测试项目，下面是测试时记录员记录的一组(10名)同学的测试成绩(单位：个/分钟)：‎ ‎176　180　184　180　170　176　172　164　186　180‎ 该组数据的众数、中位数、平均数分别为(　　)‎ A．180, 180, 178 B．180, 178, 178‎ C．180, 178, 176.8 D．178, 180, 176.8‎ ‎8．(2012年江苏盐城)甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好都是9.4环，方差分别是s＝0.90，s＝1.22，s＝0.43，s＝1.68.在本次射击测试中，成绩最稳定的是(　　)‎ A．甲 B．乙 C．丙 D．丁 ‎9．(2011年广东茂名)若一组数据 1,1,2,3，x的平均数是3，则这组数据的众数是______．‎ ‎10．(2011年山东聊城)今年“世界水日”的主题是“城市用水：应对都市化挑战”．为了解城市居民用水量的情况，小亮随机抽查了阳光小区50户居民去年每户每月的用水量，将得到的数据整理并绘制了这50户居民去年每月总用水量的折线统计图和频数、频率分布表如下：‎ 组　别 频　数 频　率 ‎3506，则小明胜；若x，y满足xy<6，则小红胜．这个游戏规则公平吗？说明理由；若不公平，怎样修改游戏规则才对双方公平？‎ 第四部分　中考专题突破 专题一　归纳与猜想 ‎1．(2012年广东肇庆)观察下列一组数：，，，，…，它们是按一定规律排列的，那么这一组数的第k个数是__________．‎ ‎2．(2012年湖南株洲)一组数据为：x，－2x2,4x2，－8x2，…，观察其规律，推断第n个数据应为________．‎ ‎3．(2011年浙江)如图X1－1，下面是按照一定规律画出的“树形图”，经观察可以发现：图A2比图A1多出2个“树枝”，图A3比图A2多出4个“树枝”，图A4比图A3多出8个“树枝”，…，照此规律，图A6比图A2多出“树枝”的个数为(　　)‎ 图X1－1‎ ‎　 　　　　　 　　　　　 　　　‎ A．28个 B．56个 C．60个 D．124个 ‎4．(2012年山东滨州)求1＋2＋22＋23＋…＋22 012的值，可令S＝1＋2＋22＋23＋…＋22 012，则2S＝2＋22＋23＋24＋…＋22 013，因此，2S－S＝22 013－1.仿照以上推理，计算出1＋5＋52＋53＋…＋52 012的值为(　　)‎ A．52 012－1　 B．52 013－1‎ C. D. ‎5．(2012年贵州毕节)在图X1－2中，每个图案均由边长为1的小正方形按一定的规律堆叠而成，照此规律，第10个图案中共有________个小正方形．‎ 图X1－2‎ ‎6．(2012年山东菏泽)一个自然数的立方，可以分裂成若干个连续奇数的和．例如：23,33和43分别可以按如图X1－3所示的方式“分裂”成2个，3个和4个连续奇数的和，即23＝3＋5；33＝7＋9＋11；43＝13＋15＋17＋19；…；若63也按照此规律来进行“分裂”，则在63“分裂”出的奇数中，最大的奇数是__________．‎ ‎　……‎ 图X1－3‎ ‎7．(2012年湖北恩施)如图X1－4，观察数表： ‎ 图X1－4‎ 根据表中数的排列规律，则B＋D＝________.‎ ‎8．(2012年湖北孝感)2008年北京成功举办了一届举世瞩目的奥运会，今年的奥运会将在英国伦敦举行，奥运会的年份与届数如表所示：‎ 年份 ‎ ‎ 1896‎ ‎ 1900‎ ‎ 1904‎ ‎…‎ ‎ 2012‎ 届数 ‎ 1‎ ‎ 2‎ ‎ 3‎ ‎…‎ ‎ n 表中n的值等于________．‎ ‎9．(2012年河北)某数学活动小组的20位同学站成一列做报数游戏，规则是：从前面第一位同学开始，每位同学依次报自己顺序的倒数加1，第1位同学报，第2位同学报，…，这样得到的20个数的积为________________．‎ ‎10．(2011年内蒙古乌兰察布)将一些半径相同的小圆按如图X1－5所示的规律摆放，请仔细观察，第n个图形有____________个小圆(用含n的代数式表示)．‎ 图X1－5‎ ‎11．(2012年江苏盐城)已知整数a1，a2，a3，a4，…，满足下列条件：a1＝0，a2＝－|a1＋1|，a3＝－|a2＋2|，a4＝－|a3＋3|，…，依此类推，则a2 012的值为(　　)‎ A．－1 005 B．－1 006 ‎ C．－1 007 D．－2 012‎ 12． ‎(2010年浙江嵊州)如图X1－6，平面内有公共端点的六条射线OA，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7，…，则“17”在射线__________上；“2 007”在射线____________上．‎ ‎ 图X1－6‎ ‎13．(2012年云南)观察图X1－7的图形的排列规律(其中▲、■、★分别表示三角形、正方形、五角星)．若第一个图形是三角形，则第18个图形是________(填图形名称)．‎ ‎▲■★■▲★▲■★■▲★▲……‎ 图X1－7‎ ‎14．(2012年广东汕头)观察下列等式：‎ 第1个等式：a1＝＝×；‎ 第2个等式：a2＝＝×；‎ 第3个等式：a3＝＝×；‎ 第4个等式：a4＝＝×；‎ ‎……‎ 请解答下列问题：‎ ‎(1)按以上规律列出第5个等式：a5＝__________＝__________；‎ ‎(2)用含有n的代数式表示第n个等式：an＝________＝________(n为正整数)；‎ ‎(3)求a1＋a2＋a3＋a4＋…＋a100的值．‎ ‎15．(2012年湖南益阳)如图X1－8，观察图形，解答问题：‎ 图X1－8‎ ‎(1)按下表已填写的形式填写表中的空格：‎ 图①‎ 图②‎ 图③‎ 三个角上三个数的积 ‎1×(－1)×2＝－2‎ ‎(－3)×(－4)×(－5)＝－60‎ 三个角上三个数的和 ‎1＋(－1)＋2＝2‎ ‎(－3)＋(－4)＋(－5)＝－12‎ 积与和的商 ‎－2÷2＝－1‎ ‎(2)请用你发现的规律求出图④中的数y和图⑤中的数x.‎ 专题二　方案与设计 ‎　　　 　　　　　 　　　　　 　　　‎ ‎1．现有球迷150人，欲同时租用A，B，C三种型号客车去观看世界杯足球赛，其中A，B，C三种型号客车载客量分别为50人，30人，10人，要求每辆车必须满载，其中A型客车最多租两辆，则球迷们一次性到达赛场的租车方案有(　　)‎ A．3种 B．4种 C．5种 D．6种 ‎2．某学校组织340名师生进行长途考察活动，带有行李170件，计划租用甲、乙两种型号的汽车共10辆．经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李．请问可行的租车方案有(　　)‎ A．2种 B．3种 C．4种 D．5种 ‎3．今年4月份，李大叔收获洋葱30吨，黄瓜13吨．现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售，已知一辆甲种货车可装洋葱4吨和黄瓜1吨，一辆乙种货车可装洋葱和黄瓜各2吨．李大叔租用甲、乙两种货车时的方案有(　　)‎ A．2种 B．3种 C．4种 D．5种 ‎4．(2012年四川泸州)某商店准备购进甲、乙两种商品．已知甲商品每件进价15元，售价20元；乙商品每件进价35元，售价45元．‎ ‎(1)若该商店同时购进甲、乙两种商品共100件，恰好用去2 700元，求购进甲、乙两种商品各多少件？‎ ‎(2)若该商店准备用不超过3 100元购进甲、乙两种商品共100件，且这两种商品全部售出后获利不少于890元，问应该怎样进货，才能使总利润最大，最大利润是多少(利润＝售价－进价)?‎ ‎5．(2011年山东枣庄)某中学为落实市教育局提出的“全员育人，创办特色学校”的会议精神，决心打造“书香校园”，计划用不超过1 900本科技类书籍和1 620本人文类书籍，组建中、小型两类图书角共30个．已知组建一个中型图书角需科技类书籍80本，人文类书籍50本；组建一个小型图书角需科技类书籍30本，人文类书籍60本．‎ ‎(1)符合题意的组建方案有几种？请你帮学校设计出来；‎ ‎(2)若组建一个中型图书角的费用是860元，组建一个小型图书角的费用是570元，试说明(1)中哪种方案费用最低，最低费用是多少元？‎ ‎6．(2012年四川南充)学校6名教师和234名学生集体外出活动，准备租用45座大车或30座小车．若租用1辆大车2辆小车共需租车费1 000元；若租用2辆大车1辆小车共需租车费1 100元．‎ ‎(1)求大、小车每辆的租车费各是多少元？‎ ‎(2)若每辆车上至少要有一名教师，且总租车费用不超过2 300元，求最省钱的租车方案．‎ ‎7．(2012年四川内江)某市为创建省卫生城市，有关部门决定利用现有的4 200盆甲种花卉和3 090盆乙种花卉，搭配A，B两种园艺造型共60个，摆放于入城大道两侧，搭配每个造型所需花卉数量的情况如下表所示：‎ ‎　　‎ 造型　　‎ 花卉 甲 乙 A ‎80‎ ‎40‎ B ‎50‎ ‎70‎ 结合上述信息，解答下列问题：‎ ‎(1)符合题意的搭配方案有哪几种？‎ ‎(2)如果搭配一个A种造型的成本为1 000元，搭配一个B种造型的成本为1 500元，试说明选用哪种方案成本最低？最低成本为多少元？‎ ‎8．(2011年湖北黄石)2011年，号称“千湖之省”的湖北正遭受大旱，为提高学生的环保意识，节约用水，某校数学教师编造了一道应用题：为了保护水资源，某市制定一套节水的管理措施，其中对居民生活用水的收费作如下规定：‎ 月用水量(单位：吨)‎ 单价(单位：元/吨)‎ 不大于10吨部分 ‎1.5‎ 大于10吨且不大于m吨 ‎2‎ 部分(20≤m≤50)‎ 大于m吨部分 ‎3‎ ‎(1)若某用户6月份的用水量为18吨，求其应缴纳的水费；‎ ‎(2)记该用户6月份的用水量为x吨，缴纳水费为y元，试列出y关于x的函数式；‎ ‎(3)若该用户6月份的用水量为40吨，缴纳水费为y元的取值范围为70≤y≤90，试求m的取值范围．‎ ‎9．(2012年江苏连云港)我市某医药公司把一批药品运往外地，现有两种运输方式可供选择．‎ 方式一：使用快递公司的邮车运输，装卸收费400元，另外每千米再加收4元；‎ 方式二：使用铁路运输公司的火车运输，装卸收费820元，另外每千米再加收2元．‎ ‎(1)请分别写出邮车、火车运输的总费用y1，y2(单位：元)与运输路程x(单位：千米)之间的函数关系式；‎ ‎(2)你认为选用哪种运输方式较好，为什么？‎ ‎10．(2012年四川达州)大学生王强积极响应“自主创业”的号召，准备投资销售一种进价为每件40元的小家电．通过试销发现，当销售单价在40元至90元之间(含40元和90元)时，每月的销售量y(单位：件)与销售单价x(单位：元)之间的关系可近似地看作一次函数，其图象如图X2－1.‎ ‎(1)求y与x的函数关系式；‎ ‎(2)设王强每月获得的利润为p(单位：元)，求p与x之间的函数关系式；如果王强想要每月获得2 400元的利润，那么销售单价应定为多少元？‎ 图X2－1‎ 专题三　阅读理解型问题 ‎　　　 　　　　　 　　　　　 　　　‎ ‎1．(2011年山东菏泽)定义一种运算☆，其规则为a☆b＝＋，根据这个规则，计算2☆3的值是(　　)‎ A. B. C．5 D．6‎ ‎2．(2012年贵州六盘水)定义：f(a，b)＝(b，a)，g(m，n)＝(－m，－n)．例如：f(2,3)＝(3,2)，g(－1，－4)＝(1,4)，则g[f(－5,6)]＝(　　)‎ A．(－6,5) B．(－5，－6) ‎ C．(6，－5) D．(－5,6)‎ ‎3．(2012年山东莱芜)对于非零的两个实数a，b，规定a⊕b＝－.若2⊕(2x－1)＝1，则x的值为(　　)‎ A. B. C. D．－ ‎4．(2012年湖南湘潭)文文设计了一个关于实数运算的程序，按此程序，输入一个数后，输出的数比输入的数的平方小1.若输入，则输出的结果为(　　)‎ A．5 B．6 C．7 D．8‎ ‎5．(2012年湖北随州)定义：平面内的直线l1与l2相交于点O，对于该平面内任意一点M，点M到直线l1，l2的距离分别为a，b，则称有序非负实数对(a，b)是点M的“距离坐标”．根据上述定义，距离坐标为(2,3)的点的个数是(　　)‎ A．2个　　　 B．1个　　　 C．4个　　　 D．3个 ‎6．(2012年四川德阳)为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密)．已知加密规则为：明文a，b，c，d对应密文a＋2b,2b＋c,2c＋3d,4d.例如：明文1,2,3,4对应的密文是5,7,18,16.当接收方收到密文14,9,23,28时，则解密得到的明文为(　　)‎ A．4,6,1,7 B．4,1,6,7‎ C．6,4,1,7 D．1,6,4,7‎ ‎7．(2012年湖北荆州)新定义：[a，b]为一次函数y＝ax＋b(a≠0，a，b为实数)的“关联数”．若“关联数”[1，m－2]的一次函数是正比例函数，则关于x的方程＋＝1的解为________．‎ ‎8．小明是一位刻苦学习、勤于思考、勇于创新的学生．一天，他在解方程时，有这样的想法：x2＝－1这个方程在实数范围内无解，如果存在一个数i2＝－1，那么方程x2＝－1可以变为x2＝i2，则x＝±i，从而x＝±i是方程x2＝－1的两个根．小明还发现i具有如下性质：‎ i1＝i，i2＝－1，i3＝i2·i＝(－1)i＝－i，i4＝(i2)2＝(－1)2＝1，i5＝i4·i＝i，i6＝(i2)3＝(－1)2＝1，i7＝i6·i＝－i，i8＝(i4)2＝1，……‎ 请你观察上述等式，根据发现的规律填空：‎ i4n＋1＝________，i4n＋2＝________，i4n＋3＝__________，i4n＝________(n为自然数)．‎ ‎9．(2012年湖南张家界)阅读材料：对于任何实数，我们规定符号的意义是＝ad－bc.例如：＝1×4－2×3＝－2，＝(－2)×5－4×3＝－22.‎ ‎(1)按照这个规定，请你计算的值；‎ ‎(2)按照这个规定，请你计算：当x2－4x＋4＝0时，的值．‎ ‎10．(2011年四川达州)给出下列命题：‎ 命题1：直线y＝x与双曲线y＝有一个交点是(1,1)；X|k | B| 1 . c |O |m 命题2：直线y＝8x与双曲线y＝有一个交点是；‎ 命题3：直线y＝27x与双曲线y＝有一个交点是；‎ 命题4：直线y＝64x与双曲线y＝有一个交点是；‎ ‎……‎ ‎(1)请你阅读、观察上面的命题，猜想出命题n(n为正整数)；‎ ‎(2)请验证你猜想的命题n是真命题．‎ ‎11．先阅读理解下列例题，再按要求完成下列问题．‎ 例题：解一元二次不等式6x2－x－2>0.‎ 解：把6x2－x－2分解因式，‎ 得6x2－x－2＝(3x－2)·(2x＋1)．‎ 又6x2－x－2>0，∴(3x－2)(2x＋1)>0.‎ 由有理数的乘法法则“两数相乘，同号得正”，有：‎ ‎(1)或(2)‎ 解不等式组(1)，得x>，‎ 解不等式组(2)，得x<－.‎ ‎∴(3x－2)(2x＋1)>0的解集为x>或x<－.‎ 因此，一元二次不等式6x2－x－2>0的解集为x>或x<－.‎ ‎(1)求分式不等式<0的解集； X|k | B| 1 . c |O |m ‎(2)通过阅读例题和解答问题(1)，你学会了什么知识和方法？‎ ‎12．(2012年江苏盐城)知识迁移 当a＞0，且x＞0时，因为≥0，所以x－2 ＋≥0，从而x＋≥2 (当x＝时，取等号)．记函数y＝x＋( a＞0，x＞0)．由上述结论，可知：当x＝ 时，该函数有最小值为2 .‎ 直接应用 已知函数y1＝x(x＞0)与函数y2＝(x＞0)，则当x＝________时，y1＋y2取得最小值为________．‎ 变形应用 已知函数y1＝x＋1(x＞－1)与函数y2＝(x＋1)2＋4(x＞－1)，求的最小值，并指出取得该最小值时相应的x的值．‎ 实际应用 ‎ 已知某汽车的一次运输成本包含以下三个部分：一是固定费用，共360元；二是燃油费，每千米1.6元；三是折旧费，它与路程的平方成正比，比例系数为0.001.设汽车一次运输路程为x千米，求当x为多少时，该汽车平均每千米的运输成本最低？最低是多少元？‎ 专题四　开放探究题 ‎　　　 　　　　　 　　　　　 　　　‎ ‎1．在四边形ABCD中，AC与BD相交于点O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下6个说法：‎ ‎①如果再加上条件“AD∥BC”，那么四边形ABCD一定是平行四边形；‎ ‎②如果再加上条件“AB＝CD”，那么四边形ABCD一定是平行四边形；‎ ‎③如果再加上条件“∠DAB＝∠DCB”，那么四边形ABCD一定是平行四边形；‎ ‎④如果再加上条件“BC＝AD”，那么四边形ABCD一定是平行四边形；‎ ‎⑤如果再加上条件“AO＝CO”，那么四边形ABCD一定是平行四边形；‎ ‎⑥如果再加上条件“∠DBA＝∠CAB”，那么四边形ABCD一定是平行四边形．‎ 其中正确的说法有(　　)‎ A．3个　　　　　 B．4个　　　　　 C．5个　　　　　　 D．6个 ‎2．已知，在四边形ABCD中，∠A＝∠B＝∠C＝90°，若添加一个条件即可判定该四边形是正方形，那么这个条件可以是________________．‎ 3． 如图X4－1，D，E分别是△ABC的边AB，AC上的点，则使△AED∽△ABC的条件是______________．‎ ‎ 图X4－1‎ ‎4．一个二元一次方程和一个二元二次方程组成的二元二次方程组的解是和试写出符合要求的方程组__________(填写一个即可)．‎ ‎5．如图X4－2，P是四边形ABCD的边DC上的一个动点，当四边形ABCD满足条件__________时，△PBA的面积始终保持不变(注：只需填上你认为正确的一种条件即可，不必考虑所有可能的情形)．‎ 图X4－2‎ ‎　　　图X4－3‎ ‎6．已知x2－ax－24在整数范围内可以分解因式，则整数a的值是__________(只需填一个)．X k B 1 . c o m ‎7．如图X4－3，已知在等腰△ABC中，∠A＝∠C，底边BC为⊙O的直径，两腰AB，AC分别与⊙O交于点D，E，有下列序号的四个结论：①AD＝AE；②DE∥BC；③∠A＝∠CBE；④BE⊥AC.其中结论正确的序号是________________(注：把你认为正确结论的序号都填上)．‎ ‎8．某初一学生在做作业时，不慎将墨水瓶打翻，使一道作业题只看到如下字样：“甲、乙两地相距40 km，摩托车的速度为45 km/h，运货汽车的速度为35 km/h，‎ ‎？”(涂黑部分表示被墨水覆盖的若干文字)，请将这道作业题补充完整，并列方程解答．‎ ‎9．如图X4－4，已知△ABC内接于⊙O，AE切⊙O于点A，BC∥AE，‎ ‎(1)求证：△ABC是等腰三角形；‎ ‎(2)设AB＝10 cm，BC＝8 cm，点P是射线AE上的点，若以A，P，C为顶点的三角形与△ABC相似，问：这样的点有几个？并求AP的长．‎ 图X4－4‎ ‎10．如图X4－5，已知△ABC内接于⊙O，‎ ‎(1)当点O与AB有怎样的位置关系时，∠ACB是直角？ ‎ ‎(2)在满足(1)的条件下，过点C作直线交AB于点D，当CD与AB有什么样的关系时，△ABC∽△CBD∽△ACD?‎ ‎(3)画出符合(1)、(2)题意的两种图形，使图形的CD＝2 cm.‎ 图X4－5‎ ‎11．(2012年河北)如图X4－6，A(－5,0)，B(－3,0)，点C在y轴的正半轴上，∠CBO＝45°，CD∥AB，∠CDA＝90°.点P从点Q(4,0)出发，沿x轴向左以每秒1个单位的速度运动，运动时间为t秒．‎ ‎(1)求点C的坐标；‎ ‎(2)当∠BCP＝15°时，求t的值；‎ ‎(3)以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边(或边所在直线)相切时，求t的值．‎ 图X4－6‎ ‎12．(2012年山东临沂)如图X4－7，点A在x轴上，OA＝4，将线段OA绕点O 顺时针旋转120°至OB位置．‎ ‎(1)求点B的坐标；‎ ‎(2)求经过点A，O，B的抛物线的解析式；‎ ‎(3)在此抛物线的对称轴上，是否存在点P，使得以点P，O，B为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，说明理由． ‎ 图X4－7‎