北京市2016年中考数学卷 12页

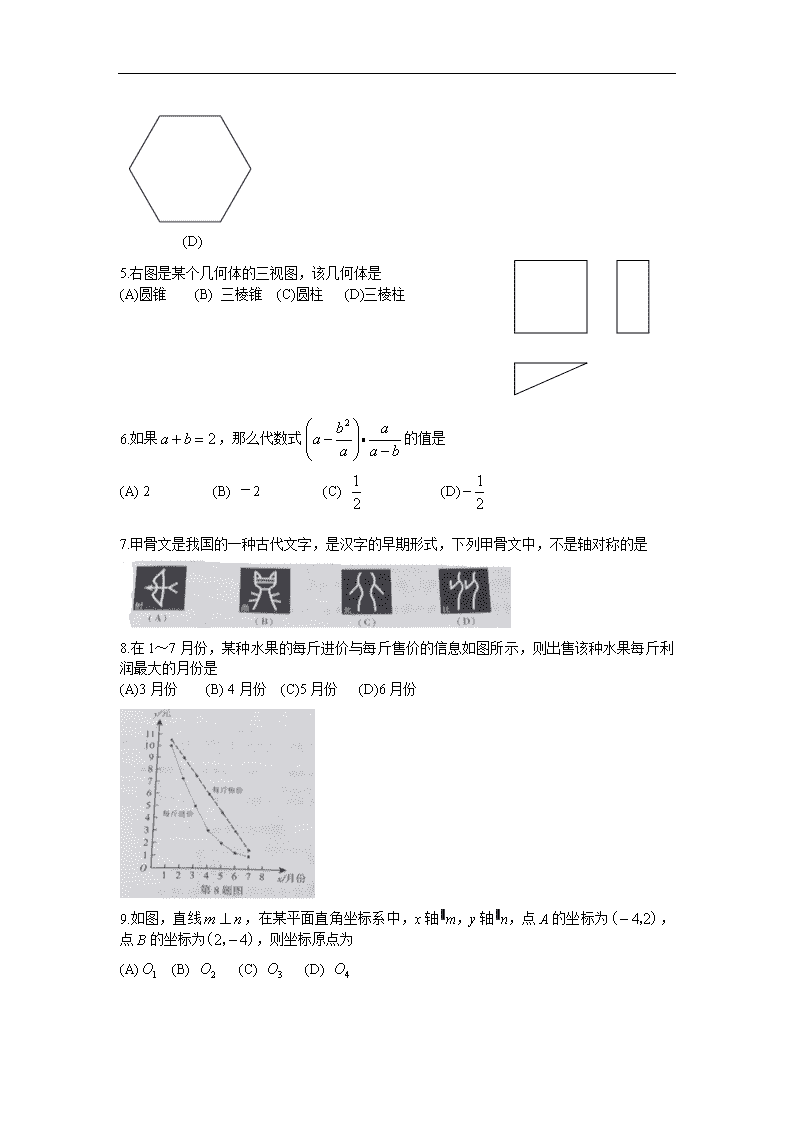
‎(A) (B) (C) (D)‎ 一、选择题（本题共30分，每小题3分）‎ ‎1.如图所示，用量角器度量，可以读出的度数为 ‎(A)45° (B)55° (C)125° (D) 135°‎ ‎2.神舟十号飞船是我国“神舟”系列飞船之一，每小时飞行约28000公里，将28000用科学记数法表示应为 ‎(A)2.8×103 (B) 28×103 (C) 2.8×104 (D)0.28×105‎ ‎3.实数a，b在数轴上的对应点的位置如图所示，则正确的结论是 ‎(A) (B) (C) (D) ‎ ‎4.内角和为540° 的多边形是 ‎(A)‎ ‎(B)‎ ‎ ‎ ‎(C)‎ ‎ ‎ ‎(D)‎ ‎5.右图是某个几何体的三视图，该几何体是 ‎(A)圆锥 (B) 三棱锥 (C)圆柱 (D)三棱柱 ‎6.如果，那么代数式的值是 ‎(A) 2 (B) －2 (C) (D)‎ ‎7.甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是 ‎8.在1～7月份，某种水果的每斤进价与每斤售价的信息如图所示，则出售该种水果每斤利润最大的月份是 ‎(A)3月份 (B) 4月份 (C)5月份 (D)6月份 ‎9.如图，直线，在某平面直角坐标系中，x轴∥m，y轴∥n，点A的坐标为，点B的坐标为，则坐标原点为 ‎(A) (B) (C) (D) ‎ ‎10.为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价，水价分档递增.计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%，15%和5%.为合理确定各档之间的界限，随机抽查了该市5万户居民家庭上一年的年用水量（单位：），绘制了统计图，如图所示.下面有四个推断：‎ ‎①年用水量不超过180的该市居民家庭按第一档水价交费 ‎②年用水量不超过240的该市居民家庭按第三档水价交费 ‎③该市居民家庭年用水量的中位数在150～180之间 ‎④该市居民家庭年用水量的平均数不超过180‎ 其中合理的是 ‎(A) ①③ (B)①④ (C) ②③ (D)②④‎ 二、填空题（本题共18分，每小题3分）‎ ‎11.如果分式有意义，那么x的取值范围是 .‎ ‎12.右图中四边形均为矩形，根据图形，写出一个正确的等式： .‎ ‎13.林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组统计数据：‎ 移植的棵数n ‎1000‎ ‎1500‎ ‎2500‎ ‎4000‎ ‎8000‎ ‎15000‎ ‎20000‎ ‎30000‎ 成活的棵数m ‎865‎ ‎1356‎ ‎2220‎ ‎3500‎ ‎7056‎ ‎13170‎ ‎17580‎ ‎26430‎ 成活的频率 ‎0.865‎ ‎0.904‎ ‎0.888‎ ‎0.875‎ ‎0.882‎ ‎0.878‎ ‎0.879‎ ‎0.881‎ 估计该种幼树在此条件下移植成活的概率为__________.‎ ‎14.如图，小军、小珠之间的距离为2.7m，他们在同一盏路灯小的影长分别为1.8m、1.5m，已知小军、小珠的身高分别为1.8m、1.5m，则路灯的高为__________m ‎15.百子回归图是由1,2,3，...，100无重复排列而成的正方形数表，它是一部数化的澳门简史，如：中央四位“19 99 12 20”标示澳门回归日期，最后一行中间两位“23 50”标示澳门面积，……，同时它也是十阶幻方，其每行10个数之和、每列10个数之和、每条对角线10个数之和均相等，则这个和为________。‎ ‎16.下面是“经过已知直线外一点作这条直线的垂线“的尺规作图过程.‎ 已知：直线l和l外一点P.‎ 求作：直线的垂线，使它经过点P 作法：如图，‎ （1） 在直线l上任意两点A、B;‎ （2） 分别以点A，B为圆心，AP，BP长为半径作弧，两弧相交于点Q；‎ （3） 作直线PQ 所以直线PQ就是所求作的垂线。‎ 请回答：该作图的依据是__________‎ 三，解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28分7分，第9题8分）解答应写出文字说明、演算步骤或证明过程。‎ ‎17.计算：.‎ ‎18.解不等式组：‎ ‎19.如图，四边形ABCD是平行四边形，AE平分，交DC的延长线于点E.‎ 求证：DA=DE ‎20.关于x的一元二次方程 有两个不想等的实数根。‎ ‎（1）求m的取值范围；‎ ‎（2）写出一个满足条件的m的值，并求此时方程的根。‎ ‎21.如图，在平面直角坐标系中，过点的直线与直线：y=2x相交于点.‎ ‎(1)求直线的表达式；‎ ‎（2）过动点且垂直与x轴的直线与，‎ 的交点分别为C，D，当点C位于点D上方时，写出n的取值范围。‎ ‎22.调查作业：了解你所在小区家庭5月份用气量情况。‎ 小天、小东和小芸三位同学住在同一小区，该小区共有300户家庭，每户家庭人数在2~5之间，这300户家庭的平均人数均为3.4。‎ 小天、小东和小芸各自对该小区家庭5月份用气量情况进行了抽样调查，将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3。‎ 表1 抽样调查小区4户家庭5月份用气量统计表（单位：m³）‎ 家庭人数 ‎2‎ ‎3‎ ‎4‎ ‎5‎ 用气量 ‎14‎ ‎19‎ ‎21‎ ‎26‎ 表2 抽样调查小区15户家庭5月份用气量统计表（单位：m³）‎ 家庭人数 ‎2‎ ‎2‎ ‎2‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎4‎ 用气量 ‎10‎ ‎11‎ ‎15‎ ‎13‎ ‎14‎ ‎15‎ ‎15‎ ‎17‎ ‎17‎ ‎18‎ ‎18‎ ‎18‎ ‎18‎ ‎20‎ ‎22‎ 表3 抽样调查小区15户家庭5月份用气量统计表（单位：m³）‎ 家庭人数 ‎2‎ ‎2‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎4‎ ‎4‎ ‎4‎ ‎4‎ ‎5‎ ‎5‎ 用气量 ‎10‎ ‎12‎ ‎13‎ ‎14‎ ‎17‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎20‎ ‎22‎ ‎26‎ ‎31‎ ‎28‎ ‎31‎ 根据以上材料回答问题：‎ 小天、小东和小芸三人中，哪一位同学抽样调查的数据能较好地反映出该小区家庭5月份用气量情况，并简要说明其他两位同学抽样调查的不足之处.‎ ‎23.如图，在四边形ABCD中，∠ABC=90°，AC=AD,M,N分别为AC,CD的中点，连接BM,MN,BN.‎ （1） 求证：BM=MN;‎ （2） 若∠BAD=60°，AC平分∠BAD,AC=2，求BN的长.‎ 24. 阅读下列材料：‎ 北京市正围绕“政治中心、文化中心、国际交往中心、科技创新中心”的定 位，深入实施“人文北京、科技北京、绿色北京”的发展战略，“十二五”期间，‎ 北京市文化创意产业展现了良好的发展基础和巨大的发展潜力，已经成为首都 经济增长的支柱产业。‎ ‎2011年，北京文化创意产业实现增加值1938.6亿元，占地区生产总值的12.1%.‎ ‎2012年，北京市文化创意产业继续呈现平稳发展态势，实现产业增加值2189.2亿元，‎ 占地区生产总值的12.3%，是第三产业中仅次于金融业、批发和零售业的第三大支 柱产业.2013年，北京市文化创意产业实现增加值2406.7亿元，比上年增长9.1%.‎ 文化创意产业作为北京市支柱产业已经排到了第二位.2014年，北京市文化创意产业 实现增加值2794.3亿元，占地区生产总值的13.1%,创历史新高.2015年，北京市文 化创意产业发展总体平稳，实现产业增加值3072.3亿元，占地区生产总值的13.4%.‎ ‎（以上数据来源于北京市统计局）‎ 根据以上材料解答下列问题：‎ （1） 用折线图将2011-2015年北京市文化创意产业实现增加值表示出来，并在图中 标明相应数据；‎ （2） 根据绘制的折线图中提供的信息，预估2016年北京市文化创意产业 实现增加值约________亿元，你的预估理由是_______________.‎ 25. 如图，AB为的直径，F为弦AC的中点，连接OF并延长交于点D，‎ 过点D作的切线，交BA的延长线于点E.‎ （1） 求证：AC∥DE；‎ （2） 连接CD，若OA=AE=a，写出求四边形ACDE面积的思路.‎ 26. 已知y是x 的函数，自变量x的取值范围是x > 0，下表是y与x 的几组对应值.‎ ‎ x ‎ ···‎ ‎ 1‎ ‎ 2 ‎ ‎ 3 ‎ ‎ 5 ‎ ‎ 7‎ ‎ 9‎ ‎···‎ ‎ y ‎ ···‎ ‎ 1.98‎ ‎ 3.95‎ ‎ 2.63‎ ‎ 1.58‎ ‎ 1.13‎ ‎ 0.88‎ ‎···‎ 小腾根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究.‎ 下面是小腾的探究过程，请补充完整：‎ （1） 如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象;‎ （2） 根据画出的函数图象，写出： ‎ ①　 x=4对应的函数值y约为＿＿＿＿；‎ ②　 该函数的一条性质：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿．‎ 27. 在平面直角坐标系中，抛物线与x轴的交点为A，B.‎ ‎ （1）求抛物线的顶点坐标;‎ ‎ （2）横、纵坐标都是整数的点叫整点. ‎ ①　 当m=1时，求线段AB上整点的个数；‎ ②　 若抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）恰有6个整点，结合函数的图象，求m 的取值范围. ‎ ‎28. 在等边中，‎ ‎（1）如图1，P，Q是BC边上两点，AP=AQ，，求的度数；‎ ‎（2）点是边上的两个动点（不与重合），点在点的左侧，且，点关于直线的对称点为，连接 ‎①依题意将图2补全；‎ ‎②小茹通过观察、实验，提出猜想：在点运动的过程中，始终有小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：‎ 想法1：要证，只需证是等边三角形。‎ 想法2：在上取一点，使得，要证，只需证.‎ 想法3：将线段绕点顺时针旋转，得到线段，要证，只需证，.‎ ‎……‎ 请参考上面的想法，帮助小茹证明.（一种方法即可）‎ ‎29. 在平面直角坐标系中，点的坐标为，点的坐标为，且，，若为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点的“相关矩形”.下图为点的“相关矩形”的示意图.‎ （1） 已知点的坐标为（1,0），‎ ‎①若点的坐标为（3,1），求点的“相关矩形”的面积；‎ ‎②点在直线x=3上，若点的“相关矩形”为正方形，求直线的表达式；‎ ‎（2）⊙的半径为，点的坐标为.若在⊙上存在一点，使得点的“相关矩形”为正方形，求的取值范围.‎