中考数学模拟试题汇编 新概念型问题模拟试题与答案 6页

新概念型问题试题 一、选择题 ‎1、如图所示为一个污水净化塔内部，污水从上方入口进入后流经形如等腰直角三角形的净化材枓表面，流向如图中箭头所示，每一次水流流经三角形两腰的机会相同，经过四层净化后流入底部的5个出口中的一个．下列判断：①5个出口的出水量相同；②2号出口的出水量与4号出口的出水量相同；③1，2，3号出水口的出水量之比约为1：4：6；④若净化材枓损耗的速度与流经其表面水的数量成正比，则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的6倍．其中正确的判断有（　　）个．　‎ A．1个B．２个C．３个D．４个 答案：B 二、填空题 ‎1、( 上海市)一个函数的图像关于y轴成轴对称图形时，我们称该函数为“偶函数”．如果二次函数是“偶函数”，该函数的图像与x轴交于点A和点B，顶点为P，那么△ABP的面积是 ▲ ．‎ 答案：8；‎ ‎2、对任意两实数a、b，定义运算“*”如下：. 根据这个规则，则方程＝9的解为________________________．‎ 答案：－3或 ‎3、定义：是不为1的有理数，我们把称为的差倒数．如：2的差倒数是，的差倒数是．已知，是的差倒数，是 的差倒数，是的差倒数，……，依此类推，则= ．‎ 答案：‎ ‎4、现定义运算“★”，对于任意实数a、b，都有a★b＝a2－‎3a+b，如：3★5＝32－3×3+5，若x★2＝6，则实数x的值是__ __．‎ 答案： —1或4 ‎ ‎5、数学家们在研究15、12、10这三个数的倒数时发现：．因此就将具有 这样性质的三个数称之为调和数，若x、y、2 (x>y>2且均为正整数)也是一组调和数．则x、y的值分别为 ▲ ．‎ 答案：6、3‎ ‎6、定义运算“※”的运算法则为: a※b= ，则(2※3) ※3 = ．‎ 答案：2‎ ‎7、现定义运算“★”，对于任意实数a、b，都有a★b＝a2－‎3a+b，如：3★5＝32－3×3+5，若x★2＝6，则实数x的值是__ __．‎ 答案： —1或4 ‎ 三、解答题 ‎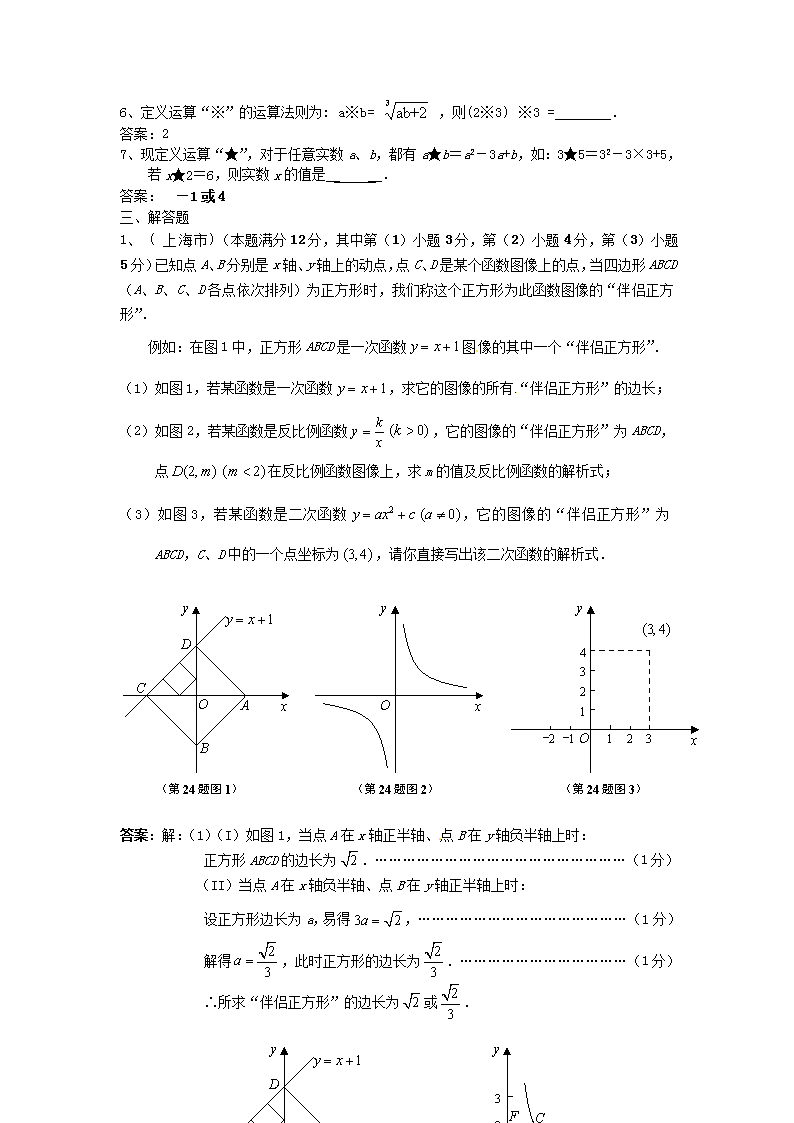1、 ( 上海市)（本题满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分）已知点A、B分别是x轴、y轴上的动点，点C、D是某个函数图像上的点，当四边形ABCD（A、B、C、D各点依次排列）为正方形时，我们称这个正方形为此函数图像的“伴侣正方形”．‎ 例如：在图1中，正方形ABCD是一次函数图像的其中一个“伴侣正方形”．‎ ‎（1）如图1，若某函数是一次函数，求它的图像的所有“伴侣正方形”的边长；‎ ‎（2）如图2，若某函数是反比例函数，它的图像的“伴侣正方形”为ABCD，点在反比例函数图像上，求m的值及反比例函数的解析式；‎ ‎（3）如图3，若某函数是二次函数，它的图像的“伴侣正方形”为ABCD，C、D中的一个点坐标为，请你直接写出该二次函数的解析式．‎ ‎（第24题图3）‎ x y ‎-2‎ ‎-1‎ O ‎1‎ ‎3‎ ‎2‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ x y O B D A C ‎（第24题图1）‎ ‎（第24题图2）‎ x y O 答案：解：（1）（I）如图1，当点A在x轴正半轴、点B在y轴负半轴上时：‎ 正方形ABCD的边长为．………………………………………………（1分）‎ ‎（II）当点A在x轴负半轴、点B在y轴正半轴上时：‎ 设正方形边长为a，易得，………………………………………（1分）‎ 解得，此时正方形的边长为．………………………………（1分）‎ ‎（第24题图2）‎ x y O ‎1‎ ‎3‎ ‎2‎ ‎1‎ ‎3‎ ‎2‎ A B C D E F x y O B D A C ‎（第24题图1）‎ ‎∴所求“伴侣正方形”的边长为或．‎ ‎（2）如图2，作DE⊥x轴，CF⊥y轴，垂足分别为点E、F，‎ 易证△ADE≌△BAO≌△CBF．‎ ‎∵点D的坐标为，，∴DE = OA = BF = m，‎ ‎∴OB = AE = CF = 2 - m．‎ ‎∴OF = BF + OB = 2，∴点C的坐标为．………………………（1分）‎ ‎∴，…………………………………………………………（1分）‎ 解得．…………………………………………………………………（1分）‎ ‎∴反比例函数的解析式为．…………………………………………（1分）‎ ‎（3）或或或．…（5分）‎ 注：第（3）小题写对一个函数解析式得2分，之后每写对一个得1分 ‎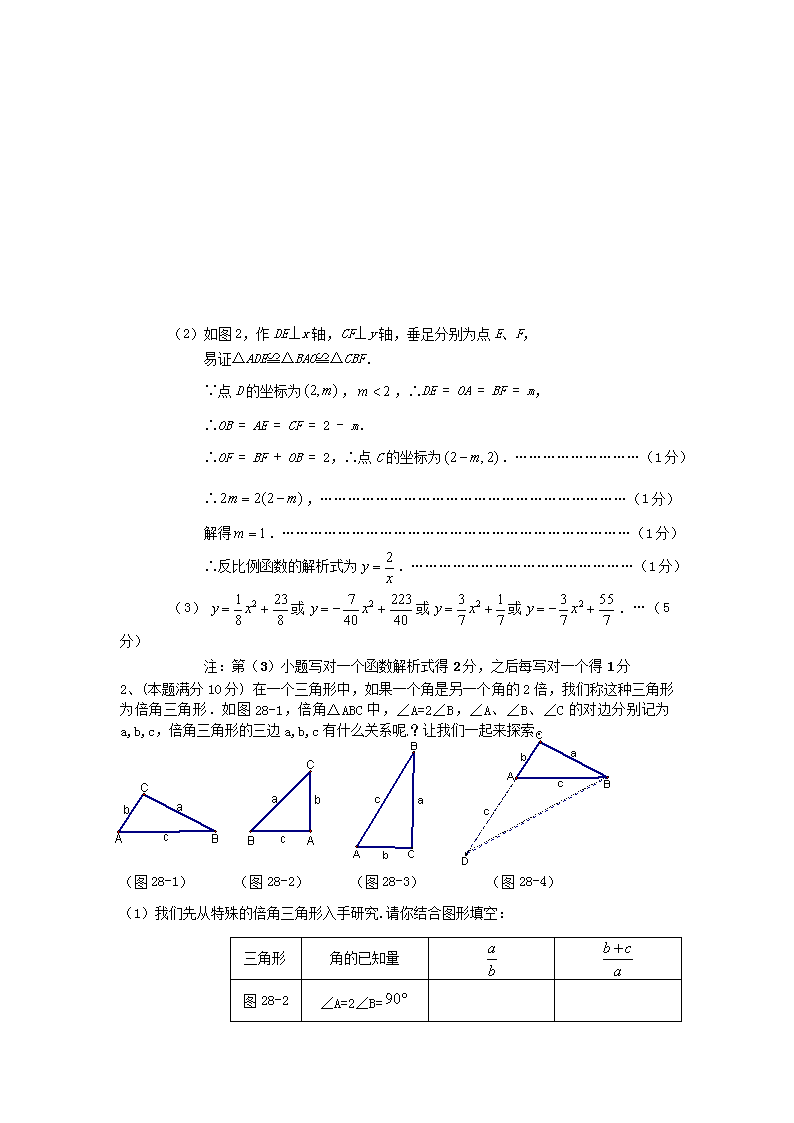2、(本题满分10分) 在一个三角形中，如果一个角是另一个角的2倍，我们称这种三角形为倍角三角形．如图28-1，倍角△ABC中，∠A=2∠B，∠A、∠B、∠C的对边分别记为a,b,c，倍角三角形的三边a,b,c有什么关系呢？让我们一起来探索．‎ ‎（图28-1） （图28-2） （图28-3） （图28-4）‎ ‎（1）我们先从特殊的倍角三角形入手研究.请你结合图形填空：‎ 三角形 角的已知量 图28-2‎ ‎∠A=2∠B=‎ 图28-3‎ ‎∠A=2∠B=‎ ‎（2）如图28-4，对于一般的倍角△ABC，若∠CAB=2∠CBA ，∠CAB、∠CBA、∠C的对边分别记为a、b、c，a、b、c三边有什么关系呢？请你作出猜测，并结合图28-4给出的辅助线提示加以证明．‎ 解：（1）‎ 三角形 角的已知量 图28-2‎ ‎∠A=2∠B=‎ 图28-3‎ ‎∠A=2∠B=‎ 每空1分共4分 ‎（2），（2分）‎ 证明正确（4分）‎ ‎3、如图，台风中心位于点，并沿东北方向移动，已知台风移动的速度为千米/时，受影响区域的半径为千米，市位于点的北偏东方向上，与点相距千米. ‎ ‎（1）请你说明本次台风会影响市；‎ ‎（2）求这次台风影响市的时间. ‎ 答案：解：作，垂足为，，（5分）；设到对市有影响，则， （10分）‎ ‎4、如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．‎ ‎⑴如图②，已知Rt△ABC中，∠ACB=90°，∠ACB＞∠A，CD是AB上的中线，过点B作BE⊥CD，垂足为E，试说明E是△ABC的自相似点．‎ ‎⑵在△ABC中，∠A＜∠B＜∠C．‎ ‎①如图③，利用尺规作出△ABC的自相似点P（写出作法并保留作图痕迹）；‎ ‎②若△ABC的内心P恰是该三角形的自相似点，求该三角形三个内角的度数．‎ ‎ ‎ 答案：解⑴在Rt △ABC中，∠ACB＝90°，CD是AB上的中线，∴，∴CD=BD．‎ ‎∴∠BCE＝∠ABC．∵BE⊥CD，∴∠BEC＝90°，∴∠BEC＝∠ACB．∴△BCE∽△ABC．‎ ‎∴E是△ABC的自相似点． ‎ ‎⑵①作图略． ‎ 作法如下：（i）在∠ABC内，作∠CBD＝∠A；‎ ‎（ii）在∠ACB内，作∠BCE＝∠ABC；BD交CE于点P．‎ 则P为△ABC的自相似点．‎ ‎②连接PB、PC．‎ ‎∵P为△ABC的内心 ‎∴，．‎ ‎∵P为△ABC的自相似点 ‎∴△BCP∽△ABC．‎ ‎∴∠PBC＝∠A，∠BCP＝∠ABC=2∠PBC =2∠A，‎ ‎∠ACB＝2∠BCP=4∠A ‎∵∠A+∠ABC+∠ACB＝180°．‎ ‎∴∠A+2∠A+4∠A＝180°．‎ ‎∴．∴该三角形三个内角的度数分别为、、．‎ ‎5、定义为一次函数的特征数．‎ ‎（1）若特征数是的一次函数为正比例函数，求的值；‎ ‎（2）已知抛物线与轴交于点，其中，点A在点B的左侧，与y轴交于点C，且的面积为4，为原点，求图象过两点的一次函数的特征数．‎ ‎（本小题满分5分） ‎ 解：(1) 由题意得 .‎ ‎∴ . -------1分 ‎ （2）由题意得 点A的坐标为（-n，0），点C的坐标为（0，-2n）. ………………2分 ‎∵ 的面积为4，‎ ‎∴ ‎ ‎∴ .‎ ‎∴ 点A的坐标为（-2，0），点C的坐标为（0，-4）. …………………………3分 设直线AC的解析式为 .‎ ‎∴ ‎ ‎∴ …………………………4分 ‎∴ 直线AC的解析式为 . ‎ ‎∴ 图象过两点的一次函数的特征数为. ………………………5分