- 1.20 MB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2015年各区分类汇编——中档解答题
(东城)
四、解答题(本题共20分,每小题5分)
23. 如图,中,,是边上的中线,分别过点,作,
的平行线交于点,且交于点,连接.
(1)求证:四边形是菱形;
(2)若,求的值.
24.为弘扬中华传统文化,某学校决定开设民族器乐选修课.为了更贴合学生的兴趣,对学生最喜爱的一种民族乐器进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查 名学生;
(2)请把条形图(图1)补充完整;
(3)求扇形统计图(图2)中,二胡部分所对应的圆心角的度数;
(4)如果该校共有学生名,请你估计最喜爱古琴的学生人数.
F
25. 如图,在⊙中,为直径,,弦与交于点,过点分别作⊙的切线交于点,且GD与的延长线交于点.
(1)求证:;
(2)已知:,⊙的半径为,求的长.
26. 在四边形中,对角线与交于点,是上任意一点,于点,交于点.
(1)如图1,若四边形是正方形,判断与的数量关系;
明明发现,与分别在和中,可以通过证明和全等,得到与的数量关系;
请回答:与的数量关系是 .
(2) 如图2,若四边形是菱形, ,请参考明明思考问题的方法,求 的值.
图1 图2
(西城)
四、解答题(本题共20分,每小题5分)
23.如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长。
A B
E D
F
C
24.在北京,乘坐地铁是市民出行时经常采用的一种交通方式,据调查,新票价改革政策的实施给北京市轨道交通客流带来很大变化.根据2015年1月公布的调价后市民当时乘坐地铁的相关调查数据,制作了以下统计表以及统计图.
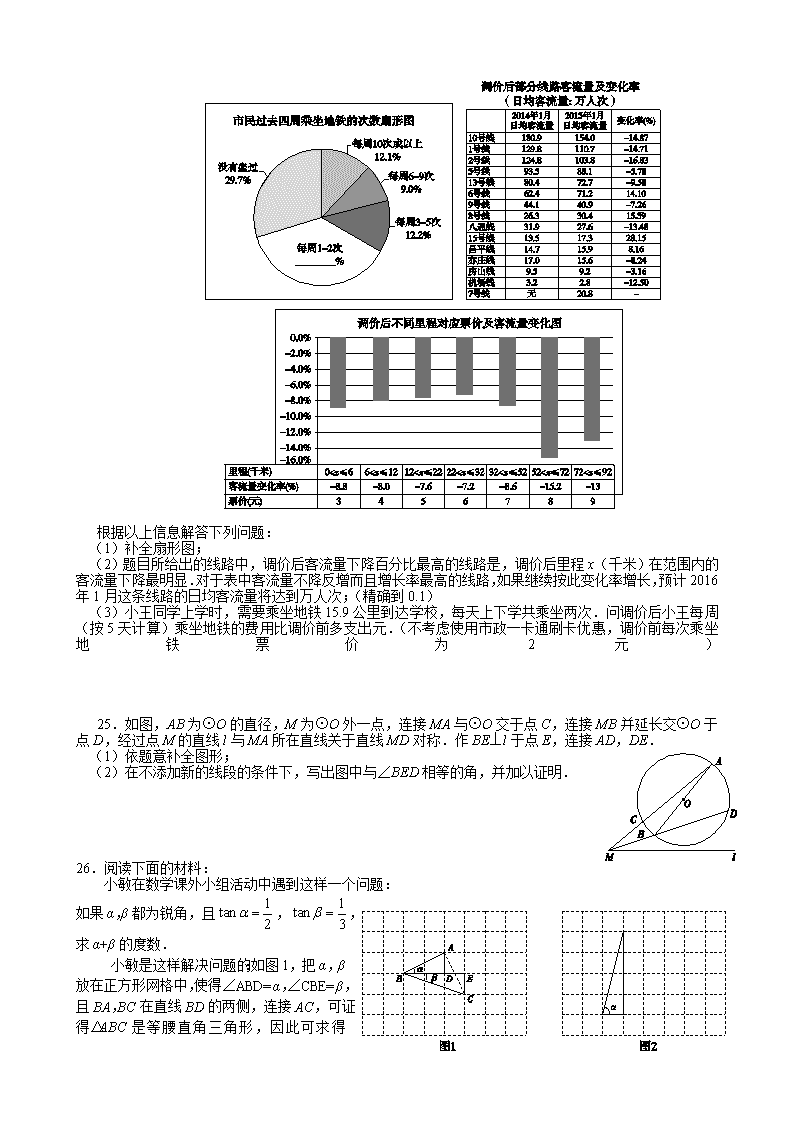
根据以上信息解答下列问题:
(1)补全扇形图;
(2)题目所给出的线路中,调价后客流量下降百分比最高的线路是,调价后里程x(千米)在范围内的客流量下降最明显.对于表中客流量不降反增而且增长率最高的线路,如果继续按此变化率增长,预计2016年1月这条线路的日均客流量将达到万人次;(精确到0.1)
(3)小王同学上学时,需要乘坐地铁15.9公里到达学校,每天上下学共乘坐两次.问调价后小王每周(按5天计算)乘坐地铁的费用比调价前多支出元.(不考虑使用市政一卡通刷卡优惠,调价前每次乘坐地铁票价为2元)
25.如图,AB为⊙O的直径,M为⊙O外一点,连接MA与⊙O交于点C,连接MB并延长交⊙O于点D,经过点M的直线l与MA所在直线关于直线MD对称.作BE⊥l于点E,连接AD,DE.
(1)依题意补全图形;
(2)在不添加新的线段的条件下,写出图中与∠BED相等的角,并加以证明.
26.阅读下面的材料:
小敏在数学课外小组活动中遇到这样一个问题:
如果α,β都为锐角,且,,求α+β的度数.
小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得
α+β=∠ABC= °.
请参考小敏思考问题的方法解决问题:
如果α,β都为锐角,当,时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α-β,由此可得α-β=______°.
(海淀)
四、解答题(本题共20分,每小题5分)
23.如图,在□中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;
(2)若AB=14,DE=8,求sin∠AEB的值.
24.根据某研究中心公布的近几年中国互联网络发展状况统计报告的部分相关数据,绘制的统计图表如下:
根据以上信息解答下列问题:
(1)直接写出扇形统计图中m的值;
(2)从2011年到2014年,中国网民人数每年增长的人数近似相等,估算2015年中国网民的人数约为 亿;
(3)据某市统计数据显示,2014年末全市常住人口为476.6万人,其中网民数约为210万人.若2014年该市的网民学历结构与2014年的中国网民学历结构基本相同,请你估算2014年末该市网民学历是大专的约有 万人.
25.如图,在△ABC中,AB=AC,AD⊥BC于点D,过点C作⊙O与边AB相切于点E,交BC于点F,CE为⊙O的直径.
(1) 求证:OD⊥CE;
(2) 若DF=1, DC=3,求AE的长.
26.阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
图1 图2 图3
请回答:BC+DE的值为_______.
参考小明思考问题的方法,解决问题:
如图3,已知□ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.
(朝阳)
四、解答题(本题共20分,每小题5分)
23. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D
作DE∥AC且DE=AC,连接 CE、OE,连接AE交OD
于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
24.为防治大气污染,依据北京市压减燃煤相关工作方案,2014年全市燃煤数量比2012年
压减450万吨,到2015年、2017年要比2012年分别压减燃煤800万吨、1300万吨.以下是根据相关数据绘制的统计图的一部分:
2012年全市燃煤各组成部分
用煤量分布扇形统计图
2012-2017年全市燃煤数量的折线统计图
(1)据报道,2012年全市燃煤由四部分组成,其中电厂用煤920万吨,则2012年全市
燃煤数量为 万吨;
(2)请根据以上信息补全2012-2017年全市燃煤数量的折线统计图,并标明相应数据;
(3)某地区积极倡导“清洁空气,绿色出行”,大力提升自行车出行比例,小颖收集了
该地区近几年公共自行车的有关信息(如下表),发现利用公共自行车出行人数与
公共自行车投放数量之间近似成正比例关系.
2012-2015年公共自行车投放数量与利用公共自行车出行人数统计表
年份
公共自行车投放数量(万辆)
利用公共自行车出行人数(万人)
2012
1.4
约9.9
2013
2.5
约17.6
2014
4
约27.6
2015
5
约
根据小颖的发现,请估计,该地区2015年利用公共自行车出行人数(直接写出结果,
精确到0.1)
25.如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O
切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
(1)求证:∠BAD=∠DAE;
(2)若AB=6,AD=5,求DF的长.
26.阅读下面材料:
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,
BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE
相交于点P,求的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和
计算能够使问题得到解决(如图2).
请回答:的值为 .
图1
图3
图2
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求 的值;
(2)若CD=2,则BP= .
(丰台)
四、解答题(本题共20分,每小题5分)
23.如图,菱形ABCD中, 分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
(1)求证:四边形DBEF是矩形;
(2)如果∠A=60°,菱形ABCD的面积为,求DF的长.
24.根据某市统计局提供的2010~2014年该市地铁运营的相关数据,绘制的统计图表如下:
2010~2014年某市地铁运营的日均客流量统计表 2014年某市居民乘地铁出行距离情况统计图
根据以上信息解答下列问题:
(1)直接写出“2014年某市居民乘地铁出行距离情况统计图”中m的值;
(2)从2010年到2014年,该市地铁的日均客流量每年的增长率近似相等,估算2015年该市地铁运营的日均客流量约为____________万人次;
(3)自2015年起,该市地铁运营实行了新票价:乘地铁5公里内(含5公里)收费2元,乘地铁5~15公里(含15公里)收费3元,乘地铁15公里以上收费4元.如果2015年该市居民乘地铁出行距离情况与2014年基本持平,估算2015年该市地铁运营平均每日票款收入约为____________万元.
25.如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD.
(1)判断直线PD与⊙O的位置关系,并加以证明;
(2)联结CO并延长交⊙O于点F,联结FP交CD于点G,如果CF=10,,
求EG的长.
26.阅读下面的材料
勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍
的一种拼图证明勾股定理的方法.
先做四个全等的直角三角形,设它们的两条直角边分别为a,b,
斜边为c,然后按图1的方法将它们摆成正方形.
图1
由图1可以得到,
整理,得.
所以.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,请
你参照上述证明勾股定理的方法,完成下面的填空:
由图2可以得到 ,
图2
整理,得 ,
所以 .
(通州)
四、解答题(每题5分,共25分)
22.为了把通州区打造成宜居的北京城市副中心,区政府对地下污水排放设施进行改造.某
施工队承担铺设地下排污管道任务共2200米,为了减少施工对周边交通环境的影响,施工队进行技术革新,使实际平均每天铺设管道的长度比原计划多10%,结果提前两天完成任务.求原计划平均每天铺设排污管道的长度.
23.已知菱形ABCD的对角线AC与BD相交于点E,点F在BC的延长线上,且CF=BC,连接DF,点G是DF中点,连接CG.求证:四边形 ECGD是矩形.
24.为倡导“1公里步行、3公里单车、5公里汽车(地铁、轻轨)”出行模式, 2013年5月环保公共自行车正式“驶入”通州,通州区分三期投放白绿环保公共自行车.第一期投放租赁点以八通线通州北苑、梨园站为中心,共投放21个租赁点。截止到2014年年底,全区公共自行车总数已达到10000辆.以下是根据相关数据绘制的通州区内分三期投放环保公共自行车的数量统计图(如图①),以及投放的租赁点统计图(如图②);
通州区2013年至2014年三期
自行车投放数量统计图(单位:辆)
通州区2013年至2014年三期所投放的
自行车租赁点百分比统计图
图① 图②
根据以上信息解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)请根据以上信息计算,通州区2014年底第三期投入使用的公共自行车租赁点有多少个?
(3)另有调查数据显示:地铁站周边的公共自行车站点的车桩日使用率较高,居住区和办公区附近站点的车桩日使用率较低,如果按全区站点的车桩日平均取车4人次/车桩,每人次骑行距离约3km,折算成驾车出行每10km消耗汽油1升,按照“消耗1升汽油=排0.63kg碳”来计算,2014年底全区约有8000个车桩.根据以上数据,请计算公共自行车租赁这一项通州区一天大约减少碳排放_______________kg
B
25.如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC,交AC于点E,交PC于点F,连接AF.
(1)求证:AF是⊙O的切线;
(2)已知⊙O的半径为4,AF=3,求线段AC的长 .
26.(1)请你根据下面画图要求,在图①中完成画图操作并填空.
如图①,△中,∠BAC=30°,∠ACB=90°,∠PAM=∠A.
操作:(1)延长BC.
(2)将∠PAM绕点A逆时针方向旋转60°后,射线AM交BC的延长线于点D.
(3)过点D作DQ//AB.
(4)∠PAM旋转后,射线AP交DQ于点G.
(5)连结BG.
结论:= .
图① 图② 图③
(2)如图②,△中,AB=AC=1,∠BAC=36°,进行如下操作:将△绕点A按逆时针方向旋转度角,并使各边长变为原来的n倍(n >1),得到△. 当点B、C、在同一条直线上,且四边形为平行四边形时(如图③),求和n的值.
(延庆)
四、 解答题(本题共20分,每小题5分)
23. 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.
24. 某区对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有
效”,有以下四个选项:
A.使用清洁能源 B.汽车限行 C.绿化造林 D.拆除燃煤小锅炉
调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的市民共有 人.
(2)请你将统计图1补充完整.
(3)已知该区人口为200000人,请根据调查结果估计该市认同汽车限行的人数.
25. 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.[w
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使CD = BC,连接AD与CM交于点E,若⊙O的半径为2,ED =1,求AC的长.
26. 阅读下面资料:
问题情境:
(1)如图1,等边△ABC,∠CAB和∠CBA的平分线交于点O,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点与点O重合,已知OA=2,则图中重叠部分△OAB的面积是 .
探究:
(2)在(1)的条件下,将纸片绕O点旋转至如图2所示位置,纸片两边分别与AB,AC交于点E,F,求图2中重叠部分的面积.
(3)如图3,若∠ABC=α(0°<α<90°),点O在∠ABC的角平分线上,且BO=2,以O为顶点的等腰三角形纸片(纸片足够大)与∠ABC的两边AB,AC分别交于点E、F,∠EOF=180°﹣α,直接写出重叠部分的面积.(用含α的式子表示)
(房山)
四、解答题(本题共20分,每小题5分)
23.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.
(1)求证:四边形BFDE是平行四边形;
(2)若AB=4,CF=1,∠ABC=60°,求的值.
24. 某校开展“人人读书”活动.小明为调查同学们的阅读兴趣,抽样调查了40名学生在本校图书馆的借阅情况(每人每次只能借阅一本图书),绘制了统计图1. 并根据图书馆各类图书所占比例情况绘制了统计图2,已知综合类图书有40本.
图2
图1
校图书馆各类图书所占比例统计图
各类图书借阅人次分布统计图
(1)补全统计图1;
(2)该校图书馆共有图书________________本;
(3)若该校共有学生1000人,试估算,借阅文学类图书的有______________人.
第25题图
25.如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE,使∠CDE=∠DFE,交AB的延长线于点E. 过点A作⊙O的切线交ED的延长线于点G.
(1)求证:GE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径为3,求AG的长.
26.小明遇到这样一个问题:
如图1,在锐角△ABC中,AD、BE、CF分别为△ABC的高,求证:∠AFE=∠ACB.
小明是这样思考问题的:如图2,以BC为直径做半⊙O,则点F、E在⊙O上,
∠BFE+∠BCE=180°,所以∠AFE=∠ACB.
请回答:若∠ABC=,则∠AEF的度数是 .
参考小明思考问题的方法,解决问题:
图1 图2 图3
如图3,在锐角△ABC中,AD、BE、CF分别为△ABC的高,求证:∠BDF=∠CDE.
(石景山)
四、解答题(本题共20分,每小题5分)
23.如图,菱形中,,分别为,上的点,且,连接并延长,交的延长线于点,连接.
(1)求证:四边形是平行四边形;w
(2)连接,若,,求的长.
24.为了解大学生参加公益活动的情况,几位同学设计了调查问卷,对几所大学的学生进行了随机调查.问卷如下:
2014—2015学年度第一学期你参加过几次公益活动?
A.没有参加过公益活动
B.参加过一次公益活动
C.参加过二次至四次公益活动
D.参加过五次或五次以上公益活动
以下是根据调查结果的相关数据绘制的统计图的一部分.
2014—2015学年度第一学期
大学生参加公益活动统计图
2014—2015学年度第一学期
大学生参加公益活动分布统计图
请回答以下问题:
(1)此次调查对象共______人,扇形统计图中m的值为__________ ;
(2)请补全条形统计图并在图上标出数据;
(3)据统计,该市某大学有学生15000人,请根据上述调查结果估计这所大学2014—2015学年度第一学期参加过至少两次公益活动的大约有____人.
25.如图,是⊙的直径,是⊙上一点,
是中点,过点作的垂线交的延长线于点.过点作⊙的切线交于点.
(1)求证:;
(2)如果,,求的长.
26.阅读下面材料:
小红遇到这样一个问题:如图1,在四边形中,,,,,求的长.
图1 图2
小红发现,延长与相交于点,通过构造Rt△,经过推理和计算能够使问题得到解决(如图2).
请回答:的长为 .
参考小红思考问题的方法,解决问题:
如图3,在四边形中,,,
,,求和的长.
图3
(门头沟)
四、解答题(本题共20分,每小题5分)
23. 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,
DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=时,求tan∠EAD的值.
24.2014年1月10日,国内成品油价格迎来了首次降低,某调查员就“汽油降价对用车的影响”这一问题向有机动车的私家车车主进行了问卷调查,并制作了统计图表的一部分如下:
车主的态度
百分比
A. 没有影响
4%
B. 影响不大
p
C. 有影响
52%
D. 影响很大
m
E. 不关心这个问题
10%
(1)结合上述统计图表可得:p= ,m= ;
(2)根据以上信息,补全条形统计图;
(3)2014年1月末,某市有机动车的私家车车主约200 000人,根据上述信息,请你估计一下持有“影响不大”这种态度的车主约有多少人?
25.如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线EF,交AB和AC的延长线于E、F.
(1)求证:FE⊥AB;
(2)当AE=6,sin∠CFD=时,求EB的长.
26.阅读下面材料:
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).
图1 图2
请回答:(1)在图2中,小明得到的全等三角形是△ ≌△ ;
(2)BC和AC、AD之间的数量关系是 .
参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.
求AB的长.
图3
(怀柔)
四、解答题(本题共20分,每小题5分)
23. 如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
24.某公司有5个股东,每个股东的利润相同,有100名工人,每名工人的工资相同.2015年第一个季度工人的工资总额与公司
月份
工人工资总额(万元)
股东总利润(万元)
1
28
14
2
30
16
3
32
18
的股东总利润情况见右表:
该公司老板根据表中数据,作出了图1,并声称股东利润和工人工资同步增长,公司和工人做到了“有福同享”.
图1
图2
针对老板的说法,解决下列问题:
(1)这三个月工人个人的月收入分别是 万元;
(2)在图2中,已经做出这三个月每个股东利润统计图,请你补出这三个月工人个人月收入的统计图;
(3)通过完成第(1),(2)问和对图2的观察,你如何看待老板的说法?(用一两句话概括)
25. 如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的
切线CN上一点,BD交AC于点E,且BA= BD.
(1)求证:∠ACD=45°;
(2)若OB=2,求DC的长.
26.阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,
图3
∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6
图1
图2
求BC的长.
小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.
这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).
请回答:(1)△BDE是_________三角形.
(2)BC的长为__________.
参考小聪思考问题的方法,解决问题:
如图3,已知△ABC中,AB=AC, ∠A=20°,
BD平分∠ABC,BD=,BC=2.
求AD的长.
(平谷)
四、解答题(本题共20分,每小题5分)
23.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,
且DE∥AB,EF∥AC.
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=12,求DE的长及四边形ADEF的面积.
24.“小组合作学习”成为我区推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“小组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
请结合图中信息解答下列问题:
(1)小组合作学习前学生学习兴趣为“高”的所占的百分比为 ;
(2)补全小组合作学习后学生学习兴趣的统计图;
(3)通过“小组合作学习”前后学生学习兴趣的对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?
25.如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,∠BAC=2∠CBE,交AC于点E,交⊙O于点F,连接AF.
(1)求证:∠CBE=∠CAF;
(2)过点E作EG⊥BC于点G,若∠C=45°,CG=1,
求⊙O的半径.
26.阅读下面材料:
图1
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪想:要想解决问题,应该对∠B进行分类研究.
图2
∠B可分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B是直角时,如图1,
在△ABC和△DEF中,AC=DF,BC=EF,
∠B=∠E=90°,根据“HL”定理,可以知道
Rt△ABC≌Rt△DEF.
第二种情况:当∠B是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是 ;
A.全等 B.不全等 C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,
∠B=∠E>90°,求证:△ABC≌△DEF.
图3