2011中考数学压轴题选 217页

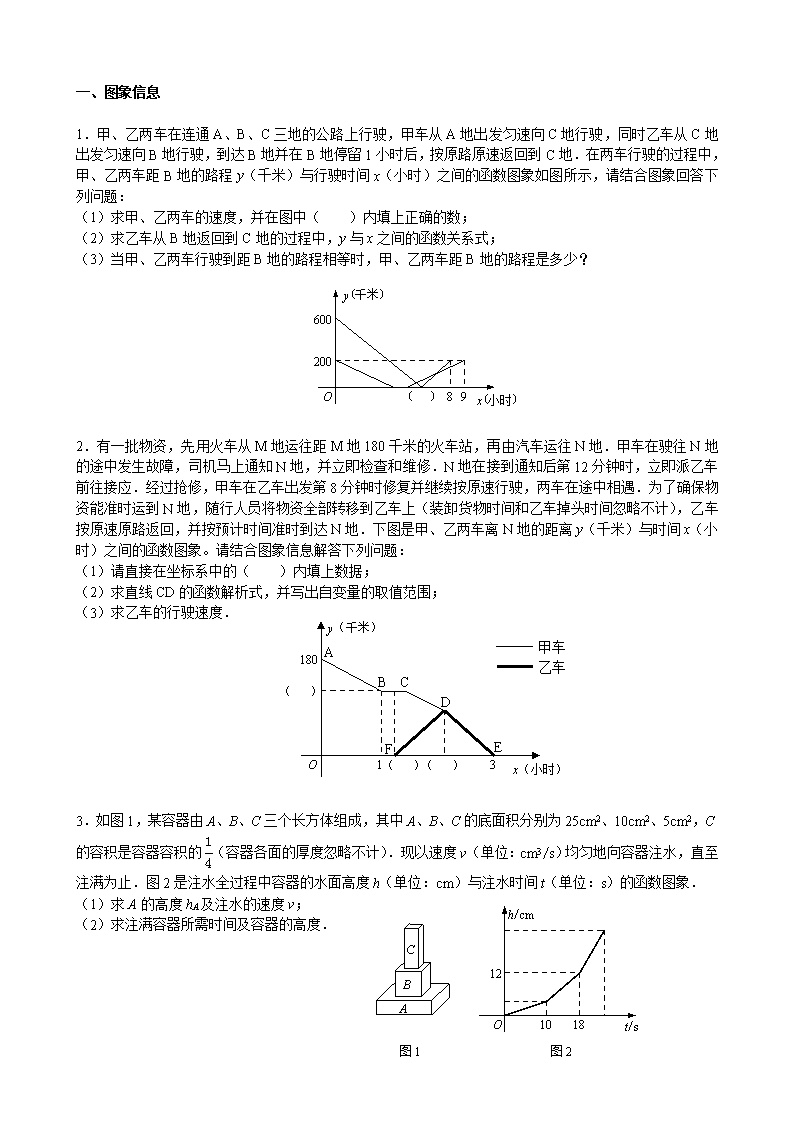
- 1 - 2011 年全国各地中考数学压轴题专集 目 录 一、图象信息 二、一元二次方程 三、反比例函数 四、二次函数 五、概率 六、三角形 七、平行四边形、矩形、菱形、正方形、梯形 八、圆 九、综合型问题 十、动态综合型问题 一、图象信息 1．甲、乙两车在连通 A、B、C 三地的公路上行驶，甲车从 A 地出发匀速向 C 地行驶，同时乙车从 C 地 出发匀速向 B 地行驶，到达 B 地并在 B 地停留 1 小时后，按原路原速返回到 C 地．在两车行驶的过程中， 甲、乙两车距 B 地的路程 y（千米）与行驶时间 x（小时）之间的函数图象如图所示，请结合图象回答下 列问题： （1）求甲、乙两车的速度，并在图中（ ）内填上正确的数； （2）求乙车从 B 地返回到 C 地的过程中，y 与 x 之间的函数关系式； （3）当甲、乙两车行驶到距 B 地的路程相等时，甲、乙两车距 B 地的路程是多少？ 2．有一批物资，先用火车从 M 地运往距 M 地 180 千米的火车站，再由汽车运往 N 地．甲车在驶往 N 地 的途中发生故障，司机马上通知 N 地，并立即检查和维修．N 地在接到通知后第 12 分钟时，立即派乙车 前往接应．经过抢修，甲车在乙车出发第 8 分钟时修复并继续按原速行驶，两车在途中相遇．为了确保物 资能准时运到 N 地，随行人员将物资全部转移到乙车上（装卸货物时间和乙车掉头时间忽略不计），乙车 按原速原路返回，并按预计时间准时到达 N 地．下图是甲、乙两车离 N 地的距离 y（千米）与时间 x（小 时）之间的函数图象。请结合图象信息解答下列问题： （1）请直接在坐标系中的（ ）内填上数据； （2）求直线 CD 的函数解析式，并写出自变量的取值范围； （3）求乙车的行驶速度． 3．如图 1，某容器由 A、B、C 三个长方体组成，其中 A、B、C 的底面积分别为 25cm2、10cm2、5cm2，C 的容积是容器容积的 1 4（容器各面的厚度忽略不计）．现以速度 v（单位：cm3/s）均匀地向容器注水，直至 注满为止．图 2 是注水全过程中容器的水面高度 h（单位：cm）与注水时间 t（单位：s）的函数图象． （1）求 A 的高度 hA 及注水的速度 v； （2）求注满容器所需时间及容器的高度． O y(千米) x(小时)8 9( ) 200 600 甲车 乙车 x（小时） A B C D E y（千米） 180 1 （ ） （ ）（ ） 3O F 图 1 图 2 12 10 t/s h/cm 18O A B C 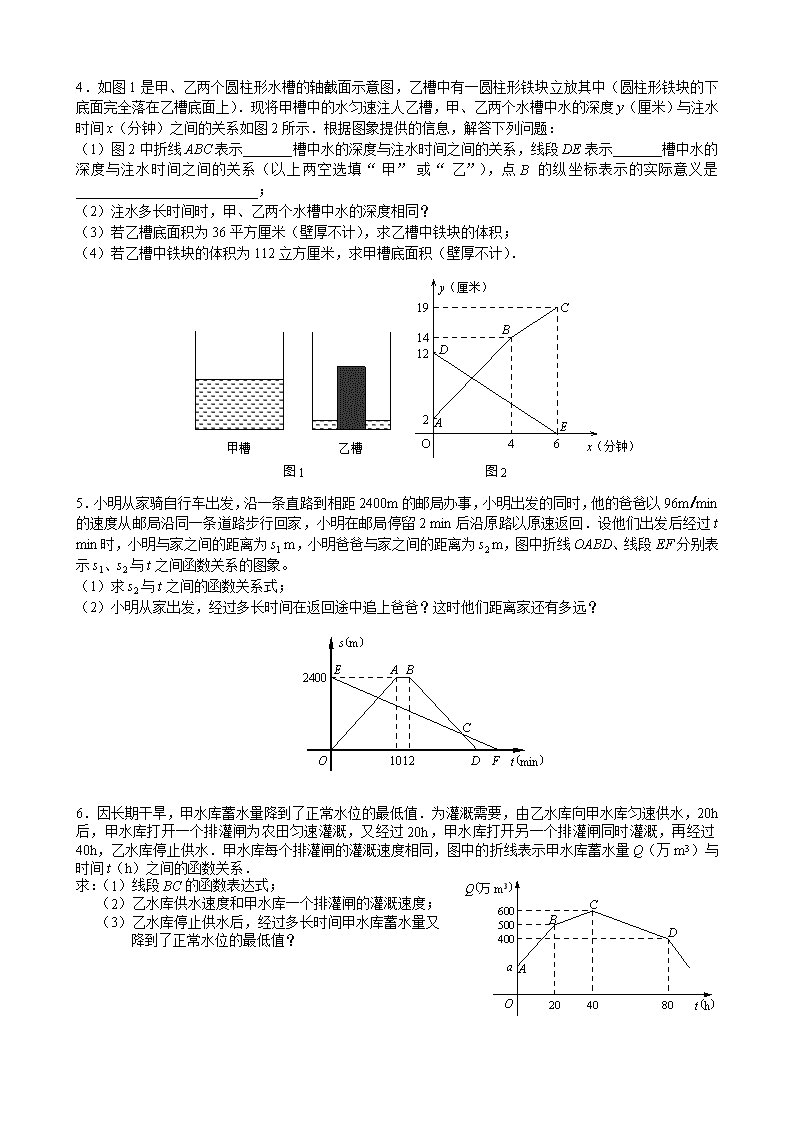4．如图 1 是甲、乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱形铁块立放其中（圆柱形铁块的下 底面完全落在乙槽底面上）．现将甲槽中的水匀速注人乙槽，甲、乙两个水槽中水的深度 y（厘米）与注水 时间 x（分钟）之间的关系如图 2 所示．根据图象提供的信息，解答下列问题： （1）图 2 中折线 ABC 表示_______槽中水的深度与注水时间之间的关系，线段 DE 表示_______槽中水的 深度与注水时间之间的关系（以上两空选填“甲”或“乙”），点 B 的纵坐标表示的实际意义是 __________________________； （2）注水多长时间时，甲、乙两个水槽中水的深度相同？ （3）若乙槽底面积为 36 平方厘米（壁厚不计），求乙槽中铁块的体积； （4）若乙槽中铁块的体积为 112 立方厘米，求甲槽底面积（壁厚不计）． 5．小明从家骑自行车出发，沿一条直路到相距 2400m 的邮局办事，小明出发的同时，他的爸爸以 96m/min 的速度从邮局沿同一条道路步行回家，小明在邮局停留 2 min 后沿原路以原速返回．设他们出发后经过 t min 时，小明与家之间的距离为 s1 m，小明爸爸与家之间的距离为 s2 m，图中折线 OABD、线段 EF 分别表 示 s1、s2 与 t 之间函数关系的图象。 （1）求 s2 与 t 之间的函数关系式； （2）小明从家出发，经过多长时间在返回途中追上爸爸？这时他们距离家还有多远？ 6．因长期干旱，甲水库蓄水量降到了正常水位的最低值．为灌溉需要，由乙水库向甲水库匀速供水，20h 后，甲水库打开一个排灌闸为农田匀速灌溉，又经过 20h，甲水库打开另一个排灌闸同时灌溉，再经过 40h，乙水库停止供水．甲水库每个排灌闸的灌溉速度相同，图中的折线表示甲水库蓄水量 Q（万 m3）与 时间 t（h）之间的函数关系． 求：（1）线段 BC 的函数表达式； （2）乙水库供水速度和甲水库一个排灌闸的灌溉速度； （3）乙水库停止供水后，经过多长时间甲水库蓄水量又 降到了正常水位的最低值？ 甲槽 乙槽 图 1 图 2 y（厘米） 19 14 12 2 O A D B C E x（分钟）4 6 O A B C E D F t(min) 2400 1012 s(m) O A B C D Q(万 m3) 600 20 40 t(h) 500 a 80 400 7．小华观察钟面（图 1），了解到钟面上的分针每小时旋转 360 度，时针毎小时旋转 30 度．他为了进一步 探究钟面上分针与时针的旋转规律，从下午 2 : 00 开始对钟面进行了一个小时的观察．为了探究方便，他 将分针与分针起始位置 OP（图 2）的夹角记为 y1，时针与 OP 的夹角记为 y2 度（夹角是指不大于平角的 角），旋转时间记为 t 分钟．观察结束后，利用获得的数据绘制成图象（图 3），并求出 y1 与 t 的函数关系 式： y1＝{ 请你完成： （1）求出图 3 中 y2 与 t 的函数关系式； （2）直接写出 A、B 两点的坐标，并解释这两点的实际意义； （3）若小华继续观察一个小时，请你在图 3 中补全图象． 8．周六上午 8∶00 小明从家出发，乘车 1 小时到郊外某基地参加社会实践活动，在基地活动 2.2 小时后， 因家里有急事，他立即按原路以 4 千米/小时的平均速度步行返回，同时他的爸爸开车从家出发沿同一路 线接他，在离家 28 千米处与小明相遇，接到小明后保持车速不变，立即按原路返回．设小明离开家的时 间为 x 小时，小名离家的路程 y （干米）与 x （小时）之间的函数图象如图所示． （1）小明去基地乘车的平均速度是______千米/小时，爸爸开车的平均速度是______千米/小时； （2）求线段 CD 所表示的函数关系式； （3）小明能否在 12∶00 前回到家？若能，请说明理由；若不能，请算出 12∶00 时他离家的路程． 9．由于受金融危机的影响，某店经销的甲型号手机今年的售价比去年每部降价 500 元．如果卖出相同数 量的手机，那么去年销售额为 8 万元，今年销售额只有 6 万元． （1）今年甲型号手机每部售价为多少元？ （2）为了提高利润，该店计划购进乙型号手机销售，已知甲型号手机每部进价为 1000 元，乙型号手机每 部进价为 800 元，预计用不多于 1.84 万元且不少于 1.76 万元的资金购进这两种手机共 20 部，请问有几 种进货方案？ （3）若乙型号手机的售价为 1400 元，为了促销，公司决定每售出一部乙型号手机，返还顾客现金 a 元， 而甲型号手机仍按今年的售价销售，要使（2）中所有方案获利相同，a 应取何值？ 10．星光中学课外活动小组准备围建一个矩形生物苗圃园．其中一边靠墙，另外三边用长为 30 米的篱笆 围成 ．已知墙长为 18 米（如图所示），设这个苗圃园垂直于墙的一边的长为 x 米． 12 39 6 图 1 12 39 6 图 2 P 图 3 30 45 60 75 90 105 120 5 15 150 5120 5 180 5 90 60 30 O t(分钟) y(度) A B A D B x(小时) C O y(千米) 10 20 30 1 28 （1）若平行于墙的一边的长为 y 米，直接写出 y 与 x 之间的函数关系式及其自变量 x 的取值范围； （2）垂直于墙的一边的长为多少米时，这个苗圃园的面积最大，并求出这个最大值； （3）当这个苗圃园的面积不小于 88 平方米时，试结合函数图像，直接写出 x 的取值范围． 11．为了保护水资源，某市制定了一套节水的管理措施，其中对居民生活用水收费作如下规定： 月用水量（吨） 单价（元／吨） 不大于 10 吨部分 1.5 大于 10 吨不大于 m 吨部分（20≤m≤50） 2 大于 m 吨部分 3 （1）若某用户六月份用水量为 18 吨，求其应缴纳的水费； （2）记该用户六月份用水量为 x 吨，缴纳水费为 y 元，试列出 y 与 x 的函数式； （3）若该用户六月份用水量为 40 吨，缴纳水费 y 元的取值范围为 70≤y≤90，试求 m 的取值范围． 12．在平面直角坐标系中，点 P 从原点 O 出发，每次向上平移 2 个单位长度或向右平移 1 个单位长度． （1）实验操作： 在平面直角坐标系中描出点 P 从点 O 出发，平移 1 次后，2 次后，3 次后可能到达的点，并把相应点 的坐标填写在表格中： （2）观察发现： 任一次平移，点 P 可能到达的点在我们学过的一种函数的图象上，如：平移 1 次后在函数 ________________的图象上；平移 2 次后在函数________________的图象上……由此我们知道，平移 次 后在函数________________的图象上．（请填写相应的解析式） （3）探索运用： 点 P 从点 O 出发经过 次平移后，到达直线 y＝x 上的点 Q，且平移的路径长不小于 50，不超过 56， 求点 Q 的坐标． 13．某学校要在围墙旁建一个长方形的中药材种植实习苗圃，苗圃的一边靠墙（墙的长度不限），另三边 用木栏围成，建成的苗圃为如图所示的长方形 ABCD．已知木栏总长为 120 米，设 AB 边的长为 x 米，长 方形 ABCD 的面积为 S 平方米． （1）求 S 与 x 之间的函数关系式，当 x 为何值时，S 取得最值（请指出是最大值还是最小值）？并求出这 个最值； （2）学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆．其圆心分别为 O1 和 O2，且 O1 到 AB、BC、AD 的距离与 O2 到 CD、BC、AD 的距离都相等，并要求在苗圃内药材种植区域外四周至少要 留够 0.5 米宽的平直路面，以方便同学们参观学习．当（1）中 S 取得最值时，请问这个设计是否可行？ 若可行，求出圆的半径；若不可行，请说明理由． P 从点 O 出发 平移次数 可能到达的点的坐标 1 次 （0，2），（1，0） 2 次 3 次1 y x1O n n 墙 18 米 苗圃园 14．王伟准备用一段长 30 米的篱笆围成一个三角形形状的小圈，用于饲养家兔．已知第一条边长为 a 米， 由于受地势限制，第二条边长只能是第一条边长的 2 倍多 2 米． （1）请用 a 表示第三条边长； （2）问第一条边长可以为 7 米吗？请说明理由，并求出 a 的取值范围； （3）能否使得围成的小圈是直角三角形形状，且各边长均为整数？若能，说明你的围法；若不能，请说 明理由． 15．李明在小岛上的 A 处，上午 8 时测得在 A 的北偏东 60º 的 D 处有一艘轮船，9 时 20 分测得该船航行 到北偏西 60º 的 C 处，9 时 40 分测得该船到达位于 A 正西方 5 千米的港口 B 处，如果该船始终保持匀速 直线运动，求： （1）A、C 之间的距离； （2）轮船的航行速度． 16．长江沿岸的甲乙两港相距 300 千米，甲港在乙港的上游，满载货物的货轮从乙港出发，到达甲港卸货 后，再空载返回乙港，货轮离开乙港的路程 s（千米）随时间 t（小时）的变化关系如图所示．已知货轮空 载时在静水中的速度比满载时在静水中的速度快 5 千米/小时． （1）求长江水流速度及货轮空载时在静水中的速度； （2）若货轮在距甲港 90 千米时接到警报，将有台风影响航道安全，预报再过 4 小时此段航道将有暴风雨， 为了安全，货船必须在 4 小时之内进入甲港避风．现决定从甲港派出一艘大马力的动力拖轮，遇到货轮后， 将其快速拖到甲港．动力拖轮拖着货轮在静水中的速度，是它们分别在静水中速度的平均值．动力拖轮在 静水中速度是 40 千米/小时．问：能否在规定时间内将货轮拖到甲港？请说明理由． 17．在海岸上 A 处，发现北偏东 45°方向、距离为 3－1 海里的 B 处有一走私船．在 A 处北偏西 75°方 向、距离为 2 海里的 C 处的我方缉私艇奉命以每小时 10 3 海里的速度向走私船追去，这时走私船正以每 小时 10 海里的速度从 B 处向北偏东 30°方向逃窜．问：缉私艇沿什么方向行驶，才能在最短时间内追上 走私船？并求出所需时间．（结果保留根号） 围墙 A D B C O1 O2 B A 北 D 东 C 0 20 30 40 300 s(千米) t(小时) A BC D 45°75° 北 30° 18．李明在进行投篮训练，他从距地面高 1.55 米处的 O 点向篮圈中心 A 点投出一球，球的飞行路线为抛 物线，当球达到距地面最高点 3.55 米时，球移动的水平距离为 2 米．以 O 点为坐标原点，建立直角坐标 系（如图所示），测得 OA 与水平方向 OB 的夹角为 30°，A、B 两点相距 1.5 米． （1）求篮球飞行路线所在抛物线的解析式； （2）判断李明这一投能否把球从 O 点直接投入篮圈 A 点（排除篮板球），如果能，请说明理由；如果不能， 那么李明应向前或向后移动多少米，才能投入篮圈 A 点？（结果保留根号） O x y A B 二、一元二次方程 1．已知△ABC 的两边 AB、AC 的长是关于 x 的一元二次方程 x 2－( 2k＋3 )x＋k 2＋3k＋2＝0 的两个实数根， 第三边长为 5． （1）当 k 为何值时，△ABC 是以 BC 为斜边的直角三角形； （2）当 k 为何值时，△ABC 是等腰三角形，并求△ABC 的周长． 2．已知△ABC 的三边长为 a、b、c，关于 x 的方程 x 2－2( a＋b )x＋c 2＋2ab＝0 有两个相等的实数根，又 sinA、sinB 是关于 x 的方程( m＋5 )x 2－( 2m－5 )x＋m－8＝0 的两个实数根． （1）求 m 的值； （2）若△ABC 的外接圆面积为 25π，求△ABC 的内接正方形的边长． 3．已知关于 x 的方程 x 2－( m＋n＋1)x＋m＝0（n≥0）的两个实数根为 α、β，且 α≤β． （1）试用含有 α、β 的代数式表示 m 和 n； （2）求证：α≤1≤β； （3）若点 P（α，β）在△ABC 的三条边上运动，且△ABC 顶点的坐标分别为 A（1，2），B（ 1 2 ，1），C （1，1），问是否存在点 P，使 m＋n＝ 5 4 ？若存在，求出点 P 的坐标；若不存在，请说明理由． 4．请阅读下列材料： 问题：已知方程 x 2＋x－1＝0，求一个一元二次方程，使它的根分别是已知方程根的 2 倍． 解：设所求方程的根为 y，则 y＝2x，所以 x＝ y 2． 把 x＝ y 2 代入已知方程，得(y 2)2＋ y 2 －1＝0． 化简，得 y 2＋2y－4＝0． 故所求方程为 y 2＋2y－4＝0． 这种利用方程根的代换求新方程的方法，我们称为“换根法”． 请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）； （1）已知方程 x 2＋x－2＝0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为： ___________________； （2）已知关于 x 的一元二次方程 ax 2＋bx＋c＝0（a≠0）有两个不等于零的实数根，求一个一元二次方程， 使它的根分别是已知方程根的倒数． 5．已知关于 x 的一元二次方程 x 2－2x－a 2－a＝0（a＞0）． （1）证明这个方程的一个根比 2 大，另一个根比 2 小； （2）如果当 a ＝1，2，3，…，2011 时，对应的一元二次方程的两个根分别为 α 1、β1，α2、β2，α3、 β3，…，α2011、β2011，求 1 α1 ＋ 1 β1 ＋ 1 α2 ＋ 1 β2 ＋ 1 α3 ＋ 1 β3 ＋ … ＋ 1 α2011 ＋ 1 β2011 的值． 6．已知关于 x 的一元二次方程 x 2－(a＋b＋c)x＋ab＋bc＋ca＝0，且 a＞b＞c＞0． （1）若方程有实数根，求证：a，b，c 不能构成一个三角形的三边长； （2）若方程有实数根 x0，求证：b＋c＜x0＜a； （3）若方程的实数根为 6 和 9，求正整数 a，b，c 的值． 7．已知方程 x 2＋2ax＋a－4＝0 有两个不同的实数根，方程 x 2＋2ax＋k＝0 也有两个不同的实数根，且其两 根介于方程 x 2＋2ax＋a－4＝0 的两根之间，求 k 的取值范围． 8．已知关于 x 的方程 x 2－4|x|＋3＝k． （1）当 k 为何值时，方程有 4 个互不相等的实数根？ （2）当 k 为何值时，方程有 3 个互不相等的实数根？ （3）当 k 为何值时，方程有 2 个互不相等的实数根？ （4）是否存在实数 k，使得方程只有 1 个实数根？若存在，求 k 的值和方程的根；若不存在，请说明理 由． 9．已知 x1，x2 是关于 x 的一元二次方程 4x 2＋4(m－1)x＋m 2＝0 的两个非零实数根，则 x1 与 x2 能否同号？ 若能同号，请求出相应的 m 的取值范围；若不能同号，请说明理由． 10．已知 α、β 为关于 x 的方程 x 2－2mx＋3m＝0 的两个实数根，且(α－β)2＝16，如果关于 x 的另一个方程 x 2－2mx＋6m－9＝0 的两个实数根都在 α 和 β 之间，求 m 的值． 11．已知 a 为实数，且关于 x 的二次方程 ax 2＋(a 2＋1)x－a＝0 的两个实数根都小于 1，求这两个实数根的 最大值． 12．求实数 a 的取值范围，使关于 x 的方程 x 2＋2(a－1)x＋2a＋6＝0 （1）有两个实根 x1、x2，且满足 0＜x1＜1＜x2＜4； （2）至少有一个正根． 13．已知 x1、x2 是方程 x 2－mx－1＝0 的两个实数根，满足 x1＜x2，且 x2≥2． （1）求 m 的取值范围； （2）若 x2＋m x1－m ＋ x1＋m x2－m ＝2，求 m 的值． 14．已知关于 x 的方程 x 2－(m－2)x－ m 2 4 ＝0（m≠0） （1）求证：这个方程总有两个异号实根； （2）若这个方程的两个实根 x1、x2 满足| x2|＝| x1|＋2，求 m 的值及相应的 x1、x2． 15．已知△ABC 的一边长为 5，另两边长恰是方程 2x 2－12x＋m＝0 的两个根，求 m 的取值范围． 16．已知：α，β（α＞β）是一元二次方程 x 2－x－1＝0 的两个实数根，设 s1＝α＋β，s2＝α 2＋β 2，…， sn＝α n＋β n．根据根的定义，有 α 2－α－1＝0，β 2－β－1＝0，将两式相加，得(α 2＋β 2)－(α＋β)－2＝0，于是， 得 s2－s1－2＝0． 根据以上信息，解答下列问题： （1）利用配方法求 α，β 的值，并直接写出 s1，s2 的值； （2）猜想：当 n≥3 时，sn，sn-1，sn-2 之间满足的数量关系，并证明你的猜想的正确性； （3）根据（2）中的猜想，求( 1＋ 2 )8 ＋( 1－ 2 )8 的值． 17．已知方程(x－1)(x 2－2x＋m)＝0 的三个实数根恰好构成△ABC 的三条边长． （1）求实数 m 的取值范围； （2）当△ABC 为直角三角形时，求 m 的值和△ABC 的面积． O A B x y OA B x y NFP E M O A B x y 三、反比例函数 1．如图，点 A、B 在反比例函数 y＝－ 4 x 的图象上，且点 A、B 的横坐标分别为 a、2a（a＜0）． （1）求△AOB 的面积； （2）若点 C 在 x 轴上，点 D 在 y 轴上，且四边形 ABCD 为正方形，求 a 的值． 2．如图，点 P 是反比例函数 y＝－ 2 x（x＜0）图象上一动点，点 A、B 分别在 x 轴，y 轴上，且 OA＝OB＝ 2，PM⊥x 轴于 M，交 AB 于 E，PN⊥y 轴于 N，交 AB 于 F． （1）当动点 P 的纵坐标为 5 3 时，连接 OE、OF，求△EOF 的面积； （2）设动点 P 的坐标为 P（a，b）（－2＜a＜0，0＜b＜2 且| a |≠| b |），其他条件不变，探索：以 AE、 EF、BF 为边的三角形是怎样的三角形？并证明你的结论． 3．如图，在△OAB 中，OA＝OB，点 A 坐标为（－3 3，3），点 B 在 x 轴负半轴上． （1）将△OAB 沿 x 轴向右平移 a 个单位后，点 A 恰好落在反比例函数 y＝ 6 x 的图象上，求 a 的值； （2）将△OAB 绕点 O 按逆时针方向旋转 α 角（0°＜α＜90°）． ①当 α＝30°时，点 B 恰好落在反比例函数 y＝ k x 的图象上，求 k 的值； ②点 A、B 能否同时落在①中的反比例函数的图象上，若能，求 α 角的大小；若不能，请说明理由． O A B x y C O A B x y 备用图 4．如图，△AOB 为等腰直角三角形，斜边 OB 在 x 轴上，一次函数 y＝3x－4 的图象经过点 A，交 y 轴于点 C，反比例函数 y＝ k x（x＞0）的图象也经过点 A． （1）求反比例函数的解析式； （2）过 O 点作 OD⊥AC 于 D 点，求 CD 2－AD 2 的值； （3）若点 P 是 x 轴上的动点，在反比例函数的图象上是否存在点 Q，使得△PAQ 为等腰直角三角形？若 存在，求点 Q 的坐标，若不存在，请说明理由． 5．如图，已知一次函数 y＝kx＋b 的图象交反比例函数 y＝ 4－2m x （x＞0）图象于点 A、B，交 x 轴于点 C． （1）求的 m 的取值范围； （2）若点 A 的坐标是（2，－4），且 BC AB ＝ 1 3 ，求 m 的值和一次函数的解析式； （3）在（2）的条件下，设点 P 是一次函数图象上的第一、四象限内的动点，点 Q 是反比例函数图象上的 动点，过点 P 作 PP1⊥x 轴于 P1，PP2⊥y 轴于 P2；过点 Q 作 QQ1⊥x 轴于 Q1，QQ2⊥y 轴于 Q2．设点 P 的横坐标为 x，请直接写出使四边形 PP1OP2 的面积小于四边形 QQ1OQ2 的面积的 x 的取值范围． 6．在平面直角坐标系 xOy 中，直线 l1 过 A（1，0）且与 y 轴平行，直线 l2 过点 B（0，2）且与 x 轴平行， 直线 l1 与 l2 相交于点 P．点 E 为直线 l2 上一点，反比例函数 y＝ k x（k＞0）的图象过点 E 且与直线 l1 相交 于点 F． （1）若点 E 与点 P 重合，求 k 的值； （2）连接 OE、OF、EF．若 k＞2，且△OEF 的面积为△PEF 的面积的 2 倍，求点 E 的坐标； （3）是否存在点 E 及 y 轴上的点 M，使得以点 M、E、F 为顶点的三角形与△PEF 全等？若存在，求点 E 的坐标，若不存在，请说明理由． A O x y B C O A B x y l 7．如图，已知直线 l 经过点 A（1，0），且与曲线 y＝ m x（x＞0）交于点 B（2，1）．过点 P（p，p－1)（p＞ 1）作 x 轴的平行线分别交曲线 y＝ m x（x＞0）和 y＝－ m x（x＜0）于 M、N 两点． （1）求 m 的值及直线 l 的解析式； （2）若点 P 在直线 y＝2 上，求证：△PMB∽△PNA； （3）是否存在实数 p，使得 S△AMN ＝4S△APM？若存在，请求出所有满足条件的 p 的值；若不存在，请说明 理由． 8．如图，在平面直角坐标系中，O 为坐标原点，P 是反比例函数 y＝ 6 x（x＞0）图象上的任意一点，以 P 为圆心，PO 为半径的圆与 x、y 轴分别交于点 A、B． （1）判断 P 是否在线段 AB 上，并说明理由； （2）求△AOB 的面积； （3）Q 是反比例函数 y＝ 6 x（x＞0）图象上异于点 P 的另一点，请以 Q 为圆心，QO 半径画圆与 x、y 轴分 别交于点 M、N，连接 AN、MB．求证：AN∥MB． E l1 O x y B P 1 l2 F A 1 l1 O x y B P 1 l2 A 1 （备用图 1） l1 O x y B P 1 l2 A 1 （备用图 2） _y O A B x y Q P A E B x F CO y A B xC O y 9．如图，将—矩形 OABC 放在直角坐标系中，O 为坐标原点，点 A 在 y 轴正半轴上，点 E 是边 AB 上的— 个动点（不与点 A、B 重合），过点 E 的反比例函数 y＝ k x（x＞0）的图象与边 BC 交于点 F． （1）若△OAE、△OCF 的面积分别为 S1、S2，且 S1＋S2＝2，求 k 的值； （2）若 OA＝2，OC＝4，问当点 E 运动到什么位置时，四边形 OAEF 的面积最大，其最大值为多少？ 10．如图，已知抛物线 y＝( 3－m )x 2＋2( m－3 )x＋4m－m 2 的顶点 A 在双曲线 y＝ 3 x 上，直线 y＝mx＋b 经过 点 A，与 y 轴交于点 B，与 x 轴交于点 C． （1）求直线 AB 的解析式； （2）将直线 AB 绕点 O 顺时针旋转 90°，与 x 轴交于点 D，与 y 轴交与点 E，求 sin∠BDE 的值； （3）过点 B 作 x 轴的平行线与双曲线交于点 F，点 M 在直线 BF 上，且到抛物线的对称轴的距离为 6．若 点 N 在直线 BF 上，直接写出使得∠AMB＋∠ANB＝45°的点 N 的坐标． 11．如图，在平面直角坐标系中，直线 y＝mx（m＞0）与双曲线 y＝ k x 交于 A、B 两点，过点 A 作 AC∥x 轴，过点 B 作 BC∥y 轴，AC 与 BC 交于点 C，AC 与 y 轴交于点 M，BC 与 x 轴交于点 N，若∠BAC＝60°， AB＝4． （1）求 m、k 的值； （2）将一把三角尺的直角顶点放在原点 O 处，绕着点 O 旋转三角尺，三角尺的两直角边分别交射线 CA、 射线 BC 于点 P、Q，设点 P 的横坐标为 x，PQ 的长为 L，当点 P 在边 AC 上运动时，求 L 与 x 的函数关 系式； A B x C O y Q N M P A B x C O y （3）当△PQC 的面积为 2 时，求点 P 的坐标． 12．如图，在平面直角坐标系中，直线 y＝ax＋1（a≠0）与 x 轴交于点 A，与 y 轴交于点 B，与双曲线 y＝ k x 在第三象限的交点为 C（－2 3，m），且△AOB 的面积为 2． （1）求 a、m、k 的值； （2）以 BC 为一边作等边三角形 BCD，求 D 点的坐标． 13．已知一次函数 y＝2 x＋8 与反比例函数 y＝ k x 的图象相交于 A、B 两点，点 A 的横坐标为 x1，点 B 的横 坐标为 x2，且 x1－x2＝2． （1）求 k 的值； （2）求△AOB 的面积； （3）若一条开口向下的抛物线经过 A、B 两点，并在过点 A 且与 OB 平行的直线上截得的线段长为 13， 求抛物线的解析式． O A B x y O A B x y D C A B x C O y F E 14．如图，已知 A、B 两点的坐标分别为 A（0，2 3），B（2，0）直线 AB 与反比例函数 y＝ m x 的图象交与 点 C 和点 D（－1，a）． （1）求直线 AB 和反比例函数的解析式； （2）求∠ACO 的度数； （3）将△OBC 绕点 O 逆时针方向旋转 α 角（α 为锐角），得到△OB′C′，当 α 为多少度时 OC′⊥AB，并求此 时线段 AB′ 的长． 15．在矩形 AOBC 中，OA＝4，OB＝6．分别以 OB、OA 所在直线为 x 轴和 y 轴，建立如图所示的平面直 角坐标系．F 是边 BC 上的一个动点（不与 B、C 重合），过 F 点的反比例函数 y＝ k x（k＞0）的图象与 AC 边交于点 E． （1）若点 E 的坐标为（2，4），求经过 O、E、F 三点的抛物线的解析式； （2）设点 P 是（1）中所求抛物线上一点，且△PEF 的面积等于△OEF 的面积，求点 P 的坐标； （3）是否存在这样的点 F，使得将△CEF 沿 EF 对折后，C 点恰好落在 OB 上？若存在，求出此时 OF 的 长；若不存在，请说明理由． 16．如图，矩形 ABCD 的顶点 A 在坐标原点，顶点 B 坐标为（－2，1），顶点 C 在 y 轴上． （1）求顶点 D 的坐标； （2）将矩形 ABCD 绕点 O 顺时针旋转，使点 D 落在 x 轴的点 G 处，得到矩形 AEFG，EF 与 AD 交于点 M，过点 M 的反比例函数图象交 FG 于点 N，求△AMN 的面积； （3）求证：△AMN 是直角三角形． G x C O y FE B (A) D M N O x y C D N B E M A（1，3） 17．如图，已知反比例函数 y＝ m x（m 是常数，m≠0），一次函数 y＝ax＋b（a、b 为常数，a≠0），其中一 次函数与 x 轴，y 轴的交点分别是 A（－4，0），B（0，2）． （1）求一次函数的关系式； （2）反比例函数图象上有一点 P 满足：①PA⊥x 轴；②PO＝ 17（O 为坐标原点），求反比例函数的关系 式； （3）求点 P 关于原点的对称点 Q 的坐标，判断点 Q 是否在该反比例函数的图象上． 18．如图，已知反比例函数 y＝ m x（m＞0）的图象与一次函数 y＝－x＋b 的图象分别交于 A（1，3）、B 两 点． （1）求 m、b 的值； （2）若点 M 是反比例函数图象上的一动点，直线 MC⊥x 轴于 C，交直线 AB 于点 N，MD⊥y 轴于 D，NE⊥y 轴于 E．设四边形 MDOC、NEOC 的面积分别为 S1、S2，S＝S2－S1，求 S 的最大值． 19．如图，已知函数 y＝ 6 x（x＞0）的图象与一次函数 y＝kx＋b 的图象交于点 A（1，m），B（n，2）两 点． （1）求一次函数的解析式； （2）将一次函数 y＝kx＋b 的图象沿 x 轴负方向平移 a（a＞0）个单位长度得到新图象，求这个新图象与 函数 y＝ 6 x（x＞0）的图象只有一个交点 M 时 a 的值及交点 M 的坐标． O x y A P B O x A B y 20．如图，一次函数的图象与反比例函数 y1＝－ 3 x（x＜0）的图象相交于 A 点，与 y 轴、x 轴分别相交于 B、C 两点，且 C（2，0）．当 x＜－1 时，一次函数值大于反比例函数值，当 x＞－1 时，一次函数值小于 反比例函数值． （1）求一次函数的解析式； （2）设函数 y2＝ a x（x＞0）的图象与 y1＝－ 3 x（x＜0）的图象关于 y 轴对称，在 y2＝ a x（x＞0）的图象上取 一点 P（P 点的横坐标大于 2），过 P 作 PQ⊥x 轴，垂足为 Q，若四边形 BCQP 的面积等于 2，求 P 点的坐 标． 21．如图，已知二次函数 y＝ax 2＋2x＋c（a＞0）图象的顶点 M 在反比例函数 y＝ 3 x 的图象上，且与 x 轴相 交于 A、B 两点． （1）若二次函数图象的对称轴为 x＝－ 1 2 ，试求 a、c 的值； （2）在（1）的条件下，求线段 AB 的长； （3）若二次函数图象的对称轴与 x 轴的交点为 N，当 NO＋MN 取最小值时，试求二次函数的解析式． 22．如图，一次函数 y＝k x＋4 的图象与反比例函数 y＝ m x（x＞0，m＞0）的图象交于 A、B 两点，与 x 轴、 y 轴分别交于 C、D 两点． O x A B C Q P y y2y1 O x y B A N M A B x C O y D E 图 2 G F A B x C O y D 图 1 P Q R （1）求证：AC＝BD； （2）若△COD 的面积是△AOB 的面积的 2 倍，求 k 与 m 之间的函数关系式； （3）在（2）的条件下，是否存在实数 k 和 m，使得以 AB 为直径的圆经过点 P（2，0）？若存在，求出 k 和 m 的值；若不存在，请说明理由． 23．已知一次函数 y＝－ 1 2 x＋b 的图象与反比例函数 y＝ 6 x（x＞0）的图象交于 A、B 两点，与 x 轴、y 轴分 别交于 C、D 两点． （1）如图 1，若 AB＝2AC，求 b 的值； （2）在（1）的条件下，将一块直角三角板的直角顶点 P 放在反比例函数 y＝ 6 x（x＞0）图象的 AB 段上滑 动，两直角边始终与坐标轴平行，且与线段 AB 分别交于 Q、R 两点．设点 P 的横坐标为 x，QR 的长为 L， 求 L 关于 x 的函数关系式，并求 L 的最大值； （3）如图 2，过点 A 作直线 AE∥x 轴，交 y 轴于点 E；过点 B 作直线 BF∥y 轴交 x 轴于点 F，交直线 AE 于点 G．当四边形 OAGB 的面积为 8 时，请判断线段 AE 与 AG 的大小关系，并说明理由． 24．如图，已知反比例函数 y＝ k x 的图象经过 A（－1，a）、B（2，a＋3 3）两点，点 C 的坐标为（－1， 0）． （1）求反比例函数的解析式； （2）在反比例函数 y＝ k x 的图象上求点 D，使得以 A、 B、C、D 为顶点的四边形是梯形． A B x C O y DP y xO C B A O C B D P E x A y 25．如图，在平面直角坐标系中，双曲线 y＝ k x 过点 A（－4，1），点 P 是双曲线上一动点（不与 A 重合）， 过点 A 和 P 分别向两坐标轴作垂线，垂足分别为 B、C 和 D、E． （1）求 k、S△ADC 及 S△PDC 的值； （2）判断 AP 和 DC 的位置关系，并说明理由； （3）若点 P 在双曲线上运动时，探索以 A、P、C、D 四点为顶点的四边形能否成为菱形和等腰梯形？若 能，请直接写出所有满足条件的点 P 的坐标；若不能，请说明理由． 26．已知关于 x 的一元二次方程( a－1 )x 2＋( 2－3a )x＋3＝0． （1）求证：当 a 取不等于 1 的实数时，此方程总有两个实数根； （2）若 m，n（m＜n）是此方程的两根，且 1 m ＋ 1 n ＝ 4 3 ，直线 l：y＝mx＋n 交 x 轴于点 A，交 y 轴于点 B， 坐标原点 O 关于直线 l 的对称点 O′ 在反比例函数 y＝ k x 的图象上，求反比例函数的解析式； （3）在（2）的条件下，将直线 l 绕点 A 逆时针旋转 θ 角（0°＜θ＜90°），得到直线 l′，l′ 交 y 轴于点 P， 过点 P 作 x 轴的平行线，与（2）中的反比例函数图象交于点 Q，当四边形 APQO′ 的面积为 9－ 3 2 时，求 θ 角的大小． O x y 27．在平面直角坐标系中，一次函数 y＝－ 1 2 x＋5 的图象交 x 轴于点 A，交 y 轴于点 B，交直线 y＝x－1 于 点 C，过点 A 作 y 轴的平行线交直线 y＝x－1 于点 D，点 E 为线段 AD 上一点，且 tan∠DCE＝ 1 2．动点 P 从原点 O 出发沿 OA 边向点 A 匀速运动，同时，动点 Q 从 B 点出发沿 BO 边向原点 O 匀速运动，点 P 与 点 Q 同时到达 A 点和 O 点，设 BQ＝m． （1）求点 E 的坐标； （2）在整个运动过程中，是否存在这样的实数 m，使得△PQD 为直角三角形．若存在，求 m 的值；若不 存在，请说明理由； （3）反比例函数 y＝ k x 的图象经过点 C，R 为 y＝ k x 图象上一点，在整个运动过程中，若以 P、Q、E、R 为顶点的四边形是平行四边形，求 R 点的坐标． O A x y C D B E O A x y C D B 备用图 2 O A x y C D B 备用图 1 四、二次函数 1．设函数 y＝kx 2＋(2k＋1)x＋1（k 为实数）． （1）写出其中的两个特殊函数，使它们的图象不全是抛物线，并在同一直角坐标系中，用描点法画出这 两个函数的图象； （2）根据所画图象，猜想出：对任意实数 k，函数的图象都具有的特征，并给予证明； （3）对任意负实数 k，当 x＜m 时，y 随着 x 的增大而增大，试求出 m 的一个值． 2．在平面直角坐标系 xOy 中，二次函数 y＝mx 2＋( m－3)x－3（m＞0）的图象与 x 轴交于 A、B 两点（点 A 在点 B 左侧），与 y 轴交于点 C． （1）求点 A 的坐标； （2）当∠ABC＝45°时，求 m 的值； （3）已知一次函数 y＝kx＋b，点 P（n，0）是 x 轴上的一个动点．在（2） 的条件下，过点 P 垂直于 x 轴的直线交这个一次函数的图象于点 M，交二次 函数 y＝mx 2＋( m－3)x－3（m＞0）的图象于 N．若只有当－2＜n＜2 时， 点 M 位于点 N 的上方，求这个一次函数的解析式． 3．已知平面直角坐标系 xOy，一次函数 y＝ 3 4 x＋3 的图象与 y 轴交于点 A，点 M 在正比例函数 y＝ 3 2 x 的图 象上，且 MO＝MA，二次函数 y＝x 2＋bx＋c 的图象经过点 A、M． （1）求线段 AM 的长； （2）求这个二次函数的解析式； （3）若点 B 在 y 轴上，点 C 在上述二次函数的图象上，点 D 在一次 函数 y＝ 3 4 x＋3 的图象上，且四边形 ABCD 是菱形，求点 C 的坐标． 4．已知二次函数 y＝ax 2＋bx＋c 和一次函数 y＝－bx，其中实数 a、b、c 满足 a＞b＞c，a＋b＋c＝0． （1）求证：这两个函数的图象交于不同的两点； （2）设这两个函数的图象交于 A、B 两点，作 AA1⊥x 轴于 A1，BB1⊥x 轴于 B1，求线段 A1B1 长的取值范 围． 5．已知二次函数 y＝ax 2－4bx＋4c（a＞0）有两个实数根 x1，x2，且 2≤x1＜x2≤3． （1）求证：存在以 a，b，c 为边长的三角形； （2）求证： c b＋c ＜ a a＋c ＋ b b＋a ． 6．已知二次函数 y＝x 2＋bx＋c（c＜0）的图象与 x 轴交于点 A、B，与 y 轴交于点 C，△ABC 的外接圆的 圆心为点 P． （1）证明：⊙P 与 y 轴的另一个交点为定点； （2）如果 AB 恰好为⊙P 的直径且 S△ABC ＝2，求 b 和 c 的值． O x y -1 -2 -3-1-3 -2 -1 -2 -3 -4 -5 -1 -2 -3 -4 -5 O x y -1 -1 7．已知关于 x 的二次函数 y1＝( m＋2)x 2－2x－1 和 y2＝( m＋2)x 2＋mx＋m＋1 的图象都经过 x 轴上的点（n， 0）． （1）求 m 的值； （2）将二次函数 y1＝( m＋2)x 2－2x－1 的图象先沿 x 轴翻折，再向下平移 3 个单位，得到一个新的二次函 数 y3 的图象． ①求 y3 的解析式； ②在所给的坐标系中画出 y2 和 y3 的大致图象，并结合函数的图象回答：当 x 取何值时，y3＞y2？ 8．已知关于 x 的方程： x 2＋a x－2 －a－1＝0 有一个增根为 b，另一根为 c． （1）求 a、c 的值； （2）若二次函数 y＝ax 2＋bx＋c＋7（－ 3 2≤x ≤ 3 2）图象与 x 轴交于 E、F 两点，在此二次函数的图象上求一 点 P，使△PEF 的面积最大，求点 P 的坐标． 9．已知：二次函数 y＝x 2＋bx－3 的图象经过点 P（－2，5）． （1）求 b 的值，并写出当 1＜x ≤3 时 y 的取值范围； （2）设 P1（m，y1）、P2（m＋1，y2）、P3（m＋2，y3）在这个二次函数的图象上． ①当 m＝4 时，y1、y2、y3 能否作为同一个三角形三边的长？请说明理由； ②当 m 取不小于 5 的任意实数时，y1、y2、y3 一定能作为同一个三角形三边的长，请说明理由． 10．已知 A（1，0），B（0，－1），C（－1，2），D（2，－1），E（4，2）五个点，抛物线 y＝a( x－1)2＋k （a＞0）经过其中的三个点． （1）求证：C，E 两点不可能同时在抛物线 y＝a( x－1)2＋k（a＞0）； （2）点 A 在抛物线 y＝a( x－1)2＋k（a＞0）上吗？为什么？ （3）求 a 与 k 的值． 11．已知二次函数 y＝x 2－(2m－1)x＋4m－6． （1）试说明不论 m 取任何实数，函数图象都经过 x 轴上的一个定点 A； （2）设函数图象与 x 轴的另一个交点为 B（A 与 B 不重合），顶点为 C，当△ABC 为直角三角形时，求 m 的值； （3）在（2）的条件下，若点 B 在点 A 的右侧，点 D 的坐标为（0，3），点 E 是函数图象上一点．问：在 x 轴上是否存在点 F，使得以 D、E、F 为顶点的三角形是等腰直角三角形？若存在，求出 F 点坐标；若不 存在，请说明理由． 1 x y O-1 12．已知二次函数 y＝x 2＋bx＋c，其中函数值 y 与自变量 x 的部分对应值如下表： x … －1 0 1 2 3 … y … 0 －5 －8 －9 －8 … （1）求该二次函数的关系式，并在给定的坐标系中画出函数的图象； （2）若 A（m，y1），B（m＋4，y2）两点都在该函数的图象上． ①试比较 y1 与 y2 的大小； ②若 A、B 两点位于 x 轴的下方，点 P 为函数图象的对称轴与 x 轴的交点，点 Q 为函数图象上的一点， 解答下列问题： （Ⅰ）求实数 m 的取值范围； （Ⅱ）是否存在实数 m，使得以 P、A、B、Q 四点为顶点的四边形为平行四边形？若存在，求出 m 的值； 若不存在，请说明理由． 13．已知二次函数 y＝x 2－( 2a＋1 )x＋2a． （1）若函数图象与 x 轴有两个不同交点，且分别位于点（2，0）的两侧，求实数 a 的取值范围； （2）若函数图象不经过第三象限，且当 x＞2 时，函数值 y 随 x 的增大而增大，求实数 a 的取值范围． 14．已知关于 x 的一元二次方程 x 2－4x＋c＝0 有实数根，且 c 为正整数． （1）求 c 的值； （2）若此方程的两根均为整数，在平面直角坐标系中，抛物线 y＝x 2－4x＋c 与 x 轴交于 A、B 两点（A 在 B 左侧），与 y 轴交于点 C．点 P 为对称轴上一点，且四边形 OBPC 为直角梯形，求 PC 的长； （3）将（2）中得到的抛物线沿水平方向平移，设顶点 D 的坐标为（m，n），当抛物线与直角梯形 OBPC 只有两个交点，且一个交点在 PC 边上时，直接写出 m 的取值范围． 15．已知一次函数 y1＝2x，二次函数 y2＝mx 2－3( m－1)x＋2m－1 的图象关于 y 轴对称，y2 的顶点为 A． （1）求二次函数 y2 的解析式； （2）将 y2 左右平移得到 y3，y3 交 y2 于点 P，过 P 点作直线 l∥x 轴交 y3 于点 Q，若△PAQ 为等腰三角形， 求 P 点坐标和函数 y3 的解析式； （3）是否存在二次函数 y4＝ax 2＋bx＋c，其图象经过点（－5，2），且对于任意一个实数 x，y1≤y4≤y2 均 成立，若存在，求出函数 y4 的解析式；若不存在，请说明理由． 16．已知二次函数 y＝ax 2＋bx＋c（a＞0）图象经过点 C（0，1），且与 x 轴交于不同的两点 A、B，点 A 的 坐标为（1，0）． （1）求 c 的值； （2）求 a 的取值范围； （3）该二次函数的图象与直线 y＝1 交于 C、D 两点，设 A、B、C、D 四点构成的四边形的对角线相交于 -2 642-2 2 -4 -10 -8 y M O M x M -6 点 P，记△PCD 的面积为 S1，△PAB 的面积为 S2，当 0＜a＜1 时，求证：S 1 － S2 为常数，并求出该常 数． 17．已知二次函数 y＝ax 2＋bx＋c 图象的顶点坐标为（2，4）． （1）试用含 a 的代数式分别表示 b，c； （2）若一次函数 y＝kx＋4（k≠0）图象与 y 轴及二次函数 y＝ax 2＋bx＋c 图象的交点依次为 D、E、F，且 S △ ODE S △ OEF ＝ 1 3 ，其中 O 为坐标原点，试用含 a 的代数式表示 k； （3）在（2）的条件下，若线段 EF 的长 m 满足 3 2≤m≤3 5，试确定 a 的取值范围． 18．已知二次函数 y＝－x 2＋bx＋c 的图象与 x 轴交于 A（x1，0），B（x2，0）两点（A 在 B 的左侧），且 x1＋ x2＝4． （1）求 b 的值及 c 的取值范围； （2）若 AB＝2，求二次函数的表达式； （3）设该二次函数的图象与 y 轴交于点 C，顶点为 D，对称轴与 x 轴交于点 E．问是否存在这样的二次函 数，使△AOC≌△BED？若存在，求二次函数的表达式；若不存在，请说明理由． 19．已知二次函数 y＝x 2＋mx－ 3 4 m 2（m＞0）的图象与 x 轴交于 A、B 两点． （1）求证：该函数图象的对称轴在 y 轴的左侧； （2）若 1 OB － 1 OA ＝ 2 3（O 为坐标原点），求二次函数的表达式； （3）设函数图象与 y 轴交于点 C，若△ABC 是直角三角形．求△ABC 的面积． 20．已知二次函数 y＝－ 1 4 x 2＋ 3 2 x 的图象如图所示． （1）求它的对称轴与 x 轴交点 D 的坐标； （2）将该函数图象沿它的对称轴向上平移，设平移后的图象与 x 轴，y 轴的交点分别为 A、B、C 三点， 若∠ACB＝90°，求此时函数的解析式； （3）设（2）中平移后的函数图象的顶点为 M，以 D 为圆心，AB 为直径作⊙D，试判断直线 CM 与⊙D 的位置关系，并说明理由. 21．已知二次函数的图象经过点 A（1，0）和点 B（2，1），且与 y 轴交点的纵坐标为 m． （1）若 m 为定值，求此二次函数的解析式； （2）若二次函数的图象与 x 轴还有异于点 A 的另一个交点，求 m 的取值范围； （3）若二次函数的图象截直线 y＝－x＋1 所得线段的长为 2 2，求 m 的值． O C A D M y xB O C A D M y xB 备用图 22．已知二次函数 y＝3ax 2＋2bx＋c． （1）若 a＝b＝1，c＝－1，求函数图象与 x 轴交点的坐标； （2）若 a＝b＝1，且当－1＜x＜1 时，函数图象与 x 轴有且只有一个交点，求 c 的取值范围； （3）若 a＋b＋c＝0，且当 x＝0 和 x＝1 时，对应的函数值 y 均大于 0．试判断当 0＜x＜1 时，函数图象与 x 轴是否有交点？请说明理由． 23．在平面直角坐标系 xOy 中，过点 P（0，2）作一直线与二次函数 y＝ax 2（a＞0）图象交于 A、B 两点， 且使∠AOB＝90°． （1）判断 A、B 两点纵坐标的乘积是否为定值，并说明理由； （2）求 a 的值； （3）当△AOB 的面积为 4 2 时，求直线 AB 的解析式． 24．已知二次函数 y＝x 2＋4x＋m（m 为常数）的图象经过点（0，4），将该函数图象先向右、再向下平移 得到一新的函数图象，已知平移后的函数图象满足下述两个条件：它的对称轴（设为直线 l2）与平移前的 函数图象的对称轴（设为直线 l1）关于 y 轴对称；它所对应的函数的最小值为－8． （1）求平移后的二次函数的表达式； （2）试问在平移后的函数图象上是否存在点 P，使得以 3 为半径的⊙P 既与 x 轴相切，又与直线 l2 相交？ 若存在，请求出点 P 的坐标，并求出直线 l2 被⊙P 所截得的弦 AB 的长度；若不存在，请说明理由． 25．使得函数值为零的自变量的值称为函数的零点．例如，对于函数 y＝x－1，令 y＝0，可得 x＝1，则 1 就是函数 y＝x－1 的零点． 己知函数 y＝x 2－2mx－2( m＋3)（m 为常数）． （1）当 m＝0 时，求该函数的零点； （2）证明：无论 m 取何值，该函数总有两个零点； （3）设函数的两个零点分别为 x1 和 x2，且 1 x1 ＋ 1 x2 ＝－ 1 4 ，此时函数图象与 x 轴的交点分别为 A、B（点 A 在点 B 左侧），点 M 在直线 y＝x－10 上，当 MA＋MB 最小时，求直线 AM 的函数解析式． 26．已知二次函数 y＝x 2－2mx＋m 2－4 的图象与 x 轴交于 A、B 两点（点 A 在点 B 的左边），且与 y 轴交于 点 D． （1）当点 D 在 y 轴正半轴时，是否存在实数 m，使得△BOD 为等腰三角形？若存在，求出 m 的值；若不 存在，请说明理由； （2）当 m＝－1 时，将函数 y＝x 2－2mx＋m 2－4 的图象在 x 轴下方的部分沿 x 轴翻折，图象的其余部分保 持不变，得到一个新的图象．当直线 y＝ 1 2 x＋b 与这个新的图象有两个公共点时，求实数 b 的取值范围． O y x 27．已知二次函数 y＝x 2－2mx＋4m－8． （1）当 x≤2 时，函数值 y 随 x 的增大而减小，求 m 的取值范围； （2）以抛物线 y＝x 2－2mx＋4m－8 的顶点 A 为一个顶点作该抛物线的内接正三角形 AMN（M，N 两点在 拋物线上），请问：△AMN 的面积是与 m 无关的定值吗？若是，请求出这个定值；若不是，请说明理由； （3）若抛物线 y＝x 2－2mx＋4m－8 与 x 轴交点的横坐标均为整数，求整数 m 的值． 28．已知二次函数 y＝ax 2＋bx＋c 图象与一次函数 y＝mx＋n 图象相交于（0，－ 1 2）和（m－b，m 2－mb＋n） 两点（a，b，c，m，n 均为实数，且 a，m 不为 0）． （1）求 c 的值； （2）设二次函数图象与 x 轴的两个交点是（x1，0）和（x2，0），求 x1x2 的值； （3）当－1≤x≤1 时，设二次函数图象上与 x 轴距离最大的点为 P（x0，y0），求此时| y0|的最小值． 29．已知二次函数 y＝ax 2＋bx＋c 的图象的顶点坐标为（0， p 2），且 ac＝ 1 4 ． （1）若该函数的图象过点（－1，－1）． ①求使 y＜0 成立的 x 的取值范围； ②若圆心在该函数的图象上的圆与 x 轴、y 轴都相切，求圆心的坐标． （2）过点 A（0，p）的直线与该函数的图象相交于 M，N 两点，过 M，N 作 x 轴的垂线，垂足分别为 M1， N1．设△MAM1，△A M1N1，△ANN1 的面积分别为 S1，S2，S3 ，是否存在 m，使得对任意实数 p≠0 都有 S2 2 ＝mS1S3 成立，若存在，求出 m 的值；若不存在，请说明理由． 30．在平面直角坐标系中，已知点 A 的坐标为（3，0），第一象限内的点 P 在直线 y＝2x 上，且∠PAO＝ 45°． （1）求点 P 的坐标； （2）若二次函数的图象经过 P、O、A 三点，求该二次函数的解析式； （3）设（2）中的二次函数图象的顶点为 M，将该二次函数图象向上或向下平移，使它的顶点落在直线 y＝ 2x 上的点 Q 处，求△APM 与△APQ 的面积之比． A O x y O x y －1 1 31．已知二次函数 y＝－ 3x 2－2 3(－a－1)x－ 3(－a 2－2a )的图象与 x 轴交于点 A（x1，0）、B（x2，0）， 且 x1＜1＜x2． （1）求 A、B 两点的坐标（用 a 表示）； （2）设二次函数图象的顶点为 C，求△ABC 的面积； （3）若 a 是整数，P 是线段 AB 上的一个动点（不与点 A、B 重合），在 x 轴上方作等边△APM 和等边△ BPN，记线段 MN 的中点为 Q，求二次函数的解析式及线段 PQ 的长的取值范围． 32．已知二次函数 y＝a( a＋1)x 2－( 2a＋1)x＋1（a 是正整数）． （1）求该函数图象与 x 轴相交所截得的线段的长； （2）当 a 依次取 1，2，3， …，n 时，该函数图象与 x 轴相交所截得的 n 条线段的长分别为 L1，L2， L3，…，Ln，求 L1＋L2＋L3＋ … ＋Ln 的值． 33．已知 a＞b＞c，且 2a＋3b＋4c＝0． （1）求证：a＋b＋c＞0； （2）若抛物线 y＝ax 2＋bx＋c 在 x 轴上截得的线段长为 6，求该抛物线的对称轴． 34．已知关于 x 的方程( a＋2)x 2－2ax＋a＝0 有两个不相等的实数根 x1 和 x2，且抛物线 y＝x 2－(2a＋1)x＋2a －5 与 x 轴的两个交点分别位于点（2，0）的两侧． （1）求实数 a 的取值范围； （2）当|x1|＋|x2|＝2 2时，求 a 的值． 35．已知二次函数 y1＝ax 2－x＋c 的图象与 x 轴交于点 A（x1，0），B（x2，0）（x1＜0，x2＞0），与 y 轴的交 点 C 在 y 轴的负半轴上，且 tan∠ACO＝ 2 3 ，S△ABC ＝3 ． （1）求该二次函数的解析式； （2）若该二次函数的图象与反比例函数 y2＝ k x（k＜0）的图象在第二象限内的交点的横坐标 x0 满足－3＜ x0＜－2，求 k 的取值范围． 36．已知方程 ax 2＋bx＋1＝x（a＞0）的两个实数根为 x1，x2． （1）若 x1＜2＜x2＜4，二次函数 y＝ax 2＋bx＋1 图象的对称轴为 x＝x0，求证：x0＞－1； （2）若| x1|＜2，| x2－x1|＝2，求 b 的取值范围． 37．已知二次函数y＝ax 2＋bx＋c（a＞0），且方程ax 2＋bx＋c＝x的两个根x1，x2满足0＜x1＜x2＜ 1 a ． 1O x y 2 3 3 2 1 （1）求证：当0＜x＜x1时，x＜ax 2＋bx＋c＜x1； （2）若二次函数y＝ax 2＋bx＋c的图象关于直线x＝x0对称，求证：x0＜ x1 2 ． 38．已知关于 x 的二次方程 x 2＋ax＋b＝0 有两个实数根 x1，x2． （1）若|x1|＜2，|x2|＜2，求证：2|a|＜4＋b 且|b|＜4； （2）若 2|a|＜4＋b 且|b|＜4，求证：|x1|＜2，|x2|＜2． 39．已知二次函数的图象与 x 轴交于 A，B 两点，与 y 轴交于点 C（0，4），且| AB|＝2 3，图象的对称 轴为 x＝1． （1）求二次函数的表达式； （2）若二次函数的图象都在直线 y＝x＋m 的下方，求 m 的取值范围． 40．已知二次函数 y＝ax 2－4ax＋b（b＜0）的图象开口向上，与 x 轴的两个交点分别为 A、B，且 |OA| |OB|＝ 1 5 （O 为坐标原点），与 y 轴的交点为 C（0，t），顶点的纵坐标为 k，且|k－ 9 5 3|≤ 24 5 3． （1）求 A、B 两点的坐标； （2）求 t 的取值范围； （3）当 t 取最小值时，求该二次函数的表达式． 41．已知 a，b 为常数，当 k 取任意实数时，函数 y＝(k 2＋k＋1)x 2－2(a＋k)2x＋(k 2＋3ak＋b)的图象与 x 轴 都交于点 A（1，0）． （1）求 a、b 的值； （2）若函数图象与 x 轴的另一个交点为 B，当 k 变化时，求|AB|的取值范围． 42．已知二次函数 y＝－x 2＋mx－m＋2． （1）若该二次函数图象与 x 轴的两个交点 A、B 分别在原点的两侧，并且 AB＝ 5，求 m 的值； （2）设该二次函数图象与 y 轴的交点为 C，二次函数图象上存在关于原点对称的两点 M、N，且 S△MNC ＝ 27，求 m 的值． 43．已知两个二次函数 y1，y2，当 x＝m（m＞0）时，y1 取最小值 6 且 y2＝5，又 y2 最小值为 5 6 ，y1＋y2＝2x 2－3x＋9． （1）求 m 的值； （2）求二次函数 y1、y2 的表达式． 44．已知 ab≠0，且函数 y1＝x 2＋2ax＋4b 与 y2＝x 2＋4ax＋2b 有相同的最小值 m，函数 y3＝－x 2＋2bx＋4a 与 y4＝－x 2＋4bx＋2a 有相同的最大值 n，求证：m＋n＝0． 45．对于 x 的二次三项式 ax 2＋bx＋c（a＞0）． （1）当 c＜0 时，求函数 y＝－2|ax 2＋bx＋c|－1 的最大值； （2）若不论 k 为任何实数，直线 y＝k(x－1)－ k 2 4 与抛物线 y＝ax 2＋bx＋c 有且只有一个公共点，求 a、b、 c 的值． 46．已知二次函数 y＝3ax 2＋2bx＋c，若 a＋b＋c＝0，且当 x＝0 和 x＝1 时，函数值 y 均大于 0． （1）求证：a＞0 且－2＜ b a ＜－1； （2）求证：方程 3ax 2＋2bx＋c＝0 有两个实数根且都大于 0 小于 1． 47．已知二次函数 y＝ax 2＋bx＋c 的图象经过点（0，3），顶点在直线 y＝－x＋1 上且在第四象限，顶点与 原点的距离为 5． （1）求该二次函数的表达式； （2）设该二次函数的图象与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），顶点为 C，直线 y＝－x＋1 交 y 轴于点 D．在 y 轴上是否存在点 P，使得以 P、O、C 为顶点的三角形与△BCD 相似？若存在，求出 P 点 的坐标．若不存在，请说明理由． 48．已知 y＝ax 2＋x－a（－1≤x≤1）． （1）若|a|≤1，求证：|y|≤ 5 4 ； （2）若 y 的最大值为 17 8 ，求 a 的值． 49．已知抛物线 y＝x 2＋mx＋n 上有一点 P（x0，y0）位于 x 轴下方． （1）求证：此抛物线与 x 轴交于两点； （2）设此抛物线与 x 轴的交点为 A（x1，0），B（x2，0），且 x1＜x2，求证：x1＜x0＜x2； （3）当点 P 坐标为（1，－2011）时，求整数 x1，x2 的值． 50．已知在 Rt△ABC 中，∠C＝90°，BC＝a，AC＝b，且 cotB＝AB·cosA． （1）求证：a＝b 2； （2）若 b＝2，抛物线 y＝m(x－b)2＋a 与直线 y＝x＋4 交于 M（x1，y1）、N（x2，y2）两点，且△MON 的 面积为 6，求 m 的值； （3）若 a＝ 1 4 b 2n 2，p－q＝3，抛物线 y＝n(x 2＋px＋3q)与 x 轴交于不同的两点，其中一个交点在原点右侧， 试判断抛物线与 y 轴的交点在 y 轴的正半轴还是负半轴，说明理由． 51．已知二次函数 y＝ax 2＋bx＋c（a≠0）的图象经过 A（－1，0）、B（0，－l）两点，它的顶点在第一象 限，它的一部分图象如图所示． （1）试确定 b 的符号； （2）当 b 变化时，求 a＋b＋c 的取值范围； （3）是否存在实数 a，使得∠ABC＝120°？若存在，求 a 的值；若不存在，请说明理由． y xO y＝－x＋1 y OA B x 52．如图，Rt△ABC 的斜边 AB 在 x 轴上（点 A 在点 B 的左侧），直角顶点 C 在 x 轴的上方，且 A（tanA， 0）、B（tanB，0），二次函数 y＝－x 2－ 5 2 mx＋(2＋2m－m 2)（x 为自变量）的图象经过 A、B 两点． （1）求该二次函数的表达式； （2）判断直角顶点 C 是否在该二次函数的图象上，请说明理由． 53．已知抛物线 F1：y＝ax 2－2amx＋am 2＋2m＋1（a＞0，m＞0）的顶点为 A，抛物线 F 2 的顶点 B 在 y 轴 上，且抛物线 F1 和 F2 关于点 M（1，3）成中心对称． （1）求 m 的值和抛物线 F2 的解析式； （2）设抛物线 F2 与 x 轴正半轴的交点为 C，当△ABC 为等腰三角形时，求 a 的值． 54．已知二次函数 y＝－x 2＋( m－2)x＋3( m＋1)． （1）求证：无论 m 为任何实数，函数图象与 x 轴总有交点； （2）设函数图象与 y 轴交于点 C，当函数图象与 x 轴有两个交点 A、B（点 A 在点 B 的左侧），且△ABC 为钝角三角形时，求 m 的取值范围； （3）在（2）的条件下，P 是函数图象的顶点，当△PAO 的面积与△ABC 的面积相等时，求二次函数的解 析式． 55．已知关于 x 的一元二次方程 x 2－2(k＋1)x＋k 2＝0 有两个整数根，k＜5 且 k 为整数． （1）求 k 的值； （2）当此方程有两个非零的整数根时，将关于 x 的二次函数 y＝x 2－2(k＋1)x＋k 2 的图象沿 x 轴向左平移 4 个单位，求平移后的二次函数图象的解析式； （3）根据直线 y＝x＋b 与（2）中的两个函数图象交点的总个数，求 b 的取值范围． 56．如图，二次函数 y＝ax 2＋bx（a＞0）与反比例函数 y＝ k x 的图象相交于 A，B 两点，且点 A 的坐标为 O x y A B C y xO （1，4），点 B 在第三象限，△AOB 的面积为 3． （1）求二次函数的表达式； （2）过点 A 作 x 轴的平行线，交二次函数 y＝ax 2＋bx 的图象于另一点 C，连接 CO，在坐标平面内求点 P，使△POC∽△AOB（点 P 与点 A 对应）． 57．已知直线 y＝ 1 2 x 和 y＝－x＋m，二次函数 y＝x 2＋bx＋c 图象的顶点为 M． （1）若 M 恰好是直线 y＝ 1 2 x 与 y＝－x＋m 的交点，试证明：无论 m 取何实数值，二次函数 y＝x 2＋bx＋c 的图象与直线 y＝－x＋m 总有两个不同的交点； （2）在（1）的条件下，若直线 y＝－x＋m 过点 D（0，－3），求二次函数 y＝x 2＋bx＋c 的表达式； （3）在（2）的条件下，若二次函数 y＝x 2＋bx＋c 的图象与 y 轴的交点为 C，与 x 轴的左交点为 A． ①在直线 y＝ 1 2 x 上求异于 M 的点 P，使点 P 在△ACM 的外接圆上； ②在二次函数图象的对称轴上是否存在点 Q，使得△QAC 为等腰三角形？若存在，直接写出点 Q 的坐 标；若不存在，请说明理由． 58．已知二次函数 y＝x 2＋(m－1)x＋m－2 的图象与 x 轴相交于 A（x1，0），B（x2，0）两点，且 x1＜x2． （1）若 x1x2＜0，且 m 为正整数，求该二次函数的表达式； （2）若 x1＜1，x2＞1，求 m 的取值范围； （3）是否存在实数 m，使得过 A、B 两点的圆与 y 轴相切于点 C（0，2），若存在，求出 m 的值；若不存 在，请说明理由； （4）若过点 D（0， 1 2）的直线与（1）中的二次函数图象相交于 M、N 两点，且 MD DN ＝ 1 3 ，求该直线的表达 式． C A O B x M y M 五、概率 1．小张同学去展览馆看展览，该展览馆有 2 个验票口 A、B（可进出），另外还有 2 个出口 C、D（不许 进）． （1）小张从进入到离开共有多少种可能的进出方式？（要求用列表或树状图） （2）小张不从同一个验票口进出的概率是多少？ 2．如图，甲、乙两个可以自由转动的均匀的转盘，甲转盘被分成 3 个面积相等的扇形，乙转盘被分成 4 个面积相等的扇形，每一个扇形都标有相应的数字，同时转动两个转盘，当转盘停止后，设甲转盘中指针 所指区域内的数字为 m，乙转盘中指针所指区域内的数字为 n（若指针指在边界线上时，重转一次，直到 指针都指向一个区域为止）． （1）请你用画树状图或列表格的方法求出|m＋n|＞1 的概率； （2）直接写出点（m，n）落在函数 y＝－ 1 x 图象上的概率． 3．经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转．如果这三种可能性大小相同，现 有两辆汽车经过这个十字路口． （1）试用树形图或列表法中的一种列举出这两辆汽车行驶方向所有可能的结果； （2）求至少有一辆汽车向左转的概率． 4．有 3 张扑克牌，分别是红桃 3、红桃 4 和黑桃 5．把牌洗匀后甲先抽取一张，记下花色和数字后将牌放 回，洗匀后乙再抽取一张． （1）先后两次抽得的数字分别记为 s 和 t，求| s－t |≥1 的概率． （2）甲、乙两人做游戏，现有两种方案．A 方案：若两次抽得相同花色则甲胜，否则乙胜．B 方案：若两 次抽得数字和为奇数则甲胜，否则乙胜． 请问甲选择哪种方案胜率更高？ 5．小国同学的父亲参加旅游团到某地旅游，准备买某种礼物送给小国．据了解，沿旅游线路依次有 A、 B、C 三个地点可以买到此种礼物，其质量相当，价格各不相同，但不知哪家更便宜．由于时间关系，随 团旅游车不会掉头行驶． （1）若到 A 处就购买，写出买到最低价格礼物的概率； （2）小国同学的父亲认为，如果到 A 处不买，到 B 处发现比 A 处便宜就马上购买，否则到 C 处购买，这 样更有希望买到最低价格的礼物．这个想法是否正确？试通过树状图分析说明． 6．甲口袋中装有两个相同的小球，它们的标号分别为 2 和 7，乙口袋中装有两个相同的小球，它们的标号 展览大厅 出口 C 出口 D 验票口 A 验票口 B 甲 1 －1－ 1 2 1 －1 02 乙 分别为 4 和 5，丙口袋中装有三个相同的小球，它们的标号分别为 3，8，9．从这 3 个口袋中各随机地取 出 1 个小球． （1）求取出的 3 个小球的标号全是奇数的概率是多少？ （2）以取出的三个小球上的标号分别表示三条线段的长度，求这些线段能构成三角形的概率． 7．6 张不透明的卡片，除正面画有不同的图形外，其它均相同，把这 6 张卡片洗匀后，正面向下放在桌上， 另外还有与卡片上图形形状完全相同的地板砖若干块，所有地板砖的长都相等． （1）从这 6 张卡片中随机抽取一张，与卡片上图形形状相对应的这种地板砖能进行平面镶嵌的概率是多 少？ （2）从这 6 张卡片中随机抽取 2 张，利用列表或画树状图计算：与卡片上图形形状相对应的这两种地板 砖能进行平面镶嵌的概率是多少？ 8．在△ABC 和△DEF 中，∠C＝∠F＝90°．有如下五张背面完全相同的纸牌①、②、③、④、⑤，其正 面分别写有五个不同的等式，小明将这五张纸牌背面朝上洗匀后先随机摸出一张（不放回），再随机摸出 一张．请结合以上条件，解答下列问题． （1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用①、②、③、④、⑤表示）； （2）用两次摸牌的结果和∠C＝∠F＝90°作为条件，求能满足△ABC 和△DEF 全等的概率． 9．如图，A 信封中装有两张卡片，卡片上分别写着 7cm、3cm；B 信封中装有三张卡片，卡片上分别写着 2cm、4cm、6cm；信封外有一张写着 5cm 的卡片．所有卡片的形状、大小都完全相同．现随机从两个信封 中各取出一张卡片，与信封外的卡片放在一起，用卡片上标明的数量分别作三条线段的长度． （1）求这三条线段能组成三角形的概率（画出树状图）； （2）求这三条线段能组成直角三角形的概率． 正三角形 正方形 B D 正六边形正五边形 C E 正八边形 F 正十边形 A A B C D E F ① AB＝DE ② ∠A＝∠D ③ BC＝EF ④ ∠B＝∠E ⑤ AC＝DF A B 5cm 10．我国不少地方农历正月十五元宵节有吃汤圆的习俗．为了增加节日的喜庆气氛，小华的妈妈在自己动 手包的 48 个汤圆中，有两个汤圆用红枣做馅，与其它汤圆不同馅．若吃到包有红枣的汤圆，被认为这一 年心情总是甜美的． （1）若只吃一个汤圆，求吃到包有红枣汤圆的概率； （2）若每碗盛 8 个汤圆，小华吃 2 碗，盛汤圆时，两个红枣汤圆被盛到不同的碗里，求小华吃到包有红 枣汤圆的概率，并说明理由； （3）若每碗盛 8 个汤圆，小华吃 2 碗，盛汤圆时，两个红枣汤圆正好被盛到同一碗里，求小华吃到包有 红枣汤圆的概率，并说明理由． 11．已知关于 的方程 ax 2＋bx＋c＝0，甲、乙两人做游戏：他们轮流确定实数 a，b，c（如甲令 b＝1，乙 令 a＝－2，甲再令 c＝10），让甲先确定数，如果方程至少有一个解 x0，满足－1≤x0≤1，那么乙胜；反之， 则甲胜． （1）若 a，b，c 只能取非零实数，甲是否有必胜策略？请说明理由； （2）若 a，b，c 可以取零，甲乙两人中谁有必胜策略？请说明理由． 12．如图 1，一小球从三角仪器的入口处落下，当它碰到每层菱形挡板时，向左或向右落下的可能性相 同． （1）求小球通过第二层 A 位置的概率是多少？ （2）求小球下落到第三层 B 位置和第四层 C 位置处的概率各是多少？ （3）如图 2，在第二层与第三层之间加一左侧隔板，求小球落到 B、C 位置处的概率各是多少？ 13．将一枚六个面分别标有 1，2，3，4，5，6 的质地均匀的正方体骰子先后投掷两次，记第一次掷出的 点数为 a，第二次掷出的点数为 b． （1）求点（a，b）落在直线 y＝2x－1 上的概率； （2）求以点 O（0，0），A（4，－3），B（a，b）为顶点能构成等腰三角形的概率； （3）求关于 x，y 的方程组 { ①只有一组解的概率； ②只有正数解的概率． 14．某俱乐部举行抽奖活动，活动规则是：每位会员交 30 元，可参加一次抽奖活动．从一个装有数字分 别为 1，2，3，4，5，6 的六个相同小球的抽奖箱中，任意摸出一个球，然后放回箱中，摇匀，再摸出第 二个球．若两次摸出的球的数字之和为 12，则获得价值为 a 元的礼品；若两次摸出的球的数字之和为 11 或 10，则获得价值 100 元的奖品；若两次摸出的球的数字之和小于 10，则不获奖． （1）求每位会员获奖的概率； （2）如果俱乐部打算这次活动既不赚钱也不赔钱，求 a 的值． 15．已知一元二次方程 ax 2＋bx＋c＝0． x A B C 图 2 A B C 图 1 （1）若 a＝1，b，c 是一枚六个面分别标有 1，2，3，4，5，6 的质地均匀的正方体骰子先后投掷两次出 现的点数，求方程有实数根的概率； （2）若 b＝－a，c＝a－3，且方程有实数根，求方程至少有一个非负实数根的概率． 16．一个不透明的口袋里装有红、黄、绿三种颜色的小球（除颜色不同外其余都相同），其中红球 2 个， 黄球 1 个，其余为绿球，从中任意摸出 1 球是绿球的概率为 1 4 ． （1）试求口袋中绿球的个数； （2）第一次从口袋中任意摸出 1 球，然后放回袋中摇匀，第二次再摸出 1 球，请用列表法求两次摸到都 是红球的概率； （3）小明和小华玩摸球游戏，游戏规则是：先由小明从口袋中任意摸出 1 球（不放回），再由小华任意摸 出 1 球．若摸出“一绿一黄”，则小明获胜；若摸出“一红一黄”，则小华获胜． 你认为这个游戏规则公平吗？请用画树状图的方法说明理由；若你认为不公平，请修改游戏规则， 使游戏变得公平． 17．有两个不同形状的计算器（分别记为A，B）和与之匹配的保护盖（分别记为a，b）（如图所示）散乱 地放在桌子上． （1）若从计算器中随机取一个，再从保护盖中随机取一个，求恰好匹配的概率． （2）若从计算器和保护盖中随机取两个，用树状图法或列表法，求恰好匹配的概率． A B a b 18．同时投掷六个面分别标有 1，2，3，4，5，6 的质地均匀的红、黄两枚正方体骰子一次，记红色和黄 色骰子正面朝上的点数分别为 m 和 n． （1）求二次函数 y＝x 2＋2mx＋n 图象的顶点落在 x 轴上的概率； （2）求一元一次方程 mx＋n＝0 有整数解的概率． 19．在一个箱子中有三个分别标有数字 1，2，3 的材质、大小都相同的小球，从中任意摸出一个小球，记 下小球的数字 x 后，放回箱中并摇匀，再摸出一个小球，又记下小球的数字 y．以先后记下的两个数字 （x，y）作为点 P 的坐标． （1）求点 P 的横坐标与纵坐标的和为 4 的概率； （2）在平面直角坐标系中，求点 P 落在以坐标原点为圆心、 10 为半径的圆的内部的概率． 20．有甲、乙两个不透明的盒子，甲盒中有四个标号分别为 0，1，2，3 的材质、大小都相同的小球，乙 盒中有三个标号分别为 0，1，2 的材质、大小都相同的小球，从甲盒中随机取出一小球，用 m 表示该球的 标号，再从乙盒中随机取出一小球，用 n 表示该球的标号． （1）用树状图的方式表示（m、n）的所有可能结果； （2）分别求出关于 x 的方程 x 2－mx＋ 1 2 n＝0 有两个相等的实数根的概率 P1 和该方程有两个不相等的实数 根的概率 P2． 六、三角形 1．△ABC 是一张等腰直角三角形纸板，∠C＝90°，AC＝BC＝2． （1）要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图 1），比较甲、乙两种剪法， 哪种剪法所得的正方形面积更大？请说明理由． （2）图 1 中甲种剪法称为第 1 次剪取，记所得正方形面积为 S1；按照甲种剪法，在余下的△ADE 和△BDF 中，分别剪取正方形，得到两个相同的正方形，称为第 2 次剪取，并记这两个正方形面积和为 S2（如图 2），则 S2＝_______；再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形， 称为第 3 次剪取，并记这四个正方形面积和为 S3（如图 3）；继续操作下去…则第 10 次剪取时，S 10＝ _______． （3）求第 10 次剪取后，余下的所有小三角形的面积之和． 2． 问题探究 （1）如图，在△ABC 中，D 是 BC 边上的中点，DE⊥DF，DE 交 AB 于点 E，DF 交 AC 于点 F，连接 EF． ①求证：BE＋CF＞EF； ②若∠A＝90°，探索线段 BE、CF、EF 之间的等量关系，并加以证明． 问题解决 （2）如图，在四边形 ABDC 中，∠B＋∠C＝180°，DB＝DC，∠BDC＝120°，以 D 为顶点作一个 60°角， 角的两边分别交 AB、AC 于 E、F 两点，连接 EF，探索线段 BE、CF、EF 之间的数量关系，并加以证 明． A BC E D F A BC 图 1 甲 乙 P N M Q A BC E D F 图 2 A BC 图 3 B M A M C M D M E M F M B M A M C M D M E M F M 3．阅读下面的情景对话，然后解答问题： （1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命 题还是假命题？ （2）在 Rt△ABC 中，∠ACB＝90°，AB＝c，AC＝b，BC＝a，且 b＞a， 若 Rt△ABC 是奇异三角形，求 a : b : c； （3）如图，AB 是⊙O 的直径，C 是⊙O 上一点（不与点 A、B 重合）， D 是半圆ADB ︵ 的中点，C、D 在直径 AB 的两侧，若在⊙O 内存在 点 E，使 AE＝AD，CB＝CE． ① 求证：△ACE 是奇异三角形； ② 当△ACE 是直角三角形时，求∠AOC 的度数． 4．如图 1，在等边△ABC 中，点 D 是边 AC 的中点，点 P 是线段 DC 上的动点(点 P 与点 C 不重合)，连 结 BP，将△ABP 绕点 P 按顺时针方向旋转 α 角（0°＜α＜180°），得到△A1B1P，连结 AA1，射线 AA1 分别 交射线 PB、射线 B1B 于点 E、F． （1）如图 1，当 0°＜α＜60°时，在 α 角变化过程中，△BEF 与△AEP 始终存在相似关系，请说明理由； （2）如图 2，设∠ABP＝β，当 60°＜α＜180°时，在 α 角变化过程中，是否存在△BEF 与△AEP 全等？若 存在，求出 α 与 β 之间的数量关系；若不存在，请说明理由； （3）如图 3，当 α＝60°时，点 E、F 与点 B 重合．已知 AB＝4，设 DP＝x，△A1BB1 的面积为 S，求 S 关 于 x 的函数关系式． 5．数学课上，李老师出示了如下框中的题目． 小明：那直角三角形 中是否存在奇异三 角形呢？ 老师：我们新定义一种三角形， 两边平方和等于第三边平方的 2 倍 的 三 角 形 叫 做 奇 异 三 角 形． 小华：等边三角形一 定是奇异三角形！ A BO C D E 图 2 A B C F D P E A1 B1 图 3 A B CD P A1 B1 图 1 A B C F D P E A1 B1 小敏与同桌小聪讨论后，进行了如下解答： （1）特殊情况，探索结论 当点 E 为 AB 的中点时，如图 1，确定线段 AE 与 DB 的大小关系．请你直接写出结论： AE_______DB（填“＞”，“＜”或“＝”）． （2）特例启发，解答题目 解：题目中，AE 与 DB 的大小关系是：AE_______DB（填“＞”，“＜”或“＝”），理由如下． 如图 2，过点 E 作 EF∥BC，交 AC 于点 F． （请你完成以下解答过程） （3）拓展结论，设计新题 在等边三角形 ABC 中，点 E 在直线 AB 上，点 D 在直线 BC 上，且 ED＝EC．若△ABC 的边长为 1， AE＝2，求 CD 的长（请你直接写出结果）． 6．如图，△ABC 的三条中线分别为 AD、BE、CF． （1）在图中利用图形变换画出并指明以 AD、BE、CF 的长度为三边长的一个三角形（保留画图痕迹）； （2）若△ABC 的面积为 1，试求以 AD、BE、CF 的长度为三边长的三角形的面积． 7．在平面直角坐标系中，点 A（3，0），B（0，4）．以点 A 为旋转中心，把△ABO 顺时针旋转，得△ ACD．记旋转转角为 α，∠ABO 为 β． （1）如图①，当旋转后点 D 恰好落在 AB 边上时，求点 D 的坐标； （2）如图②，当旋转后满足 BC∥x 轴时，求 α 与 β 之间的数量关系； （3）当旋转后满足∠AOD＝β 时，求直线 CD 的解析式． 在等边三角形 ABC 中，点 E 在 AB 上， 点 D 在 CB 的延长线上，且 ED＝EC，如图． 试确定线段 AE 与 DB 的大小关系，并说明 理由． A B C E D A B C E D 图 1 A B C E D 图 2 F A E B C F D 图① A B C O y D x 图② AO x y B D C 8．在 Rt△ABC 中，∠ACB＝90°，BC＝30，AB＝50．点 P 是 AB 边上任意一点，直线 PE⊥AB，与边 AC 或 BC 相交于 E．点 M 在线段 AP 上，点 N 在线段 BP 上，EM＝EN，sin∠EMP＝ 12 13 ． （1）如图 1，当点 E 与点 C 重合时，求 CM 的长； （2）如图 2，当点 E 在边 AC 上时，点 E 不与点 A、C 重合，设 AP＝x，BN＝y，求 y 关于 x 的函数关系 式，并写出函数的定义域； （3）若△AME∽△ENB（△AME 的顶点 A、M、E 分别与△ENB 的顶点 E、N、B 对应），求 AP 的长． 9．已知∠MON＝60°，射线 OT 是∠MON 的平分线，点 P 是射线 OT 上的一个动点，射线 PB 交射线 ON 于点 B． （1）如图，若射线 PB 绕点 P 顺时针旋转 120°后与射线 OM 交于点 A，求证：PA＝PB； （2）在（1）的条件下，若点 C 是 AB 与 OP 的交点，且满足 PC＝ 2 PB，求△POB 与△PBC 的面积之比； （3）当 OB＝2 时，射线 PB 绕点 P 顺时针旋转 120°后与直线 OM 交于点 A（点 A 不与点 O 重合），直线 PA 交射线 ON 于点 D，且满足∠PBD＝∠ABO，求 OP 的长． 10．在△ABC 中，∠ACB＝90°，∠ABC＝30°，将△ABC 绕顶点 C 顺时针旋转，旋转角为 θ（0°＜θ＜ 180°），得到△A′B′C． （1）如图 1，当 AB∥CB′ 时，设 A′B′ 与 CB 相交于点 D．证明：△A′CD 是等边三角形； （2）如图 2，连接 A′A、B′B，设△ACA′ 和△BCB′ 的面积分别为 S△ACA′ 和 S△BCB′ ． 求证：S△ACA′ : S△BCB′ ＝1 : 3； （3）如图 3，设 AC 中点为 E，A′B′ 中点为 P，AC＝a，连接 EP，当 θ＝__________°时，EP 长度最大， 最大值为__________． (E) A BP C M N 图 1 A BP C M N 图 2 E A B C 备用图 B C M A O N P T M O N T 备用图 M O N T 备用图 第 22 题图(3) A BC D A′ B′ θ 图 1 A BC A′ B′ θ 图 2 A BC A′ B′ θ 图 3 E P 11．如图，△ABC 是边长为 3 的等边三角形，点 F 在边 BC 上，CF＝1，点 E 是射线 BA 上一动点，以线 段 EF 为边向右侧作等边△EFG，直线 EG、FG 分别交直线 AC 于点 M、N． （1）设 BE＝x，MN＝y，求 y 与 x 之间的函数关系式，并写出自变量 x 的取值范围； （2）若 AE＝1，求△GMN 的面积． 12．如图，边长为 4 的等边三角形 AOB 的顶点 O 在坐标原点，点 A 在 x 轴的正半轴上，点 B 在第一象 限．点 P 从点 O 出发，沿 x 轴以每秒 1 个单位长的速度向点 A 匀速运动，当点 P 到达点 A 时停止运动， 设点 P 运动的时间是 t 秒．将线段 BP 的中点绕点 P 按顺时针方向旋转 60°得点 C，点 C 随点 P 的运动而 运动，连接 CP、CA． （1）求点 C 的坐标（用含 t 的代数式表示）； （2）在点 P 从 O 向 A 运动的过程中，△PCA 能否成为直角三角形？若能，求 t 的值．若不能，请说明理 由； （3）点 P 从点 O 运动到点 A 时，点 C 运动路线的长是多少？ 13．如图，直线 y＝－ 3 x＋2 分别交 x 轴、y 轴于 C、A 两点，将射线 AM 绕点 A 顺时针旋转 45°得到射线 AN，D 为 AM 上的动点，B 为 AN 上的动点，点 C 在∠MAN 的内部． （1）当 AM∥x 轴，且四边形 ABCD 为梯形时，求△BCD 的面积； （2）求△BCD 周长的最小值； （3）当△BCD 的周长取得最小值，且 BD＝ 5 3 时，求△BCD 的面积． A B CF E G M N A B C 备用图 A B C 备用图 A B O A x y 备用图 A C B O A P x y A x y 1O D 2 1 2 M N B 3 4C A x y 1O 2 1 2 3 4C 备用图 A x y 1O 2 1 2 3 4C 备用图 14．如图，在 Rt△ABC 中，∠C＝90°，AB＝10cm，AC : BC＝4 : 3，点 P 从点 A 出发沿 AB 方向向点 B 运 动，速度为 1cm/s，同时点 Q 从点 B 出发沿 B→C→A 方向向点 A 运动，速度为 2cm/s，当一个动点到达 终点时，另一个动点也随之停止运动． （1）设点 P 的运动时间为 x（s），△PBQ 的面积为 y（cm2），当△PBQ 存在时，求 y 与 x 的函数关系式， 并写出自变量 x 的取值范围； （2）当点 Q 在 CA 上运动，使 PQ⊥AB 时，以点 B、P、Q 为顶点的三角形与△ABC 是否相似，请说明理 由； （3）当 x＝5s 时，在直线 PQ 上是否存在一点 M，使△BCM 的周长最小，若存在，求出最小周长，若不 存在，请说明理由． 15．如图，在△ABC 中，AB＝5，AC＝3，cosA＝ 3 10 ，D 为射线 BA 上的动点（点 D 不与点 B 重合），DE∥BC 交射线 CA 于点 E． （1）设 CE＝x，BD＝y，求 y 与 x 的函数关系式； （2）若以线段 BD、CE 为直径的两圆相切，求 DE 的长度； （3）当点 D 在 AB 边上时，BC 边上是否存在点 F，使△ABC 与△DEF 相 似？若存在，请求出线段 BF 的长；若不存在，请说明理由． 16．已知：在△ABC 中，BC＝2AC，∠DBC＝∠ACB，BD＝BC，CD 交线段 AB 于点 E． （1）如图 l，当∠ACB＝90°时，则线段 DE、CE 之间的数量关系为____________________； （2）如图 2，当∠ACB＝120°时，求证：DE＝3CE； （3）如图 3，在（2）的条件下，点 F 是 BC 边的中点，连接 DF，DF 与 AB 交于点 G，△DKG 和△DBG 关于直线 DG 对称（点 B 的对称点是点 K），延长 DK 交 AB 于点 H．若 BH＝10，求 CE 的长． 17．如图，在平面直角坐标系中，点 A、B、C 的坐标分别为（0，2）、（－1，0）、（4，0）．P 是线段 OC 上的一动点（点 P 与点 O、C 不重合），过点 P 的直线 x＝t 与 AC 相交于点 Q ．设四边形 ABPQ 关于直线 x B C Q PA A B C D E C A B D E 图 1 C A B D E 图 2 C A B D E 图 3 K H G F ＝t 的对称的图形与△QPC 重叠部分的面积为 S． （1）点 B 关于直线 x＝t 的对称点 B′ 的坐标为___________； （2）求 S 与 t 的函数关系式． 18．在△ABC 中，∠A＝90°，点 D 在线段 BC 上，∠EDB ＝ 1 2∠C，BE⊥DE，垂足为 E，DE 与 AB 相交于 点 F． （1）当 AB＝AC 时，（如图 1） ①∠EBF＝_________°； ②探究线段 BE 与 FD 的数量关系，并加以证明； （2）当 AB＝kAC 时（如图 2），求 BE FD 的值（用含 k 的式子表示）． 19．如图 1，在△ABC 中，∠ABC＝90°，AB＝BC，BD 为斜边 AC 上的中线，将△ABD 绕点 D 顺时针旋 转 α（0°＜α＜180°），得到△EFD，点 A 的对应点为点 E，点 B 的对应点为点 F，连接 BE、CF． （1）判断 BE 与 CF 的位置、数量关系，并说明理由； （2）若连接 BF、CE，请直接写出在旋转过程中四边形 BFEC 能形成哪些特殊四边形； （3）如图 2，将△ABC 中 AB＝BC 改成 AB≠BC 时，其他条件不变，直接写出 α 为多少度时（1）中的两 个结论同时成立． 20．如图 11，在△ABC 中，∠ACB＝90°，AC＝BC＝2，BD 是 AC 边上的中线，CE⊥BD，垂足为 E． （1）求 sin∠DCE 的值； （2）求证：∠ABD＝∠CAE； （3）若点 F 在边 AB 上，且△AEF 为等腰三角形，求 AF 的长． A B O C x y 图 1 A B C F E D 图 2 A B C F E D A B C F E D 图 1 A B C D 备用图 A B C D 图 2 A B C D E 21．如图，点 C 为线段 AB 上任意一点（不与 A、B 两点重合），分别以 AC、BC 为一腰在 AB 的同侧作等 腰△ACD 和等腰△BCE，CA＝CD，CB＝CE，∠ACD 与∠BCE 都是锐角且∠ACD＝∠BCE，连接 AE 交 CD 于点 M，连接 BD 交 CE 于点 N，AE 与 BD 交于点 P，连接 PC． （1）求证：△ACE≌△DCB； （2）请你判断△AMC 与△DMP 的形状有何关系并说明理由； （3）求证：∠APC＝∠BPC． 22．如图①，P 为△ABC 内一点，连接 PA、PB、PC，在△PAB、△PBC 和△PAC 中，如果存在一个三角 形与△ABC 相似，那么就称 P 为△ABC 的自相似点． （1）如图②，已知 Rt△ABC 中，∠ACB＝90°，∠ACB＞∠A，CD 是 AB 上的中线，过点 B 作 BE⊥CD， 垂足为 E，试说明 E 是△ABC 的自相似点； （2）在△ABC 中，∠A＜∠B＜∠C． ①如图③，利用尺规作出△ABC 的自相似点 P（写出作法并保留作图痕迹）； ②若△ABC 的内心 P 是该三角形的自相似点，求该三角形三个内角的度数． 23．如图①，在△ABC 中，AB＝AC，BC＝a cm，∠B＝30°．动点 P 以 1cm/s 的速度从点 B 出发，沿折线 B－A－C 运动到点 C 时停止运动．设点 P 出发 x s 时，△PBC 的面积为 y cm2．已知 y 与 x 的函数图象如图② 所示，请根据图中信息，解答下列问题： （1）试判断△DOE 的形状，并说明理由； （2）当 a 为何值时，△DOE 与△ABC 相似？ 24．如图，在 Rt△ABC 中，∠C＝90°，AC＝BC＝6，点 D 为 AC 中点，点 E 为边 AB 上一动点，点 F 为 射线 BC 上一动点，且∠FDE＝90°． （1）当 DF∥AB 时，连接 EF，求 cos∠DEF 的值； （2）当点 F 在线段 BC 上时，设 AE＝x，BF＝y，求 y 关于 x 的函数关系式，并写出自变量 x 的取值范围； （3）连接 CE，若△CDE 为等腰三角形，求 BF 的长． 25．某课题研究小组就图形面积问题进行专题研究，他们发现如下结论： BA C P E D M N A B C A A C CB B ① ② ③ D EP 图① 图② A B C P D EO x y 1 1 A C B D E F （1）有一条边对应相等的两个三角形的面积之比等于这条边上的对应高之比； （2）有一个角对应相等的两个三角形的面积之比等于夹这个角的两边乘积之比； … 现请你继续对下面问题进行探究，探究过程可直接应用上述结论．（S 表示面积） 问题 1：如图 1，现有一块三角形纸板 ABC，P1，P2 三等分边 AB，R1，R2 三等分边 AC．经探究知 S 四边形 P1R1R2P2 ＝ 1 3 S△ABC ，请证明． 问题 2：若有另一块三角形纸板，可将其与问题 1 中的△ABC 拼合成四边形 ABCD，如图 2，Q1，Q2 三等 分边 DC．请探究 S 四边形 P1Q1Q2P2 与 S 四边形 ABCD 之间的数量关系． 问题 3：如图 3，P1，P2，P3，P4 五等分边 AB，Q1，Q2，Q3，Q4 五等分边 DC．若 S 四边形 ABCD ＝1，求 S 四边形 P2Q2Q3P3 ． 问题 4：如图 4，P1，P2，P3 四等分边 AB，Q1，Q2，Q3 四等分边 DC，P1Q1，P2Q2，P3Q3 将四边形 ABCD 分成四个部分，面积分别为 S1，S2，S3，S4．请直接写出含有 S1，S2，S3，S4 的一个等式． 26．在平面直角坐标系中，直线 y＝ 2 3 kx＋m（－ 1 2 ≤k ≤ 1 2）经过点 A（2 3，4），与 y 轴相交于点 C，点 B 坐标为（0，7）．记△ABC 的面积为 S． （1）求 m 的取值范围； （2）求 S 关于 m 的函数关系式； （3）当 S 取得最大值时，将△ABC 沿 AC 翻折得到△AB′C，求点 B′ 的坐标． 27．如图，Rt△ABC 中，∠ACB＝90°，AC＝3cm，CB＝4cm．点 P、Q 分别是 AB、CB 上动点，它们分别 从 A、C 同时出发向 B 点匀速移动，移动速度为 1cm/秒，设 P、Q 移动时间为 t 秒（0≤t≤4）． （1）当∠CPQ＝90°时，求 t 的值； （2）是否存在 t，使△CPQ 成为等边三角形？若存在，求出 t 的值；若不存在，能否改变 Q 的运动速度 （P 的速度不变），使△CPQ 成为等边三角形？如何改变？并求出相应的 t 值． 28．如图，在△ABC 中，∠ABC＝∠BAC＝72°，将△ABC 绕点 A 顺时针旋转 α 度（36°＜α＜180°）得到△ADE， 连接 CE，线段 BD（或其延长线）分别交 AC、CE 于点 G、F． （1）求证：△ABG∽△FCG； （2）在旋转的过程中，是否存在某一时刻，使得△ABG 与△FCG 全等？若存在，求出此时旋转角 α 的大 小；若不存在，说明理由． 图 1 图 2 图 3 图 4 A C BP1 P2 R2 R1 R1 R2 P1 P2 Q1 Q2 A C B D Q1 Q2 CD P1 P2A BP3 P4 Q3 Q4 Q1 Q2 CD P1 P2A BP3 Q3 A C B P Q A C B D E F G 29．已知 Rt△ABC 中，∠ACB＝90º，BC＝5，tan∠A＝ 3 4 ．将△ABC 绕点 C 逆时针旋转 α（45°＜α＜135°） 得到△DCE，设直线 DE 与直线 AB 相交于点 P，连接 CP． （1）如图 1，当 CD⊥AB 时，求证：PC 平分∠EPA； （2）如图 2，当点 P 在边 AB 上时，求证：PE＋PB＝6； （3）在△ABC 旋转过程中，连接 BE，当△BCE 的面积为 25 4 3 时，求∠BPE 的度数及 PB 的长． 30．已知△ABC 中，点 D 在 AC 上，点 E 在 BC 上，且 DE∥AB．将△CDE 绕点 C 按顺时针方向旋转得到 △CD′E′（∠BCE′＜180°），连接 AD′、BE′，设直线 BE′ 与 AC、AD′ 分别交于点 O、F． （1）如图 1，若△ABC 为等边三角形，则 AD′ BE′ 的值为________，∠AFB 的度数为________； （2）如图 2，若△ABC 满足∠ACB＝60°，AC＝ 3，BC＝ 2． ①求 AD′ BE′ 的值和∠AFB 的度数； ②若 E 是 BC 的中点，求△OBC 面积的最大值． 31．如图 1，△ABC 与△EFD 为等腰直角三角形，AC 与 DE 重合，AB＝AC＝EF＝9，∠BAC＝∠DEF＝ 90º．固定△ABC，将△DEF 绕点 A 顺时针旋转，当 DF 边与 AB 边重合时，旋转中止．现不考虑旋转开始 和结束时重合的情况，设 DE，DF（或它们的延长线）分别交 BC（或它的延长线）于 G，H 点，如图 2． （1）始终与△AGC 相似的三角形有___________和___________； （2）在图 2 中，设 CG＝x，BH＝y，求 y 关于 x 的函数关系式； AC B D E F P 图 1 AC B D E F P 图 2 AC B 备用图 D A F CB O D′ E E′ 图 1 D A F CB O D′ E E′ 图 2 （3）当 x 为何值时，△AGH 是等腰三角形？ 32．如图 1，已知线段 AB 的长为 2a，点 P 是 AB 上的动点（P 不与 A、B 重合），分别以 AP、PB 为边向 线段 AB 的同一侧作正△APC 和正△PBD． （1）当△APC 与△PBD 的面积之和取最小值时，AP＝_________；（直接写出结果） （2）连结 AD、BC 相交于点 Q，设∠AQC＝α，那么 α 的大小是否随点 P 的移动而变化？请说明理由； （3）如图 2，若点 P 固定，将△PBD 绕点 P 按顺时针方向旋转（旋转角小于 180°），此时 α 的大小是否发 生变化？（只需直接写出你的猜想，不必证明） 33．已知直线 l 经过 A（6，0）和 B（0，12）两点，且与直线 y＝x 交于点 C． （1）求直线 l 的解析式； （2）若点 P（x，0）在线段 OA 上运动，过点 P 作 l 的平行线交直线 y＝x 于 D，求△PCD 的面积 S 与 x 的 函数关系式；S 有最大值吗？若有，求出当 S 最大时 x 的值； （3）若点 P（x，0）在 x 轴上运动，是否存在点 P，使得△PCA 成为等腰三角形？若存在，请写出点 P 的 坐标；若不存在，请说明理由． 34．如图，Rt△ABC 中，∠A＝30°，BC＝10cm，点 Q 在线段 BC 上从 B 向 C 运动，点 P 在线段 BA 上从 B 向 A 运动．Q、P 两点同时出发，运动的速度相同，当点 Q 到达点 C 时，两点都停止运动．作 PM⊥PQ 交 CA 于点 M，过点 P 分别作 BC、CA 的垂线，垂足分别为 E、F． （1）求证：△PQE∽△PMF； A B C F(D) (E) 图 1 A B C F (D) 图 2 H E G A C BP DQ 图 1 A C B P DQ 图 2 A C B P D O x l y （2）当点 P、Q 运动时，请猜想线段 PM 与 MA 的大小有怎样的关系？并证明你的猜想； （3）设 BP＝x，△PEM 的面积为 y，求 y 关于 x 的函数关系式，当 x 为何值时，y 有最大值，并将这个值 求出来． 35．如图 1，在 Rt△ABC 中，∠C＝90°，AC＝BC，D 是 AB 边上一点，E 是 AC 边上的一个动点（与点 A、C 不重合），DF⊥DE，DF 与射线 BC 相交于点 F． （1）如图 2，若点 D 是边 AB 的中点，求证：DE＝DF； （2）若 AD : DB＝m，求 DE : DF 的值； （3）若 AC＝BC＝6，AD : DB＝1 : 2，设 AE＝x，BF＝y． ①求 y 关于 x 的函数关系式，并写出自变量 x 的取值范围； ②以 CE 为直径的圆与直线 AB 是否可相切，若可能，求出此时 x 的值，若不可能，请说明理由． 36．（1）如图 1，在△ABC 中，点 D、E、Q 分别在 AB、AC、BC 上，且 DE∥BC，AQ 交 DE 于点 P．求 证： DP BQ ＝ PE QC ． （2）如图，在△ABC 中，∠BAC＝90°，正方形 DEFG 的四个顶点在△ABC 的边上，连接 AG、AF 分别交 DE 于 M、N 两点． ①如图 2，若 AB＝AC＝1，直接写出 MN 的长； ②如图 3，求证：MN 2＝DM·EN． MF B PE Q AC 30° BDA C 图 1 E F BDA C 图 2 E F BDA C 备用图 BDA C 备用图 B Q A C D EP 图 1 B G A C D E 图 3 F MN B G A C D EM 图 2 F N 37．如图，D 是△ABC 的边 BC 的中点，过 AD 延长线上的点 E 作 AD 的垂线 EF，E 为垂足，EF 与 AB 的 延长线相交于点 F，点 O 在 AD 上，AO＝CO，BC∥EF． （1）证明：AB＝AC； （2）证明：点 O 是△ABC 的外接圆的圆心； （3）当 AB＝5，BC＝6 时，连接 BE，若∠ABE＝90°，求 AE 的长． 38．两个大小相同且含 30°角的三角板 ABC 和 DEC 如图①摆放，使直角顶点重合．将图①中△DEC 绕点 C 逆时针旋转 30°得到图②，点 F、G 分别是 CD、DE 与 AB 的交点，点 H 是 DE 与 AC 的交点． （1）不添加辅助线，写出图②中所有与△BCF 全等的三角形； （2）将图②中的△DEC 绕点 C 逆时针旋转 45°得△D1E1C，点 F、G、H 的对应点分别为 F1、G1、H1，如 图③．探究线段 D1F1 与 AH1 之间的数量关系，并写出推理过程； （3）在（2）的条件下，若 D1E1 与 CE 交于点 I，求证：G1I＝CI． 39．已知△ABC 是等腰直角三角形，∠A＝90°，D 是腰 AC 上的一个动点，过 C 作 CE 垂直于 BD 或 BD 的延长线，垂足为 E，如图 1． （1）若 BD 是 AC 的中线，如图 2，求 BD CE 的值； （2）若 BD 是∠ABC 的角平分线，如图 3，求 BD CE 的值； （3）结合（1）、（2），请你推断 BD CE 的值的取值范围（直接写出结论，不必证明），并探究 BD CE 的值能小于 4 3 吗？若能，求出满足条件的 D 点的位置；若不能，请说明理由． 40．Rt△ABC 中，∠ACB＝90°，M 为 AB 中点，将线段 BM 绕点 B 顺时针旋转 90°，得到线段 BP，连接 AP、CP，CP 交 AB 于点 N（如图 1）． B F A CD O E 图① B A C D E 图② BF A C D E H G 图③ BF A C D E H GF1 G1 D1 H1 I E1 （图 1）B A C D E （图 2）B A C D E （图 3）B A C D E （1）若 AC＝BC，求证：△NPB∽△PAB； （2）若 BC＝2，当 AC 的长为多少时，△ACB∽△ABP？ （3）图 1 中，当点 A 沿直线 AC 向下运动（其余条件不变）时，Rt△ABC、△PAB、△PBC 都会变化（如 图 2），若点 A 一直运动到 BC 下方，请在图 3 中画出相应的图形．若 BC＝2，设 AC＝x，△BCP 的面积为 S1，△PAB 的面积为 S2，试问 S1、S2 是否都为定值？若是，求出这个定值；若不是，求出其关于 x 的函数 关系式． 41．如图（1），在 Rt△ABC 中，∠ACB＝90°，CD⊥AB，垂足为 D，点 E 在 AC 上，BE 交 CD 于点 G，EF ⊥BE 交 AB 于点 F．若 AC＝mBC，CE＝nEA（m，n 为实数）． 试探究线段 EF 与 EG 的数量关系． （1）如图（2），当 m＝1，n＝1 时，EF 与 EG 的数量关系是____________； 证明： （2）如图（3），当 m＝1，n 为任意实数时，EF 与 EG 的数量关系是____________； 证明： （3）如图（1），当 m，n 为任意实数时，EF 与 EG 的数量关系是____________．（写出关系式，不必证明） 42．如图，已知在△ABC 中，AB＝4，BC＝2，以点 B 为圆心，BC 长为半径的弧交边 AC 于点 D，且∠DBC ＝∠BAC．P 是边 BC 延长线上一点，过点 P 作 PQ⊥BP，交 BD 的延长线于点 Q．设 CP＝x，DQ＝y． （1）求 CD 的长； （2）求 y 关于 x 的函数关系式，并写出自变量 x 的取值范围； （3）若∠DAQ＝2∠BAC，求 CP 的长． 43．如图，在平面直角坐标系中，等边△OAB 的边长是 12，点 A 在第一象限，OB 边在 x 轴的正半轴 上．将△OAB 沿直线 CD：y＝kx＋b 折叠，使点 A 落在 x 轴上的点 E 处． （1）若点 A 恰好落在线段 OB 上（不包括 O、B），△OCE 与△BED 相似吗？为什么？若 OE : EB＝2 : 3， 求 CE : DE 的值； 图 1 C A B N M P M BC A 图 3图 2 C A B M P 图（1） C A BF D GE 图（2） C A BF D G E 图（3） C A BF D G E A B C D Q P （2）①若点 C 是 OA 的中点，AD＝2DB，试判断以 CD 为直径的圆与 x 轴的位置关系，并说明理由； ②若点 C、D 分别在线段 OA、AB 上，试求 b 的取值范围； （3）当点 E 从点 O 移动到点 B 时，点 D 运动的总路线长为多少？ 44．Rt△ABC 的直角顶点 B 在 Rt△DEF 的斜边 DF 上，已知 AB＝DF，DE＝EF，∠A＝30°．固定△DEF 不动，将△ABC 绕点 B 旋转，并使边 AB 与边 DE 交于点 P，边 BC 与边 EF 于点 Q． （1）如图 1，若 FB BD ＝m，求 BP BQ 的值，并确定 m 的取值范围； （2）若 DF＝30， FB BD ＝2，连接 PQ，设△BPQ 的面积为 S，在旋转过程中： ①如图 2，当点 E 恰好落在边 AC 上时，求 AE 的长； ②S 是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，请说明理由； ③随着 S 取不同的值，对应△BPQ 的个数有哪些变化？求相应 S 值的取值范围． 45．如图，在 Rt△ABC 中，∠C＝90°，D，E 分别为 CA，CB 延长线上的点，AE 与 BD 相交于点 F． （1）若 BE＝AC，AD＝CE，求∠AFD 的度数； （2）若 BE＝ 3 AC，AD＝ 3 CE，求∠AFD 的度数． 46．已知：△ABC 和△ADE 都是等腰直角三角形，∠ABC＝∠ADE＝90°，点 M 是 CE 的中点，连接 BM． （1）如图①，点 D 在 AB 上，连接 DM，猜想 BD 与 BM 的数量关系，并说明理由； （2）如图②，点 D 不在 AB 上，（1）中的结论还成立吗？如果成立，请证明；如果不成立，请直接写出 此时 BD 与 BM 的数量关系． 47．如图，在四边形 ABCD 中，∠C＝90°，∠ABD＝∠DBC＝30°，E 在 BC 上，AE⊥BC，且∠ADE＝ 60°． （1）求证：CD＝EC； O E D A B C x y Q ME M D M F M B M A M P M C M图 1 Q ME M D M F M B M A M P M C M图 2 H M A C B A B C D M E M 图① M M A B C D ME M M M 图② A B C D M E M （2）若 BE＝1，求 AD、BC、CD 的长． 48．如图，△ABC 与△BCD 均为等边三角形，过 D 点的直线与 AB 交于点 M，与 CA 的延长线交于点 N， CM 与 BN 交于点 E，求∠BEC 的度数． 49．已知△ABC 是锐角三角形． （1）求证：2sinA＞cosB+cosC； （2）若点 M 在边 AC 上，作△ABM 和△CBM 的外接圆，则当 M 在什么位置时，两外接圆的公共部分面 积最小？ 50．如图，△ABC 中，AD 是∠BAC 的角平分线，AD 的垂直平分线交 AD 于点 E，交 BC 的延长线于点 F． （1）求证：DF 2＝BF·CF； （2）若 AB AC ＝ 5 3 ，求 BC CF 的值． 51．在△ABC 中，点 M 为 BC 的中点． （1）如图 1，求证：AM＜ 1 2(AB＋AC)； （2）延长 AB 到 D，使得 BD＝AC，延长 AC 到 E，使得 CE＝AB，连接 DE． ①如图 2，连接 BE，若∠BAC＝60°，请你探究线段 BE 与线段 AM 之间的数量关系．写出你的结论， 并加以证明； ②请在图 3 中证明：BC ≥ 1 2 DE． A C E B D M N A CB E D F A C B M 图 1 A C B M D E 图 2 A C B M D E 图 3 52．如图①，在 Rt△ABC 中，∠BAC＝90°，AB＝AC＝2 3，D、E 两点分别在 AC、BC 上，且 DE∥AB， CD＝2 2．将△CDE 绕点 C 顺时针旋转，得到△CD′E′（如图②，点 D′、E′分别与点 D、E 对应），点 E′ 在 AB 上，D′E′ 与 AC 相交于点 F． （1）求∠ACE′ 的度数； （2）求证：四边形 ABCD′ 是梯形； （3）求△AD′F 的面积． 53．如图，在△ABC 中，∠ABC＝45°，点 在边 上，且∠ADC＝60°，BD ＝ 1 2 CD．将△ACD 沿 AD 折叠，得到△AC′D，连接 BC′． （1）求证：BC′⊥BC； （2）求∠C 的大小． 54．已知等边三角形 ABC 中，点 D、E、F 分别为 AB、AC、BC 边的中点，P 为直线 BC 上的动点，以 DP 为一边在 DP 的右侧作等边三角形 DPQ． （1）如图，当点 P 在 BC 边上时，请你判断 PF 与 QE 有怎样的数量关系？点 F 是否在直线 QE 上？说明 理由； （2）当点 P 在 CB 的延长线或 BC 的延长线上时，你在（1）中得到的结论是否仍然成立？说明理由． 55．如图，直角三角板 ABC 中，∠A＝30°，BC＝1，将三角板 ABC 绕直角顶点 C 逆时针旋转一个角度 α （0°＜α＜120°且 α≠90°），得到 Rt△A′B′C． （1）当 A′B′边经过点 B 时，求旋转角 α 的大小； （2）在三角板旋转的过程中，边 A′C 与直线 AB 交于点 D，过点 D 作 DE∥A′B′ 交 CB′ 边于点 E，连接 D BC 图① A B CE D 图② A B C E′ D′ F A B CD C′ B C D E A FP Q B C D E A 备用图 F B C D E A 备用图 F BE． ①当 0°＜α＜90°时，设 AD＝x，BE＝y，求 y 与 x 之间的函数关系式； ②当 S△BDE ＝ 1 3 S△ABC 时，求 AD 的长． 56．如图，在平面直角坐标系中，直线 y＝－ 4 3 x＋b 与 x 轴、y 轴分别交于 A、B 两点，且 B 点的坐标为 （0，8），直线 AC 交线段 OB 于点 C（0，n）． （1）过 C 点作 CD⊥AB 于 D 点，CD＝m，求 m 与 n 的函数关系式； （2）将△AOC 沿着 AC 翻折，使点 O 落在 AB 上． ①求点 C 的坐标； ②P 是直线 AC 上的点，在 x 轴上方的平面内是否存在点 Q，使得以 O、C、P、Q 为顶点的四边形为菱 形？若存在，求点 Q 的坐标；若不存在，请说明理由． 57．如图 1 所示，直线 y＝－x＋9 与 x 轴、y 轴交于 B、A 两点，直线 y＝－ 2 3 x－4 与 x 轴、y 轴交于 C、D 两点，E（4，0），直线 l 过 B 点且垂直于 x 轴，P 是直线 上一点（与 B 点不重合），连结 AP． （1）求 A、C 两点的坐标； （2）设 M 是 AP 的中点，若 ME＝5，猜想∠CME 的度数，并说明理由； （3）如图 2 所示，连结 PE，求△PCE 外接圆面积的最小值，并求△PCE 外接圆面积最小时，圆心 G 的 坐标． l AC B 备用图 AC B A′ B′ α AC B 备用图 O x y A B 图 2 O A B x y C D P E l 图 1 O A B x y C D P E l M 58．在△ABC 中，AB＝AC，∠BAC＝α，点 D 是 BC 上一动点（不与 B、C 重合），将线段 AD 绕点 A 逆时 针旋转 α 后到达 AE 位置，连接 DE、CE，设∠BCE＝β． （1）如图 1，若 α＝90°，求 β 的大小； （2）如图 2，当点 D 在线段 BC 上运动时，试探究 α 与 β 之间的数量关系，并证明你的结论； （3）当点 D 在线段 BC 的反向延长线上运动时，（2）中的结论是否仍然成立？若成立，请证明，若不成 立，请写出 α 与 β 之间的数量关系，并说明理由． 59．已知：在平面直角坐标系中，直线 y＝kx＋4 与 y 轴、x 轴分别交于 A、B 两点，点 C 的坐标为（10， 0）． （1）如图①，若 k＝－1，在直线 y＝kx＋4 上求点 P，使∠OPC＝90°； （2）若在直线 y＝kx＋4 上只存在一个点 P，使∠OPC＝90°，求 k 的值． 60．如图 1，△ABC 和△DEF 均为等边三角形，BC 和 EF 的中点均为 O． （1）将△DEF 绕点 O 旋转到图 2 的位置时，试判断 AD 与 CF 的位置关系，并证明你的结论； （2）将△DEF 绕点 O 旋转一周，若顶点 D 与 AC 只有一个交点，且 AB＝4，求△COF 的面积． 61．把 Rt△ABC 和 Rt△DEF 按如图（1）摆放（点 C 与 E 重合），点 B、C（E）、F 在同一条直线上．已 知：∠ACB＝∠EDF＝90°，∠DEF＝45°，AC＝8cm，BC＝6cm，EF＝10cm．如图（2），△DEF 从图（1） 的位置出发，以 1cm/s 的速度沿 CB 向△ABC 匀速移动，在△DEF 移动的同时，点 P 从△ABC 的顶点 A 出发，以 2cm/s 的速度沿 AB 向点 B 匀速移动；当点 P 移动到点 B 时，点 P 停止移动，△DEF 也随之停 止移动．DE 与 AC 交于点 Q，连结 PQ，设移动时间为 t（s）． （1）用含 t 的代数式表示线段 AP 和 AQ 的长，并写出 t 的取值范围； （2）连结 PE，设四边形 APEQ 的面积为 y（cm2），试探究 y 的最大值； （3）当 t 为何值时，△APQ 是等腰三角形？ C A O B x M y M 图① CO x M y M 备用图 E D CB A 图 1 E D CB A 图 2 C A B E M D M O M F M 图 1 C A B E M D M O M F M图 2 C A B E M D M O M F M图 3 (E) A B D C F 图（1） A B D C F 图（2） Q P E 62．如图，在平面直角坐标系中，已知△AOB 为等边三角形，点 A 的坐标为（0，4），点 B 在第一象限， 点 P 是 x 轴上的一个动点，将△AOP 绕点 A 按逆时针方向旋转，使边 AO 与 AB 重合，得到△ABC． （1）求直线 AB 的解析式； （2）当点 P 运动到点（ 3，0）时，求此时 CP 的长及点 C 的坐标； （3）是否存在点 P，使△COP 的面积等于 4 ？若存在，请求出符合条件的点 P 的坐标；若不存在，请说 明理由． 63．已知△ABC 为等边三角形，AB＝6，P 是 AB 上的一个动点（与 A、B 不重合），过点 P 作 AB 的垂线 与 BC 相交于点 D，以点 D 为正方形的一个顶点，在△ABC 内作正方形 DEFG，其中 D、E 在 BC 上，F 在 AC 上． （1）设 BP 的长为 x，正方形 DEFG 的边长为 y，求 y 关于 x 的函数关系式； （2）当 BP＝2 时，求 CF 的长； （3）△GDP 是否可能成为直角三角形？若能，求出 BP 的长；若不能，请说明理由． 64．如图，在平面直角坐标系中，直线 l 的解析式为 y＝2x，点 M 的坐标为（6，2），MN⊥x 轴，垂足为 N，点 P 是 x 轴上位于点 N 右侧的一动点，连结 PM 并延长交直线 l 于点 Q． （1）当点 M 平分线段 PQ 时，试判断△POQ 的形状，并说明理由； （2）当△POQ 是等腰三角形时，求点 P 的坐标； （3）设 PM PQ ＝k，是否存在适当的 k 值，使得 S △ PMNB S四边形ONMQ ＝k？若存在，求出 k 的值；若不存在，请说明理 由． O P x B y C A O x B y A 备用图 E P DB C A FG M l O N P x Q y M l O N x y （备用图） 65．在 Rt△ABC 中，∠A＝90°，AB＝6，AC＝8，点 D 是边 AB 上的一动点（不与点 A、B 重合），过点 D 作 DE∥BC，交边 AC 于点 E． （1）如图 1，当 AD＝2BD 时，求△ADE 的面积； （2）当△ADE 的周长与四边形 BDEC 的周长相等时，求 AD 的长； （3）如图 2，将四边形 BDEC 沿 DE 向上翻折，得四边形 DEFG，设 AD 的长为 x，四边形 DEFG 与△ADE 公共部分的面积为 y，求 y 关于 x 的函数关系式，当 x 为何值时 y 最大，最大值是多少？ ED A B C 图 2 FGED A B C 图 1 七、平行四边形、矩形、菱形、正方形、梯形 1．图形既关于点 O 中心对称，又关于直线 AC，BD 对称，AC＝10，BD＝6，已知点 E，M 是线段 AB 上 的动点（不与端点重合），点 O 到 EF，MN 的距离分别为 h1，h2．△OEF 与△OGH 组成的图形称为蝶 形． （1）求蝶形面积 S 的最大值； （2）当以 EH 为直径的圆与以 MQ 为直径的圆重合时，求 h1 与 h2 满足的关系式，并求 h1 的取值范围． 2．如图 1，已知正方形 OABC 的边长为 2，顶点 A、C 分别在 x、y 轴的正半轴上，M 是 BC 的中点，P （0，m）是线段 OC 上一动点（C 点除外），直线 PM 交 AB 的延长线于点 D． （1）求点 D 的坐标（用含 m 的代数式表示）； （2）当△APD 是等腰三角形时，求 m 的值； （3）设过 P、M、B 三点的抛物线与 x 轴正半轴交于点 E，过点 O 作直线 ME 的垂线，垂足为 H（如图 2）．当点 P 从点 O 向点 C 运动时，点 H 也随之运动，请直接写出点 H 所经过的路径长．（不必写解答过 程） 3．以平行四边形 ABCD 的边 AB、BC、CD、DA 为斜边分别向外侧作等腰直角三角形，直角顶点分别为 E、F、G、H，顺次连结这四个点，得四边形 EFGH，设∠ADC＝α（0°＜α ＜90°）． （1）求∠HAE 的大小（用含 α 的代数式表示）； （2）求证：HE＝HG； （3）判断四边形 EFGH 是什么四边形？并说明理由． 4．在□ABCD 中，∠BAD 的平分线交直线 BC 于点 E，交直线 DC 于点 F． （1）在图 1 中证明 CE＝CF； （2）若∠ABC＝90°，G 是 EF 的中点（如图 2），直接写出∠BDG 的度数 （3）若∠ABC＝120°，FG∥CE，FG＝CE，分别连结 DB、DG（如图 3），求∠BDG 的度数． C A D B G P E M N F Q H O 图 1 A BM O C D P x y 图 2 A BM O C D P x y E H E B F G D H A C 图 3 A D B CE FG 图 2 A B C F D E G 图 1 A B C F D E 5．如图，有一张长为 5 宽为 3 的矩形纸片 ABCD，要通过适当的剪拼，得到一个与之面积相等的正方 形． （1）该正方形的边长为____________； （2）现要求只能用两条裁剪线．请你设计一种裁剪的方法．在图中画出裁剪线，并简要说明剪拼的过 程． 6．如图，矩形 ABCD 中，AB＝6，BC＝8，对角线 AC 与 BD 相交于点 O，点 E 在射线 BM 上． （1）连接 OE，与边 CD 交于点 F．若 CE＝OC，求 CF 的长； （2）连接 DE、AE，AE 与对角线 BD 相交于点 P．若△ADE 为等腰三角形，求 DP 的长． 7．如图，梯形 ABCD 中，AD∥BC，∠DCB＝45°，CD＝2，BD⊥CD．过点 C 作 CE⊥AB 于 E，交对角线 BD 于 F，点 G 为 BC 中点，连结 EG、AF． （1）求 EG 的长； （2）求证：CF＝AB＋AF． 8．如图，正方形 ABCD 的四个顶点分别在四条平行线 l1、l2、l3、l4 上，这四条直线中相邻两条之间的距 离依次为 h1、h2、h3（h1＞0，h2＞0，h3＞0）． （1）求证：h1＝h3； （2）设正方形 ABCD 的面积为 S，求证：S＝( h1＋h2)2＋h1 2； （3）若 3 2 h1＋h2＝1，当 h1 变化时，说明正方形 ABCD 的面积为 S 随 h1 的变化情况． 9．如图，已知四边形 ABDE、ACFG 都是△ABC 外侧的正方形，连接 DF，若 M、N 分别为 DF、BC 的中 A B CD B C DA O E M F B C DA O M 备用图 A B C D G E F C A D B h1 h2 h3 l1 l2 l3 l4 点，求证：MN⊥BC 且 MN＝ 1 2 BC． 10．矩形纸片 ABCD 中，AD＝12cm，现将这张纸片按下列图示方式折叠，AE 是折痕． （1）如图 1，P，Q 分别为 AD，BC 的中点，点 D 的对应点 F 在 PQ 上，求 PF 和 AE 的长； （2）如图 2，DP＝ 1 3 AD，CQ＝ 1 3 BC，点 D 的对应点 F 在 PQ 上，求 AE 的长； （3）如图 3，DP＝ 1 n AD，CQ＝ 1 n BC，点 D 的对应点 F 在 PQ 上． ①直接写出 AE 的长（用含 n 的代数式表示）； ②当 n 越来越大时，AE 的长越来越接近于_________． 11．如图，等腰梯形 ABCD 中，AD＝4，BC＝9，∠B＝45°．动点 P 从点 B 出发沿 BC 向点 C 运动，动点 Q 同时以相同速度从点 C 出发沿 CD 向终 D 运动，其中一个动点到达端点时，另一个动点也随之停止运 动． （1）求 AB 的长； （2）设 BP＝x，问当 x 为何值时△PCQ 的面积最大，并求出最大值； （3）探究：探究：在 AB 边上是否存在点 M，使得四边形 PCQM 为菱形？请说明理由． 12．如图①，将矩形 ABCD 折叠，使点 B 落在边 AD（含端点）上，落点记为 E，此时折痕与边 BC 或边 CD （含端点）交于点 F，然后展开铺平，则以 B、E、F 为顶点的△BEF 称为矩形 ABCD 的“折痕三角形”． （1）由“折痕三角形”的定义可知，矩形 ABCD 的任意一个“折痕△BEF”是一个_________三角形； （2）如图②，在矩形 ABCD 中，AB＝2，BC＝4，当它的“折痕△BEF”的顶点 E 位于 AD 的中点时，画 出这个“折痕△BEF”，并求出点 F 的坐标； （3）如图③，在矩形 ABCD 中，AB＝2，BC＝4，该矩形是否存在面积最大的“折痕△BEF”？若存在， 说明理由，并求出此时点 E 的坐标？若不存在，为什么？ C A F B D E G M N 图 1 C A F B D E P Q 图 2 C A F B D E P Q 图 3 C A F B D E P Q C A B D P Q C A E D FO (B) x y 图① C A E D O (B) x y 图② C A D O (B) x y 图③ 13．如图，在梯形 ABCD 中，AB∥CD，∠A＝90°，AB＝3，CD＝6，BE⊥BC 交直线 AD 于点 E． （1）当点 E 与 D 恰好重合时，求 AD 的长； （2）当点 E 在边 AD 上时（E 不与 A、D 重合），设 AD＝x，ED＝y，求 y 关于 x 的函数关系式，并写出自 变量 x 取值范围； （3）是否可能使△ABE、△CDE 与△BCE 都相似？若能，请求出此时 AD 的长；若不能，请说明理由． 14．如图，矩形 ABCD 中，AB＝3，BC＝4，M 为 CD 中点，点 E 在线段 MC 上运动，FG 垂直平分 AE， 垂足为 O，分别交 AD、BC 于 F、G． （1）求 AE FG 的值； （2）设 CE＝x，四边形 AGEF 的面积为 y，求 y 关于 x 的函数关系式；当 y 取最大值时，判断四边形 AGEF 的形 状，并说明理由． 15．如图 1，矩形 ABCD 中，AB＝10cm，BC＝6cm，在 BC 边上取一点 E，将△ABE 沿 AE 翻折，使点 B 落在 DC 边上的点 F 处． （1）求 CF 和 EF 的长； （2）如图 2，一动点 P 从点 A 出发，以每秒 1cm 的速度沿 AF 向终点 F 作匀速运动，过点 P 作 PM∥EF 交 AE 于点 M，过点 M 作 MN∥AF 交 EF 于点 N．设点 P 运动的时间为 t（0＜t ＜10），四边形 PMNF 的面 积为 S，试探究 S 的最大值？ （3）以 A 为坐标原点，AB 所在直线为 x 轴，建立平面直角坐标系，如图 3，在（2）的条件下，连接 FM，若△AMF 为等腰三角形，求点 M 的坐标． 16．如图，四边形 OABC 是矩形，点 A、C 的坐标分别为（6，0），（0，2），M 是线段 BC 上的动点（与端 点 B、C 不重合），过点 M 的直线 y＝－ 2 3 x＋m 交折线 OAB 于点 N． （1）记△MOE 的面积为 S，求 S 与 m 的函数关系式，并写出 m 的取值范围； D A B C E DA B C E M F G O （图 3） D N B C E M F A P x y （图 2） D N B C E M F A P （图 1） D B C E F A （2）当点 N 在线段 OA 上时，若矩形 OABC 关于直线 MN 的对称图形为四边形 O1A1B1C1． ①当 m 为何值时，B、N、B1 三点在同一直线上； ②试探究四边形 O1A1B1C1 与矩形 OABC 重叠部分的面积是否发生变化，若不变，求出该重叠部分的面 积；若改变，请说明理由． 17．如图，边长为 1 的正方形 ABCD 中，以 A 为圆心，1 为半径作 BD︵ ，将一块直角三角板的直角顶点 P 放置在 BD︵ （不包括端点 B、D）上滑动，一条直角边通过顶点 A，另一条直角边与边 BC 相交于点 Q，连 接 PC，设 PQ＝x． （1）△CPQ 能否为等边三角形？若能，求出 x 的值；若不能，说明理由； （2）求△CPQ 周长的最小值； （3）当△CPQ 分别为锐角三角形、直角三角形和钝角三角形时，求 x 的取值范围． 18．如图，菱形 ABCD 中，AB＝10，sinA＝ 4 5 ，点 E 在 AB 上，AE＝4，过点 E 作 EF∥AD，交 CD 于 F， 点 P 从点 A 出发，以每秒 1 个单位长的速度沿线段 AB 向终点 B 匀速运动，同时点 Q 从点 E 出发，以相同 的速度沿线段 EF 向终点 F 匀速运动，设运动时间为 t（秒）． （1）当 t＝5 秒时，求 PQ 的长； （2）当 BQ 平分∠ABC 时，直线 PQ 将菱形 ABCD 的周长分成两部分，求这两部分的比； （3）以 P 为圆心，PQ 长为半径的⊙P 是否能与直线 AD 相切？如果能，求此时 t 的值；如果不能，说明 理由． 19．如图，在平面直角坐标系中，四边形 ABCD 为菱形，AB＝10，AB 边在 x 轴上，点 D 在 y 轴上，点 A 的坐标是（－6，0）． （1）求点 C 的坐标； A M y BC O N x A y BC O x 备用图 A y BC O x 备用图 A P B CD Q A B CD 备用图 A B CD 备用图 A D CB E F Q P A D CB E 备用图 F （2）连接 BD，点 P 是线段 CD 上一动点（点 P 不与 C、D 两点重合)，过点 P 作 PE∥BC 交 BD 于点 E， 过点 B 作 BQ⊥PE 交 PE 的延长线于点 Q．设 PC 的长为 x，PQ 的长为 y，求 y 与 x 之间的函数关系式（直 接写出自变量 x 的取值范围）； （3）在（2）的条件下，连接 AQ、AE，当 x 为何值时，S△BQE ＋ S△AQE ＝ 4 5 S△DEP ？并判断此时以点 P 为 圆心，以 5 为半径的⊙P 与直线 BC 的位置关系，请说明理由． 20．在正方形 ABCD 的边 AB 上任取一点 E，作 EF⊥AB 交 BD 于点 F，如图 1． （1）将图 1 中的△BEF 绕点 B 逆时针旋转 90°，取 DF 的中点 G，连接 EG，CG，如图 2，则线段 EG 和 CG 有怎样的数量关系和位置关系？请直接写出你的猜想； （2）将图 1 中的△BEF 绕点 B 逆时针旋转 180°，取 DF 的中点 G，连接 EG，CG，如图 3，则线段 EG 和 CG 有怎样的数量关系和位置关系？请写出你的猜想，并加以证明； （3）将图 1 中的△BEF 绕点 B 逆时针旋转任意角度，取 DF 的中点 G，连接 EG，CG，如图 3，则线段 EG 和 CG 又有怎样的数量关系和位置关系？请写出你的猜想，并加以证明． 21．如图，将矩形 OABC 放置在平面直角坐标系中，点 D 在边 OC 上，点 E 在边 OA 上，把矩形沿直线 DE 翻折，使点 O 落在边 AB 上的点 F 处，且 tan∠BFD＝ 4 3 ．若线段 OA 的长是一元二次方程 x 2－7x－8＝0 的 一个根，又 2AB＝3OA．请解答下列问题： （1）求点 B、F 的坐标； （2）求直线 ED 的解析式； （3）在直线 ED、FD 上是否存在点 M、N，使以点 C、D、M、N 为顶点的四边形是等腰梯形？若存在， 求点 M 的坐标；若不存在，请说明理由． C A B y D O 备用图 x C A B y D O x C A B D E G F 图 2 C A B D E G F 图 4 C A B D E G F 图 3 BF D y A O x C E C A B D E F 图 1 22．如图，在平面直角坐标系中，四边形 OABC 是梯形，BC∥OA，点 A 的坐标为（10，0），点 C 的坐标 为（0，8），OA＝OB． （1）求点 B 的坐标； （2）点 P 从点 A 出发，沿线段 AO 以 1 个单位/秒的速度向终点 O 匀速运动，过点 P 作 PH⊥OA，交折线 A－B－O 于点 H，设点 P 的运动时间为 t 秒（0≤t≤10）． ①是否存在某个时刻 t，使△OPH 的面积等于△OAB 面积的 3 20 ？若存在，求出 t 的值，若不存在，请 说明理由； ②以 P 为圆心，PA 长为半径作⊙P，当⊙P 与线段 OB 只有一个公共点时，求 t 的值或 t 的取值范 围． 23．如图，在 Rt△OAB 中，∠A＝90°，∠ABO＝30°，OB＝ 8 3，边 AB 的垂直平分线 CD 分别与 AB、x 轴、 y 轴交于点 C、E、D． （1）求点 E 的坐标； （2）求直线 CD 的解析式； （3）在直线 CD 上和坐标平面内是否分别存在点 Q、P，使得 以 O、D、P、Q 为顶点的四边形是菱形？若存在，求出点 Q 的坐标；若不存在，请说明理由． 24．在四边形 ABCD 中，对角线 AC、BD 相交于点 O，设锐角∠DOC＝α，将△DOC 绕点 O 按逆时针方 向旋转得到△D′OC′（0°＜旋转角＜90°），连接 AC′、BD′，AC′ 与 BD′ 相交于点 M． （1）当四边形 ABCD 是矩形时，如图 1，请猜想 AC′ 与 BD′ 的数量关系以及∠AMB 与 α 的大小关系，并 证明你的猜想； （2）当四边形 ABCD 是平行四边形时，如图 2，已知 AC＝kBD，请猜想此时 AC′ 与 BD′ 的数量关系以及 ∠AMB 与 α 的大小关系，并证明你的猜想； （3）当四边形 ABCD 是等腰梯形时，如图 3，AD∥BC，此时（1）AC′ 与 BD′ 的数量关系是否成立？∠AMB 与 α 的大小关系是否成立？不必证明，直接写出结论． B A y C O x B A y C O x 备用图 B A y C O x 备用图 E B C A O D y x M B C A O D C′ D′ 图 1 M B C A O D C′ D′ 图 2 M B C A O D C′ D′ 图 3 25．如图 l，己知正方形 ABCD，点 E、F 分别在边 AB、AD 上，且 AE＝AF． （1）如图 2，将△AEF 绕点 A 顺时针旋转∠α，当 0°＜α＜90°时，连接 BE、DF，判断线段 BE、DF 的数 量关系和位置关系，并加以证明； （2）如图 3，将△AEF 绕点 A 顺时针旋转∠α，当 α＝90°时，连接 BE、DF，当 AE 与 AD 满足什么数量 关系时，直线 DF 垂直平分 BE？请说明理由； （3）如图 4，将△AEF 绕点 A 顺时针旋转∠α，当 90°＜α＜180°时，连接 BD、DE、EF、FB 得到四边形 BDEF，则顺次连接四边形 BDEF 各边中点所组成的四边形是什么特殊四边形？请说明理由． 26．如图，ABCD 是一张矩形纸片，AD＝BC＝1，AB＝CD＝5．在矩形 ABCD 的边 AB 上取一点 M，在 CD 上取一点 N，将纸片沿 MN 折叠，使 MB 与 DN 交于点 K，得到△MNK． （1）若∠1＝70°，求∠MKN 的度数； （2）△MNK 的面积能否小于 1 2 ？若能，求出此时∠1 的度数；若不能，试说明理由； （3）如何折叠能够使△MNK 的面积最大？请你用备用图探究可能出现的情况，求最大值． 27．如图，等腰梯形 MNPQ 的上底长为 2，腰长为 3，一个底角为 60°．正方形 ABCD 的边长为 1，它的一 边 AD 在 MN 上，且顶点 A 与 M 重合．现将正方形 ABCD 在梯形的外面沿边 MN、NP、PQ 进行翻滚，翻 滚到有一个顶点与 Q 重合即停止滚动． （1）请在所给的图中，用尺规画出点 A 在正方形整个翻滚过程中所经过的路线图； （2）求正方形在整个翻滚过程中点 A 所经过的路线与梯形 MNPQ 的三边 MN、NP、PQ 所围成图形的面 积 S． B D A C E F 图 1 B D A C E F 图 2 B D A C E F 图 3 B D A C E F 图 4 B D A C BD A M N C K 1 B D A C B D A C B D A N (M) Q C P 28．已知四边形 ABCD 是边长为 4 的正方形，以 AB 为直径在正方形内作半圆，P 是半圆上的动点（不与点 A、B 重合），连接 PA、PB、PC、PD． （1）如图①，当 PA 的长度等于_________时，∠PAB＝60° ； 当 PA 的长度等于_________时，△PAD 是等腰三角形； （2）如图②，以 AB 边所在直线为 x 轴、AD 边所在直线为 y 轴，建立如图所示的直角坐标系（点 A 即为 原点 O），记△PAD、△PAB、△PBC 的面积分别为 S1、S2、S3．设 P 点坐标为（a，b），试求 2S1S3－S2 2 的 最大值，并求出此时 a、b 的值． 29．如图，把边长为 1 的正方形纸片 OABC 放在直线 l 上，OA 边与直线 l 重合．将正方形纸片绕着顶点 A 按顺时针方向旋转 90°，此时点 O 运动到了点 O1 处（即点 B 处），点 C 运动到了点 C1 处，点 B 运动到了 点 B1 处；再将正方形纸片 AO1C1B1 绕顶点 B1 按顺时针方向旋转 90°，……，按上述方法经过若干次旋 转．请解答下列问题： （1）求正方形纸片 OABC 经过 3 次旋转，顶点 O 经过的路程以及顶点 O 在此过程中所形成的图形与直线 l 围成图形的面积； （2）求正方形纸片 OABC 经过 5 次旋转，顶点 O 经过的路程； （3）正方形纸片 OABC 经过多少次旋转，顶点 O 经过的路程是 41＋20 2 π？ 30．如图，将矩形纸片 ABCD 按如下顺序进行折叠：对折、展平，得折痕 EF（如图①）；沿 GC 折叠，使 点 B 落在 EF 上的点 B′ 处（如图②）；展平，得折痕 GC（如图③）；沿 GH 折叠，使点 C 落在 DH 上的点 C′ 处（如图④）；沿 GC′ 折叠（如图⑤）；展平，得折痕 GC′、GH（如图⑥）． （1）求图②中∠BCB′ 的大小； （2）图⑥中的△GCC′ 是正三角形吗？请说明理由． A P B CD （图①） A P B CD （图②） (O) x y S1 S3 S2 A BC O (O1) B1 l C1 A E D CB F 图① A E D CB F 图② B′ G A D CB 图③ G A D CB 图④ C′ G H A D CB 图⑤ C′ G H A′ A E D CB F 图⑥ G C′ H 31．如图，在边长为 2 的正方形 ABCD 中，P 为 AB 的中点，Q 为边 CD 上一动点，设 DQ＝t（0≤t≤2）， 线段 PQ 的垂直平分线分别交边 AD、BC 于点 M、N，过 Q 作 QE⊥AB 于点 E，过 M 作 MF⊥BC 于点 F． （1）当 t≠1 时，求证：△PEQ≌△NFM； （2）顺次连接 P、M、Q、N，设四边形 PMQN 的面积为 S，求出 S 与自变量 t 之间的函数关系式，并求 S 的最小值． 32．已知，矩形 ABCD 中，AB＝4cm，BC＝8cm，AC 的垂直平分线 EF 分别交 AD、BC 于点 E、F，垂足 为 O． （1）如图 1，连接 AF、CE．求证四边形 AFCE 为菱形，并求 AF 的长； （2）如图 2，动点 P、Q 分别从 A、C 两点同时出发，沿△AFB 和△CDE 各边匀速运动一周．即点 P 自 A→F→B→A 停止，点 Q 自 C→D→E→C 停止．在运动过程中， ①已知点 P 的速度为每秒 5cm，点 Q 的速度为每秒 4cm，运动时间为 t 秒，当 A、C、P、Q 四点为顶点的 四边形是平行四边形时，求 t 的值． ②若点 P、Q 的运动路程分别为 a、b（单位：cm，ab≠0），已知 A、C、P、Q 四点为顶点的四边形是平 行四边形，求 a 与 b 满足的数量关系式． 33．如图，在直角梯形 ABCD 中，AD∥BC，∠A＝90°，AB＝6，BC＝8，AD＝14，点 E、F、G 分别在 BC、AB、AD 上，且 BE＝3，BF＝2，以 EF、FG 为邻边作□EFGH，连接 CH、DH． （1）直接写出点 H 到 AD 的距离； （2）若点 H 落在梯形 ABCD 内或其边上，求△HGD 面积的最大值与最小值； （3）当△EHC 为等腰三角形时，求 AG 的长． A D C E P B FM N Q A D C E P B F 图 2 Q A D C E O B F 图 1 A D C E P B F 备用图 Q A D C G B F E H 34．已知菱形 ABCD 中，点 E、F 分别在边 BC、CD 上（点 E、F 分别不与点 C、D 重合），且 AE＝AF，∠ EAF＝54°． （1）如图 1，当 AC 平分∠EAF 时，若 AB＝AE，求∠AEB 的度数； （2）如图 2，当 AC 不平分∠EAF 时，若△ABE 是一个等腰三角形，求∠AEB 的度数． 35．如图，△ABC 是等腰直角三角形，∠BAC＝90º，BC＝2，D 是线段 BC 上一点，以 AD 为边，在 AD 的右侧作正方形 ADEF．直线 AE 与直线 BC 交于点 G，连接 CF． （1）猜想线段 CF 与线段 BD 的数量关系和位置关系，并说明理由； （2）连接 FG，当△CFG 是等腰三角形时，求 BD 的长． 36．在矩形 ABCD 中，点 E 是 AD 边上一点，∠ABE＝30°，BE＝DE，连接 BD．动点 M 从点 E 出发沿射 线 ED 运动，过点 M 作 MN∥BD 交直线 BE 于点 N． （1）如图 1，当点 M 在线段 ED 上时，求证：BE＝PD＋ 3 MN； （2）若 BC＝6，设 MN 长为 x，以 M、N、D 为顶点的三角形面积为 y，求 y 关于 x 的函数关系式； （3）在（2）的条件下，当点 M 运动到线段 ED 的中点时，连接 NC，过点 M 作 MF⊥NC 于 F，MF 交对 角线 BD 于点 G（如图 2），求线段 MG 的长． 37．在矩形 ABCD 中，点 P 在 AD 上，AB＝2，AP＝1．将直角尺的顶点放在 P 处，直角尺的两边分别交 AB、 BC 于点 E、F，连接 EF（如图 1）． （1）当点 E 与点 B 重合时，点 F 恰好与点 C 重合（如图 2），求 PC 的长； A D C B FE 图 1 A D C B F E 图 2 D CB F E A G CB A 备用图 A E M B D N C 图 1 A E B D C 备用图 A E M B D N C 图 2 G F （2）探究：将直尺从图 2 中的位置开始，绕点 P 顺时针旋转，当点 E 和点 A 重合时停止．在这个过程中， 请你观察、猜想，并解 答： ①tan∠PEF 的值是否发 生变化？请说明理由； ②直接写出从开始到停 止，线段 EF 的中点经过 的路线长． 38．已知菱形 ABCD 的边长为 1，∠ADC＝60°，等边△AEF 两边分别交边 DC、CB 于点 E、F． （1）特殊发现：如图 1，若点 E、F 分别是边 DC、CB 的中点，求证：菱形 ABCD 对角线 AC、BD 的交点 O 即为等边△AEF 的外心； （2）若点 E、F 始终分别在边 DC、CB 上移动，记等边△AEF 的外心为点 P． ①猜想验证：如图 2，猜想△AEF 的外心 P 落在哪一直线上，并加以证明； ②拓展运用：如图 3，当△AEF 面积最小时，过点 P 任作一直线分别交边 DA 于点 M，交边 DC 的延长线 于点 N，试判断 1 DM ＋ 1 DN 是否为定值．若是，请求出该定值；若不是，请说明理由． 39．如图，在直角梯形 ABCD 中，∠D＝∠BCD＝90°，∠B＝60°，AB＝6，AD＝9，点 E 是 CD 上的一个 动点（E 不与 D 重合），过点 E 作 EF∥AC，交 AD 于点 F（当 E 运动到 C 时，EF 与 AC 重合），把△DEF 沿着 EF 对折，点 D 的对应点是点 G．设 DE＝x，△GEF 与梯形 ABCD 重叠部分的面积为 y． （1）求 CD 的长及∠1 的度数； （2）若点 G 恰好在 BC 上，求此时 x 的值； （3）求 y 与 x 之间的函数关系式，并求 x 为何值时，y 的值最大？最大值是多少？ 40．如图，梯形 ABCD 中，AD∥BC，∠A＝90°，AD＝10，AB＝3，BC＝14，点 E、F 分别在 BC、DC 上， 将梯形 ABCD 沿直线 EF 折叠，使点 C 落在 AD 上一点 C′，再沿 C′G 折叠四边形 C′ABE，使 AC′ 与 C′E 重 合，且 C′A 过点 E． （1）试证明 C′G∥EF； （2）若点 A′ 与点 E 重合，求此时图形重叠部分的面积． A E B D F C P 图 1 A B D C P 图 2 (F)(E) 图 1 A E B D FC O 图 2 A E B D FC P 图 3 A E B D FC P N M A B C E DF G 1 A B C D 备用图 G A B C D E F A′ B′ C′ 41．如图，在直角梯形 ABCD 中，AD∥BC，AB⊥BC，AD＝AB＝1，BC＝2．将点 A 折叠到 CD 边上，记 折叠后 A 点对应的点为 P（P 与 D 点不重合），折痕 EF 只与边 AD、BC 相交，交点分别为 E、F．过点 P 作 PN∥BC 交 AB 于 N，交 EF 于 M，连结 PA、PE、AM，EF 与 PA 相交于 O． （1）指出四边形 PEAM 的形状（不需证明）； （2）记∠EPM＝α，△AOM、△AMN 的面积分别为 S1 、S2 ． ①求证： S1 tan ＝ 1 8 PA 2 ； ②设 AN＝x，y＝ S1 － S2 tan ，试求出以 x 为自变量的函数 y 的解析式，并确定 y 的取值范围． 42．如图 1，边长为 2 的正方形 ABCD 中，E 是 BA 延长线上一点，且 AE＝AB，点 P 从点 D 出发，以每 秒 1 个单位长度的速度沿 D→C→B 向终点 B 运动，直线 EP 交 AD 于 F，过点 F 作直线 FG⊥DE 于 G， 交 AB 于 Q．设点 P 运动时间为 t（秒）． （1）求证：AF＝AQ； （2）当 t 为何值时，四边形 PQBC 是矩形？ （3）如图 2，连接 PB，当 t 为何值时，△PQB 是等腰三角形？ 43．如图 1，已知梯形 ABCD 中，AD∥BC，∠A＝90°，AB＝AD＝4，BC＝6．点 E 为 AB 边上一点，EF∥ DC，交 BC 边于点 F，FG∥ED，交 DC 边于点 G． （1）若四边形 DEFG 为矩形，求 AE 的长； （2）如图 2，将（1）中的∠DEF 绕 E 点逆时针旋转，得到∠D′EF′，EF′ 交 BC 边于 F′ 点，且 F′ 点与 C 点 不重合，射线 ED′ 交 AD 边于点 M，作 F′N∥ED′ 交 DC 边于点 N．设 AM 的长为 x，△NF′C 中，F′C 边上 的高为 y，求 y 关于 x 的函数关系式，并确定自变量 x 的取值范围． O A B C D P E F MN A B C E D F G Q P 图 1 A B C E D F G Q P 图 2 A B C E D F G 图 1 A B C E D F′ N 图 2 M D′ 44．如图，四边形 OABC 的四个顶点坐标分别为 O（0，0），A（8，0），B（4，4），C（0，4），直线 l：y ＝kx＋b 保持与四边形 OABC 的边交于点 M、N（M 在折线 AOC 上，N 在折线 ABC 上）设四边形 OABC 在 l 右下方部分的面积为 S1，在 l 左上方部分的面积为 S2，记 S＝| S1－S2|． （1）求∠OAB 的大小； （2）当 M、N 重合时，求 l 的解析式； （3）当 b≤0 时，问线段 AB 上是否存在点 N 使得 S＝0？若存在，求 b 的值；若不存在，请说明理由； （4）求 S 与 b 的函数关系式。 45．如图，在平行四边形 ABCD 中，已知 AB＝4，AD＝5，BD＝3，以 B 点为坐标原点、AB 所在直线为 x 轴建立平面直角坐标系．将平行四边形 ABCD 绕 B 点逆时针方向旋转，使 C 点落在 y 轴正半轴上，C、D、 A 三点旋转后的位置分别是 E、F 和 G 三点． （1）求证：点 D 在 y 轴上； （2）若直线 y＝kx＋b 经过 E、F 两点，求直线 EF 的解析式； （3）将平行四边形 EFGB 沿 y 轴正半轴向上平移，得平行四边形 E′F′G′B′．设 BB′＝m（0＜m≤3），平行 四边形 E′F′G′B′ 与平行四边形 ABCD 重叠部分的面积为 S，求 S 关于 m 的函数关系式． 46．已知矩形 ABCD 中，AB＝7，AD＝6，菱形 EFGH 的三个顶点 E、G、H 分别在矩形 ABCD 的边 AB、 CD、DA 上，且 AH＝2，连接 CF． （1）当四边形 EFGH 为正方形时，求 DG 的长； （2）当△FCG 的面积为 1 时，求 DG 的长； （3）当△FCG 的面积最小时，求 DG 的长． A BC O N xM D y 2 －2 4 5 l A CD B x E F G y A CD B F E G H 47．如图，在平面直角坐标系中，已知点 A（0，2），点 P 是 x 轴上一动点，以线段 AP 为一边，在其一侧 作等边三角线 APQ．当点 P 运动到原点 O 处时，记 Q 的位置为 B． （1）求点 B 的坐标； （2）求证：当点 P 在 x 轴上运动（P 不与 O 重合）时，∠ABQ 为定值； （3）是否存在点P，使得以A、O、Q、B为顶点的四边形是梯形？若存在，请求出P点的坐标；若不存在， 请说明理由． 48．如图，在矩形 ABCD 中，AD＝4，AB＝m（m＞4），点 P 是 AB 边上的任意一（不与点 A、B 重合）， 连结 PD，过点 P 作 PQ⊥PD，交直线 BC 于点 Q． （1）当 m＝10 时，是否存在点 P 使得点 Q 与点 C 重合？若存在，求出此时 AP 的长；若不存在，说明理 由； （2）连结 AC，若 PQ∥AC，求线段 BQ 的长（用含 m 的代数式表示） （3）若△PQD 为等腰三角形，求以 P、Q、C、D 为顶点的四边形的面积 S 与 m 之间的函数关系式，并写 出 m 的取值范围． 49．已知正方形 ABCD，点 P 是对角线 AC 所在直线上的动点，点 E 在 DC 边所在直线上，且始终保持 PE ＝PD． （1）如图 1，当点 P 在对角线 AC 上时，请你通过测量、观察，猜想 PE 与 PB 有怎样的关系？（直接写 出结论不必证明）； （2）如图 2，当点 P 运动到 CA 的延长线上时，（1）中猜想的结论是否成立？如果成立，请给出证明；如 果不成立，请说明理由； （3）如图 3，当点 P 运动到 CA 的反向延长线上时，请你利用图 3 画出满足条件的图形，并判断此时 PE 与 PB 有怎样的关系？（直接写出结论不必证明） A Q y B xP O A B Q P D C A B P D CE 图 1 A B P D CE 图 2 A B P D C 图 3 50．已知菱形 ABCD 的边长为 5，∠DAB＝60°．将菱形 ABCD 绕点 A 逆时针旋转得到菱形 AEFG，设∠EAB ＝α，且 0°＜α＜90°，连接 DG、BE、CE、CF． （1）如图 1，求证：△AGD≌△AEB； （2）当 α＝60°时，在图 2 中画出图形并求出线段 CF 的长； （3）若∠CEF＝90°，在图 3 中画出图形并求出△CEF 的面积． 51．如图：菱形 ABCD 由两个等边三角形组成，点 P 是△ABD 内任一点，将△BPD 绕点 B 旋转到△BQC 的位置．则： （1）当四边形 BPDQ 是平行四边形时，求∠BPD； （2）当△PQD 是等腰直角三角形时，求∠BPD； （3）若∠APB＝100°，且△PQD 是等腰三角形时，求∠BPD． 52．探究问题： （1）方法感悟： 如图①，在正方形 ABCD 中，点 E，F 分别为 DC，BC 边上的点，且满足∠EAF＝45°，连接 EF，求证 DE ＋BF=EF． 感悟解题方法，并完成下列填空： 将△ADE 绕点 A 顺时针旋转 90°得到△ABG，此时 AB 与 AD 重合，由旋转可得： AB＝AD，BG＝DE，∠1＝∠2，∠ABG＝∠D＝90° ∴∠ABG＋∠ABF＝90°＋90°＝180° 因此，点 G，B，F 在同一条直线上 ∵∠EAF＝45°，∴∠2＋∠3＝∠BAD－∠EAF＝90°－45°＝45° ∵∠1＝∠2，∴∠1＋∠3＝45° 即∠GAF＝∠_________． 又 AG＝AE，AF＝AF，∴△GAF≌_________． ∴_________＝EF，故 DE＋BF＝EF． （2）方法迁移： 如图②，将 Rt△ABC 沿斜边 AC 翻折得到△ADC，点 E，F 分别为 DC，BC 边上的点，且∠EAF＝ 1 2 ∠DAB．试猜想 DE，BF，EF 之间有何数量关系，并证明你的猜想． （3）问题拓展： 如图③，在四边形 ABCD 中，AB＝AD，E，F 分别为 DC，BC 上的点，满足∠EAF＝ 1 2∠DAB，试猜想当∠B 与∠D 满足什么关系时，可使得 DE＋BF＝EF．请直接写出你的猜想（不必说明理由）． A B F D C E 图 1 A B D C 图 2 A B D C 图 3 A B D CP Q 53．如图，已知在直角梯形 ABCD 中，AD∥BC，AB⊥BC，AD＝11，BC＝13，AB＝12．动点 P、Q 分别在 边 AD 和 BC 上，且 BQ＝2DP．线段 PQ 与 BD 相交于点 E，过点 E 作 EF∥BC，交 CD 于点 F，射线 PF 交 BC 的延长线于点 G，设 DP＝x． （1）求 DF CF 的值． （2）当点 P 运动时，试探究四边形 EFGQ 的面积是否会发生变化？如果发生变化，请用 x 的代数式表示 四边形 EFGQ 的面积 S；如果不发生变化，请求出这个四边形的面积 S． （3）当△PQG 是等腰三角形时，求 x 的值． 54．已知 P 为正方形 ABCD 的边 BC 上任意一点，BE⊥AP 于点 E，在 AP 的延长线上取点 F，使 EF＝AE， 连接 BF、CF． （1）如图 1，求证：BF＝BC； （2）如图 2，∠CBF 的平分线交 AF 于点 G，连接 DG，求证：BG＋DG＝ 2AG； （3）若正方形 ABCD 的边长为 2，当 P 点为 BC 的中点时，求 CF 的长． 55．（1）如图①，在正方形 ABCD 中，△AEF 的顶点 E，F 分别在 BC，CD 边上，高 AG 与正方形的边长 相等，求∠EAF 的度数； （2）如图②，在 Rt△ABD 中，∠EAF＝90°，AB＝AD，点 M，N 是 BD 边上的任意两点，且∠MAN＝ 45°，将△ABM 绕点 A 逆时针旋转 90°至△ADH 位置，连接 NH，试判断 MN，ND，DH 之间的数量关系， 并说明理由． （3）在图①中，连接 BD 分别交 AE，AF 于点 M，N，若 EG＝4，GF＝6，BM＝3 2，求 AG，MN 的 长． CFBG A D E 1 2 3 图① CFB A D E 图② CFB A D E 图③ A B Q C G FE P D C F BA D E P 图 2 G C F BA D E P 图 1 C F B A D E G 图① 56．如图，点 P 是正方形 ABCD 边 AB 上一点（不与点 A，B 重合），连接 PD 并将线段 PD 绕点 P 顺时针 方向旋转 90°得到线段 PE，PE 交边 BC 于点 F．连接 BE，DF． （1）求证：∠ADP＝∠EPB； （2）求∠CBE 的度数； （3）当 AP AB 的值等于多少时，△PFD∽△BFP？并说明理由． 57．如图，梯形 ABCD 中，AB∥CD，∠ABC＝90°，AB＝8，CD＝6，P 是 AB 边上一动点，连接 DP，作 PQ⊥DP，交射线 BC 于点 E，设 AP＝x，BE＝y． （1）当 BC＝4 时， ①试写出 y 关于 x 的函数关系式； ②若△APD 是等腰三角形，求 BE 的长； ③点 E 能否与 C 点重合，若能，求出相应的 AP 的长；若不能，请说明理由； （2）当 BC 在什么范围内时，存在点 P，使得 PQ 经过 C（直接写出结果）． 58．如图，直线 l1 与 x 轴、y 轴分别交于点 A（8，0）、点 B，经过原点的直线 l2 与 AB 交于点 C（3， 15 4 ）， 与过点 A 且平行于 y 轴的直线交于点 D．E 是直线 AB 上的动点，过点 E 作 y 轴的平行线，与直线 CD 交 于点 F，以 EF 为边向右侧作正方形 EFGH．设 E 点的横坐标为 t． （1）点求直线 l1 的解析式； （2）当点 E 在线段 AC 上时，求正方形 EFGH 与△ACD 重叠部分的面积的最大值； （3）设点 M 坐标为（4， 9 2），在点 E 的运动过程中，点 M 能否在正方形 EFGH 内部？若能，求 t 的取值范 围；若不能，请说明理由． H B A DM N 图② C F BA D E P CD BA E P Q CD BA 备用图 CD BA 备用图 C D B O A x y E F G H l1 l2 59．如图，在梯形 ABCD 中，已知 AD∥BC，∠B＝90°，AB＝7，AD＝9，BC＝12，在线段 BC 上任取一 点 E，连结 DE，作 EF⊥DE，交直线 AB 于点 F． （1）若点 F 与 B 重合，求 CE 的长； （2）若点 F 在线段 AB 上，且 AF＝CE，求 CE 的长； （3）设 CE＝x，BF＝y，写出 y 关于 x 的函数关系式（直接写出结果即可）． 60．如图，等腰梯形 ABCD 中，AD∥BC，AD＝AB＝CD＝2，∠C＝60°，M 是 BC 的中点． （1）求证：△MDC 是等边三角形； （2）将△MDC 绕点 M 旋转，当 MD（即 MD′）与 AB 交于一点 E，MC（即 MC′）同时与 AD 交于点 F 时， 点 E、F 和点 A 构成△AEF．试探究△AEF 的周长是否存在最小值，如果不存在，请说明理由；如果存在， 请计算出△AEF 周长的最小值． 61．如图，正方形 ABCD 的边长是 4，M 是 AD 的中点．动点 E 在边 AB 上运动．连接 EM 并延长交射线 CD 于点 F，过 M 作 EF 的垂线交射线 BC 于点 G，连接 EG、FG． （1）求证：△EFG 是等腰三角形； （2）设 AE＝x，△EFG 的面积为 y，求 y 关于 x 的函数关系式，并写出自变量 x 的取值范围； （3）在点 E 运动过程中，△EFG 是否可以成为等边三角形？请说明理由． 62．如图，已知矩形 ABCD 中，AB＝8，BC＝6，点 E 是 AD 延长线上一点，且 DE＝9，BE 交 AC 于点 P． （1）求 AP 的长； （2）试判断以点 A 为圆心、AP 为半径的⊙A 与线段 BE 的位置关系，并说明理由； （3）若以点 A 为圆心，r1 为半径的动⊙A，使点 D 在动⊙A 的内部，点 B 在动⊙A 的外部． C D B A E F C D B A 备用图 E A B C D M F C′ D′ B G A C D E F M ①求动⊙A 的半径 r1 的取值范围； ②当以点 C 为圆心，r2 为半径的动⊙C 与动⊙A 相切时，求 r2 的取值范围． 63．如图，在□ABCD 中，点 E、F 分别是 AB、CD 的中点，CE、AF 与对角线 BD 分别相交于点 G、 H． （1）求证：DH=HG=BG； （2）如果 AD⊥BD，求证：四边形 EGFH 是菱形． 64．如图，点 F 是正方形 ABCD 的边 CD 上的动点（可与 C、D 重合），AE 平分∠BAF 交 BC 边于点 E． 点 F 在线段 CD 上运动，AE 平分∠BAF 交 BC 边于点 E． （1）求证：AF＝BE＋DF； （2）若正方形 ABCD 的边长为 1，△ABE 与△ADF 的面积之和为 S．问：S 是否存在最大值？若存在，求 出这个最大值及此时 DF 的长；若不存在，请说明理由． 65．如图，正方形 ABCD 中，E、F 分别是 BC、CD 边上的动点，满足∠EAF＝45°． （1）求证：BE＋DF＝EF； （2）若正方形 ABCD 的边长为 1，求△CEF 内切圆半径的最大值． 66．如图，直线 y＝3x＋6 交 x 轴、y 轴于 B、A 两点，点 C 在 x 轴上，点 D 的坐标为（6，6），四边形 ABCD 是等腰梯形． （1）求点 C 的坐标； （2）点 P 是坐标平面内一点，且△PAB、△PBC、△PCD、△PAD 都是等腰三角形，求点 P 的坐标． A E P D CB A C B D F E G H A CB D E F A D B E F C y xO C A B D y＝3x＋6 C A B E M D M G M O M B1 M A1 M C1 M D1 M F M 67．如图，已知正方形 ABCD 的边长为 12，对角线 AC、BD 相交 于点 O，正方形 A1B1C1D1 的顶点 A1 与点 O 重合，A1B1 交 BC 于点 E，A1D1 交 CD 于点 F，A1C1 交 BC 于点 G，连接 EF、GF． （1）求证：△A1EG≌△A1FG； （2）①若 FG＝5，求 FC 的长； ②若 A1E＝2 10，求 FC 的长； （3）设 FC＝x，△A1EF 的面积为 S，求 S 关于 x 的函数关系式； S 是否存在最小值，若存在，求出此时 x 的值，若不存在， 请说明理由． 68．已知：如图，在矩形 ABCD 中，AD＜2AB，E 为 AD 的中点，EF⊥EC 交 AB 于 F，连接 FC． （1）求证：△AEF∽△ECF； （2）设 AB BC ＝k，是否存在这样的 k 值，使得△AEF∽△BCF？若存在，请证明并求出 k 的值；若不存在， 请说明理由． 69．如图，正方形 ABCD 的边长为 2，以对角线 BD 为边作菱形 BEFD，点 C、E、F 在同一直线上． （1）求∠EBC 的度数； （2）求 CE 的长． 70．已知直线 l 过点 A（3，7），交 x 轴的正半轴于点 N，交 y 轴的正半轴于点 M． （1）如图 1，求△MON 面积的最小值； （2）如图 2，正方形 ABCD 内接于△MON，边 AD 在直线 l 上，顶点 B、C 分别在线段 OM、ON 上，求 此时直线 l 的解析式． C B D M E M A M F M A C D E F B O N x y M 图 1 A l O N x y C D M 图 2 A B l 71．如图，将边长为 a 的正方形纸片 ABCD 沿 EF 折叠（点 E、F 分别在边 AB、DC 上），使点 B 落在 AD 边上的点 G 处，点 C 落在点 H 处，GH 与 DC 交于点 M，连接 BG 与 EF 交于点 N． （1）求证：①BG＝EF；②△DGM 的周长为定值； （2）当四边形 AEFD 的面积最大时，求 AG 的长． 72．如图，矩形 ABCD 中，AB＝8，BC＝6，点 E 在边 CD 上（与点 C、D 不重合），AF⊥AE 交边 CB 的 延长线于点 F，连结 EF，交边 AB 于点 G． （1）设 DE＝x，BF＝y，求 y 关于 x 的函数关系式，并写出自变量 x 的取值范围； （2）若 AD＝BF，求证：△AEF∽△DEA； （3）当点 E 在边 CD 上移动时，△AEG 能否成为等腰三角形？若能，求出 DE 的长；若不能，请说明理 由． 73．如图，在平面直角坐标系中，正方形 ABCD 的顶点 A、D 在第二象限，顶点 B、C 在 x 轴的负半轴 上．将正方形 ABCD 绕点 B 按顺时针方向旋转，C、D、A 的对应点分别为 C1、D1、A1，且 A1、D1、O 三 点在一条直线上．记点 A1 的坐标为（a，b）． （1）若∠ABA1＝30°，b＝ 3 ①求正方形 ABCD 的边长； ②求直线 A1D1 的解析式； （2）若∠ABA1＜90°，a、b 满足 a＋b＝－2，点 D1 与点 O 之 间的距离为 5，求直线 A1D1 的解析式． 74．如图，在等腰梯形 ABCD 中，AB∥DC，对角线 AC⊥BD，垂足为 O，BC＝13 2，设 AB＝a，CD＝b， 且 a＋b＝34． （1）求：a、b 的值； A BE F C CD M C G C H C N K A B E M F C D M G A C O M B D M x y A1 M C1 M D1 M （2）设－6 2＜t＜6 2，是否存在实数 m、n，使得方程组 { 关于 x、y 的解恰好为 { ？若存在，请说明理 由，并判断点（m，n）在第几象限？若不存在，请给予证明． 75．正方形 ABCD 中，点 M、N 分别在 CB、DC 的延长线上，且 MN＝DN－BM，连接 AM、AN． （1）如图 1，求证：∠MAN＝45°； （2）如图 2，过 D 作 DP⊥AN 交 AM 于点 P，连接 PC、求证：PA＋PC＝ 2PD； （3）在（2）的条件下，若 AB＝1，C 为 DN 的中点，如图 3，求 PC 的长． 76．正方形 ABCD 中，P 为 AB 边上任一点，AE⊥DP 于 E，点 F 在 DP 的延长线上，且 DE＝EF，连接 AF、BF，∠BAF 的平分线交 DF 于 G，连接 GC． （1）求证：△AEG 是等腰直角三角形； （2）求证：AG＋CG＝ 2DG； （3）若 AB＝2，P 为 AB 的中点，求 BF 的长． 77．已知：在四边形 ABCD 中，AD∥BC，∠BAC＝∠D，点 E、F 分别在 BC、CD 上，且∠AEF＝∠ ACD． （1）如图 1，若 AB＝BC＝AC，求证：AE＝EF； （2）如图 2，若 AB＝BC，（1）中的结论是否仍然成立？证明你的结论； （3）如图 3，若 AB＝kBC，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出 AE 与 EF 之间的数量关系，并证明． O D C A B M A CB N D 图 1 M A CB N D 图 2 P M A CB N D 图 3 P A CB E D P F G E D CB A F 图 1 E D CB A F 图 2 E D CB A F 图 3 78．如图，正方形 ABCD 的边长为 2，M 是 AB 的中点，点 P 是射线 DC 上的动点，过 P 作 PE⊥DM 于 E． （1）若以 P、E、M 为顶点的三角形与△ABM 相似，求 PD 的长； （2）若以 C 为圆心，CP 为半径的⊙C 与线段 DM 只有一个公共点，求 PD 的长或 PD 的取值范围． 79．如图 1，在矩形 ABCD 中，点 E 在边 AD 上，∠ABE＝30°，BE＝DE，点 P 为线段 DE 上的任意一点， 过点 P 作 PQ∥BD，交 BE 于点 Q． （1）若 AB＝2 3，求边 AD 的长； （2）如图 2，在（1）的条件下，若点 P 为线段 DE 的中点，连接 CQ，过点 P 作 PF⊥QC 于 F，求线段 PF 的长； （3）试判断 BE、PQ、PD 这三条线段的长度之间有怎样的数量关系？请证明你的结论． 80．如图，已知点 A（－2，0），B（2，0），以 AB 为边在 x 轴上方作正方形 ABCD，点 E 是 AD 边的中点， F 是 x 轴上一动点，连接 EF，过点 E 作 EG⊥EF，交 BC 所在的直线于点 G，连接 FG． （1）当点 F 与点 A 重合时，易得 EF EG ＝ 1 2 ；若点 F 与点 A 不重合时， EF EG 的值是否改变？请说明理由； （2）设点 F 的横坐标为 x（－2＜x＜2），△BFG 的面积为 S，求 S 关于 x 的函数关系式，并求出 S 的最大 值； （3）当点 F 在 x 轴上运动时，判断有几个位置能够使得以点 E、F、G 为顶点三角形和以点 B、F、G 为 顶点的三角形全等？直接写出相应的点 F 的坐标． 81．如图，直角梯形 OABC 中，AB∥OC，O 为坐标原点，点 A 在 y 轴正半轴上，点 C 在 x 轴正半轴上， 点 B 坐标为（2，2 3），∠BCO＝60°，OH⊥BC 于点 H．动点 P 从点 H 出发，沿线段 HO 向点 O 运动， 动点 Q 从点 O 出发，沿线段 OA 向点 A 运动，两点同时出发，速度都为每秒 1 个单位长度．设点 P 运动 的时间为 t 秒． C B D A M 备用图 C B D A M P E A B C DE P Q 图 1 A B C DE P Q F 图 2 OA B x y CD E F G A B O x y C MQ P H （1）求 OH 的长； （2）若△OPQ 的面积为 S，求 S 与 t 之间的函数关系式． （3）设 PQ 与 OB 交于点 M． ①当 t 为何值时，△OPM 为等腰三角形？ ②求线段 OM 长度的最大值． 82．如图，直角梯形 OABC 的直角顶点 O 在坐标原点，∠OAB＝60°，顶点 A、C 的坐标分别为（10，0）、 （0，2 3），点 E 在线段 OA 上（不与 A 重合），点 F 在射线 AB 上．将△AEF 沿 EF 折叠，使点 A 落在射 线 AB 上点 A′ 处，设点 E 的横坐标为 x，△A′ EF 与梯形 OABC 重叠部分的面积为 S． （1）当重叠部分的图形为四边形时，求 x 的取值范围； （2）求 S 关于 x 的函数关系式； （3）S 是否存在最大值？若存在，求出这个最大值，并求此时 x 的值；若不存在，请说明理由． 83．已知在矩形 ABCD 中，AB＝1，点 P 在对角线 AC 上，直线 l 过点 P 且与 AC 垂直，与 AD 相交于点 E． （1）若 AD＝a，直线 l 与边 BC 相交于点 G（如图 1），AP＝ 1 3 AC，求 AE 的长（用含 a 的代数式表示）； （2）在（1）中，又直线 l 把矩形分成的两部分面积比为 2 : 5，求 a 的值； （3）若 AP＝ 1 4 AC，且直线 l 经过点 B（如图 2），求 AD 的长； （4）若直线 l 分别与边 AD、AB 相交于点 E、F，AP＝ 1 4 AC．设 AD 的长为 x，△AEF 的面积为 y，求 y 与 x 的函数关系式，并写出 x 的取值范围． 84．如图，在直角梯形 ABCD 中，AD∥BC，AB⊥BC，BC＝5，CD＝6，∠DCB＝60°，等边△PMN（N 为 固定点）的边长为 x，边 MN 在直线 BC 上，NC＝8．将直角梯形 ABCD 绕点 C 按逆时针方向旋转到①的 位置，再绕点 D1 按逆时针方向旋转到②的位置，如此旋转下去． （1）将直角梯形按此方法旋转四次，如果等边△PMN 的边长为 x≥5＋3 3，求梯形 ABCD 与等边△PMN O A xE B y C F A′ 60° O A x B y C 60° 备用图 l A CB DE P G 图 1 l CB DE P 图 2 重叠部分的面积； （2）将直角梯形按此方法旋转三次，如果梯形与等边三角形重叠部分的面积为 19 2 ，求等边△PMN 的边长 x 的取值范围； （3）将直角梯形按此方法旋转三次，如果梯形与等边三角形重叠部分的面积是梯形面积的一半，求等边△ PMN 的边长 x． 85．如图，在矩形 ABCD 中，AB＝4，AD＝2，点 M 是 AD 的中点，点 E 是边 AB 上的一动点．连结 EM 并延长交射线 CD 于点 F，过 M 作 EF 的垂线交 BC 的延长线于点 G，连结 EG，交边 DC 于点 H．设 AE 的长为 x，△MEG 的面积为 y． （1）求 sin∠MEG 的值； （2）求 y 关于 x 的函数解析式，并确定自变量 x 的取值范围； （3）设线段 MG 的中点为 N，连结 CN．是否存在 x 的值，使得以 N、C、G 为顶点的三角形与△EFH 相 似？若存在，求 x 和 y 的值；若不存在，请说明理由． 86．如图，在平面直角坐标系中，直线 y＝－ 1 2 x＋b（b＞0）分别交 x 轴、y 轴于 A、B 两点，以 OA、OB 为边作矩形 OACB，D 为 BC 的中点．以 M（4，0）、N（8，0）为斜边端点作等腰直角三角形 PMN，点 P 在第一象限，设矩形 OACB 与△PMN 重叠部分的面积为 S． （1）求点 P 的坐标； （2）求 S 与 b 的函数关系式； （3）若在直线 y＝－ 1 2 x＋b（b＞0）上存在点 Q，使 ∠OQM＝90°，求 b 的取值范围； （4）在 b 值的变化过程中，若△PCD 为等腰三角 形，求所有符合条件的 b 值． AD C B M P M l M ① ② M M N M ③ B1 M D1 M A1 M E F D C A B G M H D C A B M 备用图 D AO C M B x M y M P M M N M 八、圆 1．如图，已知直线 PA 交⊙O 于 A、B 两点，AE 是⊙O 的直径，点 C 为⊙O 上一点，且 AC 平分∠PAE， 过 C 作 CD⊥PA，垂足为 D． （1）求证：CD 为⊙O 的切线； （2）若 DC＋DA＝6，⊙O 的直径为 10，求 AB 的长度． 2．已知△ABC 内接于⊙O，BT 与⊙O 相切于点 B，点 P 在直线 AB 上，过点 P 作 BC 的平行线交直线 BT 于点 E，交直线 AC 于点 F． （1）如图，当点 P 在线段 AB 上时，求证：PA·PB＝PE·PF； （2）当点 P 在 BA 延长线上时，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由； （3）若 AB＝4 2，cos∠EBA＝ 1 3 ，求⊙O 的半径． 3．如图，在△ABC 中，AB＝5，AC＝6，BC＝7． （1）求 sinA 和 sinC 的值； （2）若⊙D 的圆心 D 在边 AC 上，且⊙D 与边 AB、BC 都相切，求⊙D 的半径． 4．如图，两个同心圆的圆心为 O，大圆的半径为 13，小圆的半径为 5，AD 是大圆的直径．大圆的弦 AB、 BE 分别与小圆相切于点 C、F．AD 与 BE 相交于点 G，连接 BD． （1）求 BD 的长； （3）求 BG AG 的值． C A D B P E O C A B E P O F T A B C D A C B DG F E O H A B C O D E G F 5．梯形 ABCD 中，AD∥BC，AB＝8，∠ABC＝90°，以 AB 为直径的⊙O 切 CD 于点 E． （1）如图 1，设 AD＝x，BC＝y，求 y 与 x 之间的函数关系式； （2）如图 2，BE 的延长线交 AD 的延长线于点 F，求证：AD＝ 1 2 AF； （3）如图 3，若 AD＝2，BC＝8，动点 P 以每秒 1 个单位长的速度，从点 B 沿线段 BC 向点 C 运动；同时 动点 Q 以相同的速度，从点 D 沿折线 D－A－B 向点 B 运动．当点 P 到达点 C 时，两点同时停止运 动．过点 P 作直线 PM⊥BC 与折线 B－D－C 的交于点 M．设点 P 运动的时间为 t（秒）．点 P 在线段 BC 上运动时，是否可以使得以 D、M、Q 为顶点的三角形为直角三角形？若可以，请求出 t 的值；若不可以， 请说明理由． 6．已知：在 Rt△ABC 中，∠A＝90°，AB＝3，AC＝4，⊙A 与⊙B 外切于点 D，并分别与 BC、AC 边交于 点 E、F． （1）设 EC＝x，FC＝y，求 y 关于 x 的函数关系式，并写出自变量 x 的取值范围； （2）若以 E、F、C 为顶点的三角形与△ABC 相似，求 AD BD 的值； （3）若⊙C 与⊙A、⊙B 都相切，求 AD BD 的值． 7．如图，已知∠ABC＝90º，AB＝BC，直线 l 与以 BC 为直径的⊙O 相切于点 C，点 F 是⊙O 上异于 B、C 的动点，直线 BF 与 l 相交于点 E，过点 F 作 AF 的垂线交直线 BC 于点 D． （1）如果 BE＝15，CE＝9，求 EF 的长； （2）证明：①△CDF∽△BAF；②CD＝CE； （3）探求动点 F 在什么位置时，相应的点 D 位于线段 BC 的延长线上，且使 BC＝ 3CD，请说明你的理由． 8．如图，第一象限内半径为 2 的⊙C 与 y 轴相切于点 A，作直径 AD，过点 D 作⊙C 的切线 l 交 x 轴于点 B，P 为直线 l 上一动点，已知直线 PA 的解析式为：y＝kx＋3． （1）设点 P 的纵坐标为 p，写出 p 随 k 变化的函数关系式； （2）设⊙C 与 PA 交于点 M，与 AB 交于点 N，则不论动点 P 处于直线 l 上（除点 B 以外）的什么位置时， 都有△AMN∽△ABP．请你对于点 P 处于图中位置时的两三角形相似给予证明； （3）是否存在使△AMN 的面积等于 32 25 的 k 值？若存在，求 k 的值；若不存在，请说明理由． A B C O D E M P Q 图 3 A B CD EF O l A B C O D E F 图 2 A B C O D E 图 1 A B C D E F 9．已知：AB 是⊙O 的直径，弦 CD⊥AB 于点 G，E 是直线 AB 上一动点（不与点 A、B、O、G 重合），直 线 DE 交⊙O 于点 F，直线 CF 交直线 AB 于点 P．设⊙O 的半径为 r． （1）如图 1，当点 E 在直径 AB 上时，试证明：OE·OP＝r 2； （2）当点 E 在 AB（或 BA）的延长线上时，以图 2 点 E 的位置为例，（1）中的结论是否成立？请说明理 由． 10．已知：△ABC 是边长为 4 的等边三角形，点 O 在边 AB 上，⊙O 过点 B 且分别与边 AB，BC 相交于点 D，E，EF⊥AC，垂足为 F． （1）求证：直线 EF 是⊙O 的切线； （2）当直线 DF 与⊙O 相切时，求⊙O 的半径． 11．如图，AB 是⊙O 的直径，弦 DE 垂直平分半径 OA，C 为垂足，DE＝3，连接 DB，过点 E 作 EM∥ BD，交 BA 的延长线于点 M． （1）求⊙O 的半径； （2）求证：EM 是⊙O 的切线； （3）若弦 DF 与直径 AB 相交于点 P，当∠APD＝45º 时， 求图中阴影部分的面积． 12．如图，AB 是半圆 O 的直径，AB＝2，射线 AM、BN 为半圆 O 的切线．在 AM 上取一点 D，连接 BD 交半圆于点 C，连接 AC．过 O 点作 BC 的垂线 OE，垂足为点 E，与 BN 相交于点 F．过 D 点作半圆 O 的 切线 DP，切点为 P，与 BN 相交于点 Q． CA BO x y M D l P N C A BO F D PEG （图 1） C A BO D EG （图 2） C A B O D E F C A BO D E F M P （1）求证：△ABC∽△OFB； （2）当△ABD 与△BFO 的面枳相等时，求 BQ 的长； （3）求证：当 D 在 AM 上移动时（A 点除外），点 Q 始终是线段 BF 的中点． 13．如图，在 Rt△ABC 中，∠ACB＝90°，AC＝6cm，BC＝8cm，P 为 BC 的中点．动点 Q 从点 P 出发， 沿射线 PC 方向以 2cm/s 的速度运动，以 P 为圆心，PQ 长为半径作圆．设点 Q 运动的时间为 t s． （1）当 t＝1.2 时，判断直线 AB 与⊙P 的位置关系，并说明理由； （2）已知⊙O 为△ABC 的外接圆，若⊙P 与⊙O 相切，求 t 的值． 14．如图，已知 AB 是⊙O 的弦，OB＝2，∠B＝30° ，C 是弦 AB 上的任意一点（不与点 A、B 重合），连接 CO 并延长 CO 交⊙O 于点 D，连接 AD． （1）弦长 AB 等于___________（结果保留根号）； （2）当∠D＝20° 时，求∠BOD 的度数； （3）当 AC 的长度为多少时，以 A、C、D 为顶点的三角形与以 B、C、O 为顶点的三角形相似？请写出解 答过程． 15．如图，四边形 ABCD 为正方形，⊙O 过正方形的顶点 A 和对角线的交点 M，分别交 AB、AD 于点 F、 E． （1）求证：DE＝AF； （2）若⊙O 的半径为 2 ，AB＝ 2＋1，求 AE ED 的值． 16．如图，以点 O 为圆心的两个同心圆中，矩形 ABCD 的边 BC 为大圆的弦，边 AD 与小圆相切于点 M， OM 的延长线与 BC 相交于点 N． （1）点 N 是线段 BC 的中点吗？为什么？ O A BC PQ OA B C P Q F N M D E A O BC D A O B C DE F M （2）若圆环的宽度（两圆半径之差）为 6cm，AB＝5cm，BC＝10cm，求小圆的半径． 17．如图，AB 是⊙O 的直径，AT 是经过点 A 的切线，弦 CD 垂直 AB 于 P 点，Q 为线段 CP 的中点，连 接 BQ 并延长交切线 AT 于 T 点，连接 OT． （1）求证：BC∥OT； （2）若⊙O 直径为 10，CD＝8，求 AT 的长； （3）延长 TO 交直线 CD 于 R，若⊙O 直径为 10，CD＝8，求 TR 的长． 18．如图，在 Rt△ABC 中，∠ABC＝90°，D 是 AC 的中点，⊙O 经过 A、D、B 三点，CB 的延长线交⊙O 于点 E，过点 E 作⊙O 的切线，交 AC 的延长线于点 F． （1）求证：AE＝CE； （2）若 CF＝CD＝2，求⊙O 的半径和 sin∠CAB 的值； （3）若 CF＝k·CD（k＞0），直接写出 sin∠CAB 的值（用含 k 的代数式表示）． 19．如图，Rt△ABC 中，∠ACB＝90°，AB＝5，AC＝4，点 P 是 AC 上的动点（P 不与 A、C 重合）， PQ⊥AB，垂足为 Q．设 PC＝x，PQ＝y． （1）求 y 与 x 的函数关系式； （2）求△ABC 内切圆 I 的半径，并探求 x 为何值时，直线 PQ 与内切圆 I 相切？ （3）若 0＜x＜1，试判断以 P 为圆心，半径为 y 的圆与⊙I 能否相内切，若能，求出相应的 x 的值，若不 能，请说明理由． A O B C D N M C PO D A B Q T A B C O D E F A B C I P Q 20．如图 1，⊙O 中 AB 是直径，C 是⊙O 上一点，∠ABC＝45°，等腰直角三角形 DCE 中∠DCE 是直角， 点 D 在线段 AC 上． （1）证明：B、C、E 三点共线； （2）若 M 是线段 BE 的中点，N 是线段 AD 的中点，证明：MN＝ 2OM； （3）将△DCE 绕点 C 逆时针旋转 α（0°＜α＜90°）后，记为△D1CE1（如图 2），若 M1 是线段 BE1 的中点， N1 是线段 AD1 的中点，M1N1＝ 2OM1 是否成立？若成立，请证明；若不成立，说明理由． 21．如图，AB 是⊙O 的直径，AB＝4，过点 B 作⊙O 的切线，C 是切线上一点，且 BC＝2，P 是线段 OA 上一动点，连结 PC 交⊙O 于点 D，过点 P 作 PC 的垂线，交切线 BC 于点 E，交⊙O 于点 F，连结 DF 交 AB 于点 G． （1）当 P 是 OA 的中点时，求 PE 的长； （2）若∠PDF＝∠E，求△PDF 的面积． 22．如图，△ABC 内接于⊙O，直径 DE⊥BC，交 AB 于点 F，ED、CA 的延长线相交于点 G． （1）求证：∠OBF＝∠G； （2）若 OF＝1，GF＝3，求⊙O 的半径； （3）当BEC︵ 是什么类型的弧时，△AFG 的外心在△AFG 的外部、内部、一边上？说明理由． 23．如图 1，已知在⊙O 中，点 C 为劣弧 AB 的中点，连接 AC 并延长至 D，使 CD＝CA，连接 DB 并延长 交⊙O 于点 E，连接 AE． （1）求证：AE 是⊙O 的直径； 图 2 A B O C D1 E1 M1 N1 图 1 A B O C D E M N A B O C F E D G C A B D M O P M E M F MG M （2）如图 2，连接 EC，⊙O 半径为 5，AC 的长为 4，求阴影部分的面积之和． 24．已知：如图，锐角△ABC 内接于⊙O，∠ABC＝45°；点 D 是 BC︵ 上一点，过点 D 的切线 DE 交 AC 的 延长线于点 E，且 DE∥BC；连结 AD、BD、BE，AD 的垂线 AF 与 DC 的延长线交于点 F． （1）求证：△ABD∽△ADE； （2）记△DAF、△BAE 的面积分别为 S△DAF 、S△BAE ，求证：S△DAF ＞S△BAE ． 25．如图，在以 O 为圆心的两个同心圆中，小圆的半径为 2，大圆的弦 AB 与小圆交于点 C、D，且 AB＝ 3CD，且∠COD＝60°． （1）求大圆的半径； （2）若大圆的弦 AE 与小圆切于点 F，求 AE 的长． 26．已知：如图，在△ABC 中，AB＝AC，AD 平分∠BAC 交 BC 于点 D，BE 平分∠ABC 交 AD 于点 E， F 是边 AB 上一点，以 BF 为直径的⊙O 经过点 E． （1）求证：AD 是⊙O 的切线； （2）若 BC＝4，cosC＝ 1 3 ，求⊙O 的半径． A B O C D E 图 1 A B O C D E 图 2 A B D C E O F A BDC O E F A B D C O E F 27．已知：如图，AB 是⊙O 的直径，点 P 为 BA 延长线上一点，PC 切⊙O 于点 C，BD⊥PC，垂足为 D， 交⊙O 于 E，连接 AC、BC、EC． （1）求证：BC 2＝BD·BA； （2）若 AC＝6，DE＝4，求 PC 的长． 28．如图，⊙P 与 y 轴相切于坐标原点 O（0，0），与 x 轴相交于点 A（5，0），过点 A 的直线 AB 与 y 轴 的正半轴交于点 B，与⊙P 交于点 C． （1）若 AC＝3，求点 B 的坐标； （2）若 AC＝a，D 是 OB 的中点．问：O、P、C、D 四点是否在同一圆上？请说明理由．如果这四点在同 一圆上，记这个圆的圆心为 O1，函数 y＝ k x 的图象经过点 O1，求 k 的值（用含 a 的代数式表示）． 29．己知：如图，△ABC 内接于⊙O，AB 为直径，∠CBA 的平分线交 AC 于点 F，交⊙O 于点 D，DF⊥AB 于点 E，且交 AC 于点 P，连结 AD． （1）求证：∠DAC＝∠DBA； （2）求证：P 是线段 AF 的中点； （3）若⊙O 的半径为 5，AF＝ 15 2 ，求 tan∠ABF 的值． 30．如图，已知 CD 是⊙O 的直径，AC⊥CD，垂足为 C，弦 DE∥OA，直线 AE、CD 相交于点 B． （1）求证：直线 AB 是⊙O 的切线； （2）如果 AC＝1，BE＝2，求 tan∠OAC 的值． 31．如图，在锐角△ABC 中，AC 是最短边，以 AC 中点 O 为圆心， 1 2 AC 长为半径作⊙O，交 BC 于 E， 过 O 作 OD∥BC 交⊙O 于 D，连结 AE、AD、DC． AB D C O E P y O x C AP B D y O x C AP B D 备用图 A B C D E O F P OC A D BE （1）求证：D 是 AE︵ 的中点； （2）求证：∠DAO＝∠B＋∠BAD； （3）若 S △ CEF S △ OCD ＝ 1 2 ，且 AC＝4，求 CF 的长. 32．如图，在△ABC 中，AB＝AC，以 AB 为直径的⊙O 交 BC 于点 D，过点 D 作 EF⊥AC 于点 E，交 AB 的延长线于点 F． （1）求证：EF 是⊙O 的切线； （2）如果∠A＝60º，则 DE 与 DF 有何数量关系？请说明理由； （3）如果 AB＝5，BC＝6，求 tan∠BAC 的值． 33．已知 AB 为⊙O 直径，以 OA 为直径作⊙M，过点 B 作⊙M 的切线 BC，切点为 C，交⊙O 于 E． （1）在图中 1 过点 B 作⊙M 的另一条切线 BD，切点为 D（用尺规作图，保留作图痕迹，不写作法，不用 证明）； （2）证明：∠EAC＝∠OCB； （3）若 AB＝4，在图 2 中过 O 作 OP⊥AB 交⊙O 于 P，交⊙M 的切线 BD 于 N，求 BN 的值． 34．如图，AB 是⊙O 的直径，CD 是⊙O 的切线，切点为 C．延长 AB 交 CD 于点 E．连接 AC，作∠DAC＝ ∠ACD，作 AF⊥ED 于点 F，交⊙O 于点 G． （1）求证：AD 是⊙O 的切线； （2）如果⊙O 的半径是 6cm，EC＝8cm，求 GF 的长． 35．如图所示，在以 O 为圆心的两个同心圆中，小圆的半径为 1，AB 与小圆相切于点 A，与大圆相交于点 B，大圆的弦 BC⊥AB 于点 B，过点 C 作大圆的切线 CD 交 AB 的延长线于点 D，连接 OC 交小圆于点 E， 连接 BE、BO． （1）求证：△AOB∽△BDC； O A B D CE F A BC E O D F OA B CE M 图 1 OA B CE M 图 2 P O A DCE F B G （2）设大圆的半径为 x，CD 的长为 y． ①求 y 与 x 之间的函数关系式； ②当 BE 与小圆相切时，求 x 的值． 36．如图 1，∠ABC＝90°，AB＝2，点 D 为 BC 边上的一个动点，连接 AD，将△ABD 沿 AD 翻折得到△ AED，过点 E 作 EF⊥BC 于 F． （1）当 BD＝ 2 3 时，判断直线 EF 与以 AD 为直径的⊙O 的位置关系，并加以证明； （2）如图 2，点 D 在 BC 上向点 B 运动，直线 EF 与以 AD 为直径的⊙O 交于 E、G 两点，连接 AG，当∠ EAG＝∠DAE 时，求 BD 的长． 37．如图，在边长为 8 的正方形 ABCD 中，点 O 为 AD 上一动点（4＜OA＜8），以 O 为圆心，OA 的长为 半径的⊙O 交边 CD 于点 E，连接 OE，过点 E 作⊙O 的切线交边 BC 于点 F． （1）求证：△ODE∽△ECF； （2）设 DE＝x，求 OA 的长（用含 x 的代数式表示）； （3）在点 O 运动的过程中，设△CEF 的周长为 p，试用含 x 的代数式表示 p，你能发现怎样的结论？ 38．如图，有一直径 MN＝4 的半圆形纸片，其圆心为点 P，从初始位置Ⅰ开始，在无滑动的情况下沿数轴 向右翻滚至位置Ⅴ，其中，位置Ⅰ中的 MN 平行于数轴，且半⊙P 与数轴相切于原点 O；位置Ⅱ和位置Ⅳ 中的 MN 垂直于数轴；位置Ⅲ中的 MN 在数轴上；位置Ⅴ中的点 N 到数轴的距离为 3，且半⊙P 与数轴相 切于点 A． 解答下列问题： （1）位置Ⅰ中的 MN 与数轴之间的距离为___________； 位置Ⅱ中的半⊙P 与数轴的位置关系是___________； （2）求位置Ⅲ中的圆心 P 在数轴上表示的数； （3）求半⊙P 从位置Ⅲ翻滚到位置Ⅳ时，点 N 所经过路径长及该纸片所扫过图形的面积； A O B C D E A D B EF C G 图 2 O A D B EF C 图 1 A D B CE O F （4）求 OA 的长． [（2），（3），（4）中的结果保留 π] 39．已知点 P 在线段 AB 上，点 O 在线段 AB 的延长线上，以点 O 为圆心，OP 为半径作⊙O，点 C 是⊙O 上的一点． （1）如图，如果 AP＝2PB，PB＝BO，求证：△CAO∽△BCO； （2）如果 AP＝m（m 是常数且 m＞1），BP＝1，且 OP 2＝OA·OB．当点 C 在⊙O 上运动时，求 AC : BC 的值（结果用含 m 的式子表示）； （3）在（2）的条件下，讨论以 BC 为半径的⊙B 和以 CA 为半径的⊙C 的位置关系，并写出相应的 m 取 值范围． 40．已知，AB 是⊙O 的直径，AB＝8，点 C 在⊙O 的半径 OA 上运动，PC⊥AB，垂足为 C，PC＝5，PT 为⊙O 的切线，切点为 T． （1）如图 1，当 C 点运动到 O 点时，求 PT 的长； （2）如图 2，当 C 点运动到 A 点时，连接 PO、BT，求证：PO∥BT； （3）如图 3，设 PT 2＝y，AC＝x，求 y 与 x 的函数关系式及 y 的最小值． 41．已知△ABC，分别以 AC 和 BC 为直径作半圆 O1、O2，P 是 AB 的中点． （1）如图 1，若△ABC 是等腰三角形，且 AC＝BC，在 AC︵ 、 BC︵ 上分别取点 E、F，使∠AO1E＝∠BO2F， 则有结论：①△PO1E≌△FO2P，②四边形 PO1CO2 是菱形．请给出结论②的证明； （2）如图 2，若（1）中△ABC 是任意三角形，其它条件不变，则（1）中的两个结论还成立吗？若成立， 请给出证明； （3）如图 3，若 PC 是⊙O1 的切线，求证：AB 2＝BC 2＋3AC 2． A P P Ⅴ O N P P N N Ⅳ N ⅢⅠ P Ⅱ M M M M P OA B C O BA T P (C) 图 1 O BA TP (C) 图 2 O BA TP 图 3 C 42．在等腰梯形 ABCD 中，AD∥BC，且 AD＝2，以 CD 为直径作⊙O1，交 BC 于点 E，过点 E 作 EF⊥AB 于 F，建立如图 1 所示的平面直角坐标系，已知 A，B 两点的坐标分别为 A（0，2 3），B（－2，0）． （1）求 C，D 两点的坐标； （2）求证：EF 为⊙O1 的切线； （3）探究：如图 2，线段 CD 上是否存在点 P，使得线段 PC 的长度与 P 点到 y 轴的距离相等？如果存在， 请找出 P 点的坐标；如果不存在，请说明理由． 43．如图，PA 为⊙O 的切线，A 为切点，过 A 作 OP 的垂线 AB，垂足为点 C，交⊙O 于点 B，延长 BO 与 ⊙O 交于点 D，与 PA 的延长线交于点 E． （1）求证：PB 为⊙O 的切线； （2）若 tan∠ABE＝ 1 2 ，求 sinE 的值． 44．如图，在圆内接四边形 ABCD 中，CD 为∠BCA 的外角的平分线，F 为弧AD︵ 上一点，BC＝AF，延长 DF 与 BA 的延长线交于 E． （1）求证：△ABD 为等腰三角形； （2）求证：AC·AF＝DF·FE． 45．已知⊙O1 与⊙O2 相交于 A、B 两点，点 O1 在⊙O2 上，C 为⊙O2 上一点（不与 A，B，O1 重合），直线 CB 与⊙O1 交于另一点 D． （1）如图 1，若 AC 是⊙O2 的直径，求证：AC＝CD； O1 A B C P FE O2 图 1 O1 A B C P F E O2 图 2 O1 A B C P O2 图 3 A B CEO F D O1 x y 图 1 A B CO D x y 图 2 A B C E O P D AB C E F D M （2）如图 2，若 C 是⊙O1 外一点，求证：O1C 丄 AD； （3）如图 3，若 C 是⊙O1 内的一点，判断（2）中的结论是否成立． 46．如图 1，Rt△ABC 两直角边的边长为 AC＝1，BC＝2． （1）如图 2，⊙O 与 Rt△ABC 的边 AB 相切于点 X，与边 CB 相切于点 Y．请你在图 2 中作出并标明⊙O 的圆心 O；（用尺规作图，保留作图痕迹，不写作法和证明） （2）P 是这个 Rt△ABC 上和其内部的动点，以 P 为圆心的⊙P 与 Rt△ABC 的两条边相切．设⊙P 的面积 为 S，你认为能否确定 S 的最大值？若能，请你求出 S 的最大值；若不能，请你说明不能确定 S 的最大值 的理由． 47．如图，AD 是△ABC 的边 BC 上的高，AE 是△ABC 外接圆 O 的直径，EF⊥BC 于点 F． （1）求证：BF=CD； （2）若 CD＝1，AD＝3，BD＝6，求⊙O 的直径． 48．如图，线段 AD＝5，⊙A 的半径为 1，C 为⊙A 上一动点，CD 的垂直平分线分别交 CD，AD 于点 E， B，连接 BC，AC，构成△ABC，设 AB＝x． （1）求 x 的取值范围； （2）若△ABC 为直角三角形，则 x＝____________； （3）设△ABC 的面积的平方为 W，求 W 的最大值． 49．已知：如图，以矩形 ABCD 的对角线 AC 的中点 O 为圆心、OA 长为半径作⊙O，⊙O 经过 B、D 两点， 过点 B 作 BK⊥AC，垂足为 K，过点 D 作 DH∥KB，DH 分别与 AC、AB、⊙O 及 CB 的延长线相交于点 E、F、G、H． A BC O1 D O2 图 1 A B C O1 D O2 图 2 A B C O1D O2 图 3 AB C 图 1 AB C X Y 图 2 A B C E F D O A B C D E （1）求证：AE＝CK； （2）如果 AB＝a，AD＝ 1 3 a（a 为大于零的常数），求 BK 的长； （3）若 F 是 EG 的中点，且 DE＝6，求⊙O 的半径和 GH 的长． 50．如图（1），在平面直角坐标系中，⊙O′ 是以点 O′（2，－2）为圆心，半径为 2 的圆，⊙O″ 是以点 O″ （0，4）为圆心，半径为 2 的圆． （1）将⊙O′ 竖直向上平移 2 个单位，得到⊙O1，将⊙O″ 水平向左平移 1 个单位，得到⊙O2（如图 2），分 别求出⊙O1 和⊙O2 的圆心坐标； （2）两圆平移后，⊙O2 与 y 轴交于 A、B 两点，过点 A、B 分别作⊙O2 的切线，交 x 轴与 C、D 两点，求 △O2AC 和△O2BD 的面积． 51．如图，在梯形 ABCD 中，AB∥CD，∠BAD＝90°，以 AD 为直径的半圆 O 与 BC 相切． （1）求证：OB⊥OC； （2）若 AD＝12，∠BCD＝60°，⊙O1 与半⊙O 外切，并与 BC、CD 相切，求⊙O1 的面积． 52．如图，AB 是⊙O 的直径，AC 切⊙O 于点 A，AD 是⊙O 的弦，OC⊥AD 于 F，交⊙O 于 E，连接 DE、 BE、BD、AE． （1）∠C＝∠BED； （2）如果 AB＝10，tan∠BAD＝ 3 4 ，求 AC 的长； （3）如果 DE∥AB，AB＝10，求四边形 AEDB 的面积． A B C E F D O K H G y O xO′ O″ 图（1） y O x O1 DC A B O2 图（2） O1 O A B D CM OB A D E F C 53．如图，点 P 为等边△ABC 外接圆周劣弧 BC 上的一点． （1）求∠BPC 的度数； （2）求证：PA＝PB＋PC； （3）设 PA，BC 交于点 M，若 AB＝4，PC＝2，求 CM 的长度． 54．如图，在△ABC 中，∠A＝90°，∠B＝60°，AB＝3，点 D 从点 A 以每秒 1 个单位长度的速度向点 B 运 动（点 D 不与 B 重合），过点 D 作 DE∥BC 交 AC 于点 E．以 DE 为直径作⊙O，并在⊙O 内作内接矩形 ADFE，设点 D 的运动时间为 t 秒． （1）用含 t 的代数式表示△DEF 的面积 S； （2）当 t 为何值时，⊙O 与直线 BC 相切？ 55．已知：在△ABC 中，以 AC 边为直径的⊙O 交 BC 于点 D，在劣弧AD⌒ 上取一点 E 使∠EBC＝∠DEC， 延长 BE 依次交 AC 于 G，交⊙O 于 H． （1）求证：AC⊥BH； （2）若∠ABC＝45°，⊙O 的直径等于 10，BD＝8，求 CE 的长． 56．如图，AB 是⊙O 的直径，BC 切⊙O 于点 B，连接 CO 并延长，交⊙O 于点 D、E，连接 AD 并延长， 交 BC 于点 F． （1）试判断∠CBD 与∠CEB 是否相等，并证明你的结论； （2）求证： BD BE ＝ CD BC ； （3）若 BC＝ 3 2 AB，求 tan∠CDF 的值． 57．如图，已知直线 PA 交⊙O 于 A、B 两点，AE 是⊙O 的直径，点 C 为⊙O 上一点，且 AC 平分∠PAE， 过 C 作 CD⊥PA，垂足为 D． （1）求证：CD 为⊙O 的切线； （2）若 DC＋DA＝6，⊙O 的直径为 10，求 AB 的长． A B C P M A B C D O E F O A B C G E H D OA B C E F D 58．如图，点 P 在 y 轴的正半轴上，⊙P 交 x 轴于 B、C 两点，以 AC 为直角边作等腰 Rt△ACD，BD 分别 交 y 轴和⊙P 于 E、F 两点，连接 AC、FC． （1）求证：∠ACF＝∠ADB； （2）若点 A 到 BD 的距离为 m，BF＋CF＝n，求线段 CD 的长； （3）当⊙P 的大小发生变化而其他条件不变时， DE AO 的值是否发生 变化？若不发生变化，请求出其值；若发生变化，请说明理由． 59．一量角器的直径与含 30°的较长直角板的直角边重合，且直角板 Rt△ABC 中，∠C＝90°，∠A＝60°， BC＝6，量角器半⊙O 从初始位置（点 E 与点 B 重合，EF 落在 BC 上）在线段 BC 上沿 BC 方向以每秒 1 个单位的速度平移，半⊙O 分别与 AB 相交于点 M、N．当点 F 运动到点 C 时，半⊙O 停止运动，此时半⊙O 恰好与 AB 相切，设半⊙O 平移的时间为 t． （1）求半⊙O 的半径； （2）用含 t 的代数式表示 MN 的长； （3）求 BN 的最大值． 60．如图，在梯形 ABCD 中，AD∥BC，AB⊥AD，AB＝4，AD＝CD＝5．E 为底边 BC 上的动点，以点 E 为圆心，BE 为半径的⊙E 交线段 DE 于点 F． （1）当点 F 在线段 DE 上时，设 BE＝x，DF＝y，求 y 关于 x 的函数关系式； （2）当以 CD 直径的⊙O 与⊙E 相切时，求 x 的值； （3）连接 AF、BF，当△ABF 为等腰三角形时，求 x 的值． O A B CD E P O A B C E F D P y x O A B CF M M N EO A B CF(E) A B C F E D 61．如图，四边形 ABCD 内接于圆，∠D＝90°，AB＝BC，CD＝4，AC＝8，O 是 AC 的中点． （1）设 P 是 AB 上的动点，求 OP＋PC 的最小值； （2）设 Q、R 分别是 AB、AD 上的动点，求△CQR 的周长的最小值． 62．如图，梯形 ABCD 内接于⊙O，AD∥BC，AB＝CD，E 是 DA 延长线上一点，AB 2＝AE·BC，BE 和 CA 的延长线交于点 F． （1）求证：BE 是⊙O 的切线； （2）若 BC＝18，CD＝12，AF＝16，求 BE 和 AD 的长． 63．如图，△ABC 中，AB＝AC，D 是△ABC 外接圆劣弧 AC︵ 上一点（不与点 A、C 重合），延长 BD 至 E． （1）求证：AD 的延长线平分∠CDE； （2）若∠BAC＝30°，△ABC 中 BC 边上的高为 2＋ 3，求△ABC 外接圆的半径． 64．如图，在△ABC 中，高 AE 与 CD 相交于点 H，以 DE 为直径的圆分别与 AB、AC 交于点 F、G，连接 BH．已知 AC＝25，CD＝20，CE＝7． （1）求 DE 的长； （2）求证：BH⊥FG． 65．如图，已知 AB 是⊙O 的直径，点 C 在⊙O 上，过点 C 的直线与 AB 的延长线交于点 P，且 AC＝PC， A B C D M O M A B O D M C E M F M A B C D E A B CE D H F G C O M A B P M M M ∠BOC＝2∠BCP． （1）求证：PC 是⊙O 的切线； （2）求∠P 的度数； （3）设 M 是AB ︵ 的中点，若⊙O 的半径为 2，求线段 BM、CM 及劣弧 BC 所围成的阴影部分的面积． 66．已知：如图，Rt△ABC 中，∠BAC＝90°，点 D 在斜边 BC 上，BD＝4DC，⊙O 过点 C 且与 AB 相切 于 AB 的中点 E，与 AC 相交于点 F． （1）求证：AD⊥BF； （2）若 AB＝4，AC＝2 2，求⊙O 的半径． 67．如图，△ABC 中，AB＝AC，以 AB 为直径的⊙O 分别交 AC、BC 于点 D、F，连接 BD 交 OF 于点 E． （1）求证：OF⊥BD； （2）若 AB＝ 5 2 ，DF＝ 2，求 AD 的长． 68．如图，⊙O1 与⊙O2 相交于 A、B 两点，C 是⊙O2 上一点，CA 的延长线交⊙O1 于点 D，CB 交⊙O1 于 点 E，DE 的延长线交⊙O2 于点 F，BG∥DF 交⊙O2 于点 G． （1）求证：CB＝CG； （2）若 CA＝4，AD＝2，求 CF 的长． 69．如图，在△ABC 中，∠ACB＝90°，O 是 BC 上一点，以 O 为圆心，OC 为半径的⊙O 与 AB 切于点 D， 与 BC 交于点 E，且 BD＝2，BE＝1． （1）求△ACD 的面积； （2）若 F 是线段 EC 上一动点，过 F 作 FG⊥AB 于 G，设 AG＝x，OF ＝y，求 y 与 x 之间的函数关系式． CD A B E F O C D F A B O E O1 C D E A B O2 F G C D E A B F G O 70．如图，点 D 在⊙O 的直径 AB 上，DE⊥AB 交⊙O 于点 E，OC∥AE 交⊙O 的切线 BC 于点 C，AC 与 DE 相交于点 F． （1）求证：DF＝EF； （2）延长 CO 交 ED 的延长线于点 G，当点 G 在⊙O 上时， 求 sin∠ACO 的值． 71．如图，边长为 2 3的等边三角形 ABC 内接于⊙O，点 D 在 AC︵ 上运动（与点 A、C 不重合），AD 的延 长线与 BC 的延长线相交于点 E． （1）求⊙O 的半径； （2）设 AD＝x，AE＝y，求 y 与 x 的函数关系式，并写出自变量 x 的取值范围； （3）D 点在运动过程中是否存在这样的位置，使得△BDE 成为以 BE 为底边的等腰三角形？若存在，求 AD 的长；若不存在，请说明理由． 72．如图，在 Rt△ABC 中，∠ACB＝90°，点 O 为三角形外的一点，以 O 为圆心，OC 为半径的⊙O 与边 AB 相切于点 D，与边 BC 交于点 E，直径 DF 与边 BC 交于点 G，连结 AG． （1）求证：DE∥AG； （2）当 AB＝10，AC＝6，AD＝ 34 5 时，求⊙O 的半径． 73．如图，AB 是⊙O 的直径，D 是 AC︵ 上一点，AC 与 BD 相交于点 E，且 AB＝5，sin∠CAB＝ 3 5 ． （1）设 CE＝m， DE BE ＝k，试用含 m 的代数式表示 k； （2）当 AD∥OC 时，求 CE 的长． C F O D A B EG C D A B O E A CB D F O GE A C B D E O 74．据气象台预报，一台风中心位于某沿海城市 A 东偏南 θ（cosθ＝ 10）方向 300km 的海面 B 处，正以 20km/h 的速度向西偏北 45°方向移动（如图所示），台风影响的范围为圆形区域，半径为 60km，并以 10km/h 的速度不断增大．求几小时后该市开始受到台风的影响，受影响的时间是多长？ 75．如图，点 D 为锐角三角形 ABC 外接圆的圆心，过 A、B、D 三点的⊙O 交 AC、BC 于 E、F，且 EF＝ CD． （1）求证：CD⊥EF； （2）求证：AB 是⊙O 的直径． 76．如图，⊙O 是△ABC 的外接圆，AB＝AC，直径 AD 交 BC 于点 F，E 是 OF 的中点，且 BE∥DC． （1）求证：AF＝5DF； （2）若 BC＝2 5，求 CD 的长． 77．如图，在⊙O 中，直径 AB 垂直于弦 CD，E 是 OC 的中点，AE 的延长线 交⊙O 于点 F，DF 交 BC 于点 G．求证：G 是 BC 的中点． 北 东A θ 45° B A F CB D E O A D F CB O E A C B E D F O G 78．△ABC 的内切圆⊙O 分别切 AB、BC、CA 三边于 D、E、F，G 是 DF 上一点，且 EG⊥DF，求证：EG 平分∠BGC． 79．如图，AB 是⊙O 的直径，AC 与⊙O 相切于点 A，且 AC＝AB＝2，连接 OC 交⊙O 于点 D，BD 的延 长线交 AC 于 E．求 AE 的长． 80．如图，已知⊙O 的半径为 3，点 M 为⊙O 内的一个定点，OM＝ 5，AB、CD 是⊙O 的两条相互垂直 的弦，垂足为 M． （1）当 AB＝4 时，求四边形 ADBC 的面积； （2）当 AB 变化时，求四边形 ADBC 的面积的最大值． 81．已知：如图，△ABC 内接于⊙O，AB 为直径，弦 CE⊥AB 于 F，C 是AD︵ 的中点，连结 BD 并延长交 EC 的延长线于点 G，连结 AD，分别交 CE、BC 于点 M、N． （1）求证：M 是△ACN 的外心； （2）若⊙O 的半径为 25 3 ，CE＝16，求 CN 的长． 82．如图，AB 是⊙O 的直径，以点 A 为圆心作⊙A，交⊙O 于 C、D 两点，△ACE 内接于⊙O，AE 交 CD 于点 F，连接 DE． （1）求证：AC 2＝AE·AF （2）若 AB＝15，AC＝3 5，CF : DF＝1 : 3，求 AE 和 DE 的长． A CB E D FG O A E B O D C A D B O M C A B C E F O D G M N D A B C E F O 83．如图，AB 是⊙O 的直径，点 P 是半径 OA 上的动点，MP⊥AB 交⊙O 于 C，MD 切⊙O 于 D，MP＝ 2 2． （1）当 PC＝OA 时，MD＝2，求⊙O 的半径； （2）设 MD 2＝y，AP＝x，求 y 与 x 之间的函数关系式； （3）△MPD 能否成为以 MP 为斜边的等腰直角三角形？若能，请求出△MPD 的面积；若不能，请说明理 由． 84．在平面直角坐标系中，已知点 A（－ 3，0），B（3，0），点 P 在直线 y＝ 3(x＋4)＋1 上运动，当∠APB 最大时，求 PA : PB 的值． 85．如图，在梯形 ABCD 中，AB∥CD，AD＝12，E 是边 CD 上一点，且 CE : ED＝5 : 4．设过 A、B、C、 E 四点的⊙O1 的半径为 R1，过 A、C、C 三点的⊙O2 的半径为 R2，且边 BC 与⊙O2 相切． （1）求边 CD 的长； （2）求 R1 : R2 的取值范围． 86．如图，BC 是半圆 O 的直径，点 A、F 在半圆 O 上，AD⊥BC 于 D，AB ︵ ＝ AF︵ ，BF 交 AD 于点 E． （1）求证：AE＝BE； （2）求证：AF 2＝BE·BF； （3）若 AD＝2，BD＝1，求 tan∠FBC 的值． 87．如图，扇形 AOB 中，OA＝1，∠AOB＝90°，半圆⊙O1 的圆心 O1 在 OA 上，并与AB ︵ 内切于点 A，半 圆⊙O2 的圆心 O2 在 OB 上，并与AB ︵ 内切于点 B，半圆⊙O1 与半圆⊙O2 相切．设两圆半径之和为 x，面积 之和为 y． （1）写出 y 关于 x 的函数解析式； （2）求函数 y 的最小值． OA B C D M P A B CE O1 O2 D B CO E M F MA D M A B O1 O2 O 88．已知：如图，在△ABC 中，AC＝BC，以 BC 为直径作⊙O 交 AB 于点 D，过点 D 作 DE⊥AC 于点 E， 交 BC 的延长线于点 F． （1）求证：DF 是⊙O 的切线； （2）若⊙O 的半径为 3，sin∠F＝ 3 5 ，求 DE 的长． 89．如图，⊙O 中弦 AB⊥CD，垂足为 E，过 E 作 AC 的垂线，垂足为 F，交 BD 于 G． （1）探究 BD 与 EG 之间的数量关系，并说明理由； （2）连接 OG，若 CE＝4，DE＝6，BD＝10，求 OG 的长． 90．如图，已知 AB 是⊙O 的直径，CD 是弦，AB⊥CD，垂足为 E，P 为 BC︵ 上一点，连接 AP 分别交 OC、 CD、BC 于点 F、G、H，连接 DP 交 BC 于点 Q． （1）若 P 为 BC︵ 中点，求证：CG＝CH； （2）若 F 为 OC 中点，求证：BQ＝CQ． 91．如图，在△ABC 中，AB＝AC，以 AB 为直径作⊙O 交 BC 于点 D，交 AC 于点 E，过 D 作 DG⊥AC 于 G，交 AB 的延长线于点 F． （1）求证：FG 是⊙O 的切线； （2）若 DF＝5，DG＝3，求 EC 的长． 92．如图，已知 AB 是半圆 O 的直径，C 在半圆 O 上，CD⊥AB 于 D，E 在 CD 上，⊙E 与 AB 相切于点 C，与半圆 O 相切于点 F，若 AB＝6，CD＝ 6，求：（1）⊙E 的半径；（2）阴影部分的面积． A B C E O D F A B C E O D F G O D E F C A B G H P Q O D G C A B F E D E F C A BO 93．如图，AB 是⊙O 的直径，直线 BC 与⊙O 相切于点 B，OC∥AD，DE⊥AB 于 E，交 AC 于点 F． （1）求证：CD 是⊙O 的切线； （2）若 AE＝2，BE＝4，求 sin∠DAC 和 sin∠DCA 的值． 94．如图，四边形 ABCD 内接于⊙O，BC 为⊙O 的直径，E 为 DC 上一点，若 AE∥BC，AE＝EC，BE 交 AC 于 F． （1）求证：AB＝AD； （2）若 AD＝6，AE＝7，求 BE 的长． 95．如图，四边形 ABCD 内接于⊙O，BC 是⊙O 的直径，点 E 在 CB 的延长线上，且∠BAE＝∠ADB，DF⊥BC 于点 F，交⊙O 于点 G，DG＝8． （1）求证：AE 是⊙O 的切线； （2）若 BG︵ 上有一动点 P，且 AD＝ 15，sin∠CPG＝ 3 5，求 tan∠ABD 的值． 96．如图，在△BCD 中，∠CBD＝90°，E 是 CD 的中点，⊙O 经过 B、D、E 三点，CB 的延长线交⊙O 于 点 A，过 A 作⊙O 的切线，交 DC 的延长线于点 F． （1）求证：AC＝AD； （2）若 CE＝CF＝2，求⊙O 的直径； （3）若 CF CE ＝n，求 sin∠CDB 的值． 97．如图，在△ABC 中，∠ABC＝90°，以 AB 为直径作⊙O 交 AC 于点 D，E 是 BC 的中点，连接 AE、 OD、DE，AE 与 OD 相交于点 F． （1）求证：DE 是⊙O 的切线； （2）若 AB＝10，OF＝2，求 AD 的长； O D E F C A B O D E F B A C C A OB D M F M E M G M C A OB D M E M F M C A O B E M D M F M C A O B E M D M F M （3）当四边形 AOED 是平行四边形时，求 sin∠CAE 的值． 98．如图，AB 是⊙O 的直径，C 是AB︵ 的中点，点 D 在 AC︵ 上（不与 A、C 重合），CE⊥AD 于 E，CF⊥BD 于 F． （1）求证：四边形 CEDF 是正方形； （2）若 AD＝ 6－ 2，BD＝ 6＋ 2，求阴影部分的面积． 99．如图，以正方形 ABCD 的边 CD 为直径作⊙O，以顶点 C 为圆心、边 BC 为半径作 BD︵ ，E 为 BC 延长 线的上一点，且 CD、CE 的长是方程 x 2－2( 3＋1)x＋4 3＝0 的两根，其中 CD＜CE．连结 DE 交⊙O 于 点 F． （1）求 EF 的长； （2）求图中阴影部分的面积． 100．如图，以正方形 ABCD 的边 BC 为直径，在正方形内作半圆 O，过 A 作半圆 O 的切线 AF，切点为 E，AF 交 BC 的延长线于点 F． （1）求 sin∠F 的值； （2）若 AB＝4，求 EC 的长． 101．如图，在△ABC 中，AB＝AC，⊙O 是△ABC 的外接圆，AE⊥AB 交 BC 于点 D，交⊙O 于点 E，F 在 DA 的延长线上，且 AF＝AD． （1）求证：BF 是⊙O 的切线； （2）若 AE＝4，cos∠ABF＝ 4 5 ，求 BC 的长． 102．如图，AB 是⊙O 的直径，AC 是⊙O 的切线，BC 交⊙O 于点 G，∠C 的平分线交⊙O 于点 D，点 E 在 BC 上，AE 交 BD 于点 F，∠CAD＝∠EAD．求证：DF＝DG． C A B D M O E M F M C A B D M O E M F M C A B E M O D M F M C A B E M O D MF M G M 103．如图，在 Rt△ABC 中，∠C＝90°，D 是 BC 边上一点，点 O 在线段 AD 上，以 O 为圆心、OD 为半 径的⊙O 与 AB 相切于点 E，且 ED∥AC． （1）求证：△BDE∽△ACD； （2）若 ED＝1，tan∠ADE＝ 2，求 AC、BD 的长． 104．如图，△ABC 中，AB＝AC，⊙O1 过 A、B 两点，交 AC、BC 于 D、E，⊙O2 过 C、D、E 三点，EF⊥ AC 于 F，FE 的延长线交⊙O1 于 G，AG 交 BC 于 H． （1）求证：EF 过⊙O2 的圆心 O2； （2）若 BH＝6，CD＝ 24 5 ，EC＝4，求 AG 的长． 105．如图，以矩形 ABCD 的边 AB 为直径的半圆交 CD 于 E、F 两点，CP 切半圆于 P，PQ⊥AB 于 Q．设 AQ＝m，BQ＝n． （1）用含 m、n 的代数式表示 PC 的长； （2）求证：直线 AC 平分线段 PQ； （3）求证：tg∠EBC 和 tg∠FBC 是方程 nx 2－2 mx＋ n＝0 的两个根． 106．如图，已知∠AOB＝30°，C 为 OB 上一点，OC＝ 3，DC⊥OB 于 C，交 OA 于 D，以 D 为圆心，DC 为半径作⊙D 交 OA 于 E、F 两点，M 为线段 OF 上一点（不与点 O、E 重合），过 M 作 MN⊥OA 于 M， 交 OB 于 N，设 OM＝x，四边形 CEMN 的面积为 S． （1）求 S 与 x 之间的函数关系式，并写出自变量 x 的取值范围； （2）若四边形 CEMN 的面积是△EOC 面积的 5 倍，判断此时△CMN 的形状，并说明理由． CB D M E M O A M O2 C D E A B O1 F G H B CD A F P Q E C D A BO E F M N 107．如图，点 A、B 在半径为 5 的⊙O 上，∠AOB＝90º，点 C 是 AB ︵ 上的一个动点，AC 与 OB 的延长线 相交于点 D，设 AC＝x，BD＝y． （1）求 y 关于 x 的函数关系式，并写出自变量 x 的取值范围； （2）若⊙O1 与⊙O 相交于点 A、C，且⊙O1 与⊙O 的圆心距为 2，当 BD＝ 1 3 OB 时，求⊙O1 的半径； （3）是否存在点 C，使得△DCB∽△DOC？若存在，请证明；若不存在，请说明理由． 108．如图，点 M 在 y 轴上，半径为 5 的⊙M 交 x 轴于 A、B 两点，且 AB＝4．连结 BM 并延长交⊙M 于 点 C，过点 C 的直线 y＝2x＋b 交 x 轴于点 D． （1）求点 B、M、C 的坐标； （2）求证：CD 是⊙M 的切线； （3）若二次函数 y＝－x 2＋(a＋1)x＋6 的图象经过点 B，求这个二次 函数的解析式，并写出使二次函数小于值一次函数 y＝2x＋b 值的 x 取值范围． 109．如图 1，⊙M 的直径 AB 在 y 轴的正半轴上，且点 A 与原点 O 重合，点 C 是 y 轴右侧半圆上的一点， AC＝1，BC＝2．点 A 由 O 点开始沿 x 轴的正半轴滑动，点 B 随之沿着 y 轴向原点 O 滑动（如图 2），当点 B 滑动至与原点 O 重合时运动结束． （1）在运动过程中，⊙M 始终经过原点 O，请说明理由； （2）设点 C 的坐标为（x，y），求 y 与 x 之间的函数关系式，并写出自变量 x 的取值范围； （3）求点 C 在整个运动过程中所经过的路径的长． A B D C O OA B x y C M D C M O B x y (A) 图 1 CM O B x y A 图 2 110．如图，⊙O1 和⊙O2 相交于 A、B 两点，过点 A 作⊙O2 的切线交⊙O1 于点 C，过点 B 作两圆的割线分 别交⊙O1、⊙O2 于点 D、E，DE 与 AC 相交于点 F． （1）求证： DF 2 CF 2 ＝ EF BF （2）当 AE 与⊙O1 相切，且 AF＝6，CF＝2，DF＝3 时，求 AE 的长； （3）当⊙O1 与⊙O2 为等圆，且 CF : CD : DF＝3 : 4 : 5 时，求 S△AEF : S△CDF ． 111．如图，P 是射线 y＝ 3 5 x（x＞0）上的一动点，以 P 为圆心的⊙P 与 x 轴的正半轴交于 A、B 两点，与 y 轴相切于 C 点． （1）若⊙P 的半径为 5，求点 P、A 的坐标； （2）在（1）的条件下，求以点 P 为顶点，且经过 A 点的抛物线的解析式；并判定该抛物线是否经过点 C 关于原点的对称点 D，说明理由； （3）是否存在直线 l，当点 P 在射线 y＝ 3 5 x（x＞0）上运动过程中，经过 A、B、C 三点的抛物线的顶点 都在直线 l 上？若存在，求出直线 l 的解析式；若不存在，说明理由． 112．如图，在平面直角坐标系中，O 为坐标原点，半径为 2 的⊙O 与 x 轴正半轴交于点 A，P 是 x 轴上位 于点 A 右侧的一动点，PB 切⊙O 于点 B． （1）当 PB＝4 时，求 PA 的长； （2）若点 C 在⊙O 上，且△PBC 为等边三角形，求点 C 的坐标； （3）⊙O 上是否存在点 Q，使得△PBQ 是以 PB 为底的等腰三角形，且 PB 最长？若存在，求点 Q 的坐标， 并求出此时⊙O 上能与 PB 构成等腰三角形的所有点的坐标；若不存在，请说明理由． O1 C D E A B O2 F A BO P M x y y＝ 3 5 x（x＞0） C M AO x y 备用图 AO x y 备用图 A B O P M x y 113．如图，AB 是⊙O 的直径，点 C 在⊙O 上，且 AC＝BC＝4．P 为 BC 上一动点，过 P 作 PD⊥BC 分别 交 AB、OC 于 D、E． （1）若 PC＝1，求△ODE 的面积； （2）若 PC＝a（0＜a＜2），△PCE、△ODE 的面积分别为 S1、S2． ①若 S1＝S2，求 a 的值； ②若 S＝S1＋S2，是否存在这样的实数 a，使得 S ＜ 3 ？若存在，求出 a 的值；若不存在，请说明理 由． 114．如图 1，直线 l 与⊙O 交于 E、F 两点，AB 是⊙O 的直径，且直线 l 与直径 AB 不相交．过点 A、B 分 别作直线 l 的垂线，垂足为 C、D，易证 CE＝DF． （1）若直线 l 与直径 AB 相交（如图 2），CE＝DF 是否仍然成立？请给出证明； （2）若 CD＝7，CE＝BD－AC＝1 ①求 AC、BD 的长； ②除 E、F 两点外，在线段 CD 上是否存在点 P，使得以 P，A，C 为顶点的三角形与以 P，B，D 为顶 点的三角形相似？若存在，请求出 CP 的长；若不存在，请说明理由． 115．如图，Rt△ABC 内接于⊙O，AB＝5，AC＝12，∠BAC＝90°，P 是⊙O 上的动点，且 P、C 两点在 BC 的两侧，AP 与 BC 相交于点 D，QA⊥AP 交 PC 的延长线于点 Q． （1）当点 P 与点 A 关于 BC 对称时，求 PQ 的长； （2）当点 P 是 BC︵ 的三等分点时，求 PQ 的长； （3）当点 P 运动到什么位置时，AQ 最大，并求此时 PQ 的长． A B O P M D C M E C A O B D M F M E M l M 图 1 C A O B D M F M E M l M 图 2 A P Q M CO M B D M A CO M B 备用图 116．如图，在平面直角坐标系中，半径为 5 的⊙P 经过原点 O，交 x 的正半轴于点 M（2m，0），交 y 轴 的负半轴于点 D，过点 P 作 x 轴的垂线，交⊙P 于点 A、C，将劣弧 OAM 沿 x 轴翻折，得弧 OBM． （1）当 m＝4 时 ①填空：点 B 的坐标为_________，点 C 的坐标为_________，点 D 的坐标为_________； ②若以 B 为顶点且过 D 点的抛物线交⊙P 于另一点 E，求此抛物线的函数关系式并写出点 E 的坐标； ③除 D 点外，直线 AD 与②中的抛物线有无其它公共点？说明理由． （2）是否存在实数 m，使得以 B、C、D、E 为顶点的四边形是菱形？若存在，求 m 的值；若不存在，请 说明理由． 117．如图，在△ABC 中，∠A＝75°，∠ACB＝90°，AC＝2，D 为 BC 上一点，以 CD 为直径的半圆 O 交 AB 于 E、F 两点，且 F 为 AB 的中点． （1）求 CE、AE 的长； （2）求证：BD 的长是方程 x 2＋4x－(10＋8 2)＝0 的一个根． 118．如图，AB 是⊙O 的直径，弦 CD⊥AB，垂足为 E，连结 BC，M 是 CE 的中点，连结 BM 并延长交过 A 点的切线于点 F，连结 OF 并延长交直线 CD 于点 G． （1）求证：FG∥BC； （2）若 AB＝10，CD＝8，求 AF、FG 的长． 119．如图，在以 O 为圆心的两个同心圆中，AB 经过圆心 O，且与小圆相交于点 A、与大圆相交于点 B．小 圆的切线 AC 与大圆相交于点 D，且 CO 平分∠ACB． （1）试判断 BC 所在直线与小圆的位置关系，并说明理由； （2）试判断线段 AC、AD、BC 之间的数量关系，并说明理由； （3）若 AB＝8，BC＝10，求大圆与小圆围成的圆环的面积． O A B x y C D P M O A BC E D F M C F M BO M A D M E OA C B D 120．如图，AB 为半圆 O 的直径，C 为半圆上一点，正方形 DEFG 的一边 EF 在 AB 上，另一边 FG 过△ABC 的内切圆圆心 O1，且点 G 在半圆弧上．设正方形 DEFG 的边长、半圆 O 的半径、⊙O1 的半径分别为 a、 R、r． （1）若正方形 DEFG 的顶点 D 在半圆上，求 a : R : r； （2）若 a＝10，r＝4，求 R 的值． 121．如图，AB 是⊙O 的直径，⊙O1 与⊙O 内切于点 C，且与 AB 相切于点 D，AC 交⊙O1 于点 E，EF⊥AB 于 F，交⊙O 于点 G． （1）求证：GF 是⊙O1 的切线； （2）求证：AD＝AG； （3）若 AB＝10，AG＝8，求⊙O1 的半径和 AC 的长． 122．如图，在平面直角坐标系中，Rt△AOB 的直角边 OA、OB 分别在 x 轴、y 轴上，点 M（ 12 7 ，1 2）在斜 边 AB 上，且 MA＝MB． （1）求△AOB 的内切圆⊙O1 的半径 r1； （2）若⊙O2 与⊙O1、AB 边、y 轴分别相切，⊙O3 与⊙O2、AB 边、y 轴分别相切，…，求圆心 O2011 的坐 标． 123．如图，在△ABC 中，AB＝AC＝5，BC＝6．点 D 为 BC 边上一动点（不与点 B 重合），过 D 作射线 DE 交 AB 边于点 E，使∠BDE＝∠A．以 D 为圆心，DC 长为半径作⊙D． （1）设点 BD＝x，AE＝y，求 y 关于 x 的函数关系式，并确定自变量 x 的取值范围； （2）当⊙D 与 AB 边相切时，求 BD 的长； （3）以 E 为圆心，AE 长为半径作⊙E，若⊙D 与⊙E 相切，求 BD 的长． G O D E F C A B O1 G D E F C A BO O1 M（ 12 7 ，1 2） y xAO O1 O2 B D E C A B 124．如图，在 Rt△ABC 中，∠A＝90°，AB＝AC＝4，O 是 BC 边上的点，且⊙O 与 AB、AC 都相切，切 点分别为 D、E．点 F 为 DE︵ 上的一个动点（不与点 D、E 重合），过点 F 作⊙O 的切线分别与边 AB、AC 相交于 G、H，连接 OG、OH （1）求⊙O 的半径； （2）求∠GOH 的度数； （3）设 BG＝x，阴影部分的面积为 y，求 y 关于 x 的函数 关系式；当 x 为何值时，y 有最小值？最小值是多少？ 125．如图，⊙P 与⊙Q 外切于点 N，经过点 N 的直线 AB 交⊙P 于 A，交⊙Q 于 B，以经过⊙P 的直径 AC 所在直线为 y 轴，经过点 B 的直线为 x 轴，建立直角坐标系． （1）求证：OB 是⊙Q 的切线； （2）如果 OC＝CP＝PA＝2，⊙Q 在始终保持与⊙P 外切、与 x 轴相切的情况下运动，设点 Q 的坐标为 （x，y），试求 y 与 x 之间的函数关系式； （3）在（2）的条件下，设 M 是所求函数图象上的任意一点，过点 M 分别作 x 轴、y 轴的垂线，垂足分别 为 E、F，连结 PE、PM．问是否存在△PEO 与△PMF 相似？若存在，求出 ME 的长；若不存在，请说明理 由． 126．如图，直线 AB 经过⊙O 的圆心 O，且与⊙O 交于 A、B 两点，AB＝4，半径 OC 的延长线与过点 B 的直线交于点 D，OC＝CD，BC＝ 1 2 OD，点 Q 为⊙O 上一动点． （1）若∠BCQ＝45°，求弦 CQ 的长． （2）在点 Q 运动的过程中，CQ 与直线 AB 相交于点 P，当 PO 为何值时，△BCQ 是等腰三角形？ （3）当 Q 点运动时，是否存在点 P，使得 QP＝QO？若存在，满足条件的点 P 有几个？并求出相应的∠BCP 的大小；若不存在，请说明理由． F A B CO ED G H A B C y O P x Q N A B C O D P Q 127．半径为 6 的⊙O1 与半径为 4 的⊙O2 相交于 A、B 两点，且∠O1AO2＝120°，点 C 为⊙O1 上异于点 A、 B 的动点，直线 AC 与⊙O2 交于点 D，直线 O1C 与直线 O2D 交于点 E． （1）如图 1，求∠CED 的大小； （2）当点 C 在⊙O1 上运动时，是否存在∠CED 的大小不同于（1）中结论的情况？若存在，请在图 2 中 画出一种该情况的示意图，并求出∠CED 的大小；若不存在，请在图 2 中再画出一个符合题意的图形，并 证明∠CED 的大小同于（1）中结论； （3）当点 C 在⊙O1 上运动时，若△CAO1 与△DAO2 相似，求线段 CD 的长． 128．如图 1，在边长为 1 的正方形 ABCD 内，两个动圆⊙O1 与⊙O2 互相外切，且⊙O1 与边 AB、AD 相切， ⊙O2 与边 BC、CD 相切，设⊙O1 与⊙O2 的半径分别为 r1、r2． （1）求 r1 与 r2 的关系式； （2）求⊙O1 与⊙O2 面积之和的最小值． （3）如图 2，若将正方形 ABCD 改为一个长为 3 2，宽为 1 的矩形，其它条件不变，则⊙O1 与⊙O2 面积之 和是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由． 129．如图，在平面直角坐标系中，已知△AOB 为等边三角形，点 A 坐标为（2，0），点 B 在第一象限，△AOB 的外接圆交 y 轴于另一点 C，过点 C 的圆的切线交 x 轴于点 D． （1）求 B，C 两点的坐标； （2）求直线 CD 的解析式； （3）设 E、F 别是线段 AB、AD 上的两个动点 ①当 EF 平分四边形 ABCD 的周长时，求△AEF 的最大面积； ②当 EF 平分四边形 ABCD 的面积时，求△AEF 的最小周长． 130．如图，点 P 是半圆 O 的直径 BA 延长线上的动点（不与点 A 重合），以 PO 为直径的半圆 C 与半圆 O 交于点 D，∠DPB 的平分线与半圆 C 交于点 E，过 E 作 EF⊥AB 于点 F，EG∥PB 交 PD 于点 G，连接 GA． （1）求证：PD 是半圆 O 的切线； O1 C D E A B O2 图 1 O1 A B O2 图 2 O1 A B O2 备用图 O1 A B CD O2 图 1 O1 A B CD O2 图 2 O A x B y C D （2）求证：EF＝ 1 4 AB； （3）当 GA 与半圆 O 相切时，求 tan∠POE 的值． 131．如图，已知正方形 ABCD 的边长为 4cm，动点 P 从点 B 出发，以 2cm/s 的速度沿 B→C→D 方向向 点 D 运动；动点 Q 从点 A 出发，以 1cm/s 的速度沿 A→B 方向向点 B 运动．若 P、Q 两点同时出发，运动 时间为 t（s）． （1）连结 PD、PQ、DQ，设△PQD 的面积为 S，求 S 关于 t 的函数关系式； （2）当点 P 在 BC 上运动时，是否存在 t 的值，使△PQD 是等腰三角形？若存在，请求出符合条件的 t 的 值；若不存在，请说明理由； （3）以点 P 为圆心作⊙P，使得⊙P 与对角线 BD 相切，是否存在这样的 t 值，使得⊙P 恰好经过正方形 ABCD 的某一边的中点？若存在，请求出符合条件的 t 的值；若不存在，请说明理由． 132．如图，在直角坐标系中，矩形 OABC 内接于⊙M，AB＝3，BC＝4，点 A 在 y 轴上，点 C 在 x 轴上， 过点 A 作⊙M 的切线交 x 轴于点 D． （1）求直线 AD 的解析式； （2）点 E 为线段 CD 上的一点，连接 AE，若 AE 平分四边形 ABCD 的面积，求点 E 的坐标； （3）若点 P 为线段 AD 上的一个动点（不与点 A、D 重合），且直线 PE 平分四边形 ABCD 的周长．设点 P 纵坐标为 t，△PDE 的面积为 S，求 S 关于 t 的函数关系式，并求自变量 t 的取值范围；直线 PE 能否将四 边形 ABCD 的周长和面积同时平分？若能，请求出直线 PE 的解析式；若不能，请说明理由． O BA F EG D CP C A B P D Q C A B D 备用图 C A B D 备用图 O A x B y C D E M O x y A BD C PP′ 九、综合型问题 1．如图，已知两直线 ll、l2 分别经过点 A（1，0），B（－3，0），并且当两直线同时相交于 y 轴正半轴的点 C 时，恰好有 ll⊥l2，经过 A、B、C 三点的抛物线的对称轴与直线 ll 交于点 K． （1）求点 C 的坐标和抛物线的解析式； （2）抛物线的对称轴被直线 ll、抛物线、直线 l2 和 x 轴依次截得三条线段，问这三条线段有何数量关系？ 请说明理由； （3）当直线 l2 绕点 C 旋转时，与抛物线的另一个交点为 M，请找出使△MCK 为等腰三角形的点 M，简述 理由，并写出点 M 的坐标． 2．如图，在平面直角坐标系中，点 A 的坐标为（－4，0），点 B 的坐标为（0，b）（b＞0），P 是直线 AB 上的一个动点，作 PC⊥x 轴，垂足为 C．记点 P 关于 y 轴的对称点为 P′（点 P′ 不在 y 轴上），连接 PP′， P′A，P′C．设点 P 的横坐标为 a． （1）当 b＝3 时， ①求直线 AB 的解析式； ②若点 P′ 的坐标为（－1，m），求 m 的值； （2）若点 P 在第一象限，记直线 AB 与 P′C 的交点为 D． 当 P′D : DC＝1 : 3 时，求 a 的值； （3）是否同时存在 a，b，使△P′CA 为等腰直角三角形？若存在， 请求出所有满足要求的 a，b 的值；若不存在，请说明理由． 3．如图，平面直角坐标系 xOy 中，点 A 的坐标为（－2，2），点 B 的坐标为（6，6），抛物线经过 A、O、 B 三点，连结 OA、OB、AB，线段 AB 交 y 轴于点 E． （1）求点 E 的坐标； （2）求抛物线的函数解析式； （3）点 F 为线段 OB 上的一个动点（不与点 O、B 重合），直线 EF 与抛物线交于 M、N 两点（点 N 在 y 轴右侧），连结 ON、BN，当点 F 在线段 OB 上运动时，求△BON 面积的最大值，并求出此时点 N 的坐标； （4）连结 AN，当△BON 面积最大时，在坐标平面内求使得△BOP 与△OAN 相似（点 B、O、P 分别与点 O、A、N 对应）的点 P 的坐标． AB C O K x y D E F ll l2 O x y A B N M E F 4．在平面直角坐标系中，如图 1，将 个边长为 1 的正方形并排组成矩形 OABC，相邻两边 OA 和 OC 分 别落在 x 轴和 y 轴的正半轴上，设抛物线 y＝ax 2＋bx＋c（a＜0）过矩形顶点 B、C． （1）当 n＝1 时，如果 a＝－1，试求 b 的值； （2）当 n＝2 时，如图 2，在矩形 OABC 上方作一边长为 1 的正方形 EFMN，使 EF 在线段 CB 上，如果 M，N 两点也在抛物线上，求出此时抛物线的解析式； （3）将矩形 OABC 绕点 O 顺时针旋转，使得点 B 落到 x 轴的正半轴上，如果该抛物线同时经过原点 O． ①试求当 n＝3 时 a 的值； ②直接写出 a 关于 n 的关系式． 5．如图，在平面直角坐标系中，点 A（10，0），以 OA 为直径在第一象限内作半圆 C，点 B 是该半圆周上 一动点，连结 OB、AB，并延长 AB 至点 D，使 DB＝AB，过点 D 作 x 轴垂线，分别交 x 轴、直线 OB 于点 E、F，点 E 为垂足，连结 CF． （1）当∠AOB＝30°时，求弧 AB 的长度； （2）当 DE＝8 时，求线段 EF 的长； （3）在点 B 运动过程中，是否存在以点 E、C、F 为顶点的三角形 与△AOB 相似，若存在，请求出此时点 E 的坐标；若不存在，请 说明理由． 6．已知抛物线 y＝a( x＋6 )2－3 与 x 轴交于 A，B 两点（A 在 B 的右侧），与 y 轴相交于点 C，D 为抛物线 的顶点，直线 DE⊥x 轴，垂足为 E，AE 2＝3DE． （1）求抛物线的解析式； （2）P 为直线 DE 上的一动点，以 PC 为斜边作直角三角形，使直角顶点落在 x 轴上．若在 x 轴上的直角 顶点只有一个时，求点 P 的坐标； （3）Q 为第二象限抛物线上的一动点，过点 Q 作直线 QR⊥DQ，交直线 DE 于点 R．是否存在点 Q，使点 E 三等分线段 DR？若存在，请求出所有符合条件的 Q 点坐标，若不存在，请说明理由． n 图 1 图 2 图 3 x y M O M A BC x y M O M A C B M N EF x y M O M A C B x y M O M C M E M A M F M B M D M AB C O x y D E 7．在平面直角坐标系中，A（－4，0），B（0，2），直线 x＝2 与直线 AB 交于点 C，与 x 轴交于点 D，抛 物线经过点 A，且以 C 为顶点． （1）求抛物线的解析式； （2）点 P 为抛物线上位于 A、C 两点间的一个动点，连接 PA、PC，求△PAC 面积的最大值； （3）点 Q 为 x 轴上方的抛物线上的一个动点，连接 QA、QC，设△QAC 的面积为 S，当 S＝2 时，相应的 Q 点有几个？当 S 取何值时，相应的 Q 点有且只有 1 个？ 8．已知抛物线 y＝a( x－m )2＋n 与 y 轴交于点 A，它的顶点为点 B．点 A、B 关于原点 O 的对称点分别是 点 C，D．若点 A，B，C，D 中任何三点都不在一直线上，则称四边形 ABCD 为抛物线的伴随四边形，直 线 AB 为抛物线的伴随直线． （1）如图 1，求抛物线 y＝( x－2 )2＋1 的伴随直线的解析式； （2）如图 2，若抛物线 y＝a( x－m )2＋n（m＞0）的伴随直线是 y＝x－3，伴随四边形的面积为 12，求此抛 物线的解析式； （3）如图 3，若抛物线 y＝a( x－m )2＋n 的伴随直线是 y＝－2x＋b（b＞0），且伴随四边形 ABCD 是矩 形． ①用含 b 的代数式表示 m，n 的值； ②在抛物线的对称轴上是否存在点 P，使得△PBD 是一个等腰三角形？若存在，请直接写出点 P 的坐 标（用含 b 的代数式表示）；若不存在，请说明理由． 9．抛物线 y＝－ 1 4( x－1)2＋3 与 y 轴交于点 A，顶点为 B，对称轴 BC 与 x 轴交于点 C． （1）如图 1，求点 A 的坐标及线段 OC 的长； （2）点 P 在抛物线上，直线 PQ∥BC 交 x 轴于点 Q，连结 BQ． ①若含 45°角的直角三角板如图 2 所示放置，其中一个顶点与点 C 重合，直角顶点 D 在 BQ 上，另一个 顶点 E 在 PQ 上，求直线 BQ 的函数解析式； ②若含 30°角的直角三角板一个顶点与点 C 重合，直角顶点 D 在直线 BQ 上，另一个顶点 E 在 PQ 上， A B C O x y D x＝2 A B C O x y D 图 1 O x y 图 2 O x y 图 3 求点 P 的坐标． 10．如图，在平面直角坐标系 xOy 中，我们把由两条射线 AE、BF 和以 AB 为直径的半圆所组成的图形叫 作图形 C．已知 A（－1，0），B（1，0），AE∥BF，且半圆与 y 轴的交点 D 在射线 AE 的反向延长线上． （1）求两条射线 AE、BF 所在直线的距离； （2）当一次函数 y＝x＋b 的图象与图形 C 恰好只有一个公共点时，写出 b 的取值范围； 当一次函数 y＝x＋b 的图象与图形 C 恰好只有两个公共点时，写出 b 的取值范围； （3）已知□AMPQ（四个顶点 A、M、P、Q 按顺时针方向排列）的各顶点都在图形 C 上，且不都在两条 射线上，求点 M 的横坐标 x 的取值范围． 11．已知抛物线 C1：y1＝ 1 2 x 2－x＋1，点 F（1，1）． （1）抛物线 C1 的顶点坐标为___________； （2）①若抛物线 C1 与 y 轴的交点为 A，连接 AF，并延长交抛物线 C1 于点 B，求证： 1 AF ＋ 1 BF ＝2； ②取抛物线 C1 上任意一点 P（xP，yP）（0＜xP＜1），连接 PF，并延长交抛物线 C1 于点 Q（xQ，yQ）， 试判断 1 PF ＋ 1 QF ＝2 是否成立？请说明理由； （3）将抛物线 C1 作适当的平移，得抛物线 C2：y2＝ 1 2( x－h )2，若 2＜x≤m 时，y2≤x 恒成立，求 m 的最 大值． 12．如图，在平面直角坐标系中，已知点 A（－1，0），点 B（9，0），以 AB 为直径作⊙M，交 y 轴的负半 轴于点 C，连接 AC、BC，抛物线经过 A、B、C 三点． （1）求抛物线的解析式； （2）点 E 是 AC 延长线上一点，∠BCE 的平分线 CD 交⊙M 于点 D，连 接 BD，求直线 BD 的解析式； （3）在（2）的条件下，抛物线上是否存在点 P，使得∠PDB＝∠CBD？ 若存在，求出 P 点坐标；若不存在，请说明理由． 图 1 A B O C x y 图 2 A B O C x y D E P Q A BO E D x y F 备用图 A BO E D x y F A B C M x D O y E O x M A B D y M E F 13．如图，在平面直角坐标系中，△ABC 是直角三角形，∠ACB＝90，AC＝BC，OA＝1，OC＝4，抛物线 y＝x 2＋bx＋c 经过 A、B 两点，顶点为 D． （1）求 b、c 的值； （2）点 E 是 Rt△ABC 斜边 AB 上一动点（点 A、B 除外），过点 E 作 x 轴的垂线，交抛物线于点 F，当线 段 EF 的长度最大时，求点 E 的坐标； （3）在（2）的条件下： ①求以点 E、B、F、D 为顶点的四边形的面积； ②在抛物线上是否存在一点 P，使△EFP 是以 EF 为直角边的直角三角形？若存在，求出所有点 P 的坐 标；若不存在，说明理由． 14．如图，二次函数 y＝ax 2＋bx（a＞0）的图象与反比例函数 y＝ k x 的图象相交于 A，B 两点，且点 A 的坐 标为（1，4），点 B 在第三象限． （1）求该二次函数的表达式； （2）设二次函数图象与 x 轴的另一个交点为 D，E 点为线段 OD 上的动点（与 O，D 不重合），过 E 点作 EF ∥OB，交 BD 于 F，连接 BE． ①设 OE 的长为 m，△BEF 的面积为 S，求 S 关于 m 的函数关系式； ②当△BEF 为等腰三角形时，求点 E 的坐标． 15．平面直角坐标系中，□ABOC 如图放置，点 A、C 的坐标分别为（0，3）、（－1，0），将此平行四边形 绕点 O 顺时针旋转 90°，得到□A′B′OC′． （1）若抛物线过点 C、A、A′，求此抛物线的解析式； OA B C D y x OA B C D y x 备用图 （2）求□ABOC 和□A′B′OC′ 重叠部分△OC′D 的周长； （3）点 M 是第一象限内抛物线上的一动点，问：点 M 在何处时△AMA′ 的面积最大？最大面积是多少？ 并求出此时点 M 的坐标． 16．如图，⊙M 过点 B（－2，0）、C（－4，0），且与直线 x＝－1 相切于点 A（A 在第二象限），点 A 关于 x 轴的对称点为 A1，直线 AA1 与 x 轴相交点 P． （1）求证：点 A1 在直线 MB 上； （2）求以 M 为顶点且过 A1 的抛物线的解析式； （3）设过点 A1 且平行于 x 轴的直线与（2）中的抛物线的另一交点为 D，当⊙D 与⊙M 相切时，求⊙D 的 半径和切点坐标． 17．如图，在矩形 ABCD 中，AB＝3，BC＝2，点 A 的坐标为（1，0），以 CD 为直径，在矩形 ABCD 内作 半圆 M．设过 A、B 两点的抛物线 y＝ax 2＋bx＋c 的顶点为 N． （1）求过 A、C 两点直线的解析式； （2）当点 N 在半圆 M 内时，求 a 的取值范围； （3）过点 A 作⊙M 的切线交 BC 于点 F，E 为切点，当以 A、F，B 为顶点的三角形与以 C、N、M 为顶点 的三角形相似时，求点 N 的坐标． 18．如图，直径为 5 的⊙M 圆心在 x 轴正半轴上，⊙M 与 x 轴交于 A、B 两点，与 y 轴交于 C、D 两点， 且 CD＝4，抛物线经过 A、B、C 三点，顶点为 N． C A D B O C′ A′ x y B′ C A B O A1 x y x＝－1 M P C A BO x y MD E F （1）求该抛物线的解析式； （2）直线 NC 与 x 轴交于点 E，试判断直线 CN 与⊙M 的位置关系并说明理由； （3）设点 Q 是抛物线对称轴上的一点，试问在抛物线上是否存在点 P，使得以 A、B、P、Q 为顶点的四 边形是平行四边形？若存在，求出点 P 的坐标；若不存在，请说明理由． 19．如图，二次函数 y＝ 2 3 x 2－ 1 3 x 的图象经过△AOB 的三个顶点，其中 A（－1，m），B（n，n）． （1）求点 A、B 的坐标 （2）在坐标平面上找点 C，使以 A、O、B、C 为顶点的四边形是平行四边形． ①这样的点 C 有几个？ ②能否将抛物线 y＝ 2 3 x 2－ 1 3 x 平移后经过 A、C 两点？若能，求出平移后经过 A、C 两点的抛物线的解 析式；若不能，说明理由． 20．如图，已知抛物线 y＝－x 2＋bx＋9－b 2（b 为常数）经过坐标原点 O，且与 x 轴交于另一点 E，其顶点 M 在第一象限． （1）求该抛物线所对应的函数关系式； （2）设点 A 是该抛物线上位于 x 轴上方，且在其对称轴左侧的一个动点；过点 A 作 x 轴的平行线交该抛 物线于另一点 D，再作 AB⊥x 轴于点 B，DC⊥x 轴于点 C． ①当线段 AB、BC 的长都是整数个单位长度时，求矩形 ABCD 的周长； ②求矩形 ABCD 的周长的最大值，并写出此时点 A 的坐标； ③当矩形 ABCD 的周长取得最大值时，它的面积是否也同时取得最大值？请判断并说明理由． C A BO x y M D E N A B O x y A BO x y D C E M 21．如图 1，直线 y＝－x＋1 与 x 轴、y 轴分别相交于点 C、D，一个含 45°角的直角三角板的锐角顶点 A 在线段 CD 上滑动，滑动过程中三角板的斜边始终经过坐标原点，∠A 的另一边与 x 轴的正半轴相交于点 B ． （1）试探索△AOB 能否构成以 AO、AB 为腰的等腰三角形，若能，请求出点 B 的坐标；若不能，请说明 理由； （2）若将题中“y＝－x＋1”、“∠A 的另一边与 x 轴的正半轴相交于点 B”，分别改为“直线 y＝－x＋t（ t＞0）”、“∠A 的另一边与 x 轴的负半轴相交于点 B”（如图 2），其他条件不变，试探索△AOB 能否为 等腰三角形（只考虑点 A 在线段 CD 的延长线上且不包括点 D 时的情况），若能，请求出点 B 的坐标；若 不能，请说明理由． （3）若将题中“直线 y＝－x＋1”改为“直线 y＝－ 3 x＋1”、“含 45°角的直角三角板的锐角顶点 A 在线 段 CD 上滑动”改为“含 30°角的直角三角板的 30°角的顶点 A 在线段 CD 上滑动”（如图 3），其他条件 不变，试探索△AOB 能否为等腰三角形，若能，请求出点 B 的坐标，若不能，请说明理由． 22．如图，在平面直角坐标系中，直线 y＝ 3 4 x－ 3 2 与抛物线 y＝－ 1 4 x 2＋b x＋c 交于 A、B 两点，点 A 在 x 轴 上，点 B 的横坐标为－8． （1）求该抛物线的解析式； （2）点 P 是直线 AB 上方的抛物线上一动点（不与点 A、B 重合），过点 P 作 x 轴的垂线，垂足为 C，交 直线 AB 于点 D，作 PE⊥AB 于点 E． ①设△PDE 的周长为 l，点 P 的横坐标为 x，求 l 关于 x 的函数关系式，并求出 l 的最大值； ②连接 PA，以 PA 为边作图示一侧的正方形 APFG．随着点 P 的运动，正方形的大小、位置也随之改 变．当顶点 F 或 G 恰好落在 y 轴上时，直接写出对应的点 P 的坐标． A B O x y C D 图 1 y O x A B C D 图 2 A BO x y C D 图 3 A B O x y C D P F G E A B O x y （备用图） 23．如图，在平面直角坐标系中，点 P 从原点 O 出发，沿 x 轴向右以每秒 1 个单位长的速度运动 t 秒（t＞ 0），抛物线 y＝x 2＋bx＋c 经过点 O 和点 P．已知矩形 ABCD 的三个顶点为 A（1，0），B（1，－5），D（4， 0）． （1）求 c，b（用含 t 的代数式表示）； （2）当 4＜t＜5 时，设抛物线分别与线段 AB，CD 交于点 M，N． ①在点 P 的运动过程中，你认为∠AMP 的大小是否会变化？若变化，说明理由；若不变，求出∠AMP 的值； ②求△MPN 的面积 S 与 t 的函数关系式，并求 t 为何值时，S＝ 21 8 ； （3）在矩形 ABCD 的内部（不含边界），把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好 点”分成数量相等的两部分，请直接写出 t 的取值范围． 24．将抛物线 c1：y＝－ 3x 2＋ 3 沿 x 轴翻折，得抛物线 c2，如图所示． （1）请直接写出抛物线 c2 的表达式； （2）现将抛物线 c1 向左平移 m 个单位长度，平移后得到的新抛物线的顶点为 M，与 x 轴的交点从左到右 依次为 A，B；将抛物线 c2 向右也平移 m 个单位长度，平移后得到的新抛物线的顶点为 N，与 x 轴交点从 左到右依次为 D，E． ①当 B，D 是线段 AE 的三等分点时，求 m 的值； ②在平移过程中，是否存在以点 A，N，E，M 为顶点的四边形是矩形的情形？若存在，请求出此时 m 的 值；若不存在，请说明理由． 25．某数学兴趣小组开展了一次活动，过程如下： 设∠BAC＝θ（0°＜θ＜90°）．现把小棒依次摆放在两射线 AB，AC 之间，并使小棒两端分别落在两射线 上． 活动一： 如图甲所示，从点 A1 开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直，A1A2 为第 1 根小棒． 数学思考： O x y c1 c2 A B O x y C D P N M 1 －1 O x y （1）小棒能无限摆下去吗？答：___________（填“能”或“不能”） （2）设 AA1＝A1A2＝A2A3＝1． ①θ＝_________度； ②若记小棒 A2n-1A2n 的长度为 an（n 为正整数，如 A1A2＝a1，A3A4＝a2，…），求出此时 a2，a3 的值，并 直接写出 an（用含 n 的式子表示）． 活动二： 如图乙所示，从点 A1 开始，用等长的小棒依次向右摆放，其中 A1A2 为第一根小棒，且 A1A2＝AA1． 数学思考： （3）若已经向右摆放了 3 根小棒，则 θ1＝_________，θ2＝________，θ3＝________；（用含 θ 的式子表 示）． （4）若只能摆放 4 根小棒，求 θ 的范围． 26．如图所示，抛物线 m：y＝ax 2＋b（a＜0，b＞0）与 x 轴交于点 A、B（点 A 在点 B 的左侧），与 y 轴交 于点 C．将抛物线 m 绕点 B 旋转 180°，得到新的抛物线 n，它的顶点为 C1，与 x 轴的另一个交点为 A1． （1）当 a＝－1，b＝1 时，求抛物线 n 的解析式； （2）求证：四边形 AC1A1C 是平行四边形； （3）若四边形 AC1A1C 可能是矩形吗？若能，请求出 a，b 应满足的关系式；若不能，请说明理由． 27．已知：抛物线 y＝a( x－2)2＋b（ab＜0）的顶点为 A，与 x 轴的交点为 B，C（点 B 在点 C 的左侧）． （1）直接写出抛物线对称轴方程； （2）若抛物线经过原点，且△ABC 为直角三角形，求 a，b 的值； （3）若 D 为抛物线对称轴上一点，则以 A，B，C，D 为顶点的四边形能否为正方形？若能，请写出 a，b 满足的关系式；若不能，说明理由． θ A1A A2 A3 A4 A5 A6 B C 图甲 a1 a2 a3 θ A1 A A2 A3 A4 B C 图乙 θ1 θ2 θ3 O x y C C1 A B A1 28．如图，抛物线 l1：y＝－x 2 平移得到抛物线 l2，且 l2 经过点 O（0，0）和点 A（4，0），l2 的顶点为 B， 它的对称轴与 l1 相交于点 C．设 l1、l2 与 BC 围成的阴影部分面积为 S．解答下列问题： （1）求 l2 表示的函数解析式； （2）求 S 的值； （3）在直线 AC 上是否存在点 P，使得 S△POA＝ 1 2 S ？若存在，求点 P 的坐标；若不存在，请说明理由． 29．如图，矩形 ABCD 的边 AB 在 x 轴上，且 AB＝3，BC＝2 3，直线 y＝ 3x－2 3 经过点 C，交 y 轴于点 G． （1）点 C、D 的坐标分别是 C（ ），D（ ）； （2）求顶点在直线 y＝ 3x－2 3 上且经过点 C、D 的抛物线的解析式； （3）将（2）中的抛物线沿直线 y＝ 3x－2 3 平移，平移后的抛物线交 y 轴于点 F，顶点为点 E．平移后是否存在这样的抛物线，使△EFG 为等腰 三角形？若存在，请求出此时抛物线的解析式；若不存在，请说明理由． 30．已知抛物线 y＝ax 2＋bx＋3（a≠0）经过 A（3，0）、B（4，1）两点，且与 y 轴交于点 C． （1）求抛物线的解析式； （2）如图 1，设抛物线与 x 轴的另一个交点为 D，在抛物线上是否存在点 P，使△PAB 的面积是△BDA 面 积的 3 倍？若存在，求出点 P 的坐标；若不存在，请说明理由； （3）如图 2，连接 AC，E 为线段 AC 上任意一点（不与 A、C 重合），经过 A、E、O 三点的圆交直线 AB 于点 F，当△OEF 的面积取得最小值时，求点 E 的坐标． C x y ll l2 A B O O C x y A BO D G C x y A B O 图 1 D C x y A B O 图 2 E F 31．如图，在平面直角坐标系中，抛物线 y＝ax 2＋bx＋c（a≠0）的图象经过 M（1，0）和 N（3，0）两点， 且与 y 轴交于 D（0，3），直线 l 是抛物线的对称轴． （1）求该抛物线的解析式； （2）若过点 A（－1，0）的直线 AB 与抛物线的对称轴 和 x 轴围成的三角形面积为 6，求此直线的解析式； （3）点 P 在抛物线的对称轴上，⊙P 与直线 AB 和 x 轴都相切，求点 P 的坐标． 32．如图，在平面直角坐标系中，一抛物线的顶点坐标是（0，1），且过点（－2，2），平行四边形 OABC 的顶点 A、B 在此抛物线上，AB 与 y 轴相交于点 M．已知点 C 的坐标是（－4，0），点 Q（x，y）是抛物 线上任意一点． （1）求此抛物线的解析式及点 M 的坐标； （2）在 x 轴上有一点 P（t，0），若 PQ∥CM，试用 x 的代数式表示 t； （3）在抛物线上是否存在点 Q，使得△BAQ 的面积是△BMC 的面积的 2 倍？若存在，求此时点 Q 的坐 标． 33．如图 1，在平面直角坐标系中，点 A 的坐标为（1，2），点 B 的坐标为（3，1），平移抛物线 y＝x 2， 使平移后的抛物线过 A、B 两点． （1）求平移后抛物线的函数表达式； （2）设（1）中抛物线的顶点为 C，D 为 y 轴上一点，且 S△ABD ＝S△ABC ，求点 D 的坐标； （3）请在图 2 上用尺规作图的方式探究（1）中的抛物线上是否存在点 P，使△ABP 为等腰三角形．若存 在，请判断点 P 共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由． N x y A MO D l x y O B C A 1 1 P Q M 图 1 O A B C x y 1 1 图 2 O A B x y 1 1 34．如图，抛物线 y＝－ 1 4 x 2＋4 交 x 轴于 A、B 两点（A 在 B 的左侧），交 y 轴于点 C，连接 AC、BC，D 是线段 OB 上一动点，以 CD 为一边向右侧作正方形 CDEF，连接 BF，交 DE 于点 P． （1）试判断△ABC 的形状，并说明理由； （2）求证：BF⊥AB； （3）连接 CP，记△CPF 的面积为 S1，△CPB 的面积为 S2，若 S＝S1－S2，试探究 S 的最小值． 35．已知抛物线 y＝－x 2＋2mx－m 2－m＋3． （1）m 为何值时，抛物线与 x 轴有两个交点？ （2）若抛物线与 x 轴交于 M、N 两点，当|OM|·|ON|＝3，且|OM|≠|ON| 时，求抛物线的解析式； （3）若（2）中所求抛物线顶点为 C，与 y 轴交点在原点上方，抛物线的对称轴与 x 轴交于点 B，直线 y＝－ x＋3 与 x 轴交于点 A，点 P 为抛物线对称轴上一动点，PD⊥AC 于 D．是否存在点 P，使 S△PAD ＝ 1 4 S△ABC？ 若存在，求出点 P 的坐标；若不存在，请说明理由． 36．如图，已知点 F 的坐标为（0，1），过点 F 的直线与抛物线 y＝ 1 4 x 2 交于 A、B 两点，直线 y＝－1 与 y 轴交于点 C，连接 AC、BC． （1）判断以线段 AB 为直径的圆与直线 y＝－1 的位置 关系并说明理由； （2）若以 AB 为直径的圆与 y 轴交于 C（ 3－ 2 ，0）、D （ 3＋ 2 ，0）两点，求直线 AB 对应的函数解析式； （3）求证：∠ACF＝∠BCF； （4）△ABC 的面积是否存在最小值？如果存在，求出 这个最小值；如果不存在，请说明理由． 37．如图，已知抛物线 y＝ax 2＋bx＋c 经过点 A（2，3）、B（6，1）、C（0，－2）． （1）求此抛物线的解析式，并用配方法把解析式化为顶点式； （2）点 P 是抛物线对称轴上的动点，当 AP⊥CP 时，求点 P 的坐标； （3）设直线 BC 与 x 轴交于点 D，点 H 是抛物线与 x 轴的一个交点， 点 E（t，n）是抛物线上的动点，四边形 OEDC 的面积为 S．当 S 取何 值时，满足条件的点 E 只有一个？当 S 取何值时，满足条件的点 E 有 两个？ OA BD F C P E x y y M O M x My＝－1 F MA M B M C M y M O M x M H M A M B M C M 38．已知抛物线 y1＝x 2＋4 x＋1 的图象向上平移 m 个单位（m＞0）得到的新抛物线过点（1，8）． （1）求 m 的值，并将平移后的抛物线解析式写成 y2＝a( x－h )2＋k 的形式； （2）将平移后的抛物线在 x 轴下方的部分沿 x 轴翻折到 x 轴上方，与平移后的抛物线没有变化的部分构成 一个新的图象，请写出这个图象对应的函数 y 的解析式，并在所给的平面直角坐标系中直接画出简图，同 时写出该函数在－3＜x ≤－ 3 2 时对应的函数值 y 的取值范围； （3）设一次函数 y3＝nx＋3（n≠0），问是否存在正整数 n 使得（2）中函数的函数值 y＝y3 时，对应的 x 的值为－1＜x ＜0，若存在，求出 n 的值；若不存在，说明理由． 39．如图，已知抛物线 y＝x 2＋bx＋c 与 x 轴交于 A、B 两点（A 点在 B 点左侧），与 y 轴交于点 C（0，－ 3），对称轴是直线 x＝1，直线 BC 与抛物线的对称轴交于点 D． （1）求抛物线的函数表达式； （2）求直线 BC 的函数表达式； （3）点 E 为 y 轴上一动点，CE 的垂直平分线交 CE 于点 F，交抛物线于 P、Q 两点，且点 P 在第三象 限． ①当线段 PQ＝ 3 4 AB 时，求 tan∠CED 的值； ②当以点 C、D、E 为顶点的三角形是直角三角形时，请直接写出点 P 的坐标． -1 54321-1-2-3-4-5 1 2 3 4 5 -2 -3 -4 -5 y M O M x M y O M xA B C D 1 1 x＝1 备用图 y O M xA B C D 1 1 x＝1 40．如图，已知抛物线 y＝－x 2－x＋ 11 4 ，正方形 ABCD 的边 AB 在 x 轴上，顶点 C、D 在 x 轴上方的抛物 线上，将正方形 ABCD 绕点 B 顺时针方向旋转角 α（0°＜α＜90°），得到正方形 A1BC1D1． （1）求正方形 ABCD 的边长； （2）当 tanα＝ 1 2 时 ①求正方形 A1BC1D1 与正方形 ABCD 重叠部分的面积； ②在抛物线的对称轴上存在点 P，使△PC1D1 为直角三角形，求点 P 的坐标； （3）在抛物线的对称轴上是否存在点 Q，使△QC1D1 为等腰直角三角形？若存在，求此时 tanα 的值；若 不存在，请说明理由． 41．如图，抛物线 y＝ax 2＋bx＋c 经过 A（－1，0）、B（3，0）、C（0，3）三点，对称轴与抛物线相交于 点 P、与直线 BC 相交于点 M，连接 PB． （1）求该抛物线的解析式； （2）抛物线 上是否存在一点 Q，使△QMB 与△PMB 的面积相等，若存在，求点 Q 的坐标；若不存在， 说明理由； （3）在第一象限、对称轴右侧的抛物线上是否存在一点 R，使△RPM 与△RMB 的面积相等，若存在，直 接写出点 R 的坐标；若不存在，说明理由． 42．如图 1，在平面直角坐标系中，抛物线过原点 O、点 A（10，0）和点 B（2，2），在线段 OA 上，点 P 从点 O 向点 A 运动，同时点 Q 从点 A 向点 O 运动，运动过程中保持 AQ＝2OP，当 P、Q 重合时同时停止 运动．过点 Q 作 x 轴的垂线，交直线 AB 于点 M，延长 QM 到点 D，使 MD＝MQ，以 QD 为对角线作正方 形 QCDE（正方形 QCDE 随点 Q 运动）． （1）求这条抛物线的函数表达式； （2）设正方形 QCDE 的面积为 S，P 点坐标为（m，0），求 S 与 m 之间的函数关系式； （3）过点 P 作 x 轴的垂线，交抛物线于点 N，延长 PN 到点 G，使 NG＝PN，以 PG 为对角线作正方形 PFGH y xO CD A C1 D1 A1 B y xO CD A B 备用图 y xO CD A B 备用图 y xO C A B M P （正方形 PFGH 随点 P 运动），当点 P 运动到点（2，0）时，如图 2，正方形 PFGH 的边 GF 和正方形 QCDE 的边 EQ 落在同一条直线上． ①则此时两个正方形中在直线 AB 下方的阴影部分面积的和是____________； ②若点 P 继续向点 A 运动，还存在两个正方形分别有边落在同一条直线上的情况，请直接写出每种情 况下点 P 的坐标，不必说明理由． 43．己知：二次函数 y＝ax 2＋bx＋6（a≠0）与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），点 A、点 B 的 横坐标是一元二次方程 x 2－4x－12＝0 的两个根． （1）请直接写出点 A、点 B 的坐标； （2）请求出该二次函数表达式及对称轴和顶点坐标； （3）如图 l，在二次函数对称轴上是否存在点 P，使△APC 的周长最小？若存在，请求出点 P 的坐标；若 不存在，请说明理由； （4）如图 2，连接 AC、BC，点 Q 是线段 OB 上一个动点（点 Q 不与点 O、B 重合），过点 Q 作 QD∥AC 交 BC 于点 D，设 Q 点坐标（m，0），当△CDQ 面积 S 最大时，求 m 的值． 44．如图，在平面直角坐标系中，四边形 ABCD 是梯形，BC∥AD，∠BAD＋∠CDA＝90°，且 tan∠BAD＝ 2，AD 在 x 轴上，点 A 的坐标为（－1，0），点 B 在 y 轴的正半轴上，BC＝OB． （1）求过点 A、B、C 的抛物线的解析式； （2）动点 E 从点 B（不包括点 B）出发，沿 BC 运动到点 C 停止，在运动过程中，过点 E 作 EF⊥AD 于 点 F，将四边形 ABEF 沿直线 EF 折叠，得到四边形 A1B1EF，点 A、B 的对应点分别是点 A1、B1，设四边 形 A1B1EF 与梯形 ABCD 重合部分的面积为 S，F 点的坐标是（x，0）． ①当点 A1 落在（1）中的抛物线上时，求 S 的值； ②在点 E 运动过程中，求 S 与 x 的函数关系式． y xO C D AP B E Q M 图 1 y xO C D AP B E Q M 图 2 F(N) G H y xO A B 备用图 y xO C A B 图 1 y xO C A B D Q 图 2 y xO C A B DF E y xO C A B D 备用图 45．如图，已知抛物线 y＝ax 2＋bx＋8（a≠0）与 x 轴交于点 A（－2，0）、B，与 y 轴交于点 C，tan∠ABC ＝2． （1）求抛物线的解析式及其顶点 D 的坐标； （2）设直线 CD 交 x 轴于点 E．在线段 OB 的垂直平分线上是否存在点 P，使得经过点 P 的直线 PM 垂直 于直线 CD，且与直线 OP 的夹角为 75°？若存在，求出点 P 的坐标；若不存在，请说明理由； （3）过点 B 作 x 轴的垂线，交直线 CD 于点 F，将抛物线沿其对称轴向上平移，使抛物线与线段 EF 总有 公共点，则抛物线向上最多可平移多少个单位长度？ 46．如图，在平面直角坐标系中，直线 y＝3x＋3 分别交 x 轴、y 轴于 A、B 两点，C 点坐标为（0，1），连 接 AC 并延长到 D，使∠ADB＝∠ABC． （1）求 D 点坐标； （2）求过 A、B、D 三点的抛物线的解析式； （3）若 P 是线段 AD 上一动点，过 P 点作 x 轴的垂线，交抛物线于点 H，当线段 PH 的长最大时，求 P 点坐标； （4）在（3）的条件下，将△ABD 在坐标平面内平移 ①若平移后点 H 是 AD 边中点，求点 A 的坐标； ②若平移后点 H 在△ABD 的内部（不包括三条边），设点 A 坐标为（m，n），求 m、n 的取值范围． 47．在平面直角坐标系中，对称轴平行于 y 轴的抛物线经过原点 O，其顶点坐标为（3，－ 9 2），Rt△ABC 的直角边 BC 在 x 轴上，直角顶点 C 的坐标为（ 1 2 ，0），且 BC＝5，AC＝3（如图 1）． （1）求该抛物线的解析式； （2）将 Rt△ABC 沿 x 轴向右平移，当点 A 落在（1）中所求抛物线上时，Rt△ABC 停止移动．D（0，4） y xO C A B D y xO CA B D 为 y 轴上一点．设点 B 的横坐标为 m，△DAB 的面积为 S． ①分别求出点 B 位于原点左侧、右侧（含原点 O）时，S 与 m 之间的函数关系式，并写出相应自变量 m 的 取值范围（可在图 1、图 2 中画图探求）； ②当点 B 位于原点左侧时，是否存在实数 m，使得△DAB 为直角三角形？若存在，直接写出 m 的值；若 不存在，请说明理由． 48．如图，矩形 OABC 中，点 O 为原点，点 A 的坐标为（0，8），点 C 的坐标为（6，0）．抛物线 y＝－ 4 9 x 2＋bx＋c 经过 A、C 两点，与 AB 边交于点 D． （1）求抛物线的函数表达式； （2）点 P 为线段 BC 上一个动点（不与点 C 重合），点 Q 为线段 AC 上一个动点，AQ＝CP，连接 PQ， 设 CP＝m，△CPQ 的面积为 S． ①求 S 关于 m 的函数表达式，并求出 m 为何值时，S 取得最大值； ②当 S 最大时，在抛物线 y＝－ 4 9 x 2＋bx＋c 的对称轴 l 上若存在点 F，使△FDQ 为直角三角形，请直接 写出所有符合条件的点 F 的坐标；若不存在，请说明理由． 49．如图，抛物线 y＝ax 2＋bx（a＞0）与双曲线 y＝ k x 相交于点 A，B，已知点 B 的坐标为（－2，－2）， 点 A 在第一象限内，且 tan∠AOx＝4．过点 A 作直线 AC∥x 轴，交抛物 线于另一点 C． （1）求双曲线和抛物线的解析式； （2）计算△ABC 的面积； （3）在抛物线上是否存在点 D，使△ABD 的面积等于△ABC 的面积？ 若存在，直接写出点 D 的坐标；若不存在，请说明理由． y xO D 图 2 y xO C A B D 图 1 y xO C A BD 备用图 y xO C A BD P Q C A O B x M y M 50．如图，抛物线 y＝ax 2＋bx＋c 交 x 轴于点 A（－3，0），点 B（1，0），交 y 轴于点 E（0，－3）．点 C 是 点 A 关于点 B 的对称点，点 F 是线段 BC 的中点，直线 l 过点 F 且与 y 轴平行．直线 y＝－x＋m 过点 C， 交 y 轴于 D 点． （1）求抛物线的函数表达式； （2）点 K 为线段 AB 上一动点，过点 K 作 x 轴的垂线与直线 CD 交于点 H，与抛物线交于点 G，求线段 HG 长度的最大值； （3）在直线 l 上取点 M，在抛物线上取点 N，使以点 A，C，M，N 为顶点的四边形是平行四边形，求点 N 的坐标． 51．抛物线 y＝ax 2＋bx＋c 与 y 轴交于点 C（0，－2），与直线 y＝x 交于点 A（－2，－2），B（2，2）． （1）求抛物线的解析式； （2）如图，线段 MN 在线段 AB 上移动（点 M 与点 A 不重合，点 N 与点 B 不重合），且 MN＝ 2，若 M 点的横坐标为 m，过点 M 作 x 轴的垂线与 x 轴交于点 P，过点 N 作 x 轴的垂线与抛物线交于点 Q．以点 P，M，Q，N 为顶点的四边形能否为平行四边形？若能，请求出 m 的值；若不能，请说明理由． 52．如图，在平面直角坐标系中，已知点 A（－2，－4），OB＝2，抛物线 y＝ax 2＋bx＋c 经过点 A、O、B 三点． （1）求抛物线的函数表达式； （2）若点 M 是抛物线对称轴上的一点，试求 MO＋MA 的最小值； （3）在抛物线上是否存在一点 P，使得以点 P、O、A、B 为顶点的 四边形是梯形？若存在，求点 P 的坐标；若不存在，请说明理由． CA O B x M y M F l G K D H E 备用图 CA O B x M y M F l G K D H E A O B x M y M N M C A O B x M y M A O P x M y M K y＝ 2 x 图 1 A O P x M y M B y＝ 2 x 图 2 C 53．在直角坐标系 xoy 中，已知点 P 是反比例函数 y＝ 2 x（x＞0）图象上一个动点，以 P 为圆心的圆始终 与 y 轴相切，设切点为 A． （1）如图 1，⊙P 运动到与 x 轴相切，设切点为 K，试判断四边形 OKPA 的形状，并说明理由． （2）如图 2，⊙P 运动到与 x 轴相交，设交点为 B，C．当四边形 ABCP 是菱形时： ①求出点 A，B，C 的坐标． ②在过 A，B，C 三点的抛物线上是否存在点 M，使△MBP 的面积是菱形 ABCP 面积的 1 2 ．若存在，试 求出所有满足条件的 M 点的坐标，若不存在，试说明理由． 54．如图，已知抛物线经过 A（－2，0），B（－3，3）及原点 O，顶点为 C． （1）求抛物线的解析式； （2）若点 D 在抛物线上，点 E 在抛物线的对称轴上，且以 A、O、D、E 为顶点的四边形是平行四边形， 求点 D 的坐标； （3）P 是抛物线上第一象限内的动点，过点 P 作 PM⊥x 轴，垂足为 M．是否存在点 P，使得以 P、M、A 为顶点的三角形与△BOC 相似？若存在，求出点 P 的坐标；若不存在，请说明理由． 55．如图，y 关于 x 的二次函数 y＝－ 3m( x＋m )( x－3m )（m＞0）图象的顶点为 M，图象交 x 轴于 A、B 两 点，交 y 轴正半轴于 D 点．以 AB 为直径作圆，圆心为 C．定点 E 的坐标为（－3，0），连接 ED． （1）写出 A、B、D 三点的坐标； A B O C x y （2）当 m 为何值时，M 点在直线 ED 上？判断此时直线 ED 与⊙C 的位置关系； （3）当 m 变化时，用 m 表示△AED 的面积 S，并在给出的直角坐标系中画出 S 关于 m 的函数图象的示意 图． 56．巳知二次函数 y＝a( x 2－6x＋8)（a＞0）的图象与 x 轴分别交于点 A、B，与 y 轴交于点 C．点 D 是抛 物线的顶点． （1）如图①．连接 AC，将△OAC 沿直线 AC 翻折，若点 O 的对应点 O′ '恰好落在该抛物线的对称轴上， 求实数 a 的值； （2）如图②，在正方形 EFGH 中，点 E、F 的坐标分别是（4，4）、（4，3），边 HG 位于边 EF 的右侧．小 林同学经过探索后发现了一个正确的命题：“若点 P 是边 EH 或边 HG 上的任意一点，则四条线段 PA、 PB、PC、PD 不能与任何一个平行四边形的四条边对应相等（即这四条线段不能构成平行四边形）．”若点 P 是边 EF 或边 FG 上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程； （3）如图②，当点 P 在抛物线对称轴上时，设点 P 的纵坐标 t 是大于 3 的常数，试问：是否存在一个正 数 a，使得四条线段 PA、PB、PC、PD 与一个平行四边形的四条边对应相等（即这四条线段能构成平行四 边形）？请说明理由． 57．在平面直角坐标系 xOy 中，关于 y 轴对称的抛物线 y＝－ m－1 3 x 2＋ ( m－2)x＋4m－7 与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴交于点 C，P 是抛物线 上的一点（点 P 不在坐标轴上），且点 P 关于直线 BC 的 对称点在 x 轴上，D（0，3）是 y 轴上的一点． （1）求抛物线的解析式及点 P 的坐标； （2）若 E、F 是 y 轴负半轴上的两个动点（点 E 在点 F 的上方），且 EF＝2，当四边形 PBEF 的周长最小时，求 点 E、F 的坐标； （3）若 Q 是线段 AC 上一点，且 S△COQ ＝2S△AOQ ，M 是 E O C x y B M D A O S m A B C O x y D O′ （图①） A B C O x y D （图②） E F G H O x y 1 1 直线 DQ 上的一个动点，在 x 轴上方的平面内是否存在一点 N，使得以 O、D、M、N 为顶点的四边形是菱 形？若存在，求出点 N 的坐标；若不存在，请说明理由． 58．如图，在平面直角坐标系中，点 A（m，6）（0＜m＜3），B（n，1）为两动点，且 OA⊥OB． （1）求证：mn＝－6； （2）当 S△AOB＝10 时，抛物线经过 A、B 两点且对称轴为 y 轴，求该抛物线的解析式； （3）在（2）的条件下，设直线 AB 交 y 轴于点 F，过点 F 作直线 l 交抛物线于 P、Q 两点．是否存在直线 l，使 S△POF : S△QOF＝1 : 3？若存在，求直线 l 的解析式；若不存在，请说明理由． 59．如图，已知二次函数 y＝x 2＋bx＋c 的图象与 x 轴交于 A、B 两点，与 y 轴交于点 P，顶点为 C（1，－ 2）． （1）求此函数的关系式； （2）作点 C 关于 x 轴的对称点 D，顺次连接 A、C、B、D．若在抛物线上存在点 E，使直线 PE 将四边形 ACBD 分成面积相等的两个四边形，求点 E 的坐标； （3）在（2）的条件下，抛物线上是否存在一点 F，使得△PEF 是以 P 为直角顶点的直角三角形？若存在， 求出点 F 的坐标及△PEF 的面积；若不存在，请说明理由． 60．如图，抛物线 y＝ 1 2 x 2－x＋a 与 x 轴交于点 A，B，与 y 轴交于点 C，其顶点在直线 y＝－2x 上． （1）求 a 的值； （2）求 A，B 两点的坐标； （3）以 AC，CB 为一组邻边作□ACBD，则点 D 关于 x 轴的对称点 D′ 是否在该抛物线上？请说明理由． O B A x y O BA x y C P xB y O C A 61．已知，如图，二次函数 y＝ax 2＋2ax－3a（a≠0）图象的顶点为 H，与 x 轴交于 A、B 两点（B 在 A 点 右侧），点 H、B 关于直线 l：y＝ 3x＋ 3 对称． （1）求 A、B 两点坐标，并证明点 A 在直线 l 上； （2）求二次函数解析式； （3）过点 B 作直线 BK∥AH 交直线 l 于 K 点，M、N 分别为直线 AH 和直线 l 上的两个动点，连接 HN、 NM、MK，求 HN ＋ NM ＋ MK 和的最小值． 62．如图 1，抛物线 y＝mx 2－11mx＋24m（m＜0）与 x 轴交于 B、C 两点（点 B 在点 C 的左侧），抛物线上 另有一点 A 在第一象限内，且∠BAC＝90°． （1）填空：OB＝_________，OC＝_________； （2）连结 OA，将△OAC 沿 x 轴翻折后得△ODC，当四边形 OACD 是菱形时，求此时抛物线的解析式； （3）如图 2，设垂直于 x 轴的直线 l：x＝n 与（2）中所求的抛物线交于点 M，与 CD 交于点 N，若直线 l 沿 x 轴方向左右平移，且交点 M 始终位于抛物线上 A、C 两点之间时，试探究：当 n 为何值时，四边形 AMCN 的面积取得最大值，并求出这个最大值． 63．如图，已知以点 A（2，－1）为顶点的抛物线经过点 B（4，0）． （1）求该抛物线的解析式； （2）设点 D 为抛物线对称轴与 x 轴的交点，点 E 为抛物线上一动点，过 E 作直线 y＝－2 的垂线，垂足为 N． ①探索、猜想线段 EN 与 ED 之间的数量关系，并证明你的结论； ②是否存在这样的点 E，使△EDN 为等边三角形？若存在，求点 E 的坐标；若不存在，说明理由． A l x H O B K y A l x H O B K y 备用图 A l：x＝n xO B D y CN M 图 2 A xO B D y C 图 1 y＝－2 AO BD y E N x y＝－2 AO BD y x （备用图） 64．如图，已知二次函数 y＝－ 1 2 x 2＋ 3 2 x＋2 图像与 y 轴交于点 A，与 x 轴正轴交于点 B，P 为直线 AB 上的 一个动点，过 P 作 x 轴的垂线与这个二次函数的图像交于 C 点． （1）求 A、B 两点坐标及直线 AB 的解析式； （2）连接 AC，当△APC 为直角三角形时，求点 P 的坐标； （3）在直线 AB 上是否存在一点 P，使得以 O、A、P、C 为顶点的四边形是平行四边形？若存在，请直接 写出此时点 P 的坐标；若不存在，请说明理由． 65．如图 1，在平面直角坐标系中，点 A（－2，6），B（1，3），过 A、B 分别作 x 轴的垂线，垂足为 C、 D，AD 与 BC 相交于点 E． （1）求证：点 E 在 y 轴上； （2）将 BD 水平向右移动 m 个单位（m＞0），此时 AD 与 BC 相交于点 E′（如图 2），连接 AB，求△AE′B 的面积 S 关于 m 的函数关系式； （3）过 A、E、E′ 三点的抛物线中，是否存在一条抛物线，它的顶点在 x 轴上？若存在，请求出 m 的值， 若不存在，说明理由． 66．如图，在直角坐标系中，点 A 的坐标为（0，8），点 B（b，t）（b 是大于零的常数）在直线 x＝b 上运动，点 D、E、F 分别为 OB、OA、AB 的中点． （1）判断四边形 DEFB 的形状，并证明你的结论； （2）试求四边形 DEFB 的面积 S 与 b 的关系式； （3）设直线 x＝b 与 x 轴交于点 C，问：四边形 DEFB 能不能是矩形？ 若能，求出 t 的值；若不能，说明理由． A O B P y C x C A DO x y B E 图 1 C A DO x y B E′ 图 2 x B A O y D C E F 1 1 x＝b 67．如图，在平面直角坐标系中，梯形 ABCD 的顶点 A、B 在 y 轴上，顶点 C 在 x 轴上，AB∥CD，OA＝ 2CD，∠ABC＝45°，tan∠DAB＝2，已知梯形 ABCD 的面积等于 5．直线 l 经过 B、C 两点，射线 AM∥l， 且与 x 轴交于点 M． （1）求射线 AM 所在直线的解析式； （2）将∠BAM 绕点 A 逆时针旋转，设旋转角为 α（0＜α＜90°），这个角的边 AM 与 x 轴交于点 P，另一条 边 AB 与直线 l 交于点 E．设点 P 的横坐标为 x，△PEC 的面积为 S，求 S 与 x 的函数关系式； （3）在（2）的条件下，当 S＝ 3 2 时，射线 AE 与直线 DC 交于点 F，连接 PF．问：在 x 轴上是否存在点 N，使得以 P、E、N 为顶点的三角形与△PEF 相似？若存在，求 N 点的坐标；若不存在，说明理由． 68．如图 1，已知直线 y＝ 2 5 x＋2 与 x 轴交于点 A，与 y 轴交于点 C，抛物线 y＝ax 2＋4ax＋b 经过 A、C 两 点，与 x 轴交于另一点 B． （1）求抛物线的解析式； （2）点 Q 在抛物线上，且 S△AQC ＝S△BQC ，求点 Q 的坐标； （3）如图 2，点 P 为△AOC 外接圆上 ACO︵ 的中点，直线 PC 交 x 轴于 D，∠EDF＝∠ACO．当∠EDF 绕 点 D 旋转时，DE 交 AC 于 M，DF 交 y 轴负半轴于 N．问 CN－CM 的值是否发生变化？若不变，求出其值； 若变化，求出变化范围． y O x B y＝ 2 5 x＋2 C A 图 1 y O x D y＝ 2 5 x＋2 C A 图 2 P M F N E x B M A O y D C l x B A O y D C l 备用图 1 x B A O y D C l 备用图 2 69．如图，直角梯形 OABC 中，AB∥OC，顶点 A 的坐标为（4，0），腰 BC 所在直线的解析式为 y＝－ 1 4 x ＋3． （1）求顶点 B 的坐标； （2）直线 l 经过点 C，与直线 AB 交于点 E，点 O 关于直线 l 的对称点为 O′ ，连接 CO′ 并延长交直线 AB 于第一象限的点 D，当 CD＝5 时，求直线 l 的解析式； （3）在（2）的条件下，设点 P 是直线 l 上的动点，点 Q 是直线 OD 上的动点，以 P、Q、B、C 为顶点的 四边形能否成为平行四边形？如果能，求出点 P 的坐标；如果不能，说明理由． 70．如图，在直角坐标系中，点 A 的坐标为（0，8），点 B（b，t）（b 是大于零的常数）在直线 x＝b 上运 动，点 D、E、F 分别为 OB、OA、AB 的中点． （1）判断四边形 DEFB 的形状，并证明你的结论； （2）试求四边形 DEFB 的面积 S 与 b 的关系式； （3）设直线 x＝b 与 x 轴交于点 C，问：四边形 DEFB 能不能是矩形？若能，求出 t 的值；若不能，说明 理由． 如图 1，在第一象限内，直线 y＝mx 与过点 B（0，1）且平行于 x 轴的直线 l 相交于点 A，半径为 r 的⊙Q 与直线 y＝mx、x 轴分别相切于点 T、E，且与直线 l 分别交于不同的 M、N 两点． （1）当点 A 的坐标为（3 ，p）时， ①填空：p＝_________，m＝_________，∠AOE＝_________； ②如图 2，连结 QT、QN、TM、ME、EN，当 r＝2 时，试说明：以 T、M、E、N 为顶点的四边形是等腰梯 形； （2）在图 1 中，连结 EQ 并延长交⊙Q 于点 D，试探索：对 m、r 的不同取值，经过 M、D、N 三点的抛物 线 y＝ax 2＋bx＋c，a 的值会变化吗？若不变，求出 a 的值；若变化，请说明理由． 71．已知抛物线 y＝－x 2＋2mx－m 2＋2 的顶点 A 在第一象限，过点 A 作 AB⊥y 轴，垂足为 B，C 是线段 AB 上一点（不与端点 A、B 重合），过 C 作 CD⊥x 轴，垂足为 D，并交抛物线于点 P． x B E AO y D C l O′ x B E AO y D C l 备用图 1 x B E AO y D C l 备用图 2 x B A O y M E Nl 1 1 Q T 图 1 y＝mx x B A O y M E Nl 1 1 Q T 图 2 y＝mx （1）若点 C（1，a）是线段 AB 的中点，求点 P 的坐标； （2）若直线 AP 交 y 轴的正半轴于点 E，且 AC＝CP，求△OPE 的面积 S 的取值范围． 72．如图，直线 y＝－x＋1 与直线 y＝2x、y＝x 分别交于 E、F 两点，点 P 为 x 轴上一动点，过点 P 的直线 y＝－x＋b 与直线 y＝2x、y＝x 分别交于 A、C 两点，以线段 AC 为对角线作正方形 ABCD． （1）求正方形 ABCD 各顶点的坐标（用含 b 的代数式表示）； （2）若点 P 从原点 O 出发，沿 x 轴的正方向运动，设正方形 ABCD 与△OEF 重叠部分的面积为 S，求 S 与 b 的函数关系式，并写出相应自变量 b 的取值范围． 73．如图，抛物线 y＝ax 2－4ax＋c（a≠0）经过 A（0，－1），B（5，0）两点，点 P 是抛物线上的一个动 点，且位于直线 AB 的下方（不与 A，B 重合），过点 P 作直线 PQ⊥x 轴，交 AB 于点 Q，设点 P 的横坐标 为 m． （1）求 a，c 的值； （2）设 PQ 的长为 S，求 S 与 m 的函数关系式，写出 m 的取值范围； （3）以 PQ 为直径的圆与抛物线的对称轴 l 有哪些位置关系？根据不同的位置关系，求对应的 m 取值范围． 74．已知抛物线 y＝－ 3 x 2＋ 2 3 x＋m 与 x 轴交于 A、B 两点（A 在 B 的左侧），与 y 轴交于点 C，且∠ACB＝ 90°． （1）求 m 的值和 A、B 两点的坐标； （2）过 A、B、C 的三点的⊙M 交 y 轴于另一点 D，设 P 为弧 CBD 上的动点（P 不与 C、D 重合），连接 AP 交 y 轴于点 H．是否存在一个常数 k，始终满足 AH·AP＝k？如果存在，求出 k 的值；如果不存在，请说 明理由； （3）连接 DM 并延长交 BC 于点 N，交⊙M 于点 E，过 E 点的⊙M 的切线分别交 x 轴、y 轴于点 F、G， 试探究 BC 与 FG 的位置关系，并求直线 FG 的解析式． x B A O y C D y＝2x y＝x y＝－x＋1 y＝－x＋b P E F xB A O y l Q P A B C D F E y G O N xM 75．如图，抛物线 y＝ax 2＋bx＋c 与 x 轴交于 A、B 两点（点 A 在点 B 左侧），与 y 轴交于点 C，且当 x＝0 和 x＝4 时，y 的值相等．直线 y＝4x－16 与抛物线相交于两点，其中一点的横坐标是 3，另一点是抛物线 的顶点 D． （1）求抛物线的解析式； （2）P 为线段 OD 上一点，过点 P 作 PQ⊥x 轴于点 Q．若点 P 在线段 OD 上运动（点 P 不与点 O 重合， 但可以与点 D 重合），设 OQ 的长为 m，四边形 PQCO 的面积为 S，求 S 与 m 之间的函数关系式； （3）随着点 P 的运动，四边形 PQCO 的面积 S 有最大值吗？如果有，求出 S 的最大值，并指出点 Q 的具 体位置和四边形 PQCO 的特殊形状；如果没有，说明理由； （4）是否存在实数 m，使得 PO＝OC？如果存在，求出 m 的值；如果不存在，说明理由． 76．已知抛物线 y＝ax 2＋bx＋c 的对称轴为直线 x＝2，且与 x 轴交于 A（1，0）、B 两点，与 y 轴交于点 C （0，－3）． （1）求抛物线的解析式； （2）若点 P 在抛物线上运动（点 P 异于点 A）． ①如图 l，当△PBC 面积与△ABC 面积相等时，求点 P 的坐标； ②如图 2，当∠PCB＝∠BCA 时，求直线 CP 的解析式． 77．定义：对于抛物线 y＝ax 2＋bx＋c（a、b、c 是常数，a≠0），若 b 2＝ac，则称该抛物线为黄金抛物 A B C D Q y O P x 图 2 A B C O x y P 图 1 A B C O x y P 线．例如 y＝2x 2－2x＋2 是黄金抛物线． （1）请再写出一个与上例不同的黄金抛物线的解析式：_________________________； （2）若抛物线 y＝ax 2＋bx＋c（a、b、c 是常数，a≠0）是黄金抛物线，请探究该黄金抛物线与 x 轴的公共 点个数的情况（要求说明理由）； （3）将黄金抛物线 y＝2x 2－2x＋2 沿对称轴向下平移 3 个单位． ① 直接写出平移后的新抛物线的解析式； ② 设①中的新抛物线与 y 轴交于点 A，对称轴与 x 轴交于点 B，动点 Q 在对称轴上，问新抛物线上是否 存在点 P，使以点 P、Q、B 为顶点的三角形与△AOB 全等？若存在，直接写出所有符合条件的点 P 的坐 标；若不存在，请说明理由． 78．如图，在平面直角坐标系中，点 A、B 的坐标分别为（0，3）、（5，0），将△AOB 绕点 O 按逆时针方 向旋转 90°，得到△COD（点 C、D 分别与点 A、B 对应）． （1）求经过 B、C、D 三点的抛物线的解析式； （2）将（1）中抛物线向右平移 2 个单位，点 B 的对应点为点 E，平移后的抛物线与原抛物线相交于点 F， P 为平移后的抛物线对称轴上一个动点，连接 PE、PF ①当| PE－PF|取得最大值时，求点 P 的坐标； ②当点 P 在抛物线对称轴上运动时，是否存在点 P 使△EPF 为直角三角形？如果存在，求出点 P 的坐标； 如果不存在，说明理由． 79．如图，已知抛物线 y＝－ 4 9 x 2＋bx＋c 与 x 轴相交于 A、B 两点，顶点为 C，其对称轴为直线 x＝2，且与 x 轴交于点 D，AO＝1． （1）填空：b＝______，c＝______，点 B 的坐标为（______，______）； （2）若线段 BC 的垂直平分线 EF 交 BC 于点 E，交 x 轴于点 F，求 FC 的长； （3）探究：在抛物线的对称轴上是否存在点 P，使⊙P 与 x 轴、直线 BC 都相切？若存在，请求出点 P 的 坐标；若不存在，请说明理由． O x y 1 2 3-1-2 -2 -1 1 2 3 O x y 3 5 A B O x y A B C E F D 80．如图，抛物线 y＝－ 5 4 x 2＋ 17 4 x＋1 与 y 轴交于 A 点，过点 A 的直线与抛物线交于另一点 B，过点 B 作 BC ⊥x 轴，垂足为点 C（3，0）． （1）求直线 AB 的函数关系式； （2）动点 P 在线段 OC 上从原点 O 出发以每秒一个单位的速度向 C 移动，过点 P 作 PN⊥x 轴，交直线 AB 于点 M，交抛物线于点 N．设点 P 移动的时间为 t 秒，MN 的长度为 s 个单位，求 s 与 t 的函数关系式，并 写出 t 的取值范围； （3）设在（2）的条件下（不考虑点 P 与点 O、点 C 重合的情况），连接 CM、BN，当 t 为何值时，四边 形 BCMN 为平行四边形？对于所求的 t 值，平行四边形 BCMN 是否菱形？请说明理由． 81．已知抛物线 y＝ax 2＋bx＋c 经过点 A（0，4）、B（1，4）、C（3，2），与 x 轴正半轴交于点 D． （1）求抛物线的解析式及点 D 的坐标； （2）在 x 轴上求一点 E，使得△BCE 是以 BC 为底边的等腰三角形； （3）在（2）的条件下，设 P（x，0）是线段 ED 上的动点，过 P 作 PF∥BC，分别交 BE、CE 于点 F、 G，将△EFG 沿 FG 翻折得到△E′FG．记△E′FG 与四边形 BFGC 重叠部分的面积为 S，求 S 与 x 的函数关 系式及自变量 x 的取值范围． 82．如图 1，y＝ax 2＋bx＋c（a≠0）的顶点为 C（l，4），交 x 轴于 A、B 两点，交 y 轴于点 D，其中点 B 的坐标为（3，0）． （1）求抛物线的解析式； O x y A B CP N M O x y A B C E F G E′ DP （2）如图 2，过点 A 的直线与抛物线交于点 E，交 y 轴于点 F，其中点 E 的横坐标为 2，若直线 PQ 为抛 物线的对称轴，点 G 为直线 PQ 上的一动点，则 x 轴上是否存在一点 H，使 D、G、H、F 四点所围成的四 边形周长最小．若存在，求出这个最小值及点 G、H 的坐标；若不存在，请说明理由； （3）如图 3，在抛物线上是否存在一点 T，过点 T 作 x 轴的垂线，垂足为点 M，过点 M 作 MN∥BD，交 线段 AD 于点 N，连接 MD，使△DNM∽△BMD，若存在，求出点 T 的坐标；若不存在，请说明理由． 83．如图 1，在平面直角坐标系中，点 A 的坐标为（3，0），以 A 为圆心，半径为 2 的⊙A 交 x 轴于 B、C 两点，过点 D（－1，0）作⊙A 的切线，切点为 E，过点 E 作 x 轴的垂线，垂足为 G，交⊙A 于点 F，抛物 线 y＝ax 2＋bx＋c 经过 A、D、F 三点． （1）求抛物线的函数表达式； （2）点 P 是抛物线上位于 D、F 两点之间的一动点，设点 P 的横坐标为 x，四边形 DPFE 的面积为 S，求 S 与 x 之间的函数关系式，并求 S 的最大值和此时点 P 的坐标； （3）如图 2，将弧 EBF 沿弦 EF 对折后得到弧 EB′F，试判断直线 EC 与弧 EB′F 的位置关系，并说明理 由． 84．抛物线 y＝ax 2＋bx＋c 与 x 轴交于点 A（－2，0）、B（8，0），与 y 轴交于点 C（0，－4），直线 y＝x＋ m 与抛物线交于点 D、E（D 在 E 的左侧），与抛物线的对称轴交于点 F． （1）求抛物线的解析式； （2）当 m＝2 时，求∠DCF 的大小； （3）若在直线 y＝x＋m 下方的抛物线上存在点 P，使得∠DPF＝45°，且满足条件的点 P 只有两个，求 m 的值． A B O C D E P Q x F y 图 2 A B O C D x y 图 1 A B O C D x y 图 3 ABO C D E x F y 图 1 G O CD x F y 图 2 E B G A B′ O x y C BA 85．已知抛物线 y＝ 1 4 x 2－ 3 4 mx＋n 与直线 l：y＝x＋m 的左交点为 A，抛物线与 y 轴相交于点 C，直线 l 与 抛物线的对称轴相交于点 E． （1）直接写出抛物线顶点 D 的坐标（用含 m、n 的代数式表示）； （2）当 m＝2，n＝－4 时，求∠ACE 的大小； （3）是否存在正实数 m＝n，使得在直线 l 下方的抛物线上有且仅有两个点 P1 和 P2，且∠AP1E＝∠AP2E＝ 45°？若存在，求 m 的值和点 P1、P2 的坐标；若不存在，请说明理由． 86．如图，抛物线 y＝ax 2＋bx＋c 经过点 O（0，0），A（4，0），B（5，5），点 C 是 y 轴负半轴上一点， 且 tan∠OCB＝ 5 9 ．点 P 是直线 OB 上一动点，过点 P 作 PQ∥y 轴，交抛物线于点 Q． （1）求抛物线的解析式； （2）当直线 BC 平分△PQB 的面积时，求点 P 的坐标； （3）是否存在这样的点 P，使得以 P、Q、B 为顶点的三角形与△OBC 相似？若存在，求点 P 的坐标；若 不存在，请说明理由． 87．如图，在平面直角坐标系中，点 C 的坐标为（0，2），点 D 在 x 轴的正半轴上，∠ODC＝30°，OE 为 y O xA C E D l y O x C D 备用图 y O x C A B Q P △COD 的中线，过 C、E 两点的抛物线 y＝ax 2＋ 6 x＋c 与 x 轴相交于 A、B 两点（A 在 B 的左侧）． （1）求抛物线的解析式； （2）等边△OMN 的顶点 M、N 在线段 AE 上，求 AE 及 AM 的长； （3）点 P 为△AOC 内的一个动点，求 PA＋PC＋PO 的最小值，并求此时点 P 的坐标． 88．如图，在平面直角坐标系中，二次函数 y＝－x 2＋4x＋5 的图象与 x 轴交于点 A、B（A 在 B 的左侧）， 与 y 轴交于点 C，顶点为 D．点 P 是 x 轴正半轴上的一个动点，点 Q 是 x 轴负半轴上一点，QE⊥CP 于 E， 交 y 轴于点 F，且 QF＝CP．设 OP＝m． （1）求证：OF＝OP． （2）当 m 为何值时，以 C、P、D 为顶点的三角形是直角三角形？ （3）是否存在实数 m，使直线 QE 与以 AB 为直径的圆相切？若存在，求出相应的 m 值；若不存在，请说 明理由． 89．如图，抛物线 y＝－ 4 3 x 2＋ 8 3 x＋4 交 x 轴于 A、B 两点（点 A 在点 B 的左侧），交 y 轴于点 C，以 OB、OC 为边作矩形 OBDC，CD 交抛物线于 G． （1）求 OB 和 OC 的长； （2）抛物线的对称轴在边 OB（不包括 O、B 两点）上作平行移动，交 x 轴于点 E，交 CD 于点 F，交 BC 于点 M，交抛物线于点 P．设 OE＝m，PM＝h，求 h 与 m 的函数关系式，并求 PM 的最大值； （3）连接 PC，在 CD 上方的抛物线部分是否存在这样的点 P，使得以 P、C、F 为顶点的三角形与△BEM 相似？若存在，求出相应的 m 的值，并判断△PCM 的形状；若不存在，请说明理由． y O xA C E DB y O xA C E D BPQ F y O xA C E D B G F M P 90．如图，直线 y＝－ 3 4 x 经过抛物线 y＝ax 2＋8ax－3 的顶点 M，点 P 是抛物线上的动点，点 Q 是抛物线 对称轴上的动点． （1）求抛物线的解析式； （2）当 PQ∥OM 时，设点 P 的横坐标为 x，线段 PQ 的长为 d，求 d 关于 x 的函数关系式； （3）当以 P、Q、O、M 四点为顶点的四边形是平行四边形时，求 P、Q 两点的坐标． 91．如图 1，在平面直角坐标系中，抛物线 y＝－ 1 16 x 2＋16 与 x 轴正半轴交于点 F、与 y 轴正半轴交于点 E，边长为 8 的正方形 ABCD 的边 CD 在 x 轴上，且顶点 C 与点 F 重合，抛物线与边 AB 交于点 P． （1）求点 F、点 P 的坐标； （2）如图 2，若正方形 ABCD 在平面内运动，并且边 BC 所在的直线始终与 x 轴垂直，抛物线始终与边 AB 交于点 P 且同时与边 CD 交于点 Q．当 P、Q 分别经过 AB、CD 的三等分点时，设点 A 的坐标为（m，n） （m＞0），求 m 的值； （3）当正方形 ABCD 左右平移时，抛物线始终与边 AB 交于点 P，且同时与边 CD 交于点 Q，设点 A 的坐 标为（m，n）（m＞0），求 m 的取值范围． 92．已知抛物线 y＝－ 4 9( x－2)2＋c 与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴正半轴交于点 C， 顶点为 D，DE⊥x 轴于点 E，DA 交 y 轴于点 F，sin∠DOE＝ 2 5 ． y O x Q M P 图 1 O x B y A D F (C) P 图 2 O x B y A C FD P Q （1）求抛物线的解析式； （2）过 E 点的直线与 y 轴相交于点 P，过 O、D 两点作直线 PE 的垂线，垂足分别为 G、H，若 EG EH ＝ 1 2 ， 求点 P 的坐标； （3）点 A 关于 y 轴的对称点为 A′，Q 为抛物线上一动点，直线 FQ 交 x 轴于点 K．是否存在这样的点 Q， 使△AFK 与△AA′D 相似？若存在，求出所有符合条件的直线 QK 的解析式；若不存在，请说明理由． 93．已知二次函数 y＝ax 2＋bx＋c（a≠0）的图象经过点 A（－3，0），B（1，0），与 y 轴负半轴交于点 C， sin∠OBC＝ 2 5 ，点 D 的坐标为（0，－9）． （1）求二次函数的解析式； （2）点 E 在二次函数 y＝ax 2＋bx＋c 的图象上，四边形 ABCE 是 以 AB 为一底边的梯形，求点 E 的坐标； （3）在（2）的条件下，过点 E 作直线 EF⊥x 轴于 F，直线 EF 与线段 AD 相交于点 G．问：在二次函数的图象上是否存在点 P， 使直线 PG 与 y 轴相交所成的锐角等于梯形 ABCE 的底角？若存 在，求出点 P 的坐标；若不存在，请说明理由． 94．如图，在 Rt△OAB 中，∠OAB＝90°，AO＝AB，点 B 坐标为（10，0），过原点 O 的抛物线，又过点 A 和 G，点 G 坐标为（7，0）． （1）求抛物线的解析式； （2）边 OB 上有一动点 T（t，0）（T 不与点 O、B 重合），过点 T 作 OA、AB 的垂线，垂足分别为 C、 D．设△TCD 的面积为 S，求 S 与 t 之间的函数关系式，并求 S 的最大值； （3）已知 M（2，0），过点 M 作 MK⊥OA，垂足为 K，作 MN⊥OB，交 OA 于点 N．在线段 OA 上是否存 在一点 Q，使得 Rt△KMN 绕点 Q 旋转 180°后，点 M、K 恰好落在（1）中所求抛物线上，若存在，请求 出点 Q 和抛物线上与 M、K 对应的点的坐标；若不存在，请说明理由． y xOA B F D E C y xO y xO A B D T C M K N G 95．如图，点 M 坐标为（－4，0），以点 M 为圆心，2 为半径的圆与 x 轴交于 A、B 两点（A 在 B 的左 侧），抛物线 y＝ax 2＋bx＋c 经过 A、B 两点，与 y 轴交于点 C（0，2）． （1）求抛物线的解析式； （2）点 D（m， 16 3 ）（m＜0）是抛物线 y＝ 1 6 x 2＋bx＋c 上一点，点 P 是抛物线对称轴上的一个动点，求 PB＋ PD 的最小值； （4）CE 切⊙M 于点 E，且点 E 在第三象限．在抛物线上是否存在一点 Q，使△QOC 的面积等于△EOC 的面积？若存在，求点 Q 的坐标，若不存在，请说明理由． 96．抛物线 y＝ax 2＋2x＋3（a＜0）交 x 轴于 A、B 两点，交 y 轴于点 C，顶点为 D，连接 BD 并以 BD 为 直径作⊙M． （1）写出抛物线的对称轴及 C、D 两点的坐标（用含 a 的代数式表示）； （2）当 a＝－1 时，判断⊙M 是否经过点 C，并说明理由； （3）在（2）的条件下，点 P 是抛物线上任意一点，过 P 作对称轴的垂线，垂足为 Q．那么是否存在这样 的点 P，使△PQD 与以 B、C、D 为顶点的三角形相似？若存在，求出点 P 的坐标；若不存在，请说明理 由． 97．如图，在平面直角坐标系中，已知抛物线经过点 A（0，4）， B（1，0），C（5，0），抛物线的对称轴 l 与 x 轴相交于点 M． （1）求抛物线的解析式和对称轴； （2）设点 P 为抛物线（x ＞5）上的一点，若以 A、O、M、P 为 顶点的四边形四条边的长度为四个连续的正整数，请直接写出 y OAB E C M x y O x C A B D M y O A B C x －1 －2 －3 1 2 3 4 1 2 3 4 5 6 7－1 点 P 的坐标； （3）连接 AC．探索：在直线 AC 下方的抛物线上是否存在一点 N，使△NAC 的面积最大？若存在，求点 N 的坐标；若不存在，请说明理由． 98．如图，抛物线 y＝x 2＋bx＋c 与 x 轴交于 A、B 两点（点 A 在点 B 的左侧），与 y 轴交于点 C（0，－3）， 顶点为 D（－1，－4），连接 AC、CD． （1）求抛物线的解析式； （2）试在 x 轴上找一点 E，使∠CED 最大，求点 E 的坐标； （3）点 Q 是抛物线上的动点，在 x 轴上是否存在点 P，使以 A、C、P、Q 四点为顶点的四边形为平行四 边形？若存在，求出所有满足条件的点 P 的坐标；若不存在，请说明理由． 99．如图，在平面直角坐标系中，抛物线 y＝x 2＋mx＋n 经过 A（3，0）、B（0，－3）两点，点 P 是直线 AB 上一动点，过点 P 作 x 轴的垂线交抛物线于点 M． （1）若点 P 在第四象限，连接 AM、BM，当△ABM 的面积最大时，求△ABM 的 AB 边上的高； （2）若四边形 PMBO 为等腰梯形，求点 P 的坐标 （3）是否存在这样的点 P，使得以点 P、M、B、O 为顶点的四边形为平行四边形？若存在，请直接写出 点 P 的坐标；若不存在，请说明理由． 100．如图，一次函数 y＝－4x－4 的图象与 x 轴、y 轴分别交于 A、 C 两点，抛物线 y＝ 4 3 x 2＋b x＋c 的图象经过 A、C 两点，且与 x 轴 交于点 B． （1）求抛物线的函数表达式； （2）设抛物线的顶点为 D，求四边形 ABDC 的面积； （3）作直线 MN 平行于 x 轴，分别交线段 AC、BC 于点 M、N． 问在 x 轴上是否存在点 P，使得△PMN 是等腰直角三角形？如果 存在，求出所有满足条件的 P 点的坐标；如果不存在，请说明理 由． y xOA B D C －2 －4 O 2 4 5 B A P x y M O BA x y C 101．如图，在平面直角坐标系中，抛物线与 x 轴交于 A、B 两点（A 在 B 的左侧），与 y 轴交于点 C（0， 4），顶点为（1， 9 2）． （1）求抛物线的函数关系式； （2）设抛物线的对称轴与轴交于点 D，试在对称轴上找出点 P，使△CDP 为等腰三角形，请直接写出满 足条件的所有点 P 的坐标； （3）若点 E 是线段 AB 上的一个动点（与点 A、B 不重合），分别连结 AC、BC，过点 E 作 EF∥AC 交线 段 BC 于点 F，连接 CE，记△CEF 的面积为 S，S 是否存在最大值？若存在，求出 S 的最大值及此时 E 点 的坐标；若不存在，请说明理由． 102．如图，已知直线 y＝－ 1 2 x＋2 与抛物线 y＝a( x＋2)2 相交于 A、B 两点，与 x 轴相交于 C 点，点 B 在 y 轴上，D 为抛物线的顶点．P 为线段 AB 上一个动点（点 P 不与 A、B 重合），过 P 点作 x 轴的垂线与抛物 线交于 Q 点． （1）求抛物线的解析式； （2）设直线与抛物线的对称轴交于点 E，如果以 P、Q、E 为顶点的三角形与△BOC 相似，求点 P 的坐标； （3）连接 QD，探究四边形 PQDE 的形状：①能否成为菱形；②能否成为等腰梯形？如果能，求点 P 的 坐标；如果不能，请说明理由． 103．已知抛物线 y＝ax 2－2ax－3a（a＜0）与 x 轴交于 A、 B 两点（点 A 在点 B 的左侧），与 y 轴交于点 C，点 D 为 抛物线的顶点． （1）求 A、B 的坐标； （2）过点 D 作 DH⊥y 轴于点 H，若 DH＝HC，求 a 的值 O BA x y C D O A B x y CD E 备用图 O A B x y CD E O H D x y BA E C F N 和直线 CD 的解析式； （3）在（2）的条件下，直线 CD 与 x 轴交于点 E，过线段 OB 的中点 N 作 NF 丄 x 轴，交直线 CD 于点 F，则直线 NF 上是否存在点 M，使得点 M 到直线 CD 的距离等于点 M 到原点 O 的距离？若存在，求出点 M 的坐标；若不存在，请说明理由． 104．如图，半径为 1 的⊙M 经过直线坐标系的原点 O，且分别与 x 轴正半轴、y 轴正半轴交于点 A、B，∠ OMA＝60°，过点 B 的切线交 x 轴负半轴于点 C，抛物线经过点 A、B、C． （1）求点 A、B 的坐标； （2）求抛物线的函数关系式； （3）若点 D 为抛物线对称轴上的一个动点，问是否存在这样的点 D，使得△BCD 是等腰三角形？若存在， 求出符合条件的点 D 的坐标；若不存在，请说明理由． 105．已知抛物线 y＝ 1 6( x－2)( x－2t－3)（t＞0）与 x 轴相交于点 A、B（点 A 在点 B 的左侧），与 y 轴交于 点 C，且△ABC 的面积为 21 2 ． （1）求抛物线的解析式； （2）设 l 为过点 B 且经过第一、二、四象限的一条直线，过原点 O 的直线与 l 交于点 E，与以 AC 为直径 的圆交于点 D，若△OAD∽△OEB，求直线 l 的解析式； （3）在（2）的条件下，若点 Q 为直线 l 上的动点，在坐标平面内是否存在点 P，使得以 P、Q、A、C 四 点为顶点的四边形为菱形？若存在，直接写出点 P 的坐标；若不存在，请说明理由． 106．抛物线 y＝ax 2＋bx＋c 与 x 轴交于点 A（1，0）、B（5，0），与 y 轴交于点 C，顶点的纵坐标为 4． （1）求抛物线的解析式； （2）若△ABC 的外接圆⊙M 与 y 轴的另一交点为 D，⊙M 的弦 DE∥x 轴，求直线 CE 的解析式； （3）在 x 轴上是否存在点 F，使以 O、C、F 为顶点的三角形与△CDE 相似？若存在，求出所有符合条件 的点 F 的坐标，并判定直线 CF 与⊙M 的位置关系（要求写出判断根据）；若不存在，请说明理由． 107．如图，抛物线 y＝ax 2＋bx 经过点 A（－4，0）、B（－2，2），连接 OB、AB． O y x O x y B A C M1 －1 （1）求该抛物线的解析式； （2）求证：△OAB 是等腰直角三角形； （3）将△OAB 绕点 O 按逆时针方向旋转 135°，得到△OA′B′，写出 A′B′ 中点 P 的坐标，试判断点 P 是否在 此抛物线上. （4）在抛物线上是否存在这样的点 M，使得四边形 ABOM 成直角梯形，若存在，请求出点 M 坐标及该直 角梯形的面积；若不存在，请说明理由． 108．九（1）班数学课题学习小组为了研究学习二次函数问题，他们经历了实践——应用——探究的过程： （1）实践：他们对一条公路上横截面为抛物线的单向双车道的隧道（如图①）进行测量，测得一隧道的 路面宽为 10m，隧道顶部最高处距地面 6.25m，并画出了隧道截面图，建立了如 图②所示的直角坐标系， 请你求出抛物线的解析式． （2）应用：按规定机动车辆通过隧道时，车顶部与隧道顶部在竖直方向上的高度差至少为 0.5m．为了确 保安全，问该隧道能否让最宽 3m，最高 3.5m 的两辆厢式货车居中并列行驶（两车并列行驶时不考虑两车 间的空隙）？ （3）探究：该课题学习小组为进一步探索抛物线的有关知识，他们借助上述抛物线模型，提出了以下两 个问题，请予解答： Ⅰ．如图③，在抛物线内作矩形 ABCD，使顶点 C、D 落在抛物线上．顶点 A、B 落在 x 轴上．设矩形 A BCD 的周长为 l，求 l 的最大值． Ⅱ．如图④，过原点作一条 y＝x 的直线 OM，交抛物线于点 M，交抛物线对称轴于点 N，P 为直线 OM 上 一动点，过 P 点作 x 轴的垂 线交抛物线于点 Q．问在直线 OM 上是否存在点 P，使以 P、N、Q 为顶点的 三角形是等腰直角三角形？若存在，请求出 P 点的坐标；若不存在，请说明理由． O x y B A－5 －2 －4 －6 2 图② 5 10 6.25 O x y 图③ 5 10 6.25 O x y A B D C 图④ 5 10 6.25 O x y P Q N M 图① 109．已知抛物线 y＝ 1 2 x 2－mx＋2m－ 7 2 ． （1）试说明：无论 m 为何实数，该抛物线与 x 轴总有两个不同的交点； （2）如图，当该抛物线的对称轴为直线 x＝3 时，抛物线的顶点为点 C，直线 y＝x－1 与抛物线交于 A、B 两点，并与它的对称轴交于点 D． ①抛物线上是否存在一点 P 使得四边形 ACPD 是正方形？若存在，求出点 P 的坐标；若不存在，说明理 由； ②平移直线 CD，交直线 AB 于点 M，交抛物线于点 N，通过怎样的平移能使得 C、D、M、N 为顶点的四 边形是平行四边形． 110．如图，在直角坐标 系中 ，点 P 的坐标为（n，0）（n＞0），抛物线 y＝－x 2＋bx＋c 经过原点 O 和点 P， 正方形 ABCD 的三个顶点为 A（2，2），B（3，2），D（2，3）． （1）求 c、b 的值并写出抛物线对称轴及 y 的最大值（用含有 n 的代数式表示）； （2）求证：抛物线的顶点在函数 y＝x 2 的图象上； （3）若抛物线与直线 AD 交于点 N，求 n 为何值时，△NPO 的面积为 1； （4）若抛物线经过正方形区域 ABCD（含边界），请直接写出 n 的取值范围． 111．如图，已知抛物线经过原点 O 和点 A，点 B（2，3）是该抛物线对称轴上一点，过点 B 作 BC∥x 轴 交抛物线于点 C，连接 BO、CA，若四边形 OACB 是平行四边形． （1）求这条抛物线的函数关系式； （2）设抛物线的顶点为 D，试在线段 AC 上找出这样的点 P，使△PBD 是等腰三角形，求点 P 的坐标； （3）经过点 D 的直线把平行四边形 OACB 的面积分为 1 : 3 两部分，求该直线的函数关系式． B A xO y D C BA xO y D C N P 1 1 O B A xO y C D 112．如图，在平面直角坐标系中，正方形 ABCD 的边长为 5，点 A 在 y 轴正半轴上，点 B 在 x 轴负半轴 上，B（－1，0），C、D 两点在抛物线 y＝ 1 2 x 2＋bx＋c 上． （1）求此抛物线的表达式； （2）正方形 ABCD 沿射线 CB 以每秒 5个单位长度平移，1 秒后停止，此时 B 点运动到 B1 点，试判断 B1 点是否在抛物线上，并说明理由； （3）正方形 ABCD 沿射线 BC 平移，得到正方形 A2B2C2D2，A2 点在 x 轴正半轴上，求正方形 ABCD 的平 移距离． 113．如图 1，直线 y＝－x＋3 与 x 轴、y 轴分别交于点 B、点 C，经过 B、C 两点的抛物线 y＝x 2＋bx＋c 与 x 轴的另一个交点为 A，顶点为 P． （1）求该抛物线的解析式； （2）在该抛物线的对称轴上是否存在点 M，使以 C、P、M 为顶点的三角形为等腰三角形？若存在，请直 接写出所有符合条件的点 M 的坐标；若不存在，请说明理由； （3）连结 AC，在 x 轴上是否存在点 Q，使以 P、B、Q 为顶点的三角形与△ABC 相似？若存在，请求出 点 Q 的坐标；若不存在，请说明理由； （4）当 0＜x＜3 时，在抛物线上求一点 E，使△CBE 的面积有最大值． （图 2、图 3 供画图探究） 114．如图，直线 y＝x－3 与 x 轴、y 轴分别相交于点 B、点 C，经过 B、C 两点的抛物线 y＝ax 2＋bx＋c 与 x 轴的另一交点为 A，顶点为 D，且对称轴是直线 x＝1． D A O C B A1 B1 A2 B2 C2 D2 x y A O C B x y P 图 1 A O C B x y P 图 2 A O C B x y P 图 3 （1）求抛物线的解析式； （2）若平行于 x 轴的直线 y＝m 与△BCD 的外接圆有公共点，求 m 的取值范围； （3）点 P 是线段 BC 上的动点，过点 P 作 x 轴的垂线，交折线 C－D－B 于点 E，将△BCD 沿直线 PE 向 右翻折．设点 P 的横坐标为 x，翻折后的图形与△BCD 重叠部分的面积为 S，求 S 关于 x 的函数关系式， 并求 S 的最大值； （4）在抛物线上是否存在点 M，使∠AMB＝∠CBD？若存在，直接写出点 M 的坐标；若不存在，请说明 理由． 115．如图，已知抛物线经过点 A（4，0）、B（3，2）、C（0，4），BD⊥y 轴，垂足为 D． （1）求抛物线对应的函数关系式； （2）点 P 从点 B 出发，沿折线 B→D→C 以每秒 1 个单位的速度运动，过点 P 作 PE⊥DB，交抛物线于 E，点 F 是 x 轴上一点，且始终保持∠PFA＝45°．设点 P 的运动时间为 t（秒），△PEF 的面积为 S（平方 单位）． ①求 S 关于 t 的函数关系式； ②当 t 为何值时，S 有最大值，并求这个最大值； ③在 S 取得最大值时，判断以 EF 为对角线的平行四边形 QEPF 的顶点 Q 是否在（1）中的抛物线上，并 说明理由． 116．如图，在平面直角坐标系中，点 A 的坐标为（10，0），点 B 在第一象限，且 AB＝3 5，cos∠OAB＝ 2 5 ，点 B 关于 x 轴的对称点为点 C，一条抛物线经过 O、C、A 三点． （1）求该抛物线的解析式； （2）在第一象限的抛物线上是否存在点 P，使以点 P、O、C、A 为顶点的四边形是梯形？若存在，求出 点 P 的坐标；若不存在，请说明理由； （3）若将点 O、A 分别变换为点 E（－4m，0）、F（6m，0）（m 为常数且 m＞0），设过 E、F 两点且以 EF 的垂直平分线为对称轴的抛物线（开口向上）与 y 轴的交点为 G，其顶点为 D，求 S△EGD : S△EGF 的值． OA B x y C D x＝1 x B A y E D F O C P O A B x y 117．如图，在平面直角坐标系中，A、B 两点的坐标分别是（0，1）和（1，0），P 是线段 AB 上的一动点 （不与 A、B 重合），坐标为（m，1－m）（m 为常数）． （1）求经过 O、P、B 三点的抛物线的解析式； （2）当 P 点在线段 AB 上移动时，过 O、P、B 三点的抛物线的对称 轴是否会随着 P 的移动而改变？请说明理由； （3）当 P 点移动到（ 1 2， 1 2）时，请你在过 O、P、B 三点的抛物线上至 少找出两点，使每个点都能与 P、B 两点构成等腰三角形，并求出这 两点的坐标． 118．孔明是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线 y＝ax 2（a＜0）的性质时，将 一把直角三角板的直角顶点置于平面直角坐标系的原点 O，两直角边与该抛物线交于 A、B 两点，请解答 以下问题： （1）若测得 OA＝OB＝2 2（如图 1），求 a 的值； （2）对同一条抛物线，孔明将三角板绕点 O 旋转到如图 2 所示位置时，过 BF 作 BF⊥x 轴于点 F，测得 OF ＝1，写出此时点 B 的坐标，并求点 A 的横坐标； （3）对该抛物线，孔明将三角板绕点 O 旋转任意角度时惊奇地发现，交点 A、B 的连线段总经过一个固 定的点，试说明理由并求出该点的坐标． 119．如图，直线 y＝3x＋3 交 x 轴于 A 点，交 y 轴于 B 点，过 A、B 两 点的抛物线交 x 轴于另一点 C（3，0），顶点为 D． （1）求抛物线的解析式； （2）若点 E 的坐标为（1，－2），点 M 是抛物线上一点（D 点除外），且 △MOE 的面积与△DOE 的面积相等，求 M 点坐标； （3）若点 P 是抛物线的对称轴上的动点，在坐标平面内是否存在点 Q， O A B x y P 1 1 O B x y A 图 2 FO B x y A 图 1 xO y B A D E C 使以点 P、Q、A、B 为顶点的四边形是菱形？若存在，求出 Q 点坐标；若不存在，请说明理由． 120．在平面直角坐标系中，O 为坐标原点，点 A 坐标为（1，0），以 OA 为边在第一象限内作等边△OAB， C 为 x 轴正半轴上的一个动点（OC＞1），连接 BC，以 BC 为边在第一象限内作等边△BCD，直线 DA 交 y 轴于 E 点． （1）如图，当 C 点在 x 轴上运动时，设 AC＝x，请用 x 表示线段 AD 的长； （2）随着 C 点的变化，直线 AE 的位置变化吗？若变化，请说明理由；若不变，请求出直线 AE 的解析 式． （3）以线段 BC 为直径作圆，圆心为点 F，当 C 点运动到何处时直线 EF∥直线 BO？此时⊙F 和直线 BO 的位置关系如何？请说明理由． （4）G 为 CD 与⊙F 的交点，H 为直线 DF 上的一个动点，连结 HG、HC，求 HG＋HC 的最小值，并将此 最小值用 x 表示． 121．已知直线 y＝－ 3 4 x＋6 与 x 轴、y 轴分别相交于点 A、B，将∠OBA 对折，使点 O 的对应点 E 落在直 线 AB 上，折痕交 x 轴于点 C． （1）求经过 A、B、C 三点的抛物线的解析式； （2）若抛物线的顶点为 D，在直线 BC 上是否存在点 P，使得四边形 OPAD 为平行四边形？若存在，求出 点 P 的坐标；若不存在，说明理由； （3）设抛物线的对称轴与直线 BC 的交点为 F，Q 为线段 BF 上一点，求|QA－QO|的取值范围． xO y B A D C E －1 1 xO y B A D C E F 122．如图，已知抛物线过点 A（0，6），B（2，0），C（7， 5 2）． （1）求抛物线的解析式； （2）若 D 是抛物线的顶点，E 是抛物线的对称轴与直线 AC 的交点，F 与 E 关于 D 对称，求证：∠CFE＝∠ AFE； （3）在 y 轴上是否存在这样的点 P，使△AFP 与△FDC 相似，若有，请求出所有符合条件的点 P 的坐标； 若没有，请说明理由． 123．如图 1，抛物线 y＝ax 2＋bx＋3 经过 A（－3，0），B（－1，0）两点． （1）求抛物线的解析式； （2）设抛物线的顶点为 M，直线 y＝－2x＋9 与 y 轴交于点 C，与直线 OM 交于点 D．现将抛物线平移， 保持顶点在直线 OD 上，若平移的抛物线与射线 CD（含端点 C）只有一个公共点，求它的顶点横坐标的 值或取值范围； （3）如图 2，将抛物线平移，当顶点至原点时，过 Q（0，3）作不平行于 x 轴的直线交抛物线于 E、F 两 点．问在 y 轴的负半轴上是否存在点 P，使△PEF 的内心在 y 轴上.若存在，求出点 P 的坐标；若不存在， 请说明理由． 124．如图所示，过点 F（0，1）的直线 y＝kx＋b 与抛物线 y＝ 1 4 x 2 交于 M（x1，y1）和 N（x2，y2）两点 （其中 x1＜0，x2＞0）． （1）求 b 的值； （2）求 x1·x2 的值； A B C O x y D E F A B C O x y D M 图 1 Q E O x y F 图 2 F O x y N M l N1M1 F1 （3）分别过 M、N 作直线 l：y＝－1 的垂线，垂足分别是 M 1 和 N1，判断△M1FN1 的形状，并证明你的结 论； （4）对于过点 F 的任意直线 MN，是否存在一条定直线 m，使 m 与以 MN 为直径的圆相切．如果有，请 求出这条直线 m 的解析式；如果没有，请说明理由． 125．如图，已知抛物线 l1：y＝x 2－4 与 x 轴相交于 A、C 两点，B 是抛物线 l1 上的动点（B 不与 A、C 重 合），抛物线 l2 与 l1 关于 x 轴对称，以 AC 为对角线的平行四边形 ABCD 的第四个顶点为 D． （1）求证：点 D 一定在 l2 上； （2）试判断动点 B 运动到什么位置时平行四边形 ABCD 恰好是菱形，并求这个菱形的面积； （3）平行四边形 ABCD 能否为矩形？如果能为矩形，求这些矩形公共部分的面积（若只有一个矩形符合 条件，则求此矩形的面积）；如果不能为矩形，请说明理由． 126．如图，分别以两个彼此相邻的正方形 OABC 与 CDEF 的边 OC、OA 所在直线为 x 轴、y 轴建立平面 直角坐标系（O、C、F 三点在 x 轴正半轴上）．若⊙P 过 A、B、E 三点（圆心在 x 轴上），抛物线 y＝ 1 4 x 2＋ bx＋c 经过 A、C 两点，与 x 轴的另一交点为 G，M 是 FG 的中点，正方形 CDEF 的面积为 1． （1）求 B 点坐标； （2）求证：ME 是⊙P 的切线； （3）设直线 AC 与抛物线对称轴交于 N，Q 点是此对称轴上不与 N 点重合的一动点． ①求△ACQ 周长的最小值； ②若 FQ＝t，S△ACQ＝S，直接写出 S 与 t 之间的函数关系式． 127．如图，在平面直角坐标系中，已知点 A（－4，0），点 C（0，2），点 B 是 x 轴上一点（位于点 A 的右 CA O x y l2 l1：y＝x 2－4 C A O x y D E G F B 备用图 C A O x y P D E M G F B 侧），以 AB 为直径的圆恰好经过点 C，抛物线 y＝ax 2＋bx＋c 经过 A、B、C 三点． （1）求抛物线的解析式； （2）D 是抛物线的顶点，在抛物线上是否存在点 P，使△ADP 为锐角三角形？若存在，求出 Q 点横坐标 的取值范围； （3）Q 是 y 轴上一点，M 是抛物线的对称轴上一点，且四边形 BCMQ 为等腰梯形，直接写出 M 点坐 标． 128．如图，已知抛物线 y＝x 2＋bx＋c 与 x 轴交于点 A（1，0）和点 B，与 y 轴交于点 C（0，－3）． （1）求抛物线的解析式； （2）如图（1），已知点 H（0，－1）．问在抛物线上是否存在点 G（点 G 在 y 轴的左侧），使得 S△GHC ＝S△GHA？ 若存在，求出点 G 的坐标，若不存在，请说明理由； （3）如图（2），抛物线上点 D 在 x 轴上的正投影为点 E（－2，0），F 是 OC 的中点，连接 DF，P 为线段 BD 上的一点，若∠EPF＝∠BDF，求线段 PE 的长． 129．如图，在平面直角坐标系 xOy 中，AB 在 x 轴上，AB＝10．以 AB 为直径的⊙O′ 与 y 轴正半轴交于点 C，连接 BC、AC．CD 是⊙O′ 的切线，AD⊥CD 于点 D，tan∠CAD＝ 1 2 ，抛物线 y＝ax 2＋bx＋c 过 A、B、 C 三点． （1）求证：∠CAD＝∠CAB； （2）①求抛物线的解析式； ②判断抛物线的顶点 E 是否在直线 CD 上，并说明理由； （3）在抛物线上是否存在一点 P，使四边形 PBCA 是直角梯形．若存在，直接写出点 P 的坐标；若不存 在，请说明理由． y xO A B C D y xO A B C D 备用图 y xO A B C D 备用图 C AO x y B FP 图（2） E DC AO x y B H G 图（1） y xOA B C D O′ 130．如图，直径为 5 的⊙M 圆心在 x 轴正半轴上，⊙M 与 x 轴交于 A、B 两点，与 y 轴交于 C、D 两点且 CD＝4，抛物线 y＝ax 2＋bx＋c 经过 A、B、C 三点，顶点为 N． （1）求抛物线的解析式； （2）直线 NC 与 x 轴交于点 E，试判断直线 CN 与⊙M 的位置关系并说明理由； （3）设点 Q 是抛物线对称轴上的一点，试问在抛物线上是否存在点 P，使以点 A、B、P、Q 为顶点的四 边形是平行四边形？若存在，求出点 P 的坐标；若不存在，请说明理由． 131．如图，抛物线 y＝x 2－4x＋c 交 x 轴于点 A、B（－1，0），交 y 轴于点 C，抛物线的对称轴交 x 轴于点 D． （1）求抛物线的解析式； （2）若点 E 在抛物线上，且位于第四象限，当四边形 ADCE 面积最大时，求点 E 的坐标； （3）在抛物线上是否存在这样的点 P，使△PAB 的内角中有一边与 x 轴所夹锐角的正切值为 1 2 ？若存在， 求出点 P 的坐标；若不存在，请说明理由． 132．如图，抛物线 y＝ax 2＋bx＋c 与 x 轴相交于 O、A 两点，直线 y＝－x＋3 与 y 轴交于 B 点，与该抛物 线交于 A、D 两点，已知点 D 的横坐标为－1． （1）求这条抛物线的解析式； x D y MO C BAE N OB A y C x 备用图 OB AD y C x E OB A y C x 备用图 （2）在线段 OA 上有一动点 H（不与 O、A 重合），过 H 作 x 轴的垂线分别交 AB 于 P 点，交抛物线于 Q 点，若 x 轴把△POQ 成两部分的面积之比为 1：2，请求出 H 点的坐标； （3）在抛物线上是否存在点 C，使△ABC 为直角三角形？若存在，求出点 C 的坐标；若不存在，请说明 理由． 133．如图，在平面直角坐标系 xOy 中，△ABC 的 A、B 两个顶点在 x 轴上，顶点 C 在 y 轴的负半轴上． 已知|OA|:|OB|＝1 : 5，|OB|＝|OC|，△ABC 的面积 S△ABC ＝15，抛物线 y＝ax 2＋bx＋c（a≠0）经过 A、 B、C 三点． （1）求此抛物线的函数表达式； （2）设 E 是 y 轴右侧抛物线上异于点 B 的一个动点，过点 E 作 x 轴的平行线交抛物线于另一点 F，过点 F 作 FG 垂直于 x 轴于点 G，再过点 E 作 EH 垂直于 x 轴于点 H，得到矩形 EFGH．则在点 E 的运动过程中， 当矩形 EFGH 为正方形时，求出该正方形的边长； （3）在抛物线上是否存在异于 B、C 的点 M，使△MBC 中 BC 边上的高为 7 2？若存在，求出点 M 的坐 标；若不存在，请说明理由． 134．在平面直角坐标系中，抛物线 y＝ax 2＋bx＋3 与 x 轴的两个交点分别为 A（－3，0）、B（1，0），过顶 点 C 作 CH⊥x 轴于点 H． （1）求抛物线的解析式； （2）在 y 轴上是否存在点 D，使得△ACD 是以 AC 为斜边的直角三角形？若存在，求出点 D 的坐标；若 不存在，说明理由； （3）若点 P 为 x 轴上方的抛物线上一动点（点 P 与顶点 C 不重合），PQ⊥AC 于点 Q，当以点 P、C、Q 为顶点的三角形与△ACH 相似时，求点 P 的坐标． O B A y D x O B A y D x 备用图 O B A y D x 备用图 OA x y B C O BA y H x C 备用图 O BA y H x C 135．如图，已知二次函数 y＝ax 2＋bx＋c 的图象的对称轴为直线 x＝1，且与 x 轴有两个不同的交点，其中 一个交点坐标为（－1，0）． （1）求二次函数的关系式； （2）在抛物线上有一点 A，其横坐标为－2，直线 l 过点 A 并绕着点 A 旋转，与抛物线的另一个交点是点 B，点 B 的横坐标满足－2＜xB＜ 3 2 ，当△AOB 的面积最大时，求出此时直线 l 的关系式； （3）抛物线上是否存在点 C，使△AOC 的面积与（2）中△AOB 的最大面积相等．若存在，求出点 C 的 横坐标；若不存在，说明理由． 136．已知抛物线 y＝x 2－2x＋m－1 与 x 轴只有一个交点，且与 y 轴交于 A 点，如图，设它的顶点为 B． （1）求 m 的值； （2）过 A 作 x 轴的平行线，交抛物线于点 C，求证△ABC 是等腰直角三角形； （3）将此抛物线向下平移 4 个单位后，得到抛物线 C′，且与 x 轴的左半轴交于 E 点，与 y 轴交于 F 点， 如图．请在抛物线 C′上求点 P，使得△EFP 是以 EF 为直角边的直角三角形． 137．已知二次函数 y＝－ 1 2 x 2＋2x＋ 5 2 图象交 x 轴于点 A，B（A 在 B 的左侧），交 y 轴于点 C，点 D 是该函 数图像上一点，且点 D 的横坐标为 3，连接 BD．点 E 是线段 AB 上一动点（不与点 A 重合），过 E 作 EF⊥AB 交射线 AD 于点 F，以 EF 为一边在 EF 的右侧作正方形 EFGH．设 E 点的坐标为（t，0）． x＝1y O x B A （－1，0） B A C OE F x y （1）求射线 AD 的解析式； （2）在线段 AB 上是否存在点 E，使△OCG 为等腰三角形？ 若存在，求正方形 EFGH 的边长；若不存在，请说明理由； （3）设正方形 EFGH 与△ABD 重叠部分面积为 S，求 S 与 t 的函数关系式． 138．已知在平面直角坐标系 xOy 中，⊙O 的半径为 1． （1）当直线 l：y＝x＋b 与⊙O 只有一个交点时，求 b 的值； （2）当反比例函数 y＝ k x 的图象与⊙O 有四个交点时，求 k 的取值范围； （3）试探究当 m 取不同的数值时，二次函数 y＝x 2＋m 的图象与⊙O 交点个数情况． 139．如图，抛物线经过原点 O，与 x 轴交于另一点 A，它的对称轴 x＝2 与 x 轴交于点 C，直线 y＝2x＋1 经过抛物线上一点 B（m，－3），且与 y 轴、直线 x＝2 分别交于点 D、E． （1）求抛物线对应的函数解析式； （2）求证：CD⊥BE； （3）在对称轴 x＝2 上是否存在点 P，使△PBE 是直角三角形，如 果存在，请求出点 P 的坐标，并求出△PAB 的面积；如果不存 在，请说明理由． 140．已知抛物线 C：y＝ax 2＋bx＋c（a＜0）过原点，与 x 轴的另一个交点为 B（4，0），A 为抛物线 C 的 顶点． （1）如图 1，若∠AOB＝60°，求抛物线 C 的解析式； （2）如图 2，若直线 OA 的解析式为 y＝x，将抛物线 C 绕原点 O 旋转 180°得到抛物线 C′，求抛物线 C、 C′ 的解析式； （3）在（2）的条件下，设 A′ 为抛物线 C′ 的顶点，求抛物线 C 或 C′ 上使得 PB＝PA′ 的点 P 的坐标． O x y A C E D B F G H O x y O x y AC E D B x＝2 y B O A C x 图 1 y BO A C x 图 2 C′ A′ 141．如图，已知抛物线与 x 轴交于 A（1，0），B（－3，0）两点，与 y 轴交于点 C（0，3），抛物线的顶 点为 P，连接 AC． （1）求此抛物线的解析式； （2）在抛物线上找一点 D，使得 DC 与 AC 垂直，且直线 DC 与 x 轴交于点 Q，求点 D 的坐标； （3）抛物线对称轴上是否存在一点 M，使 得 S△MAP ＝2S△ACP ，若存在，求出 M 点坐 标；若不存在，请说明理由． 142．如图，抛物线与 x 轴交于 A（x1，0）、B（x2，0）两点，且 x1＜x2，与 y 轴交于点 C（0，－4），其中 x1，x2 是方程 x 2－4x－12＝0 的两个根． （1）求抛物线的解析式； （2）点 M 是线段 AB 上的一个动点，过点 M 作 MN∥BC， 交 AC 于点 N，连接 CM，当△CMN 的面积最大时，求点 M 的坐标； （3）点 D（4，k）在（1）中抛物线上，点 E 为抛物线上一 动点，在 x 轴上是否存在点 F，使以 A、D、E、F 为顶点的 四边形是平行四边形？若存在，求出所有满足条件的点 F 的 坐标，若不存在，请说明理由． 143．已知顶点为 A（1，5）的抛物线 y＝ax 2＋bx＋c 经过点 B（5，1）． （1）求抛物线的解析式； （2）如图（1），设 C、D 分别是 x 轴、y 轴上的两个动点，求四边形 ABCD 周长的最小值； （3）在（2）中，当四边形 ABCD 周长最小时，作直线 CD．设点 P（x，y）（x＞0）是直线 y＝x 上的一个 动点，Q 是 OP 的中点，以 PQ 为斜边按图（2）所示构造等腰直角三角形 PRQ． ①当△PRQ 与直线 CD 有公共点时，求 x 的取值范围； ②在①的条件下，记△PRQ 与△COD 公共部分的面积为 S．求 S 关于 x 的函数关系式，并求 S 的最大 值． O x y A C D B Q P O x y A C M B N O C B A y x D 图（1） O C B A y x D 图（2） R Q P 144．如图（1），矩形 ABCD 的一边 BC 在直角坐标系中 x 轴上，AB＝8，AD＝10．折叠边 AD，使点 D 落 在 x 轴上点 F 处，折痕为 AE，设点 B 坐标为（m，0），其中 m＞0． （1）求点 E、F 的坐标（用含 m 的式子表示）； （2）连接 OA，若△OAF 是等腰三角形，求 m 的值； （3）如图（2），设抛物线 y＝a( x－m－6)2＋h 经过 A、E 两点，其顶点为 M，连接 AM，若∠OAM＝90°， 求 a、h、m 的值． 145．如图．在直角坐标系中，已知点 A（0，1），B（－4，4），将点 B 绕点 A 顺时针方向旋转 90°得到点 C，顶点在坐标原点的抛物线经过点 B． （1）求抛物线的解析式和点 C 的坐标； （2）抛物线上一动点 P，设点 P 到 x 轴的距离为 d1，点 P 到点 A 的距离为 d2，试说明 d2＝d1＋1； （3）在（2）的条件下，请探究当点 P 位于何处时，△PAC 的周长有最小值，并求出△PAC 的周长的最小 值． 146．已知抛物线 y＝ax 2＋2x＋3（a≠0）有如下两个特点：①无论实数 a 怎样变化，其顶点都在某一条直 线 l 上；②若把顶点的横坐标减少 1 a ，纵坐标增加 1 a 分别作为点 A 的横、纵坐标；把顶点的横坐标增加 1 a ， 纵坐标增加 1 a 分别作为点 B 的横、纵坐标，则 A、B 两点也在抛物线 y＝ax 2＋2x＋3（a≠0）上． （1）求出当实数 a 变化时，抛物线 y＝ax 2＋2x＋3（a≠0）的顶点所在直线 l 的解析式； （2）请找出在直线 l 上但不是该抛物线顶点的所有点，并说明理由； （3）你能根据特点（2）的启示，对一般二次函数 y＝ax 2＋bx＋c（a≠0）提出一个猜想吗？请用数学语言 把你的猜想表达出来，并给予证明． 147．已知抛物线的顶点是 C（0，a）（a＞0，a 为常数），并经过点（2a，2a），点 D（0，2a）为一定 点． （1）求含有常数 a 的抛物线的解析式； （2）设点 P 是抛物线任意一点，过 P 作 PH⊥x 轴，垂足是 H，求证：PD＝PH； （3）设过原点 O 的直线 l 与抛物线在第一象限相交于 A、B 两点，若 DA＝2DB，且 S△ABD ＝4 2，求 a 的 A y CO xB D E 图（2） M A y CO xB F D E 图（1） O A B x y C P O B x y C AD 值． 148．如图：抛物线 y＝ax 2－4ax＋m 与 x 轴交于 A、B 两点，点 A 的坐标是（1，0），与 y 轴负半轴交于点 C． （1）求抛物线的对称轴和点 B 的坐标； （2）过点 C 作对称轴的垂线 CP，垂足为 P，连结 BC 交对称轴于点 D，连结 AC、BP，若∠BPD＝∠ BCP，求抛物线的解析式； （3）在（2）的条件下，设抛物线的顶点为 G，连结 AG．问：对称轴上是否存在点 M，使△MCG 的面积 等于△ACG 的面积，若存在，求出 M 点的坐标，若不存在，请说明理由． 149．抛物线 y＝ax 2＋bx＋c 与 x 轴的交点为 A（m－4，0）和 B（m，0），与直线 y＝－x＋p 相交于点 A 和 点 C（2m－4，m－6）． （1）求抛物线的解析式； （2）若点 P 在抛物线上，且以点 P 和 A、C 以及另一点 Q 为顶点的平行四边形 ACQP 面积为 12，求点 P、Q 的坐标； （3）在（2）条件下，若点 M 是 x 轴下方抛物线上的动点， 当△PQM 的面积最大时，请求出△PQM 的最大面积及点 M 的坐标． 150．如图，抛物线 y＝ 1 3 x 2－m x＋n 与 x 轴交于 A、B 两点（A 在 B 的左侧），与 y 轴交于点 C（0．－1）， 且对称抽为 x＝l． （1）求出抛物线的解析式及 A、B 两点的坐标； O A B x y C P D G A B C y x O D （2）在 x 轴下方的抛物线上是否存在点 D，使四边形 ABDC 的面积为 3，若存在，求出点 D 的坐标；若 不存在，说明理由（使用图 1）； （3）点 Q 在 y 轴上，点 P 在抛物线上，要使 Q、P、A、B 为顶点的四边形是平行四边形，请求出所有满 足条件的点 P 的坐标（使用图 2）． 151．如图，抛物线 y＝ax 2＋2ax＋c（a≠0）与 y 轴交于点 C（0，4），与 x 轴交于 A、B 两点，点 A 的坐标 为（－4，0）． （1）求该抛物线的解析式； （2）点 Q 是线段 AB 上的动点，过点 Q 作 QE∥AC，交 BC 于点 E，连接 CQ，当△CQE 的面积最大时， 求点 Q 的坐标； （3）若平行于 x 轴的动直线 l 与该抛物线交于点 P，与直线 AC 交于点 F，点 D 的坐标为（－2，0）．问是 否有这样的直线 l，使得△ODF 是等腰三角形？若存在，请求出点 P 的坐标；若不存在，请说明理由． 152．如图所示，在平面直角坐标系中，四边形 ABCD 是直角梯形，BC∥AD，∠BAD＝90°，A（－1，0）， B（－1，2），D（3，0）．BC 与 y 轴相交于点 M，且 M 是 BC 的中点．连接 DM，并把线段 DM 沿 DA 方 向平移到 ON．抛物线 y＝ax 2＋bx＋c 经过 D、M、N 三点． （1）求抛物线的解析式； （2）抛物线上是否存在点 P，使得 PA＝PC，若存在，求出点 P 的坐标；若不存在，请说明理由； （3）设抛物线与 x 轴的另一个交点为 E，点 Q 是抛物线的对称轴上的一个动点，当点 Q 在什么位置时，|QE －QC|最大？并求出最大值． A O B xQ C D E y OA B C x y 图 1 x＝l OA B C x y 图 2 x＝l A O B xE M D N C y 153．如图，抛物线 y＝x 2－2mx＋n＋1 的顶点 A 在 x 轴负半轴上，与 y 轴交于点 B，C 是抛物线上一点，且 点 C 的横坐标为 1，AC＝3 10． （1）求抛物线的函数关系式； （2）若 D 是抛物线上一点，直线 BD 经过第一、二、四象限，且原点 O 到直线 BD 的距离为 8 5，求点 D 的坐标； （3）在（2）的条件下，直线 BD 上是否存在点 P，使得以 A、B、P 为顶点的三角形与△AOB 相似？若存 在，求出点 P 的坐标；若不存在，请说明理由． 154．如图，在平面直角坐标系中，抛物线 y＝－2x 2＋4x＋6 与 x 轴交于点 A、B（A 在 B 的左侧），与 y 轴 交于点 C，顶点为 D．过 C、D 两点的直线与 x 轴交于点 E，以 OE 为直径的⊙O 1 交直线 CD 于另一点 F． （1）求点 E 的坐标； （2）连接 FO1、FA，求证：△FO1A∽△BCD； （3）以点 O2（0，m）为圆心的⊙O2 经过点 C 且与⊙O1 相切． ①求实数 m 的值； ②在坐标轴上是否存在点 O3，使得以 O3 为圆心的⊙O3 与 ⊙O1、⊙O2 都相切？若存在，直接写出点 O3 的坐标；若不存 在，请说明理由． 155．如图，直线 y＝2x＋6 与 x 轴、y 轴分别交于点 A、C，抛物线 y＝－ x 2＋bx＋c 经过 A、C 两点，与 x 轴交于另一点 B． B OA x C y BOA x C y D E F O1 O M B M A M x M C M y M （1）求抛物线的解析式； （2）点 D 是直线 AC 上一点，且 S△ABD : S△BDC ＝1 : 3，求点 D 的坐标； （3）设直线 y＝ 1 2 x＋a 与抛物线交于 E、F 两点，问：∠EOF 能否为钝角？如果能，求 a 的取值范围；如 果不能，请说明理由． 156．如图，抛物线过 A（0，m）、B（－3，0）、C（12，0）三点，过 A 点作 x 轴的平行线交抛物线于点 D，P 是线段 OC 上的动点，连接 DP，作 PE⊥DP，交 y 轴于点 E． （1）求 AD 的长； （2）若在线段 OC 上存在不同的两点 P1、P2，使相应的点 E1、E2 都与点 A 重合，试求 m 的取值范围． （3）设抛物线的顶点为点 M，当 60°≤∠BMC≤90°时，求 m 的变化范围． 157．如图，抛物线 y＝ax 2＋bx＋c 交 x 轴于点 A（－3，0），点 B（1，0），交 y 轴于点 C（0，－3）．点 D 是点 A 关于点 B 的对称点，点 E 是线段 BD 的中点，直线 l 过点 E 且与 y 轴平行，直线 y＝－x＋m 过点 D， 交 y 轴于点 F． （1）求抛物线的函数表达式； （2）点 P 是线段 AB 上一动点，过点 P 作 x 轴的垂线，交直线 DF 于点 G，交抛物线于点 H，求线段 GH 长度的最大值； （3）点 M 在直线 l 上运动，在抛物线上是否存在点 N，使以点 A，D，M，N 为顶点的四边形是平行四边 形？若存在，求出点 N 的坐标；若不存在，请说明理由． 158．如图，在平面直角坐标系中，矩形 ABCD 的边 AB 在 x 轴的正半轴上，顶点 C、D 在第一象限，AB＝ O M B M A M x M C M y M E M D M P M O M B M A M x M C M y M D M E M l MF M P M G M H M 3，AD＝2，直线 y＝ 3 2 x－1 经过顶点 C、D 中的一个． （1）求矩形的顶点 A、B、C、D 的坐标； （2）以 AB 为直径作⊙M，经过 A、B 两点的抛物线 y＝ax 2＋bx＋c 的顶点为 P． ①若点 P 在⊙M 外部且在矩形 ABCD 内部，求 a 的取值范围； ②过点 C 作⊙M 的切线交 AD 于点 E，当 PE∥AB 时，试判断 抛物线与 y 轴的交点 Q 是在直线 y＝ 3 2 x－1 的上方还是下 方？还是正好落在此直线上？并说明理由． 159．如图，矩形 OABC 的顶点 A、C 分别在 x 轴、y 轴上，顶点 B 在第一象限，E、F 分别是 OA、AB 上的点，将△AEF 沿 EF 翻折，使点 A 落在线段 BC 上的点 D 处．经过 抛物线 y＝ax 2－14ax＋49a＋4（a≠0）顶点 M 的每一条直线总平分矩形 OABC 的面积． （1）求点 E、F 的坐标； （2）若点 M 在线段 DE 上，AF 的长为整数，且抛物线与线段 EF 有两个不同的交点，求实数 a 的取值范 围． 160．已知点 P（m，n）在抛物线 y＝x 2－1 上，以 P 为圆心的⊙P 与 x 轴有两个交点 A、B，且 A、B 两点 的横坐标是关于 x 的方程 x 2－2mx＋n＝0 的两个根． （1）当 P 在抛物线上运动时，⊙P 在 x 轴上截得的弦长是否变化？说明理由； （2）当⊙P 与 y 轴相切时，求圆心 P 的坐标； （3）当⊙P 与 x 轴的两个交点和抛物线的顶点 C 构成一个等腰三角形时，求圆心 P 的坐标． 161．已知二次函数 y＝x 2＋bx＋c 的图象经过点 A（－1，0），且顶点 D 在直线 y＝－4x 上． （1）求该二次函数的表达式； （2）设该二次函数与 x 轴的另一个交点为 B，与 y 轴的交点为 C，求经过 B、C、D 三点的⊙O′ 的半径； （3）设⊙O′ 与 y 轴的另一个交点为 E，经过 P（－2，0）、E 两点的直线为 l，则圆心 O′ 是否在直线 l 上？ 请说明理由． BA CD y xO O A x y C F B E D M O x y A B C P O A B x y C D O′ E 162．已知顶点为 C 的抛物线 y＝ax 2－4ax＋c 经过点（－2，0），与 y 轴交于点 A（0，3），点 B 是抛物线上 的点，且满足 AB∥x 轴． （1）求抛物线的表达式； （2）求该抛物线上关于原点中心对称的两个点的坐标； （3）在线段 AB 上是否存在点 P，使得以 P、A、C 为顶点 的三角形与△AOC 相似？若存在，求点 P 的坐标；若不存 在，请说明理由． 163．如图，在 Rt△ABC 中，∠ACB＝90°，AC＝BC，边 BC 在 x 轴上，点 A 坐标为（3，m）（m＞0），边 AB 与 y 轴相交于点 D，以 M（1，0）为顶点的抛物线经过点 A、D． （1）用含 m 的代数式表示点 B、D 的坐标； （2）求该抛物线的解析式； （3）点 P 为抛物线上点 M 至点 A 之间的一点，且点 P 到△ABC 的 边 AC、BC 的距离相等，连接 AP、PM， 求四边形 ABMP 的面积． 164．如图，顶点为 D 的抛物线与 y 轴交于点 A，直线 y＝ax＋3 与 y 轴也交于点 A，矩形 OCBA 的面积为 12，且顶点 B 在此抛物线上． （1）求该抛物线的对称轴； （2）⊙P 是经过 A、B 两点的一个动圆，当⊙P 与 y 轴相交，且在 y 轴上两交点的距离为 4 时，求圆心 P 的坐标； （3）若线段 DO 与 AB 交于点 E，以 D、A、E 为顶点的三角形是否有可能与以 D、O、A 为顶点的三角形 相似？如果有可能，请求出点 D 的坐标及抛物线的解析式；如果不可能，请说明理由． y xO y xO C A B M D C A O D M B x M y M 165．如图，直线 y＝－2x＋m（m＞0）与轴、y 轴分别交于点 A、B，S△AOB＝16，抛物线 y＝ax 2＋bx（a≠ 0）经过点 A，顶点 M 在直线 y＝－2x＋m 上． （1）求 m 的值； （2）求抛物线的解析式； （3）设抛物线的对称轴与 x 轴交于点 N，问：在抛物线的对称轴上是否存 在一点 P，使得以 O、P、N 为顶点的三角形与△AMN 相似？若存在，求出 点 P 的坐标；若不存在，请说明理由． 166．已知抛物线 y＝ax 2＋bx＋c 的对称轴为 x＝ 3，且经过点 C（0，－3） 和点 F（3，－2 3）． （1）求该抛物线的解析式； （2）如图 1，设该抛物线与 x 轴交于 A、B 两点，与 y 轴交于点 C，过 A、B、C 三点的⊙M 交 y 轴于另一 点 D，连接 AD、DB，设∠CDB＝α，∠ADC＝β，求 cot(α－β)的值； （3）如图 2，作∠CDB 的平分线 DE 交⊙M 于点 E，连接 BE．在坐标轴上是否存在点 P，使得以 P、D、 E 为顶点的三角形与△DEB 相似？若存在，求出所有满足条件的点 P 的坐标（不包括点 B）；若不存在， 请说明理由． 167．如图，已知抛物线 y＝ax 2－2ax＋b（a＞0）与 x 轴交于 A、B（3，0）两点，与 y 轴交于点 C，且 OC ＝3OA，抛物线的顶点为 D． （1）求抛物线的解析式； （2）如图 1，E 为 x 轴上一点，且 S△ACD ＝ 1 2 S△EAC ，求 E 点的坐标； （3）如图 2，P 为抛物线上一动点，问在对称轴上是否存在点 Q，使得以 P、D、Q 为顶点的三角形与△BOD 相似（只考虑顶点 D 与顶点 O 对应的情况），若存在，求出所有符合条件的 Q 点的坐标；若不存在，请说 明理由． A O B x M y M A B M MO x y D C 图 1 A B M MO x y D C 图 2 E A B O x y D C 图 1 A B O x y D C 图 2 168．已知抛物线 y＝ax 2＋3ax＋b 与 x 轴交于 A、B（1，0）两点，与 y 轴交于点 C（0，2）． （1）求此抛物线的解析式； （2）如图（1），P 为抛物线第三象限的点，若 S△PAC ＝ 4 3 S△PBC ，求 P 点坐标； （3）如图（2），D 为抛物线的顶点，在抛物线上是否存在点 Q，使△ADQ 为锐角三角形？若存在，求出 Q 点横坐标的取值范围． 169．如图，已知直线 y＝2x＋2 与 x 轴交于点 C，与 y 轴交于点 B，抛物线 y＝ax 2－2ax＋c 过点 C 且与直 线 y＝2x＋2 交于点 A（5，12）． （1）求该抛物线的解析式； （2）D 为 x 轴上方抛物线上一点，若△DCO 与△DBO 的面积相等，求 D 点的坐标； （3）在线段 AB 上是否存在点 P，过 P 作 x 轴的垂线交抛物线于 E 点，使得以 P、B、E 为顶点的三角形 与△BOC 相似？若存在，求出点 P 的坐标；若不存在，请说明理由． y xO A B C P 图 1 y xO A B C P 图 2 D y xO A B C 170．已知抛物线 y＝ax 2－2x＋c 与 x 轴交于 A（－1，0）、B 两点，与 y 轴交于点 C，对称轴为 x＝1，顶点 为 E，直线 y＝－ 1 3 x＋1 交 y 轴于点 D． （1）求抛物线的解析式； （2）求证：△BCE∽△BOD； （3）点 P 是抛物线上的一个动点，当点 P 运动到什么位置时， △BDP 的面积等于△BOE 的面积？ 171．如图，抛物线 y＝ax 2＋( a－3)x－3（a＞0）与 x 轴交于点 A、 B（A 在 B 的左侧），与 y 轴交于点 C，顶点为 D，且 sin∠ABD＝ 2 5 ． （1）求 a 的值； （2）⊙M 过 A、B、C 三点，P 是抛物线上一点，连接 PA，当 PA 与⊙M 相切时，求点 P 的坐标； （3）点 R 在 y 轴上，抛物线上是否存在点 Q，使得四边形 ACQR 是以 AC 为底的等腰梯形？若存在，求 出点 Q 的坐标；若不存在，说明理由．（用备用图作答） 172．如图，在平面直角坐标系中，将直线 y＝－ 3 4 x－ 3 2 沿 x 轴翻折，得到一条新直线与 x 轴交于点 A，与 y 轴交于点 B，将抛物线 y＝ 2 3 x 2 沿 x 轴平移，得到一条新抛物线与 y 轴交于点 C，与直线 AB 交于点 E、 F． （1）求直线 AB 的解析式； （2）若线段 CF∥x 轴，求平移后抛物线的解析式； （3）在（2）的条件下，若点 F 在 y 轴右侧，过 F 作 FH⊥x 轴于点 G，与直线 y＝－ 3 4 x－ 3 2 交于点 H．是 否存在不过△AFH 顶点且同时平分△AFH 的周长和面积的直线 l？若存在，求直线 l 的解析式；若不存在， 请说明理由． B D A C E y xO D O M C A B x y y O xA B C 备用图 O x y -1 -1 173．已知二次函数 y＝ax 2＋bx＋c 的图象与 x 轴交于点 A（x1，0），B（x2，0）（0＜x1＜x2），与 y 轴交于 点 C（0，1），过点 C 的直线与 x 轴交于点 D，与抛物线交于另一点 E，且△BCD 是等腰直角三角形，S△ABE ＝ 5 2 S△ABC ． （1）求点 B、D 的坐标； （2）求该二次函数的表达式； （3）设 AE 与 BC 交于点 F，在坐标平面内是否存在点 P，使得以 A、C、F、P 为顶点的四边形是等腰梯 形？若存在，求出点 P 的坐标；若不存在，请说明理由． 174．如图，抛物线 y＝ax 2＋bx－4a 与 x 轴交于 A（－1，0）、B（4，0）两点，与 y 轴交于点 C，点 C 关于 抛物线对称轴的对称点为 D． （1）求点 D 关于直线 AC 对称的点的坐标； （2）点 E 为抛物线上一点，且∠DBE＝45°，求点 E 的坐标． （3）若点 P 为抛物线上 BC 段上的一动点（点 P 不与 B，C 重合），过点 P 作 PG⊥x 轴于 G，交线段 BC 于点 F．是否存在点 P，使得四边形 PCOF 为平行四边形？若存在，请求出满足条件的点 P 的坐标；若不 存在，请说明理由． 175．如图，已知抛物线 y＝ax 2＋(a－2)x－2（a＞0）与 x 轴交于 A（x1，0）、B（x2，0）两点（x1＜x2），与 y 轴交于点 C，且 AB＝5，⊙M 过 A、B、C 三点． （1）求抛物线的解析式； （2）求图中阴影部分的面积； （3）抛物线上是否存在点 P，过 P 作 PD⊥x 轴，垂足为 D，使得△PBD 的面积被直线 BC 分成 2 : 3 的两 部分？若存在，求点 P 的坐标；若不存在，请说明理由． y C O A B x y O xA B M C y O xA B C 备用图 176．如图，在平面直角坐标系中，矩形 OABC 的顶点 A、B 的坐标分别为（4，0），（4，2），点 D 在第一 象限，以 D 为圆心，半径为 1 的⊙D 与 y 轴及矩形 OABC 的边 BC 都相切． （1）若⊙D 与矩形 OABC 组合得到的图形的面积能被一条直线平分，求这条直线的解析式； （2）求经过 O、D、A 三点的抛物线的解析式； （3）若点 E 在（2）中的抛物线上，那么，在 x 轴上是否存在点 F，使得以 F 为圆心的⊙F 与△ADE 的三 边 AD、AE、DE 所在直线都相切？若存在，请求出 F 点的坐标；若不存在，请说明理由． 177．如图，抛物线经过坐标原点，顶点 D 的坐标为（2，4），直线 AD 交 y 轴于点 A（0，－2），点 P 是抛 物线上点 O 至点 D 之间（不与 O、D 重合）的动点，连接 PO，以 P 为顶点、PO 为腰的等腰三角形 POQ 的另一顶点 Q 在 x 轴上，QR⊥x 轴交直线 AD 于点 R，连接 PR． （1）求抛物线的解析式； （2）设点 P 的横坐标为 x，△PQR 的面积为 S，求 S 与 x 之间的函数关系式，并写出自变量 x 的取值范围； （3）直线 AD 是否能将△PQR 分成面积比为 1 : 2 的两部分？如果能，求此时点 P 的坐标；如果不能，请 说明理由． 178．已知抛物线 y＝ax 2＋bx＋c（a＜0）与 x 轴交于 A、B 两点，与 y 轴交于点 C，点 A 的坐标为（－1， 0），抛物线的对称轴为直线 x＝1，tan∠ACB＝2． （1）求抛物线的解析式； （2）在抛物线上找一点 D，使得△BCD 是以点 D 为直角顶点的直角三角形，求点 D 的坐标； （3）以 OB 为直径作⊙E，在 y 轴左侧的抛物线上是否存在点 P，过点 P 作 x 轴的平行线与⊙E 交于 M、N 两点，与抛物线交于另一点 Q，使得 PM＋QN＝MN？若存在，求点 P 的坐标；若不存在，请说明理由． A y O B x C D O A Q x y R D P 179．已知抛物线 y＝ax 2＋x＋c 与 x 轴交于 A（－3，0）、B（m，0）两点，对称轴为直线 x＝－1，顶点为 C，且∠ACB＝90°． （1）求 m 的值和抛物线的解析式； （2）若过点 B 的直线 y＝－x＋1 交抛物线于另一点 D，点 P 在 x 轴上，且以 P、A、C 为顶点的三角形与△ ABD 相似，求点 P 的坐标； （3）在（2）的条件下，求△PAC 的外接圆半径． 180．已知抛物线 y＝ax 2＋bx＋c（a＞0）与 x 轴交于 A（－3，0）、B（2，0）两点，与 y 轴相交于点 C，且∠ ACB≥45°，抛物线的顶点为 D． （1）求 a、b、c 的取值范围； （2）求△BCD 中 CD 边上的高 h 的最大值； （3）当 a 取得最大值时 ①求△BCD 外接圆的半径； ②在 x 轴上是否存在点 P，使得直线 PD 将△ABC 的面积平分？若存在，求出点 P 的坐标；若不存在， 请说明理由． OA B x y C x＝1 A BO D M x y C A BO D C x y 181．已知抛物线 y＝－x 2＋(1－2m)x－m 2＋4（x 为自变量）． （1）求证：不论 m 取何值，抛物线的顶点都在同一条直线上； （2）若抛物线经过坐标原点，顶点在第二象限，P 是抛物线上位于 x 轴上方、对称轴左侧的一个动点， PQ∥x 轴交抛物线于另一点 Q，PM⊥x 轴于 M，QN⊥x 轴于 N．问：四边形 PQNM 的周长是否存在最大 值？若存在，请求出这个最大值；若不存在，请说明理由； （3）设（2）中的抛物线与 x 轴的另一交点为 A，抛物线的顶点为 D，O′ 为△AOD 外接圆的圆心，O′′ 为 矩形 PQNM 的中心，试探究△O′AO 的周长与△O′′AO 的周长之间的大小关系，并写出此时点 P 横坐标的 取值范围． 182．如图，在平面直角坐标系中，已知 A（－1，0）、B（0，2），点 C 在第二象限，CD⊥x 轴，垂足为 D，且△CDA≌△AOB．E 为 BC 延长线上的动点，过 A、B、E 三点作⊙O′，连结 AE，在⊙O′ 上另有一点 F，且 AF＝AE，AF 交 BC 于点 G，连接 BF． （1）求证：AF·BG＝AG·BF； （2）若抛物线 y＝ax 2＋ax－2 经过点 C，求抛物线的解析式； （3）在（2）的抛物线上是否存在 P、Q 两点，使得四边形 ABPQ 为正方形？若存在，求 P、Q 两点的坐 标，若不存在，请说明理由（用备用图作答）． 183．如图，抛物线 y＝－ 1 2 x 2－( m＋3)x＋m 2－12 与 x 轴交于点 A（x1，0）、B（x2，0）（x1＜0，x2＞0）， 与 y 轴交于点 C，且 OB＝2OA． （1）求抛物线的解析式； （2）在 x 轴上，点 A 的左侧，求一点 E，使△ECO 与△CAO 相似，并说明直线 EC 经过抛物线的顶点 D； （3）过（2）中的点 E 的直线 y＝ 1 4 x＋b 与抛物线相交于 M、N 两点，分别过 M、N 作 x 轴的垂线，垂足 x y O y xO C B AD F E O′ G y xO C B AD 备用图 为 M ′、N ′，点 P 为线段 MN 上一点，点 P 的横坐标为 t，过点 P 作 x 轴的垂线交抛物线于点 Q．是否存在 t 值，使 S △ QMN S梯形MM ′ N ′ N ＝ 12 35 ？若存在，求出满足条件的 t 值；若不存在，请说明理由． 184．如图，已知点 A（2 3，2），点 B（4，0），将△OAB 绕点 O 顺时针旋转 α 角（0°＜α＜90°）得到△OCD （O、A、B 的对应点分别为 O、C、D），将△OAB 沿 x 轴负方向平移 m 个单位得到△EFG（m＞0，O、 A、B 的 对应点分别为 E、F、G），α，m 的值恰好使点 C、D、F 落在同一反比例函数 y＝ k x(k≠0)的图象 上． （1）∠AOB＝________°，α＝________°； （2）求经过点 A、B、F 三点的抛物线的解析式； （3）若（2）中抛物线的顶点为 M，抛物线与直线 EF 的另一个交点为 H，抛物线上的点 P 满足以 P、M、 F、A 为顶点的四边形的面积与四边形 MFAH 的面积相等（点 P 不与点 H 重合），请直接写出满足条件的 点 P 的个数，并求位于直线 EF 上方的点 P的坐标． 185．如图，已知直线 y＝－2 x＋4 与 x 轴、y 轴分别相交于点 A、C，抛物线 y＝－2x 2＋bx＋c 经过 A、C 两 点，与 x 轴的另一交点为 B． （1）求抛物线的解析式； （2）设抛物线的顶点为 D，点 E 为抛物线上一点，且 S△AEC ＝4S△ADC ，求点 E 的坐标； （3）点 P 是直线 y＝－2 x＋4 上的动点，过点 P 作 PG⊥x 轴于 G，在 y 轴上（原点除外）是否存在点 Q， 使得△PQG 为等腰直角三角形？若存在，求出点 Q 的坐标；若不存在，请说明理由． OA B x y C D M N M ′ N ′ Q E P O A B x y O A B x y 备用图 y C O AB x D 十、动态综合型问题 1．已知直线 y＝kx＋3（k＜0）分别交 x 轴、y 轴于 A、B 两点，线段 OA 上有一动点 P 由原点 O 向点 A 运 动，速度为每秒 1 个单位长度，过点 P 作 x 轴的垂线交直线 AB 于点 C，设运动时间为 t 秒． （1）当 k＝－1 时，线段 OA 上另有一动点 Q 由点 A 向点 O 运动，它与点 P 以相同速度同时出发，当点 P 到达点 A 时两点同时停止运动（如图 1）． ① 直接写出 t＝1 秒时 C、Q 两点的坐标； ② 若以 Q、C、A 为顶点的三角形与△AOB 相似，求 t 的值． （2）当 k＝－ 3 4 时，设以 C 为顶点的抛物线 y＝( x＋m )2＋n 与直线 AB 的另一交点为 D（如图 2）． ① 求 CD 的长； ② 设△COD 的 OC 边上的高为 ，当 t 为何值时，h 的值最大？ 2．已知二次函数的图象经过 A（2，0）、C（0，12）两点，与 x 轴的另一交点为点 B，且对称轴为直线 x＝ 4，设顶点为点 D． （1）求二次函数的解析式及顶点 D 的坐标； （2）如图 1，在直线 y＝2x 上是否存在点 E，使四边形 ODBE 为等腰梯形？若存在，求出点 E 的坐标；若 不存在，请说明理由； （3）如图 2，点 P 是线段 OD 上的一个动点（不与 O、D 重合），以每秒 2 个单位长度的速度由点 D 向 点 O 运动，过点 P 作直线 PQ∥x 轴，交 BD 于点 Q，将△DPQ 沿直线 PQ 对折，得到△D1PQ．在点 P 运 动的过程中，设△D1PQ 与梯形 OPQB 的重叠部分的面积为 S，运动时间为 t 秒，求 S 关于 t 的函数关系 式． h O x y A B 1 1 C P Q 图 1 O x y A B 1 1 C P D 图 2 A B C O x y D P Q 图 2 A B C O x y D 图 1 3．如图 1，在梯形 ABCD 中，AD∥BC，∠C＝90°，点 E 从点 B 出发，以某一速度沿折线 BA－AD－DC 向点 C 匀速运动；点 F 从点 C 出发，以每秒 1 个单位长的速度向点 B 匀速运动，点 E、F 同时出发同时停 止．设运动时间为 t 秒时，△BEF 的面积为 y，已知 y 与 t 的函数关系如图 2 所示．请根据图中的信息，解 答下列问题： （1）点 E 运动到 A、D 两点时，y 的值分别是_______和_______； （2）求 BC 和 CD 的长； （3）求点 E 的运动速度； （4）当 t 为何值时，△BEF 与梯形 ABCD 的面积之比为 1 : 3？ 4．如图，矩形 ABCD 中，AB＝6，BC＝2 3，点 O 是 AB 的中点，点 P 在 AB 的延长线上，且 BP＝3．一 动点 E 从 O 点出发，以每秒 1 个单位长度的速度沿 OA 匀速运动，到达 A 点后，立即以原速度沿 AO 返回； 另一动点 F 从 P 点出发，以每秒 1 个单位长度的速度沿射线 PA 匀速运动，点 E、F 同时出发，当两点相 遇时停止运动，在点 E、F 的运动过程中，以 EF 为边作等边△EFG，使△EFG 和矩形 ABCD 在射线 PA 的同侧．设运动的时间为 t 秒（t≥0）． （1）当等边△EFG 的边 FG 恰好经过点 C 时，求运动时间 t 的值； （2）在整个运动过程中，设等边△EFG 和矩形 ABCD 重叠部分的面积为 S，请直接写出 S 与 t 之间的函数 关系式和相应的自变量 t 的取值范围； （3）设 EG 与矩形 ABCD 的对角线 AC 的交点为 H，是否存在这样的 t，使△AOH 是等腰三角形？若存在， 求出对应的 t 的值；若不存在，请说明理由． 5．如图所示，已知 A、B 两点的坐标分别为（28，0）和（0，28）．动点 P 从点 A 开始，在线段 AO 上以 每秒 3 个单位长的速度向原点 O 运动，动直线 EF 从 x 轴开始，以每秒 1 个单位长的速度向上平行移动（即 EF∥x 轴），且分别与 y 轴、线段 AB 交于点 E、F，连接 FP．设动点 P 与动直线 EF 同时出发，运动时间 为 t 秒． （1）当 t＝1 秒时，求梯形 OPFE 的面积．当 t 为何值时，梯形 OPFE 的面积最大，最大面积是多少？ （2）当梯形 OPFE 的面积等于三角形 APF 的面积时，求线段 PF 的长； （3）设 t 的值分别取 t1、t2 时（t1≠t2），所对应的三角形分别为△AF1P1 和△AF2P2，判断这两个三角形是 否相似，请证明你的结论． A B D CF E 图 1 M O t(秒)42.5 y N P 图 2 4 7 A B CD O F PE A B E O y P x F A B P D E C F G Q K 6．如图，在 Rt△ABC 中，∠C＝90°，AB＝50，AC＝30，D、E、F 分别是 AC、AB、BC 的中点，点 P 从 点 D 出发，沿折线 DE－EF－FC－CD 以每秒 7 个单位长的速度匀速运动；点 Q 从点 B 出发，沿 BA 方向 以每秒 4 个单位长的速度匀速运动．过点 Q 作射线 QK⊥AB，交折线 BC－CA 于点 G．点 P、Q 同时出发， 当点 P 绕行一周回到点 D 时停止运动，点 Q 也随之停止．设点 P、Q 运动的时间为 t 秒（t＞0）． （1）射线 QK 能否将四边形 CDEF 分成面积相等的两部分？若能， 求出 t 的值．若不能，说明理由； （2）当 t 为何值时，点 P 恰好落在射线 QK 上？ （3）连接 PG，当 PG∥AB 时，请直接写出 t 的值． 7．如图，在平面直角坐标系中．四边形 OABC 是平行四边形．直线 l 经过 O、C 两点．点 A 的坐标为（8， 0），点 B 的坐标为（11，4），动点 P 在线段 OA 上从点 O 出发以每秒 1 个单位的速度向点 A 运动，同时动 点 Q 从点 A 出发以每秒 2 个单位的速度沿 A→B→C 的方向向点 C 运动，过点 P 作 PM 垂直于 x 轴，与折 线 O－C－B 相交于点 M．当 P、Q 两点中有一点到达终点时，另一点也随之停止运动，设点 P、Q 运动的 时间为 t 秒（t＞0），△MPQ 的面积为 S． （1）点 C 的坐标为_____________，直线 l 的解析式为_____________； （2）试求点 Q 与点 M 相遇前 S 与 t 的函数关系式，并写出相应的 t 的取值范围； （3）试求题（2）中当 t 为何值时，S 的值最大，并求出 S 的最大值； （4）随着 P、Q 两点的运动，当点 M 在线段 CB 上运动时，设 PM 的延长线与直线 l 相交于点 N．试探究： 当 t 为何值时，△QMN 为等腰三角形？请直接写出 t 的值． 8．如图，在△ABC 中，∠B＝90°，AB＝6 米，BC＝8 米，动点 P 以 2 米/秒的速度从 A 点出发，沿 AC 向 点 C 移动，同时，动点 Q 以 1 米/秒的速度从 C 点出发，沿 CB 向点 B 移动．当其中有一点到达终点时， 它们都停止移动，设移动的时间为 t 秒． （1）①当 t＝2.5 秒时，求△CPQ 的面积； ②求△CPQ 的面积 S（平方米）关于时间 t（秒）的函数解析式； （2）在 P、Q 移动的过程中，当△CPQ 为等腰三角形时，直接写出 t 的值； （3）以 P 为圆心，PA 为半径的圆与以 Q 为圆心，QC 为半径的圆相切时，求出 t 的值． 9．如图，在 Rt△ABC 中，∠B＝90°，BC＝5 3，∠C＝30°．点 D 从点 C 出发沿 CA 方向以每秒 2 个单位 A B P x C O QM y l A B P CQ 长的速度向点 A 匀速运动，同时点 E 从点 A 出发沿 AB 方向以每秒 1 个单位长的速度向点 B 匀速运动，当 其中一个点到达终点时，另一个点也随之停止运动．设点 D、E 运动的时间是 t 秒（t＞0）．过点 D 作 DF⊥ BC 于点 F，连接 DE、EF． （1）求证：AE＝DF； （2）四边形 AEFD 能够成为菱形吗？如果能，求出相应的 t 值；如果不能，说明理由； （3）当 t 为何值时，△DEF 为直角三角形？请说明理由． 10．如图，梯形 ABCD 中，AD∥BC，∠BAD＝90°，CE⊥AD 于点 E，AD＝8cm，BC＝4cm，AB＝5cm．从 初始时刻开始，动点 P、Q 分别从点 A、B 同时出发，运动速度均为 1cm/s，动点 P 沿 A→B→C→E 的方 向运动，到点 E 停止；动点 Q 沿 B→C→E→D 的方向运动，到点 D 停止，设运动时间为 x s，△PAQ 的面 积为 y cm2．（这里规定：线段是面积为 0 的三角形）解答下列问题： （1）当 x＝2s 时，y＝_________cm2；当 x＝ 9 2 s 时，y＝_________cm2； （2）当 5≤x ≤14 时，求 y 与 x 之间的函数关系式； （3）当动点 P 在线段 BC 上运动时，求出使 y＝ 4 15 S 梯形 ABCD 的 x 的值； （4）直接写出在整个运动过程中，使 PQ 与四边形 ABCE 的对角线平行的所有 x 的值． 11．如图，∠C＝90°，点 A、B 在∠C 的两边上，CA＝30，CB＝20，连结 AB．点 P 从点 B 出发，以每秒 4 个单位长度的速度沿 BC 方向运动，到点 C 停止．当点 P 与 B、C 两点不重合时，作 PD⊥BC 交 AB 于 D，作 DE⊥AC 于 E．F 为射线 CB 上一点，且∠CEF＝∠ABC．设点 P 的运动时间为 x（秒）． （1）用含有 x 的代数式表示 CE 的长； （2）求点 F 与点 B 重合时 x 的值； （3）当点 F 在线段 CB 上时，设四边形 DECP 与四边形 DEFB 重叠部分图形的面积为 y（平方单位），求 y 与 x 之间的函数关系式； （4）当 x 为某个值时，沿 PD 将以 D、E、F、B 为顶点的四边形剪开，得 到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形，请 直接写出所有符合上述条件的 x 值． A B D CF E C DA B E P Q C DA B E 备用图 C D A B E F P 12．如图，矩形 OABC 的两边分别在 x 轴和 y 轴上 OA＝10cm，OC＝6cm．动点 P、Q 分别从 O、A 同时 出发，点 P 在线段 OA 上沿 OA 方向作匀速运动；点 Q 在线段 AB 上沿 AB 方向作匀速运动，已知点 P 的运 动速度为 1cm/s． （1）设点 Q 的运动速度为 1 2 cm/s，运动时间为 t 秒． ①当△CPQ 的面积最小时，求点 Q 的坐标； ②当△COP 与△PAQ 相似时，求点 Q 的坐标． （2）设点 Q 的运动速度为 a cm/s，是否存在 a 的值，使得△OCP 与△PAQ 和△CBQ 都相似？若存在，求 出 a 的值，并写出此时点 Q 的坐标；若不存在，请说明理由． 13．如图，梯形 ABCD 中，AD∥BC，BC＝20cm，AD＝10cm，现有两个动点 P、Q 分别从 B、D 两点同 时出发，点 P 以每秒 2cm 的速度沿 BC 向终点 C 移动，点 Q 以每秒 1cm 的速度沿 DA 向终点 A 移动，线 段 PQ 与 BD 相交于点 E，过 E 作 EF∥BC 交 CD 于点 F，射线 QF 交 BC 的延长线于点 H，设动点 P、Q 移动的时间为 t（单位：秒，0＜t＜10）． （1）当 t 为何值时，四边形 PCDQ 为平行四边形？ （2）在 P、Q 移动的过程中，线段 PH 的长是否发生改变？如果不变，求出线段 PH 的长；如果改变，请 说明理由． 14．如图所示，Rt△ABC 是一张放在平面 直角坐标系中的纸片，点 C 与原点 O 重合，点 A 在 x 轴的正半 轴上，点 B 在 y 轴的正半轴上，已知 OA＝3，OB＝4．将纸片的直角部分翻折，使点 C 落在 AB 边上，记 为 D 点，AE 为折痕，E 在 y 轴上． （1）求点 E 的坐标及 AE 的长； （2）线段 AD 上有一动点 P（不与 A、D 重合）自 A 点沿 AD 方向以每秒 1 个单位长度向 D 点作匀速运动， 设运动时间为 t 秒（0＜t ＜3），过 P 点作 PM∥DE 交 AE 于 M 点，过点 M 作 MN∥AD 交 DE 于 N 点，求 四边形 PMND 的面积 S 与时间 t 之间的函数关系式，当 t 取何值时，S 有最大值？最大值是多少？ （3）当 t（0＜t ＜3）为何值 时，A、D、M 三点构成等腰三角形？并求出点 M 的坐标． C y Q B AO P x C Q B A E P H F D A x y P 1O D E 2 1 2 3 M N B (C) B COA x y 15．如图所示，正方形 OABC 的边长为 2cm，点 A、C 分别在 y 轴的负半轴和 x 轴的正半轴上，抛物线 y＝ ax 2＋bx＋c 经过点 A、B 和 D（4，－ 2 3）． （1）求抛物线的表达式； （2）如果点 P 由点 A 出发，沿 AB 边以 2cm/s 的速度向点 B 运动，同时点 Q 由点 B 出发，沿 BC 边以 1cm/s 的速度向点 C 运动，当其中一点到达终点时，另一点也随之停止运动．设 S＝PQ 2（cm2）． ①试求出 S 与运动时间 t 之间的函数关系式，并写出 t 的取值范围； ②当 S 取 5 4 时，在抛物线上是否存在点 R，使得以点 P、B、Q、R 为顶点的四边形是平行四边形？如果存 在，求出 R 点的坐标；如果不存在，请说明理由； （3）在抛物线的对称轴上求点 M，使得 M 到 D、A 的距离之差最大，求出点 M 的坐标． 16．在梯形 OABC 中，CB∥OA，∠AOC＝60°，∠OAB＝90°，OC＝2，BC＝4，以 O 点为原点，OA 所在 的直线为 x 轴，建立平面直角坐标系，另有一边长为 2 的等边△DEF，DE 在 x 轴上（如图 1），如果让△DEF 以每秒 1 个单位的速度向左作匀速直线运动，开始时点 D 与点 A 重合，当点 D 到达坐标原点时运动停 止． （1）设△DEF 运动时间为 t，△DEF 与梯形 OABC 重叠部分的面积为 S，求 S 关于 t 的函数关系式； （2）探究：在△DEF 运动过程中，如果射线 DF 交经过 O、C、B 三点的抛物线于点 G，是否存在这样的 时刻 t，使得△OAG 的面积与梯形 OABC 的面积相等？若存在，求出 t 的值；若不存在，请说明理由． 17．已知直线 y＝ 3x＋4 3 与 x 轴、y 轴分别交于 A、B 两点，∠ABC＝60°，BC 与 x 轴交于点 C． （1）试确定直线 BC 的解析式； （2）若动点 P 从 A 点出发沿 AC 向点 C 运动（不与 A、C 重合）， 同时动点 Q 从 C 点出发沿 CBA 向点 A 运动（不与 C、A 重合），动点 P 的运动速度是每秒 1 个单位长度，动点 Q 的运动速度是每秒 2 个 单位长度．设△APQ 的面积为 S，P 点的运动时间为 t 秒，求 S 与 t 的 函数关系式，并写出自变量的取值范围； （3）在（2）的条件下，当△APQ 的面积最大时，y 轴上有一点 M， 平面内是否存在一点 N，使以 A、Q、M、N 为顶点的四边形为菱形？ 若存在，请直接写出 N 点的坐标；若不存在，请说明理由． 18．已知：如图，在△ABC 中，AB＝AC＝10cm，BD⊥AC 于 D，且 O A B x y C Q D P BC E F O A(D) x y 图 1 BC E F O A x y 图 2 D BD＝8cm．点 M 从点 A 出发，沿 AC 的方向匀速运动，速度为 2cm/s；同时直线 PQ 由点 B 出发沿 BA 方 向匀速运动，速度为 1cm/s，运动过程中始终保持 PQ∥AC，直线 PQ 交 AB 于 P，交 BC 于 Q，交 BD 于 F，连接 PM，设运动时间为 t（s）（0＜t＜5）．解答下列问题： （1）当 t 为何值时，四边形 PQCM 是平行四边形？ （2）设四边形 PQCM 的面积为 y（cm2），求 y 与 t 之间的函数关系式； （3）是否存在某一时刻 t，使 S 四边形 PQCM ＝ 9 16 S△ABC？若存在，求出 t 的值；若不存在，说明理由； （4）连接 PC，是否存在某一时刻 t，使点 M 在线段 PC 的垂直平分线上？若存在，求出此时 t 的值；若 不存在，说明理由． 19．如图，在直角坐标系中，梯形 ABCD 的底边 AB 在 x 轴上，底边 CD 的端点 D 在 y 轴上，直线 CB 的 表达式为 y＝－ 4 3 x＋ 16 3 ，点 A，D 的坐标分别为（－4，0），（0，4）．动点 P 自 A 点出发，在 AB 上匀速运 行，动点 Q 自点 B 出发，在折线 BCD 上匀速运行，速度均为每秒 1 个单位，当其中一个动点到达终点时， 它们同时停止运动．设点 P 运动 t（秒）时，△OPQ 的面积为 S（不能构成△OPQ 的动点除外）． （1）求出点 B，C 的坐标； （2）求 S 随 t 变化的函数关系式（注明 t 的取值范围）； （3）当 t 为何值时 S 有最大值？并求出最大值． 20．如图，在矩形 ABCD 中，AB＝12cm，BC＝8cm，点 E、F、G 分别从 A、B、C 三点同时出发，沿矩形 的边按逆时针方向移动，点 E、G 的速度为 2cm/s，点 F 的速度为 4cm/s，当点 F 追上点 G（即点 F 与点 G 重合）时，三个点随之停止移动．设移动开始后第 t 秒时，△EFG 的面积为 S（cm2）． （1）当 t＝1 秒时，S 的值是多少？ （2）写出 S 和 t 之间的函数解析式，并指出自变量 t 的取值范围； （3）若点 F 在矩形的边 BC 上移动，当 t 为何值时，以点 E、B、F 为 顶点的三角形与以点 F、C、G 为顶点的三角形相似？请说明理由． 21．如图，已知 O（0，0）、A（4，0）、B（4，3）．动点 P 从 O 点出发， A B C D M P F Q B C OA x y D P Q B C OA x y D （备用图 1） B C OA x y D （备用图 2） A D B C E F G 以每秒 3 个单位的速度，沿△OAB 的边 OA、AB、BO 作匀速运动；动直线 l 从 AB 位置出发，以每秒 1 个 单位的速度向 x 轴负方向作匀速平移运动．若它们同时出发，运动的时间为 t 秒，当点 P 运动到 O 时， 它们都停止运动． （1）当 P 在线段 OA 上运动时，求直线 l 与以 P 为圆心、1 为半径的圆相交时 t 的取值范围； （2）当 P 在线段 AB 上运动时，设直线 l 分别与 OA、OB 交于 C、D．试问：四边形 CPBD 是否可能为菱 形？若能，求出此时 t 的值；若不能，请说明理由，并说明如何改变直线 l 的出发时间，使得四边形 CPBD 会是菱形． 22．在平面直角坐标系 xOy 中，一次函数 y＝ 3 4 x＋3 的图象是直线 l1，l1 与 x 轴、y 轴分别相交于 A、B 两 点，直线 l2 过点 C（a，0）（a＞0）且与 l1 垂直．点 P、Q 同时从 A 点出发，其中点 P 沿射线 AB 运动，速 度为每秒 4 个单位；点 Q 沿射线 AO 运动，速度为每秒 5 个单位． （1）写出 A 点的坐标和 AB 的长； （2）当点 P、Q 运动了 t 秒时，以点 Q 为圆心，PQ 为半径的⊙Q 与直线 l 2、y 轴都相切，求此时 a 的 值． 23．在△ABC 中，∠BAC＝90°，AB＜AC，M 是 BC 边的中点，MN⊥BC 交 AC 于点 N．动点 P 从点 B 出 发沿射线 BA 以每秒 3 厘米的速度运动．同时，动点 Q 从点 N 出发沿射线 NC 运动，且始终保持 MQ⊥ MP．设运动时间为 t 秒（t＞0）． （1）△PBM 与△QNM 相似吗？以图 1 为例说明理由； （2）若∠ABC＝60°，AB＝4 3厘米． ①求动点 Q 的运动速度； ②设△APQ 的面积为 S（平方厘米），求 S 与 t 的函数关系式； （3）探求 BP 2、PQ 2、CQ 2 三者之间的数量关系，以图 1 为例说明理由． B O A x y A Q l1 O x y B P 1 1 A B M C P Q 图 1 N A B M C 图 2（备用图） N 24．在平面直角坐标系 xOy 中，边长为 a（a 为大于 0 的常数）的正方形 ABCD 的对角线 AC、BD 相交于 点 P，顶点 A 在 x 轴正半轴上运动，顶点 B 在 y 轴正半轴上运动（x 轴的正半轴、y 轴的正半轴都不包含 原点 O），顶点 C、D 都在第一象限． （1）当∠BAO＝45°时，求点 P 的坐标； （2）求证：无论点 A 在 x 轴正半轴上、点 B 在 y 轴正半轴上怎样运动，点 P 都在∠AOB 的平分线上； （3）设点 P 到 x 轴的距离为 h，试确定 h 的取值范围，并说明理由． 25．如图，已知一次函数 y＝－x＋7 与正比例函数 y＝ 4 3 x 的图象交于点 A，且与 x 轴交于点 B． （1）求点 A 和点 B 的坐标； （2）过点 A 作 AC⊥y 轴于点 C，过点 B 作直线 l∥y 轴．动点 P 从点 O 出发，以每秒 1 个单位长的速度， 沿 O－C－A 的路线向点 A 运动；同时直线 l 从点 B 出发，以相同速度向左平移，在平移过程中，直线 l 交 x 轴于点 R，交线段 BA 或线段 AO 于点 Q．当点 P 到达点 A 时，点 P 和直线 l 都停止运动．在运动 过程中，设动点 P 运动的时间为 t 秒． ①当 t 为何值时，以 A、P、R 为顶点的三角形的面积为 8？ ②是否存在以 A、P、Q 为顶点的三角形是等腰三角形？若存在，求 t 的值；若不存在，请说明理由． 26．如图，在 Rt△ABC 中，∠C＝90°，AC＝8，BC＝6，点 P 在 AB 上，AP＝2．点 E、F 同时从点 P 出发， 分别沿 PA、PB 以每秒 1 个单位长度的速度向点 A、B 匀速运动，点 E 到达点 A 后立刻以原速度沿 AB 向 点 B 运动，点 F 运动到点 B 时停止，点 E 也随之停止．在点 E、F 运动过程中，以 EF 为边作正方形 EFGH，使它与△ABC 在线段 AB 的同侧．设 E、F 运动的时间为 t 秒（t＞0），正方形 EFGH 与△ABC 重 叠部分面积为 S． （1）当 t＝1 时，正方形 EFGH 的边长是_________， 当 t＝3 时，正方形 EFGH 的边长是_________； AO x y B P C D A B O x y y＝－x＋7 y＝ 4 3 x （备用图） A B O x y y＝－x＋7 y＝ 4 3 x （2）当 0＜t≤2 时，求 S 与 t 的函数关系式； （3）直接答出：在整个运动过程中，当 t 为何值时，S 最大？最大面积是多少？ 27．如图，在平面直角坐标系中，等腰梯形 OABC 的底角为 60°，下底 OA 在 x 轴的正半轴上，O 为坐标 原点，点 A 的坐标为（m，0），对角线 AC 平分∠OAB，动点 P 在 AC 上以每秒一个单位长度的速度由点 A 向点 C 运动（点 P 不与 A、C 重合）．过 P 作 AC 的垂线，交 OA 于点 D，交折线 A－B－C 于点 E． （1）线段 OC 的长为_________；（用含 m 的代数式表示） （2）当直线 DE 经过点 B 时，它的解析式为 y＝ 3x－2 3，求 m 的值； （3）在（2）的条件下，设动点 P 运动了 t 秒时，△ODE 的面积为 S，求 S 关于 t 的函数关系式；当 t 为 何值时，S 取得最大值，最大值是多少？ 28．如图，在平面直角坐标系中，直线 l：y＝2x＋b 与 x 轴交于点 A（－4，0），与 y 轴交于点 B．点 P 是 y 轴上的一个动点，以 P 为圆心，3 为半径作⊙P． （1）若 PA＝PB，试判断⊙P 与直线 l 的位置关系，并说明理由； （2）当⊙P 与直线 l 相切时，求点 P 与原点 O 间的距离； （3）如果以⊙P 与直线 l 的两个交点和圆心 P 为顶点的三角形是等边三角形，求点 P 的坐标． 29．如图 1，在平面直角坐标系中，直线 y＝ 1 2 x＋ 5 与 x 轴、y 轴分别交于 A、B 两点，将△AOB 绕原点 O 顺时针旋转得到△A′OB′，并使 OA′⊥AB，垂足为 D，直线 AB 与线段 A′B′ 相交于点 G．动点 E 从原点 O 出发，以 1 个单位/秒的速度沿 x 轴正方向运动，设动点 E 运动的时间为 t 秒． （1）求点 D 的坐标； A E P F B GH C ADO x y B E C P x B P A O l y x B A O l y （备用图） （2）连接 DE，当 DE 与线段 OB′ 相交，交点为 F，且四边形 DFB′G 是平行四边形时（如图 2），求此时 线段 DE 所在直线的解析式； （3）若以动点为 E 圆心，以 2 5 为半径作⊙E，连接 A′E，当 t 为何值时，tan∠EA′B′＝ 1 8 ？并判断此时直 线 A′O 与⊙E 的位置关系，请说明理由． 30．如图，在四边形 ABCD 中，∠BAC＝∠ACD＝90º，∠B＝∠D． （1）求证：四边形 ABCD 是平行四边形； （2）若 AB＝3 厘米，BC＝5 厘米，AE＝ 1 3 AB，点 P 从 B 点出发，以 1 厘米/秒的速度沿 BC→CD→DA 运 动至 A 点停止．从运动开始，经过多少时间，以点 E、B、P 为顶点的三角形成为等腰三角形？ 31．如图，直线 y＝x－6 与 x 轴、y 轴分别交于点 A、B，点 E 从 B 点出发，以每秒 1 个单位的速度沿线段 BO 向 O 点移动（与点 B、O 不重合），过 E 作 EF∥AB，交 x 轴于 F 点．将四边形 ABEF 沿 EF 折叠，得 到四边形 DCEF，设点 E 的运动时间为 t 秒． （1）①直线 y＝x－6 与坐标轴交点坐标是 A（____，____），B（____，____）； ②画出 t＝2 时，四边形 ABEF 沿 EF 折叠后的图形（不写画法）； （2）若 CD 交 y 轴于 H 点，求证：四边形 DHEF 为平行四边形；并求 t 为何值时，四边形 DHEF 为菱形； （3）设四边形 DCEF 落在第一象限内的图形面积为 S，求 S 关于 t 的函数表达式，并求出 S 的最大值． 图 1 x B G A O y D A′ B′ 图 2 x B G A O y D A′ B′F E 备用图 x B G A O y D A′ B′ A CB D E A O E B F x y 1 -1 -2 -3 -4 -5 -6 -1-2-3 2 3 4 1 2 3 4 5 6 7 32．如图，在平面直角坐标系中，△ABC 是直角三角形，∠ACB＝90°，点 A（－15，0），AB＝25，AC＝ 15，点 C 在第二象限，点 P 是 y 轴上的一个动点，连接 AP，将△AOP 绕点 A 逆时针方向旋转，使边 AO 与 AC 重合，得到△ACD． （1）求直线 AC 的解析式； （2）当点 P 运动到点（0，5）时，求此时点 D 的坐标及 DP 的长； （3）是否存在点 P，使△OPD 的面积等于 5，若存在，请求出符合条件的点 P 的坐标；若不存在，请说 明理由． 33．已知直线 y＝ 3x－6 3与 x 轴、y 轴分别相交于 A、B 两点，点 C 在射线 BA 上以每秒 3 个单位的速度 运动，以 C 点为圆心，半径为 1 作⊙C．点 P 以每秒 2 个单位的速度在线段 OA 上来回运动，过点 P 作直 线 l⊥x 轴． （1）填空：A 点坐标为（____，____），B 点坐标为（____，____）； （2）若点 C 与点 P 同时从点 B、点 O 开始运动，求直线 l 与⊙C 第二次相切时点 P 的坐标； （3）在整个运动过程中，直线 l 与⊙C 有交点的时间共有多少秒？ 34．已知二次函数 y＝ax 2＋bx－2 的图象与 x 轴交于 A、B 两点，与 y 轴交于点 C，点 A 的坐标为（4，0）， 且当 x＝－2 和 x＝5 时二次函数的函数值 y 相等． （1）求实数 a、b 的值； （2）如图 1，动点 E、F 同时从 A 点出发，其中点 E 以每秒 2 个单位长度的速度沿 AB 边向终点 B 运动， 点 F 以每秒 5 个单位长度的速度沿射线 AC 方向运动．当点 E 停止运动时，点 F 随之停止运动．设运动 时间为 t 秒．连接 EF，将△AEF 沿 EF 翻折，使点 A 落在点 D 处，得到△DEF． ①当 t 为何值时，线段 DF 平分△ABC 的面积？ ②是否存在某一时刻 t，使得△DCF 为直角三角形？若存在，求出 t 的值；若不存在，请说明理由． ③设△DEF 与△ABC 重叠部分的面积为 S，求 S 关于 t 的函数关系式； （3）如图 2，点 P 在二次函数图象上运动，点 Q 在二次函数图象的对称轴上运动，四边形 PQBC 能否成 为以 PQ 为底的等腰梯形？如果能，直接写出 P、Q 两点的坐标；如果不能，请说明理由． A B P C D O x y A B C O x y （备用图） A B C O x y （备用图） C O P A B x ly 35．如图，等边三角形 ABC 的边长为 4cm，AD⊥BC 于 D．点 E、F 分别从 B、C 两点同时出发，其中点 E 以 1cm/s 的速度沿 BC 向终点 C 运动；点 F 以 2cm/s 的速度沿 CA、AB 向终点 B 运动，设运动时间为 t （s）． （1）当 t 为何值时，EF⊥AC？当 t 为何值时，EF⊥AB？ （2）设△DEF 的面积为 S（cm2），求 S 与 t 之间的函数关系式； （3）探索以 EF 为直径的圆与 AC 的位置关系，并写出相应位置关系的 t 的取值范围． 36．如图，梯形 OABC 的顶点 C 在 x 轴的正半轴上，A、B 两点在第一象限，且 AB∥OC，AO＝BC＝2，AB ＝3，OC＝5．动点 P 从点（－2，0）出发，以每秒 1 个单位长度的速度沿 x 轴的正方向运动，过点 P 作 直线 l，使 l 与 x 轴正方向的夹角为 30°．设点 P 运动了 t 秒，直线 l 扫过梯形 OABC 的面积为 S． （1）求 A、B 两点的坐标； （2）当 t＝2 秒时，求 S 的值； （3）求 S 与 t 的函数关系式，并求直线 l 扫过梯形 OABC 面积的 3 4 时点 P 的坐标． y O xAB C E F 图 1 D y O xAB C 图 2 E D A B C F y O xC A l B P 30° y O xC A B 备用图 y O xC A B 备用图 y O xC A B 备用图 37．在平面直角坐标系中，Rt△AOB 的直角顶点 O 在坐标原点，直角边 OA、OB 分别在 x 轴正半轴和 y 轴正半轴上，且 OA＝4，OB＝3．动点 P、Q 分别从 O、A 同时出发，其中点 P 以每秒 1 个单位长度的速 度沿 OA 方向向 A 点匀速运动，到达 A 点后立即以原速沿 AO 返回；点 Q 以每秒 1 个单位长度的速度沿 AB 向 B 点匀速运动．当 Q 到达 B 时，P、Q 两点同时停止运动．设运动时间为 t（秒）． （1）求△APQ 的面积 S 与 t 之间的函数关系式； （2）如图 1，在某一时刻将△APQ 沿 PQ 翻折，使点 A 恰好落在 AB 边的点 C 处，求此时△APQ 的面积； （3）在点 P 从 O 向 A 运动的过程中，在 y 轴上是否存在点 D，使四边形 PQBD 为等腰梯形？若存在，求 点 D 的坐标；若不存在，请说明理由； （4）如图 2，在 P、Q 两点运动过程中，线段 PQ 的垂直平分线 EF 交 PQ 于点 E，交折线 QB－BO－OP 于点 F．问：是否存在某一时刻 t，使 EF 恰好经过原点 O，若存在，求相应的 t 值；若不存在，请说明理 由． 38．如图，直线 y＝ 3 4 x－3 与 x 轴、y 轴分别交于点 A、B，圆心在坐标原点、半径为 1 的动圆以每秒 0.4 个单位的速度向 x 轴正方向运动，动点 P 从 B 点同时出发，以每秒 0.5 个单位的速度沿 BA 方向运动．设 运动时间为 t（秒）． （1）直接写出 A、B 两点的坐标； （2）当 t 为何值时，动圆与直线 AB 相切？ （3）问在整个运动过程中，点 P 在动圆的圆面（圆上和圆的内部）上一共运动了多长时间？ y O x Q AP B C 图 1 y O xA B 备用图 y O x Q AP B 图 2 F E y O xA B 备用图 y O xA B 备用图 y O xA B 备用图 y O xA B 39．已知直线 l：y＝ 3 4 x＋8 与 x 轴、y 轴分别交于点 A、B，P 是 x 轴上一点，以 P 为圆心的⊙P 与直线 l 相切于 B 点． （1）求点 P 的坐标和⊙P 的半径； （2）若⊙P 以每秒 10 3 个单位向 x 轴负方向运动，同时⊙P 的半径以每秒 3 2 个单位变小，设⊙P 的运动时 间为 t 秒，且⊙P 始终与直线 l 有公共点，试求 t 的取值范围； （3）在（2）中，设⊙P 被直线 l 截得的弦长为 a，问是否存在 t 的值，使 a 最大？若存在，求出 t 的值； 若不存在，请说明理由； （4）在（2）中，设⊙P 与直线 l 的一个公共点为 Q，若以 A、P、Q 为顶点的三角形与△ABO 相似，请直 接写出此时 t 的值． 40．如图，直线 y＝－ 4 3 x＋4 与 x 轴交于点 B，与 y 轴交于点 C，二次函数的图象经过 A（－1，0）、B、C 三点． （1）求二次函数的表达式； （2）设二次函数图象的顶点为 D，求四边形 OCDB 的面积； （3）若动点 E、F 同时从 O 点出发，其中点 E 以每秒 3 2 个单位长度的速度沿折线 OBC 按 O→B→C 的路 线运动，点 F 以每秒 4 个单位长度的速度沿折线 OCB 按 O→C→B 的路线运动，当 E、F 两点相遇时，整 个运动随之结束．设运动时间为 t（秒），△OEF 的面积为 S（平方单位）． ①在 E、F 两点运动过程中，是否存在 EF∥OC？若存在，求出此时 t 的值；若不存在，请说明理由； ②求 S 关于 t 的函数关系式，并求 S 的最大值． 41．已知：在△ABC 中，∠C＝90°，AC＝4，BC＝3，动点 P 从点 A 出发，以每秒 5 4 个单位的速度沿 AB 方向向终点 B 运动；同时，动点 Q 也从点 A 出发，以每秒 1 个单位的速度沿 AC 方向向终点 C 运动．连接 PC、BQ 相交于点 D．设两点运动的时间为 t 秒（0＜t＜4）． y O xA B l P y O x C A B D 备用图 y O x C A B D （1）记△PQD 的面积为 S，求 S 关于 t 的函数关系式； （2）当 t 为何值时，PC⊥BQ？ （3）把△PQB 沿直线 PQ 折叠成△PQB′，设 B′Q 与 AB 交于点 E．是否存在 t 的值，使△BEQ 是直角三角 形，若存在，求 t 的值；若不存在，请说明理由． 42．如图，梯形 ABCD 中，AD∥BC，AD＝AB＝CD＝2cm，BC＝4cm，点 P、Q 分别从 A、C 两点出发， 点 P 沿射线 AB、点 Q 沿 BC 的延长线均以 1cm/s 的速度作匀速运动． （1）求∠B 的度数； （2）若 P、Q 同时出发，当 AP 的长为何值时，△PCQ 的面积是梯形 ABCD 面积的一半？ （3）设 PQ 交直线 CD 于点 E，作 PF⊥CD 于 F，若 Q 点比 P 点先出发 2 秒，请问 EF 的长是否改变？证 明你的结论． 43．已知抛物线 y＝ax 2＋bx＋c 经过 O（0，0），A（4，0），B（3， 3）三点，连接 AB，过点 B 作 BC∥ 轴交抛物线于点 C．动点 E、F 分别从 O、A 两点同时出发，其中点 E 沿线段 OA 以每秒 1 个单位长度的 速度向 A 点运动，点 F 沿折线 A→B→C 以每秒 1 个单位长度的速度向 C 点运动．设动点运动的时间为 t （秒）． （1）求抛物线的解析式； （2）记△EFA 的面积为 S，求 S 关于 t 的函数关系式，并求 S 的最大值，指出此时△EFA 的形状； （3）是否存在这样的 t 值，使△EFA 是直角三角形？若存在，求出此时 E、F 两点的坐标；若不存在，请 说明理由． 44．如图，在平行四边形 ABCD 中，AB 在 x 轴上，D 点 y 轴上，∠C＝60°，BC＝6，B 点坐标为（4， 0）．点 M 是边 AD 上一点，且 DM : AD＝1 : 3．点 E、F 分别从 A、C 同时出发，以 1 个单位/秒的速度分 别沿 AB、CB 向点 B 运动，当点 F 运动到点 B 时，点 E 随之停止运动，EM、CD 的延长线交于点 P，FP x y O x C A B E F C A B 备用图 C A B D P Q A D CB E Q P 交 AD 于点 Q．⊙E 的半径为 5 2，设运动时间为 t 秒． （1）求直线 BC 的解析式； （2）当 t 为何值时，PF⊥AD？ （3）在（2）的条件下，⊙E 与直线 PF 是否相切？如果相切，加以证明，并求出切点的坐标；如果不相 切，说明理由． 45．如图，在等腰梯形 OABC 中，BC∥OA，AB＝BC．将梯形 ABCD 沿 AC 折叠，使点 B 恰好落在 x 轴上 点 D 处，过 C、D 两点的直线与 y 轴交于点 E． （1）试判断四边形 ABCD 是怎样的特殊四边形，并说明你的理由； （2）若∠OAB＝60°，AB＝2，在 y 轴上是否存在一点 P，使以 P、D、E 为顶点的三角形构成等腰三角形， 若存在，请求出所有可能的 P 点坐标，若不存在，请说明理由； （3）在（2）的条件下，将△ODE 沿 x 轴正方向以每秒 1 个单位的速度平移，得到△O′DE，当点 O′ 与点 A 重合时停止平移．设△O′DE 在平移过程中与△OAC 重合部分的面积为 S，平移时间为 t 秒，求 S 与 t 之 间的函数关系式，并求出何时 S 有最大值，最大值是多少？ 46．如图，抛物线 y＝ax 2＋bx＋4 与 x 轴交于 A（－2，0）、B（4，0）两点，与 y 轴交于 C 点． （1）求抛物线的解析式； （2）T 是抛物线对称轴上的一点，且△ATC 是以 AC 为底的等腰三角形，求点 T 的坐标； （3）M、Q 两点分别从 A、B 点以每秒 1 个单位长度的速度沿 x 轴同时出发相向而行，当点 M 到达原点时， 点 Q 立刻掉头并以每秒 3 2 个单位长度的速度向点 B 方向移动，当点 M 到达抛物线的对称轴时，两点停止 运动．过点 M 的直线 l⊥x 轴交 AC 或 BC 于点 P．求点 M 的运动时间 t 与△APQ 面积 S 的函数关系式，并 求出 S 的最大值． y O x C A BE F DP M Q y O x C AD E 备用图 y O x C A B D E y O x C A B l M T P Q 47．如图，在直角梯形 ABCD 中，AD∥BC，∠B＝90°，AD＝6cm，AB＝8cm，BC＝14cm．动点 P、Q 都从 点 C 出发，点 P 沿 C→B 方向做匀速运动，点 Q 沿 C→D→A 方向做匀速运动，当 P、Q 其中一点到达终 点时，另一点也随之停止运动． （1）求 CD 的长； （2）若点 P 以 1cm/s 速度运动，点 Q 以 2 2cm/s 的速度运动，连接 BQ、PQ，设△BQP 面积为 S（cm2）， 点 P、Q 运动的时间为 t（s），求 S 与 t 的函数关系式，并写出 t 的取 值范围； （3）若点 P 的速度仍是 1cm/s，点 Q 的速度为 a cm/s，要使在运动过程中出现 PQ∥DC，请你直接写出 a 的取值范围． 48．如图，对称轴为直线 x＝－1 的抛物线经过点 A（－3，0）和点 C（0，3），与 x 轴的另一交点为 B．点 P、Q 同时从 B 点出发，均以每秒 1 个单位长度的速度分别沿 BA、BC 边运动，其中一个点到达终点时， 另一点也随之停止运动．设运动时间为 t（秒）． （1）求抛物线的解析式； （2）连接 PQ，将△BPQ 沿 PQ 翻折，所得的△B′PQ 与△ABC 重叠部分的面积记为 S，求 S 与 t 之间的函 数关系式，并求 S 的最大值； （3）若点 D 的坐标为（－4，3），当点 B′ 恰好落在抛物线上时，在抛物线的对称轴时是否存在点 M，使 四边形 MADB′ 的周长最小，若存在，求出这个最小值；若不存在，请说明理由． 49．如图，直线 l 与 x 轴、y 轴分别交于点 A（8，0）、点 B（0，6），点 P 以每秒 3 个单位长度的速度沿 BO 由 B 向 O 运动，点 Q 以每秒 5 个单位长度的速度沿 AB 由 A 向 B 运动．已知 P、Q 两点同时出发，且当一 点到达终点时，另一点也随之停止运动，设运动时间为 t 秒． y O x C Q B D PA B′ x＝－1 D C A B P Q （1）当四边形 PQAO 为梯形时，求 t 的值； （2）当△POQ 为等腰三角形时，求 t 的值； （3）在整个运动过程中，以 PQ 为直径的圆能否与 x 轴相切？若能，请求出运动时间 t；若不能，请说明 理由； （4）在整个运动过程中，若以点 P 为圆心、PB 为直径的圆与以点 Q 为圆心、QA 为直径的圆相切，请直 接写出 t 的值． 50．如图，抛物线 y＝ax 2＋bx＋ 15 2 （a≠0）经过 A（－3，0）、C（5，0）两点，点 B 为抛物线的顶点，抛 物线的对称轴与 x 轴交于点 D． （1）求此抛物线的解析式； （2）动点 P 从点 B 出发，沿线段 BD 向终点 D 作匀速运动，速度为每秒 1 个单位长度，运动时间为 t s， 过点 P 作 PM⊥BD 交 BC 于点 M，过点 M 作 MN∥BD，交抛物线于点 N． ①当 t 为何值时，线段 MN 最长； ②在点 P 运动的过程中，是否有某一时刻，使得以 O、P、M、C 为顶点的四边形为等腰梯形？若存在， 求出此刻的 t 值；若不存在，请说明理由． 51．如图，直线 y＝kx＋b（k≠0）与坐标轴分别交于 A、B 两点，OA＝8，OB＝6．动点 P 从 O 点出发， 沿路线 O→B→A 以每秒 1 个单位长度的速度运动，到达 A 点时运动停止． （1）求直线 AB 的解析式； （2）设点 P 的运动时间为 t（秒），△OPA 的面积为 S，求 S 与 t 之间的函数关系式； （3）当 S＝12 时，在坐标轴上是否存在点 Q，使以 O、A、P、 Q 为顶点的四边形是梯形？若存在，求 P、Q 两点的坐标；若不 存在，请说明理由． 52．如图，在平面直角坐标系中，平行四边形的顶点 A 的坐 y O xl Q B P A y O xA B M N P CD xAO P B y xA O CD y B F E G 标为（－6，0），顶点 C 的坐标为（8，8），边 AB 在 x 轴上，顶点 D 在 y 轴上，点 E 为线段 AD 的中点，点 F 在线段 DC 上，且横坐标为 3，直线 EF 与 y 轴交于点 G．点 P 以每秒 1 个单位长度的速度，从点 A 开始 沿折线 A－B－C－F 运动，当点 P 到达点 F 时停止运动，设点 P 运动时间为 t 秒． （1）求直线 EF 的表达式及点 G 的坐标； （2）记△PEF 的面积为 S，求 S 与 t 之间的函数关系式； （3）是否存在点 P，使得△PFG 为直角三角形，若存在，请直接写出所有符合条件的点 P 的坐标；若不存 在，请说明理由． 53．如图，在平面直角坐标系中，点 A 的坐标为（0，10），点 B 的坐标为（5，0），点 P 从点 A 出发，以 每秒 3 个单位长度的速度沿线段 AO 向点 O 运动，点 Q 从 B 出发，以每秒 1 个单位长度的速度沿线段 BO 向点 O 运动，当其中一个点到达 O 点时，另一点也随即停止运动．设运动时间为 t（秒）．以 P、Q 为圆心 作⊙P 和⊙Q，且⊙P 和⊙Q 的半径分别为 4 和 1． （1）若⊙P 与 Rt△AOB 的一边相切，求点 P 的坐标； （2）若⊙P 与线段 AB 有两个公共点，求 t 的取值范围； （3）在运动的过程中，是否存在⊙P 和⊙Q 相切？若存在， 求出相应的 t 的值；若不存在，说明理由． 54．如图，直线 y＝ m 3 x＋m（m≠0）交 x 轴负半轴于点 A，交 y 轴正半轴于点 B，且 AB＝5，过点 A 作直 线 AC⊥AB 交 y 轴于点 C．点 E 从原点 O 出发，以 0.8 个单位/秒的速度沿 y 轴向上运动；与此同时直线 l 从与直线 AC 重合的位置出发，以 1 个单位/秒的速度沿射线 AB 方向平行移动．直线 l 在平移过程中交射 线 AB 于点 F，交 y 轴于点 G．设点 E 离开原点 O 的时间为 t 秒（t≥0）． （1）求直线 AC 的解析式； （2）直线 l 在平移过程中，请直接写出△BOF 为等腰三角形时点 F 的坐标； （3）直线 l 在平移过程中，设点 E 到直线 l 的距离为 d，求 d 与 t 的函数关系． 55．如图，抛物线 y＝－x 2－2x＋3 与 x 轴相交于点 A、B（A 在 B 的左侧），与 y 轴交于点 C． （1）求线段 AC 所在直线的解析式； x A O y B x B A y O l F E 1 1 G C x B A y O l F E 1 1 G C 备用图 （2）点 M 是第二象限内抛物线上的一点，且 S△MAC ＝ 1 2 S△MAB ，求点 M 的坐标； （3）点 P 以每秒 1 个单位长度的速度，沿线段 BA 由 B 向 A 运动，同时，点 Q 以每秒 2 个单位长度的速 度，从 A 开始沿射线 AC 运动，当 P 到达 A 时，整个运动随即结束．设运动的时间为 t 秒． ①求△APQ 的面积 S 与 t 的函数关系式，并求当 t 为何值时，△APQ 的面积最大，最大面积是多少？ ②在整个运动过程中，以 PQ 为直径的圆能否与直线 BC 相切？若能，请直接写出相应的 t 值；若不能，请 说明理由； ③直接写出线段 PQ 的中点在整个运动过程中所经过路径的长． 55．如图，四边形 OABC 为正方形，点 A 在 x 轴上，点 C 在 y 轴上，点 B（8，8），点 P 在边 OC 上，点 M 在边 AB 上．把四边形 OAMP 沿 PM 对折，PM 为折痕，使点 O 落在 BC 边上的点 Q 处．动点 E 从点 O 出 发，沿 OA 边以每秒 1 个单位长度的速度向终点 A 运动，运动时间为 t，同时动点 F 从点 O 出发，沿 OC 边以相同的速度向终点 C 运动，当点 E 到达点 A 时，E、F 同时停止运动． （1）若点 Q 为线段 BC 边中点，直接写出点 P、点 M 的坐标； （2）在（1）的条件下，设△OEF 与四边形 OAMP 重叠面积为 S，求 S 与 t 的函数关系式； （3）在（1）的条件下，在正方形 OABC 边上是否存在点 H，使△PMH 为等腰三角形，若存在，求点 H 的坐标，若不存在，请说明理由； （4）若点 Q 为线段 BC 上任一点（不与点 B、C 重合），△BNQ 的周长是否发生变化，若不变，求出其值； 若变化，请说明理由． 56．如图，在平面直角坐标系中，直线 AC：y＝ 4 3 x＋8 与 x 轴交于点 A，与 y 轴交于点 C，抛物线 y＝ax 2＋ bx＋c 过点 A、点 C，且与 x 轴的另一交点为 B（x0，0）（x0＞0），点 P 是抛物线的对称轴 l 上一动点． （1）求点 A 的坐标，并在图 1 中的 l 上找一点 P0，使 P0 到点 A 与点 C 的距离之和最小； （2）若△PAC 周长的最小值为 10＋2 41，求抛物线的解析式及顶点 N 的坐标； （3）如图 2，在线段 CO 上有一动点 M 以每秒 2 个单位的速度从点 C 向点 O 移动（M 不与端点 C、O 重 合），过点 M 作 MH∥CB 交 x 轴于点 H．设 M 移动的时间为 t 秒，试把△P0HM 的面积 S 表示成时间 t 的 O A B x y P Q C O A B x y C 备用图 O A B x C y M N D Q P E F 函数，当 t 为何值时，S 有最大值，并求出最大值； （4）在（3）的条件下，当 S＝ 75 32 时，过 M 作 x 轴的平行线交抛物线于 E、F 两点，问：过 E、F、C 三 点的圆与直线 CN 能否相切于点 C？请证明你的结论．（用图 3 解答） 57．如图，在平面直角坐标系中，直线 y＝ 4 3 x＋4 分别交 x 轴，y 轴于 A，B 两点，点 C 为 OB 的中点，点 D 在第二象限，且四边形 AOCD 为矩形． （1）直接写出点 A，B 的坐标，并求直线 AB 与 CD 交点的坐标； （2）动点 P 从点 C 出发，沿线段 CD 以每秒 1 个单位长度的速度向终点 D 运动；同时，动点 M 从点 A 出 发，沿线段 AB 以每秒 5 3 个单位长度的速度向终点 B 运动．过点 P 作 PH⊥OA，垂足为 H，连接 MP， MH．设点 P 的运动时间为 t 秒． ①若△MPH 与矩形 AOCD 重合部分的面积为 1，求 t 的值； ②点 Q 是点 B 关于点 A 的对称点，问 BP＋PH＋HQ 是否有最小值，如果有，求出相应的点 P 的坐标； 如果没有，请说明理由． 58．如图，在直角坐标系中，点 A 在 y 轴正半轴上，点 B 为 x 轴正半轴上一点，点 D 的坐标为（－ 3， 1），△AOD 和△BDC（点 B、D、C 沿顺时针方向排列）都为等边三角形． （1）求证：△BOD≌CAD； （2）若△BDC 的边长为 7，求 AC 的长及点 C 的坐标； （3）设（2）中点 B 的位置为初始位置，点 B 在 x 轴上由初始位置以 1 个单位/秒的速度向左运动，等边 △BCD 的大小也随之变化，在运动过程中△AOC 是否能成为等腰三角形？如果能，请直接写出运动时间 t 的值；如果不能，请说明理由． O A B x C y P l 图 1 y＝ 4 3 x＋8 O A B x C y P l 图 3 y＝ 4 3 x＋8 O A B x C y P l M 图 2 y＝ 4 3 x＋8 OA B x C y PD M H OA B x C y D （备用图 1） OA B x C y D （备用图 2） O x A y B D C O x A y D 备用图 59．如图 1，在平面直角坐标系 xOy 中，直线 MN 分别与 x 轴正半轴、y 轴正半轴交于点 M、N，且 OM＝ 6，∠OMN＝30°，等边△ABC 的顶点 B 与原点 O 重合，BC 边落在 x 轴正半轴上，点 A 恰好落在线段 MN 上．如图 2，将等边△ABC 从图 1 的位置沿 x 轴正方向以每秒 1 个单位长度的速度平移，边 AB、AC 分别 与线段 MN 交于点 E、F．在△ABC 平移的同时，点 P 从△ABC 的顶点 B 出发，以每秒 2 个单位长度的速 度沿折线 B→A→C 运动，当点 P 达到点 C 时，点 P 停止运动，△ABC 也随之停止平移．设△ABC 平移时 间为 t（s），△PEF 的面积为 S． （1）求等边△ABC 的边长； （2）当点 P 在线段 BA 上运动时，求 S 与 t 的函数关系式，并写出自变量 t 的取值范围； （3）点 P 沿折线 B→A→C 运动的过程中，是否在某一时刻，使△PEF 为等腰三角形，若存在，求出此时 t 值；若不存在，请说明理由． 60．如图（1），在平面直角坐标系中，O 是坐标原点，Rt△AOB 的直角顶点 A 在第一象限，斜边 OB 在 x 轴正半轴上，∠AOB＝60°，OB＝2 3，∠AOB 的平分线 OC 交 AB 于 C．动点 P 从点 B 出发沿折线 BC－CO 以每秒 1 个单位长度的速度向点 O 运动，运动时间为 t 秒，同时动点 Q 从点 C 出发沿折线 CO－Oy 以相同 的速度运动，当点 P 到达点 O 时 P、Q 同时停止运动． （1）求 OC、BC 的长； （2）设△CPQ 的面积为 S，求 S 与 t 的函数关系式； （3）当 P 在 OC 上、Q 在 y 轴上运动时，如图（2），设 PQ 与 OA 交于点 M．当 t 为何值时，△OPM 为等 腰三角形？ 61．如图，在平面直角坐标系中，四边形 OABC 是梯形，BC∥AO，顶点 O 在坐标原点，顶点 A（4，0）， 顶点 B（1，4）．动点 P 从 O 出发，以每秒 1 个单位长度的速度沿 OA 的方向向 A 运 动；同时，动点 Q 从 N A y CO xM(B) 图 1 N A y CO xM 图 2 B E F P A y C O xB 图（2） P Q M A y C O xB 图（1） P Q A 出发，以每秒 2 个单位长度的速度沿 A→B→C 的方向向 C 运动．当其中一个点到达终点时，另一个也 随之停止．设运动时间为 t 秒． （1）当 t 为何值时， PB 与 AQ 互相平分？ （2）设△PAQ 的面积为 S，求 S 与 t 的函数关系式．当 t 为何值时，S 有最大值？最大值是多少？ （3）在整个运动过程中，是否存在某一时刻 t，使得以 PQ 为直径的圆与 y 轴相切？若存在，求出相应的 t 值；若不存在，请说明理由． 62．如图，在平面直角坐标系中，O 为坐标原点，△AOB 为等边三角形，点 A 的坐标为（4 3，0），点 B 在第一象限，∠OAB 的平分线 AC 与 y 轴交于点 E． （1）动点 P、Q 同时从点 C 出发，其中点 P 以 3cm/s 的速度沿折线 C→O→A 向终点 A 运动；点 Q 以 1cm/s 的速度沿射线 CA 方向运动，当点 P 达到点 A 时，P、Q 两点停止运动．设运动时间为 t 秒．求△PQC 的面积 S 与 t 的函数关系式； （2）点 M 为直线 AC 上一个动点，把△AOM 绕点 A 顺时针旋转，使边 AO 与边 AB 重合，得到△ABD．问： 是否存在点 M，使△OMD 的面积等于 3 3？若存在，求出点 M 的坐标；若不存在，请说明理由． 63．如图，直线 AB 与 CD 相交于点 E，直线 AB、CD 的解析式分别是 y＝－x＋6，y＝－ 1 2 x＋4，点 P 在线 段 CD 上由 C 向点 D 以每秒 5 个单位的速度运动（不运动到 D 点），过点 P 作 PQ∥x 轴，交 AB 于点 Q， 再过 Q 作 QR⊥x 轴于点 R． （1）求点 E 的坐标； （2）设点 P 运动的时间为 t 秒，△PQR 的面积为 S，求 S 关于 t 的函数关系式，并求 S 的最大值； （3）在点 P 运动过程中，是否存在点 P，使得以 P、Q、R 为顶点的三角形与△OCD 相似，若存在，求出 t 值；若不 存在，请说明理由． 64．Rt△ABC 中，∠C＝90°，∠A＝60°，BC＝6，等边三角形 DEF 从初始位置（点 E 与点 B 重合，EF 落 在 BC 上，如图 1）在线段 BC 上沿 BC 方向以每秒 1 个单位的速度平移，DE、DF 分别与 AB 相交于点 M、 B y C O xAP Q B y C O xA 备用图 B y C O xA 备用图 B y C O xA E A y C O xB Q DR P E N．当点 F 运动到点 C 时，△DEF 停止运动，此时点 D 恰好落在 AB 上，设△DEF 平移的时间为 t 秒． （1）求△DEF 的边长； （2）求 M 点、N 点在 BA 上的移动速度； （3）在△DEF 开始运动的同时，如果点 P 以每秒 2 个单位的速度从 D 点出发沿 DE→EF 运动，最终运动 到 F 点．设△PMN 的面积为 S． ①求 S 与 t 的函数关系式，当 P 点在何处时，△PMN 的面积最大？ ②是否存在这样的 t 值，使得 S＝ 8 ？若存在，求出 t 的值；若不存在，请说明理由． 65．如图，在 Rt△ABC 中，∠C＝90°，AB＝10，BC＝8，动点 P 从点 A 出发，沿 AB 以每秒 1 个单位的速 度向点 B 运动，动点 Q 从点 B 同时出发，沿 BC 以相同的速度向点 C 运动，当其中一个点到达终点时，另 一个点随之停止运动．设动点的运动时间为 t（秒），△PBQ 的面积为 S． （1）求 S 关于 t 的函数关系式； （2）当△PBQ 为等腰三角形时，求 t 的值； （3）若动点 R 从点 C 同时出发，沿 CA 以每秒 1 个单位的速度向点 A 运动，当点 R 到达终点时，P、Q 两 点随之停止运动．问：是否存在某一时刻 t（t＝0 除外），使得△PBQ 为直角三角形？若存在，求出 t 的值； 若不存在，请说明理由． 66．如图，矩形 ABCD 中，AB＝4，BC＝2，动点 M、N 分别从点 A、B 同时出发，动点 M 沿 AB 边以每秒 1 个单位的速度向点 B 运动，动点 N 沿 BC →CD 边以每秒 3 2 个单位的速度向点 D 运动，连结 MN，设运 动时间为 t（s）． （1）当 t 为何值时，MN∥BC ？ （2）当点 N 在 CD 边上运动时，设 MN 与 BD 相交于点 P，求证： 点 P 的位置固定不变； （3）以 AD 为直径作半圆 O，问：是否存在某一时刻 t，使得 MN 与半圆 O 相切？若存在，求 t 的值，并判断此时△MON 的形状； 若不存在，请说明理由． 67．如图，在△ABC 中，AB＝AC＝5cm，BC＝6cm，点 P 从点 B 出发沿 BC 边以 1cm/s 的速度向点 C 运 动，点 Q 从点 C 出发沿 CA 边以 2cm/s 的速度向点 A 运动，DE 保持垂直平分 PQ，且交 PQ 于点 D，交 BC B A D C P E F N M 图 2 B A D CF 图 1 (E) A B P M Q C A C B D M M M N M 于点 E．P、Q 两点同时出发，当点 Q 运动到点 A 时，P、Q 两点停止运动，设运动时间为 t（s）． （1）当 t＝________秒时，DE 经过点 C； （2）当点 Q 运动时，设四边形 ABPQ 的面积为 S（cm2），求 S 关于 t 的函数关系式； （3）当点 Q 运动时，是否存在以 P、Q、C 为顶点的三角形与△PDE 相似？若存在，求出 t 的值；若不存 在，请说明理由． 68．如图，在平面直角坐标系中，直线 l1：y＝ 3x＋ 3与 y 轴、x 轴交于点 A、B，直线 l2 经过点 A 和点 C （1，0），动点 P 从 B 点出发，以每秒 1 个单位的速度沿射线 BA 运动，连结 PC． （1）设△APC 的面积为 S，点 P 的运动时间为 t 秒，求 S 与 t 的函数关系式，并写出自变量的取值范围； （2）是否存在点 P，使得以 P、A、C 为顶点的三角形与 AOC 相似？若存在，求出点 P 的坐标；若不存在， 请说明理由． 69．如图，在平面直角坐标系中，矩形 OABC 的顶点 A 的坐标为（6，0），将△ABC 沿 AC 翻折，使点 B 落到点 B′ 处，B′ C 交 x 轴于点 D，且 CD＝2DB′ ．动点 P 从点 C 出发，沿 CO 以每秒 1 个单位的速度向点 O 运动；动点 Q 从点 O 出发，沿 OA、AB 以每秒 3 个单位的速度向点 B 运动，连接 PQ．若 P、Q 两点同 时出发，当其中一点到达终时整个运动随之结束，设运动时间为 t 秒． （1）求点 B′ 的坐标； （2）若以 P、Q、D、C 为顶点的凸四边形的面积为 S，求 S 与 t 之间的函数关系式； （3）当 t ＞ 2 3 时，设 PQ 与 B′ C 相交于点 M，问：是否存在这样的 t 值，使得△PCM 为等腰三角形？若存 在，请求出 t 的值；若不存在，请说明理由． 70．如图，在平面直角坐标系中，动点 P 从点 A（0，10）出发，以 3 个单位/秒的速度沿 y 轴向点 O 匀速 运动，动点 Q 从点 B（5，0）同时出发，以 1 个单位/秒的速度沿 x 轴向点 O 匀速运动，当其中一个点到 达终点时，另一点也随即停止运动．设运动的时间为 t（秒）．以 P、Q 为圆心作⊙P 和⊙Q，且⊙P 和⊙Q 的半径分别为 4 和 1． Q D E C A B P y xO CB A l1 l2 P O x y A BC P Q D B′ （1）若⊙P 与 Rt△AOB 的一边相切，求此时动点 P 的坐标； （2）若⊙P 与线段 AB 有两个公共点，求 t 的取值范围； （3）是否存在某一时刻 t，使⊙P 和⊙Q 相切？若存在，求出 t 的值； 若不存在，请说明理由． 71．如图所示，菱形 ABCD 的边长为 6cm，∠DAB＝60°，点 E 是边 AD 上一点，且 DE＝2cm，动点 P、Q 分别从 A、C 两点同时出发，以 1cm/s 的速度分别沿边 AB、CB 向点 B 运动，PE、CD 的延长线相交于点 F，FQ 交 AD 于点 G．设运动时间为 t（s），△CFQ 的面积为 S（cm2）． （1）求 S 与 t 之间的函数关系式； （2）是否存在某一时刻，使得线段 FQ 将菱形 ABCD 分成上、下两部分的面积之比为 1 : 5？若存在，求 出此时 t 的值；若不存在，请说明理由． 72．如图，直线 y＝－ 3 4 x＋9 与 x 轴、y 轴分别交于点 B、C，抛物线 y＝－ 1 4 x 2＋b x＋c 经过 B，C 两点，与 x 轴的另一个交点为点 A，动点 P 从点 A 出发沿 AB 以每秒 3 个单位长度的速度向点 B 运动，运动时间为 （0＜t＜5）秒． （1）求抛物线的解析式及点 A 的坐标； （2）以 OC 为直径的⊙O′ 与 BC 交于点 M，当 t 为何值时，PM 与⊙O′ 相切？请说明理由； （3）在点 P 从点 A 出发的同时，动点 Q 从点 B 出发沿 BC 以每秒 3 个单位长度的速度向点 C 运动，动点 N 从点 C 出发沿 CA 以每秒 3 5 个单位长度的速度向点 A 运动，运动时间与点 P 相同． ①记△BPQ 的面积为 S，当 t 为何值时，S 最大，最大值是多少？ ②是否存在△NCQ 为直角三角形的情形，若存在，求出相应的 t 值；若不存在，请说明理由． 73．如图，点 M 在第一象限，半径为 6 的⊙M 交 x 轴于点 A、B，交 y 轴于点 C、D，且∠AMB＝60°，CD ＝4 5． t O x y A BQ P C PA B Q E DF G O M C BA x y P QN O′ O C BA x y O′ 备用图 M （1）求直线 AM 的解析式； （2）若⊙M 以每秒 1 个单位长的速度沿直线 AM 向右上方匀速运动 ①当⊙M 开始运动时，动点 N 同时从点 A 出发，沿 x 轴正方向以每秒 3 个单位长的速度匀速运动．在整 个运动过程中，点 N 在动圆的圆面（圆上和圆的内部）上一共运动了多长时间？ ②在①中，若动点 N 的运动速度为每秒 a 个单位，当动点 N 离开⊙M 时，⊙M 恰好与 x 轴相切，求 a 的 值； （3）设 P 为直线 AM 上一点，在坐标平面内是否存在点 Q，使得以 A、B、P、Q 为顶点的四边形是一个 有三边相等且有一个内角为 60°的等腰梯形？若存在，请直接写出点 Q 的坐标；若不存在，请说明理 由． 74．如图，在等腰梯形 ABCD 中，AD∥BC，AB＝DC＝10，AD＝15，BC＝27．动点 P 从点 B 出发，以每 秒 5 个单位长的速度沿折线段 BA－AD－DC 向点 C 匀速运动；动点 Q 从点 C 出发，以每秒 3 个单位长的 速度沿线段 CB 向点 B 匀速运动，过点 Q 作 QE⊥BC，交折线段 CD－DA－AB 于点 E．设 P、Q 两点同时 出发，运动时间为 t 秒，当点 P 与点 C 重合时整个运动随之结束． （1）当点 P 在 AD 上运动时，若 PQ∥DC，求 t 的值； （2）设直线 QE 扫过梯形 ABCD 的面积为 S，求 S 与 t 的函数关系式； （3）△PQE 能否成为直角三角形？若能，求 t 的取值范围；若不能，请说明理由． 75．如图，在平面直角坐标系中，四边形 OABC 是矩形，A（0，－4），B（8，－4），将矩形 OABC 沿直线 AC 折叠，点 B 落在点 D 处，AD 交 OC 于点 E． （1）求 OE 的长； （2）求经过 O、D、C 三点的抛物线的解析式； （3）设 M 为（2）中抛物线的顶点，动点 P 从点 A 出发，沿射 线 AB 以每秒 1 个单位长度的速度匀速运动，是否存在时刻 t， 使得△MAC 被直线 PM 分成面积比为 1 : 3 的两部分？若存 在，求 t 的值；若不存在，请说明理由． 76．如图，在平面直角坐标系中，四边形 OABC 为矩形，顶点 A、C 的坐标分别为（8，0）、（0，6）．动点 C A B M M D O x y B C A D P Q E y O x D C BA E P 从点 O 出发，以每秒 1 个 单位长度的速度沿 OA 匀速向终点 A 运动．过点 P 作 PM⊥OB，垂足为 M．设 点 P 运动的时间为 t（s）． （1）设△OPM 的面积为 S，求 S 与 t 的函数关系式； （2）当点 O 关于直线 CP 的对称点 O′ 恰好落在对角线 OB 上时，求直线 CP 的函数表达式； （3）在点 P 运动的过程中，是否存在时刻 t，使得 S△PCM ＝ 1 8 S 矩形 OABC ？若存在，请求出 t 的值；若不存 在，请说明理由． O A B x y C P M