- 7.06 MB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2010 年中考数学压轴题 100 题精选(1-10 题)答案
【001】解:(1)抛物线 2( 1) 3 3( 0)y a x a 经过点 ( 2 0)A , ,
30 9 3 3 3a a ···············································································1 分
二次函数的解析式为: 23 2 3 8 3
3 3 3y x x ············································3 分
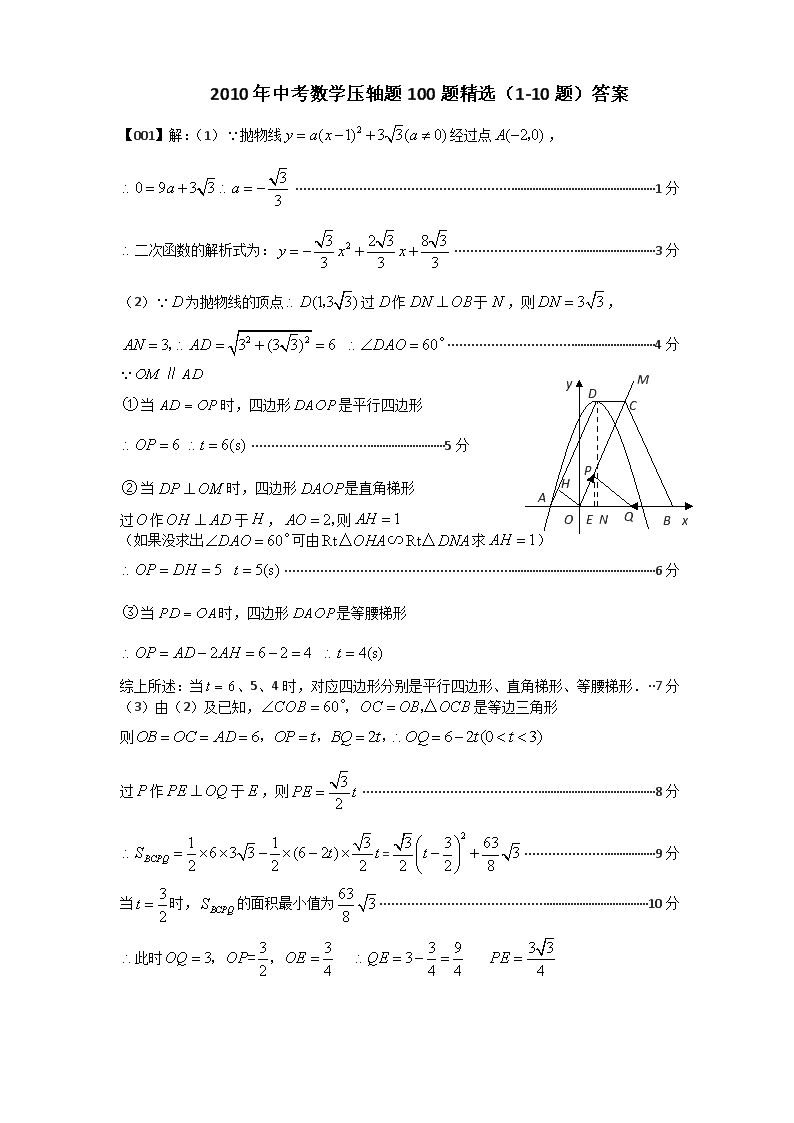
(2) D 为抛物线的顶点 (13 3)D , 过 D 作 DN OB 于 N ,则 3 3DN ,
2 23 3 (3 3) 6 60AN AD DAO , °·············································4 分
OM AD ∥
① 当 AD OP 时,四边形 DAOP 是平行四边形
6 6(s)OP t ·········································· 5 分
② 当 DP OM 时,四边形 DAOP 是直角梯形
过O 作 OH AD 于 H , 2AO ,则 1AH
(如果没求出 60DAO °可由 Rt RtOHA DNA△ ∽ △ 求 1AH )
5 5(s)OP DH t ·················································································6 分
③ 当 PD OA 时,四边形 DAOP 是等腰梯形
2 6 2 4 4(s)OP AD AH t
综上所述:当 6t 、5、4 时,对应四边形分别是平行四边形、直角梯形、等腰梯形.· 7 分
(3)由(2)及已知, 60COB OC OB OCB °, ,△ 是等边三角形
则 6 2 6 2 (0 3)OB OC AD OP t BQ t OQ t t , , ,
过 P 作 PE OQ 于 E ,则 3
2PE t ································································8 分
1 1 36 3 3 (6 2 )2 2 2BCPQS t t =
23 3 63 32 2 8t
···························· 9 分
当 3
2t 时, BCPQS 的面积最小值为 63 38
·························································· 10 分
此时 3 3 3 9 3 33 32 4 4 4 4OQ OP OE QE PE , = ,
x
y M
C
D
P
QO
A
BNE
H
2 2
2 2 3 3 9 3 3
4 4 2PQ PE QE
··············································· 11 分
【002】解:(1)1, 8
5
;
(2)作 QF⊥AC 于点 F,如图 3, AQ = CP= t,∴ 3AP t .
由△AQF∽△ABC, 2 25 3 4BC ,
得
4 5
QF t .∴ 4
5QF t . ∴ 1 4(3 )2 5S t t ,
即 22 6
5 5S t t .
(3)能.
①当 DE∥QB 时,如图 4.
∵DE⊥PQ,∴PQ⊥QB,四边形 QBED 是直角梯形.
此时∠AQP=90°.
由△APQ ∽△ABC,得 AQ AP
AC AB
,
即 3
3 5
t t . 解得 9
8t .
②如图 5,当 PQ∥BC 时,DE⊥BC,四边形 QBED 是直角梯形.
此时∠APQ =90°.
由△AQP ∽△ABC,得 AQ AP
AB AC
,
即 3
5 3
t t . 解得 15
8t .
(4) 5
2t 或 45
14t .
【注:①点 P 由 C 向 A 运动,DE 经过点 C.
方法一、连接 QC,作 QG⊥BC 于点 G,如图 6.
PC t , 2 2 2QC QG CG 2 23 4[ (5 )] [4 (5 )]5 5t t .
由 2 2PC QC ,得 2 2 23 4[ (5 )] [4 (5 )]5 5t t t ,解得 5
2t .
方法二、由 CQ CP AQ ,得 QAC QCA ,进而可得
B BCQ ,得 CQ BQ ,∴ 5
2AQ BQ .∴ 5
2t .
②点 P 由 A 向 C 运动,DE 经过点 C,如图 7.
2 2 23 4(6 ) [ (5 )] [4 (5 )]5 5t t t , 45
14t 】
【003】解.(1)点 A 的坐标为(4,8) …………………1 分
将 A (4,8)、C(8,0)两点坐标分别代入 y=ax2+bx
8=16a+4b
A C
B
P
Q
E
D
图 4
A C
)
B
P
Q
D
图 3
E
)
F
A C
B
P
Q
ED
图 5
A C(E)
B
P
Q
D
图 6
G
A C(E)
B
P
Q
D
图 7
G
得
0=64a+8b
解 得 a=- 1
2 ,b=4
∴抛物线的解析式为:y=- 1
2
x2+4x …………………3 分
(2)①在 Rt△APE 和 Rt△ABC 中,tan∠PAE= PE
AP = BC
AB ,即 PE
AP = 4
8
∴PE= 1
2
AP= 1
2
t.PB=8-t.
∴点E的坐标为(4+ 1
2
t,8-t).
∴点 G 的纵坐标为:- 1
2
(4+ 1
2
t)2+4(4+ 1
2
t)=- 1
8
t2+8. …………………5 分
∴EG=- 1
8
t2+8-(8-t) =- 1
8
t2+t.
∵- 1
8
<0,∴当 t=4 时,线段 EG 最长为 2. …………………7 分
②共有三个时刻. …………………8 分
t1=16
3
, t2= 40
13
,t3= 8 5
2 5
. …………………11 分
【004】(1)解:由 2 8 03 3x ,得 4x A . 点坐标为 4 0 , .
由 2 16 0x ,得 8x B . 点坐标为 8 0, .∴ 8 4 12AB .(2 分)
由
2 8
3 3
2 16
y x
y x
,
.
解得 5
6
x
y
,
.∴C 点的坐标为 5 6, .(3 分)
∴ 1 1 12 6 362 2ABC CS AB y △ · .(4 分)
(2)解:∵点 D 在 1l 上且 2 88 8 83 3D B Dx x y , .∴ D 点坐标为 8 8, .(5 分)又∵点
E 在 2l 上且 8 2 16 8 4E D E Ey y x x , . .∴ E 点坐标为 4 8, .(6 分)
∴ 8 4 4 8OE EF , .(7 分)
(3)解法一:① 当 0 3t ≤ 时,如图 1,矩形 DEFG 与 ABC△ 重叠部分为五边形CHFGR( 0t
时,为四边形 CHFG ).过C 作CM AB 于 M ,则 Rt RtRGB CMB△ ∽ △ .
A
D
B
E
O
R
F x
y
1l2l
M
(图 3)
G
C
A
D
B
E
O
C
F x
y
1l2l
G
(图 1)
R
M A
D
B
E
O
C
F x
y
1l2l
G
(图 2)
R
M
∴ BG RG
BM CM
,即
3 6
t RG ,∴ 2RG t . Rt RtAFH AMC △ ∽ △ ,
∴ 1 1 236 2 8 82 2 3ABC BRG AFHS S S S t t t t △ △ △ .
即 24 16 44
3 3 3S t t .(10 分)
【005】(1)如图 1,过点 E 作 EG BC 于点G.················
∵ E 为 AB 的中点,
∴ 1 22BE AB .
在 Rt EBG△ 中, 60B ∠ ,∴ 30BEG ∠ .············
∴ 2 21 1 2 1 32BG BE EG , .
即点 E 到 BC 的距离为 3.······································
(2)①当点 N 在线段 AD 上运动时, PMN△ 的形状不发生改变.
∵ PM EF EG EF , ,∴ PM EG∥ .
∵ EF BC∥ ,∴ EP GM , 3PM EG .
同理 4MN AB .···················································································4 分
如图 2,过点 P 作 PH MN 于 H ,∵ MN AB∥ ,
∴ 60 30NMC B PMH ∠ ∠ ,∠ .
∴ 1 3
2 2PH PM .
∴ 3cos30 2MH PM .
则 3 54 2 2NH MN MH .
在 Rt PNH△ 中,
22
2 2 5 3 72 2PN NH PH
.
∴ PMN△ 的周长= 3 7 4PM PN MN .······································· 6 分
②当点 N 在线段 DC 上运动时, PMN△ 的形状发生改变,但 MNC△ 恒为等边三角形.
当 PM PN 时,如图 3,作 PR MN 于 R ,则 MR NR .
类似①, 3
2MR .
∴ 2 3MN MR .····················································································7 分
∵ MNC△ 是等边三角形,∴ 3MC MN .
此时, 6 1 3 2x EP GM BC BG MC .···································· 8 分
图 1
A D
E
B
F
CG
图 2
A D
E
B
F
C
P
N
MG
H
当 MP MN 时,如图 4,这时 3MC MN MP .
此时, 6 1 3 5 3x EP GM .
当 NP NM 时,如图 5, 30NPM PMN ∠ ∠ .
则 120PMN ∠ ,又 60MNC ∠ ,
∴ 180PNM MNC ∠ ∠ .
因此点 P 与 F 重合, PMC△ 为直角三角形.
∴ tan30 1MC PM .
此时, 6 1 1 4x EP GM .
综上所述,当 2x 或 4 或 5 3 时, PMN△ 为等腰三角形.
【006】解:(1)OC=1,所以,q=-1,又由面积知 0.5OC×AB=
4
5 ,得 AB= 5
2
,
设 A(a,0),B(b,0)AB=b a= 2( ) 4a b ab = 5
2
,解得 p= 3
2
,但 p<0,所以 p= 3
2
。
所以解析式为: 2 3 12y x x
(2)令 y=0,解方程得 2 3 1 02x x ,得 1 2
1 , 22x x ,所以 A( 1
2
,0),B(2,0),在直角三角形 AOC
中可求得 AC= 5
2 ,同样可求得 BC= 5 ,显然 AC2+BC2=AB2,得△ABC 是直角三角形。AB 为斜
边,所以外接圆的直径为 AB= 5
2 ,所以 5 5
4 4m 。
(3)存在,AC⊥BC,①若以 AC 为底边,则 BD//AC,易求 AC 的解析式为 y=-2x-1,可设 BD 的解析式
为 y=-2x+b,把 B(2,0)代入得 BD 解析式为 y=-2x+4,解方程组
2 3 12
2 4
y x x
y x
得 D( 5
2
,9)
②若以 BC 为底边,则 BC//AD,易求 BC 的解析式为 y=0.5x-1,可设 AD 的解析式为 y=0.5x+b,把
A( 1
2
,0)代入得 AD 解析式为 y=0.5x+0.25,解方程组
2 3 12
0.5 0.25
y x x
y x
得 D( 5 3,2 2 ) 综上,
图 3
A D
E
B
F
C
P
N
M
图 4
A D
E
B
F
C
P
M
N
图 5
A D
E
B
F(P)
C
M
N
GG
R
G
所以存在两点:( 5
2
,9)或( 5 3,2 2 )。
【007】
【008】证明:(1)∵∠ABC=90°,BD⊥EC,
∴∠1 与∠3 互余,∠2 与∠3 互余,
∴∠1=∠2…………………………………………………1 分
∵∠ABC=∠DAB=90°,AB=AC
∴△BAD≌△CBE…………………………………………2 分
∴AD=BE……………………………………………………3 分
(2)∵E 是 AB 中点,
∴EB=EA 由(1)AD=BE 得:AE=AD……………………………5 分
∵AD∥BC∴∠7=∠ACB=45°∵∠6=45°∴∠6=∠7
由等腰三角形的性质,得:EM=MD,AM⊥DE。
即,AC 是线段 ED 的垂直平分线。……………………7 分
(3)△DBC 是等腰三角(CD=BD)……………………8 分
理由如下:
由(2)得:CD=CE 由(1)得:CE=BD∴CD=BD
∴△DBC 是等腰三角形。……………………………10 分
【009】解:(1)① AC x ⊥ 轴, AE y⊥ 轴,
四边形 AEOC 为矩形.
BF x⊥ 轴, BD y⊥ 轴,
四边形 BDOF 为矩形.
AC x ⊥ 轴, BD y⊥ 轴,
四边形 AEDK DOCK CFBK, , 均为矩形.···········1 分
1 1 1 1OC x AC y x y k , , ,
1 1AEOCS OC AC x y k 矩形
2 2 2 2OF x FB y x y k , , ,
2 2BDOFS OF FB x y k 矩形 .
AEOC BDOFS S矩形 矩形 .
AEDK AEOC DOCKS S S 矩形 矩形 矩形 ,
CFBK BDOF DOCKS S S 矩形 矩形 矩形 ,
AEDK CFBKS S矩形 矩形 .·················································································· 2 分
②由(1)知 AEDK CFBKS S矩形 矩形 .
AK DK BK CK .
AK BK
CK DK
.······························································································4 分
90AKB CKD °,
AKB CKD△ ∽△ .····················································································5 分
O C F M
D
E
N
K
y
x
A
B
图 1
CDK ABK .
AB CD∥ .······························································································· 6 分
AC y∥ 轴,
四边形 ACDN 是平行四边形.
AN CD .······························································································· 7 分
同理 BM CD .
AN BM .·······························································································8 分
(2) AN 与 BM 仍然相等.············································································· 9 分
AEDK AEOC ODKCS S S 矩形 矩形 矩形 ,
BKCF BDOF ODKCS S S 矩形 矩形 矩形 ,
又 AEOC BDOFS S k 矩形 矩形 ,
AEDK BKCFS S矩形 矩形 .·····························10 分
AK DK BK CK .
CK DK
AK BK
.
K K ,
CDK ABK△ ∽△ .
CDK ABK .
AB CD∥ .······························································································11 分
AC y∥ 轴,
四边形 ANDC 是平行四边形.
AN CD .
同理 BM CD .
AN BM .·····························································································12 分
【010】解:(1)根据题意,得
3 4 2 3
1.2
a a b
b
a
,
····2 分
解得 1
2.
a
b
,
抛物线对应的函数表达式为 2 2 3y x x . 3 分
(2)存在.
在 2 2 3y x x 中,令 0x ,得 3y .
令 0y ,得 2 2 3 0x x , 1 21 3x x , .
( 1 0)A , , (3 0)B , , (0 3)C , .
O C
D K
F
E
N
y
x
A
B
M
图 2
y
x
E
D
N
OA
C
M
P
N1
F
(第 26 题图)
又 2( 1) 4y x ,顶点 (1 4)M , .·······························································5 分
容易求得直线 CM 的表达式是 3y x .
在 3y x 中,令 0y ,得 3x .
( 3 0)N , , 2AN .················································································ 6 分
在 2 2 3y x x 中,令 3y ,得 1 20 2x x , .
2CP AN CP , .
AN CP ∥ ,四边形 ANCP 为平行四边形,此时 (2 3)P , .····························· 8 分
(3) AEF△ 是等腰直角三角形.
理由:在 3y x 中,令 0x ,得 3y ,令 0y ,得 3x .
直线 3y x 与坐标轴的交点是 (0 3)D , , (3 0)B , .
OD OB , 45OBD °.······································································· 9 分
又点 (0 3)C , , OB OC . 45OBC °.············································ 10 分
由图知 45AEF ABF °, 45AFE ABE °.···································· 11 分
90EAF °,且 AE AF . AEF△ 是等腰直角三角形.·····························12 分
(4)当点 E 是直线 3y x 上任意一点时,(3)中的结论成立. 14 分
2010 年中考数学压轴题 100 题精选(11-20 题)答案
【011】解:(1)证明:在 Rt△FCD 中,∵G 为 DF 的中点,∴ CG= FD.………1 分
同理,在 Rt△DEF 中,EG= FD.…………2 分∴ CG=EG.…………………3 分
(2)(1)中结论仍然成立,即 EG=CG.…………………………4 分
证法一:连接 AG,过 G 点作 MN⊥AD 于 M,与 EF 的延长线交于 N 点.
在△DAG 与△DCG 中,∵ AD=CD,∠ADG=∠CDG,DG=DG,
∴ △DAG≌△DCG.∴ AG=CG.………………………5 分
在△DMG 与△FNG 中,∵ ∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴ △DMG≌△FNG.∴ MG=NG 在矩形 AENM 中,AM=EN. ……………6 分
在 Rt△AMG 与 Rt△ENG 中,∵ AM=EN, MG=NG,
∴ △AMG≌△ENG.∴ AG=EG.∴ EG=CG. ……………………………8 分
证法二:延长 CG 至 M,使 MG=CG,
连接 MF,ME,EC, ……………………4 分
在△DCG 与△FMG 中,∵FG=DG,∠MGF=∠CGD,MG=CG,
∴△DCG ≌△FMG.∴MF=CD,∠FMG=∠DCG.
∴MF∥CD∥AB.………………………5 分∴ 在 Rt△MFE 与 Rt△CBE 中,
∵ MF=CB,EF=BE,∴△MFE ≌△CBE.∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°.∴ △
MEC 为直角三角形.∵ MG = CG,∴ EG= MC.………8 分
(3)(1)中的结论仍然成立,即 EG=CG.其他的结论还有:EG⊥CG.……10 分
【012】解:(1)圆心O 在坐标原点,圆O 的半径为 1,
点 A B C D、 、 、 的坐标分别为 ( 1 0) (0 1) (1 0) (01)A B C D ,、 , 、 ,、 ,
抛物线与直线 y x 交于点 M N、 ,且 MA NC、 分别与圆O 相切于点 A 和点C ,
( 1 1) (11)M N , 、 , .点 D M N、 、 在抛物线上,将 (01) ( 1 1) (11)D M N ,、 , 、 , 的坐标代入
2y ax bx c ,得:
1
1
1
c
a b c
a b c
解之,得:
1
1
1
a
b
c
抛物线的解析式为: 2 1y x x .····························································· 4 分
(2)
2
2 1 51 2 4y x x x
抛物线的对称轴为 1
2x ,
1 1 512 4 2OE DE , .··················6 分
连结 90BF BFD , °,
BFD EOD△ ∽△ , DE OD
DB FD
,
又 5 1 22DE OD DB , , ,
4 5
5FD ,
4 5 5 3 5
5 2 10EF FD DE .···························································· 8 分
(3)点 P 在抛物线上.··················································································· 9 分
设过 D C、 点的直线为: y kx b ,
O x
y
N
C
D
E
F
BM
A
P
将点 (1 0) (01)C D,、 , 的坐标代入 y kx b ,得: 1 1k b , ,
直线 DC 为: 1y x .··········································································· 10 分
过点 B 作圆O 的切线 BP 与 x 轴平行, P 点的纵坐标为 1y ,
将 1y 代入 1y x ,得: 2x .
P 点的坐标为 (2 1), ,当 2x 时, 2 21 2 2 1 1y x x ,
所以, P 点在抛物线 2 1y x x 上.····························································12 分
【013】解:(1)该抛物线过点 (0 2)C , ,可设该抛物线的解析式为 2 2y ax bx .
将 (4 0)A , , (1 0)B , 代入,
得 16 4 2 0
2 0
a b
a b .
,
解得
1
2
5
2
a
b .
,
此抛物线的解析式为 21 5 22 2y x x .·················································(3 分)
(2)存在.····························································································· (4 分)
如图,设 P 点的横坐标为 m ,
则 P 点的纵坐标为 21 5 22 2m m ,
当1 4m 时,
4AM m , 21 5 22 2PM m m .
又 90COA PMA °,
①当 2
1
AM AO
PM OC
时,
APM ACO△ ∽△ ,
即 21 54 2 22 2m m m
.
解得 1 22 4m m , (舍去), (21)P , .·····················································(6 分)
②当 1
2
AM OC
PM OA
时, APM CAO△ ∽△ ,即 21 52(4 ) 22 2m m m .
解得 1 4m , 2 5m (均不合题意,舍去)
当1 4m 时, (2 1)P , .······································································· (7 分)
O x
y
AB
C
41
2
(第 26 题图)
D P
M
E
类似地可求出当 4m 时, (5 2)P , .·························································(8 分)
当 1m 时, ( 3 14)P , .
综上所述,符合条件的点 P 为 (2 1), 或 (5 2), 或 ( 3 14) , .··························(9 分)
(3)如图,设 D 点的横坐标为 (0 4)t t ,则 D 点的纵坐标为 21 5 22 2t t .
过 D 作 y 轴的平行线交 AC 于 E .由题意可求得直线 AC 的解析式为 1 22y x .(10 分)
E 点的坐标为 1 22t t
, . 2 21 5 1 12 2 22 2 2 2DE t t t t t
.· (11 分)
2 2 21 1 2 4 4 ( 2) 42 2DACS t t t t t △ .
当 2t 时, DAC△ 面积最大. (2 1)D , .··············································(13 分)
【014】(1)解:∵ A 点第一次落在直线 y x 上时停止旋转,∴OA 旋转了 045 .
∴OA 在旋转过程中所扫过的面积为
245 2
360 2
.……………4 分
(2)解:∵ MN ∥ AC ,∴ 45BMN BAC , 45BNM BCA .
∴ BMN BNM .∴ BM BN .又∵ BA BC ,∴ AM CN .
又 ∵ OA OC , OAM OCN , ∴ OAM OCN . ∴ AOM CON . ∴
1 (90 452AOM .∴旋转过程中,当 MN 和 AC 平行时,正方形 OABC 旋转的度
数为 45 .……………………………………………8 分
(3)答: p 值无变化. 证明:延长 BA 交 y 轴于 E 点,则 045AOE AOM ,
0 0 090 45 45CON AOM AOM , ∴ AOE CON . 又 ∵ OA OC ,
0 0 0180 90 90OAE OCN .∴ OAE OCN .∴ ,OE ON AE CN .
又∵ 045MOE MON ,OM OM , ∴ OME OMN .
∴ MN ME AM AE .∴ MN AM CN ,
∴ 4p MN BN BM AM CN BN BM AB BC .
∴在旋转正方形OABC 的过程中, p 值无变化. ……………12 分
(第 26 题)
O
A
B
C
M
N
y x
x
y
E
【015】⑴设二次函数的解析式为:y=a(x-h)2+k∵顶点 C 的横坐标为 4,且过点(0, 39
7 )
∴y=a(x-4)2+k ka 1639
7 ………………①
又∵对称轴为直线 x=4,图象在 x 轴上截得的线段长为 6 ∴A(1,0),B(7,0)
∴0=9a+k ………………②由①②解得 a=
9
3 ,k= 3- ∴二次函数的解析式为:y=
9
3 (x-4)2- 3
⑵∵点 A、B 关于直线 x=4 对称 ∴PA=PB ∴PA+PD=PB+PD≥DB ∴当点 P 在线段 DB 上时 PA+PD 取得
最小值 ∴DB 与对称轴的交点即为所求点 P
设直线 x=4 与 x 轴交于点 M ∵PM∥OD,∴∠BPM=∠BDO,又∠PBM=∠DBO
∴△BPM∽△BDO∴
BO
BM
DO
PM ∴
3
3
7
339
7
PM ∴点 P 的坐标为(4,
3
3 )
⑶由⑴知点 C(4, 3 ),又∵AM=3,∴在 Rt△AMC 中,cot∠ACM=
3
3 ,
∴∠ACM=60o,∵AC=BC,∴∠ACB=120o
①当点 Q 在 x 轴上方时,过 Q 作 QN⊥x 轴于 N 如果 AB=BQ,由△ABC∽△ABQ 有
BQ=6,∠ABQ=120o,则∠QBN=60o ∴QN=3 3 ,BN=3,ON=10,此时点 Q(10, 33 ),
如果 AB=AQ,由对称性知 Q(-2, 33 )
②当点 Q 在 x 轴下方时,△QAB 就是△ACB,此时点 Q 的坐标是(4, 3 ),
经检验,点(10, 33 )与(-2, 33 )都在抛物线上
综上所述,存在这样的点 Q,使△QAB∽△ABC
点 Q 的坐标为(10, 33 )或(-2, 33 )或(4, 3 ).
【016】解:(1)设正比例函数的解析式为 1 1( 0)y k x k ,
因为 1y k x 的图象过点 (3 3)A , ,所以 13 3k ,解得 1 1k .
这个正比例函数的解析式为 y x .······························································(1 分)
设反比例函数的解析式为 2
2( 0)ky kx
.因为 2ky x
的图象过点 (3 3)A , ,所以
23 3
k ,解得 2 9k .这个反比例函数的解析式为 9y x
.······························ (2 分)
(2)因为点 (6 )B m, 在 9y x
的图象上,所以 9 3
6 2m ,则点 36 2B
, .·······(3 分)
设一次函数解析式为 3 3( 0)y k x b k .因为 3y k x b 的图象是由 y x 平移得到的,
所以 3 1k ,即 y x b .又因为 y x b 的图象过点 36 2B
, ,所以
3 62 b ,解得 9
2b ,一次函数的解析式为 9
2y x .·························· (4 分)
(3)因为 9
2y x 的图象交 y 轴于点 D ,所以 D 的坐标为 90 2
, .
设二次函数的解析式为 2 ( 0)y ax bx c a .
因为 2y ax bx c 的图象过点 (3 3)A , 、 36 2B
, 、和 D 90 2
, ,
所以
9 3 3
336 6 2
9 .2
a b c
a b c
c
,
,·················(5 分) 解得
1
2
4
9 .2
a
b
c
,
,
这个二次函数的解析式为 21 942 2y x x .·············································· (6 分)
(4) 9
2y x 交 x 轴于点C ,点C 的坐标是 9 02
, ,
如图所示, 15 1 1 3 16 6 6 3 3 32 2 2 2 2S
9 945 18 4 2
81
4
.
假设存在点 0 0( )E x y, ,使 1
2 81 2 27
3 4 3 2S S .
四边形CDOE 的顶点 E 只能在 x 轴上方, 0 0y ,
y
xO C
D
B
A
3
3 6
E
1 OCD OCES S S △ △ 0
1 9 9 1 9
2 2 2 2 2 y 0
81 9
8 4 y .
0
81 9 27
8 4 2y , 0
3
2y . 0 0( )E x y , 在二次函数的图象上,
2
0 0
1 9 342 2 2x x .解得 0 2x 或 0 6x .
当 0 6x 时,点 36 2E
, 与点 B 重合,这时CDOE 不是四边形,故 0 6x 舍去,
点 E 的坐标为 32 2
, . (8 分)
【017】解:(1)已知抛物线 2y x bx c 经过 (1 0) (0 2)A B,, , ,
0 1
2 0 0
b c
c
解得 3
2
b
c
所求抛物线的解析式为 2 3 2y x x .·························································· 2 分
(2) (1 0)A , , (0 2)B , , 1 2OA OB ,
可得旋转后C 点的坐标为 (31), ··········································································· 3 分
当 3x 时,由 2 3 2y x x 得 2y ,
可知抛物线 2 3 2y x x 过点 (3 2),
将原抛物线沿 y 轴向下平移 1 个单位后过点 C .
平移后的抛物线解析式为: 2 3 1y x x .·····················································5 分
(3)点 N 在 2 3 1y x x 上,可设 N 点坐标为 2
0 0 0( 3 1)x x x ,
将 2 3 1y x x 配方得
23 5
2 4y x
,其对称轴为 3
2x .·························· 6 分
①当 0
30 2x 时,如图①,
1 1
2NBB NDDS S △ △
0 0
1 1 31 2 12 2 2x x
0 1x
y
x
C
B
A
O
N
D
B1
D1
图①
此时 2
0 03 1 1x x
N 点的坐标为 (1 1), .················································································· 8 分
②当 0
3
2x 时,如图②
同理可得 0 0
1 1 31 22 2 2x x
0 3x
此时 2
0 03 1 1x x
点 N 的坐标为 (31), .
综上,点 N 的坐标为 (1 1), 或 (31), .······························································· 10 分
【018】解:(1)抛物线 2 4y ax bx a 经过 ( 1 0)A , , (0 4)C , 两点,
4 0
4 4.
a b a
a
,
解得 1
3.
a
b
,
抛物线的解析式为 2 3 4y x x .
(2)点 ( 1)D m m , 在抛物线上, 21 3 4m m m ,
即 2 2 3 0m m , 1m 或 3m .
点 D 在第一象限,点 D 的坐标为 (3 4), .
由(1)知 45OA OB CBA , °.
设点 D 关于直线 BC 的对称点为点 E .
(0 4)C , , CD AB ∥ ,且 3CD ,
45ECB DCB °,
E 点在 y 轴上,且 3CE CD .
1OE , (01)E , .
即点 D 关于直线 BC 对称的点的坐标为(0,1).
(3)方法一:作 PF AB⊥ 于 F , DE BC⊥ 于 E .
由(1)有: 4 45OB OC OBC , °,
45DBP CBD PBA °, .
(0 4) (3 4)C D ,, , , CD OB ∥ 且 3CD .
y
x
C
B
A
O D
B1
D1
图②
N
y
xO
A B
C D
EP
F
y
xO
A B
C D
E
45DCE CBO °,
3 2
2DE CE .
4OB OC , 4 2BC , 5 2
2BE BC CE ,
3tan tan 5
DEPBF CBD BE
.
设 3PF t ,则 5BF t , 5 4OF t ,
( 5 4 3 )P t t , .
P 点在抛物线上,
23 ( 5 4) 3( 5 4) 4t t t ,
0t (舍去)或 22
25t , 2 66
5 25P
, .
方法二:过点 D 作 BD 的垂线交直线 PB 于点Q ,过点 D 作 DH x⊥ 轴于 H .过Q 点作QG DH⊥
于G .
45PBD QD DB °, .
QDG BDH 90 °,
又 90DQG QDG °, DQG BDH .
QDG DBH△ ≌△ , 4QG DH , 1DG BH .
由(2)知 (3 4)D , , ( 13)Q , .
(4 0)B , ,直线 BP 的解析式为 3 12
5 5y x .
解方程组
2 3 4
3 12
5 5
y x x
y x
,
,
得 1
1
4
0
x
y
,
;
2
2
2
5
66 .25
x
y
,
点 P 的坐标为 2 66
5 25
, .
【019】(1)EO>EC,理由如下:
由折叠知,EO=EF,在 Rt△EFC 中,EF 为斜边,∴EF>EC, 故 EO>EC …2 分
(2)m 为定值
∵S 四边形 CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO―EC)=CO·(EO―EC)
y
xO
A B
C D
P
Q G
H
S 四边形 CMNO=CM·CO=|CE―EO|·CO=(EO―EC) ·CO
∴ 1
CMNO
CFGH
S
Sm
四边形
四边形 ……………………………………………………4 分
(3)∵CO=1,
3
2
3
1 QFCE , ∴EF=EO= QF
3
2
3
11
∴cos∠FEC=
2
1 ∴∠FEC=60°,
∴ 30602
60180 EAOOEAFEA ,
∴△EFQ 为等边三角形,
3
2EQ …………………………………………5 分
作 QI⊥EO 于 I,EI=
3
1
2
1 EQ ,IQ=
3
3
2
3 EQ
∴IO=
3
1
3
1
3
2 ∴Q 点坐标为 )3
1,3
3( ……………………………………6 分
∵抛物线 y=mx2+bx+c 过点 C(0,1), Q )3
1,3
3( ,m=1
∴可求得 3b ,c=1
∴抛物线解析式为 132 xxy ……………………………………7 分
(4)由(3), 33
23 EOAO
当 33
2x 时,
3
1133
23)33
2( 2 y <AB
∴P 点坐标为 )3
1,3
32( …………………8 分
∴BP=
3
2
3
11 AO
方法 1:若△PBK 与△AEF 相似,而△AEF≌△AEO,则分情况 如
下:
①
3
32
3
2
3
2 BK 时,
9
32BK ∴K 点坐标为 )1,9
34( 或 )1,9
38(
②
3
2
3
2
3
32
BK 时,
3
32BK ∴K 点坐标为 )1,3
34( 或 )1,0( …………10 分
故直线 KP 与 y 轴交点 T 的坐标为
)1,0()3
1,0()3
7,0()3
5,0( 或或或 …………………………………………12 分
方法 2:若△BPK 与△AEF 相似,由(3)得:∠BPK=30°或 60°,过 P 作 PR⊥y 轴于 R,则∠RTP=60°
或 30°
①当∠RTP=30°时, 233
32 RT
②当∠RTP=60°时,
3
233
32 RT
∴ )1,0()3
1,0()3
5,0()3
7,0( 4321 TTTT ,,, ……………………………12 分
【020】解:(1)①CF⊥BD,CF=BD
②成立,理由如下:∵∠FAD=∠BAC=90° ∴∠BAD=∠CAF
又 BA=CA ,AD=AF ∴△BAD≌△CAF∴CF=BD ∠ACF=∠ACB=45°
∴∠BCF=90° ∴CF⊥BD ……(1 分)
(2)当∠ACB=45°时可得 CF⊥BC,理由如下:
如图:过点 A 作 AC 的垂线与 CB 所在直线交于 G
则∵∠ACB=45° ∴AG=AC ∠AGC=∠ACG=45°
∵AG=AC AD=AF ………(1 分)
∴△GAD≌△CAF(SAS) ∴∠ACF=∠AGD=45°
∴∠GCF=∠GCA+∠ACF=90° ∴CF⊥BC …………(2 分)
(3)如图:作 AQBC 于 Q
∵∠ACB=45° AC=4 2 ∴CQ=AQ=4
∵∠PCD=∠ADP=90°∴∠ADQ+∠CDP=∠CDP+∠CPD=90°
∴△ADQ∽△ DPC
…(1 分)
∴
DQ
PC = AQ
CD
设 CD 为 x ( 0 < x < 3 ) 则 DQ=CQ - CD=4 - x 则
x
PC
4 = 4
x …………(1 分)
∴PC= 4
1 (-x2+4x)=-
4
1 (x-2)2+1≥1
当 x=2 时,PC 最长,此时 PC=1 ………(1 分)
2010 年中考数学压轴题 100 题精选(31-40 题)答案
【 031 】 解 : ( 1 ) 5 , 24,
5
24 …………………………………3 分
(2)①由题意,得 AP=t,AQ=10-2t. ……………………………………1 分
如图 1,过点 Q 作 QG⊥AD,垂足为 G,由 QG∥BE 得
△AQG∽△ABE,∴
BA
QA
BE
QG ,
∴QG=
25
48
5
48 t , …………………………1 分
∴ ttQGAPS 5
24
25
24
2
1 2 (
2
5 ≤t≤5).
∵ 6)2
5(25
24 2 tS (
2
5 ≤t≤5).
∴当 t=
2
5 时,S 最大值为 6.…………………1 分
② 要使△APQ 沿它的一边翻折,翻折前后的两个三角形 组成
的四边形为菱形,根据轴对称的性质,只需△APQ 为等腰三角形即可.
当 t=4 秒时,∵点 P 的速度为每秒 1 个单位,∴AP= 4 .………………1 分
以下分两种情况讨论:
第一种情况:当点 Q 在 CB 上时, ∵PQ≥BE>PA,∴只存在点 Q1,使 Q1A=Q1P.
如图 2,过点 Q1 作 Q1M⊥AP,垂足为点 M,Q1M 交 AC 于点 F,则 AM= 1 22 AP .
由△AMF∽△AOD∽△CQ1F,得
4
3
1
1
AO
OD
CQ
FQ
AM
FM ,
2
3FM ,
∴
10
33
11 FMMQFQ . … … … … ……1 分
∴CQ1= QF3
4 = 22
5
.则
1
1
CQ
AP
tk
t
,
∴ 1 11
10
CQk AP
.……………………………1 分
第二种情况:当点 Q 在 BA 上时,存在两点 Q2,Q3,
分别使 A P= A Q2,PA=PQ3.
①若 AP=AQ2,如图 3,CB+BQ2=10-4=6.
则
2
1
BQCB
AP
tk
t
,∴ 2 3
2
CB BQk AP
.……1 分
②若 PA=PQ3,如图 4,过点 P 作 PN⊥AB,垂足为 N,
由△ANP∽△AEB,得
AB
AP
AE
AN .
∵AE=
5
722 BEAB , ∴AN= 28
25
.
∴AQ3=2AN= 56
25
, ∴BC+BQ3=10-
25
194
25
56
则
3
1
BQCB
AP
tk
t
.∴
50
973
AP
BQCBk .
………………………1 分
综上所述,当 t= 4 秒,以所得的等腰三角形 APQ 沿底边翻折,
翻折后得到菱形的 k 值为
10
11 或
2
3 或
50
97 .
�
G
�
x
�
y
�
A
�
B
�
C
�
D
�
O
�
E
�
(图1)�
�
P
�
Q
�
(图3)
�
x
�
y
�
A
�
B
�
C
�
D
�
O
�
Q
�
2
�
P
�
N
�
E
�
(图4)
�
x
�
y
�
A
�
B
�
C
�
D
�
O
�
Q
�
3
�
P
�
E
�
Q
�
1
�
F
�
M
�
O
�
D
�
C
�
B
�
A
�
y
�
x
�
(图2)
�
P
【032】解:(1)在△ABC 中,∵ 1AC , xAB , xBC 3 .
∴
xx
xx
31
31 ,解得 21 x . ·····································································4 分
(2)①若 AC 为斜边,则 22 )3(1 xx ,即 0432 xx ,无解.
②若 AB 为斜边,则 1)3( 22 xx ,解得
3
5x ,满足 21 x .
③若 BC 为斜边,则 22 1)3( xx ,解得
3
4x ,满足 21 x .
∴
3
5x 或
3
4x . ························································································ 9 分
(3)在△ABC 中,作 ABCD 于 D,
设 hCD ,△ABC 的面积为 S,则 xhS 2
1 .
①若点 D 在线段 AB 上,
则 xhxh 222 )3(1 .
∴ 22222 112)3( hhxxhx ,即 431 2 xhx .
∴ 16249)1( 222 xxhx ,即 16248 222 xxhx .
∴ 4624
1 2222 xxhxS 2
1)2
3(2 2 x ( 4 23 x ≤ ). ·························· 11 分
当
2
3x 时(满足 4 23 x ≤ ), 2S 取最大值
2
1 ,从而 S 取最大值
2
2 .····················13 分
②若点 D 在线段 MA 上,
则 xhhx 222 1)3( .
同理可得, 4624
1 2222 xxhxS
2
1)2
3(2 2 x ( 41 3x ≤ ),
易知此时
2
2S .
综合①②得,△ABC 的最大面积为
2
2 .···························································· 14 分
【033】
C
A B NM
(第 24 题-1)
D
C
BADM N
(第 24 题-2)
第(2)题
x
y
B
C
O
D
A
M
N N′
x
y
B
C
O
A
M
N
P1
P2
备用图
(1) 4 11 1 3 3M a N a a
, , , .……………4 分
(2)由题意得点 N 与点 N ′关于 y 轴对称, N 4 1
3 3a a
, ,
将 N ′的坐标代入 2 2y x x a 得 21 16 8
3 9 3a a a a ,
1 0a (不合题意,舍去), 2
9
4a .……………2 分
33 4N
, ,点 N 到 y 轴的距离为 3.
90 4A , , N 33 4
, ,直线 AN 的解析式为 9
4y x ,
它与 x 轴的交点为 9 04D
, , 点 D 到 y 轴的距离为 9
4 .
1 9 1 9 9 18932 2 2 2 4 16ACN ACDADCNS S S △ △四边形 .……………2 分
(3)当点 P 在 y 轴的左侧时,若 ACPN 是平行四边形,则 PN 平行且等于 AC ,
把 N 向上平移 2a 个单位得到 P ,坐标为 4 7
3 3a a
, ,代入抛物线的解析式,
得: 27 16 8
3 9 3a a a a
1 0a (不舍题意,舍去), 2
3
8a , 1
2P
7,8 .……………2 分
当点 P 在 y 轴的右侧时,若 APCN 是平行四边形,则 AC 与 PN 互相平分,
OA OC OP ON , .
P 与 N 关于原点对称, 4 1
3 3P a a
, ,
将 P 点坐标代入抛物线解析式得: 21 16 8
3 9 3a a a a ,
1 0a (不合题意,舍去), 2
15
8a , 5 5
2 8P
, .……………2 分
存在这样的点 1
1 7
2 8P
, 或 2
5 5
2 8P
, ,能使得以 P A C N, , , 为顶点的四边形是平行四边
形.
【034】解:(1)2 3 . ……………2 分
(2)证明:在 BB 上取点 P ,使 120BPC °,
连结 AP ,再在 PB 上截取 PE PC ,连结CE .
120BPC °, 60EPC °, PCE△ 为正三角形,
60PC CE PCE CEB , °, =120°,
ACB△ 为正三角形, AC B C ACB, = 60°,
PCA ACE ACE ECB = 60°,
PCA ECB ′, ACP B△ ≌△ CE .
APC B 120CE PA EB °, ,
120APB APC BPC °, P 为 ABC△ 的费马点,
BB 过 ABC△ 的费马点 P ,且 BB = EB + PB PE PA PB PC .………2 分
【035】解:(1) Q (1,0)··············································································1 分
点 P 运动速度每秒钟 1 个单位长度.··································································2 分
(2) 过点 B 作 BF⊥y 轴于点 F , BE ⊥ x 轴于点 E ,则 BF =8, 4OF BE .
∴ 10 4 6AF .
在 Rt△AFB 中, 2 28 6 10AB 3 分
过点 C 作 CG ⊥ x 轴于点 G ,与 FB 的延长线交于点 H .
∵ 90 ,ABC AB BC ∴△ABF≌△BCH.
∴ 6, 8BH AF CH BF .
∴ 8 6 14, 8 4 12OG FH CG .
∴所求 C 点的坐标为(14,12). 4 分
(3) 过点 P 作 PM⊥y 轴于点 M,PN⊥ x 轴于点 N,
则△APM∽△ABF.
∴ AP AM MP
AB AF BF
.
10 6 8
t AM MP .
∴ 3 4
5 5AM t PM t , . ∴ 3 410 ,5 5PN OM t ON PM t .
设△OPQ 的面积为 S (平方单位)
∴ 21 3 47 3(10 )(1 ) 52 5 10 10S t t t t (0≤ t ≤10) ················································· 5 分
说明:未注明自变量的取值范围不扣分.
∵ 3
10a <0 ∴当
47
4710
3 62 ( )10
t
时, △OPQ 的面积最大.···························6 分
此时 P 的坐标为( 94
15
, 53
10
) .·······································································7 分
A
CB
P
E
第(25)题
B
(4) 当 5
3t 或 295
13t 时, OP 与 PQ 相等.·················································· 9 分
对一个加 1 分,不需写求解过程.
【036】解:(1)由已知,得 (3 0)C , , (2 2)D , ,
90ADE CDB BCD ° ,
1tan 2 tan 2 12AE AD ADE BCD . (01)E , .····················· (1 分)
设过点 E D C、 、 的抛物线的解析式为 2 ( 0)y ax bx c a .将点 E 的坐标代入,得 1c .[来源:学&
将 1c 和点 D C、 的坐标分别代入,得 4 2 1 2
9 3 1 0.
a b
a b
,
································· (2 分)
解这个方程组,得
5
6
13
6
a
b
[来源:学#科#网]
故抛物线的解析式为 25 13 16 6y x x .·········· (3 分)
(2) 2EF GO 成立.············································································· (4 分)
点 M 在该抛物线上,且它的横坐标为 6
5
,点 M 的纵坐标为12
5
.················ (5 分)
设 DM 的解析式为 1( 0)y kx b k ,
将点 D M、 的坐标分别代入,得
1
1
2 2
6 12 .5 5
k b
k b
,
解得
1
1
2
3
k
b
,
.
DM 的解析式为 1 32y x . (0 3)F , , 2EF .·································(7 分)
过点 D 作 DK OC⊥ 于点 K ,则 DA DK . 90ADK FDG °,
FDA GDK .又 90FAD GKD °, DAF DKG△ ≌△ .
1KG AF .[来 1GO . 2EF GO .
(3)点 P 在 AB 上, (1 0)G , , (3 0)C , ,则设 (1 2)P , .
2 2 2( 1) 2PG t , 2 2 2(3 ) 2PC t , 2GC .
①若 PG PC ,则 2 2 2 2( 1) 2 (3 ) 2t t ,
解得 2t . (2 2)P , ,此时点 Q 与点 P 重合. (2 2)Q , .
②若 PG GC ,则 2 2( 1) 2 2t ,解得 1t , (1 2)P , ,此时GP x⊥ 轴.
GP 与该抛物线在第一象限内的交点Q 的横坐标为 1,点Q 的纵坐标为 7
3
. 71 3Q
, .
y
x
D B
C
A
EE
O
MF
KGG
③若 PC GC ,则 2 2 2(3 ) 2 2t ,[来
解得 3t , (3 2)P , ,此时 2PC GC , PCG△ 是等腰直角三角形.
过点 Q 作QH x⊥ 轴于点 H ,则QH GH ,设QH h ,
( 1 )Q h h , .
25 13( 1) ( 1) 16 6h h h .
解得 1 2
7 25h h , (舍去). 12 7
5 5Q
, .(12 分)
综上所述,存在三个满足条件的点Q ,即 (2 2)Q , 或 71 3Q
, 或 12 7
5 5Q
, .
【037】解:(1)设第一象限内的点 B(m,n),则 tan∠POB
9
1
m
n ,得 m=9n,又点 B 在函数
xy 1
的图象上,得
mn 1 ,所以 m=3(-3 舍去),点 B 为 )3
1,3( ,
而 AB∥x 轴,所以点 A(
3
1 ,
3
1 ),所以
3
8
3
13 AB ;
(2)由条件可知所求抛物线开口向下,设点 A(a , a),B(
a
1 ,a),则 AB=
a
1 - a =
3
8 ,
所以 0383 2 aa ,解得
3
13 aa 或 .
当 a = -3 时,点 A(―3,―3),B(―
3
1 ,―3),因为顶点在 y = x 上,所以顶点为(-
3
5 ,
-
3
5 ),所以可设二次函数为
3
5)3
5( 2 xky ,点 A 代入,解得 k= -
4
3 ,所以所求函数解析
式为
3
5)3
5(4
3 2 xy .
同理,当 a =
3
1 时,所求函数解析式为
3
5)3
5(4
3 2 xy ;
(3)设 A(a , a),B(
a
1 ,a),由条件可知抛物线的对称轴为
a
ax 2
1
2
.
设所求二次函数解析式为: )2)1()(2(5
9
aaxxy .
点 A(a , a)代入,解得 31 a ,
13
6
2 a ,所以点 P 到直线 AB 的距离为 3 或
13
6 。
y
x
D B
C
A
EE
O
Q
P
HGG
(P)
(Q)
Q
(P)
【038】解:(1)矩形(长方形); 4
7
BP
BQ
.
(2)① POC B OA , PCO OA B 90 °, COP A OB △ ∽△ .
CP OC
A B OA
,即 6
6 8
CP , 9
2CP , 7
2BP BC CP .····························4 分
同理 B CQ B C O △ ∽△ , CQ B C
C Q B C
,即 10 6
6 8
CQ ,
3CQ , 11BQ BC CQ . 7
22
BP
BQ
.················································6 分
②在 OCP△ 和 B A P △ 中,
90
OPC B PA
OCP A
OC B A
,
°,
,
[来源:学科网 ZXXK]
(AAS)OCP B A P △ ≌△ .········································7 分
OP B P .设 B P x ,[来源:学科网]在 Rt OCP△ 中, 2 2 2(8 ) 6x x ,解得 25
4x .···8 分
1 25 7562 4 4OPBS △ .············································································ 9 分
(3)存在这样的点 P 和点Q ,使 1
2BP BQ .··················································10 分
点 P 的坐标是 1
39 6 62P
, , 2
7 64P
, .·················································· 12 分
对于第(3)题,我们提供如下详细解答,对学生无此要求.
过点 Q 画QH OA⊥ 于 H ,连结OQ ,则QH OC OC ,
1
2POQS PQ OC △ , 1
2POQS OP QH △ ,
PQ OP .设 BP x , 1
2BP BQ , 2BQ x ,
1 如图 1,当点 P 在点 B 左侧时,
3OP PQ BQ BP x ,
在 Rt PCO△ 中, 2 2 2(8 ) 6 (3 )x x ,[来源:学科网 ZXXK]
解得 1
31 62x , 2
31 62x (不符实际,舍去).
39 62PC BC BP , 1
39 6 62P
, .
②如图 2,当点 P 在点 B 右侧时, OP PQ BQ BP x , 8PC x .
Q
C
B
A O x
P
A
B
C
y
H
QCB
A O x
P
A
B
C
y
H
在 Rt PCO△ 中, 2 2 2(8 ) 6x x ,解得 25
4x . PC BC BP 25 78 4 4
,
2
7 64P
, .综上可知,存在点 1
39 6 62P
, , 2
7 64P
, ,使 1
2BP BQ .
【039】(1) 将点 A(-4,8)的坐标代入 2y ax ,解得 1
2a .……1 分
将点 B(2,n)的坐标代入 21
2y x ,求得点 B 的坐标为(2,2),
则点 B 关于 x 轴对称点 P 的坐标为(2,-2). ……1 分
直线 AP 的解析式是 5 4
3 3y x . ……1 分
令 y=0,得 4
5x .即所求点 Q 的坐标是( 4
5
,0). ……1 分
(2)① 解法 1:CQ=︱-2- 4
5
︱=14
5
, ……1 分
故将抛物线 21
2y x 向左平移 14
5
个单位时,A′C+CB′最短,
此时抛物线的函数解析式为 21 14( )2 5y x . ……1 分
解法 2:设将抛物线 21
2y x 向左平移 m 个单位,则平移后 A′,B′的
坐标分别为 A′(-4-m,8)和 B′(2-m,2),点 A′关于 x 轴对称点的坐
标为 A′′(-4-m,-8).
直线 A′′B′的解析式为 5 5 4
3 3 3y x m . 要使 A′C+CB′最短,点
C 应在直 线 A′′B′上,将点 C(-2,0)代入直线 A′′B′的解析式,
解得 14
5m .
故将抛物线 21
2y x 向左平移14
5
个单位时 A′C+CB′最短,此时抛物线
的函数解析式为 21 14( )2 5y x . ……1 分
② 左右平移抛物线 21
2y x ,因为线段 A′B′和 CD 的长是定值,所以要使四边形 A′B′CD 的
周长最短,只要使 A′D+CB′最短; ……1
分
第一种情况:如果将抛物线向右平移,显然有 A′D+CB′>AD+CB,因此不存
在某个位置,使四边形 A′B′CD 的周长最短.……1 分
第二种情况:设抛物线向左平移了 b 个单位,则点 A′和点 B′的坐标分别为
A′(-4-b,8)和 B′(2-b,2).
因为 CD=2,因此将点 B′向左平移 2 个单位得 B′′(-b,2),
要使 A′D+CB′最短,只要使 A′D+DB′′最短. ……1 分
点 A′关于 x 轴对称点的坐标为 A′′(-4-b,-8),直线 A′′B′′的解析式
为 5 5 22 2y x b .要使 A′D+DB′′最短,点 D 应在直线 A′′B′′上,
(第 24 题(1))
4 x2
2
A 8
-2O
-2
-4
y
6
B
CD
-4
4
Q
P
(第 24 题(2)①)
4 x2
2
A′ 8
-2O
-2
-4
y
6
B′
CD
-4
4
A′′
(第 24 题(2)②)
4 x2
2
A′ 8
-2O
-2
-4
y
6
B′
CD
-4
4
A′′
B′′
将点 D(-4,0)代入直线 A′′B′′的解析式,解得 16
5b .故将抛物线向左平移时,存在某个位置,
使四边形 A′B′CD 的周长最短,此时抛物线的函数解析式为 21 16( )2 5y x .……1 分
【040】(1)解 ①如图 1,当 B 在△ABC 内时,重叠部分是平行四边形,由题意得:
2
232 x 解得 x=
2
3 ……(2 分)
②如图 3,当 A 在△ABC 内时,重叠部分是平行四边形,由题意得:
A N= x26 列式得( x26 )× 2 =
2
23
解得 x= 26 2
3 ……(2 分)
综上所述,当△ CBA 与△ ABC 重叠部分面积 为 22
3 平方厘米时,△ CBA 移动的时
间为
2
3 或( 26 2
3 )秒。
(2) ①如图 1,当 0≤x≤ 22 时 xy 2 ……(1 分)
②如图 2,当 22 ≤x≤ 24 时,如图,△D B N, △ MEA ,△ FGC 是等腰直角三角形,
B N= 2x ,GF=MN= 22 , xMA 24
22 )24(4
1)22(4
1222
1442
1 xxy
即 4232
1 2 xxy …(3 分)
③如图 3,当 24 ≤x≤ 26 时, 122 xy …(1 分)
(3)①当 0≤x≤ 22 时, 4=
最大值y ……(1 分)
②当 22 ≤x≤ 24 时, 5=
最大值y ……(2 分)
③当 24 ≤x≤ 26 时, 4=
最大值y ……(1 分)
图 3图 1 图 2
所以,△ CBA 与△ ABC 重叠部分面积的最大值为 5。
2010 年中考数学压轴题 100 题精选(41-50 题)答案
【041】(1)如图 (3 分)
(2)2 次·································································································(5 分)
(3)如图,设直线 AB 的解析式为 1 1y k x b ,
图象过 (4 0) (6150)A B,, , ,
1 1
1 1
4 0
6 150.
k b
k b
, 1
1
75
300.
k
b
,
75 300y x .①········································(7 分)
设直线CD 的解析式为 2 2y k x b ,
图象过 (7 0) (5150)C D,, , ,
2 2
2 2
7 0
5 150.
k b
k b
, 2
2
75
525.
k
b
,
75 525y x .②··································· (7 分)
解由①、②组成的方程组得 5.5
112.5.
x
y
,
最后一次相遇时距离乌鲁木齐市的距离为 112.5 千米. (12 分)
【042】解:(1)∵点 D 是OA 的中点,∴ 2OD ,∴OD OC .
又∵ OP 是 COD 的角平分线,∴ 45POC POD °,
∴ POC POD△ ≌△ ,∴ PC PD .······························································· 3 分
(2)过点 B 作 AOC 的平分线的垂线,垂足为 P ,点 P 即为所求.
易知点 F 的坐标为(2,2),故 2BF ,作 PM BF⊥ ,
∵ PBF△ 是等腰直角三角形,∴ 1 12PM BF ,
∴点 P 的坐标为(3,3).
y(千米)
x(小时)
150
100
50
-1 10 2 3 4 5 6 7 8
A C
BD
E
y
O xD
B
(4 0)A ,
C
P
E
(0 2), F
M
∵抛物线经过原点,∴设抛物线的解析式为 2y ax bx .
又∵抛物线经过点 (3 3)P , 和点 (2 0)D , ,∴有 9 3 3
4 2 0
a b
a b
解得 1
2
a
b
∴抛物线的解析式为 2 2y x x .·····································································7 分
(3)由等腰直角三角形的对称性知 D 点关于 AOC 的平分线的对称点即为 C 点.
连接 EC ,它与 AOC 的平分线的交点即为所求的 P 点(因为 PE PD EC ,而两点之间线段
最短),此时 PED△ 的周长最小.
∵抛物线 2 2y x x 的顶点 E 的坐标 (1 1), ,C 点的坐标 (0 2), ,
设CE 所在直线的解析式为 y kx b ,则有 1
2
k b
b
,解得 3
2
k
b
.
∴CE 所在直线的解析式为 3 2y x .
点 P 满足 3 2y x
y x
,解得
1
2
1
2
x
y
,故点 P 的坐标为 1 1
2 2
, .
PED△ 的周长即是 10 2CE DE .
(4)存在点 P ,使 90CPN °.其坐标是 1 1
2 2
, 或 (2 2), .····························· 14 分
【043】解(Ⅰ) 2
1 2 1 2 0y x y x bx c y y , , ,
2 1 0x b x c .··············································································· 1 分
将 1 1
3 2
, 分别代入 2 1 0x b x c ,得
2 21 1 1 11 0 1 03 3 2 2b c b c
, ,
解得 1 1
6 6b c , .函数 2y 的解析式为 2y 2 5 1
6 6x x .·····························3 分
(Ⅱ)由已知,得 2
6AB ,设 ABM△ 的高为 h ,
3
1 2 1
2 12 12ABMS AB h h △ · ,即 12 144h .
根据题意, 2t T h ,由 2 1 1
6 6T t t ,得 2 5 1 1
6 6 144t t .
当 2 5 1 1
6 6 144t t 时,解得 1 2
5
12t t ;
当 2 5 1 1
6 6 144t t 时 , 解 得
3 4
5 2 5 2
12 12t t , .
t 的值为 5 5 2 5 2
12 12 12
, , .·····································································
( Ⅲ ) 由 已 知 , 得
2 2 2b c b c T t bt c , , .
T t t b , T t t b ,
2 2b c b c ,化简得 1 0b .
0 1 ,得 0 , 1 0b .
有 1 0 1 0b b , .
又 0 1t , 0t b , 0t b ,
当 0 t a ≤ 时,T ≤ ≤ ;当 t ≤ 时, T ≤ ;
当 1t 时, T .············································································· 10 分
【044】(1) 配方,得 y= 1
2
(x–2)2 –1,∴抛物线的对称轴为直线 x=2,顶点为 P(2,–1) .
取 x=0 代入 y= 1
2
x2 –2x+1,得 y=1,∴点 A 的坐标是(0,1).由抛物线的对称性知,点 A(0,
1)与点 B 关于直线 x=2 对称,∴点 B 的坐标是(4,1). 2 分
设直线 l 的解析式为 y=kx+b(k≠0),将 B、P 的坐标代入,有
1 4 ,
1 2 ,
k b
k b
解得 1,
3.
k
b
∴直线 l 的解析式为 y=x–3.3 分
(2) 连结 AD 交 O′C 于点 E,∵ 点 D 由点 A 沿 O′C 翻折后得到,∴ O′C 垂直平分 AD.[来源:Z。xx。k.Com]
由(1)知,点 C 的坐标为(0,–3),∴ 在 Rt△AO′C 中,O′A=2,AC=4,∴ O′C=2 5 .
据面积关系,有 1
2
×O′C×AE= 1
2
×O′A×CA,∴ AE= 4 55
,AD=2AE= 8 55
.
作 DF⊥AB 于 F,易证 Rt△ADF∽Rt△CO′A,∴ AF DF AD
AC O A O C
,
∴ AF= AD
O C ·AC= 16
5
,DF= AD
O C ·O′A= 8
5
,5 分
又 ∵OA=1,∴点 D 的纵坐标为 1– 8
5
= – 3
5
,
∴ 点 D 的坐标为( 16
5
,– 3
5
).
(3) 显然,O′P∥AC,且 O′为 AB 的中点,
∴ 点 P 是线段 BC 的中点,∴ S△DPC= S△DPB .
故要使 S△DQC= S△DPB,只需 S△DQC=S△DPC .
过 P 作直线 m 与 CD 平行,则直线 m 上的任意一点与 CD 构成的三角形的面积都等于 S△DPC ,故
m 与抛物线的交点即符合条件的 Q 点.
容易求得过点 C(0,–3)、D( 16
5
,– 3
5
)的直线的解析式为 y= 3
4
x–3,
据直线 m 的作法,可以求得直线 m 的解析式为 y= 3
4
x– 5
2
.[来源:学_科_网]
令 1
2
x2–2x+1= 3
4
x– 5
2
,解得 x1=2,x2= 7
2
,代入 y= 3
4
x– 5
2
,得 y1= –1,y2= 1
8
,
因此,抛物线上存在两点 Q1(2,–1)(即点 P)和 Q2( 7
2
, 1
8
),使得 S△DQC= S△DPB.
【045】(1)将 A(0,1)、B(1,0)坐标代入 21
2y x bx c 得
1
1 02
c
b c
解得
3
2
1
b
c
∴抛物线的解折式为 21 3 12 2y x x …(2 分)
(2)设 点 E 的横 坐标 为 m ,则 它的 纵坐 标为
21 3 12 2m m
即 E 点的坐标( m , 21 3 12 2m m )又∵点 E 在直线
1 12y x 上[来源:Z§xx§k.Com]
∴ 21 3 11 12 2 2m m m 解得 1 0m (舍去), 2 4m
∴E 的坐标为(4,3)……(4 分)
(Ⅰ)当 A 为直角顶点时
过 A 作 AP1 ⊥DE 交 x 轴于 P1 点,设 P1(a,0) 易知 D 点坐标为(-2,0) 由 Rt△AOD
∽Rt△POA 得
DO OA
OA OP
即 2 1
1 a
,∴a=
2
1 ∴P1(
2
1 ,0)……(5 分)
(Ⅱ)同理,当 E 为直角顶点时,P2 点坐标为(11
2
,0)……(6 分)
(Ⅲ)当 P 为直角顶点时,过 E 作 EF⊥x 轴于 F,设 P3(b 、3 )由∠OPA+∠FPE=90°,得∠
OPA=∠FEP Rt△AOP∽Rt△PFE
由 AO OP
PF EF
得 1
4 3
b
b
解得 1 3b , 2 1b
∴此时的点 P3 的坐标为(1,0)或(3,0)……(8 分)
综上所述,满足条件的点 P 的坐标为(
2
1 ,0)或(1,0)或(3,0)或(11
2
,0)[来源:学科网](Ⅲ)
抛物线的对称轴为 3
2x …(9 分)∵B、C 关于 x=
2
3 对称 ∴MC=MB
要使| |AM MC 最大,即是使| |AM MB 最大
由三角形两边之差小于第三边得,当 A、B、M 在同一直线上时| |AM MB 的值最大.易知直
线 AB 的解折式为 1y x ∴由
1
3
2
y x
x
得
3
2
1
2
x
y
∴M(
2
3 ,-
2
1 )……(11 分)
【046】网](1)解:由 2 8 03 3x ,得 4x A . 点坐标为 4 0 , .
由 2 16 0x ,得 8x B . 点坐标为 8 0, .∴ 8 4 12AB .······························ ( 2
分)
由
2 8
3 3
2 16
y x
y x
,
.
解得 5
6
x
y
,
.∴C 点的坐标为 5 6, .··················································( 3
分)
∴ 1 1 12 6 362 2ABC CS AB y △ · .······································································( 4
分)
(2)解:∵点 D 在 1l 上且 2 88 8 83 3D B Dx x y , .
∴ D 点坐标为 8 8, .(5 分)又∵点 E 在 2l 上且 8 2 16 8 4E D E Ey y x x , . .
∴ E 点坐标为 4 8, .(6 分)∴ 8 4 4 8OE EF , .(7 分)
(3)解法一: ① 当 0 3t ≤ 时,如图 1,矩形 DEFG 与 ABC△ 重叠部分为五边形 CHFGR
( 0t 时,为四边形CHFG ).过C 作CM AB 于 M ,则 Rt RtRGB CMB△ ∽ △ .
A
D
B
E
O
R
F x
y
1l2l
M
(图 3)
G
C
A
D
B
E
O
C
F x
y
1l2l
G
(图 1)
R
M A
D
B
E
O
C
F x
y
1l2l
G
(图 2)
R
M
∴ BG RG
BM CM
,即
3 6
t RG ,∴ 2RG t . Rt RtAFH AMC △ ∽ △ ,
∴ 1 1 236 2 8 82 2 3ABC BRG AFHS S S S t t t t △ △ △ .
即
24 16 44
3 3 3S t t .
【047】解:方法一:如图(1-1),连接 BM EM BE, , .
由题设,得四边形 ABNM 和四边形 FENM 关于直线 MN 对称.
∴ MN 垂直平分 BE .∴ BM EM BN EN , .·············································· 1 分
∵四边形 ABCD 是正方形,∴ 90 2A D C AB BC CD DA °, .
∵ 1 12
CE CE DECD
, .设 BN x ,则 NE x , 2NC x .
在 Rt CNE△ 中, 2 2 2NE CN CE .∴ 22 22 1x x .解得 5
4x ,即 5
4BN .3 分
在 Rt ABM△ 和在 Rt DEM△ 中, 2 2 2AM AB BM , 2 2 2DM DE EM ,
2 2 2 2AM AB DM DE .········································································ 5 分
设 AM y ,则 2DM y ,∴ 22 2 22 2 1y y .
解得 1
4y ,即 1
4AM . ∴ 1
5
AM
BN
.·········································· 7 分
方法二:同方法一, 5
4BN .········································································ 3 分
如图(1-2),过点 N 做 NG CD∥ ,交 AD 于点G ,连接 BE.
∵ AD BC∥ ,∴四边形GDCN 是平行四边形.
∴ NG CD BC .
同理,四边形 ABNG 也是平行四边形.∴ 5
4AG BN .
∵ 90MN BE EBC BNM , °.
N
图(1-1)
A
B C
D
E
FM
N
图(1-2)
A
B C
D
E
FM G
90NG BC MNG BNM EBC MNG , °, .
在 BCE△ 与 NGM△ 中
90
EBC MNG
BC NG
C NGM
,
,
°.
∴ BCE NGM EC MG△ ≌△ , .··························5分
∵ 11 4AM AG MG AM 5, = .4 ∴ 1
5
AM
BN
.·····································7 分
类比归纳
2
5
(或 4
10
); 9
17
; 2
2
1
1
n
n
2 2
2 2
2 1
1
n m n
n m
········································· 12 分
【048】解:(1)由题意得 6=a(-2+3)(-2-1),∴a=-2,
∴抛物线的函数解析式为 y=-2(x+3)(x-1)与 x 轴交于 B(-3,0)、A(1,0)
设直线 AC 为 y=kx+b,则有 0=k+b,6=-2k+b,解得 k=-2,b=2,
∴直线 AC 为 y=-2x+2
(2)①设 P 的横坐标为 a(-2≤a≤1),则 P(a,-2a+2),M(a,-2a2-4a+6)
∴PM=-2a2-4a+6-(-2a+2)=-2a2-2a+4=-2a2+a+14+92
=-2a+122+92,∴当 a=-12 时,PM 的最大值为 926 分
②M1(0,6)M2-14,678
【049】解:(1)由题意得 12
9 3 0
2
b
a
a b c
c
解得
2
3
4
3
2
a
b
c
∴此抛物线的解析式为 22 4 23 3y x x ··················································3 分
(2)连结 AC 、 BC .因为 BC 的长度一定,所以 PBC△ 周长最小,就是使 PC PB 最小. B 点
关于对称轴的对称点是 A 点, AC 与对称轴 1x 的交点即为所求的点 P .
设直线 AC 的表达式为 y kx b 则 3 0
2
k b
b
,
解得
2
3
2
k
b
∴此直线的表达式为 2 23y x .
把 1x 代入得 4
3y ∴ P 点的坐标为 41 3
,
(3) S 存在最大值,理由:∵ DE PC∥ ,即 DE AC∥ .
∴ OED OAC△ ∽△ .∴ OD OE
OC OA
,即 2
2 3
m OE .
∴ 3 33 32 2OE m AE OE m , ,
方法一:连结 OP , OED POE POD OEDPDOES S S S S S △ △ △ △四边形
(第 24 题图)
OA
C
x
y
B
E
P
D
= 1 3 4 1 1 33 2 1 3 22 2 3 2 2 2m m m m [来源:Z。xx。k.Com]
= 23 3
4 2m m
,
∵ 3 04
∴当 1m 时, 3 3 3
4 2 4S 最大 ·················9 分
方法二: OAC OED AEP PCDS S S S S △ △ △ △
= 1 1 3 1 3 4 13 2 3 2 12 2 2 2 2 3 2m m m m
= 223 3 3 314 2 4 4m m m
,
∵ 3 04
∴当 1m 时, 3
4S 最大 ·····················9 分
【050】解:(1)∵ PE AB∥ ∴ DE DP
DA DB
.而 10DE t DP t , ,
∴ 10
6 10
t t ,∴ 15
4t .∴当 15 (s)4t PE AB , ∥ .
(2)∵ EF 平行且等于CD ,[来源:学科网]
∴四边形 CDEF 是平行四边形.
∴ DEQ C DQE BDC , .
∵ 10BC BD ,∴ DEQ C DQE BDC .∴ DEQ BCD△ ∽△ .
∴ DE EQ
BC CD
.
10 4
t EQ .∴ 2
5EQ t .
过 B 作 BM CD⊥ ,交CD 于 M ,过 P 作 PN EF⊥ ,交 EF 于 N .
2 210 2 100 4 96 4 6BM .∵ ED DQ BP t ,
∴ 10 2PQ t .又 PNQ BMD△ ∽△ , PQ PN
BD BM
,10 2
10 4 6
t PN ,
4 6 1 5
tPN ,
21 1 2 4 6 4 64 6 12 2 5 5 25 5PEQ
tS EQ PN t t t △ .
(3) 1 1 4 4 6 8 62 2BCDS CD BM △ .
若 2
25PEQ BCDS S△ △ ,则有 24 6 4 6 2 8 625 5 25t t ,解得 1 21 4t t , .
(4)在 PDE△ 和 FBP△ 中, 10
DE BP t
PD BF t PDE FBP
PDE FBP
,
, △ ≌△
,
∴ PDEPFCDE PFCDS S S △五边形 四边形 FBP PFCDS S △ 四边形 8 6BCDS △ .
A E D
Q
P
B F C
N M
∴在运动过程中,五边形 PFCDE 的面积不变.
2010 年中考数学压轴题 100 题精选(51-60 题)答案
【051】解:(1) 3k ,(-1,0),B(3,0).··················3 分
(2)如图 14(1),抛物线的顶点为 M(1,-4),连结 OM.
则 △AOC 的面积=
2
3 ,△MOC 的面积=
2
3 ,△MOB 的面积=6,∴ 四边形 ABMC 的面积=△AOC
的面积+△MOC 的面积+△MOB 的面积=9.··························6 分
说明:也可过点 M 作抛物线的对称轴,将四边形 ABMC 的面
积转化为求 1 个梯形与 2 个直角三角形面积的和.
(3)如图 14(2),设 D(m, 322 mm ),连结 OD.
则 0<m<3, 322 mm <0. 且 △AOC 的面积=
2
3 ,△DOC 的面积= m2
3 ,
△DOB 的面积=-
2
3 ( 322 mm ),
∴ 四边形 ABDC 的面积=△AOC 的面积+△DOC 的面积+△DOB 的面积
= 62
9
2
3 2 mm =
8
75)2
3(2
3 2 m .
∴ 存在点 D 3 15( )2 4
, ,使四边形 ABDC 的面积最大为
8
75 .
(4)有两种情况:
如图 14(3),过点 B 作 BQ1⊥BC,交抛物线于点 Q1、交 y 轴于点 E,连接 Q1C.
∵ ∠CBO=45°,∴∠EBO=45°,BO=OE=3.
∴ 点 E 的坐标为(0,3). ∴ 直线 BE 的解析式为 3y x .······················12 分
由 2
3
2 3
y x
y x x
,
解得 1
1
2
5
x
y
,
;
ì =-ïïíï =ïî
2
2
3
0.
x
y
,ì =ïïíï =ïî
∴ 点 Q1 的坐标为(-2,5).······· 13 分
如图 14(4),过点 C 作 CF⊥CB,交抛物线于点 Q2、交 x 轴于点 F,连接 BQ2.
∵ ∠CBO=45°,∴∠CFB=45°,OF=OC=3.
∴ 点 F 的坐标为(-3,0).∴ 直线 CF 的解析式为 3y x .······················14 分
由 2
3
2 3
y x
y x x
,
解得 1
1
0
3
x
y
,
;
ì =ïïíï =-ïî
2
2
1
4
x
y
,
.
ì =ïïíï =-ïî
∴点 Q2 的坐标为(1,-4).综上,在抛物线上存在点 Q1(-2,5)、Q2(1,-4),
使△BCQ1、△BCQ2 是以 BC 为直角边的直角三角形.
图 14(2)
图 14(3) 图 14(4)
【052】解:(1)根据题意,得
0
4 2 0
2.
a b c
a b c
c
,
,
解得 1 3 2a b c , , . 2 3 2y x x .(2 分)
(2)当 EDB AOC△ ∽△ 时,得 AO CO
ED BD
或 AO CO
BD ED
,
∵ 1 2 2AO CO BD m , , ,当 AO CO
ED BD
时,得 1 2
2ED m
,
∴ 2
2
mED ,∵点 E 在第四象限,∴ 1
2
2
mE m
, .·································(4 分)
当 AO CO
BD ED
时,得 1 2
2m ED
,∴ 2 4ED m ,
∵点 E 在第四象限,∴ 2 ( 4 2 )E m m, .························································ (6 分)
(3)假设抛物线上存在一点 F ,使得四边形 ABEF 为平行四边形,则
1EF AB ,点 F 的横坐标为 1m ,
当点 1E 的坐标为 2
2
mm
, 时,点 1F 的坐标为 21 2
mm
, ,
∵点 1F 在抛物线的图象上,∴ 22 ( 1) 3( 1) 22
m m m ,∴ 22 11 14 0m m ,
∴ (2 7)( 2) 0m m ,∴ 7 22m m , (舍去),∴ 1
5 3
2 4F
, ,
∴ 3 31 4 4ABEFS .··············································································(9 分)
当点 2E 的坐标为 ( 4 2 )m m, 时,点 2F 的坐标为 ( 1 4 2 )m m , ,
∵点 2F 在抛物线的图象上,∴ 24 2 ( 1) 3( 1) 2m m m ,∴ 2 7 10 0m m ,
∴ ( 2)( 5) 0m m ,∴ 2m (舍去), 5m ,∴ 2 (4 6)F , ,∴ 1 6 6ABEFS .
【053】解:(1)设 ( 1)( 3)y a x x ,把 (0 3)C , 代入,得 1a ,······················· 2 分
∴抛物线的解析式为: 2 2 3y x x .顶点 D 的坐标为 (1 4), .···························5 分
(2)设直线 BD 解析式为: y kx b ( 0k ),把 B D、 两点坐标代入,
得 3 0
4.
k b
k b
,
解得 2 6k b , .∴直线 AD 解析式为 2 6y x .··················· 7 分
y
xO
BA D
C
(x=m)
(F2)F1
E1 (E2)
21 1 1 ( 2 6) 32 2 2s PE OE xy x x x x ,∴ 2 3 (1 3)s x x x ··············9 分
2
2 9 9 3 93 4 4 2 4s x x x
.·····················································10 分
∴当 3
2x 时, s 取得最大值,最大值为 9
4
.······················································11 分
(3)当 s 取得最大值, 3
2x , 3y ,∴ 3 32P
, .∴四边形 PEOF 是矩形.
作点 P 关于直线 EF 的对称点 P,连接 P E P F 、 .
法一:过 P作 P H y ⊥ 轴于 H , P F 交 y 轴于点 M .
设 MC m ,则 33 2MF m P M m P E , , .
在 Rt P MC△ 中,由勾股定理,
2
2 23 (3 )2 m m
.
解得 15
8m .∵CM P H P M P E ,∴ 9
10P H .
由 EHP EP M △ ∽△ ,可得 EH EP
EP EM
, 6
5EH .∴ 6 93 5 5OH .
∴ P坐标 9 9
10 5
, .····················································································13 分
法二:连接 PP ,交CF 于点 H ,分别过点 H P、 作 PC 的垂线,垂足为 M N、 .
易证 CMH HMP△ ∽△ .∴ 1
2
CM MH
MH PM
.
设CM k ,则 2 4MH k PM k , .∴ 35 2PC k , 3
10k .
由三角形中位线定理, 12 68 45 5PN k P N k , .
∴ 12 3 9
5 2 10CN PN PC ,即 9
10x .
6 93 5 5y PF P N ∴ P坐标 9 9
10 5
, .················································ 13 分
把 P坐标 9 9
10 5
, 代入抛物线解析式,不成立,所以 P不在抛物线上.················ 14 分
【054】(1)由抛物线经过点 A(0,1),C(2,4),
得 2
1,
1 2 2 4.4
c
b c
解得 2,
1.
b
c
(E)
1
123 1 2 3
3
1
D
y
C
BA
P
2
xO F
P
M
H
(E)
1
123 1 2 3
3
1
D
y
C
BA
P
2
xO F
P
M
H
N M
∴抛物线对应的函数关系式为: 21 2 14y x x .··························· (2 分)
(2)当 1t 时,P 点坐标为(1,1),∴Q 点坐标为(2,0).
当 4t 时,P 点坐标为(2,3),∴Q 点坐标为(5,0).························· (5 分)
(3)当 0 t ≤2 时, 21 1( 2 1 1) 12 4S t t .S 21
8t t .
当 2 t ≤5 时, 1 (5 )(2 2 1 2)2S t t .S 21 532 2t t . (8 分)
当 3t 时,S 的最大值为 2.························································(10 分)
【055】(1)过点 B 作 BD x 轴,垂足为 D ,
90 90BCD ACO ACO CAO °, °
BCD CAO ;
又 90BDC COA CB AC °; ,
BCD CAO△ ≌△ , 1 2BD OC CD OA ,
点 B 的坐标为 ( 31) , ;······································ 4 分
(2)抛物线 2 2y ax ax 经过点 ( 31)B , ,则得到1 9 3 2a a ,·····················5 分
解得 1
2a ,所以抛物线的解析式为 21 1 22 2y x x ;········································7 分
(3)假设存在点 P ,使得 ACP△ 仍然是以 AC 为直角边的等腰直角三角形:
① 若以点C 为直角顶点;
则延长 BC 至点 1P ,使得 1PC BC ,得到等腰直角三角形 1ACP△ ,······················· 8 分
过点 1P 作 1PM x 轴, 1 1 1 90CP BC MCP BCD PMC BDC , , °;
1MPC DBC△ ≌△ 12 1CM CD PM BD , ,可求得点 1P(1,-1);········11 分
② 若以点 A 为直角顶点;
则过点 A 作 2AP CA ,且使得 2AP AC ,得到等腰直角三角形 2ACP△ ,············ 12 分
过点 2P 作 2P N y 轴,同理可证 2AP N CAO△ ≌△ ;·········································13 分
2 2 1NP OA AN OC , ,可求得点 2 (21)P , ;·········································· 14 分
经检验,点 1(1 1)P , 与点 2 (21)P , 都在抛物线 21 1 22 2y x x 上.························ 16 分
【056】解:(1) C(3,0);
(2)①抛物线 cbxaxy 2 ,令 x =0,则 y = c , ∴A 点坐标(0,c).
∵ acb 22 ,∴
24
2
4
24
4
4 2 c
a
ac
a
acac
a
bac ,∴点 P 的坐标为(
2,2
c
a
b ).
B
A
D C O M
N
x
y
P1
P2
�
D
�
P
�
2
�
P
�
1
�
y
�
x
B
A
O
∵ PD ⊥ x 轴 于 D , ∴ 点 D 的 坐 标 为 ( 0,2a
b ). … … … … … … … … … … … … … … 5 分
根据题意,得 a=a′,c= c′,∴抛物线 F′的解析式为 cxbaxy '2 .
又 ∵ 抛 物 线 F ′ 经 过 点 D ( 0,2a
b ), ∴ ca
bb
a
ba )2('
4
0 2
2
. … … … … … 6 分
∴ acbbb 4'20 2 .又∵ acb 22 ,∴ '230 2 bbb .∴b:b′=
3
2 .
②由①得,抛物线 F′为 cbxaxy
2
32 .
令 y=0,则 02
32 cbxax . ∴
a
bxa
bx 21 ,2
.
∵点 D 的横坐标为 ,2a
b ∴点 C 的坐标为( 0,a
b ).
设直线 OP 的解析式为 kxy .∵点 P 的坐标为(
2,2
c
a
b ),
∴ ka
bc
22
,∴
222
2 2 b
b
b
b
ac
b
ack ,∴ xby 2
.
∵点 B 是抛物线 F 与直线 OP 的交点,∴ xbcbxax 2
2 .∴
a
bxa
bx 21 ,2
.
∵点 P 的横坐标为
a
b
2
,∴点 B 的横坐标为
a
b .
把
a
bx 代入 xby 2
,得 ca
ac
a
b
a
bby
2
2
2)(2
2
.
∴点 B 的坐标为 ),( ca
b .∴BC∥OA,AB∥OC.(或 BC∥OA,BC =OA),
∴四边形 OABC 是平行四边形.
又∵∠AOC=90°,∴四边形 OABC 是矩形.
【057】(1) )6,0(),0,8( BA
(2)∵ 8OA , 6OB ,∴ 10AB
当点 P 在OB 上运动时, tOP 1 ,
ttOPOAS 482
1
2
1
1 ;
当点 P 在 BA 上运动时,作 OADP 2 于点 D ,
有
AB
AP
BO
DP 22 ∵ ttAP 161062 ,∴
5
348
2
tDP
∴
5
192
5
12
5
34882
1
2
1
2 ttDPOAS
(3)当 124 t 时, 3t , )3,0(1P ,
此时,过 AOP 各顶点作对边的平行线,与坐标轴无第二个交点,所以点 M 不存在;
当 125
192
5
12 t 时, 11t , )3,4(2P ,此时, )3,0(1M 、 )6,0(2 M
【058】解:(1)令 0y ,得 2 1 0x 解得 1x ,令 0x ,得 1y
∴ A ( 1,0) B (1,0) C (0, 1) ·········· 3 分
(2)∵OA=OB=OC=1 ∴ BAC= ACO= BCO= 45
∵AP∥CB,∴ PAB= 45 ,过点 P 作 PE x 轴于 E,
则 APE 为等腰直角三角形
令 OE= a ,则 PE= 1a ∴P ( , 1)a a
∵点 P 在抛物线 2 1y x 上 ∴ 21 1a a
解得 1 2a , 2 1a (不合题意,舍去) ∴PE=3··········································· 4 分
∴四边形 ACBP 的面积 S = 1
2
AB•OC+ 1
2
AB•PE= 1 12 1 2 3 42 2
························ 5 分
(3). 假设存在∵ PAB= BAC = 45 ∴PA AC
∵MG x 轴于点 G, ∴ MGA= PAC =90
在 Rt△AOC 中,OA=OC=1 ∴AC= 2 ,在 Rt△PAE 中,AE=PE=3 ∴AP= 3 2 ····· 6 分
设 M 点的横坐标为 m ,则 M 2( , 1)m m
①点 M 在 y 轴左侧时,则 1m
(ⅰ) 当 AMG ∽ PCA 时,有 AG
PA = MG
CA
∵AG= 1m ,
MG= 2 1m 即
21 1
3 2 2
m m 解得 1 1m (舍去)
2
2
3m (舍去)………7 分
(ⅱ) 当 MAG ∽ PCA 时有 AG
CA = MG
PA
即
21 1
2 3 2
m m
,
解得: 1m (舍去)
2 2m ∴M ( 2,3) ····················································································· 8 分
G
M
C
B
y
P
A o x
G
M
C
B
y
P
A o x
E
C
B
y
P
A o x
② 点 M 在 y 轴右侧时,则 1m
(ⅰ) 当 AMG ∽ PCA 时有 AG
PA = MG
CA
∵AG= 1m ,MG= 2 1m
∴
21 1
3 2 2
m m 解得 1 1m (舍去) 2
4
3m ∴M 4 7( , )3 9
(ⅱ) 当 MAG∽ PCA 时有 AG
CA = MG
PA
即
21 1
2 3 2
m m
解得: 1 1m (舍去) 2 4m ∴M (4,15) ∴存在点 M,使以 A、M、G 三点为顶点的三
角形与 PCA 相似,M 点的坐标为 ( 2,3) , 4 7( , )3 9
, (4,15)
【059】解:(1)∵四边形 ABCD 和四边形 AEFG 是正方形
∴AB=AD,AE=AG,∠BAD=∠EAG=90º
∴∠BAE+∠EAD=∠DAG+∠EAD
∴∠BAE=∠DAG
∴△ BAE≌△DAG …………4 分
(2)∠FCN=45º …………5 分
理由是:作 FH⊥MN 于 H
∵∠AEF=∠ABE=90º
∴∠BAE +∠AEB=90º,∠FEH+∠AEB=90º
∴∠FEH=∠BAE 又∵AE=EF,∠EHF=∠EBA=90º
∴△EFH≌△ABE …………7 分
∴FH=BE,EH=AB=BC,∴CH=BE=FH
∵∠FHC=90º,∴∠FCH=45º …………8 分
(3)当点 E 由 B 向 C 运动时,∠FCN 的大小总保持不变,…………9 分
理由是:作 FH⊥MN 于 H
由已知可得∠EAG=∠BAD=∠AEF=90º
结合(1)(2)得∠FEH=∠BAE=∠DAG
又∵G 在射线 CD 上,∠GDA=∠EHF=∠EBA=90º
∴△EFH≌△GAD,△EFH∽△ABE ……11 分
∴EH=AD=BC=b,∴CH=BE,∴ EH
AB
=FH
BE
=FH
CH
∴在 Rt△FEH 中,tan∠FCN=FH
CH
= EH
AB
=b
a
∴当点 E 由 B 向 C 运动时,∠FCN 的大小总保持不变,tan∠FCN=b
a
【060】解:(1)根据题意,得
4 2 0
36 6 0
a c
a c
,解得
1
4
3
a
c
抛物线的解析式为 21 34y x x ,顶点坐标是(2,4)
(2) (4 3)D , ,设直线 AD 的解析式为 ( 0)y kx b k
M B E
A
C N
D
F
G
图(2)
H
M B E
A
C N
D
F
G
图(1)
H
BA O
C
y
x
第 26 题图
Q4
Q3
Q1
Q2
P3
P1P2
D
C
P4
直线经过点 ( 2 0)A ,、点 (4 3)D , 2 0
4 3
k b
k b
1
2
1
k
b
1 12y x
(3)存在. 1(2 2 2 0)Q , , 2 ( 2 2 2 )Q ,0 , 3 (6 2 6 0)Q , , 4 (6 2 6 0)Q ,
2010 年中考数学压轴题 100 题精选(61-70 题)答案
【061】解(1)A( 4 ,0),B(0,3)···································2 分(每对一个给 1 分)
(2)满分 3 分.其中过 F 作出垂线 1 分,作出 BF 中垂线 1 分,找出圆心并画出⊙P 给 1 分. (注:
画垂线 PF 不用尺规作图的不扣分)
(3)过点 P 作 PD⊥ y 轴于 D,则 PD= x ,BD= 3 y ,············6 分
PB=PF= y ,∵△BDP 为直角三形,∴ 2 2 2PB PD BD
∴ 2 2 2BP PD BD ,即 2 2 23y x y
即 2 2 2(3 )y x y ∴ y 与 x 的函数关系为 21 3
6 2y x
(4)存在
解法 1:∵⊙P 与 x 轴相切于点 F,且与直线l 相切于点 B
∴ AB AF ,∵ 2 2 2 25AB OA OB ,∴ 2 25AF
∵AF= 4x , ∴ 2 2( 4) 5x ,∴ 1 9x x 或 11 分
把 1 9x x 或 代入 21 3
6 2y x ,得 5 153y y 或
∴点 P 的坐标为(1, 5
3
)或( 9,15)12 分
【062】解:实践应用(1)2; l
c
. 1
6
; 1
3
.(2) 5
4
.
拓展联想(1)∵△ABC 的周长为 l,∴⊙O 在三边上自转了 l
c
周.
又∵三角形的外角和是 360°,
∴在三个顶点处,⊙O 自转了 360 1360
(周).
∴⊙O 共自转了( l
c +1)周.
(2) l
c +1.
【063】(1)① 对称轴 4 22x ····························································· (2 分)
② 当 0y 时,有 2 4 3 0x x ,解之,得 1 1x , 2 3x
∴ 点 A 的坐标为( 3 ,0).··························································(4 分)
y
xO
A
B
D P
F
(2)满足条件的点 P 有 3 个,分别为( 2 ,3),(2,3),( 4 , 3 ).······ (7 分)
(3)存在.当 0x 时, 2 4 3 3y x x ∴ 点 C 的坐标为(0,3)
∵ DE∥ y 轴,AO 3,EO 2,AE 1,CO 3
∴ AED△ ∽ AOC△ ∴ AE DE
AO CO
即 1
3 3
DE ∴ DE 1··········(9 分)
∴ DEOCS 梯形
1 (1 3) 22
4
在 OE 上找点 F,使 OF 4
3
,此时 COFS △
1 4 32 3
2,直线 CF 把四边形 DEOC
分成面积相等的两部分,交抛物线于点 M.·················································(10 分)
设直线 CM 的解析式为 3y kx ,它经过点 4 03F
, .则 4 3 03 k ·(11 分)
解之,得 9
4k ∴ 直线 CM 的解析式为 9 34y x ······················· (12 分)
【064】解:(1)抛物线 21 24y x x 与 y 轴的交于点 B,令 x=0 得 y=2.
∴B(0,2)
∵ 2 21 12 ( 2) 34 4y x x x ∴A(—2,3)
(2)当点 P 是 AB 的延长线与 x 轴交点时,
ABPBPA .
当点 P 在 x 轴上又异于 AB 的延长线与 x 轴的交点时,
在点 P、A、B 构成的三角形中, ABPBPA .
综合上述: PA PB AB ≤
(3)作直线 AB 交 x 轴于点 P,由(2)可知:当 PA—PB 最大时,点 P 是所求的点 ····· 8 分
作 AH⊥OP 于 H.∵BO⊥OP,∴△BOP∽△AHP
∴ AH HP
BO OP
由(1)可知:AH=3、OH=2、OB=2,∴OP=4,故 P(4,0)
【065】解:(1)∵AB 是⊙O 的直径(已知)
∴∠ACB=90º(直径所对的圆周角是直角)
∵∠ABC=60º(已知)
∴∠BAC=180º-∠ACB-∠ABC= 30º(三角形的内角和等于 180º)
∴AB=2BC=4cm(直角三角形中,30º锐角所对的直角边等于斜边的一半)
即⊙O 的直径为 4cm.
(2)如图 10(1)CD 切⊙O 于点 C,连结 OC,则 OC=OB=1/2·AB=2cm.
∴CD⊥CO(圆的切线垂直于经过切点的半径)
∴∠OCD=90º(垂直的定义) ∵∠BAC= 30º(已求)
∴∠COD=2∠BAC= 60º ∴∠D=180º-∠COD-∠OCD= 30º∴OD=2OC=4cm ∴BD=OD
-OB=4-2=2(cm)
∴当 BD 长为 2cm,CD 与⊙O 相切.
(3)根据题意得:
BE=(4-2t)cm,BF=tcm;
B
O
A
·
x
y
第 28 题图
PH
如图 10(2)当 EF⊥BC 时,△BEF 为直角三角形,此时△BEF∽△BAC
∴BE:BA=BF:BC 即:(4-2t):4=t:2 解得:t=1
如图 10(3)当 EF⊥BA 时,△BEF 为直角三角形,此时△BEF∽△BCA
∴BE:BC=BF:BA 即:(4-2t):2=t:4 解得:t=1.6
∴当 t=1s 或 t=1.6s 时,△BEF 为直角三角形.
【066】(1)由 11 2C
, 得 (1 2)A , ,代入反比例函数 my x
中,得 2m
∴反比例函数解析式为: 2 ( 0)y xx
····································································· 2 分
解方程组
1 5
2 2
2
y x
y x
由 1 5 2
2 2x x
化简得: 2 5 4 0x x
( 4)( 1) 0x x , 1 24 1x x , 所以 14 2B
, ·························································5 分
(2)无论 P 点在 AB 之间怎样滑动, PMN△ 与 CAB△ 总能相似.因为 B C、 两点纵坐标相
等,所以 BC x∥ 轴.
又因为 AC y∥ 轴,所以 CAB△ 为直角三角形.
同时 PMN△ 也是直角三角形, AC PM BC PN∥ , ∥ .
PMN CAB△ ∽△ .·················································································8 分
(在理由中只要能说出 BC x∥ 轴, 90ACB °即可得分.)
【067】(1)解:∵直角梯形 ABCD,AD BC∥
PD QC ∥
当 PD QC 时,四边形 PQCD
为平行四边形.
由题意可知: 2AP t CQ t ,
8 2t t
3 8t
8
3t
当 8
3t s 时,四边形 PQCD 为平行四边形.·························································3 分
(2)解:设 PQ 与 O⊙ 相切于点 H,
过点 P 作 PE BC ,垂足为 E
直角梯形 ABCD AD BC, ∥
PE AB
由题意可知: 2AP BE t CQ t ,
O
A P D
B Q
C
O
A P D
B Q
C
H
E
22 2BQ BC CQ t
22 2 22 3EQ BQ BE t t t
AB 为 O⊙ 的直径, 90ABC DAB °
AD BC 、 为 O⊙ 的切线
AP PH HQ BQ ,
22 2 22PQ PH HQ AP BQ t t t ·············································· 5 分
在 Rt PEQ△ 中, 2 2 2PE EQ PQ ,
2 2 212 (22 3 ) (22 )t t
即: 28 88 144 0t t , 2 11 18 0t t , ( 2)( 9) 0t t
1 22 9t t , ,因为 P 在 AD 边运动的时间为 8 81 1
AD 秒
而 9 8t , 9t (舍去),当 2t 秒时, PQ 与 O⊙ 相切.···························8 分
【068】解:(1)如图 4,过 B 作 BG OA G 于 ,
则 2 2 2 212 15 10 169 13AB BG GA ( )
过 Q 作 ,于HOAQH
则 2 2 2 2 212 10 2 ) 144 (10 3 )QP QH PH t t t (
··············································································(2 分)
要使四边形 PABQ 是等腰梯形,则 AB QP ,
即 ,13)310(144 2 t
t 5
3
或 5t (此时 PABQ 是平行四边形,不合题意,舍去)······················ (3 分)
(2)当 2t 时, 4 10 2 8 2OP CQ QB , , 。
1 .2
QB QE QD QBCB DE OF AF EF DP OP
∥ ∥ , ·········································(4 分)
2 2 2 4 15 4 19.AF QB OF , ··············································(5 分)
.1741219102
1 )(梯形OFBCS ···························································(6 分)
(3)①当QP PF 时,则 2 212 (10 2 ) 15 2 2t t t t ,
.3
19
3
1 tt 或 ················································································ (7 分)
②当QP QF 时, 222222 )]10(215[1212)210(12 ttFHtt 则
即 2 2 2 2 512 (10 3 ) 12 (5 3 ) 6t t t , ···············································(8 分)
③当QF PF 时, 2 2 4 1412 (5 3 ) 15 ( .3 3t t t 则 , 或 舍去)······· (9 分)
综上,当 1 19 5 4
3 3 6 3t t t t , , , 时,
△
PQF 是等腰三角形.·············· (10 分)
【069】解 (1)易求得点C 的坐标为 (0 )k,
由题设可知 1 2x x, 是方程 0)( 22 mkmx 即 022 kmxx 的两根,
所以
2
1 2
2 ( 2 ) 4
2
m m kx , ,所 1 2 1 22x x m x x k , ·······················
如图 3,∵⊙P 与 y 轴的另一个交点为 D,由于 AB、CD 是⊙P 的两
条相交弦,设它们的交点为点 O,连结 DB,∴△AOC∽△DOC,则
.121
k
k
k
xx
OC
OBOAOD ····································· (2 分)
由题意知点C 在 y 轴的负半轴上,从而点 D 在 y 轴的正半轴上,
所以点 D 的坐标为(0,1)···································································(3 分)
(2)因为 AB⊥CD, AB 又恰好为⊙P 的直径,则 C、D 关于点 O 对称,
所以点C 的坐标为 (0 1), ,即 1k ·····················································(4 分)
又 2 2 2 2
2 1 2 1 1 2( ) 4 ( 2 ) 4 2 2 1AB x x x x x x m k m k m ,
所以 21 1 2 1 1 52 2ABCS AB OC m △ 解得 .2m ··················· (6 分)
【070】解:(1)6.(2)8.········································································(3 分)
(3)①当 0 3x ≤ 时,
2
1
1 1 3 3sin 60 22 2 2 2APQy S AP AQ x x x 1 3△ 1· · ·· · . ······························ (5 分)
②当 3 x ≤ 6 时,
QA B
CD
Q
P
Q
E
P
P
O
1 2 2 2 2
2 2
1
2
1 sin 602
1 3(12- 2 )2 2
APQy S AP P Q
AP CQ
x x
△ = ·
· ·
· ·
= 23 3 3 .2 x x ····················································································· (7 分)
③当 6 9x≤ ≤ 时,设 3 3PQ 与 AC 交于点O .
(解法一)
过 3Q 作 3 ,Q E CB∥ 则 3CQ E△ 为等边三角形.
3 3
3
3 3
2 12.
.
Q E CE CQ x
Q E CB
COP EOQ
∥
△ ∽△
3
3
6 1 ,2 12 2
1 1 (2 12),3 3
CPOC x
OE EQ x
OC CE x
3
3 3
3 3
1 1sin 60 sin 602 2
AQP
ACP COP
y S
S
CP AC OC CP
△
△ △- S
· · ° · · °
1 3 1 1 3( 6) (2 12)( 6)2 2 2 3 2x x x ·6 .
23 7 3 15 36 2x x .···································································· (10 分)
(解法二)
如右图,过点 O 作 3OF CP 于点 F , 3OG CQ ,于点 ,G
过点 3P 作 3P H DC 交 DC 延长线于点 H .
,
.
ACB ACD
OF OG
又 3 3,6, 2 12 2( 6),CP x CQ x x
PO
A B
CD Q G H
F
3 3
1
2CQP COQS S △ △
3 3 3
3 3
2
1 ,3
1 1
3 2
1 1 (2 12)( 6)3 2 2
3 ( 6) .6
COP CP QS S
CQ P H
x x
x
△ △
· ·
3·
又 3 3
1 sin 602ACPS CP AC△ · · °
1 3( 6) 62 2
3 3 ( 6).2
x
x
3AOPy S △
3 3
23 3 3( 6) ( 6)2 6
ACP OCPS S
x x
△ △
23 7 3 15 3.6 2x x ······································································· (10 分)
2010 年中考数学压轴题 100 题精选(71-80 题)答案
【071】解:(1)由题意得
12
9 3 0
2
b
a
a b c
c
,解得
2
3
4
3
2
a
b
c
∴此抛物线的解析式为 22 4 23 3y x x 3 分
(2)连结 AC 、 BC .因为 BC 的长度一定,所以 PBC△ 周长最小,就是使 PC PB 最
小. B 点关于对称轴的对称点是 A 点, AC 与对称轴 1x 的交点即为所求的点 P .
设直线 AC 的表达式为 y kx b
则 3 0
2
k b
b
,
解得
2
3
2
k
b
∴此直线的表达式为 2 23y x .……5 分
把 1x 代入得 4
3y ∴ P 点的坐标为 41 3
, ···································6 分
(3) S 存在最大值··············································································7 分
理由:∵ DE PC∥ ,即 DE AC∥ .
∴ OED OAC△ ∽△ .∴ OD OE
OC OA
,即 2
2 3
m OE .
∴ 3 33 32 2OE m AE OE m , ,
方法一:
连结 OP OED POE POD OEDPDOES S S S S S △ △ △ △四边形
= 1 3 4 1 1 33 2 1 3 22 2 3 2 2 2m m m m
= 23 3
4 2m m ·················································································8 分
∵ 3 04
,∴当 1m 时, 3 3 3
4 2 4S 最大 ·····································9 分
方法二:
OAC OED AEP PCDS S S S S △ △ △ △
= 1 1 3 1 3 4 13 2 3 2 12 2 2 2 2 3 2m m m m
= 223 3 3 314 2 4 4m m m ························································8 分
∵ 3 04
,∴当 1m 时, 3
4S 最大 ···················································9 分
【072】解:(1)① 2AB , 8 42OA , 4OC ,S 梯形 OABC=12
②当 42 t 时,直角梯形 OABC 被直线l 扫过的面积=直角梯形 OABC 面积-直角三角开 DOE 面积
2112 (4 ) 2(4 ) 8 42S t t t t
(2) 存在 , 1 2 3 4 5
8( 12,4), ( 4,4), ( ,4), (4,4), (8,4)3P P P P P
对于第(2)题我们提供如下详细解答(评分无此要求).下面提供参考解法二:
(第 24 题图)
OA
C
x
y
B
E
P
D
1 以点 D 为直角顶点,作 1PP x 轴
Rt ODE在 中, 2OE OD , 设 2OD b OE b , . 1Rt ODE Rt PPD ,(图示阴影)
4b ,2 8b ,在上面二图中分别可得到 P 点的生标为 P(-12,4)、P(-4,4)E 点在 0 点
与 A 点之间不可能;
② 以点 E 为直角顶点
同理在②二图中分别可得 P 点的生标为 P(- 8
3
,4)、P(8,4)E 点在 0 点下方不可能.
3 以点 P 为直角顶点
同理在③二图中分别可得 P 点的生标为 P(-4,4)(与①情形二重合舍去)、P(4,4),
E 点在 A 点下方不可能.
综上可得 P 点的生标共 5 个解,分别为 P(-12,4)、P(-4,4)、P(- 8
3
,4)、
P(8,4)、P(4,4).
下面提供参考解法二:
以直角进行分类进行讨论(分三类):
第一类如上解法⑴中所示图 2 2P DE y x b 为直角:设直线 : , D此时 (-b,o),E(O,2b)
的中点坐标为 b(- ,b)2 ,直线 DE 的中垂线方程: 1 ( )2 2
by b x ,令 4y 得 3( 8,4)2
bP .由
已知可得 2PE DE 即 2 2 2 232 ( 8) (4 2 ) 42 b b b b 化简得 23 32 64 0b b 解
得 1 2 1
88 3b b P P 3b, 将之代入( -8,4) (4,4)、2 2 ( 4,4)P ;
第二类如上解法②中所示图 2 2E DE y x b 为直角:设直线 : , D此时 (-b,o),E(O,2b)
,直线 PE 的方程: 1 22y x b ,令 4y 得 (4 8,4)P b .由已知可得 PE DE 即
2 2 2 2(4 8) (4 2 ) 4b b b b 化简得 2 2(2 8)b b 解之得 ,
1 2 3
44 3b b P P , 将之代入(4b-8,4) (8,4)、 4
8( ,4)3P
第三类如上解法③中所示图 2 2D DE y x b 为直角:设直线 : , D此时 (-b,o),E(O,2b)
,直线 PD 的方程: 1 ( )2y x b ,令 4y 得 ( 8,4)P b .由已知可得 PD DE 即
2 2 2 28 4 4b b 解得 1 2 54 4b b P P , 将之代入(-b-8,4) (-12,4)、
6 ( 4,4)P ( 6 ( 4,4)P 与 2P 重合舍去).
综上可得 P 点的生标共 5 个解,分别为 P(-12,4)、P(-4,4)、P(- 8
3
,4)、
P(8,4)、P(4,4).
事实上,我们可以得到更一般的结论:
如果得出 AB a OC b 、 、OA h 、设 b ak h
,则 P 点的情形如下
直角分类情形 1k 1k
P 为直角
1( , )P h h
1( , )P h h
2 ( , )P h h
E 为直角
3( , )1
hkP hk
2 ( , )2
hP h
4 ( , )1
hkP hk
D 为直角
5 ( ( 1), )P h k h 3 (0, )P h
6 ( ( 1), )P h k h 4 ( 2 , )P h h
【073】(1)∵∠A、∠C 所对的圆弧相同,∴∠A=∠C.
∴Rt△APD∽Rt△CPB,∴ AP PD
CP PB ,∴PA·PB=PC·PD;………………………3 分
(2)∵F 为 BC 的中点,△BPC 为 Rt△,∴FP=FC,∴∠C=∠CPF.
又∠C=∠A,∠DPE=∠CPF,∴∠A=∠DPE.∵∠A+∠D=90°,
∴∠DPE+∠D=90°.∴EF⊥AD.
(3)作 OM⊥AB 于 M,ON⊥CD 于 N,同垂径定理:
∴OM2=(2 5 )2-42=4,ON2=(2 5 )2-32=11
又易证四边形 MONP 是矩形,
∴OP= 2 2 15OM ON
【074】(1)解:由题意得 | 4 | |8| 12OA ,
A 点坐标为 ( 12 0) , .在 Rt AOC△ 中, 60OAC °,
tan 12 tan 60 12 3OC OA OAC °
C 点的坐标为 (0 12 3), .
设直线l 的解析式为 y kx b ,由l 过 A C、 两点,得 12 3
0 12
b
k b
解得 12 3
3
b
k
直线l 的解析式为: 3 12 3y x .
(2)如图,设 2O⊙ 平移t 秒后到 3O⊙ 处与 1O⊙ 第一次外切于点 P ,
3O⊙ 与 x 轴相切于 1D 点,连接 1 3 3 1O O O D, .则 1 3 1 3 8 5 13O O O P PO
3 1O D x ⊥ 轴, 3 1 5O D ,
在 1 3 1Rt O O D△ 中, 2 2 2 2
1 1 1 3 3 1 13 5 12O D O O O D .································6 分
1 1 4 13 17O D O O OD , 1 1 1 1 17 12 5D D O D O D ,
5 51t (秒) 2O⊙ 平移的时间为 5 秒.······················································8 分
【075】解:(1)对称轴是直线: 1x ,
点 A 的坐标是(3,0).···················································· 2 分
(说明:每写对 1 个给 1 分,“直线”两字没写不扣分)
(2)如图 11,连接 AC、AD,过 D 作 轴�yDM 于点 M,
解法一:利用 AOC CMD△ ∽△
∵点 A、D、C 的坐标分别是 A (3,0),D(1, ba )、C(0, b ),
O
y
x
C
DBA D1
O1
O2
O3P
60°
(第 22 题答图)
l
∴AO=3,MD=1.由
MD
OC
CM
AO 得
1
3 b
a
∴ 03 ab ······································· 3 分
又∵ baa )1(2)1(0 2 ∴由
03
03
ba
ab 得
3
1
b
a
∴函数解析式为: 322 xxy ·································································6 分
解法二:利用以 AD 为直径的圆经过点 C
∵点 A、D 的坐标分别是 A (3,0) 、D(1, ba )、C(0, b ),
∴ 29 bAC , 21 aCD , 2)(4 baAD ∵ 222 ADCDAC
∴ 03 ab …① 又∵ baa )1(2)1(0 2 …② ······································4 分
由①、②得 1 3a b , ∴函数解析式为: 322 xxy ····························6 分
(3)如图所示,当 BAFE 为平行四边形时,则 BA ∥ EF ,并且 BA = EF .
∵ BA =4,∴ EF =4 ,由于对称为 1x ,∴点 F 的横坐标为 5.······················· 7 分
将 5x 代入 322 xxy 得 12y ,∴F(5,12).
根据抛物线的对称性可知,在对称轴的左侧
抛物线上也存在点 F,使得四边形 BAEF 是
平行四边形,此时点 F 坐标为( 3 ,12).
当四边形 BEAF 是平行四边形时,
点 F 即为点 D,此时点 F 的坐标为(1, 4 ).
综上所述,点 F 的坐标为(5,12),
( 3 ,12)或(1, 4 ).
【076】解:(1)∵四边形 OBHC 为矩形,∴CD∥AB,
又 D(5,2), ∴C(0,2),OC=2 .
∴
2552
1
2
2 nm
n
解得
2
2
5
n
m
∴抛物线的解析式为: 22
5
2
1 2 xxy …… 4 分
(2)点 E 落在抛物线上. 理由如下:……… 5 分
由 y = 0,得 022
5
2
1 2 xx . 解得 x1=1,x2=4. ∴A(4,0),B(1,0).
∴OA=4,OB=1. 由矩形性质知:CH=OB=1,BH=OC=2,∠BHC=90°,
由旋转、轴对称性质知:EF=1,BF=2,∠EFB=90°,∴点 E 的坐标为(3,-1).
把 x=3 代入 22
5
2
1 2 xxy ,得 1232
532
1 2 y , ∴点 E 在抛物线上.
(3)法一:存在点 P(a,0),延长 EF 交 CD 于点 G,易求 OF=CG=3,PB=a-1.
S 梯形 BCGF = 5,S 梯形 ADGF = 3,记 S 梯形 BCQP = S1,S 梯形 ADQP = S2,
下面分两种情形: ①当 S1∶S2 =1∶3 时, 52)35(4
1
1 S ,
y
xO AB
C D
图 11
E F
此时点 P 在点 F(3,0)的左侧,则 PF = 3-a,由△EPF∽△EQG,得
3
1
EG
EF
QG
PF ,则 QG=9
-3a,∴CQ=3-(9-3a) =3a -6,由 S1=2,得 22)163(2
1 aa ,解得
4
9a ;
②当 S1∶S2=3∶1 时, 56)35(4
3
1 S
,
此时点 P 在点 F(3,0)的右侧,则 PF = a-
3,由△EPF∽△EQG,得 QG = 3a-9,∴CQ = 3 +(3 a-9)= 3 a-6,
由 S1= 6,得 62)163(2
1 aa ,解得
4
13a ,综上所述:所求点 P 的坐标为(
4
9 ,0)或(
4
13 ,
0)……… 14 分
法二:存在点 P(a,0). 记 S 梯形 BCQP = S1,S 梯形 ADQP = S2,易求 S 梯形 ABCD = 8.
当 PQ 经过点 F(3,0)时,易求 S1=5,S2 = 3,此时 S1∶S2 不符合条件,故 a≠3.
设直线 PQ 的解析式为 y = kx+b(k≠0),则
0
13
bak
bk ,解得
3
3
1
a
ab
ak
,
∴
33
1
a
axay . 由 y = 2 得 x = 3a-6,∴Q(3a-6,2) ……… 10 分
∴CQ = 3a-6,BP = a-1, 742)163(2
1
1 aaaS .
下面分两种情形:①当 S1∶S2 = 1∶3 时, 84
1S4
1
ABCD1 梯形S = 2;
∴4a-7 = 2,解得
4
9a ;……………………………………………… 12 分
②当 S1∶S2 = 3∶1 时, 684
3S4
3
ABCD1 梯形S ; ∴4a-7 = 6,解得
4
13a ;
综上所述:所求点 P 的坐标为(
4
9 ,0)或(
4
13 ,0)………… 14 分
[说明:对于第(3)小题,只要考生能求出
4
9a 或
4
13a 两个答案,就给 6 分. ]
【077】解:(1)把 B(0,6)代入 my
4
3 ,得 m =6………………………1 分
把 y =0 代入 64
3 y ,得 x =8
∴点 A 的坐标为(8,0)…………… 3 分
(2)在矩形 OACB 中,AC=OB=6,
BC=OA=8,∠C=90°
∴AB= 1086 2222 BCAC
∵PD⊥AB∴∠PDB=∠C=90°
BA
BC
BP
BDCBA cos , ∴
10
8
a
BD ∴
aBD 5
4 ∴ aAD 5
410
又∵BC∥AE,∴△PBD∽△EAD
∴
BD
AD
BP
AE ,即
5
4
5
410
a
a
a
AE
,∴ aaAE 5.12)5
410(4
5
∵ ACAEPCS PEAC )(2
1 梯形 ,∴ 5.6166)5.128(2
1 aaas
( 8 ao )……………………………7 分 (注:写成 8 ao 不扣分)
② ⊙Q 是△OAB 的内切圆 ,可设⊙Q 的半径为 r
∵ 862
1)1086(2
1 rS OAB ,解得 r=2.………………………………………8 分
设⊙Q 与 OB、AB、OA 分别切于点 F、G、H
可知,OF=2∴BF=BG=OB-OF=6-2=4,设直线 PD 与⊙Q 交于点 I、J ,过 Q 作 QM⊥IJ 于点
M,连结 IQ、QG, ∵QI=2, 2.12
1 IJIM
∴ 6.122 IMQIQM ∴ 在矩形 GQMD 中,GD=QM=1.6
∴BD=BG+GD=4+1.6=5.6,由
10
8cos
BA
BC
BP
BDCBA ,得 74
5 BDBP
∴点 P 的坐标为(7,6)…………………………………………………………………11 分
当 PE 在圆心 Q 的另一侧时,同理可求点 P 的坐标为(3,6)………………………12 分
综上,P 点的坐标为(7,6)或(3,6).………………………………………………13 分。
【078】(1) 1y x ·······················································································2 分
(2)∵OP t ,∴Q 点的横坐标为 1
2 t ,
①当 10 12 t ,即 0 2t 时, 11 2QM t ,
∴ 1 112 2OPQS t t △ .················································································· 3 分
②当 2t ≥ 时, 1 11 12 2QM t t ,
∴ 1 1 12 2OPQS t t △ .∴
1 11 0 22 2
1 1 1 2.2 2
t t t
S
t t t
, ,
, ≥
·········································4 分
当 10 12 t ,即 0 2t 时, 21 1 1 11 ( 1)2 2 4 4S t t t
,
∴当 1t 时, S 有最大值 1
4
.··········································································· 6 分
(3)由 1OA OB ,所以 OAB△ 是等腰直角三角形,若在 1L 上存在点C ,使得 CPQ△ 是以Q
为直角顶点的等腰直角三角形,则 PQ QC ,所以OQ QC ,又 1L x∥ 轴,则C ,O 两点关于
直线 L 对称,所以 1AC OA ,得 (11)C , .······················································ 7 分
下证 90PQC °.连CB ,则四边形OACB 是正方形.
法一:(i)当点 P 在线段OB 上,Q 在线段 AB 上
(Q 与 B C、 不重合)时,如图–1.
由对称性,得 BCQ QOP QPO QOP , ,
∴ 180QPB QCB QPB QPO °,
∴ 360 ( ) 90PQC QPB QCB PBC ° °.······································· 8 分
(ii)当点 P 在线段OB 的延长线上,Q 在线段 AB 上时,如图–2,如图–3
∵ 1 2QPB QCB , , ∴ 90PQC PBC °. ····················· 9 分
(iii)当点 Q 与点 B 重合时,显然 90PQC °.
综合(i)(ii)(iii), 90PQC °.
∴在 1L 上存在点 (11)C , ,使得 CPQ△ 是以Q 为直角顶点的等腰直角三角形.·········· 11 分
法二:由 1OA OB ,所以 OAB△ 是等腰直角三角形,若在 1L 上存在点C ,使得 CPQ△ 是以Q
为直角顶点的等腰直角三角形,则 PQ QC ,所以OQ QC ,又 1L x∥ 轴, 则 C , O 两点关
于直线 L 对称,所以 1AC OA ,得 (11)C , . ················································· 7 分
延长 MQ 与 1L 交于点 N .
(i)如图–4,当点Q 在线段 AB 上(Q 与 A B、 不重合)时,
∵四边形 OACB 是正方形,
∴四边形OMNA 和四边形 MNCB 都是矩形, AQN△ 和 QBM△ 都是等腰直角三角形.
L
A
O P B x
y
L1
23 题图-1
Q
C
L
A
O PB x
L1
23 题图-2
Q
C
2
1
y
y
L
A
O PB x
L1
23 题图-3
Q
C
2
1
∴ 90NC MB MQ NQ AN OM QNC QMB , , °.
又∵ OM MP , ∴ MP QN ,
∴ QNC QMP△ ≌△ ,
∴ MPQ NQC ,
又∵ 90MQP MPQ °,
∴ 90MQP NQC °.
∴ 90CQP °. ······················································································ 8 分
(ii)当点 Q 与点 B 重合时,显然 90PQC °. ·····································9 分
(iii)Q 在线段 AB 的延长线上时,如图–5,
∵ BCQ MPQ ,∠1=∠2
∴ 90CQP CBM °
综合(i)(ii)(iii), 90PQC °.
∴在 1L 上存在点 (11)C , ,使得 CPQ△ 是以Q 为直角顶点的等腰直角三角形. ······ 11 分
法三:由 1OA OB ,所以 OAB△ 是等腰直角三角形,若在 1L 上存在点C ,使得 CPQ△ 是以Q
为直角顶点的等腰直角三角形,则 PQ QC ,所以OQ QC ,又 1L x∥ 轴,
则C ,O 两点关于直线 L 对称,所以 1AC OA ,得 (11)C , . ····················9 分
连 PC ,∵ |1 |PB t , 1
2OM t , 1 2
tMQ ,
∴ 2 2 2 2 2(1 ) 1 2 2PC PB BC t t t ,
L
A
O P B x
y
L1
23 题图-1
Q
C
23 题图-4
L
A
O M P B x
y
L1
Q
CN
y
L
A
O PB x
L1
23 题图-5
Q
C
2
1
2 2 2
2 2 2 2 2 1 12 2 2
t t tOQ OP CQ OM MQ t
.
∴ 2 2 2PC OP QC ,∴ 90CQP °.·························································10 分
∴在 1L 上存在点 (11)C , ,使得 CPQ△ 是以Q 为直角顶点的等腰直角三角形. ········· 11 分
【079】解:(1)解 2 7 12 0x x 得 1 24 3x x ,
OA OB , 4 3OA OB , ···································································· 1 分
在 Rt AOB△ 中,由勾股定理有 2 2 5AB OA OB , 4sin 5
OAABC AB
(2)∵点 E 在 x 轴上, 16
3AOES △ , 1 16
2 3AO OE , 8
3OE
8 80 03 3E E
, 或 , ·········································································1 分
由已知可知 D(6,4),设 DEy kx b ,当 8 03E
, 时有
4 6
80 3
k b
k b
解得
6
5
16
5
k
b
6 16
5 5DEy x ,同理 8 03E
, 时, 6 16
13 13DEy x ·· 1 分
在 AOE△ 中, 890 4 3AOE OA OE °, ,
在 AOD△ 中, 90 4 6OAD OA OD °, , , OE OA
OA OD
, AOE DAO△ ∽△
(3)满足条件的点有四个, 1 2 3 4
75 22 42 44(3 8) ( 3 0) 14 7 25 25F F F F
,; ,; , ; , ·· 4 分
说明:本卷中所有题目,若由其它方法得出正确结论,可参照本评
【080】(1)过点C 作CD AB ,垂足为 D .则 2AD ,
当 MN 运动到被CD 垂直平分时,四边形 MNQP 是矩形,
即 3
2AM 时,四边形 MNQP 是矩形,
3
2t 秒时,四边形 MNQP 是矩形.
3tan 60 32PM AM °= , 3 32MNQPS 四边形
(2)1°当 0 1t 时,
1 ( )2MNQPS PM QN MN 四边形 · 1 3 3( 1)2 t t
33 2t
C
P
Q
BA M N
C
P
Q
C
P Q
BA M D N
2°当1 2t≤ ≤ 时
1 ( )2MNQPS PM QN MN 四边形 ·
1 3 3(3 ) 12 t t · 3 32
3°当 2 3t 时,
1 ( )2MNQPS PM QN MN 四边形 ·
1 3(3 ) 3(4 )2 t t
73 32t ················································10 分
2010 年中考数学压轴题 100 题精选(81-90 题)答案
【081】解:(1)(0,-3),b=- 9
4
,c=-3.·····················································3 分
(2)由(1),得 y= 3
4
x2- 9
4
x-3,它与 x 轴交于 A,B 两点,得 B(4,0).
∴OB=4,又∵OC=3,∴BC=5.
由题意,得
△
BHP∽△BOC,
∵OC∶OB∶BC=3∶4∶5,
∴HP∶HB∶BP=3∶4∶5,
∵PB=5t,∴HB=4t,HP=3t.
∴OH=OB-HB=4-4t.
由 y= 3
4t
x-3 与 x 轴交于点 Q,得 Q(4t,0).
∴OQ=4t.··············································································· 4 分
①当 H 在 Q、B 之间时,
QH=OH-OQ
=(4-4t)-4t=4-8t.························································5 分
②当 H 在 O、Q 之间时,
QH=OQ-OH
=4t-(4-4t)=8t-4.························································6 分
综合①,②得 QH=|4-8t|;······················································· 6 分
(3)存在 t 的值,使以 P、H、Q 为顶点的三角形与△COQ 相似.··················7 分
①当 H 在 Q、B 之间时,QH=4-8t,
若△QHP∽△COQ,则 QH∶CO=HP∶OQ,得 4 8
3
t = 3
4
t
t
,
∴t= 7
32
.················································································7 分
若△PHQ∽△COQ,则 PH∶CO=HQ∶OQ,得 3
3
t = 4 8
4
t
t
,
即 t2+2t-1=0.
∴t1= 2 -1,t2=- 2 -1(舍去).·········································· 8 分
②当 H 在 O、Q 之间时,QH=8t-4.
若△QHP∽△COQ,则 QH∶CO=HP∶OQ,得 8 4
3
t = 3
4
t
t
,
C
P
Q
BA M N
∴t= 25
32
.················································································9 分
若△PHQ∽△COQ,则 PH∶CO=HQ∶OQ,得 3
3
t = 8 4
4
t
t
,
即 t2-2t+1=0.
∴t1=t2=1(舍去).································································ 10 分
综上所述,存在t 的值,t1= 2 -1,t2= 7
32
,t3= 25
32
.·····················10 分
附加题:解:(1)8;·······················································································5 分
(2)2.····················································································· 10 分
【082】(09 上海)略
【083】. 解:(1)B(1, 3 )
(2)设抛物线的解析式为 y=ax(x+a),代入点 B(1, 3 ),得 3
3a ,
因此 23 2 3
3 3y x x
(3)如图,抛物线的对称轴是直线 x=—1,当点 C 位于对称轴与线段 AB 的交点时,△BOC
的周长最小.
设直线 AB 为 y=kx+b.所以
3
3, 3
2 0. 2 3
3
kk b
k b b
解得 ,
因此直线 AB 为 3 2 3
3 3y x ,
当 x=-1 时, 3
3y ,
因此点 C 的坐标为(-1, 3 ).
(4)如图,过 P 作 y 轴的平行线交 AB 于 D.
2
2
2
1 ( )( )2
1 3 2 3 3 2 3 32 3 3 3 3
3 3 32 2
3 1 9 3
2 2 8
PAB PAD PBD D P B AS S S y y x x
x x x
x x
x
当 x=- 1
2
时,△PAB 的面积的最大值为 9 3
8
,此时 1 3,2 4P
.
【084】解:(1)⊙P 与 x 轴相切.
∵直线 y=-2x-8 与 x 轴交于 A(4,0),与 y 轴交于 B(0,-8),
C
B
A O
y
x
D
B
A O
y
x
P
∴OA=4,OB=8.由题意,OP=-k,∴PB=PA=8+k.
在 Rt△AOP 中,k2+42=(8+k)2,
∴k=-3,∴OP 等于⊙P 的半径,
∴⊙P 与 x 轴相切.
(2)设⊙P 与直线 l 交于 C,D 两点,连结 PC,PD 当圆心 P 在线段 OB 上时,作 PE⊥CD 于 E.
∵△PCD 为正三角形,∴DE= 1
2
CD= 3
2
,PD=3,
∴PE= 3 3
2
.
∵∠AOB=∠PEB=90°, ∠ABO=∠PBE,
∴△AOB∽△PEB,
∴
3 3
4 2, =
4 5
AO PE
AB PB PB
即 ,
∴ 3 15 ,2PB ∴ 3 158 2PO BO PB ,
∴ 3 15(0, 8)2P ,∴ 3 15 82k .
当圆心 P 在线段 OB 延长线上时,同理可得 P(0,- 3 15
2
-8),
∴k=- 3 15
2
-8,∴当 k= 3 15
2
-8 或 k=- 3 15
2
-8 时,以⊙P 与直线 l 的两个交点和圆心 P
为顶点的三角形是正三角形.
【085】解: (1)由题知:
0339
03
ba
ba ……………………………………1 分
解得:
2
1
b
a ……………………………………………………………2 分
∴ 所求抛物线解析式为: 322 x--xy ……………………………3 分
(2) 存在符合条件的点 P, 其坐标为 P (-1, 10 )或 P(-1,- 10 )
或 P (-1, 6) 或 P (-1,
3
5 )………………………………………………………7 分
(3)解法①:
过点 E 作 EF⊥x 轴于点 F , 设 E ( a ,- 2a -2a+3 )( -3< a < 0 )
∴EF=- 2a -2a+3,BF=a+3,OF=-a ………………………………………………8 分
∴S 四边形 BOCE =
2
1 BF·EF +
2
1 (OC +EF)·OF
=
2
1 ( a+3 )·(- 2a -2a+3) +
2
1 (- 2a -2a+6)·(-a)……………………………9 分
=
2
9
2
9
2
3 2 aa ………………………………………………………………………10 分
=-
2
3 2)2
3( a +
8
63
∴ 当 a =-
2
3 时,S 四边形 BOCE 最大, 且最大值为
8
63 .……………………………11 分
此时,点 E 坐标为 (-
2
3 ,
4
15 )……………………………………………………12 分
解法②:
过点 E 作 EF⊥x 轴于点 F, 设 E ( x , y ) ( -3< x < 0 ) …………………………8 分
则 S 四边形 BOCE =
2
1 (3 + y )·(-x) +
2
1 ( 3 + x )·y ………………………………………9 分
=
2
3 ( y-x)=
2
3 ( 332 x--x ) …………………………………10 分
= -
2
3 2)2
3( x +
8
63
∴ 当 x =-
2
3 时,S 四边形 BOCE 最大,且最大值为
8
63 . …………………………11 分
此时,点 E 坐标为 (-
2
3 ,
4
15 ) ……………………………………………………12 分
【086】⑴证明:∵BC 是⊙O 的直径
∴∠BAC=90o
又∵EM⊥BC,BM 平分∠ABC,
∴AM=ME,∠AMN=EMN
又∵MN=MN,
∴△ANM≌△ENM
⑵∵AB2=AF·AC
∴
AB
AF
AC
AB
又∵∠BAC=∠FAB=90o
∴△ABF∽△ACB
∴∠ABF=∠C
又∵∠FBC=∠ABC+∠FBA=90o
∴FB 是⊙O 的切线
⑶由⑴得 AN=EN,AM=EM,∠AMN=EMN,
又∵AN∥ME,∴∠ANM=∠EMN,
∴∠AMN=∠ANM,∴AN=AM,
∴AM=ME=EN=AN
∴四边形 AMEN 是菱形
∵cos∠ABD=
5
3 ,∠ADB=90o
∴
5
3
AB
BD
设 BD=3x,则 AB=5x,,由勾股定理 xx-xAD 435 22
而 AD=12,∴x=3
∴BD=9,AB=15
∵MB 平分∠AME,∴BE=AB=15
∴DE=BE-BD=6
∵ND∥ME,∴∠BND=∠BME,又∵∠NBD=∠MBE
∴△BND∽△BME,则
BE
BD
ME
ND
设 ME=x,则 ND=12-x,
15
912
x
x ,解得 x=
2
15
∴S=ME·DE=
2
15 ×6=45
【087】(天门)略
【088】解:(1)法一:由图象可知:抛物线经过原点,
设抛物线解析式为 2 ( 0)y ax bx a .
把 (11)A , , (31)B , 代入上式得:········································································· 1 分
1
1 9 3 1
a b
a b
解得
1
3
4
3
a
b
············································································3 分
∴所求抛物线解析式为 21 4
3 3y x x ······························································· 4 分
法二:∵ (11)A , , (31)B , ,
∴抛物线的对称轴是直线 2x .
设抛物线解析式为 2( 2)y a x h ( 0a )······················································1 分
把 (0 0)O , , (11)A , 代入得
2
2
0 (0 2)
1 (1 2)
a h
a h
解得
1
3
4
3
a
h
··································································3 分
∴所求抛物线解析式为 21 4( 2)3 3y x x .·····················································4 分
(2)分三种情况:
①当 0 2t ≤ ,重叠部分的面积是 OPQS△ ,过点 A 作 AF x⊥ 轴于点 F ,
∵ (11)A , ,在 Rt OAF△ 中, 1AF OF , 45AOF °,
在 Rt OPQ△ 中,OP t , 45OPQ QOP °,
∴ 2cos45 2PQ OQ t t ° ,
2
O
A B
C
x
y
1
1 3P
第 26 题图 1
Q
F
∴
2
21 2 1
2 2 4S t t
.········································· 6 分
②当 2 3t ≤ ,设 PQ 交 AB 于点G ,作GH x⊥ 轴于点 H ,
45OPQ QOP °,则四边形OAGP 是等腰梯形,
重叠部分的面积是 OAGPS梯形 .
∴ 2AG FH t ,
∴ 1 1( ) ( 2) 1 12 2S AG OP AF t t t .··········8 分
③当 3 4t ,设 PQ 与 AB 交于点 M ,交 BC 于点 N ,重叠部分的面积是 OAMNCS五边形 .
因 为 PNC△ 和 BMN△ 都 是 等 腰 直 角 三 角 形 , 所 以 重 叠 部 分 的 面 积 是
OAMNCS五边形 BMNOABCS S △梯形 .
∵ (31)B , ,OP t ,
∴ 3PC CN t ,
∴ 1 ( 3) 4BM BN t t ,
∴ 21 1(2 3) 1 (4 )2 2S t
21 1142 2S t t .·········································· 10 分
(3)存在 1 1t ······················································································· 12 分
2 2t ······················································································14 分
【089】解:(1)圆心O 在坐标原点,圆O 的半径为 1,
点 A B C D、 、 、 的坐标分别为 ( 1 0) (0 1) (1 0) (01)A B C D ,、 , 、 ,、 ,
抛物线与直线 y x 交于点 M N、 ,且 MA NC、 分别与圆O 相切于点 A 和点C ,
( 1 1) (11)M N , 、 , .··················································································· 2 分
点 D M N、 、 在抛物线上,将 (01) ( 1 1) (11)D M N ,、 , 、 , 的坐标代入
2y ax bx c ,得:
1
1
1
c
a b c
a b c
解之,得:
1
1
1
a
b
c
抛物线的解析式为: 2 1y x x .····························································· 4 分
2
O
A B
C
x
y
1
1 3
第 26 题图 2
Q
F
G
PH
2
O
A B
C
x
y
1
1 3
第 26 题图 3
Q
F
M
P
N
(2)
2
2 1 51 2 4y x x x
抛物线的对称轴为 1
2x ,
1 1 512 4 2OE DE , .··················6 分
连结 90BF BFD , °,
BFD EOD△ ∽△ , DE OD
DB FD
,
又 5 1 22DE OD DB , , ,
4 5
5FD ,
4 5 5 3 5
5 2 10EF FD DE .···························································· 8 分
(3)点 P 在抛物线上.··················································································· 9 分
设过 D C、 点的直线为: y kx b ,
将点 (1 0) (01)C D,、 , 的坐标代入 y kx b ,得: 1 1k b , ,
直线 DC 为: 1y x .··········································································· 10 分
过点 B 作圆O 的切线 BP 与 x 轴平行, P 点的纵坐标为 1y ,
将 1y 代入 1y x ,得: 2x .
P 点的坐标为 (2 1), ,··············································································· 11 分
当 2x 时, 2 21 2 2 1 1y x x ,
所以, P 点在抛物线 2 1y x x 上.····························································12 分
说明:解答题各小题中只给出了 1 种解法,其它解法只要步骤合理、解答正确均应得到相应的分数.
O x
y
N
C
D
E
F
BM
A
P
【090】(1)解:把 A( 1 ,0),C(3, 2 )代入抛物线 2 3y ax ax b 得
299
0)1(3)1( 2
baa
baa ······································································ 1 分
整理得
2
04
b
ba ············· ……………… 2 分 解得
2
2
1
b
a ………………3 分
∴抛物线的解析式为 22
3
2
1 2 xxy ·························································· 4 分
(2)令 022
3
2
1 2 xx 解得 1 21 4x x ,
∴ B 点坐标为(4,0)
又∵D 点坐标为(0, 2 ) ∴AB∥CD ∴四边形 ABCD 是梯形.
∴S 梯形 ABCD = 82)35(2
1 ························· 5 分
设直线 )0(1 kkxy 与 x 轴的交点为 H,
与 CD 的交点为 T,
则 H(
k
1 ,0), T(
k
3 , 2 )·················6 分
∵直线 )0(1 kkxy 将四边形 ABCD 面积二等分
∴S 梯形 AHTD =
2
1 S 梯形 ABCD=4
∴ 42)311(2
1
kk
································ 7 分
∴
3
4k ···················································· 8 分
E
F
M
N
G
O BA x
y
图(9) -2
Q
D
O BA x
y
C
y=kx+1
图(9) -1
H
T
(3)∵MG⊥ x 轴于点 G,线段 MG︰AG=1︰2
∴设 M(m,
2
1 m ),···································9 分
∵点 M 在抛物线上 ∴ 22
3
2
1
2
1 2 mmm
解得 1 23 1m m , (舍去) ························ 10 分
∴M 点坐标为(3, 2 )··········································································11 分
根据中心对称图形性质知,MQ∥AF,MQ=AF,NQ=EF,
∴N 点坐标为(1, 3 ) ········································································· 12 分
2010 年中考数学压轴题 100 题精选(91-100 题)答案
【091】(1)解:法 1:由题意得 n=2+c,
2n-1=2+c.
……1 分
解得 n=1,
c=-1.
……2 分
法 2:∵ 抛物线 y=x2-x+c 的对称轴是 x=1
2
,
且 1
2
-(-1) =2-1
2
,∴ A、B 两点关于对称轴对称.
∴ n=2n-1 ……1 分
∴ n=1,c=-1. ……2 分
∴ 有 y=x2-x-1 ……3 分
=(x-1
2
)2-5
4
.
∴ 二次函数 y=x2-x-1 的最小值是-5
4
. ……4 分
(2)解:∵ 点 P(m,m)(m>0),
∴ PO= 2m.
∴ 2 2≤ 2m ≤ 2+2.
∴ 2≤m≤1+ 2. ……5 分
法 1: ∵ 点 P(m,m)(m>0)在二次函数 y=x2-x+c 的图象上,
∴ m=m2-m+c,即 c=-m2+2m.
∵ 开口向下,且对称轴 m=1,
∴ 当 2≤m≤1+ 2 时,
有 -1≤c≤0. ……6 分
法 2:∵ 2≤m≤1+ 2,
∴ 1≤m-1≤ 2.
∴ 1≤(m-1)2≤2.
∵ 点 P(m,m)(m>0)在二次函数 y=x2-x+c 的图象上,
∴ m=m2-m+c,即 1-c=(m-1)2.
∴ 1≤1-c≤2.
∴ -1≤c≤0. ……6 分
∵ 点 D、E 关于原点成中心对称,
法 1: ∴ x2=-x1,y2=-y1.
∴ y1=x12-x1+c,
-y1=x12+x1+c.
∴ 2y1=-2x1, y1=-x1.
设直线 DE:y=kx.
有 -x1=kx1.
由题意,存在 x1≠x2.
∴ 存在 x1,使 x1≠0. ……7 分
∴ k=-1.
∴ 直线 DE: y=-x. ……8 分
法 2:设直线 DE:y=kx.
则根据题意有 kx=x2-x+c,即 x2-(k+1) x+c=0.
∵ -1≤c≤0,
∴ (k+1)2-4c≥0.
∴ 方程 x2-(k+1) x+c=0 有实数根. ……7 分
∵ x1+x2=0,
∴ k+1=0.
∴ k=-1.
∴ 直线 DE: y=-x. ……8 分
若
y=-x,
y=x2-x+c+3
8
.
则有 x2+c+3
8
=0.即 x2=-c-3
8
.
① 当 -c-3
8
=0 时,即 c=-3
8
时,方程 x2=-c-3
8
有相同的实数根,
即直线 y=-x 与抛物线 y=x2-x+c+3
8
有唯一交点. ……9 分
② 当 -c-3
8
>0 时,即 c<-3
8
时,即-1≤c<-3
8
时,
方程 x2=-c-3
8
有两个不同实数根,
即直线 y=-x 与抛物线 y=x2-x+c+3
8
有两个不同的交点. ……10 分
③ 当 -c-3
8
<0 时,即 c>-3
8
时,即-3
8
<c≤0 时,
方程 x2=-c-3
8
没有实数根,
即直线 y=-x 与抛物线 y=x2-x+c+3
8
没有交点. ……11 分
【092】解:(1)如图,在坐标系中标出 O,A,C 三点,连接 OA,OC.
∵∠AOC≠90°, ∴∠ABC=90°,
A B
C
故 BC⊥OC, BC⊥AB,∴B( 7
2
,1).(1 分,)
即 s= 7
2
,t=1.直角梯形如图所画.(2 分)
(大致说清理由即可)
(2)由题意,y=x2+mx-m 与 y=1(线段 AB)相交,
得,
1
2y = x mx m,
y = .
(3 分)∴1=x2+mx-m,
由 (x-1)(x+1+m)=0,得 1 21, 1x x m .
∵ 1x =1< 3
2
,不合题意,舍去. (4 分)
∴抛物线 y=x2+mx-m 与 AB 边只能相交于( 2x ,1),
∴ 3
2
≤-m-1≤ 7
2
,∴ 9
2
5
2
m . ①(5 分)
又∵顶点 P(
2 4
2 4
,m m m )是直角梯形 OABC 的内部和其边上的一个动点,
∴ 70
2 2
m ,即 7 0m . ② (6 分)
∵
2 2
24 ( 2) 4 ( 1)
4 4 2
1 1m m m m ,
(或者抛物线 y=x2+mx-m 顶点的纵坐标最大值是 1)
∴点 P 一定在线段 AB 的下方. (7 分)
又∵点 P 在 x 轴的上方,
∴
2 4
4
0m m , ( 4) 0,m m
∴ 0, 0,
4 0 4 0
m m
m m
或者 . (*8 分)
4 (9 ) 0.�m 分 ③(9 分)
又∵点 P 在直线 y= 2
3
x 的下方,∴
2 4 2 ( )
4 3 2
m m m ,(10 分)即 (3 8) 0.m m
0, 0,
3 8 0 3 8 0.
m m
m m
或者 (*8 分处评分后,此处不重复评分)
8 0.
3
m m (11分),或 ④
由①②③④ ,得 4 8
3
m .(12 分)
说明:解答过程,全部不等式漏写等号的扣 1 分,个别漏写的酌情处理.
【093】解:(1)连结BO 与 AC 交于点 H ,则当点 P 运动到点H 时,直线DP 平分矩形OABC 的面积.理
由如下:
∵矩形是中心对称图形,且点 H 为矩形的对称中心.
又据经过中心对称图形对称中心的任一直线平分此中心对称图形的面积,因为直线 DP 过矩形
OABC 的对称中心点 H ,所以直线 DP 平分矩形 OABC 的面积.…………2 分
由已知可得此时点 P 的坐标为 3( 2 )2P , .
设直线 DP 的函数解析式为 y kx b .
则有
5 0
3 2.2
k b
k b
,
解得 4
13k , 20
13b .
所以,直线 DP 的函数解析式为: 4 20
13 13y x .·············································5 分
(2)存在点 M 使得 DOM△ 与 ABC△ 相似.
如图,不妨设直线 DP 与 y 轴的正半轴交于点 (0 )mM y, .
因为 DOM ABC ,若△DOM 与△ABC 相似,则有 OM BC
OD AB
或 OM AB
OD BC
.
当 OM BC
OD AB
时,即 3
5 4
my ,解得 15
4my .所以点 1
15(0 )4M , 满足条件.
当 OM AB
OD BC
时,即 4
5 3
my ,解得 20
3my .所以点 2
20(0 )3M , 满足条件.
由对称性知,点 3
15(0 )4M , 也满足条件.
综上所述,满足使 DOM△ 与 ABC△ 相似的点 M 有 3 个,分别为 1
15(0 )4M , 、 2
20(0 )3M , 、
3
15(0 )4M , .·································································································9 分
(3)如图 ,过 D 作 DP⊥AC 于点 P,以 P 为圆心,半径长为 5
2
画圆,过点 D 分别作 P 的切线 DE、
DF,点 E、F 是切点.除 P 点外在直线 AC 上任取一点 P1,半径长为 5
2
画圆,过点 D 分别作 P 的切
线 DE1、DF1,点 E1、F1 是切点.
在△DEP 和△DFP 中,∠PED=∠PFD,PF=PE,PD=PD,∴
△
DPE≌
△
DPF.
∴S四边形 DEPF=2S
△
DPE=2× 1 5
2 2DE PE DE PE DE .
∴当 DE 取最小值时,S四边形 DEPF 的值最小. y
BC
P
E
F
∵ 2 2 2DE DP PE , 2 2 2
1 1 1 1DE DP PE ,
∴ 2 2 2 2
1 1DE DE DP DP .
∵ 1DP DP ,∴ 2 2
1 0DE DE .
∴ 1DE DE .由 1P 点的任意性知:DE 是
D 点与切点所连线段长的最小值.……12 分
在△ADP 与△AOC 中,∠DPA=∠AOC,
∠DAP=∠CAO, ∴△ADP∽△AOC.
∴ DP CO
DA CA
,即 4
8 5
DP .∴ 32
5DP .
∴ 2 2 1024 25 3471
25 4 10DE DP PE .
∴S四边形DEPF= 3471
4
,即S= 3471
4
.···························································· 14 分
(注:本卷中所有题目,若由其它方法得出正确结论,请参照标准给分.)
【094】解:(1)令二次函数 2y ax bx c ,则
16 4 0
0
2
a b c
a b c
c
····························································································1 分
1
2
3
2
2
a
b
c
···································································································· 2 分
过 A B C, , 三点的抛物线的解析式为 21 3 22 2y x x ···································4 分
(2)以 AB 为直径的圆圆心坐标为 3 02O
,
5
2O C 3
2O O ····················································································· 5 分
CD 为圆O 切线 OC CD ····································································· 6 分
90O CD DCO °
90CO O O CO ° CO O DCO
O CO CDO△ ∽△ / /O O OC OC OD ······················································ 8 分
3 / 2 2/2 OD 8
3OD
D 坐标为 80 3
, ···························································································9 分
(3)存在·····································································································10 分
抛物线对称轴为 3
2X
设满足条件的圆的半径为 r ,则 E 的坐标为 3( )2 r r , 或 3( )2F r r ,
而 E 点在抛物线 21 3 22 2y x x 上
21 3 3 3( ) ( ) 22 2 2 2r r r
1
291 2r 2
291 2r
故在以 EF 为直径的圆,恰好与 x 轴相切,该圆的半径为 291 2
, 291 2
··········12 分
注:解答题只要方法合理均可酌情给分
【095】(1) B (4,0), (0 2)C , .································································· 2 分
21 3 22 2y x x .························································································4 分
(2) ABC△ 是直角三角形.············································································5 分
证明:令 0y ,则 21 3 2 02 2x x .
1 21 4x x , .
( 1 0)A , .·································································································· 6 分
解法一: 5 5 2 5AB AC BC , , .·······················································7 分
2 2 25 20 25AC BC AB .
ABC△ 是直角三角形.················································································· 8 分
解法二: 11 2 4 2
CO AOAO CO BO BO OC
, , ,
90AOC COB °,
AOC COB△ ∽△ .·····················································································7 分
ACO CBO .
90CBO BCO °,
90ACO BCO °.即 90ACB °.
ABC△ 是直角三角形.················································································· 8 分
(3)能. ① 当矩形两个顶点在 AB 上时,如图 1,CO 交GF 于 H .
G
A O B x
y
D E
FHC
GF AB ∥ ,
CGF CAB△ ∽△ .
GF CH
AB CO
.·················································9 分
解法一:设GF x ,则 DE x , 2
5CH x ,
22 5DG OH OC CH x .
22 22 25 5DEFGS x x x x 矩形 ·
=
22 5 5
5 2 2x
.······················································································ 10 分
当 5
2x 时, S 最大.
5 12DE DG , .
ADG AOC△ ∽△ ,
1 1 22 2
AD DG AD OD OEAO OC
, , , .
1 02D
, , (2 0)E , .················································································ 11 分
解法二:设 DG x ,则 10 5
2
xDE GF .
2 210 5 5 5 55 ( 1)2 2 2 2DEFG
xS x x x x 矩形 · .····································· 10 分
当 1x 时, S 最大.
51 2DG DE , .
ADG AOC△ ∽△ ,
1 1 22 2
AD DG AD OD OEAO OC
, , , .
1 02D
, , (2 0)E , .················································································ 11 分
② 当矩形一个顶点在 AB 上时, F 与C 重合,如图 2,
DG BC ∥ ,
AGD ACB△ ∽△ .
GD AG
BC AF
.
解法一:设GD x , 5, 2 5AC BC ,
C
A O B x
y
图 2
D
G G
5 2
xGF AC AG .
215 52 2DEFG
xS x x x 矩形 ·
= 21 552 2x .····················································································· 12 分
当 5x 时, S 最大.
55 2GD AG , , 2 2 5
2AD AG GD . 3
2OD
3 02D
, ···································································································13 分
解法二:设 DE x , 5AC , 2 5BC , GC x , 5AG x . 2 5 2GD x .
22 5 2 2 2 5DEFGS x x x x 矩形 ·
=
2
5 52 2 2x
························································································ 12 分
当 5
2x 时, S 最大,
55 2GD AG , . 2 2 5
2AD AG GD . 3.2OD
3 02D
, ·································································································· 13 分
综上所述:当矩形两个顶点在 AB 上时,坐标分别为 1 02
, ,(2,0);
当矩形一个顶点在 AB 上时,坐标为 3 02
, ························································ 14 分
【096】(1)因所求抛物线的顶点 M 的坐标为(2,4),
故可设其关系式为 22 4y a x ………………(1 分)
又抛物线经过 O(0,0),于是得 20 2 4 0a , ………………(2 分)
解得 a=-1 ………………(3 分)
∴ 所求函数关系式为 22 4y x ,即 2 4y x x . ……………(4 分)
(2)① 点 P 不在直线 ME 上. ………………(5 分)
根据抛物线的对称性可知 E 点的坐标为(4,0),
又 M 的坐标为(2,4),设直线 ME 的关系式为 y=kx+b.
于是得
42
04
bk
bk ,解得
8
2
b
k
所以直线 ME 的关系式为 y=-2x+8. ……(6 分)
由已知条件易得,当 t
2
5 时,OA=AP
2
5 ,
2
5,2
5P ……………(7 分)
∵ P 点的坐标不满足直线 ME 的关系式 y=-2x+8.
∴ 当 t
2
5 时,点 P 不在直线 ME 上. ………………(8 分)
② S 存在最大值. 理由如下: ………………(9 分)
∵ 点 A 在 x 轴的非负半轴上,且 N 在抛物线上, ∴ OA=AP=t.
∴ 点 P,N 的坐标分别为(t,t)、(t,-t 2+4t) ∴ AN=-t 2+4t (0≤t≤3) ,
∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3- t)≥0 , ∴ PN=-t 2+3 t …(10 分)
(ⅰ)当 PN=0,即 t=0 或 t=3 时,以点 P,N,C,D 为顶点的多边形是三角形,此三角形的高为
AD,∴ S=
2
1 DC·AD=
2
1 ×3×2=3. ………………(11 分)
(ⅱ)当 PN≠0 时,以点 P,N,C,D 为顶点的多边形是四边形
∵ PN∥CD,AD⊥CD,
∴ S=
2
1 (CD+PN)·AD=
2
1 [3+(-t 2+3 t)]×2=-t 2+3 t+3=
4
21
2
3 2
t
其中(0<t<3),由 a=-1,0<
2
3 <3,此时
4
21最大S . …………(12 分)
综上所述,当 t
2
3 时,以点 P,N,C,D 为顶点的多边形面积有最大值,
这个最大值为
4
21 . ………………(13 分)
说明:(ⅱ)中的关系式,当 t=0 和 t=3 时也适合.
【097】解:(1)点 D 的坐标为 (4 3), .······················································ (2 分)
(2)抛物线的表达式为 23 9
8 4y x x .·······················································(4 分)
(3)抛物线的对称轴与 x 轴的交点 1P 符合条件.
∵OA CB∥ ,
∴ 1POM CDO .
∵ 1 90OPM DCO °,
∴ 1Rt RtPOM CDO△ ∽ △ .······················· (6 分)
∵抛物线的对称轴 3x ,
y
O
3 C D B
6
A
x
3
4y x
A
M
P1
P2
∴点 1P 的坐标为 1(3 0)P , .·········································································· (7 分)
过点 O 作OD 的垂线交抛物线的对称轴于点 2P .
∵对称轴平行于 y 轴,
∴ 2P MO DOC .
∵ 2 90P OM DCO °,
∴ 2 1Rt RtP M O DOC△ ∽ △ .····································································(8 分)
∴点 2P 也符合条件, 2OP M ODC .
∴ 1 2 13 90PO CO P PO DCO , °,
∴ 2 1Rt RtP PO DCO△ ≌ △ .····································································· (9 分)
∴ 1 2 4PP CD .
∵点 2P 在第一象限,
∴点 2P 的坐标为 2P (3 4), ,
∴符合条件的点 P 有两个,分别是 1(3 0)P , , 2P (3 4), .·································· (11 分)
【098】解:(1)当 t=4 时,B(4,0)
设直线 AB 的解析式为 y= kx+b .
把 A(0,6),B(4,0) 代入得:
b=6
4k+b=0 , 解得:
k =-3
2
b=6
,
∴直线 AB 的解析式为:y=-3
2
x+6.………………………………………4 分
(2) 过点 C 作 CE⊥x 轴于点 E
由∠AOB=∠CEB=90°,∠ABO=∠BCE,得△AOB∽△BEC.
∴ 1
2
BE CE BC
AO BO AB
,
∴BE= 1
2
AO=3,CE= 1
2
OB= t
2
,
∴点 C 的坐标为(t+3,t
2
).…………………………………………………………2 分
方法一:
S 梯形 AOEC= 1
2
OE·(AO+EC)= 1
2
(t+3)(6+t
2
)=1
4
t2+15
4
t+9,
S△ AOB= 1
2
AO·OB= 1
2×6·t=3t,
y
O
C
A
B x
D
E
S△ BEC= 1
2
BE·CE= 1
2×3×t
2
= 3
4
t,
∴S△ ABC= S 梯形 AOEC- S△ AOB-S△ BEC
= 1
4
t2+15
4
t+9-3t-3
4
t = 1
4
t2+9.
方法二:
∵AB⊥BC,AB=2BC,∴S△ ABC= 1
2
AB·BC= BC2.
在 Rt△ABC 中,BC2= CE2+ BE2 = 1
4
t2+9,
即 S△ ABC= 1
4
t2+9.…………………………………………………………2 分
(3)存在,理由如下:
①当 t≥0 时.
Ⅰ.若 AD=BD.
又∵BD∥y 轴
∴∠OAB=∠ABD,∠BAD=∠ABD,
∴∠OAB=∠BAD.
又∵∠AOB=∠ABC,
∴△ABO∽△ACB,
∴ 1
2
OB BC
AO AB
,
∴t
6
= 1
2
,
∴t=3,即 B(3,0).
Ⅱ.若 AB=AD.
延长 AB 与 CE 交于点 G,
又∵BD∥CG
∴AG=AC
过点 A 画 AH⊥CG 于 H.
∴CH=HG=1
2
CG
由△AOB∽△GEB,
得GE
BE
=AO
OB
,
∴GE= 18
t .
又∵HE=AO=6,CE=t
2
∴18
t
+6=1
2
×(t
2
+18
t
)
∴t2-24t-36=0
解得:t=12±6 5. 因为 t≥0,
y
O
C
A
B x
D
E
y
O
A
D
E
y
O
C
A
B
D
E
H
G x
所以 t=12+6 5,即 B(12+6 5,0).
Ⅲ.由已知条件可知,当 0≤t<12 时,∠ADB 为钝角,故 BD ≠ AB.
当 t≥12 时,BD≤CE