- 902.50 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
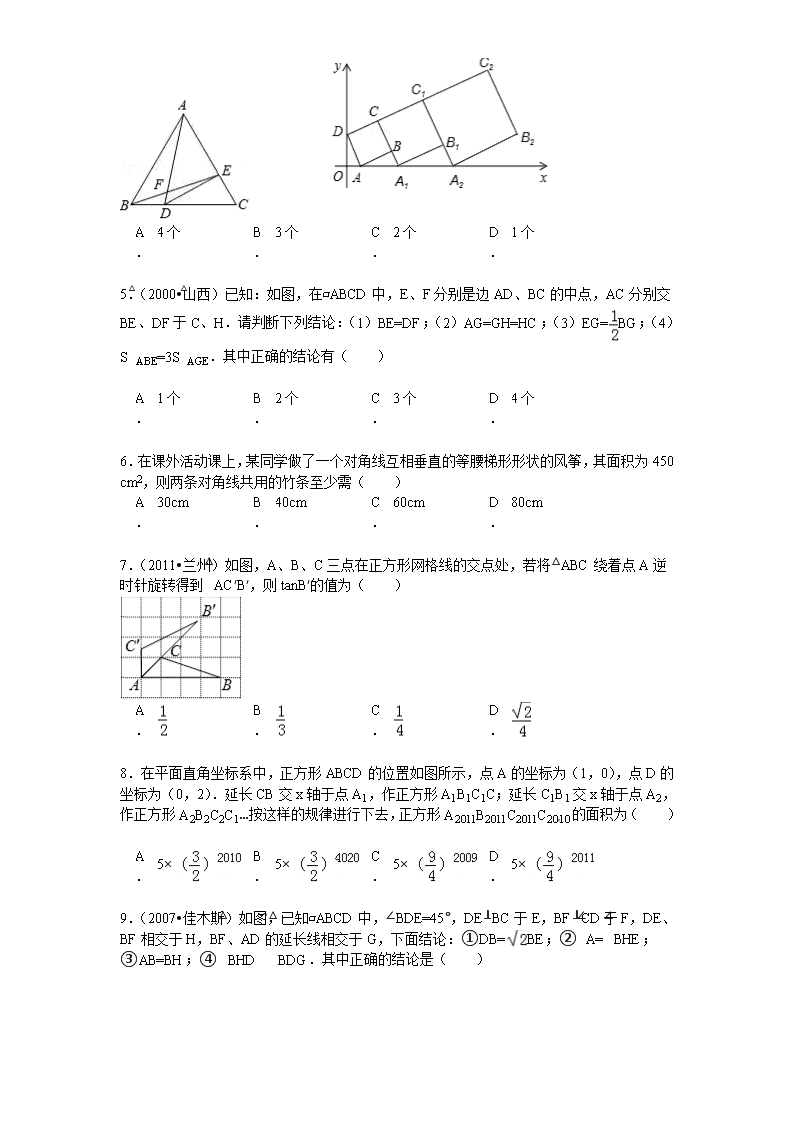
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
易错题错题二
一.选择题(共11小题)
1.(2010•武汉)如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=;③.其中正确的是( )
A.
①②③
B.
只有②③
C.
只有②
D.
只有③
2.(2006•武汉)(北师大版)如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB.其中相似的为( )
A.
①④
B.
①②
C.
②③④
D.
①②③
3.(2008•齐齐哈尔)如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=AB;②∠BAF=∠CAF;③S四边形ADFE=AF•DE;④∠BDF+∠FEC=2∠BAC,正确的个数是( )
A.
1
B.
2
C.
3
D.
4
4.(2007•黑龙江)如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=BC,CE=AC,BE、AD相交于点F,连接DE,则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF•DA;④AF•BE=AE•AC,正确的结论有( )
A.
4个
B.
3个
C.
2个
D.
1个
5.(2000•山西)已知:如图,在▱ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
A.
1个
B.
2个
C.
3个
D.
4个
6.在课外活动课上,某同学做了一个对角线互相垂直的等腰梯形形状的风筝,其面积为450 cm2,则两条对角线共用的竹条至少需( )
A.
30cm
B.
40cm
C.
60cm
D.
80cm
7.(2011•兰州)如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A.
B.
C.
D.
8.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,正方形A2011B2011C2011C2010的面积为( )
A.
5×
B.
5×
C.
5×
D.
5×
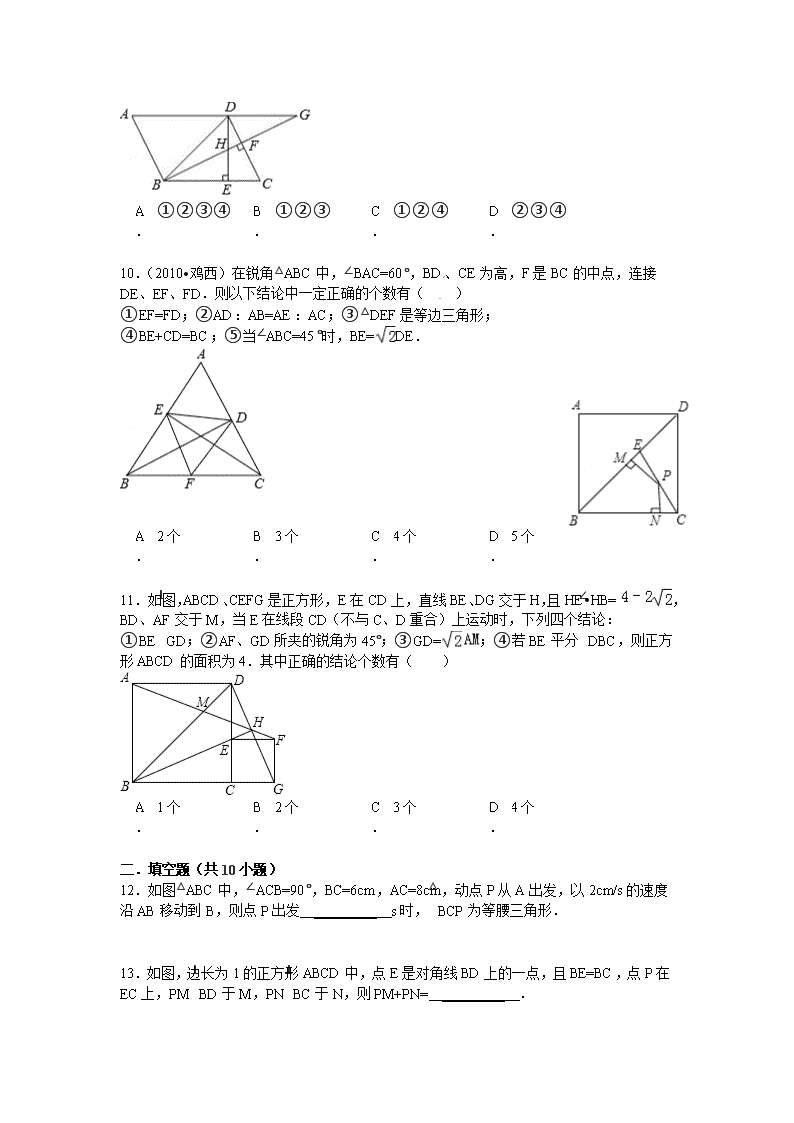
9.(2007•佳木斯)如图,已知▱ABCD中,∠BDE=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.其中正确的结论是( )
A.
①②③④
B.
①②③
C.
①②④
D.
②③④
10.(2010•鸡西)在锐角△ABC中,∠BAC=60°,BD、CE为高,F是BC的中点,连接DE、EF、FD.则以下结论中一定正确的个数有( )
①EF=FD;②AD:AB=AE:AC;③△DEF是等边三角形;
④BE+CD=BC;⑤当∠ABC=45°时,BE=DE.
A.
2个
B.
3个
C.
4个
D.
5个
11.如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE•HB=,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=;④若BE平分∠DBC,则正方形ABCD的面积为4.其中正确的结论个数有( )
A.
1个
B.
2个
C.
3个
D.
4个
二.填空题(共10小题)
12.如图△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从A出发,以2cm/s的速度沿AB移动到B,则点P出发 _________ s时,△BCP为等腰三角形.
13.如图,边长为1的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN= _________ .
14.(2010•眉山)如图,已知梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB=3,则下底BC的长为 _________ .
15.在半径为5的⊙O中,有两平行弦AB.CD,且AB=6,CD=8,则弦AC的长为 _________ .
16.如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是 _________ .
17.(2011•锦州)如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是 _________ .
18.(2010•牡丹江)开学初,小明到某商场购物,发现商场正在进行购物返券活动,活动规则如下:购物每满100元,返购物券50元,此购物券在本商场通用,且用购物券购买商品不再返券.小明只购买了单价分别为60元、80元和120元的书包、T恤、运动鞋,在使用购物券参与购买的情况下,他的实际花费为 _________ 元.
19.⊙O的弦AB的长等于半径,那么弦AB所对的圆周角等于 _________ 度.
20.如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且;②∠BAF=∠CAF ;③;
④∠BDF+∠FEC=2∠BAC,正确结论的序号是 ___ .
21.(2008•江西)如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5﹣x(0≤x≤5),给出以下四个结论:①AF=2;②BF=5;③OA=5;④OB=3.其中正确结论的序号是 _________ .
三.解答题(共4小题)
22.在平面直角坐标系中,点A、B分别在x轴、y 轴上,线段OA、OB的长(OA<OB)是关于x的方程x2﹣(2m+6)x+2m2=0的两个实数根,C是线段AB的中点,OC=3,D在线段OC上,OD=2CD.
(1)求OA、OB的长;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
23.(2009•朝阳)如图①,点A′,B′的坐标分别为(2,0)和(0,﹣4),将△A′B′O绕点O按逆时针方向旋转90°后得△ABO,点A′的对应点是点A,点B′的对应点是点B.
(1)写出A,B两点的坐标,并求出直线AB的解析式;
(2)将△ABO沿着垂直于x轴的线段CD折叠,(点C在x轴上,点D在AB上,点D不与A,B重合)如图②,使点B落在x轴上,点B的对应点为点E.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.
①试求出S与x之间的函数关系式(包括自变量x的取值范围);
②当x为何值时,S的面积最大,最大值是多少?
③是否存在这样的点C,使得△ADE为直角三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.
24.如图所示,在平面直角坐标系中,四边形OABC是等腰梯形.BC∥OA,∠COA=60°,OA、AB(OA>AB)是方程x2﹣11x+28=0的两个根.
(1)求点B的坐标;
(2)求线段AC的长;
(3)在x轴上是否存在一点P,使以点P、A、C为顶点的三角形为等腰三角形?若存在,请接写出点P的坐标;若不存在,请说明理由.
25.(2010•山西)在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F,求直线DE的解析式;
(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一个点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
2013年5月29龙江易错题错题二参考答案与试题解析
一.选择题(共11小题)
1.(2010•武汉)如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=;③.其中正确的是( )
A.
①②③
B.
只有②③
C.
只有②
D.
只有③
考点:
直角梯形.2611726
分析:
①如图,过H作HM⊥BC于M,根据角平分线的性质可以得到DH=HM,而在Rt△BHM中BH>HM,所以容易判定①是错误的;
②设HM=x,那么DH=x,由于∠ABC=90°,BD⊥DC,BD=DC,由此得到∠DBC=45°,而AD∥CB,由此可以证明△ADB是等腰直角三角形,又CE平分∠BCD,∠BDC=∠ABC=90°,由此可以证明△DCH∽△EBC,再利用相似三角形的性质可以推出∠BEH=∠DHC,然后利用对顶角相等即可证明∠BHC=∠BEH,接着得到BH=BE,然后即可用x分别表示BE、EN、CD,又由EN∥DC可以得到△DCH∽△NEH,再利用相似三角形的性质即可结论②;
③利用(2)的结论可以证明△ENH∽△CBE,然后利用相似三角形的性质和三角形的面积公式即可证明结论③.
解答:
解:①如图,过H作HM⊥BC于M,
∵CE平分∠BCD,BD⊥DC
∴DH=HM,
而在Rt△BHM中BH>HM,
∴BH>HD,
∴所以容易判定①是错误的;
②∵CE平分∠BCD,
∴∠DCE=∠BCE,而∠EBC=∠BDC=90°,
∴∠BEH=∠DHC,
而∠DHC=∠EHB,
∴∠BEH=∠EHB,
∴BE=BH,
设HM=x,那么DH=x,
∵BD⊥DC,BD=DC,
∴∠DBC=∠ABD=45°,
∴BH=x=BE,
∴EN=x,
∴CD=BD=DH+BH=(+1)x,
即=+1,
∵EN∥DC,
∴△DCH∽△NEH,
∴=+1,即CH=(+1)EH;
③由②得∠BEH=∠EHB,
∵EN∥DC,
∴∠ENH=∠CDB=90°,
∴∠ENH=∠EBC,
∴△ENH∽△CBE,
∴EH:EC=NH:BE,
而,
∴.
所以正确的只有②③.
故选B.
点评:
此题比较复杂,综合性很强,主要考查了梯形的性质,相似三角形的判定和性质以及等腰直角三角形的性质.
2.(2006•武汉)(北师大版)如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB.其中相似的为( )
A.
①④
B.
①②
C.
②③④
D.
①②③
解答:
解:根据题意得:∠BAE=∠ADC=∠AFE=90°
∴∠AEF+∠EAF=90°,∠DAC+∠ACD=90°
∴∠AEF=∠ACD
∴①中两三角形相似;
容易判断△AFE∽△BAE,得=,
又∵AE=ED,
∴=
而∠BED=∠BED,
∴△FED∽△DEB.
故②正确;
∵AB∥CD,
∴∠BAC=∠GCD,
∵∠ABE=∠DAF,∠EBD=∠EDF,且∠ABG=∠ABE+∠EBD,
∴∠ABG=∠DAF+∠EDF=∠DFC;
∵∠ABG=∠DFC,∠BAG=∠DCF,
∴△CFD∽△ABG,故③正确;
所以相似的有①②③.
故选D.
点评:
此题考查了相似三角形的判定:
①有两个对应角相等的三角形相似;
②有两个对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似.
3.(2008•齐齐哈尔)如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=AB;②∠BAF=∠CAF;③S四边形ADFE=AF•DE;④∠BDF+∠FEC=2∠BAC,正确的个数是( )
A.
1
B.
2
C.
3
D.
4
分析:
根据对折的性质可得AE=EF,∠DAF=∠DFA,∠EAF=∠AFE,∠BAC=∠DFE,据此和已知条件判断图中的相等关系.
解答:
解:①由题意得AE=EF,BF=FC,但并不能说明AE=EC,∴不能说明EF是△ABC的中位线,故①错;
②题中没有说AB=AC,那么中线AF也就不可能是顶角的平分线,故②错;
③易知A,F关于D,E对称.那么四边形ADFE是对角线互相垂直的四边形,那么面积等于对角线积的一半,故③对;
④∠BDF=∠BAF+∠DFA,∠FEC=∠EAF+∠AFE,∴∠BDF+∠FEC=∠BAC+∠DFE=2∠BAC,故④对.
正确的有两个,故选B.
点评:
翻折前后对应线段相等,对应角相等.
4.(2007•黑龙江)如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=BC,CE=AC,BE、AD相交于点F,连接DE,则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF•DA;④AF•BE=AE•AC,正确的结论有( )
A.
4个
B.
3个
C.
2个
D.
1个
分析:
本题是开放题,对结论进行一一论证,从而得到答案.
①利用△ABD≌△BCE,再用三角形的一个外角等于与它不相邻的两个内角和,即可证∠AFE=60°;
②从CD上截取CM=CE,连接EM,证△CEM是等边三角形,可证明DE⊥AC;
③△BDF∽△ADB,由相似比则可得到CE2=DF•DA;
④只要证明了△AFE∽△BAE,即可推断出AF•BE=AE•AC.
解答:
解:∵△ABC是等边三角形
∴AB=BC=AC,∠BAC=∠ABC=∠BCA=60°
∵BD=BC,CE=AC
∴BD=EC
∴△ABD≌△BCE
∴∠BAD=∠CBE,
∵∠ABE+∠EBD=60°
∴∠ABE+∠CBE=60°
∵∠AFE是△ABF的外角
∴∠AFE=60°
∴①是对的;
如图,从CD上截取CM=CE,连接EM,则△CEM是等边三角形
∴EM=CM=EC
∵EC=CD
∴EM=CM=DM
∴∠CED=90°
∴DE⊥AC,
∴②是对的;
由前面的推断知△BDF∽△ADB
∴BD:AD=DF:DB
∴BD2=DF•DA
∴CE2=DF•DA
∴③是对的;
在△AFE和△BAE中,∠BAE=∠AFE=60°,∠AEB是公共角
∴△AFE∽△BAE
∴AF•BE=AE•AC
∴④是正确的.
故选A.
点评:
本题主要应用到了三角形外角与内角的关系,直角三角形的判定,全等三角形和相似三角形的判定及性质,内容较多,较为复杂.
5.(2000•山西)已知:如图,在▱ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
A.
1个
B.
2个
C.
3个
D.
4个
分析:
(1)根据BF∥DE,BF=DE可证BEDF为平行四边形;(2)根据平行线等分线段定理判断;(3)根据△AGE∽△CGB可得;
(4)由(3)可得△ABG的面积=△AGE面积×2.
解答:
解:(1)∵▱ABCD,∴AD=BC,AD∥BC.
E、F分别是边AD、BC的中点,
∴BF∥DE,BF=DE.
∴BEDF为平行四边形,BE=DF.故正确;
(2)根据平行线等分线段定理可得AG=GH=HC.故正确;
(3)∵AD∥BC,AE=AD=BC,
∴△AGE∽△CGB,AE:BC=EG:BG=1:2,
∴EG=BG.故正确.
(4)∵BG=2EG,∴△ABG的面积=△AGE面积×2,
∴S△ABE=3S△AGE.故正确.
故选D.
点评:
此题考查了平行四边形的判定及性质、相似三角形的判定及性质等知识点,难度中等.
6.在课外活动课上,某同学做了一个对角线互相垂直的等腰梯形形状的风筝,其面积为450 cm2,则两条对角线共用的竹条至少需( )
A.
30cm
B.
40cm
C.
60cm
D.
80cm
考点:
等腰梯形的性质.2611726
专题:
应用题.
分析:
设对角线的长是x,根据面积公式可求得对角线的长,从而可得到两条对角线所用的竹条至少需要多少.
解答:
解:等腰梯形的对角线互相垂直且相等,可以设对角线的长是x,则x2=450,则x=30cm,两条对角线所用的竹条至少需要60cm.
故选C
点评:
对角线互相垂直的四边形的面积的计算方法是需要注意记忆的问题,两对角线长若是a,b则面积是ab.
7.(2011•兰州)如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A.
B.
C.
D.
分析:
过C点作CD⊥AB,垂足为D,根据旋转性质可知,∠B′=∠B,把求tanB′的问题,转化为在Rt△BCD中求tanB.
解答:
解:过C点作CD⊥AB,垂足为D.
根据旋转性质可知,∠B′=∠B.
在Rt△BCD中,tanB==,
∴tanB′=tanB=.
故选B.
点评:
本题考查了旋转的性质,旋转后对应角相等;三角函数的定义及三角函数值的求法.
8.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,正方形A2011B2011C2011C2010的面积为( )
A.
5×
B.
5×
C.
5×
D.
5×
分析:
先利用ASA证明△AOD和△A1BA相似,根据相似三角形对应边成比例可以得到AB=2A1B,所以正方形A1B1C1C的边长等于正方形ABCD边长的以此类推,后一个正方形的边长是前一个正方形的边长的然后即可求出第2011个正方形的边长与第1个正方形的边长的关系,从而求出第2011个正方形的面积.
解答:
解:∵四边形ABCD是正方形,
∴∠ABC=∠BAD=90°,AB=BC,
∴∠ABA1=90°,∠DAO+∠BAA1=180°﹣90°=90°,
又∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∴∠ADO=∠BAA1,
在△AOD和A1BA中,
∵,
∴△AOD∽△A1BA,
∴==2,
∴BC=2A1B,
∴A1C=BC,
以此类推A2C1=A1C,A3C2=A2C1即后一个正方形的边长是前一个正方形的边长的倍,
∴第2011个正方形的边长为()2011BC,
∵A的坐标为(1,0),D点坐标为(0,2),
∴BC=AD==,
∴正方形A2011B2011C2011C2010的面积为[()2011BC]2=5×()4022=5×()2011.
故选D.
点评:
本题考查的是一次函数综合题,涉及到正方形的性质及直角三角形的性质、相似三角形的判定与性质,属规律性题目.
9.(2007•佳木斯)如图,已知▱ABCD中,∠BDE=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.其中正确的结论是( )
A.
①②③④
B.
①②③
C.
①②④
D.
②③④
分析:
根据已知及相似三角形的判定方法对各个结论进行分析从而得到最后答案.
解答:
解:∵∠BDE=45°,DE⊥BC
∴DB=BE,BE=DE
∵DE⊥BC,BF⊥CD
∴∠BEH=∠DEC=90°
∵∠BHE=∠DHF
∴∠EBH=∠CDE
∴△BEH≌△DEC
∴∠BHE=∠C,BH=CD
∵▱ABCD中
∴∠C=∠A,AB=CD
∴∠A=∠BHE,AB=BH
∴正确的有①②③
故选B.
点评:
此题考查了相似三角形的判定和性质:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.相似三角形的对应边成比例,对应角相等.
10.(2010•鸡西)在锐角△ABC中,∠BAC=60°,BD、CE为高,F是BC的中点,连接DE、EF、FD.则以下结论中一定正确的个数有( )
①EF=FD;②AD:AB=AE:AC;③△DEF是等边三角形;
④BE+CD=BC;⑤当∠ABC=45°时,BE=DE.
A.
2个
B.
3个
C.
4个
D.
5个
分析:
①EF、FD是直角三角形斜边上的中线,都等于BC的一半;②可证△ABD∽△ACE;③证明∠EFD=60°;④假设结论成立,在BC上取满足条件的点H,证明其存在性;⑤当∠ABC=45°时,EF不一定是BC边的高.
解答:
解:①∵BD、CE为高,∴△BEC、△BDC是直角三角形.
∵F是BC的中点,∴EF=DF=BC.故正确;
②∵∠ADB=∠AEC=90°,∠A公共,∴△ABD∽△ACE,得AD:AB=AE:AC.故正确;
③∵∠A=60°,∴∠ABC+∠ACB=120°.
∵F是BC的中点,∴EF=BF,DF=CF.∴∠ABF=∠BEF,∠ACB=∠CDF.
∴∠BFE+∠CFD=120°,∠EFD=60°.又EF=FD,∴△DEF是等边三角形.故正确;
④若BE+CD=BC,则可在BC上截取BH=BE,则HC=CD.
∵∠A=60°,∴∠ABC+∠ACB=120°.又∵BH=BE,HC=CD,
∴∠BHE+∠CHD=120°,∠EHD=60°.
所以存在满足条件的点,假设成立,但一般情况不一定成立,故错误;
⑤当∠ABC=45°时,在Rt△BCE中,BC=BE,在Rt△ABD中,AB=2AD,
由B、C、D、E四点共圆可知,△ADE∽△ABC,
∴==,即=,∴BE=DE,故正确;
故此题选C.
点评:
此题考查了相似三角形的判定和性质,综合性很强.
11.如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE•HB=,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=;④若BE平分∠DBC,则正方形ABCD的面积为4.其中正确的结论个数有( )
A.
1个
B.
2个
C.
3个
D.
4个
分析:
①由已知条件可证得△BEC≌△DGC,∠EBC=∠CDG,因为∠BDC+∠DBH+∠EBC=90°,所以∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;
②若以BD为直径作圆,那么此圆必经过A、B、C、H、D五点,根据圆周角定理即可得到∠AHD=45°,所以②的结论也是正确的.
③此题要通过相似三角形来解;由②的五点共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45°,由此可判定△ABM∽△DBG,根据相似三角形的比例线段即可得到AM、DG的比例关系;
④若BE平分∠DBC,那么H是DG的中点;易证得△ABH∽△BCE,得BD•BC=BE•BH,即BC2=BE•BH,因此只需求出BE•BH的值即可得到正方形的面积,可先求出BE、EH的比例关系,代入已知的乘积式中,即可求得BE•BH的值,由此得解.
解答:
解:①正确,证明如下:
∵BC=DC,CE=CG,∠BCE=∠DCG=90°,
∴△BEC≌△DGC,∴∠EBC=∠CDG,
∵∠BDC+∠DBH+∠EBC=90°,
∴∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;
②由于∠BAD、∠BCD、∠BHD都是直角,因此A、B、C、D、H五点都在以BD为直径的圆上;
由圆周角定理知:∠DHA=∠ABD=45°,故②正确;
③由②知:A、B、C、D、H五点共圆,则∠BAH=∠BDH;
又∵∠ABD=∠DBG=45°,
∴△ABM∽△DBG,得AM:DG=AB:BD=1:,即DG=AM;
故③正确;
④过H作HN⊥CD于N,连接EG;
若BH平分∠DBG,且BH⊥DG,易知:BH垂直平分DG;
得DE=EG,H是DG中点,HN为△DCG的中位线;
设CG=x,则:HN=x,EG=DE=x,DC=BC=(+1)x;
∵HN⊥CD,BC⊥CD,∴HN∥BC,
∴∠NHB=∠EBC,∠ENH=∠ECB,
∴△BEC∽△HEN,则BE:EH=BC:HN=2+2,即EH=;
∴HE•BH=BH•=4﹣2,即BE•BH=4;
∵∠DBH=∠CBE,且∠BHD=∠BCE=90°,
∴△DBH∽△CBE,得:DB•BC=BE•BH=4,
即BC2=4,得:BC2=4,即正方形ABCD的面积为4;
故④正确;
因此四个结论都正确,故选D.
点评:
本题主要考查三角形相似和全等的判定及性质、正方形的性质以及圆周角定理等知识的综合应用,能够判断出A、B、C、D、H五点共圆是解题的关键.
二.填空题(共10小题)
12.如图△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从A出发,以2cm/s的速度沿AB移动到B,则点P出发 2,2.5,1.4 s时,△BCP为等腰三角形.
分析:
根据∠ACB=90°,BC=6cm,AC=8cm,利用勾股定理求出AB的长,再分别求出BC=BP,BP=PC时,AP的长,然后利用P点的运动速度即可求出时间.
解答:
解;∵△ABC中,∠ACB=90°,BC=6cm,AC=8cm,
∴AB===10,
∵当BC=BP时,△BCP为等腰三角形,
即BC=BP=6cm,△BCP为等腰三角形,
∴AP=AB﹣BP=10﹣6=4,
∵动点P从A出发,以2cm/s的速度沿AB移动,
∴点P出发 =2s时,△BCP为等腰三角形,
当点P从A出发,以2cm/s的速度沿AB移动到AB的中点时,
此时AP=BP=PC,则△BCP为等腰三角形,
点P出发=2.5s时,△BCP为等腰三角形,
当BC=PC时,
过点C作CD⊥AB于点D,
则△BCD∽△BAC,
∴,
解得:BD=3.6,
∴BP=2BD=7.2,
∴AP=10﹣7.2=2.8,
∴点P出发1.4s时,△BCP为等腰三角形.
故答案为:2;2.5;1.4.
点评:
此题主要考查勾股定理和等腰三角形的判定,解答此题的关键是首先根据勾股定理求出AB的长,然后再利用等腰三角形的性质去判定.
13.如图,边长为1的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN= .
分析:
连接BP,作EF⊥BC于点F,由正方形的性质可知△BEF为等腰直角三角形,BE=1,可求EF,利用面积法得S△BPE+S△BPC=S△BEC
,将面积公式代入即可.
解答:
解:连接BP,作EF⊥BC于点F,则∠EFB=90°,
由正方形的性质可知∠EBF=45°,
∴△BEF为等腰直角三角形,
又根据正方形的边长为1,得到BE=BC=1,
在直角三角形BEF中,sin∠EBF=,
即BF=EF=BEsin45°=1×=,
又PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
即BE×PM+×BC×PN=BC×EF,
∵BE=BC,
PM+PN=EF=;
故答案为:.
点评:
解决本题的关键是作出辅助线,构造矩形和全等三角形,把所求的线段转移到正方形的对角线上.
14.(2010•眉山)如图,已知梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB=3,则下底BC的长为 10 .
分析:
过A作AE∥CD,把梯形分成平行四边形和直角三角形,利用平行四边形的对边相等得到CE=AD,所以BE可以求出,在直角三角形中,根据∠B=30°,利用勾股定理求出BE,BC的长也就可以求出了.
解答:
解:如图,过A作AE∥CD交BC于点E,
∵AD∥BC,∴四边形AECD是平行四边形,
∴CE=AD=4,
∵∠B=30°,∠C=60°,
∴∠BAE=90°,
∴AE=BE(直角三角形30°角所对的直角边等于斜边的一半),
在Rt△ABE中,BE2=AB2+AE2,
即BE2=(3)2+(BE)2,
BE2=27+BE2,
BE2=36,
解得BE=6,
∴BC=BE+EC=6+4=10.
故答案为:10.
点评:
通过作腰的平行线,把梯形分成平行四边形和直角三角形,再利用直角三角形30°角所对的直角边等于斜边的一半和勾股定理求解,考虑本题的突破口在于两个已知角的和是90°.
15.在半径为5的⊙O中,有两平行弦AB.CD,且AB=6,CD=8,则弦AC的长为 或5 .
解答:
解:利用垂径定理和勾股定理可知:OE=3,OF=4,
①如图,∵4﹣3=1,(8﹣6)÷2=1,
∴AC==;
②如图,∵4+3=7,(8﹣6)÷2=1,
∴AC==5.
点评:
本题综合考查了垂径定理和勾股定理的运用.
16.如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是 (26,50) .
分析:
解决本题的关键是分析出题目的规律,以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为100÷2=50;其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到P100的横坐标.
解答:
解:经过观察可得:以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为100÷2=50;
其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到:Pn的横坐标为n÷4+1(n是4的倍数).
故点P100的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点P第100次跳动至点P100的坐标是(26,50).
故答案填(26,50).
点评:
本题的关键是分析出题目的规律,找出题目中点的坐标的规律,总结规律是近几年出现的常见题目.
17.(2011•锦州)如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是 (51,50) .
考点:
坐标与图形性质;规律型:图形的变化类.2611726
专题:
规律型.
分析:
根据图形观察发现,第偶数次跳动至点的坐标,横坐标是次数的一半加上1,纵坐标是次数的一半,然后写出即可.
解答:
解:观察发现,第2次跳动至点的坐标是(2,1),
第4次跳动至点的坐标是(3,2),
第6次跳动至点的坐标是(4,3),
第8次跳动至点的坐标是(5,4),
…
第2n次跳动至点的坐标是(n+1,n),
∴第100次跳动至点的坐标是(51,50).
故答案为:(51,50).
点评:
本题考查了坐标与图形的性质,以及图形的变化问题,结合图形得到偶数次跳动的点的横坐标与纵坐标的变化情况是解题的关键.
18.(2010•牡丹江)开学初,小明到某商场购物,发现商场正在进行购物返券活动,活动规则如下:购物每满100元,返购物券50元,此购物券在本商场通用,且用购物券购买商品不再返券.小明只购买了单价分别为60元、80元和120元的书包、T恤、运动鞋,在使用购物券参与购买的情况下,他的实际花费为 210或200 元.
分析:
根据题意读懂商场的活动规则,应该分两种情况:让其先买120元的运动鞋,得50元购物券,再用购物券去买那两样东西,依此计算实际花费;若先购买120元和80元,可得到100元的购物券,那么60元的就不用再掏钱了.所以应该是200或210.
解答:
解:他的实际花费=120+60﹣50+80=210元
或若现购买120元和80元,可得到100元的购物券,那么60元的就不用再掏钱了,即120+80=200(元).
点评:
本题旨在学生养成仔细读题的习惯.
19.⊙O的弦AB的长等于半径,那么弦AB所对的圆周角等于 30或150 度.
分析:
一条弦所对的圆周角有两种情况:当圆周角的顶点在优弧上,圆周角应是一个锐角;当圆周角的顶点在劣弧上,圆周角是一个钝角.
解答:
解:∵弦AB的长等于半径,
∴当把圆心分别与点A,B连接,可得等边三角形,等边三角形的内角是60°,
∴弦AB所对的圆心角是60°,
∴弦AB把圆分成60°和300°的两段弧,
根据弧的度数等于它所对的圆心角的度数,而一条弧所对的圆周角的度数等于所对圆心角度数的一半,
∴弦AB所对的圆周角等于30°或150°.
故弦AB所对的圆周角等于30°或150°.
点评:
一条弦(非直径)把圆分成两条弧,两条弧对应两个不同度数的圆周角.
20.如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且;②∠BAF=∠CAF;③;④∠BDF+∠FEC=2∠BAC,正确结论的序号是 ③④ .
分析:
根据折叠得到DE垂直平分AF,再根据对角线互相垂直的四边形的面积等于两条对角线的乘积的一半即可证明③,根据三角形的外角的性质即可证明④.
解答:
解:①要使EF∥AB且,则需EF是△ABC的中位线,根据折叠得AE=EF,显然本选项不一定成立;
②要使∠BAF=∠CAF,则需AD=AE,显然本选项不一定成立;
③根据折叠得到DE垂直平分AF,故本选项正确;
④根据三角形的外角的性质,得∠BDF=∠DAF+∠AFD,∠CEF=∠EAF+∠AFE,又∠BAC=∠DFE,则∠BDF+∠FEC=2∠BAC,故本选项成立.
故答案为③④.
点评:
此题综合考查了折叠的性质、对角线互相垂直的四边形的面积等于两条对角线的乘积的一半、三角形的外角的性质.
21.(2008•江西)如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5﹣x(0≤x≤5),给出以下四个结论:①AF=2;②BF=5;③OA=5;④OB=3.其中正确结论的序号是 ①②③ .
分析:
一次函数与正比例函数动点函数图象的问题.
解答:
解:此题由解析式求点的坐标,再求线段长,是数形结合的典范.当x=5时,d=2=AF,故①正确;当x=0时,d=5=BF,故②正确;OA=OF+FA=5,故③正确.当x=0时,BF=5,OF=3,OB=4,故④错误.故答案为①②③.
点评:
本题是今年出现的一种新题型,以多选题的形式出现,从考生所填的项中,能看出学生思维层次上的差异,弥补了填空题的不足.答题时,不少学生选择④,有的考生甚至填入⑤,说明学生对这类新题型的缺乏答题策略,对没有把握的结论宁可少选,也不可乱选;即宁缺勿滥.
三.解答题(共4小题)
22.在平面直角坐标系中,点A、B分别在x轴、y 轴上,线段OA、OB的长(OA<OB)是关于x的方程x2﹣(2m+6)x+2m2=0的两个实数根,C是线段AB的中点,OC=3,D在线段OC上,OD=2CD.
(1)求OA、OB的长;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
分析:
(1)求出AB=2OC=6,根据OA+OB=2m+6,OA×OB=2m2,得出方程(2m+6)2﹣4m2=180,求出m的值,代入方程,求出方程的解即可;
(2)过C作CM⊥OA于M,过D作DN⊥OA于N,求出C、D的坐标,设直线AD的解析式是y=kx+b,把A、D的坐标代入求出即可;
(3)求出AD与y轴的交点F的坐标,求出AF,①以OA为一边时,共有4个点,根据A坐标和OP=OA即可求出R、T的坐标,K(3,﹣3),同理求出G、K的坐标;②以OA为对角线,作OA的垂直平分线交AD于P,交OA于M,在OA的下方作MP=MQ,把x=3代入y=﹣x+6求出y,即可得出此时Q的坐标.
解答:
解:(1)∵AB=2OC=6,
∴OA2+OB2=AB2==180,
∵OA+OB=2m+6,OA×OB=2m2,
∴(OA+OB)2﹣2OA×OB=180,
即(2m+6)2﹣4m2=180,
∴m=6,
即方程为x2﹣18x+72=0,
∴x1=12,x2=6,
∵OA<OB,
∴OA=6,OB=12.
(2)过C作CM⊥OA于M,过D作DN⊥OA于N,
∵CM∥OB,
∴===,
∵OA=6,OB=12,
∴CM=6,AM=3,OM=3,
∴C(3,6),
∵OD=2CD,
∴===,
∴DN=4,ON=2,
∴D(2,4),
设直线AD的解析式是y=kx+b,
∵A(6,0),
代入得:,
解得:k=﹣1,b=6,
∴直线AD的解析式是y=﹣x+6.
(3)设直线y=﹣x+6交y轴于F,
把x=0代入y=﹣x+6得:y=6,
∴F(0,6),OF=6=OA,
由勾股定理得:AF=6,
分为两种情况:
①以OA为一边时,如图,共有3个点,如图,AP=OA=AP′=6,RT∥OA∥KG,
点Q在点T、K点时,以O、A、P(P′)、Q为顶点的四边形是菱形,
∵A(6,0),OP=OA,
∴OP=6=PR=PT,
∴此时Q的坐标是(6,6),
过P′作P′H⊥OA于H,
AP′=6,
由勾股定理得:P′H=AH=3,
K(3,﹣3),
K点在直线AD上关于A点对称的点(3,3)也可以.
②以OA为对角线,作OA的垂直平分线交AD于P,交OA于M,在OA的下方,MP=MQ,以O、A、P、Q为顶点的四边形是菱形,
把x=3代入y=﹣x+6得:y=3,
此时Q的坐标是(3,﹣3),
综合上述:P是直线AD上的点,在平面内存在点Q,使以O、A、P、Q为顶点的四边形是菱形,点Q的坐标是(6,6)或
(3,﹣3)或(3,3)或(3,﹣3).
点评:
本题考查了菱形的判定,用待定系数法求一次函数的解析式,勾股定理,平行线分线段
成比例定理等知识点的运用,本题综合性比较强,难度偏大,主要培养了学生综合运用性质进行推理和计算的能力.分类讨论思想的运用.
23.(2009•朝阳)如图①,点A′,B′的坐标分别为(2,0)和(0,﹣4),将△A′B′O绕点O按逆时针方向旋转90°后得△ABO,点A′的对应点是点A,点B′的对应点是点B.
(1)写出A,B两点的坐标,并求出直线AB的解析式;
(2)将△ABO沿着垂直于x轴的线段CD折叠,(点C在x轴上,点D在AB上,点D不与A,B重合)如图②,使点B落在x轴上,点B的对应点为点E.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.
①试求出S与x之间的函数关系式(包括自变量x的取值范围);
②当x为何值时,S的面积最大,最大值是多少?
③是否存在这样的点C,使得△ADE为直角三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.
分析:
(1)根据旋转的性质可以得到OA=OA′,OB=OB′,则A,B的坐标就可以得到,根据待定系数法就可以求出直线AB的解析式.
(2)①OB=4,C点的位置应分两种情况进行讨论,当C在OB的中点或在中点与B之间时,重合部分是△CDE;当C在OB的中点与O之间时,重合部分是梯形,就可以得到函数解析式.
②求出S与x之间的函数解析式,根据函数的性质就可以得到面积的最值.
③分△ADE以点A为直角顶点和△ADE以点E为直角顶点,两种情况进行讨论.根据相似三角形的对应边的比相等,求出OE的长,就可以得到C点的坐标.
解答:
解:
(1)A(0,2),B(4,0)(2分)
设直线AB的解析式y=kx+b,则有
解得
∴直线AB的解析式为(3分)
(2)i)①点E在原点和x轴正半轴上时,重叠部分是△CDE.
则S△CDE=
=
当E与O重合时,
∴2≤x<4(4分)
②当E在x轴的负半轴上时,设DE与y轴交于点F,则重叠部分为梯形
∵△OFE∽△OAB
∴,
∴
又∵OE=4﹣2x
∴
∴
=(5分)
当点C与点O重合时,点C的坐标为(0,0)
∴0<x<2(6分)
综合①②得(7分)
ii)①当2≤x<4时,
∴对称轴是直线x=4
∵抛物线开口向上,
∴在2≤x<4中,S随x的增大而减小
∴当x=2时,S的最大值=(8分)
②当0<x<2时,
∴对称轴是直线
∵抛物线开口向下∴当时,S有最大值为(9分)
综合①②当时,S有最大值为(10分)
iii)存在,点C的坐标为(,0)和(,0)(14分)
附:详解:①当△ADE以点A为直角顶点时,作AE⊥AB交x轴负半轴于点E,
∵△AOE∽△BOA
∴
∵AO=2∴EO=1
∴点E坐标为(﹣1,0)
∴点C的坐标为(,0)②当△ADE以点E为直角顶点时
同样有△AOE∽△BOA
∴EO=1∴E(1,0)
∴点C的坐标(,0)
综合①②知满足条件的坐标有(,0)和(,0).
以上仅提供本试题的一种解法或解题思路,若有不同解法请参照评分标准予以评分.
点评:
本题主要考查了待定系数法求函数的解析式,求函数的最值,以及相似三角形的对应边的比相等.
24.如图所示,在平面直角坐标系中,四边形OABC是等腰梯形.BC∥OA,∠COA=60°,OA、AB(OA>AB)是方程x2﹣11x+28=0的两个根.
(1)求点B的坐标;
(2)求线段AC的长;
(3)在x轴上是否存在一点P,使以点P、A、C为顶点的三角形为等腰三角形?若存在,请接写出点P的坐标;若不存在,请说明理由.
分析:
(1)首先解方程x2﹣11x+28=0,得出AB,AO的长,再利用∠COA=60°,得出EO的长,进而求出CE的长以及FO的长,从而得出B点坐标;
(2)利用等腰梯形的性质得出BO=AC,进而求出其长度;
(3)利用等腰三角形的性质以及线段垂直平分线的性质,即可得符合要求的点P的坐标.
解答:
解:(1)∵OA、AB(OA>AB)是方程x2﹣11x+28=0的两个根,
∴(x﹣7)(x﹣4)=0,
∴x1=4,x2=7,
∴AO=7,AB=4,
∴CO=AB=4,
∵∠COA=60°,
∴∠OCE=30°,
∴OE=CO=2,
∴CE==2,
∴FO=EO+EF=2+3=5,
BF=2,
∴点B的坐标为:(5,2);
(2)∵四边形OABC是等腰梯形,
∴CA=OB,
∴AC=BO==,
(3)存在.
如图所示即可得出:
①当AP=AC时,P1(7+,0),P2(7﹣,0),
②当AC=PC时,P3(﹣3,0),
③当AP=CP时,P4(3.3,0).
综上可得:P1(7+,0),P2(7﹣,0),P3(﹣3,0),P4(3.3,0).
点评:
此题主要考查了一次函数的综合应用以及等腰梯形的性质和等腰三角形的性质等知识,第(3)题容易漏解注意此类问题的解题方法应熟练应用.
25.(2010•山西)在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F,求直线DE的解析式;
(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一个点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
分析:
(1)过B作BH⊥x轴于H,则OH=BC=3,进而可求得AH的长,在Rt△ABH中,根据勾股定理即可求出BH的长,由此可得B点坐标;
(2)过E作EG⊥x轴于G,易得△OGE∽△OHB,根据相似三角形的对应边成比例可求出EG、OG的长,即可得到E点的坐标,进而可用待定系数法求出直线DE的解析式;
(3)此题应分情况讨论:
①以OD、ON为边的菱形ODMN,根据直线DE的解析式可求出F点的坐标,即可得到OF的长;过M作MP⊥y轴于P,通过构建的相似三角形可求出M点的坐标,将M点向下平移OD个单位即可得到N点的坐标;
②以OD、OM为边的菱形ODNM,此时MN∥y轴,延长NM交x轴于P,可根据直线DE的解析式用未知数设出M点的坐标,进而可在Rt△OMP中,由勾股定理求出M点的坐标,将M点向上平移OD个单位即可得到N点的坐标;
③以OD为对角线的菱形OMCN,根据菱形对角线互相垂直平分的性质即可求得M、N的纵坐标,将M点纵坐标代入直线DE的解析式中即可求出M点坐标,而M、N关于y轴对称,由此可得到N点的坐标.
解答:
解:(1)作BH⊥x轴于点H,则四边形OHBC为矩形,
∴OH=CB=3,(1分)
∴AH=OA﹣OH=6﹣3=3,
在Rt△ABH中,BH===6,(2分)
∴点B的坐标为(3,6);(3分)
(2)作EG⊥x轴于点G,则EG∥BH,
∴△OEG∽△OBH,(4分)
∴,
又∵OE=2EB,
∴,
∴=,
∴OG=2,EG=4,
∴点E的坐标为(2,4),(5分)
又∵点D的坐标为(0,5),
设直线DE的解析式为y=kx+b,
则,
解得k=﹣,b=5,
∴直线DE的解析式为:y=﹣x+5;(7分)
(3)答:存在(8分)
①如图1,当OD=DM=MN=NO=5时,四边形ODMN为菱形.作MP⊥y轴于点P,则MP∥x轴,∴△MPD∽△FOD
∴,
又∵当y=0时,﹣x+5=0,
解得x=10,
∴F点的坐标为(10,0),
∴OF=10,
在Rt△ODF中,FD===5,
∴,
∴MP=2,PD=,
∴点M的坐标为(﹣2,5+),
∴点N的坐标为(﹣2,);(10分)
②如图2,当OD=DN=NM=MO=5时,四边形ODNM为菱形.延长NM交x轴于点P,则MP⊥x轴.
∵点M在直线y=﹣x+5上,
∴设M点坐标为(a,﹣a+5),
在Rt△OPM中,OP2+PM2=OM2,
∴a2+(﹣a+5)2=52,
解得:a1=4,a2=0(舍去),
∴点M的坐标为(4,3),
∴点N的坐标为(4,8);(12分)
③如图3,当OM=MD=DN=NO时,四边形OMDN为菱形,连接NM,交OD于点P,则NM与OD互相垂直平分,
∴yM=yN=OP=,
∴﹣xM+5=,
∴xM=5,
∴xN=﹣xM=﹣5,
∴点N的坐标为(﹣5,),(14分)
综上所述,x轴上方的点N有三个,分别为N1(﹣2,),N2(4,8),N3(﹣5,).
(其它解法可参照给分)
点评:
此题主要考查了梯形的性质、相似三角形的判定和性质、一次函数解析式的确定以及菱形的判定和性质等知识的综合应用,需注意的是(3)题要根据菱形的不同构成情况分类讨论,以免漏解.