湖北省咸宁市2008年中考（数学）试题（含答案） 11页

湖北省咸宁市2008年初中毕业生学业考试 数 学 试 卷 ‎（参考答案及评分标准附后）‎ 考生注意：1．本试卷共8页，24小题；满分120分(附加2分)；考试时间120分钟．‎ ‎2．答题前，请将密封线内的项目填写清楚、完整．‎ 参考公式：总分 题号 一 二 三 ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ 得分 抛物线y＝ax2＋bx＋c(,,是常数，a≠0)的顶点坐标是().‎ 得 分 评卷人 一、精心选一选（本大题共8小题，每小题3分，共24分）每小题给出的4个选项中只有一个符合题意，请将所选选项的字母代号写在题目后的括号内 ‎1．-5的相反数是 【 】 ‎ ‎ A．5 B．‎-5 C． D．‎ ‎2．化简的结果为 　　 【 】‎ A． B． C． D．‎ ‎3．2008年北京奥运会火炬接力传递距离约为137　000千米，将137　000用科学记数法表示为 【 】‎ A. 13.7‎‎× B. 137×‎103 C. 1.37×105 D． 0.137×106‎ ‎4．在Rt△ABC 中， ∠C=90，AB=4，AC=1，则的值是 　　　　　【 】‎ A． B． C． D．４‎ ‎5. 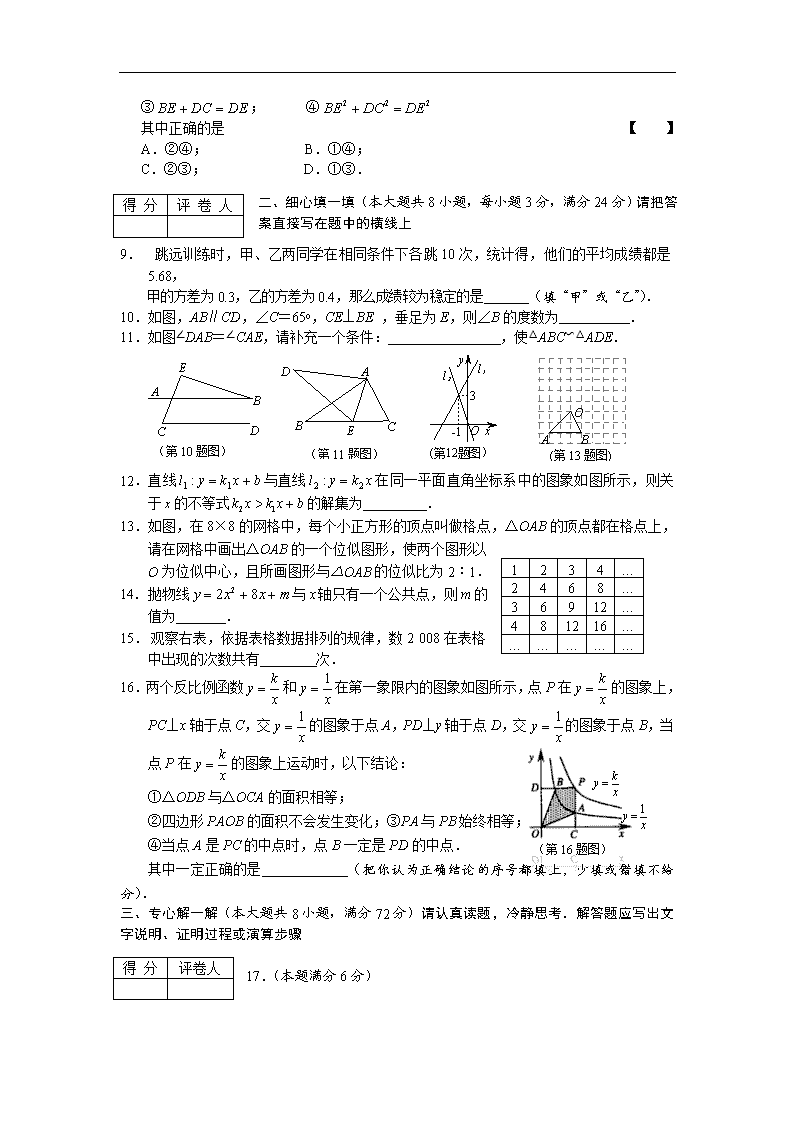右图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该班40名同学一周参加体育锻炼时间的说法错误的是　　 　　　　　　　　　　　　【 】‎ A．极差是3　　 B．中位数为8‎ C．众数是8 　 D．锻炼时间超过8小时的有21人 ‎6．两个完全相同的长方体的长、宽、高分别为3、2、1，把 它们叠放在一起组成一个新的长方体，在这些新长方体中，‎ 表面积最小值为 【 】‎ A．42 　 B． ‎38 ‎ 　C．20 　D．32‎ ‎7．下列说法：①对角线互相平分且相等的四边形是菱形； ②计算的结果为1；‎ ‎③正六边形的中心角为60； ④函数的自变量的取值范围是≥3．‎ 其中正确的个数有　　　　　　　　　　　　　　　　　　　　　　　　　　 【 】‎ A．1个 B．2个 C．3个 D．4个 ‎8．如图，在Rt△ABC 中，，D、E是斜边BC上两点，且∠DAE=45°，将△‎ 绕点顺时针旋转90后，得到△，连接，下列结论：‎ ‎①△≌△； ②△∽△；　　‎ ‎③； ④‎ 其中正确的是 【 】‎ A．②④；　　　　　　 B．①④；　　‎ 得 分 评 卷 人 C．②③；　　　　　　　 D．①③．‎ 二、细心填一填（本大题共8小题，每小题3分，满分24分）请把答案直接写在题中的横线上 ‎ ‎ ‎9． 跳远训练时，甲、乙两同学在相同条件下各跳10次，统计得，他们的平均成绩都是5.68，‎ 甲的方差为0.3，乙的方差为0.4，那么成绩较为稳定的是 （填“甲”或“乙”）．‎ ‎10．如图，AB∥CD，∠C＝65o，CE⊥BE ，垂足为E，则∠B的度数为 ．‎ ‎11．如图∠DAB＝∠CAE，请补充一个条件： ，使△ABC∽△ADE．‎ E ‎（第11题图）‎ D A C B A ‎(第13题图)‎ B O ‎ ‎ ‎（第10题图）‎ ‎12．直线与直线在同一平面直角坐标系中的图象如图所示，则关于的不等式的解集为 ．‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎…‎ ‎3‎ ‎6‎ ‎9‎ ‎12‎ ‎…‎ ‎4‎ ‎8‎ ‎12‎ ‎16‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎13．如图，在8×8的网格中，每个小正方形的顶点叫做格点，△OAB的顶点都在格点上，请在网格中画出△OAB的一个位似图形，使两个图形以 ‎ O为位似中心，且所画图形与△OAB的位似比为2︰1．‎ ‎14．抛物线与轴只有一个公共点，则的 值为 ．‎ ‎15．观察右表，依据表格数据排列的规律，数2 008在表格 中出现的次数共有 　　 次．‎ ‎16．两个反比例函数和在第一象限内的图象如图所示，点P在的图象上，PC⊥x轴于点C，交的图象于点A，PD⊥y轴于点D，交的图象于点B，当点P在的图象上运动时，以下结论：‎ ‎①△ODB与△OCA的面积相等；‎ ‎②四边形PAOB的面积不会发生变化；③PA与PB始终相等；‎ ‎（第16题图）‎ ‎④当点A是PC的中点时，点B一定是PD的中点．‎ 其中一定正确的是 （把你认为正确结论的序号都填上，少填或错填不给分）．‎ 三、专心解一解（本大题共8小题，满分72分）请认真读题，冷静思考．解答题应写出文字说明、证明过程或演算步骤 得 分 评卷人 ‎17．（本题满分6分）‎ ‎ ‎ 先化简，再求值： ，其中．‎ 得分 评卷人 ‎18．（本题满分8分）‎ Ａ、Ｂ两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运20千克，A型机器人搬运1000千克所用时间与B型机器人搬运800千克所用时间相等，两种机器人每小时分别搬运多少化工原料？‎ 得分 评卷人 ‎19．（本题满分8分）‎ ‎ ‎ 如图，在△ABC 中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．‎ ‎（1）求证：EO=FO；‎ ‎（2）当点O运动到何处时，四边形AECF是矩形？‎ ‎ 并证明你的结论．‎ 得分 评卷人 ‎20．（本题满分9分）‎ 有四张卡片（形状、大小和质地都相同），正面分别写有字母A、B、C、D和一个算式．将这四张卡片背面向上洗匀，从中随机抽取一张(不放回)，接着再随机抽取一张．‎ A B C ‎ ‎ D ‎(1)用画树形图或列表法表示抽取两张卡片可能出现的所有情况（卡片可用A、B、C、D表示）；(2)分别求抽取的两张卡片上的算式都正确的概率和只有一个算式正确的概率．‎ 得分 评卷人 ‎21．（本题满分9分）‎ 如图，BD是⊙O的直径，AB与⊙O相切于点B，过点D作OA的平行线交⊙O于点C，AC与BD的延长线相交于点E．‎ (1) 试探究A E与⊙O的位置关系，并说明理由；‎ (2) 已知EC＝a，ED＝b，AB＝c，请你思考后，选用以上适当的数据，设计出计算⊙O的半径r的一种方案：‎ ‎①你选用的已知数是　　　　　　　　；‎ ‎ ②写出求解过程（结果用字母表示）．‎ 得 分 评卷人 ‎22．（本题满分10分）‎ ‎ 如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．‎ 实验与探究：‎ (1) 由图观察易知A（0，2）关于直线l的对称点的坐标为（2，0），请在图中分别标明 B(5,3) 、C(-2,5) 关于直线l的对称点、的位置，并写出他们的坐标: ‎ ‎ 、 ；‎ 归纳与发现：‎ (2) 结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点的坐标为 （不必证明）；‎ 运用与拓广：‎ (3) 已知两点D(1,-3)、E(-1,-4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．‎ 得 分 评卷人 ‎23．（本题满分10分）‎ ‎“5·12”四川汶川大地震的灾情牵动全国人民的心，某市Ａ、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后，决定调运蔬菜支援灾区．已知Ａ蔬菜基地有蔬菜200吨，B蔬菜基地有蔬菜300吨，现将这些蔬菜全部调往C、D两个灾民安置点．从A地运往C、D两处的费用分别为每吨20元和25元，从B地运往C、D两处的费用分别为每吨15元和18元．设从B地运往C处的蔬菜为x吨．‎ (1) 请填写下表，并求两个蔬菜基地调运蔬菜的运费相等时x的值；‎ Ｃ Ｄ 总计 Ａ ‎200吨 Ｂ x吨 ‎300吨 总计 ‎240吨 ‎260吨 ‎500吨 (2) 设Ａ、B两个蔬菜基地的总运费为w元，写出w与x之间的函数关系式，并求总运费最小的调运方案；‎ (3) 经过抢修，从B地到C处的路况得到进一步改善，缩短了运输时间，运费每吨减少元（＞０），其余线路的运费不变，试讨论总运费最小的调运方案．‎ 得 分 评卷人 ‎24．（本题(1)～(3)小题满分12分，(4)小题为附加题另外附加2分）‎ 如图①，正方形 ABCD中，点A、B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形 ABCD的边上，从点A出发沿A→B→C→D匀速运动，同时动点Q以相同速度在x轴上运动，当P点到D点时，两点同时停止运动，设运动的时间为t秒．‎ (1) 当P点在边AB上运动时，点Q的横坐标（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；‎ ‎(2) 求正方形边长及顶点C的坐标；‎ ‎(第24题图①)‎ ‎（第24题图②）‎ ‎(3) 在(1)中当t为何值时，△OPQ的面积最大，并求此时P点的坐标．‎ (1) 附加题：（如果有时间，还可以继续 解答下面问题，祝你成功！）‎ 如果点P、Q保持原速度速度不 变，当点P沿A→B→C→D匀 速运动时，OP与PQ能否相等，‎ 若能，写出所有符合条件的t的 值；若不能，请说明理由．‎ 湖北省咸宁市2008年初中毕业生学业考试 数学试题参考答案及评分说明 说明：‎ 1． 如果考生的解法与本参考答案不同，可参照本评分说明制定相应的评分细则．‎ 2． 当考生的解答在某一步出现错误，影响了后继部分时，如果这一步以后的解答为改变这道题的内容和难度，可视影响程度决定后面部分的给分，但不得超过后面部分应给分数的一半；如果这一步以后的解答有较严重的错误，就不给分．‎ 3． 为阅卷方便，本解答中的推算步骤写得较为详细，但允许考生在解答过程中，合理省略非关键性的步骤．‎ 4． 解答中右端所注分数，表示考生正确做到这一步应得的累加分数．‎ 一．精心选一选（每小题３分，本大题满分24分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 A C C B B D C B 二．细心填一填 ‎ ‎9．甲 10．25° 11．或或 ‎ ‎12．<-1 13．(如右图) 14．8 15．8 16．①②④；‎ 说明：（1）本大题每小题3分，满分24分；‎ ‎ （2）第11小题为开放题，考生只需填一个正确的即可；‎ ‎ （3）第16小题少填、多填、错填的均不得分．‎ 三．专心解一解（本大题满分72分，附加题另附加3分）‎ ‎17．解：原式 ---------------------------------------------------------2分 ‎ ------------------------------------------------------------------------3分 ‎. --------------------------------------------------------------------------------4分 当时，原式．---------------------------------------------------6分 ‎18．解：设 A型机器人每小时搬运化工原料千克，则B型机器人每小时搬运（-20）千克，依题意得： . -----------------------------------------------------3分 ‎ 解这个方程得： . ----------------------------------------------------------------6分 ‎ 经检验是方程的解，所以-20=80. --------------------------------------------7分 答：Ａ、Ｂ两种机器人每小时分别搬运化工原料100千克和80千克．-----------8分 ‎19．解（1）证明： ∵CE平分，　　 ∴，‎ 又∵MN∥BC，　∴，　　∴，　　　　　‎ ‎∴．　　------------2分 ‎ 同理，． -----3分 ‎∴ ．------------------4分 ‎（2）当点O运动到AC的中点时，四边形AECF是矩形. ----------------------------------5分 ‎∵，点O是AC的中点． ∴四边形AECF是平行四边形. ------------------6分 又∵，． ∴，即． ----7分 ‎∴四边形AECF是矩形． -------------------------------------------------------------------8分 ‎20．解：（1）可能出现的情况共有12种（画树形图或列表略）；-----------------------------3分 ‎ （2）抽取的两张卡片上的算式都正确的有2种，‎ ‎ ∴(两张卡片上的算式都正确)= ． ---------------------------------------6分 抽取的两张卡片上的算式只有一个正确的有8种，‎ ‎ ∴(两张卡片上的算式只有一个正确)=． -------------------------------9分 ‎21．解：（1）A E与⊙O相切．------------------------------------------------------------------------1分 理由：连接OC ．‎ ‎∵CD∥OA ∴， ．‎ 又∵ODOC， ∴．∴．‎ ‎ 在△AOC和△AOB中 ‎ OA=OA， ，OB=OC，‎ ‎∴△AOC≌△AOB， ∴．‎ ‎∵AB与⊙O相切， ∴=90°．‎ ‎∴A E与⊙O相切． ----------------------------------------------------------------------------5分 ‎（2）①选择a、b、c，或其中2个 ‎② 解答举例：‎ 若选择a、b、c，‎ 方法一：由CD∥OA， ，得．‎ 方法二：在Rt△ABE中 ，由勾股定理，‎ 得 ．‎ ‎ 方法三：由Rt△OCE∽Rt△ABE，，得．‎ 若选择a、b ‎　方法一：在Rt△OCE中 ，由勾股定理：，得；‎ 方法二：连接BC，由△DCE∽△CBE，得．‎ 若选择a、c；需综合运用以上多种方法，得．‎ 说明：（１）此问满分４分，考生只需选择一组数据并正确完成计算即可；‎ ‎（２）若考生作出选择，但未完成计算或计算错误不给分．‎ ‎22．解：（1）如图：，-----------------2分 ‎(2) (b，a) 　　----------------------------------4分 ‎(3)由(2)得，D(1,-3) 关于直线l的对称点 的坐标为(-3,1)，连接E交直线l于点 Q，此时点Q到D、E两点的距离之和最小 ‎ -------------------------------------6分 设过(-3,1) 、E(-1,-4)的设直线的解析式 为，则 ‎　 ∴‎ ‎∴．‎ 由 　 得 ∴所求Q点的坐标为（，）-----10分 ‎ 说明：由点E关于直线l的对称点也可完成求解．‎ ‎23．解：(1)填表 Ｃ Ｄ 总计 Ａ ‎（240-x）吨 ‎（x-40）吨 ‎200吨 Ｂ x吨 ‎（300-x）吨 ‎300吨 总计 ‎240吨 ‎260吨 ‎500吨 ‎ ---------------------------------------------------------------1分 依题意得：. ------------------------------2分 ‎ 解得： . -----------------------------------------------------------------3分 ‎ (2) w与x之间的函数关系为：. -------------------------------------4分 依题意得： . ∴40≤≤240 ----------------------------------5分 ‎ 在中，∵2>0，　∴随的增大而增大， 表一：‎ ‎ ‎ Ｃ Ｄ Ａ ‎200吨 ‎0吨 Ｂ ‎40吨 ‎260吨 故当＝40时，总运费最小， ---------------------6分 ‎ 此时调运方案为如右表一. ----------------------7分 ‎ (3)由题意知 ‎ ∴0<<2时，（2）中调运方案总运费最小；-----8分 ‎ ‎ Ｃ Ｄ Ａ ‎0吨 ‎200吨 Ｂ ‎240吨 ‎60吨 ‎ =2时，在40≤≤240的前提下调运 表二：‎ 方案的总运费不变； ------9分 ‎ ‎ 2<<15时，＝240总运费最小，‎ 其调运方案如右表二 .-------------------------10分 ‎ 说明：讨论时按大于0、等于0、小于0不扣分 ‎24．解：（1）(1,0) ----------------------------------------------------------------------------------1分 ‎ 点P运动速度每秒钟1个单位长度．----------------------------------------------3分 ‎ (2) 过点作BF⊥y轴于点，⊥轴于点，则＝8，.‎ ‎ ∴.‎ ‎ 在Rt△AFB中，.-----------------------------------------------5分 ‎ 过点作⊥轴于点,与的延长线交于点.‎ ‎∵ ∴△ABF≌△BCH. ‎ ‎ ∴. ‎ ‎∴.‎ ‎∴所求C点的坐标为（14，12）.------------7分 ‎ (3) 过点P作PM⊥y轴于点M，PN⊥轴于点N，‎ 则△APM∽△ABF.‎ ‎ ∴. . ‎ ‎ ∴. ∴.‎ 设△OPQ的面积为(平方单位)‎ ‎∴(0≤≤10) --------------------10分 ‎ 说明:未注明自变量的取值范围不扣分.‎ ‎ ∵<0 ∴当时, △OPQ的面积最大.------------------11分 ‎ 此时P的坐标为(，) . ---------------------------------------------------12分 ‎ (4) 当 或时, OP与PQ相等.-----------------------------------------14分 ‎ 对一个加1分,不需写求解过程.‎