2017广州中考数学解析 13页

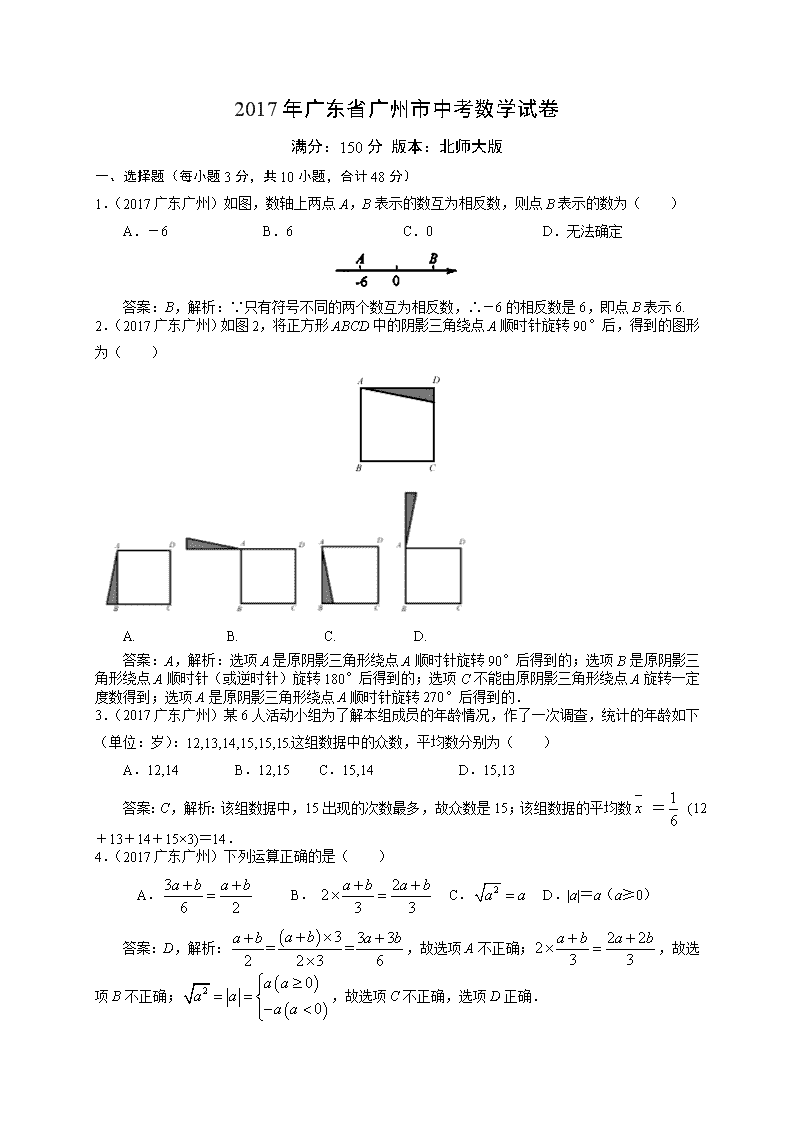
‎2017年广东省广州市中考数学试卷 满分：150分 版本：北师大版 一、选择题（每小题3分，共10小题，合计48分）‎ ‎1．（2017广东广州）如图，数轴上两点A，B表示的数互为相反数，则点B表示的数为（ ）‎ ‎ A．－6 B．6 C．0 D．无法确定 ‎ 答案：B，解析：∵只有符号不同的两个数互为相反数，∴－6的相反数是6，即点B表示6.‎ ‎2．（2017广东广州）如图2，将正方形ABCD中的阴影三角绕点A顺时针旋转90°后，得到的图形为（ ）‎ ‎ ‎ ‎ A. B. C. D. ‎ ‎ 答案：A，解析：选项A是原阴影三角形绕点A顺时针旋转90°后得到的；选项B是原阴影三角形绕点A顺时针（或逆时针）旋转180°后得到的；选项C不能由原阴影三角形绕点A旋转一定度数得到；选项A是原阴影三角形绕点A顺时针旋转270°后得到的．‎ ‎3．（2017广东广州）某6人活动小组为了解本组成员的年龄情况，作了一次调查，统计的年龄如下（单位：岁）：12,13,14,15,15,15.这组数据中的众数，平均数分别为（ ） ‎ ‎ A．12,14 B．12,15 C．15,14 D．15,13‎ ‎ 答案：C，解析：该组数据中，15出现的次数最多，故众数是15；该组数据的平均数 ＝ (12＋13＋14＋15×3)＝14．‎ ‎4．（2017广东广州）下列运算正确的是（ ）‎ ‎ A． B． C． D．|a|＝a（a≥0）‎ ‎ 答案：D，解析：，故选项A不正确；，故选项B不正确；，故选项C不正确，选项D正确．‎ ‎5．（2017广东广州）关于x的一元二次方程x2＋8x＋q＝0有两个不相等的实数根，则q的取值范围是（ ）‎ ‎ A．q＜16 B．q＞16 C．q≤4 D．q≥4‎ ‎ 答案：A，解析：根据一元二次方程根的判别式，得△＝82－4q＞0，解得q＜16.‎ ‎6．（2017广东广州）如图，⊙O是△ABC的内切圆，则点O是△ABC的（ ） ‎ ‎ A．三条边的垂直平分线的交点 B．三条角平分线的交点 ‎ C．三条中线的交点 D．三条高的交点 ‎ 答案：B，解析：如图，三角形内切圆的圆心是三个内角平分线的交点.‎ ‎7．（2017广东广州）计算，结果是（ ）‎ ‎ A．a5b5 B．a4b5 C．ab5 D．a5b6‎ ‎ 答案：A，解析：原式＝a6b3·＝a5b5．‎ ‎8．（2017广东广州）如图，E,F分别是ABCD的边AD，BC上的点，EF＝6，∠DEF＝60°，将四边形EFCD沿EF翻折，得到 EFC’D’，ED’交BC于点G，则△GEF的周长为（ ）‎ ‎ A．6 B．12 C.18 D.24‎ ‎ 答案：C，解析：由折叠的性质可知，∠GEF＝∠DEF＝60°.又∵AD∥BC，∴∠GFE＝∠DEF＝60°，∴△GEF是等边三角形.∵EF＝6，∴△GEF的周长为18．‎ ‎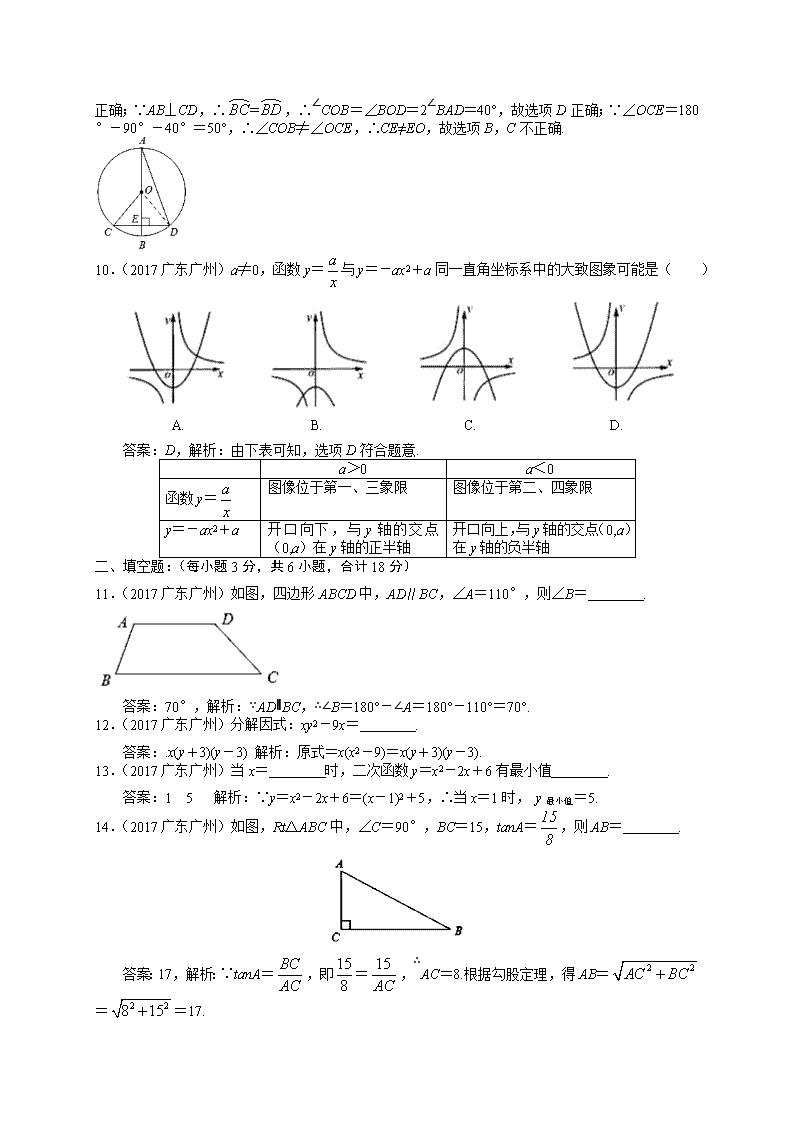9．（2017广东广州）如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，连接CO,AD,∠BAD＝20°，则下列说法中正确的是（ ）‎ A．AD＝2OB B．CE＝EO C．∠OCE＝40° D．∠BOC＝2∠BAD ‎ 答案：D，解析：如图，连接OD.∵AD是非直径的弦，OB是半径，∴AD≠2OB，故选项A 不正确；∵AB⊥CD，∴，∴∠COB＝∠BOD＝2∠BAD＝40°，故选项D正确；∵∠OCE＝180°－90°－40°＝50°，∴∠COB≠∠OCE，∴CE≠EO，故选项B，C不正确.‎ ‎10．（2017广东广州）a≠0，函数y＝与y＝－ax2＋a同一直角坐标系中的大致图象可能是（ ）‎ ‎ A. B. C. D.‎ ‎ 答案：D，解析：由下表可知，选项D符合题意.‎ a＞0‎ a＜0‎ 函数y＝‎ 图像位于第一、三象限 图像位于第二、四象限 y＝－ax2＋a 开口向下，与y轴的交点（0,a）在y轴的正半轴 开口向上，与y轴的交点（0,a）在y轴的负半轴 二、填空题：（每小题3分，共6小题，合计18分）‎ ‎11．（2017广东广州）如图，四边形ABCD中，AD∥BC，∠A＝110°，则∠B＝ .‎ ‎ 答案：70°，解析：∵AD∥BC，∴∠B＝180°－∠A＝180°－110°＝70°.‎ ‎12．（2017广东广州）分解因式：xy2－9x＝ .‎ ‎ 答案：.x(y＋3)(y－3) 解析：原式＝x(x2－9)＝x(y＋3)(y－3).‎ ‎13．（2017广东广州）当x＝ 时，二次函数y＝x2－2x＋6有最小值 .‎ ‎ 答案：1 5 解析：∵y＝x2－2x＋6＝(x－1)2＋5，∴当x＝1时， y最小值＝5.‎ ‎14．（2017广东广州）如图，Rt△ABC中，∠C＝90°，BC＝15，tanA＝，则AB＝ .‎ ‎ 答案：17，解析：∵tanA＝，即＝，∴AC＝8.根据勾股定理，得AB＝＝＝17.‎ ‎15．（2017广东广州）如图，圆锥的侧面展开图是一个圆心角为120°的扇形，若圆锥的底面圆半径是，则圆锥的母线l＝ .‎ ‎ 答案：3 解析：圆锥的侧面展开图是扇形，且扇形的弧长等于圆锥底面圆的周长，扇形的半径长等于圆锥的母线长，即＝2π×，解得l＝3.‎ ‎16．（2017广东广州）如图，平面直角坐标系中O是原点，□ABCD的顶点A,C的坐标分别是（8，0），（3,4），点D,E把线段OB三等分，延长CD,CE分别交OA，AB于点F，G，连接FG，则下列结论：①F是OA的中点；②△OFD与△BEG相似；③四边形DEGF的面积是；④OD＝；其中正确的结论是 ．（填写所有正确结论的序号）‎ ‎ 答案：①③ 解析：∵BC∥OA，且点D，E是OB的三等分点，∴，∴OF＝BC＝OA，∴点F是OA的中点，故①正确；易证点G是AB的中点，∴S△COF＝S△BCG＝S□OABC，∴S四边形AFCG＝ S□OABC.由点A，C的坐标可知S□OABC＝8×4＝32，S△CDE＝S△BOC＝×S□OABC＝.∵FG是△AOB的中位线，∴S△AFG＝S△AFG＝×S□OABC＝4，∴S四边形DEGF＝S四边形AFCG－S△CDE－S△AFG＝S□OABC－S△CDE－S△AFG＝16－－4＝，故③正确；由平行四边形的性质可知点B的坐标为(11，4)，则OB＝＝，∴OD＝OB＝，故④不正确.由于△OFD与△BEG相似的条件不充足，故②不正确.‎ 三、解答题：本大题共9个小题，满分102分．‎ ‎17．（本小题满分9分）解方程组：.‎ ‎ 思路分析：利用加减消元法或代入消元法求解.‎ 解：①×3，得 ‎3x＋3y＝15③，‎ ‎③－②，得 x＝4.‎ 将x＝4代入①，得 y＝1.‎ ‎∴方程组得解为.‎ ‎18．（2017广东广州）（本小题满分9分）如图，点E,F在AB上，AD＝BC，∠A＝∠B，AE＝BF.‎ 求证：△ADF≌△BCE.‎ ‎ 思路分析：根据SAS证明两个三角形全等.‎ 证明：∵AE＝BF，‎ ‎∴AE＋EF＝BF＋EF，‎ 即AF＝BE.‎ 在△ADF和△BCE中，‎ ‎∴△ADF≌△BCE（SAS）.‎ ‎19．（2017广东广州）（本小题满分10分）某班为了解学生一学期做义工的时间情况，对全班50名学生进行调查，按做义工的时间 （单位：小时），将学生分成五类：A类（0≤t≤2），B类（2＜t≤4），C类（4＜t≤6），D类（6＜t≤8），E类（t＞8），绘制成尚不完整的条形统计图如图11.‎ 根据以上信息，解答下列问题：‎ ‎（1）E类学生有_________人，补全条形统计图；‎ ‎（2）D类学生人数占被调查总人数的__________%；‎ ‎（3）从该班做义工时间在0≤t≤4的学生中任选2人，求这2人做义工时间都在2＜t≤4中的概率．‎ 思路分析：（1）∵全班人数为50，∴E类学生人数为50－（2+3+22+18）＝5；（2）D类学生人数占被调查人数的百分比为×100%＝36%；（3）先列举所有可能的结果，再利用概率计算公式求解.‎ 解：（1）5，补全条形统计图如图所示：‎ ‎（2）36；‎ ‎（3）该班做义工时间在0≤t≤4的学生有5人，其中A类（0≤t≤2）的学生有2人，B类（0≤t≤2）的学生有3人.设这5人分别为A1，A2，B1，B2，B3，从中任选2人，所有可能的结果为：（A1，A2），（A1，B1），（A1，B2），（A1，B3），（A2，B1），（A2，B2），（A2，B3），（B1，B2），（B1，B3），（B2，B3），共10种，其中两人都在2＜t≤4的结果有3种：（B1，B2），（B1，B3），（B2，B3），∴P（这2人做义工时间都在2＜t≤4）＝.‎ ‎20．（2017广东广州）（本小题满分10分）如图12，在Rt△ABC中，∠B＝90°，∠A＝30°，AC＝2.‎ ‎（1）利用尺规作线段AC的垂直平分线DE，垂足为E，交AB于点D；（保留作图痕迹，不写作法）‎ ‎（2）若△ADE的周长为a，先化简T＝（a＋1）2－a（a－1），再求T的值．‎ 思路分析：（1）按照线段垂直平分线的尺规作图方法作图；（2）通过解直角三角形求出△ADE的周长为a，再化简、代入求值.‎ 解：（1）如图所示：‎ ‎（2）∵DE是线段AC的垂直平分线，‎ ‎∴∠AED＝90°，AE＝AC＝×2＝.‎ 在RtADE中，∠A＝30°，AE＝，∴DE＝AE·tanA＝×＝1，AD＝2DE＝2.‎ ‎∴a＝AD+DE+AE＝2+1+＝3＋.‎ T=（a＋1）2－a（a－1）＝a2＋2a＋1－a2＋a＝3a＋1＝3（3+）+1＝3+10.‎ ‎21．（2017广东广州）（本小题满分12分）甲、乙两个工程队均参与某筑路工程，先由甲队筑路60公里，再由乙队完成剩下的筑路工程，已知乙队筑路总公里数是甲队筑路总公里数的倍，甲队比乙队多筑路20天．‎ ‎（1）求乙队筑路的总公里数；‎ ‎（2）若甲、乙两队平均每天筑路公里数之比为5：8，求乙队平均每天筑路多少公里．‎ ‎ 思路分析：（1）根据“乙队筑路总公里数是甲队筑路总公里数的倍”求解；（2）根据“甲队比乙队多筑路20天”列分式方程求解，注意检验.‎ ‎ 解：（1）60×＝80（公里），即乙队筑路的总公里数为80公里.‎ ‎（2）设甲队每天筑路8x公里，乙队每天筑路5x公里，根据题意，得 解得x＝. ‎ 经检验，x＝是原方程的解且符合题意,‎ ‎×8＝.‎ 答：乙队平均每天筑路公里.‎ ‎22．（2017广东广州）（本小题满分12分）将直线y＝3x＋1向下平移1个单位长度，得到直线y＝3x＋m，若反比例函数y＝的图象与直线y＝3x＋m相交于点A，且点A的纵坐标是3．‎ ‎（1）求m和k的值；‎ ‎（2）结合图象求不等式3x＋m＞的解集．‎ ‎ 思路分析：（1）将直线y＝3x＋1向下平移1个单位长度后得到直线y＝3x+1－1，故3x＋m＝3x+1－1，从而求得m的值和点A的坐标，将点A代入y＝可得到k的值；（2）直线y＝3x＋m在双曲线y＝上方时x的取值范围，即为不等式3x＋m＞的解集.‎ ‎ 解：（1）根据题意，得3x＋m＝3x+1－1，解得m＝0.∴y＝3x.‎ 将y＝3代入y＝3x，得3x＝3，解得x＝1，∴点A的坐标为（1,3）.‎ 将（1,3）代入y＝，得k＝3.‎ ‎（2）如图，可知不等式3x＋m＞的解集为－1＜x＜0或x＞1.‎ ‎23．（2017广东广州）（本小题满分12分）已知抛物线y1＝－x2＋mx＋n，直线y2＝kx＋b，y1的对称轴与y2交于点A（－1,5），点A与y1的顶点B的距离是4．‎ ‎（1）求y1的解析式；‎ ‎（2）若y2随着x的增大而增大，且y1与y2都经过x轴上的同一点，求y2的解析式．‎ ‎ 思路分析：（1）由“y1的对称轴经过点A（－1,5）”可知对称轴为x＝－1，从而求得m的值，进而可用含n的式子表示出顶点B的坐标，再由“点A与y1的顶点B的距离是4”求得n的值；（2）由（1）中所求y1的函数解析式求得y2与x轴的交点，利用待定系数法求出y2的解析式.注意“y2随着x的增大而增大”这一条件的限制.‎ 解：（1）∵y1的对称轴与y2交于点A（－1,5），‎ ‎∴y1的对称轴为x＝－1.‎ ‎∴＝－1，解得m＝－2.‎ ‎∴y1＝－x2－2x＋n＝－（x+1）2＋n＋1.‎ ‎∴顶点B的坐标为（－1，n＋1）.‎ ‎∵AB＝4，∴|（n＋1）－5|＝4，解得n1＝0，n2＝8.‎ 当n＝0时，y1＝－x2－2x；当n＝8时，y1＝－x2－2x＋8.‎ 即y1的解析式为y1＝－x2－2x或y1＝－x2－2x＋8.‎ ‎（2）当y1＝－x2－2x时，‎ 将y＝0代入y1＝－x2－2x，得x1＝0，x2＝－2，∴y1与x轴的交点为（0,0），（－2,0）.‎ ‎∵y2随x的增大而增大，∴k＞0.‎ ‎①当y2经过A（－1，5），（0，0）时，则有，解得，∴y2＝－5x.（不合题意，舍去）.‎ ‎②当y2经过A（－1，5），（－2，0）时，则有，解得，∴y2＝5x+10.‎ 当y1＝－x2－2x+8时，将y＝0代入y1＝－x2－2x+8，得x1＝2，x2＝－4，∴y1与x轴的交点为（2,0），（－4,0）.‎ ‎①当y2经过A（－1，5），（2，0）时，则有，解得，∴y2＝x+.（不合题意，舍去）.‎ ‎②当y2经过A（－1，5），（－4，0）时，则有，解得，∴y2＝x+.‎ 综上可知，y2的解析式为y2＝5x+10或y2＝x+.‎ ‎24．（2017广东广州）（本小题满分14分）如图，矩形ABCD的对角线AC，BD相交于点O，△COD关于CD的对称图形为△CED．‎ ‎（1）求证：四边形OCED是菱形；‎ ‎（2）连接AE，若AB＝6cm，BC＝cm.‎ ‎①求sin∠EAD的值；‎ ‎②若点P为线段AE上一动点（不与点A重合），连接OP，一动点Q从点O出发，以1cm/s的速度沿线段OP匀速运动到点P，再以1.5cm/s的速度沿线段PA匀速运动到点A，到达点A后停止运动．当点Q沿上述路线运动到点A所需要的时间最短时，求AP的长和点Q走完全程所需的时间．‎ 思路分析：（1）根据矩形的性质和轴对称的性质证明四边形OCED的四条边都相等；（2）①连接OE，设直线OE交AB于点F，交DC于点G，可知∠EAD＝∠AEF，在△AEF中求得sin∠AEF即可；②过点P作PM⊥AB，垂足为点M. Q由O运动到P所需时间就是OP+MA最小.‎ 解：（1）证明：∵四边形ABCD是为矩形，‎ ‎∴AC＝BD.‎ ‎∵AC与BD交于点O，且△COD与△CED关于CD对称，‎ ‎∴DO＝CO，且DO＝DE，OC＝EC，‎ ‎∴DO＝OC＝EC＝ED，‎ ‎∴四边形OCED是菱形.‎ ‎（2）①连接OE，设直线OE交AB于点F，交DC于点G.‎ ‎∵△COD与△CED关于CD对称，∴OE⊥DC.‎ ‎∵DC∥AB，∴OF⊥AB，EF∥AD.‎ ‎∵G为DC的中点，O为AC的中点，∴OG是△CAD的中位线，∴OG＝GE＝.‎ 同理可得OF＝，AF＝3，∴AE＝.‎ ‎∵∠EAD＝∠AEF，∴sin∠EAD＝sin∠AEF＝.‎ ‎①过点P作PM⊥AB，垂足为点M.‎ ‎∴Q由O运动到P所需时间为3s.‎ 由①可知AM＝AP.‎ ‎∴点Q以1.5cm/s的速度从点P到A所需时间等同于以1cm/s的速度从M运动到A,‎ 即t＝tOP+tPA＝，‎ ‎∴Q由O运动到P所需时间就是OP+MA最小.‎ 如图，当P运动到P1，即P1O∥AB时，所用时间最短.‎ ‎∴t＝＝3s.‎ 在Rt△AP1M1中，设AM1＝2x，则AP1＝3x，∵AP12＝AM12+P1M12，∴（3x）2＝（2x）‎ ‎2+，解得x1＝，x2＝－（舍去），∴AP＝.‎ 答：AP的长为cm，点Q走完全程需时3s.‎ ‎25．（2017广东广州）（本小题满分14分）如图14，AB是⊙O的直径，，AB＝2，连接AC.‎ ‎（1）求证：∠CAB＝45°；‎ ‎（2）若直线l为⊙O的切线，C是切点，在直线L上取一点D，使BD＝AB，BD所在的直线与AC所在的直线相交于点E，连接AD．‎ ‎①试探究AE与AD之间的数量关系，并证明你的结论；‎ ‎②是否为定值？若是，请求出这个定值；若不是，请说明理由．‎ ‎ 思路分析：（1）连接BC，根据“同弧所对的圆周角等于圆角角的一半”求解；（2）①当BD＝AB时，有∠ABD为锐角和∠ABD为钝角两种情形；②分D在点C左侧或D在点C右侧两种情况求解.‎ 解：（1）证明：如图，连接BC.‎ ‎∵AB是⊙O的直径，∴∠ACB＝90°.‎ ‎∵AC＝BC，∴∠CAB＝∠CBA＝（180°－90°）＝45°.‎ ‎（2）①当∠ABD为锐角时，如图所示，作BF⊥l于F.‎ 由（1）可知△ABC为等腰直角三角形.‎ ‎∵O是AB的中点，∴CO＝AO＝BO，∴△COB为等腰直角三角形.‎ ‎∵l是⊙O的切线，∴OC⊥l.‎ ‎∵BF⊥l，∴四边形OBEC为矩形.‎ ‎∴AB＝2BF，∴BD＝2BF，∴∠BDF＝30°，∴∠DBA＝30°，‎ ‎∴∠BDA＝∠BAD＝75°，∠CBE＝15°，∠CEB＝90°－15°＝75°，∴∠CEB＝∠DEA，∴AD＝AE.‎ ‎②当∠ABD为钝角时，如图所示，同样BF＝BD，∠BDC＝30°，‎ ‎∴∠ABD＝150°，∠AEB＝90°－∠CBE＝15°，∠ADB＝（180°－150°）＝15°，‎ ‎∴∠AED＝∠ADE，∴AE＝AD.‎ ‎②当D在C左侧时，由①可知CD∥AB，∠ACD＝∠BAE，∠DAC＝∠EBA＝30°，‎ ‎∴△CAD∽△BAE，∴，∴AE＝CD.‎ ‎∵BA＝BD，∠BAD＝∠BDA＝15°，∴∠IBE＝30°.‎ 在Rt△IBE中，BE＝2EI＝2×AE＝AE＝CD＝2CD.‎ ‎∴.‎ 当D在C右侧时，过E走EI⊥AB与I.‎ 由①可知∠ADC＝∠BEA＝15°.‎ ‎∵AB∥CD，∴∠EAB＝∠ACD，‎ ‎∴△ACD∽△BAE，‎ ‎∴，∴AE＝CD.‎ ‎∵BA＝BD，∠BAD＝∠BDA＝15°，∴∠IBE＝30°.‎ 在Rt△IBE中，BE＝2EI＝2×AE＝AE＝CD＝2CD.‎ ‎∴.‎ 综上所述，为定值，其值为2.‎