专题14相似三角形问题攻破15个特色专题之备战2018中考数学高端精品原卷 9页

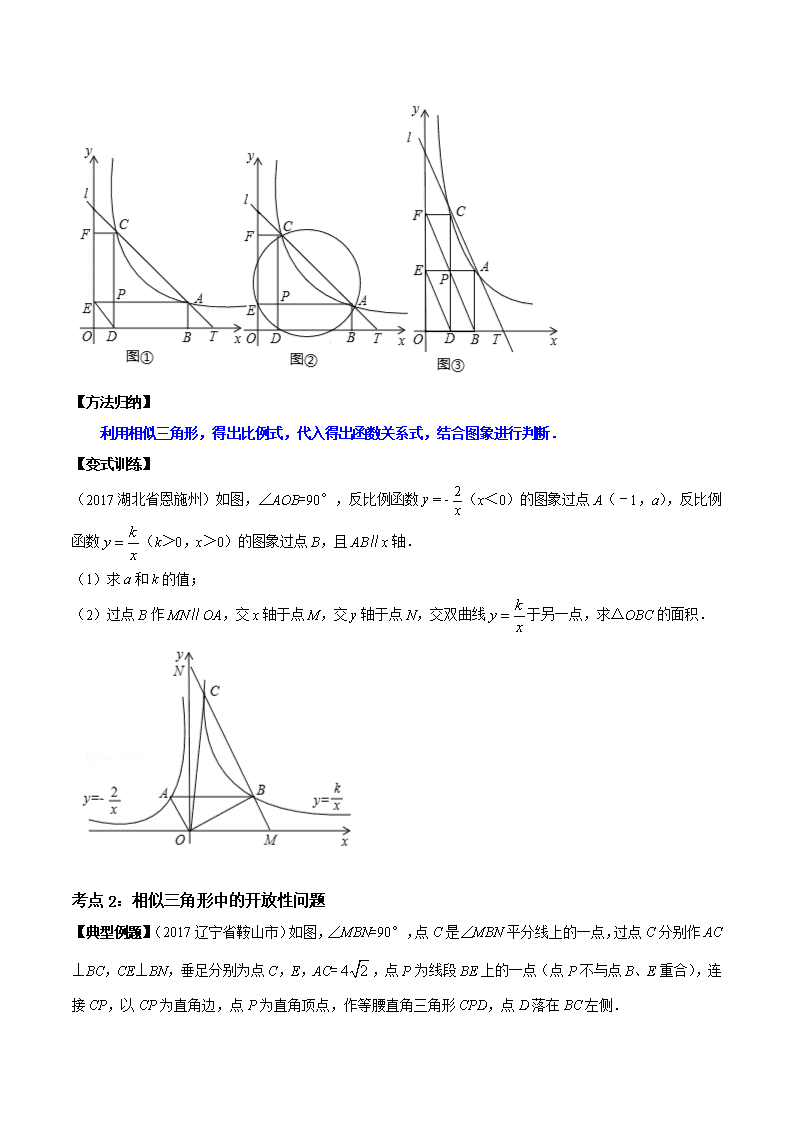
专题14 相似三角形问题 ‎【考点综述评价】‎ 因动点产生的相似三角形问题，常常出现在综合题中．‎ 一是以几何图形为载体，赋予动点、动线和动面，来探究相似三角形问题，进而研究面积、函数最值等问题；二是以动态问题为背景或与函数图象、圆结合探究相似三角形的存在性问题；三是以相似三角形为背景，经历“问题情境，建立模型，求解，应用”的基本过程，设置探究性问题．问题设置常常具有开放性． ‎ 相似三角形由于对应边、对应角的不确定，或者是图形的不确定，常常需要进行分类讨论，解题时根据对应角或对应边来分类．要注意确定分类标准，按一个标准进行分类，做到“不重复，不遗漏”．‎ ‎【考点分类总结】‎ 考点1：利用三角形相似与图象的判断 ‎ ‎【典型例题】（2017湖北省黄石市）如图，直线l：y=kx+b（k＜0）与函数（x＞0）的图象相交于A、C两点，与x轴相交于T点，过A、C两点作x轴的垂线，垂足分别为B、D，过A、C两点作y轴的垂线，垂足分别为E、F；直线AE与CD相交于点P，连接DE，设A、C两点的坐标分别为（a，）、（c，），其中a＞c＞0．‎ ‎（1）如图①，求证：∠EDP=∠ACP；‎ ‎（2）如图②，若A、D、E、C四点在同一圆上，求k的值；‎ ‎（3）如图③，已知c=1，且点P在直线BF上，试问：在线段AT上是否存在点M，使得OM⊥AM？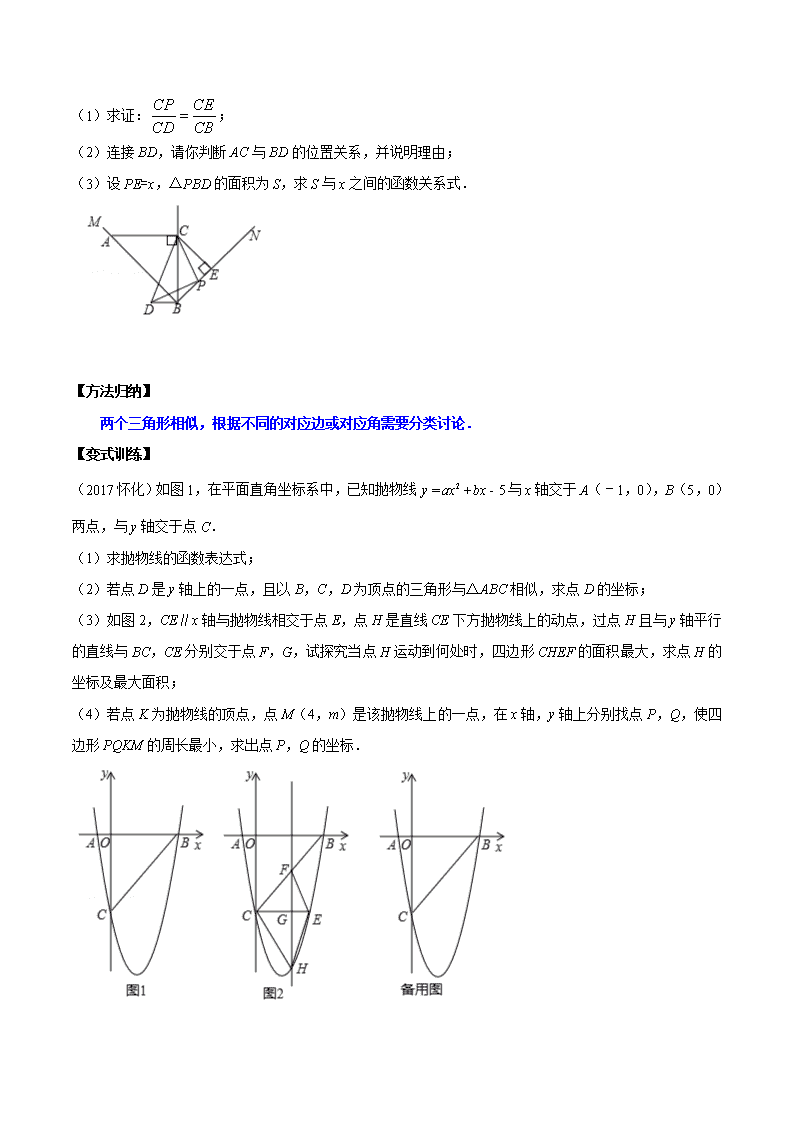请求出点M的坐标；若不存在，请说明理由．‎ ‎【方法归纳】‎ 利用相似三角形，得出比例式，代入得出函数关系式，结合图象进行判断．‎ ‎【变式训练】‎ ‎（2017湖北省恩施州）如图，∠AOB=90°，反比例函数（x＜0）的图象过点A（﹣1，a），反比例函数（k＞0，x＞0）的图象过点B，且AB∥x轴．‎ ‎（1）求a和k的值；‎ ‎（2）过点B作MN∥OA，交x轴于点M，交y轴于点N，交双曲线于另一点，求△OBC的面积．‎ 考点2：相似三角形中的开放性问题 ‎ ‎【典型例题】（2017辽宁省鞍山市）如图，∠MBN=90°，点C是∠MBN平分线上的一点，过点C分别作AC⊥BC，CE⊥BN，垂足分别为点C，E，AC=，点P为线段BE上的一点（点P不与点B、E重合），连接CP，以CP为直角边，点P为直角顶点，作等腰直角三角形CPD，点D落在BC左侧．‎ ‎（1）求证：；‎ ‎（2）连接BD，请你判断AC与BD的位置关系，并说明理由；‎ ‎（3）设PE=x，△PBD的面积为S，求S与x之间的函数关系式．‎ ‎【方法归纳】‎ 两个三角形相似，根据不同的对应边或对应角需要分类讨论．‎ ‎【变式训练】‎ ‎（2017怀化）如图1，在平面直角坐标系中，已知抛物线与x轴交于A（﹣1，0），B（5，0）两点，与y轴交于点C．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）若点D是y轴上的一点，且以B，C，D为顶点的三角形与△ABC相似，求点D的坐标；‎ ‎（3）如图2，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积；‎ ‎（4）若点K为抛物线的顶点，点M（4，m）是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标．‎ 考点3：相似三角形的存在性问题 ‎【典型例题】（2017山东省莱芜市）抛物线过A（2，3），B（4，3），C（6，﹣5）三点．‎ ‎（1）求抛物线的表达式；‎ ‎（2）如图①，抛物线上一点D在线段AC的上方，DE⊥AB交AC于点E，若满足，求点D的坐标；‎ ‎（3）如图②，F为抛物线顶点，过A作直线l⊥AB，若点P在直线l上运动，点Q在x轴上运动，是否存在这样的点P、Q，使得以B、P、Q为顶点的三角形与△ABF相似，若存在，求P、Q的坐标，并求此时△BPQ的面积；若不存在，请说明理由．‎ ‎【方法归纳】‎ 一是求相似三角形的第三个顶点时，先要分析已知三角形的边和角的特点，进而得出已知三角形是否为特殊三角形，根据未知三角形中已知边与已知三角形的可能对应边分类讨论；二是利用已知三角形中的对应角，在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小； 三是若两个三角形的各边均未给出，则应先设所求点的坐标进而用函数解析式来表示各边的长度，之后利用相似来列方程求解．‎ ‎【变式训练】‎ ‎（2017济宁）定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点．‎ 例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠PCB=∠ABC，则△BCP∽△ABC，故点P是△ABC的自相似点．‎ 请你运用所学知识，结合上述材料，解决下列问题：‎ 在平面直角坐标系中，点M是曲线（x＞0）上的任意一点，点N是x轴正半轴上的任意一点．‎ ‎（1）如图2，点P是OM上一点，∠ONP=∠M，试说明点P是△MON的自相似点；当点M的坐标是（，3），点N的坐标是（，0）时，求点P的坐标；‎ ‎（2）如图3，当点M的坐标是（3，），点N的坐标是（2，0）时，求△MON的自相似点的坐标；‎ ‎（3）是否存在点M和点N，使△MON无自相似点？若存在，请直接写出这两点的坐标；若不存在，请说明理由．‎ ‎【新题好题训练】‎ ‎1．（2017江苏省泰州市）如图，P为反比例函数（k＞0）在第一象限内图象上的一点，过点P分别作x轴，y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B．若∠AOB=135°，则k的值是（　　）‎ A．2　　　　　　B．4　　　　　　C．6　　　　　　D．8‎ ‎2．（2017山东省潍坊市）如图，在△ABC中，AB≠AC．D、E分别为边AB、AC上的点．AC=3AD，AB=3AE，点F为BC边上一点，添加一个条件： ，可以使得△FDB与△ADE相似．（只需写出一个）‎ ‎3．（2017湖北省随州市）在△ABC在，AB=6，AC=5，点D在边AB上，且AD=2，点E在边AC上，当AE= 时，以A、D、E为顶点的三角形与△ABC相似．‎ ‎4．（2017江苏省南通市）我们知道，三角形的内心是三条角平分线的交点，过三角形内心的一条直线与两边相交，两交点之间的线段把这个三角形分成两个图形．若有一个图形与原三角形相似，则把这条线段叫做这个三角形的“內似线”．‎ ‎（1）等边三角形“內似线”的条数为 ；‎ ‎（2）如图，△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求证：BD是△ABC的“內似线”；‎ ‎（3）在Rt△ABC中，∠C=90°，AC=4，BC=3，E、F分别在边AC、BC上，且EF是△ABC的“內似线”，求EF的长．‎ ‎5．（2017河南省）如图，直线与x轴交于点A（3，0），与y轴交于点B，抛物线经过点A，B．‎ ‎（1）求点B的坐标和抛物线的解析式；‎ ‎（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．‎ ‎①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；‎ ‎②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”．请直接写出使得M，P，N三点成为“共谐点”的m的值．‎ ‎6．（2017辽宁省葫芦岛市）如图，∠MAN=60°，AP平分∠MAN，点B是射线AP上一定点，点C在直线AN上运动，连接BC，将∠ABC（0°＜∠ABC＜120°）的两边射线BC和BA分别绕点B顺时针旋转120°，旋转后角的两边分别与射线AM交于点D和点E．‎ ‎（1）如图1，当点C在射线AN上时，①请判断线段BC与BD的数量关系，直接写出结论；‎ ‎②请探究线段AC，AD和BE之间的数量关系，写出结论并证明；‎ ‎（2）如图2，当点C在射线AN的反向延长线上时，BC交射线AM于点F，若AB=4，AC=，请直接写出线段AD和DF的长．‎ ‎7．（2017新疆）如图，抛物线与x轴交于点A，B，与y轴交于点C．‎ ‎（1）试求A，B，C的坐标；‎ ‎（2）将△ABC绕AB中点M旋转180°，得到△BAD．‎ ‎①求点D的坐标；‎ ‎②判断四边形ADBC的形状，并说明理由；‎ ‎（3）在该抛物线对称轴上是否存在点P，使△BMP与△BAD相似？若存在，请直接写出所有满足条件的P点的坐标；若不存在，请说明理由．‎ ‎8．（2017内蒙古赤峰市）如图，一次函数的图象与x轴、y轴分别交于点A、B，以线段AB为边在第一象限作等边△ABC．‎ ‎（1）若点C在反比例函数的图象上，求该反比例函数的解析式；‎ ‎（2）点P（，m）在第一象限，过点P作x轴的垂线，垂足为D，当△PAD与△OAB相似时，P点是否在（1）中反比例函数图象上？如果在，求出P点坐标；如果不在，请加以说明．‎ ‎9．（2017海南省）抛物线 经过点A（1，0）和点B（5，0）．‎ ‎（1）求该抛物线所对应的函数解析式；‎ ‎（2）该抛物线与直线 相交于C、D两点，点P是抛物线上的动点且位于x轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M、N．‎ ‎①连结PC、PD，如图1，在点P运动过程中，△PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；‎ ‎②连结PB，过点C作CQ⊥PM，垂足为点Q，如图2，是否存在点P，使得△CNQ与△PBM相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由．‎ ‎10．（2017辽宁省抚顺市）如图，OF是∠MON的平分线，点A在射线OM上，P，Q是直线ON上的两动点，点Q在点P的右侧，且PQ=OA，作线段OQ的垂直平分线，分别交直线OF、ON交于点B、点C，连接AB、PB．‎ ‎（1）如图1，当P、Q两点都在射线ON上时，请直接写出线段AB与PB的数量关系；‎ ‎（2）如图2，当P、Q两点都在射线ON的反向延长线上时，线段AB，PB是否还存在（1）中的数量关系？若存在，请写出证明过程；若不存在，请说明理由；‎ ‎（3）如图3，∠MON=60°，连接AP，设=k，当P和Q两点都在射线ON上移动时，k是否存在最小值？若存在，请直接写出k的最小值；若不存在，请说明理由．‎