中考数学专题复习卷四边形解析版 18页

‎2019年中考数学专题复习卷: 四边形 一、选择题 ‎1.下列命题正确的是（   ） ‎ A.对角线相等的四边形是平行四边形 B.对角线相等的四边形是矩形 C.对角线互相垂直的平行四边形是菱形 D.对角线互相垂直且相等的四边形是正方形 ‎2.正十边形的每一个内角的度数为（   ） ‎ A.                                    B.                                    C.                                    D.  ‎ ‎3.在四边形ABCD中，∠A，∠B，∠C，∠D度数之比为1：2：3：3，则∠B的度数为（    ） ‎ A. 30°                                      B. 40°                                      C. 80°                                      D. 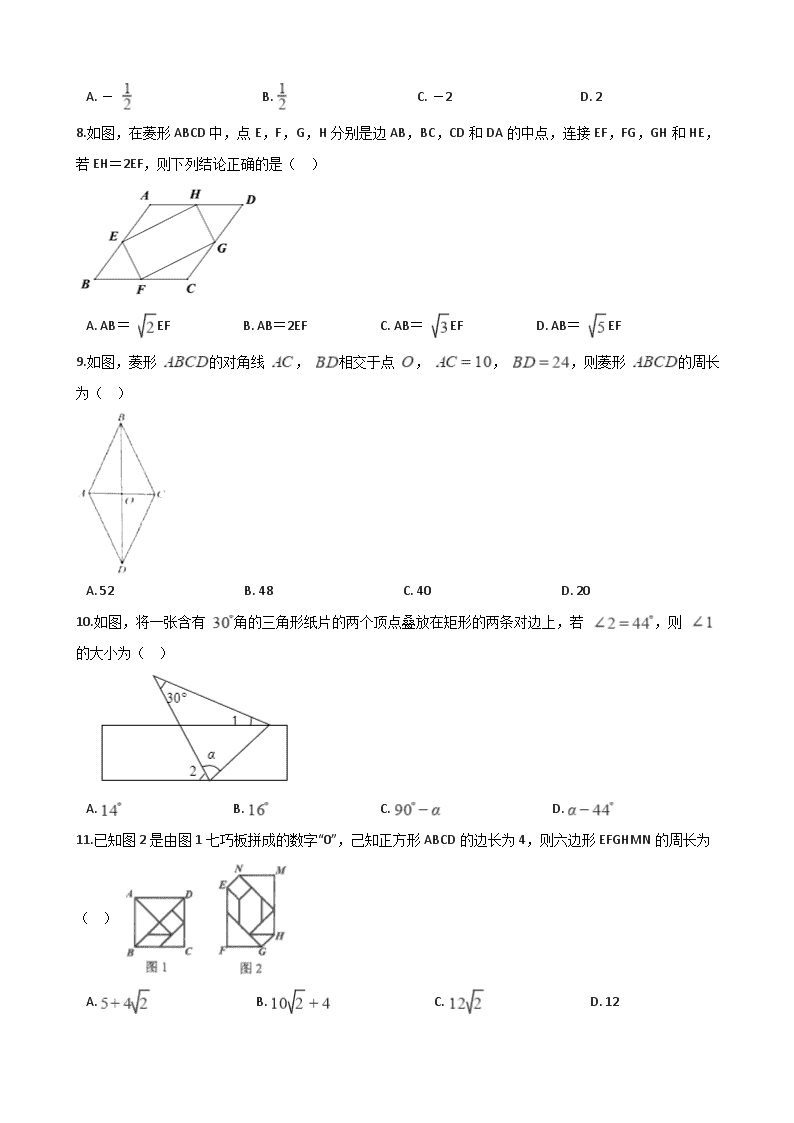120°‎ ‎4.如图，在▱ABCD中，对角线AC与BD交于点D，若增加一个条件，使▱ABCD成为菱形，下列给出的条件正确的是（    ）‎ A. AB=AD                         B. AC=BD                         C. ∠ABC=90°                         D. ∠ABC=∠ADC ‎5.如图，三角板的直角顶点落在矩形纸片的一边上，若∠1＝35°，则∠2的度数是（    ）。 ‎ A.35° B.45° C.55° D.65°‎ ‎6.如图，菱形ABCD的对角线AC、BD的长分别为6和8，则这个菱形的周长是（    ）。 ‎ A.20 B.24 C.40 D.48‎ ‎7.如图，在矩形ACBO中，A(－2，0)，B(0，1)．若正比例函数y＝kx的图像经过点C，则k的取值为（   ） ‎ A. －                                         B.                                         C. －2                                        D. 2‎ ‎8.如图，在菱形ABCD中，点E，F，G，H分别是边AB，BC，CD和DA的中点，连接EF，FG，GH和HE，若EH＝2EF，则下列结论正确的是（   ） ‎ A. AB＝ EF                      B. AB＝2EF                      C. AB＝ EF                      D. AB＝ EF ‎9.如图，菱形 的对角线 ， 相交于点 ， ， ，则菱形 的周长为（   ） ‎ A. 52                                         B. 48                                         C. 40                                         D. 20‎ ‎10.如图，将一张含有 角的三角形纸片的两个顶点叠放在矩形的两条对边上，若 ，则 的大小为（   ） ‎ A.                                    B.                                    C.                                    D. ‎ ‎11.已知图2是由图1七巧板拼成的数字“0”，己知正方形ABCD的边长为4，则六边形EFGHMN的周长为（    ）‎ A.                                 B.                                 C.                                 D. 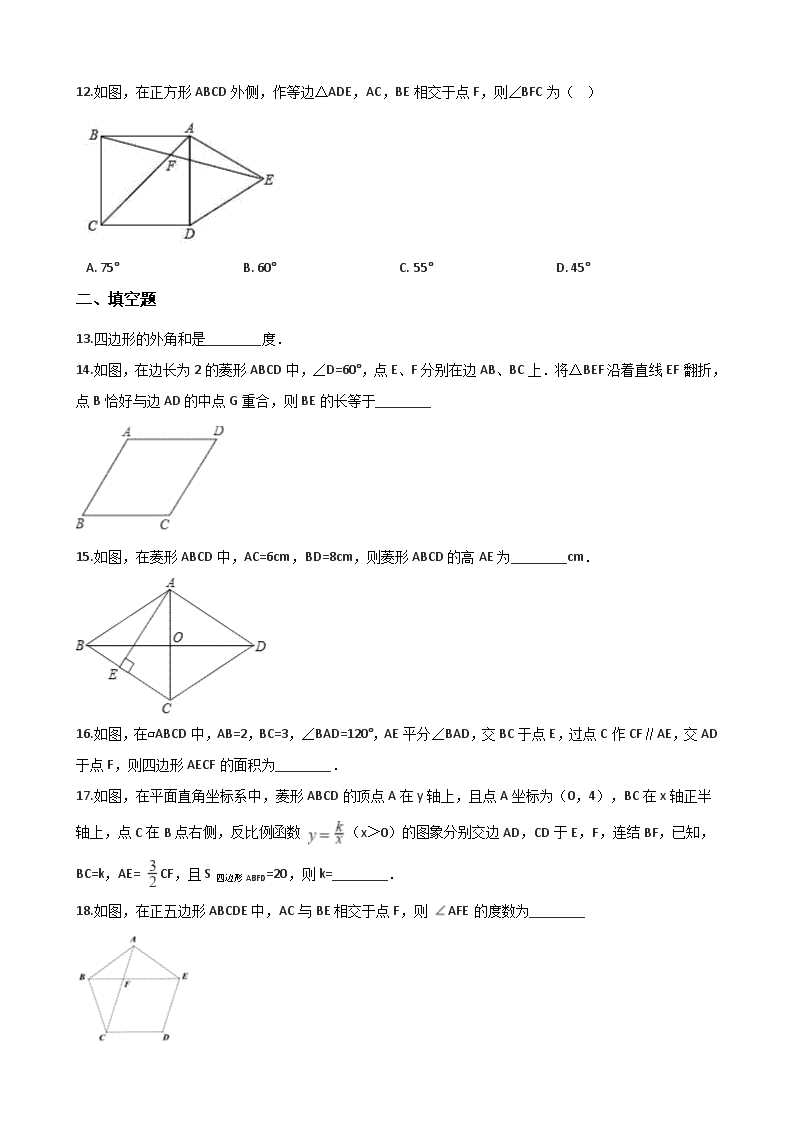12‎ ‎12.如图，在正方形ABCD外侧，作等边△ADE，AC，BE相交于点F，则∠BFC为（    ）‎ A. 75°                                       B. 60°                                       C. 55°                                       D. 45°‎ 二、填空题 ‎ ‎13.四边形的外角和是________度． ‎ ‎14.如图，在边长为2的菱形ABCD中，∠D=60°，点E、F分别在边AB、BC上．将△BEF沿着直线EF翻折，点B恰好与边AD的中点G重合，则BE的长等于________ ‎ ‎15.如图，在菱形ABCD中，AC=6cm，BD=8cm，则菱形ABCD的高AE为________cm． ‎ ‎16.如图，在▱ABCD中，AB=2，BC=3，∠BAD=120°，AE平分∠BAD，交BC于点E，过点C作CF∥AE，交AD于点F，则四边形AECF的面积为________．‎ ‎17.如图，在平面直角坐标系中，菱形ABCD的顶点A在y轴上，且点A坐标为（0，4），BC在x轴正半轴上，点C在B点右侧，反比例函数 （x＞0）的图象分别交边AD，CD于E，F，连结BF，已知，BC=k，AE= CF，且S四边形ABFD=20，则k=________．‎ ‎18.如图，在正五边形ABCDE中，AC与BE相交于点F，则 AFE的度数为________ ‎ ‎19.  如图,在平行四边形ABCD中,对角线AC、BD相交于点0,AB=OB，点E、点F分别是OA、OD的中点,连接EF,∠CEF=45°EM⊥BC于点M,EM交BD于点N,FN= ,则线段BC的长为________. ‎ ‎20.如图，矩形ABCD中，BC=4，CD=2，以AD为直径的半圆O与BC相切于点E，连接BD，则阴影部分的面积为________．（结果保留π） ‎ 三、解答题 ‎ ‎21.如图， ， ， ， 在一条直线上，已知 ， ， ，连接 .求证：四边形 是平行四边形. ‎ ‎22.如图，等边△AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF=45°。‎ ‎ 求证：矩形ABCD是正方形 ‎ ‎23.已知：如图，□ABCD的对角线AC、BD相交于点O，过点O的直线分别与AD、BC相交于点E、F，求证：AE＝CF．‎ ‎24.已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断 ①  OA＝OC    ②  AB＝CD    ③  ∠BAD＝∠DCB    ④  AD∥BC 请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题： ‎ ‎（1）构造一个真命题，画图并给出证明； ‎ ‎（2）构造一个假命题，举反例加以说明. ‎ ‎25.如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE． ‎ ‎（1）求证：△ADE≌△CED； ‎ ‎（2）求证：△DEF是等腰三角形． ‎ ‎26.如图，矩形ABCD中，E是AD的中点，延长CE、BA交于点F，连接AC、DF． ‎ ‎（1）求证：四边形ACDF是平行四边形； ‎ ‎（2）当CF平分∠BCD时，写出BC与CD的数量关系，并说明理由． ‎ 答案解析 ‎ 一、选择题 ‎1.【答案】C ‎ ‎【解析】 ：A.改成为：对角线“互相平分”的四边形是平行四边形，故A不符合题意；B．改成为：对角线相等的“平行四边形”是矩形，故B不符合题意； C．正确，故C符合题意； D．改成为：对角线互相垂直且相等的“平行四边形”是正方形，故D不符合题意； 故答案为：C. 【分析】特殊四边形的对角线是比较特殊的，当两条对角线具有如下性质“互相平分，相等，互相垂直”中的一个或二个或三个时，这个四边形或是平行四边形、或是矩形、或是菱形、或是正方形．‎ ‎2.【答案】D ‎ ‎【解析】 ：方法一： ；方法二： ． 故答案为：D. 【分析】方法一：根据内角和公式180°×(n-2)求出内角和，再求每个内角的度数；方法二：根据外角和为360°，求出每个外角的度数，而每个外角与它相邻的内角是互补的，则可求出内角．‎ ‎3.【答案】C ‎ ‎【解析】 ：∵∠A，∠B，∠C，∠D度数之比为1：2：3：3， ∴设∠A=x，∠B=2x，∠C=3x，∠D=3x ∴x+2x+3x+3x=360° 解之：x=40° ∴∠B=2×40°=80° 故答案为：C 【分析】根据已知条件设∠A=x，∠B=2x，∠C=3x，∠D=3x，利用四边形的内角和=360°，建立方程，就可求出∠B的度数。‎ ‎4.【答案】A ‎ ‎【解析】 ：∵▱ABCD，AB=AD ∴四边形ABCD是菱形，因此A符合题意； B、∵▱ABCD，AC=BD ∴四边形ABCD是矩形，因此B不符合题意； C、▱ABCD，∠ABC=90° ∴四边形ABCD是矩形，因此C不符合题意； D、∵▱ABCD， ∴∠ABC=∠ADC，因此D不符合题意； 故答案为：A 【分析】根据菱形的判定定理，对各选项逐一判断，即可得出答案。‎ ‎5.【答案】C ‎ ‎【解析】 ：如图，‎ ‎ 依题可得：∠1＝35°，∠ACB＝90°， ∴∠ECA+∠1=90°，    ∴∠ECA=55°， 又∵纸片EFGD为矩形， ∴DE∥FG， ∴∠2=∠ECA=55°， 故答案为：C. 【分析】由补角定义结合已知条件得出∠ECA度数，再根据矩形性质和平行线性质得∠2度数.‎ ‎6.【答案】A ‎ ‎【解析】 ：设对角线AC、BC交于点O，‎ ‎ ∵四边形ABCD是菱形，AC=6,BD=8 ∴A0=3,BO=4,AC⊥BC， ∴AB=5, ∴C菱形ABCD=4×5=20. 故答案为：A. 【分析】根据菱形性质可得A0=3,BO=4,AC⊥BC，再由勾股定理可得菱形边长，根据周长公式即可得出答案.‎ ‎7.【答案】A ‎ ‎【解析】 ∵A(－2，0)，B(0，1)， ∴OA=2，OB=1， ∵四边形OACB是矩形， ∴BC=OA=2，AC=OB=1， ‎ ‎∵点C在第二象限，∴C点坐标为（-2，1）， ∵正比例函数y＝kx的图像经过点C， ∴-2k=1， ∴k=－ ， 故答案为：A. 【分析】根据A,B两点的坐标，得出OA=2，OB=1，根据矩形的性质得出BC=OA=2，AC=OB=1，根据C点的位置得出C点的坐标，利用反比例函数图像上的点的坐标特点得出k的值。‎ ‎8.【答案】D ‎ ‎【解析】 连接AC、BD交于点O， ∵四边形ABCD是菱形，∴OA= AC，OB= BD，AC⊥BD， ∵E、F、G、H分别是边AB、BC、CD和DA的中点， ∴EH= BD，EF= AC， ∵EH=2EF， ∴OA=EF，OB=2OA=2EF， 在Rt△AOB中，AB= = EF， 故答案为：D. 【分析】连接AC、BD交于点O，根据菱形的性质，得出OA= AC，OB= BD，AC⊥BD，根据三角形的中位线定理得出EH= BD，EF= AC，又EH=2EF，故OA=EF，OB=2OA=2EF，在Rt△AOB中，由勾股定理得出AB的长。‎ ‎9.【答案】A ‎ ‎【解析】 ：∵菱形ABCD中，BD=24，AC=10， ∴OB=12，OA=5，BD⊥AC 在Rt△ABO中，AB= =13， ∴菱形ABCD的周长=4AB=52， 故答案为：A． ‎ ‎【分析】根据菱形的对角线互相平分且垂直得出OB=12，OA=5，再根据勾股定理得出AB的长度，从而得出菱形的周长。‎ ‎10.【答案】A ‎ ‎【解析】 ：如图， ∵矩形的对边平行，∴∠2=∠3=44°， 根据三角形外角性质，可得：∠3=∠1+30°，∴∠1=44°﹣30°=14°． 故答案为：A． 【分析】根据矩形的对边平行及平行线的性质，可求出∠3的度数，再根据三角形外角的性质，可求出结果。‎ ‎11.【答案】B ‎ ‎【解析】 ∵正方形的边长为4 ∴BD= ∴MN=FG= GH=EN==EN, ∴EF=MH= ∴六边形EFGHMN的周长为：EF+EN+GH+MH+MN+FG =+++++ = 【分析】根据正方形的性质和勾股定理，求出六边形EFGHMN的各边的长，再求出其周长即可。‎ ‎12.【答案】B ‎ ‎【解析】 ：∵等边△ADE和正方形ABCD ∴AD=AE=AB，∠BAD=∠ABC=90°，∠DAE=60° ∴∠ABE=∠AEB，∠BAE=90°+60°=150° ∴∠ABE=（180°-150°）÷2=15° ∴∠CBF=90°-15°=75° ‎ ‎∵AC是正方形ABCD的对角线 ∴∠ACB=45° ∴∠BFC=180°-∠ACB-∠CBF=180°-45°-75°=60° 故答案为：B 【分析】根据等边三角形和正方形的性质，可证得AD=AE=AB，∠BAD=∠ABC=90°，∠DAE=60°及∠ACB的度数，可求得∠BAE，再利用三角形内角和定理求出∠CBF的度数，然后根据BFC=180°-∠ACB-∠CBF，就可求出结果。‎ 二、填空题 ‎13.【答案】360 ‎ ‎【解析】 ：四边形的外角和是360° 故答案为：360° 【分析】根据任意多边形的外角和都是360°，可得出答案。‎ ‎14.【答案】‎ ‎【解析】 如图，作GH⊥BA交BA的延长线于H，EF交BG于O． ∵四边形ABCD是菱形，∠D=60°， ∴△ABC，△ADC度数等边三角形，AB=BC=CD=AD=2， ∴∠BAD=120°，∠HAG=60°， ∵AG=GD=1， ∴AH= AG= ，HG= ， 在Rt△BHG中，BG= ， ∵△BEO∽△BGH， ∴ ， ‎ ‎∴ ， ∴BE= ， 故答案为： ． 【分析】先根据题意作出图，先根据题目中的条件，解直角三角形AGH，从而求得AH与HG的长度，再解直角三角形BGH求得BG的长度，再由△BEO∽△BGH得到对应线段成比例，进而求得BE的值.‎ ‎15.【答案】‎ ‎【解析】 ：∵四边形ABCD是菱形， ∴AC、BD互相垂直平分， ∴BO=  BD=  ×8=4（cm），CO=  AC=  ×6=3（cm）， 在△BCO中，由勾股定理，可得 BC= = =5（cm） ∵AE⊥BC， ∴AE•BC=AC•BO， ∴AE===  （cm）， 即菱形ABCD的高AE为  cm． 故答案为：  ． 【分析】根据菱形的两条对角线互相垂直平分，结合勾股定理求得BC的长度，再利用菱形的面积等于底乘以高，也等于两条对角线的乘积的一半，可以求得AE的长.‎ ‎16.【答案】‎ ‎【解析】 ：过点A作AG⊥BC于点G ∵▱ABCD ∴AD∥BC ∴∠DAE=∠AEB，∠BAD+∠B=180° ‎ ‎∴∠B=180°-120°=60° ∵AE平分∠BAD ∴∠DAE=∠BAE ∴∠BAE=∠AEB ∴AB=BE=2 ∴CE=3-2=1 ∴△ABE是等边三角形 ∴BG=1 AG= ∵CF∥AE,AD∥BC ∴四边形AECF是平行四边形 ∴四边形AECF的面积=CEAG= 故答案为： 【分析】根据平行四边形的性质及角平分线的定义，证明AB=BE=2，求出CE的长，再证明△ABE是等边三角形，就可求出BG的长，利用勾股定理求出AG的长，然后证明四边形AECF是平行四边形，利用平行四边形的面积公式，可求解。‎ ‎17.【答案】‎ ‎【解析】 ：过点F作CH⊥x轴 ∵菱形ABCD ∴AD∥x轴，AB=BC，AB∥DC ∴∠ABO=∠DCO，S菱形ABCD=4k ∴△ABO∽△FHC ∴ ∵点A（0，4） ∴OA=4 ‎ ‎∴点E ∵AE=CF， ∴ 解之CF= ∴ ∴FH= ∵S菱形ABCD=4k，S四边形ABFD=20， ∴S△BFC=S菱形ABCD-S四边形ABFD=4k-20= ∴ 故答案为： 【分析】根据菱形的性质得出AD∥x轴，AB=BC，AB∥DC，根据点A得出OA的长，表示出点E的坐标，再根据AE=CF，求出CF的长，证明△ABO∽△FHC，求出FH的长，然后根据S菱形ABCD=4k，S四边形ABFD=20，建立关于k的方程，求出k的值即可。‎ ‎18.【答案】72° ‎ ‎【解析】 ∵五边形ABCDE为正五边形， ∴AB=BC=AE，∠ABC=∠BAE=108°， ∴∠BAC=∠BCA=∠ABE=∠AEB=（180°−108°）÷2=36°， ∴∠AFE=∠BAC+∠ABE=72°， 故答案为：72°． 【分析】根据正五边形的性质得出AB=BC=AE，∠ABC=∠BAE=108°，根据等腰三角形的性质及三角形的内角和即可得出∠BAC=∠BCA=∠ABE=∠AEB=（180°−108°）÷2=36°，根据三角形的外角定理即可得出答案。‎ ‎19.【答案】‎ ‎【解析】 ：连接BE，‎ ‎ ∵平行四边形ABCD ∴AD∥BC，AD=BC ∵AB=OB，点E时OA的中点 ∴BE⊥OA ∵点E、点F分别是OA、OD的中点 ∴EF是△AOD的中位线 ∴ ∴∠FEN=∠BMN=90° ∴∠CEF=∠ECB=45° ∴△BEC是等腰直角三角形 ∵EM⊥BC即EM是斜边BC边上的高 ∴EF=BM 在△FEN和△BMN中 ∴△FEN≌△BMN ∴EN=MN即EF=2EN，BC=4EN 在Rt△FEN中，EN2+EF2=FN2 ∴EN2+4EN2=10， 【分析】根据已知条件先证明BE⊥AC，再证EF是△AOD的中位线，根据∠CEF=45°，可证得△BEC 是等腰直角三角形，可证得EF=BM，然后证明△FEN≌△BMN，证得EF=2EN，利用勾股定理求出EN的长，就可求出BC的长。‎ ‎20.【答案】π ‎ ‎【解析】 ：连接OE，如图， ∵以AD为直径的半圆O与BC相切于点E， ∴OD=2，OE⊥BC， 易得四边形OECD为正方形， ∴由弧DE、线段EC、CD所围成的面积=S正方形OECD﹣S扇形EOD=22﹣ =4﹣π， ∴阴影部分的面积= ×2×4﹣（4﹣π）=π． 故答案为：π． 【分析】连接OE，如图，根据题意得出OD=2，OE⊥BC，易得四边形OECD为正方形，由弧DE、线段EC、CD所围成的面积=S正方形OECD﹣S扇形EOD ， 又图中阴影部分的面积等于矩形面积的一半再减去由弧DE、线段EC、CD所围成的面积即可得出答案。‎ 三、解答题 ‎21.【答案】证明：∵AB∥DE，AC∥DF， ∴∠B=∠DEF，∠ACB=∠F． ∵BE=CF， ∴BE+CE=CF+CE， ∴BC=EF． 在△ABC和△DEF中， ， ∴△ABC≌△DEF（ASA）， ∴AB=DE． 又∵AB∥DE， ∴四边形ABED是平行四边形 ‎ ‎【解析】【分析】根据二直线平行，同位角相等得出∠B=∠DEF，∠ACB=∠F．根据等式性质由BE=CF，得出BC=EF．然后用ASA判断出△ABC≌△DEF，根据全等三角形对应边相等得出AB=DE．根据一组对边平行且相等的四边形是平行四边形得出结论。‎ ‎22.【答案】∵四边形ABCD是矩形， ∴∠B=∠D=∠C=90° ∵△AEF是等边三角形 ∴AE=AF，∠AEF=∠AFE=60°， 又∠CEF=45°， ∴∠CFE=∠CEF=45°， ∴∠AFD=∠AEB=180°-45°-60°=75°， ∴△AEB≌△AFD（AAS）， ∴AB=AD, ∴矩形ABCD是正方形。 ‎ ‎【解析】【分析】证明矩形ABCD是正方形，根据有一组邻边相等的矩形是正方形，则可证一组邻边相等 ‎23.【答案】证明：∵四边形ABCD是平行四边形，∴AO=CO,AD∥BC， ∴∠DAO=∠BCO， 在△AEO和△CFO中， ∵ , ∴△AEO≌△CFO（ASA）, ∴AE=CF. ‎ ‎【解析】【分析】根据平行四边形性质可得AO=CO,AD∥BC，根据平行线性质可得∠DAO=∠BCO，再由全等三角形判定ASA得△AEO≌△CFO，由全等三角形性质即可得证.‎ ‎24.【答案】（1）解：①④作为条件时，如图， ∵AD∥BC， ∴∠ADB=∠DBC， 在△AOD和△COB中， ‎ ‎∵ , ∴△AOD≌△COB（AAS）， ∴AD=CB， ∴四边形ABCD是平行四边形. （2）解：②④作为条件时，此时一组对边相等，一组对边平行，是等腰梯形. ‎ ‎【解析】【分析】（1）如果①②作为条件，则两个三角形中的条件是SSA，不能证到三角形全等，就不能证明四边形是平行四边形；如果①③作为条件，也不能得到四边形是平行四边形；如果②③作为条件，也不能得到四边形是平行四边形；只有①④作为条件时，可根据全等三角形的判定AAS得两个三角形全等，总而得线段相等，再根据一组对边平行且相等的四边形是平行四边形； （2）如果②④作为条件时，根据梯形的定义，可知其为等腰梯形.‎ ‎25.【答案】（1）解：∵四边形ABCD是矩形， ∴AD=BC，AB=CD． 由折叠的性质可得：BC=CE，AB=AE， ∴AD=CE，AE=CD． 在△ADE和△CED中， ， ∴△ADE≌△CED（SSS） （2）解：由（1）得△ADE≌△CED， ∴∠DEA=∠EDC，即∠DEF=∠EDF， ∴EF=DF， ∴△DEF是等腰三角形 ‎ ‎【解析】【分析】（1）根据矩形的性质得出AD=BC，AB=CD．由折叠的性质可得：BC=CE，AB=AE，从而得出AD=CE，AE=CD．然后利用SSS判断出△ADE≌△CED； （2）根据全等三角形对应角相等由△ADE≌△CED，得出∠DEA=∠EDC，根据等角对等边即可得出结论。‎ ‎26.【答案】（1）证明：∵四边形ABCD是矩形，∴AB∥CD，∴∠FAE=∠CDE. ∵E是AD的中点，∴AE=DE. 又∵∠FEA=∠CED,∴△FAE≅△CDE（AAS）， ∴CD=FA. 又∵CD∥AF， ∴四边形ACDF是平行四边形. ‎ ‎（2）BC=2CD. 理由如下： ∵CF平分∠BCD，∴∠DCE=45°. ∵∠CDE=90°，∴△CDE是等腰直角三角形， ∴CD=DE， ∵E是AD的中点，∴AD=2CD. ∵AD=BC，∴BC=2CD. ‎ ‎【解析】【分析】（1）此题方法不唯一，例如：证明△FAE≅△CDE，则CD=FA，又由CD∥FA即可判定，依据是：有一组对边平行且相等的四边形是平行四边形；（2）由CF平分∠BCD，得∠DCE=45°，则CD=DE，而BC=AD=2DE，从而可证明.‎