2017中考数学菱形专题素材 25页

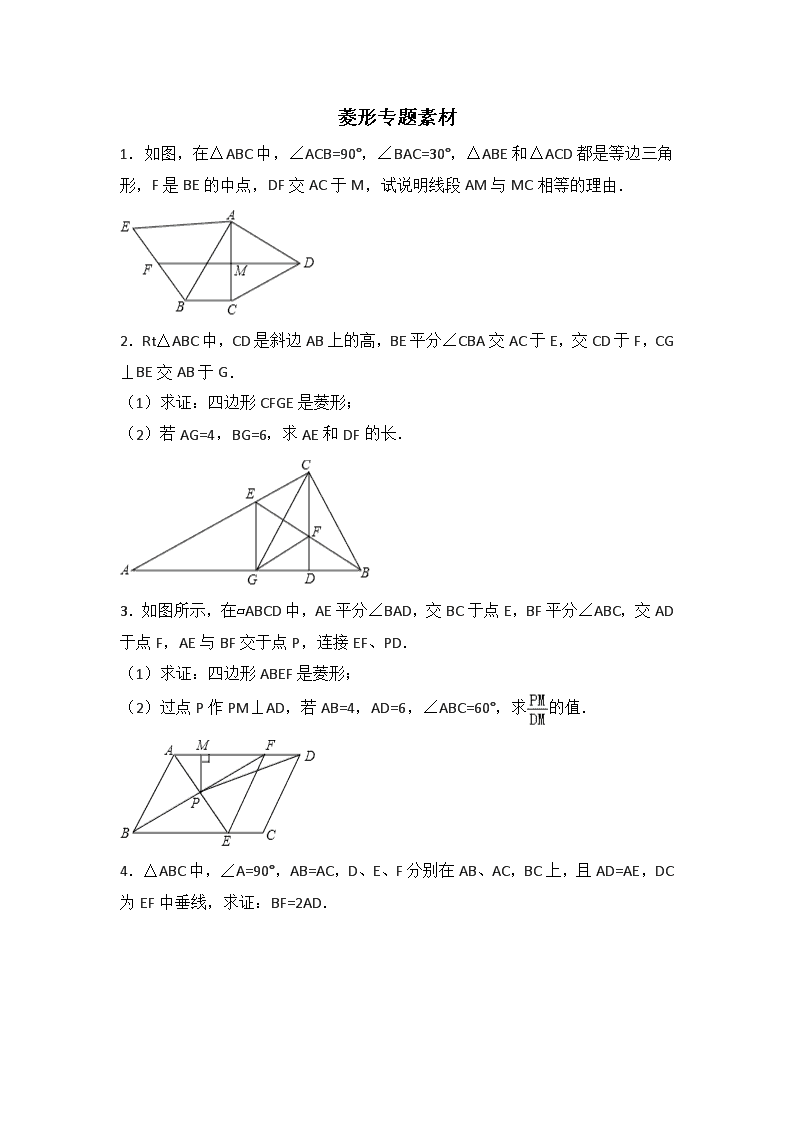
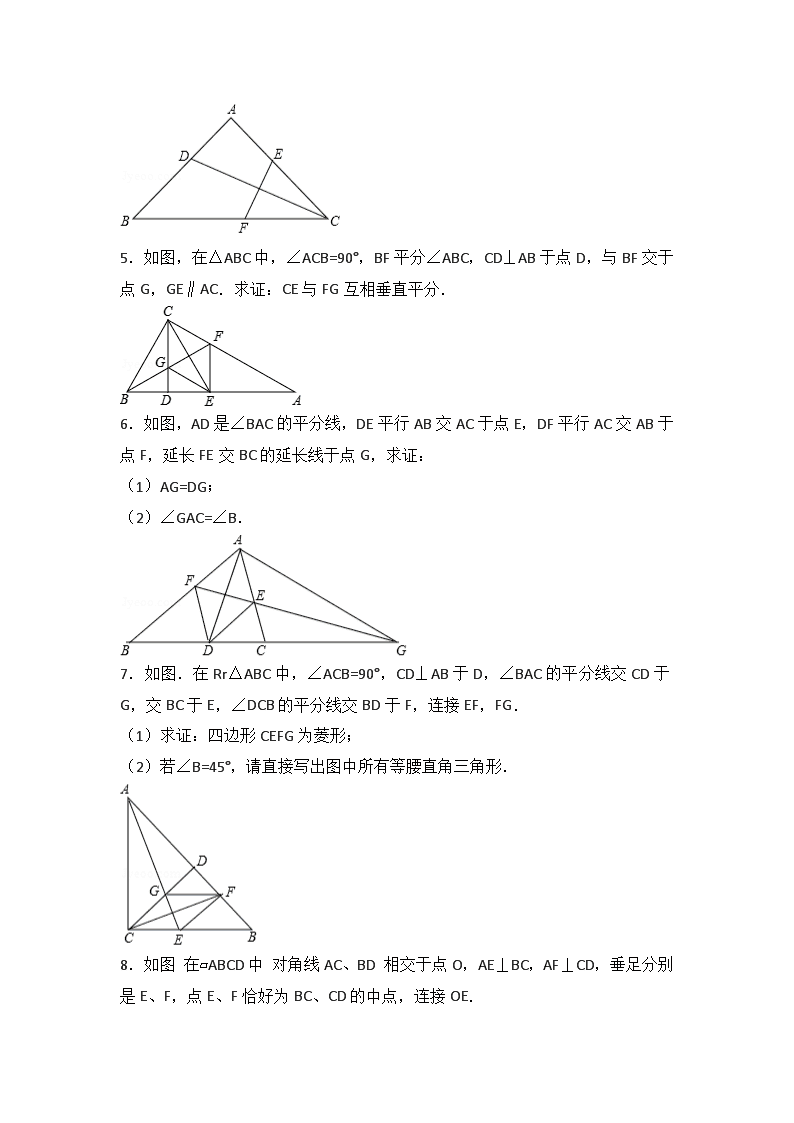
菱形专题素材 ‎1．如图，在△ABC中，∠ACB=90°，∠BAC=30°，△ABE和△ACD都是等边三角形，F是BE的中点，DF交AC于M，试说明线段AM与MC相等的理由．‎ ‎2．Rt△ABC中，CD是斜边AB上的高，BE平分∠CBA交AC于E，交CD于F，CG⊥BE交AB于G．‎ ‎（1）求证：四边形CFGE是菱形；‎ ‎（2）若AG=4，BG=6，求AE和DF的长．‎ ‎3．如图所示，在▱ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF、PD．‎ ‎（1）求证：四边形ABEF是菱形；‎ ‎（2）过点P作PM⊥AD，若AB=4，AD=6，∠ABC=60°，求的值．‎ ‎4．△ABC中，∠A=90°，AB=AC，D、E、F分别在AB、AC，BC上，且AD=AE，DC为EF中垂线，求证：BF=2AD．‎ ‎5．如图，在△ABC中，∠ACB=90°，BF平分∠ABC，CD⊥AB于点D，与BF交于点G，GE∥AC．求证：CE与FG互相垂直平分．‎ ‎6．如图，AD是∠BAC的平分线，DE平行AB交AC于点E，DF平行AC交AB于点F，延长FE交BC的延长线于点G，求证：‎ ‎（1）AG=DG；‎ ‎（2）∠GAC=∠B．‎ ‎7．如图．在Rr△ABC中，∠ACB=90°，CD⊥AB于D，∠BAC的平分线交CD于G，交BC于E，∠DCB的平分线交BD于F，连接EF，FG．‎ ‎（1）求证：四边形CEFG为菱形；‎ ‎（2）若∠B=45°，请直接写出图中所有等腰直角三角形．‎ ‎8．如图 在▱ABCD中 对角线AC、BD 相交于点O，AE⊥BC，AF⊥CD，垂足分别是E、F，点E、F恰好为BC、CD的中点，连接OE．‎ ‎（1）▱ABCD是什么特殊四边形？请证明你的结论．‎ ‎（2）求∠AEO的度数．‎ ‎9．如图所示，已知在矩形ABCD和矩形AECF中，CD=CE，AD与CF相交于点H，BC与AE相交于点G，连接AC、GH．‎ ‎（1）求证：AC、GH互相垂直平分；‎ ‎（2）如果AC=9，GH=4，那么四边形AHCG的面积是多少？‎ ‎10．已知：如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD⊥AB交AB于点E，且CD=AC，DF∥BC分别与AB、AC交于点G、F，连接CG．‎ ‎（1）求证：四边形BCGD是菱形；‎ ‎（2）若BC=1，求DF的长．‎ ‎11．如图1，已知平行四边形ABCD中，对角线AC，BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．‎ ‎（1）求证：四边形ABCD是菱形；‎ ‎（2）如图2，若∠AED=2∠EAD，AC=8．求DE的长．‎ ‎12．如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．‎ ‎（1）证明：∠BAC=∠DAC，∠AFD=∠CFE．‎ ‎（2）若AB∥CD，试证明四边形ABCD是菱形；‎ ‎（3）在（2）的条件下，试确定E点的位置，使得∠EFD=∠BCD，并说明理由．‎ ‎13.如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过A作BD的平行线，交CE的延长线与点F，在AF的延长线上截取FG=BD，连接BG，DF．若AF=8，CF=6，‎ ‎（1）求证：四边形BDFG是菱形，（2）求四边形BDFG的周长为多少？‎ ‎14．如图，在△ABC中，∠ABC=90°，D为AC的中点，过点C作CE⊥BD于点E，作∠GAB=∠CAB，CE的延长线与AG交于点F，点G在AF的延长线上，且FG=BD，连结BG、DF（23题的变式题）‎ ‎（1）求证：①BD∥AG；②四边形BGFD为菱形；‎ ‎（2）已知AG=15，CF=3，求菱形BGFD的边长．‎ ‎2017年03月17日菱形正方形专题素材 参考答案与试题解析 ‎　‎ ‎1．如图，在△ABC中，∠ACB=90°，∠BAC=30°，△ABE和△ACD都是等边三角形，F是BE的中点，DF交AC于M，试说明线段AM与MC相等的理由．‎ ‎【分析】连接AF、FC，由等边三角形的性质可得AF是∠BAE的平分线，然后求出∠BAF=∠BAC=30°，再利用“角角边”证明△ABF和△ABC全等，由全等三角形对应边相等可得AF=AC，然后求出△AFC是等边三角形，再由等边三角形的性质求出AF=FC=CD=AD=AC，然后求出四边形AFCD是菱形，由菱形的对角线互相平分可得AM=MC．‎ ‎【解答】证明：连AF，FC，如图所示：‎ ‎∵△ABE是等边三角形，F是BE的中点，‎ ‎∴AF是∠BAE的平分线，‎ ‎∴∠BAF=∠BAE=×60°=30°，‎ ‎∵∠BAC=30°，‎ ‎∴∠BAF=∠BAC=30°，‎ 在△ABF和△ABC中，‎ ‎，‎ ‎∴△ABF≌△ABC（AAS），‎ ‎∴AF=AC，‎ ‎∵∠FAC=∠BAF+∠BAC=30°+30°=60°，‎ ‎∴△AFC是等边三角形，‎ 又∵△ACD是等边三角形，‎ ‎∴AF=FC=CD=AD=AC，‎ ‎∴四边形AFCD是菱形，‎ ‎∴AM=MC．‎ ‎【点评】本题考查了菱形的判定与性质、等边三角形的性质、全等三角形的判定与性质；作辅助线构造出全等三角形和菱形是解题的关键，也是本题的难点．‎ ‎　‎ ‎2．Rt△ABC中，CD是斜边AB上的高，BE平分∠CBA交AC于E，交CD于F，CG⊥BE交AB于G．‎ ‎（1）求证：四边形CFGE是菱形；‎ ‎（2）若AG=4，BG=6，求AE和DF的长．‎ ‎【分析】（1）先证明△BMG≌△BMC，得出MC=MG，再由线段垂直平分线性质证出EC=EG，FG=FC，然后证明EC=FC，即可证出结论；‎ ‎（2）先求出BC=BG=6，再求出AC=8，然后证明△AEG∽△ABC，得出比例式，求出AE=5，EC=CF=3，最后根据面积公式得到AB•CD=AC•BC，求出CD==4.8．即可得出DF=CD﹣CF．‎ ‎【解答】解：（1）证明：设BE交CG于M．如图所示：‎ ‎∵BE是∠CBA的平分线，‎ ‎∴∠1=∠2，‎ ‎∵CG⊥BE，‎ ‎∴∠3=∠4=90°，‎ 在△BMG和△BMC中，‎ ‎，‎ ‎∴△BMG≌△BMC（ASA），‎ ‎∴MC=MG，‎ ‎∴EC=EG，FG=FC，‎ ‎∵CD⊥AB，‎ ‎∴∠DFB+∠1=90°，‎ ‎∵∠CEF+∠2=90°，∠CFE=∠DFB，‎ ‎∴∠CEF=∠CFE，‎ ‎∴EC=FC，‎ ‎∴EC=EG=FG=FC，‎ ‎∴四边形CFGE是菱形；‎ ‎（2）根据题意得：△BEG≌△BEC，‎ ‎∴BC=BG=6，∠BGE=∠BCA=90°，‎ ‎∵AB=AG+BG=10，‎ ‎∴AC=，‎ ‎∵∠A=∠A，∠ABG=∠BCA=90°，‎ ‎∴△AEG∽△ABC，‎ ‎∴，即，‎ ‎∴AE=5．‎ ‎∴EC=AC﹣AE=3，‎ ‎∴CF=3，‎ ‎∵AB•CD=AC•BC，‎ ‎∴CD===4.8，‎ ‎∴DF=CD﹣CF=4.8﹣3=1.8．‎ ‎【点评】本题考查了菱形的判定、三角形全等的判定与性质以及勾股定理的运用等知识；培养学生综合运用定理进行推理和计算的能力．‎ ‎　‎ ‎3．如图所示，在▱ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF、PD．‎ ‎（1）求证：四边形ABEF是菱形；‎ ‎（2）过点P作PM⊥AD，若AB=4，AD=6，∠ABC=60°，求的值．‎ ‎【分析】（1）由四边形ABCD是平行四边形，得到AD∥BC，从而得到∠AFB=∠FBE，再由∠ABF=∠FBE，推出∠ABF=∠AFB，于是得到AB=AF，同理得出AB=BE，于是得出结论；‎ ‎（2）由菱形的性质得出AE⊥BF，得到∠ABF=30°，∠BAP=∠FAP=60°从而得出AP=2，又有PM⊥AD，得到PM=，AM=1，从而得到，DM=5，于是推出结论．‎ ‎【解答】证明：（1）∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，‎ ‎∴∠AFB=∠FBE，‎ ‎∵∠ABF=∠FBE，‎ ‎∴∠ABF=∠AFB，‎ ‎∴AB=AF，‎ 同理AB=BE，‎ ‎∴四边形ABEF是菱形；‎ ‎（2）∵四边形ABEF是菱形，‎ ‎∴AE⊥BF，‎ ‎∵∠ABC=60°，‎ ‎∴∠ABF=30°，∠BAP=∠FAP=60°，‎ ‎∵AB=4，‎ ‎∴AP=2，‎ ‎∵PM⊥AD，‎ ‎∴PM=，AM=1，‎ ‎∵AD=6，‎ ‎∴DM=5，‎ ‎∴．‎ ‎【点评】本题主要考查了平行四边形的性质，平行线的性质和菱形的判定，特殊三角形的性质，通过等量代换推出角相等推出等腰三角形是解决问题的关键．‎ ‎　‎ ‎4．△ABC中，∠A=90°，AB=AC，D、E、F分别在AB、AC，BC上，且AD=AE，DC为EF中垂线，求证：BF=2AD．‎ ‎【分析】连接DE，DF，设DC与EF相交于点O，设AD=x，表示DE，然后根据平行线分线段成比例定理求出DE∥BC，再求出DE=FC，从而判断出四边形DECF是平行四边形，根据线段垂直平分线上的点到两端点的距离相等可得FC=DF，判断出四边形DECF是菱形，根据菱形的四条边都相等可得DE=EC=x，再求出BC，然后根据BF=BC﹣FC表示出BF，从而得证．‎ ‎【解答】证明：连接DE，DF，设DC与EF相交于点O，‎ 设AD=x，则AE=x，‎ ‎∵AD=AE，∠A=90°，‎ ‎∴DE=x，‎ ‎∵AB=AC，AD=AE，‎ ‎∴=，‎ ‎∴DE∥BC，‎ ‎∴=，‎ ‎∵DC为EF中垂线，‎ ‎∴EO=FO，‎ ‎∴DE=FC，‎ 又∵DE∥FC，‎ ‎∴四边形DECF是平行四边形，‎ ‎∵DC为EF中垂线，‎ ‎∴FC=DF，‎ ‎∴四边形DECF是菱形，‎ ‎∴DE=EC=x，‎ ‎∴AC=x+x，‎ ‎∵∠A=90°，AB=AC，‎ ‎∴∠B=45°，‎ ‎∴BC=AC=（x+x）=x+2x，‎ ‎∴BF=BC﹣FC=x+2x﹣x=2x，‎ ‎∴BF=2AD．此法麻烦！！‎ 编者按：BF是DF的根2倍，DF=DE,DE是AD的根2倍，即可得出BF=2AD ‎【点评】本题考查了菱形的判定与性质，等腰直角三角形的判定与性质，线段垂直平分线上的点到两端点的距离相等的性质，熟记各性质并用AD表示出BF是解题的关键．‎ ‎　‎ ‎5．如图，在△ABC中，∠ACB=90°，BF平分∠ABC，CD⊥AB于点D，与BF交于点G，GE∥AC．求证：CE与FG互相垂直平分．‎ ‎【分析】延长EG交BC于点K．由角平分线的性质可得∠GBK=∠GBD，GK=GD，由全等三角形的判定定理可知△GBK≌△GBD，△CBD≌△EBK，由平行四边形的判定定理可知FCGE为平行四边形，根据CG=GE即平行四边形的邻边相等可知此四边形是菱形，由菱形的对角线互相垂直平分即可求解．‎ ‎【解答】证明：延长EG交BC于点K． 编者：此题不必作辅助线！！！！‎ ‎∵GE∥AC，∠ACB=90°，‎ ‎∴∠BKE=∠ACB=90°，即EK⊥BC．‎ 又∵CD⊥AB，BF平分∠ABC，‎ ‎∴GK=GD．‎ 在Rt△GKB与Rt△GDB中，‎ ‎，‎ ‎∴Rt△GKB≌Rt△GDB（HL），‎ ‎∴DB=BK．‎ 在△CBD与△EBK中，‎ ‎，‎ ‎∴△CBD≌△EBK（ASA），‎ ‎∴BC=BE，‎ ‎∴BF垂直平分CE（三合一）．‎ ‎∴CO=EO，‎ 在△COF与△EOG中，‎ ‎，‎ ‎∴△COF≌△EOG（ASA）‎ ‎∴FC=GE，‎ 又∵GE∥AC．‎ ‎∴四边形FCGE为平行四边形，‎ ‎∵CG=GE，‎ ‎∴四边形FCGE为菱形，‎ ‎∴CE与GF互相垂直平分．‎ ‎【点评】本题考查的是角平分线的性质、全等三角形的判定与性质、平行四边形及菱形的判定与性质，涉及面较广，难度适中．‎ ‎　‎ ‎6．如图，AD是∠BAC的平分线，DE平行AB交AC于点E，DF平行AC交AB于点F，延长FE交BC的延长线于点G，求证：‎ ‎（1）AG=DG；‎ ‎（2）∠GAC=∠B．‎ ‎【分析】（1）由DE∥AB，DF∥AC，可证得四边形AEDF是平行四边形，∠DAF=∠ADE，又由AD是∠BAC的平分线，可证得AE=DE，即可证得四边形AEDF是菱形，则可得EF是AD的垂直平分线，继而证得结论；‎ ‎（2）由AG=DG，AE=DE，可得∠GAD=∠GDA，∠EAD=∠EDA，继而证得∠GAC=∠GDE，又由DE∥AB，可得∠GDC=∠B，继而证得结论．‎ ‎【解答】证明：（1）∵DE∥AB，DF∥AC，‎ ‎∴四边形AEDF是平行四边形，∠DAF=∠ADE，‎ ‎∵AD是∠BAC的平分线，‎ ‎∴∠DAF=∠DAE，‎ ‎∴∠DAE=∠ADE，‎ ‎∴AE=DE，‎ ‎∴四边形AEDF是菱形，‎ ‎∴EF是AD的垂直平分线，‎ ‎∵延长FE交BC的延长线于点G，‎ ‎∴AG=DG；‎ ‎（2）∵AG=DG，AE=DE，‎ ‎∴∠GAD=∠GDA，∠EAD=∠EDA，‎ ‎∵∠GAC=∠GAD﹣∠EAD，∠GDE=∠GDA﹣∠EDA，‎ ‎∴∠GAC=∠GDE，‎ ‎∵DE∥AB，‎ ‎∴∠GDE=∠B，‎ ‎∴∠GAC=∠B．‎ ‎【点评】此题考查了菱形的判定与性质、线段垂直平分线的性质以及等腰三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．‎ ‎　‎ ‎7．如图．在Rr△ABC中，∠ACB=90°，CD⊥AB于D，∠BAC的平分线交CD于G，交BC于E，∠DCB的平分线交BD于F，连接EF，FG．‎ ‎（1）求证：四边形CEFG为菱形； 证AE⊥CF是关键！！！‎ ‎（2）若∠B=45°，请直接写出图中所有等腰直角三角形．‎ ‎【分析】（1）根据四边相等的四边形是菱形，即可证明．‎ ‎（2）等腰直角三角形有：△ABC，△ACD，△CDB，△GDF，△EFB．‎ ‎【解答】（1）证明：∵∠ACB=90°，CD⊥AB，‎ ‎∴∠CAD+∠ACD=90°，∠ACD+∠BCD=90°，‎ ‎∴∠CAD=∠BCD，同理∠ACD=∠B，‎ ‎∵∠CAE=∠EAB，∠BCF=∠FCD，‎ ‎∴∠BCF=∠CAE，‎ ‎∵∠BCF+∠ACF=90°，‎ ‎∴∠CAE+∠ACF=90°，‎ ‎∴AE⊥CF，‎ ‎∴∠CAE+∠ACF=90°，∠EAF+∠AFC=90°，‎ ‎∴∠ACF=∠AFC，‎ ‎∴AC=AF，‎ 在△ACG和△AFG中，‎ ‎，‎ ‎∴△AGC≌△AGF，‎ ‎∴CG=GF，同理证明CE=EF，‎ ‎∵∠CGE=∠ACG+∠CAG，∠CEG=∠EAB+∠B，‎ ‎∴∠CGE=∠CEG，‎ ‎∴CG=CE=FG=EF，‎ ‎∴四边形CEFG是菱形．‎ ‎（2）当∠B=45°时，图中等腰直角三角形有：△ABC，△ACD，△CDB，△GDF，△EFB．‎ ‎【点评】本题考查菱形的判定和性质、等腰直角三角形的性质、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，本题的证明方法比较多，属于中考常考题型．‎ ‎　‎ ‎8．如图 在▱ABCD中 对角线AC、BD 相交于点O，AE⊥BC，AF⊥CD，垂足分别是E、F，点E、F恰好为BC、CD的中点，连接OE．‎ ‎（1）▱ABCD是什么特殊四边形？请证明你的结论．‎ ‎（2）求∠AEO的度数．‎ ‎【分析】（1）根据线段垂直平分线的性质证出AB=AD，即可得出结论；‎ ‎（2）先证明△ABC是等边三角形，得出∠BAC=60°，∠CAE=30°，再证明OE=OA，即可得出结果．‎ ‎【解答】（1）答：▱ABCD是菱形；‎ 证明：∵AE⊥BC，AF⊥CD，垂足分别是E、F，点E、F恰好为BC、CD的中点，‎ ‎∴AB=AC，AD=AC，‎ ‎∴AB=AD，‎ ‎∴▱ABCD是菱形；‎ ‎（2）解：∵▱ABCD是菱形，‎ ‎∴AB=BC，‎ ‎∵AB=AC，‎ ‎∴AB=AC=BC，‎ ‎∴∠BAC=60°，‎ ‎∵AE⊥BC，OA=OC，‎ ‎∴∠CAE=∠BAC=30°，OE=AC=OA，‎ ‎∴∠AEO=∠CAE=30°．‎ ‎【点评】本题考查了菱形的判定与性质、线段垂直平分线的性质以及直角三角形的中线性质；证明四边形是菱形以及等边三角形是解决问题的关键．‎ ‎　‎ ‎9．如图所示，已知在矩形ABCD和矩形AECF中，CD=CE，AD与CF相交于点H，BC与AE相交于点G，连接AC、GH．‎ ‎（1）求证：AC、GH互相垂直平分；‎ ‎（2）如果AC=9，GH=4，那么四边形AHCG的面积是多少？‎ ‎【分析】（1）先证得四边形AGCH是平行四边形，然后利用SAS证明△HDC≌△GEC，得到CH=CG，进而根据菱形的判定方法得到平行四边形AGCH是菱形，再根据菱形的对角线互相垂直平分的性质可得结论；‎ ‎（2）根据菱形的面积等于两条对角线乘积的一半，可求得菱形的面积．‎ ‎【解答】（1）证明：∵四边形ABCD与四边形AECF都是矩形，‎ ‎∴AH∥GC，AG∥CH，‎ ‎∴四边形AGCH是平行四边形．‎ ‎∵四边形ABCD与四边形AECF都是矩形，‎ ‎∴∠D=∠E=90°，∠BCD=∠ECF=90°，‎ ‎∴∠ECG=∠DCH，‎ 在△HDC与△GEC中，‎ ‎，‎ ‎∴△HDC≌△GEC（SAS），‎ ‎∴CH=CG，‎ ‎∴平行四边形AGCH是菱形，‎ ‎∴AC、GH互相垂直平分；‎ ‎（2）解：∵四边形AGCH是菱形，AC=9，GH=4，‎ ‎∴．‎ ‎【点评】本题考查了菱形的判定与性质，矩形的性质，全等三角形的判定与性质，菱形面积的计算等知识，通过推理得出四边形AGCH是解题的关键．‎ ‎　‎ ‎10．（2012•枣阳市校级模拟）已知：如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD⊥AB交AB于点E，且CD=AC，DF∥BC分别与AB、AC交于点G、F，连接CG．‎ ‎（1）求证：四边形BCGD是菱形；‎ ‎（2）若BC=1，求DF的长．‎ ‎【分析】（1）根据已知条件易证明Rt△AEC≌Rt△‎ DFC，得CE=CF，则DE=AF，从而进一步证明Rt△AFG≌Rt△DEG，就可得到GE=GF；‎ ‎（2）根据直角三角形的性质可以得到CE=AC，则CE=CD，即AB是CE的垂直平分线，则BC=BD=1．再根据直角三角形的性质进一步求得AB、BE的长，则AE=AB﹣BE，结合（1）中的全等三角形，知DF=AE．‎ ‎【解答】（1）证明：∵∠A=30°，CD⊥AB，‎ ‎∴CE=AC，‎ ‎∵CD=AC，‎ ‎∴CE=AC，‎ ‎∴CE=DE，‎ ‎∵DF∥BC，‎ ‎∴∠EDG=∠ECB，‎ 在△EDG和△ECB中，‎ ‎，‎ ‎∴△DEG≌△CEB（ASA），‎ ‎∴EG=BE，‎ ‎∴四边形BCGD是平行四边形，‎ ‎∵CD⊥AB，‎ ‎∴▱BCGD是菱形．‎ ‎（2）解：∵CD⊥AB，∠A=30°，‎ ‎∴CE=AC=CD，‎ ‎∴CE=ED．‎ ‎∴BC=BD=1．‎ 又∵∠ECB+∠ACE=90°，∠A+∠ACE=90°，‎ ‎∴∠ECB=∠A=30°，∠CEB=90°，‎ ‎∴BE=BC=BD=，‎ 在直角三角形ABC中，∠A=30°，‎ 则AB=2BC=2．‎ 则AE=AB﹣BE=，‎ ‎∵Rt△AEC≌Rt△DFC，‎ ‎∴DF=AE=．‎ ‎【点评】此题综合运用了全等三角形的判定和性质、直角三角形的性质以及线段垂直平分线的性质；用到的知识点为：直角三角形中30°所对的直角边是斜边的一半．‎ ‎　‎ ‎11．（2013•海安县校级模拟）如图1，已知平行四边形ABCD中，对角线AC，BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．‎ ‎（1）求证：四边形ABCD是菱形；‎ ‎（2）如图2，若∠AED=2∠EAD，AC=8．求DE的长．‎ ‎【分析】（1）根据对角线互相垂直的平行四边形是菱形．由四边形ABCD是平行四边形，可得AO=CO．又由△ACE是等边三角形，可得AE=CE．根据三线合一，对角线垂直，即可得四边形既为菱形；‎ ‎（2）根据有一个角是90°的菱形是正方形．由题意易得∠BAO=∠EAO﹣∠‎ EAB=60°﹣15°=45°，即四边形ABCD是正方形，利用正方形的性和等边三角形的性质即可求出DE的长．‎ ‎【解答】证明：（1）∵四边形ABCD是平行四边形 ‎∴OA=OC，‎ ‎∵△ACE是等边三角形．‎ ‎∴OE⊥AC，‎ ‎∴BD⊥AC，‎ ‎∴四边形ABCD是菱形；‎ ‎（2）∵△ACE是等边三角形，OE⊥AC，‎ ‎∴∠AEO=∠AEC=30°，‎ ‎∵∠AED=2∠EAD，‎ ‎∴∠EAD=15°‎ ‎∴∠ADB=45°，‎ ‎∵四边形ABCD是菱形，‎ ‎∴AD=DC，BD⊥AC，‎ ‎∴∠CDB=∠ADB=45°‎ ‎∴∠ADC=90°，‎ ‎∴△ADC是等腰直角三角形，‎ ‎∴OA=OC=OD=AC=4，‎ ‎∵△ACE是等边三角形，‎ ‎∴∠EAO=60°‎ 在Rt△AOE中，OE=OAtan60°=4‎ ‎∴DE=OE﹣OD=4﹣4．‎ ‎【点评】此题主要考查菱形和正方形的判定．本题考查知识点较多，综合性强，能力要求全面，难度中等．注意灵活运用正方形和菱形的判定方法．‎ ‎　‎ ‎12．（2013•泰安）如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．‎ ‎（1）证明：∠BAC=∠DAC，∠AFD=∠CFE．‎ ‎（2）若AB∥CD，试证明四边形ABCD是菱形；‎ ‎（3）在（2）的条件下，试确定E点的位置，使得∠EFD=∠BCD，并说明理由．‎ ‎【分析】（1）首先利用SSS定理证明△ABC≌△ADC可得∠BAC=∠DAC，再证明△ABF≌△ADF，可得∠AFD=∠AFB，进而得到∠AFD=∠CFE；‎ ‎（2）首先证明∠CAD=∠ACD，再根据等角对等边可得AD=CD，再有条件AB=AD，CB=CD可得AB=CB=CD=AD，可得四边形ABCD是菱形；‎ ‎（3）首先证明△BCF≌△DCF可得∠CBF=∠CDF，再根据BE⊥CD可得∠BEC=∠DEF=90°，进而得到∠EFD=∠BCD．‎ ‎【解答】（1）证明：在△ABC和△ADC中，‎ ‎，‎ ‎∴△ABC≌△ADC（SSS），‎ ‎∴∠BAC=∠DAC，‎ 在△ABF和△ADF中，‎ ‎，‎ ‎∴△ABF≌△ADF（SAS），‎ ‎∴∠AFD=∠AFB，‎ ‎∵∠AFB=∠CFE，‎ ‎∴∠AFD=∠CFE；‎ ‎（2）证明：∵AB∥CD，‎ ‎∴∠BAC=∠ACD，‎ 又∵∠BAC=∠DAC，‎ ‎∴∠CAD=∠ACD，‎ ‎∴AD=CD，‎ ‎∵AB=AD，CB=CD，‎ ‎∴AB=CB=CD=AD，‎ ‎∴四边形ABCD是菱形；‎ ‎（3）当EB⊥CD时，即E为过B且和CD垂直时垂线的垂足，∠EFD=∠BCD，‎ 理由：∵四边形ABCD为菱形，‎ ‎∴BC=CD，∠BCF=∠DCF，‎ 在△BCF和△DCF中，‎ ‎，‎ ‎∴△BCF≌△DCF（SAS），‎ ‎∴∠CBF=∠CDF，‎ ‎∵BE⊥CD，‎ ‎∴∠BEC=∠DEF=90°，‎ ‎∴∠BCD+∠CBE=∠CDF+∠EFD，‎ ‎∴∠EFD=∠BCD．‎ ‎【点评】此题主要考查了全等三角形的判定与性质，以及菱形的判定与性质，全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．‎ ‎　‎ ‎13．（2014春•沛县期末）如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过A作BD的平行线，交CE的延长线与点F，在AF的延长线上截取FG=BD，连接BG，DF．若AF=8，CF=6，则四边形BDFG的周长为多少？‎ ‎【分析】首先可判断四边形BGFD是平行四边形，再由直角三角形斜边中线等于斜边一半，可得BD=FD，则可判断四边形BGFD是菱形，设GF=x，则AF=13﹣x，AC=2x，在Rt△ACF中利用勾股定理可求出x的值．‎ ‎【解答】解：∵AG∥BD，BD=FG，‎ ‎∴四边形BGFD是平行四边形，‎ ‎∵CF⊥BD，‎ ‎∴CF⊥AG，‎ 又∵点D是AC中点，‎ ‎∴BD=DF=AC=5，‎ ‎∴四边形BGFD是菱形，‎ ‎∴四边形BDFG的周长=4GF=20．‎ ‎【点评】本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质，解答本题的关键是判断出四边形BGFD是菱形．‎ ‎　‎ ‎14．（2014春•慈溪市期末）如图，在△ABC中，∠ABC=90°，D为AC的中点，过点C作CE⊥BD于点E，作∠GAB=∠CAB，CE的延长线与AG交于点F，点G在AF的延长线上，且FG=BD，连结BG、DF ‎（1）求证：‎ ‎①BD∥AG；‎ ‎②四边形BGFD为菱形；‎ ‎（2）已知AG=15，CF=3，求菱形BGFD的边长．‎ ‎【分析】（1）首先可判断四边形BDFG是平行四边形，再由直角三角形斜边中线等于斜边一半，可得BD=FD，则可判断四边形BDFG是菱形；‎ ‎（2）设GF=x，则AF=15﹣x，AC=2x，在Rt△ACF中利用勾股定理可求出x的值．‎ ‎【解答】解：（1）①∵∠ABC=90°，D为AC的中点，‎ ‎∴BD=AD=DC，‎ ‎∴∠CAB=∠DBA，‎ ‎∵∠GAB=∠CAB，‎ ‎∴∠GAB=∠DBA，‎ ‎∴AG∥BD；‎ ‎②∵AG∥BD，BD=FG，‎ ‎∴四边形BGFD是平行四边形，‎ ‎∵CE⊥BD，‎ ‎∴CE⊥AG，‎ 又∵BD为AC的中线，‎ ‎∴BD=DF=AC，‎ ‎∴四边形BDFG是菱形；‎ ‎（2）设GF=x，则AF=15﹣x，AC=2x，‎ ‎∵在Rt△ACF中，∠CFA=90°，‎ ‎∴AF2+CF2=AC2，即（15﹣x）2+（3）2=（2x）2，‎ 解得：x=6，‎ ‎∴菱形BGFD的边长为6．‎ ‎【点评】本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质，解答本题的关键是判断出四边形BGFD是菱形．‎ ‎　‎