2014山东省泰安市中考数学试卷 9页

‎2014年山东省泰安市中考试题 数学 ‎（满分120分，考试时间120分钟）‎ 第一部分（选择题 共60分）‎ 一、选择题（本大题共20小题，每小题3分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的。）‎ ‎1.（2014山东省泰安市，1，3分）在，0，-1，-这四个数中，最小的数是（ ）‎ ‎（A） （B）0 （C）- (D)-1‎ ‎【答案】D。‎ ‎2. （2014山东省泰安市，2，3分）下列运算，正确的是（ ）‎ ‎（A）4a-2a=2 （B）a6÷a3=a2 （C）（-a3b）2=a6b2 (D)（a-b）2=a2-b2‎ ‎【答案】C。‎ ‎3. （2014山东省泰安市，3，3分）下列几何体，主视图和左视图都为矩形的是（ ）‎ ‎【答案】D.‎ ‎4. （2014山东省泰安市，4，3分）PM2.5是指大气中直径≤0.0000025米的颗粒物，将0.0000025用科学计数法表示为（ ）‎ ‎（A）2．5×10-7 （B）2.5×10-6 （C）25×10-7 (D)0.25×10-5‎ ‎【答案】B。‎ ‎5. （2014山东省泰安市，5，3分）如图，把一直尺放置在一个三角形纸片上，则下列结论正确的是（ ）‎ ‎（A）∠1+∠6＞180° ‎ ‎（B）∠2+∠5＜180° ‎ ‎（C）∠3+∠4＜180°‎ ‎（D）∠3+∠7＞180°‎ ‎【答案】D。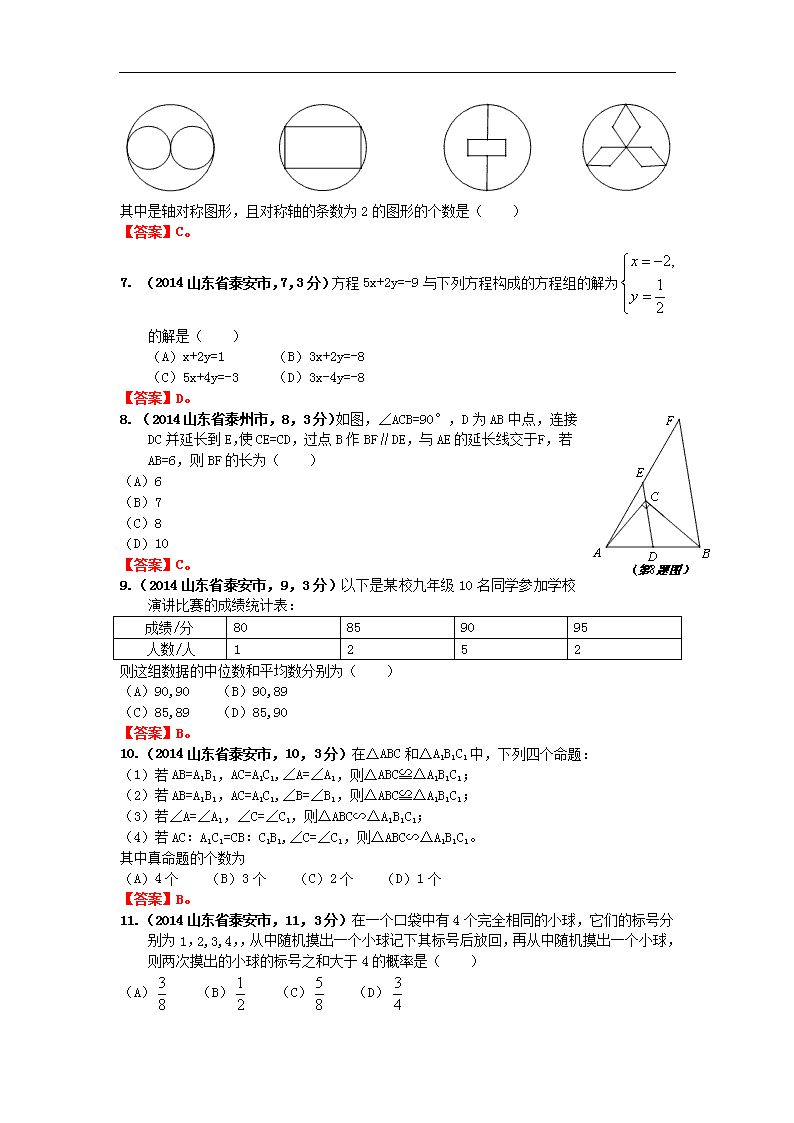‎ ‎6. （2014山东省泰安市，6，3分）下列四个图形：‎ 其中是轴对称图形，且对称轴的条数为2的图形的个数是（ ）‎ ‎【答案】C。‎ ‎7. （2014山东省泰安市，7，3分）方程5x+2y=-9与下列方程构成的方程组的解为的解是（ ）‎ ‎ （A）x+2y=1 （B）3x+2y=-8 ‎ ‎（C）5x+4y=-3 （D）3x-4y=-8‎ ‎【答案】D。‎ ‎8. （2014山东省泰州市，8，3分）如图，∠ACB=90°，D为AB中点，连接DC并延长到E，使CE=CD，过点B作BF∥DE，与AE的延长线交于 F，若AB=6，则BF的长为（ ）‎ ‎（A）6 ‎ ‎（B）7 ‎ ‎（C）8‎ ‎（D）10‎ ‎【答案】C。‎ ‎9.（2014山东省泰安市，9，3分）以下是某校九年级10名同学参加学校演讲比赛的成绩统计表：‎ 成绩/分 ‎80‎ ‎85‎ ‎90‎ ‎95‎ 人数/人 ‎1‎ ‎2‎ ‎5‎ ‎2‎ 则这组数据的中位数和平均数分别为（ ）‎ ‎（A）90,90 （B）90,89 ‎ ‎（C）85,89 （D）85,90‎ ‎【答案】B。‎ ‎10.（2014山东省泰安市，10，3分）在△ABC和△A1B1C1中，下列四个命题：‎ ‎（1）若AB=A1B1，AC=A1C1,∠A=∠A1，则△ABC≌△A1B1C1；‎ ‎（2）若AB=A1B1，AC=A1C1,∠B=∠B1，则△ABC≌△A1B1C1；‎ ‎（3）若∠A=∠A1，∠C=∠C1，则△ABC∽△A1B1C1；‎ ‎（4）若AC﹕A1C1=CB﹕C1B1,∠C=∠C1，则△ABC∽△A1B1C1。‎ 其中真命题的个数为 ‎（A）4个 （B）3个 （C）2个 （D）1个 ‎【答案】B。‎ ‎11.（2014山东省泰安市，11，3分）在一个口袋中有4个完全相同的小球，它们的标号分别为1，2,3,4，，从中随机摸出一个小球记下其标号后放回，再从中随机摸出一个小球，则两次摸出的小球的标号之和大于4的概率是（ ）‎ ‎（A） （B） （C） （D）‎ ‎【答案】C。 ‎ ‎12.（2014山东省泰安市，12，3分）如图（1）是直角三角形纸片，∠A=30°，BC=4cm，将其折叠为BD，如图（2），再将（2）沿DE折叠，使点A落在DC`的延长线上的点A`处，如图（3），则折痕DE的长为（ ）‎ ‎（A）cm （B）cm （C）cm （D）3cm ‎【答案】A。‎ ‎13．（2014山东省泰安市，13，3分）某种花卉每盆的盈利与每盆的株数有一定的关系。每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元。要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则可以列出方程是（ ）‎ ‎（A）（3+x）（4-0.5x）=15 （B）（x+3）（4+0.5x）=15‎ ‎（C）（x+4）（3-0.5x）=15 （D）（x+1）（4-0.5x）=15‎ ‎【答案】A。‎ ‎14.（2014山东省泰安市，14，3分）如图，△ABC中，∠ACB=90°，∠A=30°，AB=16.点P是斜边AB上一点，过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q。设AP=x，△APQ的面积为y，则y与x之间的函数图象大致为（ ）‎ ‎【答案】B。‎ ‎15.（2014山东省泰安市，15，3分）若不等式有解，则实数a的取值范围是（ ）‎ ‎（A）a＜-36 （B）a≤-36 （C）a＞-36 （D）a≥-36‎ ‎【答案】C。‎ ‎16.（2014山东省泰安市，16，3分）将两个斜边长相等的三角形纸片如图（1）放置，其中∠ACH=∠CED=90°，∠A=45°，‎ ‎∠D=30°，把△DCE绕点C顺时针旋转15°得到△D`CE`。如图（2），连接DB，则∠E`D`B的度数为（ ）‎ ‎（A）10° （B）20° （C）7.5° （D）15°‎ ‎【答案】D。‎ ‎17.（2014山东省泰安市，17，3分）已知函数y=（x-m）（x-n）（其中m＜n＝的图像如图所示，则一次函数y=mx+n与反比例函数y=的图像可能是（ ）‎ ‎【答案】C。‎ ‎18.（2014山东省泰安市，18，3分）如图，P为⊙O的直径BA延长线上一点，PC与⊙O相切，切点为C，点D是⊙O上一点，连接PD。已知PC=PD=BC。下列结论：（1）PD与⊙O相切；（2）四边形PCBD是菱形：（3）PO=AB；（4）∠PDB=120°。其中正确的个数为 ‎（A）4个 （B）3个 （C）2个 （D）1个 ‎【答案】A。‎ ‎19.（2014山东省泰安市，19，3分）如图，半径为2cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则圆中阴影部分的面积为（ ）‎ ‎（A）（-1）cm2 （B）（+1）cm2 ‎ ‎（C）1cm2 （D）cm2‎ ‎【答案】A。‎ ‎20．（2014山东省泰安市，20，3分）二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：‎ x ‎-1‎ ‎0‎ ‎1‎ ‎3‎ y ‎-1‎ ‎3‎ ‎5‎ ‎3‎ 下列结论：（1）ac＜0；（2）当x＞1时，y的值随x值的增大而减小；‎ ‎（3）3是方程ax2+（b-1）x+c=0的一个根；‎ ‎（4）当-1＜x＜3时，ax2+（b-1）x+c＞0.‎ 其中正确的个数为（ ）‎ ‎（A）4个 （B）3个 （C）2个 （D）1个 ‎【答案】B.‎ 第二部分(非选择题，共60分)‎ 二、填空题（本大题共4小题，满分12分。）‎ ‎21.（2014山东省泰安市，21，4分）化简（1+）÷的结果为＿＿。‎ ‎【答案】x-1.‎ ‎22.（2014山东省泰安市，22，4分）七年（1）班同学为了了解2013年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据整理如下表：‎ 月均用水量x/m3‎ ‎0＜x≤5‎ ‎5＜x≤10‎ ‎10＜x≤15‎ ‎15＜x≤20‎ x＞20‎ 频数/户 ‎12‎ ‎20‎ ‎3‎ 频率 ‎0.12‎ ‎0.07‎ 若该小区有800户家庭，据此估计该小区月均用水量不超过10m3的家庭有＿＿户。‎ ‎【答案】560.‎ ‎23.（2014山东省泰安市，23，4分）如图，AB是半圆的直径，点O为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E，交⊙O于D，连接BE，设∠BEC=α，则sinα的值为＿＿。‎ ‎【答案】。‎ ‎24.（2014山东省泰安市，24，4分）如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去……。若点A（，0），B（0,4），则点B2014的横坐标为＿＿。‎ ‎【答案】10070。‎ 三、解答题（本大题共5小题，满分48分，解答应写出文字说明、证明过程或演算步骤）‎ ‎25.（2014山东省泰安市，25，8分）某超市用3000元购进某种干果销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，但这次的进价比第一次的进价提高20％，购进干果数量是第一次的2倍还多300千克。如果超市按每千克9元的价格出售，当大部分干果售出后，余下的600千克按售价的8折售完。‎ ‎（1）该种干果的第一次进价是每千克多少元？‎ ‎（2）超市销售这种干果共盈利多少元？‎ ‎【答案】解：（1）设该种干果第一次进价是每千克x元，则第二次进价为（1+20％）x元，由题意，得=2×+300‎ 解之，得x=5‎ 经检验x=5是所求的解，‎ 所以该种果干第一次的进价为每千克5元。‎ ‎（2）盈利：【+】9+600×9×80％-（3000+9000）‎ ‎=5820（元）‎ 所以超市销售该干果共盈利5820元。‎ ‎26.（2014山东省泰安市，26，8分）如图①，△OAB中，A（0,2），B（4,0），将△AOB向右平移m个单位，得△O`A`B`.‎ ‎(1)当m=4时，如图②。若反比例函数y=的图像经过点A`，一次函数y=ax+b的图像经过A`，B`两点，求反比例函数及一次函数的表达式；‎ ‎（2）若反比例函数y=的图像经过点A`及A`B`的中点，求m的值。‎ ‎【答案】解：（1）由图②知：A`点的坐标为（4,2），B`点的坐标（8,0）‎ ‎∴k=4×2=8‎ ‎∴y=‎ 把（4,2），（8,0）代入y=ax+b，‎ 得 ‎∴‎ 所以经过A`，B`两点的一次函数表达式为y=-x+4.‎ ‎（2）当△AOB向右平移m个单位时，A`点的坐标为（m，2），B`点的坐标为（m+4,0），则A`B`的中点M的坐标为[（m+4）-2，1]‎ ‎∴m×2=[（m+4）-2]×1‎ 即m=2.‎ ‎∴当m=2时，反比例函数y=的图像经过点A`及A`B`的中点M。‎ ‎27.（2014山东省泰安市，27，10分）如图，∠ABC=90°，D,E分别在BC、AC上，AD⊥DE，且AD=DE，点F是AE的中点，FD与AB相交于点M。‎ ‎（1）求证：∠FMC=∠FCM;‎ ‎(2)AD与MC垂直吗？并说明理由。‎ ‎【答案】（1）证明：∵△ADE是等腰三角形，F是AE的中点，‎ ‎∴DF⊥AE，DF=AF=EF 又∵∠ABC=90°，∠DCF,∠AMF都与∠MAC互余 ‎∴∠DCF=∠AMF 又∵∠DFC=AFM=90°‎ ‎∴△DFC≌△AFM ‎∴CF=MF ‎∴∠FMC=∠FCM ‎（2）AD⊥MC 由（1）知∠MFC=90°，FD=FE,FM=FC ‎∴∠FDE=∠FMC=45°‎ ‎∴DE∥CM ‎∴AD⊥MC。‎ ‎28．（2014山东省泰安市，28，11分）如图，在四边形ABCD中，AB=AD,AC与BD交于点E，∠ADB=∠ACB.‎ ‎（1）求证：;‎ ‎（2）若AB⊥AC，AE﹕EC=1﹕2，F是BC中点，求证：四边形ABFD是菱形。‎ ‎【答案】解：（1）证明：∵AB=AD ‎∴∠ADB=∠ABE 又∵∠ADB=∠ACB ‎∴∠ABE=∠ACB 又∵∠BAE=∠CAB ‎∴△ABE∽△ACB ‎∴‎ 又∵AB=AD，‎ ‎∴‎ ‎（2）证明：设AE=x ‎∵AE:EC=1:2‎ ‎∴EC=2x 由（1）得AB2=AE·AC ‎∴AB=x 又∵BA⊥AC ‎∴BC=2x ‎∴∠ACB=30°‎ 又∵F是BC的中点 ‎∴BF=x ‎∴BF=AB=AD 又∵∠ADB=∠ACB=∠ABD ‎∴∠ADB=∠CBD=30°‎ ‎∴AD∥BF ‎∴四边形ABFD是平行四边形 又AD=AB ‎∴四边形ABDF是菱形。‎ ‎29.（2014山东省泰安市，29，11分）二次函数y=ax2+bx+c的图像经过点（-1,4），且与直线y=-x+1相交于A，B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（-3，0）。‎ ‎（1）求二次函数的表达式；‎ ‎（2）点N是二次函数图像上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；‎ ‎（3）在（2）的条件下，点N在何位置时，BM与NC互相垂直平分？并求出所有满足条件的N的坐标。‎ ‎【答案】解：（1）由题设得A（0,1），B（-3，）‎ 由二次函数y=ax2+bx+c的图像经过A、B及点（-1,4）‎ ‎∴‎ 解得 ‎∴二次函数的表达式为y=-x2-x+1.‎ ‎（2）设N（x，-x2-x+1）‎ 则M/P点的坐标分别为（x，-x+1），（x，0）‎ ‎∴MN=PN-PM=-x2-x+1-（-x+1）=-x2-x=-（x+）2+‎ ‎∴当x=-时，MN的最大值为。‎ ‎（3）连接CM,BN,BM与NC互相垂直平分 即四边形BCMN为菱形 由于BC∥MN 即MN=BC,且BC=MC 即-x2-x=，且（-x+1）2+（x+3）2=‎ 即x=-1‎ 故当点N（-1,4）时，BM与NC互相垂直平分。‎